STATISTIKA-38 APROKSIMASI TABEL MORTALITA MENGGUNAKAN PERSAMAAN DUFRESNE

(1)

(2)

Makalah dipresentasikan dalam Seminar Nasional Matematika dan Statistika dengan tema ”

Penguatan Peran Matematika dan Statistika Dalam Percepatan Pembangunan Nasional " pada tanggal 27 Februari 2014 di Jurusan Matematika FMIPA Universitas Tanjungpura.

STATISTIKA-38

APROKSIMASI TABEL MORTALITA

MENGGUNAKAN PERSAMAAN DUFRESNE

Lexy Janzen Sinay

1

, Neva Satyahadewi

2

1_{PS Matematika FMIPA Universitas Pattimura Ambon,} 2_{PS Statistika FMIPA Universitas Tanjungpura Pontianak}

1_{lexyjz@gmail.com,}2_{neva.satya@gmail.com} Abstrak

Persamaan Dufresne merupakan sebuah persamaan matematika yang diperkenalkan oleh Daniel Dufresne.Persamaan Dufresne dibangun dari polinomial Jacobi teralihkan yang diterapkan pada komplemen fungsi peluang.Secara analitis, persamaan ini menghasilkan sebuah barisan-barisan kombinasi eksponensial. Dengan demikian, penulisan ini memberikan suatu cara untuk mengaproksimasi tabel mortalita dengan menerapkan persamaan Dufresne pada distribusi Makeham.

Kata kunci: Aproksimasi Dufresne, komplemen fungsi peluang, distribusi

Makeham, kombinasi eksponensial, polinomial Jacobi teralihkan, tabel mortalita. PENDAHULUAN

Pada umumnya bentuk eksponensial sering ditemukan dalam model matematika ataupun statistika.Secara numerik, bentuk ekponensial memberikan kemudahan dalam penghitungan.Oleh karena itu, bentuk eksponensial digunakan sering digunakan dalam membentuk fungsi-fungsi khusus untuk menentukan suatu distribusi peluang.Distribusi peluang yang menggunakan bentuk eksponensial adalah distribusi eksponensial.

Kombinasi eksponensial merupakan suatu bentuk kombinasi dari fungsi kepadatan peluang distribusi eksponensial.Secara numerik bentuk kombinasi eksponesial tersebut memiliki kemudahan untuk diterapkan.Hal ini dikarenakan distribusi eksponensial memberikan suatu penghitungan yang sangat sederhana, sehingga mudah untuk dapat diaplikasikan ke berbagai bidang seperti teori resiko, teori antrian, teori keuangan, teori aktuaria, dan lain-lain. Salah satu sifat penting dari kombinasi eksponensial adalah suatu bentuk yang dense dalam himpunan distribusi peluang atas



0,



.

Ada berbagai metode yang dapat digunakan untuk menentukan dan mengaproksimasi sebuah distribusi peluang.Pada tahun 2006, Daniel Dufresne memberikansuatu metode aproksimasi distribusi peluang yang didasarkan atas kombinasi eksponensial dengan menggunakan sifat-sifat dari polinomial Jacobi.Aproksimasi iniadalahsebuahpersamaan yang terdiri atas barisan-barisan yang berbentuk kombinasi eksponensial, yang mana barisan-barisan tersebut merupakan barisan-barisan yang konvergen.Persamaan tersebutmerupakan sebuahformula yang konstruktif untuk mengaproksimasi distribusi peluang.Kemudian, formula ini dikenal sebagai persamaan Dufresne.

Dengan demikian, Penulisan ini memberikan suatu cara untuk mengaproksimasi sebuah tabel mortalita dengan menggunakan persamaan Dufresne, yaitu denganmengkonstruksi suatu bentuk aproksimasi distribusi waktu hidup yang akan datang (future lifetime) ke dalam bentuk kombinasi eksponensial dan kemudian memperlihatkan keakuratan dari hasil-hasil aproksimasi tersebut secara numerik.

(3)

PROSIDING ISBN: 978-602-8355-39-1

Seminar Nasional Matematika dan Statistika FMIPA UNTAN Pontianak, 27 Februari 2014

446 PEMBAHASAN

Bagian ini membahas tentang teori-teori dan studi kasus.Teori-teori yang dimaksud merupakan beberapa definisi dasar yang digunakan untuk memperoleh persamaan Dufresne dan mendukung studi kasus.Sementara itu, studi kasus yang diberikan pada bagian ini merupakan implementasi numerik dari aproksimasi distribusi waktu hidup (lifetime), dimana hasil dari implementasi numerik tersebut digunakan untuk menentukan tabel mortalita.Tabel mortalita yang diperoleh pada bagian ini merupakan sebuah ilustrasi, karena diperoleh dengan membuat asumsi parameter distribusi waktu hidup.

A. Distribusi Waktu Hidup

Distribusi waktu hidup (lifetime) merupakan sebuah distribusi peluang dari usia hidup seseorang. Usia hidup yang dimaksud adalah usia sesorang dari kelahiran sampai usia kematian. Bagian iniakan diberikan beberapa definisi penting mengenai distribusi waktu hidup yang akan digunakan dalam pembahasan ini. Definisi-definisi yang digunakan pada bagian ini merupakan definisi-definisi dasar.

1. Fungsi Kelangsungan Hidup (Survival)

Misal X adalah variabel random kontinu yang mengikuti usia hidup seseorang (dari kelahiran sampai kematian). Misal FX

 

x merupakan cdf dari X,

 





,

X

F x P Xx xR_ dan ccdf didefinisikan seperti berikut:

 

1 _X

 





,

S x  F x P Xx xR_,

dengan asumsi bahwa F_X

 

0 0 yang berakibat S

 

0 1. Fungsi S x

 

sering disebut juga

sebagai fungsi kelangsungan hidup (survival). 2. Percepatan Mortalitas (Force of Mortality)

Misal X adalah variabel random kontinu yang mengikuti usia hidup seseorang (dari kelahiran sampai kematian), dengan fungsi distribusinya adalahFX

 

x . Dengan demikian, pdf dari X yang dinotasikan dengan fX

 

x adalah

 

X X

f x  dF x , xR_

sehingga dapat didefinisikan sebuah fungsi sebagai berikut:

 

_{ }

 

1 X X f x dS x x F x S x



    , xR ekuivalen dengan

 

0 exp x S x  _  y dy_ 



, xR di mana S x

 

adalah fungsi survival dari variabel random X.

Dalam aktuaria dan demografi fungsi



 

x disebut juga sebagai percepatan

mortalita.Dalam teori reliabilitas fungsi



 

x disebut sebagai tingkat kegagalan (failure rate)

(4)

447 3. Fungsi-Fungsi pada Tabel Mortalita

Jumlah individu yang hidup dari suatu kelompok individu-individu berusia x, dinotasikan dengan lx, merupakan suatu fungsi seperti berikut ini:

 

0

x

l l S x ,

dimanaS x

 

merupakan fungsi survival, dan l₀ merupakan suatu konstanta yang sering disebut

dengan radix. Dengan demikian peluang hidup seorang berusia x adalah 1 x x x l p l   .

Kemudian, dx merupakan jumlah orang yang meninggal dari suatu kelompok orang yang berusia x, diberikan seperti berikut ini:

1

x x x

d  l l _ .

Dengan demikian, peluang meninggal orang yang berusia x adalah

1 x x x x d q p l    .

B. Distribusi Waktu Hidup yang didasarkan atas Hukum Makeham

Bagian ini merupakan penerapan langsung dari distribusi waktu hidup yang dijelaskan pada Bagian A di atas.Bagian ini membahas tentang distribusi waktu hidup yang didasarkan atas hukum Makeham.Distribusi tersebut sering disebut sebagai distribusi Makeham.

Misal X adalah variabel random kontinu yang mengikuti usia hidup seseorang (dari kelahiran sampai kematian). Untuk usia hidupx, diberikan percepatan mortalitas yang didasarkan atas hukum Makeham seperti berikut

 

x A Bcx, x

   R_

Bentuk ini sering disebut sebagai hazard rate atau failure rate.

Berdasarkan percepatan mortalitas hukum Makehammaka dapat diperoleh fungsi

survival dari distribusi Makeham seperti berikut

 

exp





x 1





S x  Axm c  ,dengan log B m c  ₍₁₎

C. Penurunan Persamaan Dufresne 1. Fungsi Hipergeometri Gauss

Simbol Pochhammer untuk suatu bilangan a dinotasikan dengan

 

a _n, didefinisikan

seperti berikut,

 

a ₀ 1,

 

a _n a a



1

 

a n 1



, n1, 2, .

Fungsi hipergeometri Gauss yang dinotasikan dengan 2 1F



, , ;



, dapat didefinisikan

seperti berikut,





_{  }

 

_{ }

1







₁ 1 2 1 0 , , ; c 1 a b 1 c b F a b c z zt t t dt b c b           



   

 

0 ! n n n n n a b z c n   



dengan z1, Re

 

c Re

 

b 0.

(5)

PROSIDING ISBN: 978-602-8355-39-1

448 2. Kombinasi Eksponensial dari Aproksimasi Distribusi Peluang

a. Kombinasi Eksponensial

Berikut ini, akan diberikan bentuk umum dari suatu kombinasi ekponensial dengan mendefinisikan sebuah fungsi yang berbentuk

 

_{ }0 1 j n t j j t j f t a  e _  



1 (2)

dimana

 

aj ,

 

j adalah konstan. Fungsi ini adalah fungsi densitas peluang (pdf) jika (a) 1 1 n j j a  



; (b)



_j 0, untuk setiap j; (c) f x

 

0, untuk setiap x0.

Kondisi (a) dan (b) menyatakan bahwa fungsi f

 

terintegral untuk 1 atas

R

_, namun tidak

untuk kondisi (c). Jika a_j0 untuk semua j, maka persamaan (2) disebut sebuah mixture of

exponentials atau disebut juga sebagai distribusi hiper-eksponensial.

Teorema 1 memperlihatkan kekonvergenan dari barisan variabel random yang mana pdf dari variabel random tersebut merupakan suatu kombinasi eksponensial.

Teorema 1

(a) Misal T variabel random non negatif. Maka terdapat suatu barisan variabel random

 

T_n

masing-masing dengan suatu pdf yang diberikan oleh suatu kombinasi eksponensial dan sedemikian sehingga

T

_n konvergen dalam distribusi ke T.

(b) Jika distribusi T tidak mempunyai atom, maka

 

0 lim sup 0 n T T n  _t F t F t  b. Polinomial Jacobi Teralihkan

Pada umumnya, bentuk polinomial Jacobi dapat didefinisikan seperti berikut

 , 

_{  }



2 1 1 ₁ , 1, 1; , ! 2 n n x P x F n n n   _  _ _{  }_{ } __       untukn0,1, dan ,  1.

Diketahui juga bahwa polinomial Jacobi ortogonal atas interval



1, 1



, untuk fungsi bobot



1x

 

 1x



.

Kemudian bentuk polinomial Jacobi teralihkan (shifted Jacobian polynomials) dapat diturunkan seperti berikut:

 , 

_{ }

 , 

_

_

2 1 n n R  x  P  x



1



₂ ₁



, 1, 1;1



! n _F _{n n} _x n             0 n j nj j x   



,

dimana2 1

F

adalah fungsi hipergeometri Gauss dan

  

   







1 1 1 ! ! n n j j nj j n n n j           .

(6)

449 Dengan demikian, polinomial Jacobi teralihkan ortogonal atas

 

0, 1 , dengan fungsi bobotnya adalah  , 

_{  }

_

1 x x x   _{ }  w .

Sifat-sifat dari polinomial Jacobi teralihkan dapat diberikan untuk suatu fungsi



 

yang terdefinisi atas

 

0, 1 (termasuk semua fungsi kontinu dan terbatas) sedemikan sehinga,

 , 

_{  }

_

1 x x  x   _{ }  w , 1

 



 _, 

_{ }

0 1 1 n n n c x x x R x dx h      



 ,





 

_{ }

2 1 _, 0 1 n n h 



x x_R  x _ dx



 











1 1 2 ! n n n n n               c. Persamaan Dufresne

Berdasarkan teori shifted Jacobi polynomials yang diberikan pada bagian sebelumnya, maka teori tersebut dapat diterapkan ke dalam suatu distribusi peluang atas

R

 dengan cara

seperti berikut ini.

Misal F t

 

adalah cdf, dan misal F t

 

 1 F t

 

P



Tt



.F t

 

merupakan ccdf

(komplemen cdf). F t

 

sering disebut juga sebagai fungsi survival. Jika F

 

0 1dan F

 

 1, untuk0 t  . Misal T menyatakan waktu dari kelahiran sampai kematian dari usia hidup x, maka F t

 

tpx. Diketahui bahwa r  0,

 

1

 

log g x F x r       , 0 x 1, g

 

0 0.

Pemetaan yang terjadi dari bentuk ini merupakan pemetaan



0,



pada



0, 1



, yang mana t0 berkorespondensi dengan x1, dan

t

 

berkorespondensi dengan x 0 . Diketahui juga bahwa F

 

 0, maka dapat diperoleh sedemikian rupa sehingga g

 

0 0.

Misal parameter-parameter , , p dan

 

bk diketahui sedemikian sehingga, dengan menerapkan shifted Jacobi polynomials dapat diperoleh

 

 , 

_{ }

0 p k k k g x x b R  x   



, 0 x 1. Ekuivalen dengan

 

rt F t  g e 0 prt jrt k kj k j e b  e     

 

  0 j p rt k kj j k b



e        _ _  

 

.

Bentuk di atas memiliki kesamaan dengan persamaan (2), jika j 



j p r



, untuk 0,1, 2,

j . Jika p0, suatu kombinasi eksponensial dapat diperoleh dengan cara pemotongan jumlahan dari deret di atas. Berdasarkan bentuk dari deret yang diberikan di atas, maka konstanta

 

bk dapat ditemukan seperti berikut:

 

_{ }

_

1 _, 0 1 1 p k k k b x g x R x x x dx h      



 (3)

(7)

PROSIDING ISBN: 978-602-8355-39-1

Seminar Nasional Matematika dan Statistika FMIPA UNTAN Pontianak, 27 Februari 2014 450  1





 , 

 

_{ }

0 1 p rt rt rt k r e e R e F t dt h_k           



 .

Dengan demikian, bentuk (3) merupakan kombinasi dari bentuk

 1





_{ }

0 1 p j rt rt e  e F t dt      _ 



, j 0, 1, ,k

Jika  0, maka dapat diperoleh

 

0 0 1 1 1 st st st e F t dt F t d e e s s  _  _ _      _  _



E ,dengan s 0

Hal ini berarti, konstanta

 

bk dapat diperoleh dengan menggunakan transformasi Laplace dari distribusi T.

Teorema 2.

Misal ,   1, F

 

kontinu atas



0,



dan diberikan fungsi berikut ini.

 

prt

e F t

yang memiliki sebuah limit yang berhingga untuk t menuju tak hingga, untuk beberapa pR

(hal ini selalu benar di mana p0). Maka berlaku

 

 , 

 

0 prt rt k k k F t e b R  e     



(4)

Untuk setiap t

 

0, dan konvergen seragam atas setiap interval

 

a b, , untuk 0 a b   .

Tidak semua distribusi terkondisi dalam Teorema 2.Hasil dalam teorema berikut tidak membutuhkan asumsi ini.

Teorema 3.

Misal ,   1dan untuk beberapa pR dan r0

 1 2 





_{ }

2 0 1 p rt rt e  e F t dt     _  _{ }



(ini selalu benar jika 1

2 p ). Maka

 

 , 

 

2  1 2 





0 0

lim

1

0

N p rt prt rt rt k k N k

F t

e

b R

 

e



e



dt

 _ _ _{  } _  _

 





_



_





 









Selanjutnya, persamaan (4) lebih dikenal sebagai persamaan Dufresne.Pemotongan jumlahan dari deret yang diperoleh dari persamaaan Dufresne bukanlah fungsi distribusi yang sebenarnya. Hasil pemotongan deret pada persamaan Dufresne merupakan suatu aproksimasi dari bentuk ccdf distribusi T. Nilai fungsi yang diperoleh dari persamaan Dufresne, bisa lebih kecil dari 0 atau lebih besar dari 1, atau fungsi tersebut mungkin saja turun pada beberapa interval.

D. Studi Kasus

Bagian ini memuat tentang implementasi numerik dari persamaan Dufresne untuk mengaproksimasi distribusi waktu hidup, yang bertujuan untuk menghasilkan sebuah tabel

(8)

451 mortalita.Hasil aproksimasi pada bagian ini, diperoleh dengan cara mensubtitusi parameter-parameter  =  = 0, p = 10–9_{, r = 0.015 ke dalam persamaan (4).}

Langkah awal yang perlu dilakukan adalah mengaproksimasi distribusi waktu hidup.Dalam penulisan ini distribusi yang digunakan adalah distribusi Makeham.

a. Aproksimasi Distribusi Waktu Hidup

Bagian ini merupakan penerapan langsung dari bagian-bagian sebelumnya.Hasil-hasil yang diperoleh pada bagian ini didasarkan atas hukum Makeham seperti yang diberikan pada persamaan (1), dengan menggunakan asumsi parameter-parameter seperti berikut

0.0007

A ; B 5 105; c100.04, (5) mengikuti Bowers et al (1997).

Misalkan X menyatakan usia hidup dari seseorang, berarti X 0. Kemudian, subtitusi parameter-parameter (5) ke dalam persamaan (1) maka diperoleh fungsi survival dari Xseperti berikut

 

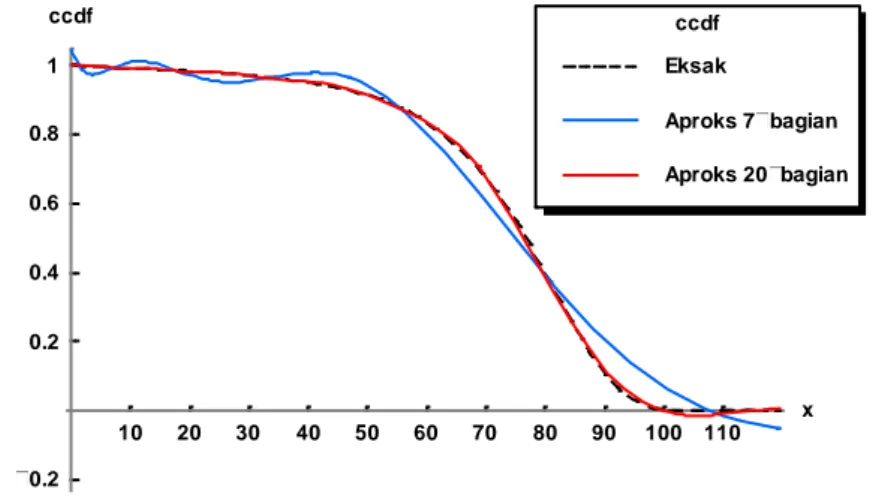
0.00054 1.09648  0.0007 1.00054 x x S x  e  , x0

Kemudian, hasil ini dapat diterapkan pada persamaan Dufresne.Secara visual hasil aproksimasi distribusi waktu hidup untuk N7 dan N20dapat dilihat pada Gambar 1. Dengan demikian, tingkat ketelitian aproksimasi pada saat N20lebih baik dibandingkan N7. Berdasarkan Gambar 1, aproksimasi yang diperoleh pada saat N20sangat akurat, karena hampir keseluruhan grafiknya berimipitan dengan grafik eksak.

10 20 30 40 50 60 70 80 90 100 110 x 0.2 0.2 0.4 0.6 0.8 1 ccdf Aproks 20 bagian Aproks 7 bagian Eksak ccdf

Gambar 1. Distribusi waktu hidup yang akan datang

Untuk melihat lebih jelas mengenai tingkat ketelitian (keakuratan) hasil aproksimasi untuk masing-masing N, maka diberikan pada Tabel 1.

Tabel 1

Hasil Estimasi tingkat ketelitian dari N-bagian aproksimasiF t

 

3 0.323073

7 0.142532

10 0.0796111 15 0.037354 20 0.0146908

(9)

PROSIDING ISBN: 978-602-8355-39-1

452 b. Ilustrasi Tabel Mortalita

Berdasarkan keakuratan hasil aproksimasi distribusi waktu hidup di atas, maka dipilih hasil aproksimasidengan N20. Kemudian hasil tersebut diterapkan pada fungsi-fungsi tabel mortalita maka diperoleh tabel mortalita sebagai berikut:

Tabel 2

Ilustrasi Tabel Mortalita

Usia lx Eksak Aproksimasi (N = 20) 13 96.808 96.897 14 96.724 96.835 15 96.638 96.730 16 96.550 96.590 17 96.460 96.432 18 96.369 96.279 19 96.275 96.147 KESIMPULAN

Dari hasil yang diperoleh dapat disimpulkan bahwa: 1. Persamaan Dufresne berbentuk seperti berikut ini

 

 , 

 

0 prt rt k k k F t e b R  e     



_,

merupakanbentuk aproksimasi ccdf (fungsi survival) dari sebuahdistribusi peluang (distribusi waktu hidup), yaitu dengan melakukan pemotongan terhadap jumlahan dari deret tersebut. Jika pemotongan deret tersebut dalam N bagian, maka hasil dari aproksimasi tersebut dapat dinyatakan dalam bentuk

 

0 j N t j j F t c e  



dengan j



jp r



, j0,1, ,N.

2. Penggunaan persamaan Dufresne dalam mengaproksimasi tabel mortalita cukup akurat. Keakuratan aproksimasi tersebut bergantung pada pemilihan parameter-parameter yang terdapat pada persamaan Dufresne.

DAFTAR PUSTAKA

Abramowitz, M., dan Stegun, I. A., 1972,Handbook of Mathematical Functional,(cetakan kesepuluh), Dover, New York.

Bain, L. J., dan Engelhardt, M., 1992,Introduction to Probability and Mathematical Statistics, edisi kedua,Duxburry Press, California.

Billingsley, P., 1986,Probability and Measure,edisi kedua,John Wiley & Sons, Inc., New York. Bowers, N. L. Jr., Gerber, H. U., Hickman, J. C., Jones, D. A., dan Nesbitt, C. J., 1997,Actuarial

Mathematics. edisi kedua,Society of Actuaries, Schaumburg, IL.

Dufresne, D., 2006,Fitting Combinations of Exponentials to Probability Distributions,To appear in Applied Stochastic Models in Business and Industry.

Dufresne, D., 2007,Stochastic Life Annuities, North American Actuarial Journal.

Feller, W., 1971,An Introduction to Probability Theory and its Applications II, Edisi kedua,John Wiley & Sons, Inc., New York.

(10)

453 Higgins, J. R.,1977, Completeness and Basis Properties of Sets of Special Functions,

Cambridge University Press,London.

Hogg, R. H., dan Craig, A. T.,1991.Introduction to Mathematical Statistics, edisi kelima.Higher Education Press.

Khuri, A. I., 2003, Advanced Calculus with Applications in Statistics, edisi kedua, John Willey & Sons, Inc., New Jersey.

Lebedev, N. N., 1972,Special Functions and Their Applications, Dover, New York.

Luke, Y. L., 1969,TheSpecial Functions and Their Applications, Academic Press,New York. Sinay, L. J., 2010, Anuitas Hidup yang didasarkan atas Kombinasi Eksponensial dari

Aproksimasi Distribusi Waktu Hidup Yang Akan Datang, Tesis pada Program Studi S2

Matematika Fakultas MIPA, Universitas Gadjah Mada, Yogyakarta.

Stahl, S., 1999,Real Analysis: A Historical Approach,John Wiley & Sons, Inc., New York. Stoll, M.,2001,Introduction to Real Analysis,Edisi kedua, Addison Wesley Longman, Inc.