MODEL STATE SPACE UNTUK DATA DERET WAKTU PEUBAH TUNGGAL MUTIA RAMADHANTI HAFLIL

(1)

MUTIA RAMADHANTI HAFLIL

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(2)

MUTIA RAMADHANTI HAFLIL. Model State Space untuk Data Deret Waktu Peubah Tunggal. Dibimbing oleh KUSMAN SADIK dan FARIT MOCHAMAD AFENDI.

Deret waktu adalah rangkaian data yang diukur berdasarkan waktu dengan interval yang sama. Dasar pemikiran deret waktu adalah pengamatan sekarang tergantung pada satu atau beberapa pengamatan sebelumnya. Dengan kata lain, model deret waktu dibuat karena ada korelasi antarderet pengamatan. Analisis data deret waktu pada dasarnya digunakan untuk melakukan analisis data yang mempertimbangkan pengaruh waktu. Analisis data deret waktu dibagi menjadi dua, yaitu analisis data deret waktu peubah tunggal dan analisis data deret waktu peubah ganda. Metode yang dapat digunakan untuk analisis data deret waktu peubah tunggal maupun peubah ganda adalah model State Space.

Tahapan yang dilakukan adalah menduga model-model autoregressive dan menghitung nilai AIC tiap model. Model AR yang terpilih (dengan nilai AIC terkecil) digunakan dalam analisis korelasi kanonik. Unsur pada state vector disusun dari variabel dengan korelasi kanonik yang nyata. Jika state vector telah ditentukan, maka model State Space dapat diterapkan pada data tersebut. Parameter-parameter dalam model State Space diduga dengan pendekatan maximum

likelihood dengan proses iterasi.

Model State Space mempunyai penyajian dalam bentuk ARMA dan juga sebaliknya setiap

model ARMA mempunyai penyajian dalam bentuk State Space.

Pada model AR (2), model MA (1), dan model ARMA (2,1) proses iterasi dilakukan sebanyak tujuh, delapan, dan lima kali. Model State Space yang diperoleh dari hasil iterasi tersebut dapat digunakan untuk peramalan. Peramalan pada model State Space menggunakan teknik Kalman

(3)

MUTIA RAMADHANTI HAFLIL

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Statistika

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(4)

Menyetujui :

Pembimbing I,

Pembimbing II,

Kusman Sadik, M.Si

NIP. 13218751

Farit Mochamad Afendi, M.Si

NIP. 132314007

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA

NIP. 131578806

(5)

PRAKATA

Puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat serta salam semoga selalu tercurahkan kepada Rasulullah SAW, keluarga, sahabat dan pengikutnya hingga akhir zaman. Judul yang dipilih dalam penelitian ini adalah Model State Space untuk Data Deret Waktu Peubah Tunggal.

Terima kasih penulis ucapkan kepada semua pihak yang telah membantu dalam penyelesaian karya ilmiah ini, diantaranya :

1. Bapak Kusman Sadik, M.Si dan Bapak Farit Mochamad Afendi, M.Si selaku dosen pembimbing atas bimbingan, saran dan kritik yang telah diberikan.

2. Kedua orang tua serta abangku Dhani Aulia Haflil atas doa, kasih sayang, serta dukungan yang telah diberikan kepada penulis.

3. Segenap staf pengajar di Departemen Statistika FMIPA IPB atas ilmu yang bermanfaat sehingga membantu penulis dalam menyelesaikan karya ilmiah ini, serta kepada seluruh staf Departemen Statistika (Bu Markonah, Bu Sulis, Bu Dedeh, Bu Aat, Pak Yaya, Mang Sudin, Mang Herman, Mang Dur) atas segala bantuannya.

4. Bapak Ir. Budi Waryanto, M.Si, Ibu Ir. Sabarella, M.Si, dan seluruh staf Pusat Data dan Informasi Pertanian (Pusdatin) Departemen Pertanian atas bimbingan dan kerjasama selama praktik lapang, serta teman-teman baru di tempat PL (Dede, Santi, Rini, Rina, Yosy, Dennis, Ade, Jefry) atas kebersamaan selama dua bulan penuh, semoga kita dapat bertemu kembali.

5. Teman satu bimbingan, Ipunk, atas diskusi dan masukannya selama proses pengerjaan karya ilmiah ini.

6. Lintang, Ash, Memei, Esi, Indri, Suci atas persahabatan yang indah selama ini.

7. Ema, Ari L, Anggoro, Adit, Rosit, Dian, Lala, Arta, Rani, Rina, Edo, Arief, Yudi, Rio, Dwi dan rekan-rekan Statistika 40 lainnya (sahabat-sahabat terbaikku adalah kalian semua).

8. Kakak-kakak kelas dan adik-adik kelas Statistika.

9. Teman-teman A2 254 (Hera, Tia, Yuyun), Puri 9, Pondok Mentari (Kak Nely, Kak Pur, Indri, Lusy, Renta) dan Fahmeda (Kiki, Aslih, Ade, Anum, Uul) atas kebersamaan dan keceriaan selama penulis menghuni rumah kedua di Darmaga.

10. Semua pihak yang telah membantu dan memberikan dukungan kepada penulis yang tidak bisa disebutkan satu persatu sehingga karya ilmiah ini dapat diselesaikan.

Penulis berharap semoga karya ilmiah ini dapat bermanfaat bagi semua pihak.

Bogor, Januari 2008kk

(6)

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 29 Mei 1985 dari pasangan Yudhawarman dan Johainil Fitri. Penulis merupakan anak bungsu dari dua bersaudara.

Tahun 1997 penulis menyelesaikan pendidikan dasar di SDN Cipinang Melayu 03 Pagi Jakarta Timur, kemudian melanjutkan studi ke sekolah menengah pertama di SLTPN 109 Jakarta Timur hingga tahun 2000. Tahun 2003 penulis menyelesaikan pendidikan menengah atas di SMUN 61 Jakarta Timur dan pada tahun yang sama diterima di Departemen Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB).

Semasa menjadi mahasiswa, penulis aktif diorganisasi kemahasiswaan tingkat departemen. Tahun 2004-2005 penulis menjadi Kepala Departemen Kesekretariatan himpunan profesi Gamma Sigma Beta (GSB). Praktik lapang dilakukan penulis di Pusat Data dan Informasi Pertanian (Pusdatin) Departemen Pertanian, Jakarta pada bulan Februari-April 2007.

(7)

DAFTAR ISI

Halaman

DAFTAR GAMBAR ...vii

DAFTAR LAMPIRAN ...viii

PENDAHULUAN Latar Belakang ...1

Tujuan ...1

TINJAUAN PUSTAKA Data Deret Waktu ...1

Model Regresi Diri (Autoregressive) ...1

Model Rataan Bergerak (Moving Average)...1

Model ARMA (p,q)...2

Model State Space...2

Hubungan antara ARMA dan State Space ...2

Vector Autoregressive (VAR) ...2

Akaike Information Criterion...3

Analisis Korelasi Kanonik ...3

Pemilihan Komponen State vector...3

Pendugaan Parameter ...3

Kalman Filter...4

BAHAN DAN METODE Bahan ...4

Metode ...4

HASIL DAN PEMBAHASAN Model AR (2) ...5

Model MA (1) ...6

Model ARMA (2,1)...7

KESIMPULAN DAN SARAN Kesimpulan ...7

Saran ...8

DAFTAR PUSTAKA ...8

(8)

DAFTAR GAMBAR

Halaman

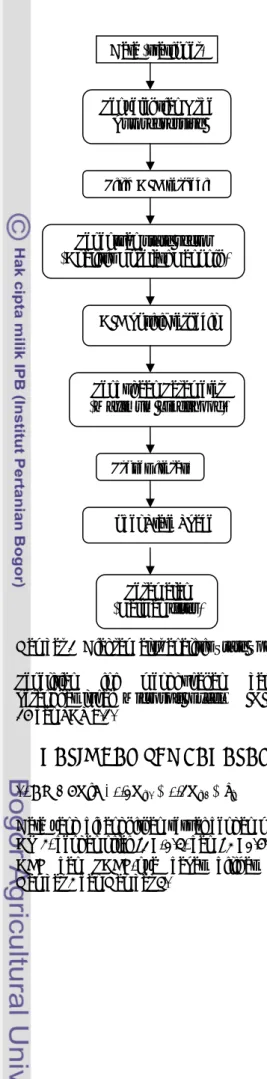
Gambar 1 Diagram alur analisis State Space ... 4

Gambar 2 Plot ACF pada data awal (AR 2) ... 5

Gambar 3 Plot PACF pada data awal (AR 2)... 5

Gambar 4 Plot Peramalan (AR 2)... 6

Gambar 5 Plot Aktual, model AR2, dan model State Space ... 6

Gambar 6 Plot Peramalan (MA1)... 7

Gambar 7 Plot Aktual, model MA1, dan model State Space ... 7

Gambar 8 Plot Peramalan (ARMA 2,1) ... 7

(9)

DAFTAR LAMPIRAN

Halaman

1. Hubungan antara ARMA dan State Space... 10

Model AR (2) : Xt= -0.3Xt-1 + 0.4Xt-2+et 2. Penyeleksian Orde VAR Berdasarkan IC Terkecil... 12

3. Analisis Korelasi Kanonik... 12

4. Dugaan Awal Model State Space ... 12

5. Proses Iterasi Pendugaan Maksimum Likelihood... 13

6. Model State-space yang disesuaikan (fitted) ... 13

Model MA (1) : Xt= et - 0.8et-1 7. Penyeleksian Orde VAR Berdasarkan IC Terkecil... 14

11. Model State Space yang disesuaikan (fitted) ... 15

Model ARMA (2,1) : Xt= -0.3Xt-1 - 0.6Xt-2+et - 0.8et-1 12. Penyeleksian Orde VAR Berdasarkan IC Terkecil... 16

16. Model State Space yang disesuaikan (fitted)... 17

17. Nilai pendugaan parameter dan nilai AIC pada model AR 2 ... 18

18. Nilai pendugaan parameter dan nilai AIC pada model MA 1... 18

19. Nilai pendugaan parameter dan nilai AIC pada model ARMA 2,1 ... 18

(10)

PENDAHULUAN

Latar Belakang

Deret waktu adalah rangkaian data yang diukur berdasarkan waktu dengan interval yang sama. Dasar pemikiran deret waktu adalah pengamatan sekarang tergantung pada satu atau beberapa pengamatan sebelumnya. Dengan kata lain, model deret waktu dibuat karena ada korelasi antarderet pengamatan. Analisis data deret waktu pada dasarnya digunakan untuk melakukan analisis data yang mempertimbangkan pengaruh waktu. Analisis data deret waktu dibagi menjadi dua, yaitu analisis data deret waktu peubah tunggal dan analisis data deret waktu peubah ganda. Metode untuk analisis data deret waktu peubah tunggal antara lain Metode Dekomposisi, Pemulusan Eksponensial Tunggal, Pemulusan Eksponensial Ganda,

Winter, dan ARIMA. Metode untuk analisis

data deret waktu peubah ganda antara lain model Fungsi Transfer, Analisis Intervensi, Analisis Fourier, Analisis Spectral, dan

Vector Autoregressive (VAR). Sedangkan

metode yang dapat digunakan untuk analisis data deret waktu peubah tunggal maupun peubah ganda adalah model State Space (Wei 1989). Oleh karena model State Space merupakan metode baru pada analisis data deret waktu, maka pada penelitian ini akan dibahas lebih lanjut mengenai model State

Space untuk data deret waktu peubah tunggal.

Tujuan

Penelitian ini bertujuan untuk memodelkan data deret waktu, melihat hubungan antara ARMA dan State Space, dan melakukan peramalan dengan menggunakan model State

Space.

TINJAUAN PUSTAKA

Data Deret Waktu

Data deret waktu merupakan data yang dikumpulkan dari beberapa tahapan waktu secara kronologis. Umumnya data ini merupakan kumpulan dari fenomena tertentu yang didapat dalam interval tertentu, misalnya dalam waktu mingguan, bulanan, atau tahunan (Montgomery, et. al., 1990).

Model Regresi Diri (Autoregressive) Menurut Montgomery, et. al., 1990, model

regresi diri berordo p, yang disingkat AR (p) merupakan model yang menggambarkan bahwa peubah tak bebas dipengaruhi oleh peubah tak bebas itu sendiri pada waktu-waktu yang sebelumnya. Dengan kata lain menyatakan ketergantungan nilai pengamatan Xt terhadap Xt-1, Xt-2, ..., Xt-p.

Secara umum bentuk model AR adalah:

t e t X B P =μ+ φ ( ) dimana: ) ... 2 2 1 1 1 ( ) (B B B _pBp p φ φ φ φ = − − − − t

X : nilai pengamatan pada waktu ke-t

µ : konstanta

p

φ : parameter model AR et : sisaan pada waktu ke-t

Syarat kestasioneran pada model AR (p) dapat menggunakan polinomial karakteristik AR yaitu equivalen dengan persamaan karakteristik AR: 0 ... 2 2 1 1− − − − _xp = p x x φ φ φ

AR (p) akan stasioner jika dan hanya jika akar-akar persamaan dari persamaan di atas secara absolut lebih besar dari satu.

Model Rataan Bergerak (Moving Average) Menurut Montgomery, et. al., 1990, perbedaan model Moving Average (MA) dengan model Autoregressive terletak pada jenis peubah bebasnya. Pada model MA peubah bebasnya adalah nilai sisaan pada periode sebelumnya, atau dengan kata lain proses MA menyatakan ketergantungan nilai Xt terhadap et,et-1,…, et-q.

Dari proses linier umum dapat diambil

q q=−θ

Ψ , sehingga secara umum bentuk model MA adalah: Xt = µ + θq(B) et dimana: θq(B) = (1-θ1B1- θ2B2-...- θqBq) µ : konstanta θq : parameter model MA

et : galat acak ke-t

Model rataan bergerak derajat q ini dilambangkan dengan MA (q).

(11)

Model ARMA (p,q)

Menurut Montgomery, et. al., 1990, model

ARMA (p,q) merupakan campuran model

Autoregressive (AR) dan model Moving Average (MA). Untuk data yang stasioner

kombinasi model AR dan MA menghasilkan model ARMA (p,q). Model ARMA (p,q) ini dapat ditulis dalam bentuk umum:

φ_p(B)X_t =μ+θ_q(B)e_t dimana: µ : konstanta p φ : parameter model AR q θ : parameter model MA et : galat acak ke-t.

Model State Space

Model State Space adalah metode yang

digunakan untuk analisis data deret waktu peubah tunggal maupun peubah ganda. Model

State Space merupakan suatu pendekatan

untuk memodelkan dan memprediksi secara bersama beberapa data deret waktu yang saling berhubungan, serta peubah-peubah tersebut mempunyai interaksi yang dinamis. Model State Space menggambarkan data

deret waktu melalui peubah tambahan (state

vector). State vector berisi ringkasan semua

informasi dari nilai sebelumnya dan nilai sekarang dari suatu deret waktu yang sesuai dengan prediksi dari nilai yang akan datang (SAS User’ Guide 2002).

Model State Space merepresentasikan proses stokastik dari zt yang stasioner. Model

ini didefinisikan sebagai persamaan transisi: zt+1 = Fzt + Get+1

dan persamaan pengukuran: xt = H zt

dimana:

xt : vektor observasi berdimensi r×1

H : matriks koefisien berukuran r×s yang

disebut matriks observasi.

zt : state vector dimensi s×1, s≥r, dimana r

elemen pertama adalah xt dan s−r elemen terakhir adalah syarat untuk peramalan xt ke depan

F : matriks koefisien berukuran s×s yang

disebut matriks transisi, yang menentukan sifat dinamis dari model

G : matriks koefisien berukuran s×r yang

disebut matriks input, yang menentukan struktur ragam dari persamaan transisi. Untuk identifikasi model, r baris dan kolom pertama dari G disusun menjadi matriks identitas (Ir) berukuran r× r

et : vektor inovasi atau shock vector, vektor sisaan bersifat acak yang menyebar normal berdimensi r dengan nilai tengah 0 dan matriks kovarian ∑.

Pada persamaan transisi, model State

Space pada umumnya meliputi satu

persamaan pengukuran dimana xt sebagai

fungsi state vector, zt. Persamaan pengukuran yang digunakan oleh prosedur SAS adalah

xt = [Ir,0] zt

dimana Ir adalah matriks identitas r x r. SAS

melakukan ekstraksi xt dari zt tanpa penyajian

ke dalam persamaan pengukuran.

Hubungan antara ARMA dan State Space Setiap model State Space mempunyai

penyajian dalam bentuk ARMA, dan sebaliknya setiap model ARMA mempunyai penyajian dalam bentuk State Space.

Model ARMA: t e B t x B) ( ) ( =Θ Φ atau q t e q t e t e p t x p t x t x−Φ₁ ₋₁−...−Φ ₋ = +Θ₁ ₋₁+...+Θ ₋

dimana et adalah galat acak yang menyebar

normal dengan nilai tengah nol dan matriks ragam ∑ee, B adalah backshift operator

) 1

(BX_t _{= t}X ₋ ,Φ(B)dan adalah

matriks polinomial dalam B, dan X

) (B Θ

t adalah

observasi.

Untuk melihat contoh dari hubungan ARMA dengan State Space dapat dilihat pada Lampiran 1.

Vector Autoregressive (VAR)

Vector Autoregressive atau yang lebih

dikenal dengan VAR adalah suatu sistem persamaan yang memperlihatkan setiap peubah sebagai fungsi linear dari konstanta dan nilai lag (masa lampau) dari peubah itu sendiri serta nilai lag dari peubah lain yang ada dalam sistem. Jadi, peubah penjelas dalam VAR meliputi nilai lag seluruh peubah tak bebas dalam sistem.

Secara umum VAR dengan ordo p dapat dimodelkan sebagai berikut:

t e p t X p A t X A t X A A t X = ₀+ ₁ ₋₁+ ₂ ₋₂+...+ ₋ + dengan:

Xt : vektor peubah endogen berukuran n x 1

A0 : vektor intersep berukuran n x 1

Ai : matrik parameter berukuran n x n

untuk setiap i = 1, 2, …, p et : vekor sisaan berukuran n x 1

(12)

Akaike Information Criterion (AIC)

AIC digunakan sebagai acuan dalam pemilihan model terbaik. Pada State Space nilai AIC terkecil digunakan untuk memilih model VAR terbaik (SAS User’ Guide 2002). AIC untuk model orde-p dihitung dengan persamaan: 2 2 ˆ ln _p pr n p AIC = ∑ + dengan : n = jumlah observasi

r = dimensi dari vektor proses xt

| ˆ

| pΣ = determinan dari matriks kovarian sisaan yang bersifat white noise pada pemodelan AR (p)

Analisis Korelasi Kanonik

Penentuan unsur dari state vector melalui serangkaian analisis korelasi kanonik dari matriks autokovarian contoh. Variabel dengan korelasi kanonik yang nyata dimasukkan dalam state vector, sedangkan variabel yang tidak nyata dikeluarkan dari state vector. (SAS User’ Guide, 2002).

Dalam Wei (1989), state vector ditentukan secara unik melalui analisis korelasi kanonik. pt adalah vektor dari nilai sekarang dan lampau yang relevan untuk memprediksi x . t+1

pt = (x’t, x’t-1, ... , x’t-p)’

f adalah vektor dari nilai sekarang dan yang akan datang t

f = (t x’t, x’t+1, ... , x’t+p)’

Pada analisis korelasi kanonik, submatriks ditentukan dari matriks kovarian contoh pt dan f . t Γ adalah matriks kovarian yang didasarkan pada Block Hankel:

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ Γ + Γ + Γ Γ + Γ Γ Γ Γ Γ Γ Γ Γ = Γ ) 2 ( ) 2 ( ) 1 ( ) ( ) 1 ( ) 3 ( ) 2 ( ) 1 ( ) ( ) 2 ( ) 1 ( ) 0 ( p p p p p p L M M M M L L

Pemilihan nilai p didasarkan pada model

VAR dengan nilai AIC terkecil. Analisis korelasi kanonik didasarkan pada Block

Hankel dari matriks kovarian contoh, yaitu:

⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ Γ + Γ + Γ Γ + Γ Γ Γ Γ Γ Γ Γ Γ = Γ ) 2 ( ˆ ) 2 ( ˆ ) 1 ( ˆ ) ( ˆ ) 1 ( ˆ ) 3 ( ˆ ) 2 ( ˆ ) 1 ( ˆ ) ( ˆ ) 2 ( ˆ ) 1 ( ˆ ) 0 ( ˆ ˆ p p p p p p L M M M M L L

dimana adalah matriks

kovarian contoh.

( )

j,j 0,1,...,2p ˆ ₌ Γ ∑− − ₊ − = = Γ n j t j X j t X X t X n j) 1 ( )( )', 1,2,.. ( ˆ

Dimana X=(X₁,X₂,...,X_t)' adalah vektor nilai

tengah contoh.

Pemilihan Komponen State vector Analisis korelasi kanonik membentuk satu urutan dari state vector. Korelasi kanonik terkecil digunakan di dalam pemilihan komponen-komponen state vector.

Pada setiap langkah dari serangkaian analisis korelasi kanonik, korelasi kanonik terkecil yang signifikan (ρmin) dihitung

berdasarkan kriteria informasi dari Akaike (1976): ] 1 ) 1 ( [ 2 ) min 2 1 ln( − − + − + − = n r p q AIC ρ dimana:

q = banyaknya komponen state vector r = banyaknya variabel pada state vector p = orde AR optimal

Jika AIC≤0, ρ_{min =}0, jika nilai AIC>0 maka nilai ρ_{min >}0.

Untuk menguji kesignifikanan korelasi kanonikρ , salah satu pendekatan yang dapat digunakan adalah uji chi-square dengan hipotesis: ) 2 (χ H0 : ρ=0 H1 : ρ>0

Bentuk statistik ujinya:

) 2 min 1 ln( )) 1 ) 1 ( ( 5 . 0 ( 2 _ρ χ hit=−n− r p+ −q+ −

Mendekati sebaran chi-square dengan derajat bebas (db), db = [r(p+1)−q+1].

Jika χ2_hit >χ2α

( )

_db maka keputusan H0

ditolak, artinya korelasi kanonik significant. Pendugaan Parameter

Setelah model State Space diidentifikasi,

pendugaan parameter model State Space dapat dilakukan salah satunya dengan menggunakan pendekatan. Prosedur ini dilakukan secara iteratif. Dugaan ini didapatkan dari analisis korelasi kanonik dan digunakan untuk memperoleh penduga Г yang efisien bagi nilai-nilai parameternya, yaitu F, G, dan ∑. Pada proses pendugaan ini, salah satu elemen pada F dan G, pasti ada yang bernilai konstan seperti 0 dan 1 (Wei, 1989).

Untuk serangkaian n observasi x1,x2,...,xt

karena

xt = (I - FB)-1Get

B sebagai backshift operator , maka diperoleh xt = H(I - FB)-1Get

dan

(13)

sehingga diperoleh fungsi log likelihood sebagai berikut : 1 1 ln | | S(F,G) 2 2 n trace − − ∑ − ∑ dimana _∑ = ′ = n t 1t t e e G) S(F, Kalman Filter

Kalman filter adalah prosedur rekursif yang digunakan untuk melakukan peramalan dari state vector. Kalman filter terdiri dari pembentukan dugaan awal dari state kemudian merevisi dugaan dengan menambahkan koreksi pada dugaan awal. Besarnya koreksi ditentukan oleh sebaik apa dugaan awal memprediksi observasi baru. (Wei 1989).

Ketepatan peramalan bergantung pada pendugaan dari state vector . Ketika sebuah informasi yang baru tersedia, harus dilakukan pembaharuan state vector, begitu pula dengan peramalannya.

) ( ˆ l X_t t Zˆ Zt

Melalui pendekatan teorema Bayes diperoleh :

p(Zt+1| Xt+1) ∞ p(Xt+1| Zt+1,Xt)p(Zt+1| Xt)

Sebaran posterior p(Zt+1| Xt) menjadi sebaran

prior untuk mengetahui sebaran posterior yang baru, yaitu p(Zt+1| Xt+1), dimana observasi Xt+1

tersedia.

Sebaran posterior dari state vector Zt pada

waktu ke t yaitu p(Zt| Xt) mengikuti sebaran

normal dengan rataan Zt dan matriks kovarian

Гt

(Zt| Xt) ~ N( , ГZˆ_t t)

Pada waktu t+1, ketika observasi Xt+1

tersedia, state vector dapat diperbaharui dan diperoleh sebaran posterior baru p(Zt+1| Xt+1).

Xt+1 ekivalen dengan peramalan error et+1,

maka untuk memperoleh p(Zt+1|Xt+1) hanya

perlu menemukan sebaran posterior dari (Zt+1|et+1,Xt), yaitu (Zt+1|Xt) ~ N(F , RZˆt t+1) dimana Rt+1 = FГtF’+G∑G’ ( ) 1 1 1 1 1 ˆ ˆ − ₊ + + + = t + t ′ Ω + t ′ t t FX R H HR H e Z ˆ

(

ˆ ( )₁

)

1 1 t t t t K X X X F + − = ₊ ₊ ( ) 1 1 1 1 1 1 + − + + + + = − ′ Ω + ′ Γ_t R_t R_t H HR _t H HR_t = Rt₊₁−Kt₊₁HRt₊₁ =

(

I = Kt+1H

)(

FΓtF′+G ∑G′

)

dengan:

(

)

G G F F R H HR H R K t t t t t ′ ∑ + ′ Γ = ′ + Ω ′ = + − + + + 1 1 1 1 1

(

F,G,∑| x1,x2,...,xt

)

∞ lnL

Persamaan di atas merupakan formula rekursif dasar yang digunakan untuk memperbaharui rataan dan matriks kovarian serta sebaran dari state vector Zt+1 setelah

observasi baru, yaitu Xt+1 tersedia. Dugaan

dari state yang telah diperbaharui yaitu adalah penjumlahan dari , yaitu dugaan dari observasi sampai waktu t, dengan peramalan error 1 langkah ke depan yaitu

. Matriks K 1 ˆ + t Z t Z F ˆ ) 1 ( ˆ 1 1 t t t X X e+ = + − t+1 dinamakan

Kalman gain, yang menentukan bobot untuk peramalan error.

BAHAN DAN METODE

Bahan

Data yang digunakan dalam penelitian ini adalah data simulasi dengan membangkitkan data yang berasal dari model AR, MA, dan ARMA.

Metode 1) Simulasi data

a) Membangkitkan 200 data (et),

dimana et ~ N(0,1).

b) Melakukan transformasi ke dalam model AR(2), MA(1), dan ARMA(2,1).

2) Pemodelan State Space

Tahapan yang dilakukan adalah menduga model-model autoregressive dan menghitung nilai AIC tiap model. Model AR yang terpilih (dengan nilai AIC terkecil) digunakan dalam analisis korelasi kanonik.

Unsur pada state vector disusun dari

variabel dengan korelasi kanonik yang nyata. Jika state vector telah ditentukan, maka

model State Space dapat diterapkan pada data tersebut. Parameter-parameter dalam model

State Space (F, G, dan ∑) diduga dengan

pendekatan maximum likelihood. 3) Peramalan

Setelah parameter-parameter diduga, Peramalan lima periode ke depan dilakukan secara subjektif berdasarkan model State

Space yang fitted dengan teknik Kalman filter.

(14)

Gambar 1 Diagram alur analisis State Space

Penelitian ini menggunakan bantuan perangkat lunak Microsoft Excel, MINITAB 14 dan SAS 9.1.

HASIL DAN PEMBAHASAN

1. AR 2 : Xt= - 0.3Xt-1 + 0.4Xt-2 + et

Data yang dibangkitkan sesuai dengan model AR 2, dengan nilai φ =-0.3, dan ₁ φ =0.4. Plot ₂ ACF dan PACF-nya dapat dilihat pada Gambar 2 dan Gambar 3.

La g A u to co rr e la ti o n 5 0 4 5 4 0 3 5 3 0 2 5 2 0 1 5 1 0 5 1 1 .0 0 .8 0 .6 0 .4 0 .2 0 .0 - 0 .2 - 0 .4 - 0 .6 - 0 .8 - 1 .0 A u to c o r r e la ti o n F u n c tio n

(w ith 5 % s ig n ific a n ce lim its fo r th e a u to c o r r e la tio n s )

Gambar 2 Plot ACF pada data awal Penentuan state vector

(Analisis Korelasi Kanonik)

Pendugaan Parameter (Maximum Likelihood) Penyeleksian Orde Autoregressive Peramalan (Kalman filter) Data (stasioner)

Pilih AIC terkecil

AIC positif terkecil

Proses iterasi Model State Space

L a g P a rt ia l A u to co rr e la tio n 5 0 4 5 4 0 3 5 3 0 2 5 2 0 1 5 1 0 5 1 1 .0 0 .8 0 .6 0 .4 0 .2 0 .0 - 0 .2 - 0 .4 - 0 .6 - 0 .8 - 1 .0

P a r tia l A u to c o r r e la tio n F u n c tio n

( w ith 5 % s ig n ific a n c e lim its fo r th e p a r tia l a u to c o r r e la tio n s )

Gambar 3 Plot PACF pada data awal Penyeleksian Orde Autoregressive Sebelum menentukan model State Space, dilakukan pemilihan orde optimal pada AR. Nilai AIC terkecil -9.31294 terdapat pada lag ke-2 (Lampiran 2), lag ini menunjukkan orde AR optimal yang dipilih adalah 2 (p=2). Banyaknya lag pada AR ada 10. Nilai ini diperoleh dari hasil simulasi yang telah dicoba.

Jumlah lag = n-2, untuk n<10 10, untuk n>10 dimana n = banyaknya observasi

Penentuan State Vector

Penentuan unsur dari state vector melalui serangkaian analisis korelasi kanonik dari matriks autokovarian contoh dengan orde p=2 (Lampiran 3).

Nilai IC yang negatif (tidak nyata) dikeluarkan dari state vector, sedangkan nilai IC yang positif (nyata) dan terkecil dimasukkan dalam state vector. Pada Lampiran 3 dapat dilihat bahwa nilai IC dari korelasi kanonik x(T+1;T) bernilai positif yaitu sebesar 27.2766 oleh karena itu dimasukkan dalam state vector. Kemudian komponen ditambah, dan dihitung nilai AIC nya. Karena nilai AIC yang diperoleh bernilai negatif yaitu sebesar -1.87419, maka x(T+2;T) tidak dimasukkan dalam state vector. Dapat juga dilihat dari uji kesignifikanan korelasi kanonik dengan menggunakan uji chi-square

. Nilai < ,

yang artinya korelasi kanonik tidak )

2

(15)

significant, komponen tersebut tidak

dimasukkan ke dalam state vector.

Dari pengujian kesignifikanan analisis korelasi kanonik, diperoleh komponen yang nyata adalah xt, xt+1|t. Komponen ini menjadi

final komponen state vector, yang dapat dituliskan sebagai berikut:

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + = t t x t x t Z | 1

Pendugaan Parameter Model State Space Informasi dari tahap sebelumnya, yaitu tahap penyeleksian orde VAR dan penentuan

state vector melalui serangkaian analisis

korelasi kanonik, digunakan untuk membentuk dugaan awal parameter model

State Space.Nilai dugaan awal ini (Lampiran

4) digunakan sebagai nilai awal proses pendugaan parameter. Pendugaan parameter dilakukan dengan menggunakan pendekatan

maximum likelihood dengan proses iteratif.

Setelah mengalami tujuh kali iterasi (Lampiran 5), diperoleh penduga efisien bagi F, G, dan ∑ sebagai berikut (Lampiran 6):

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.09101 -0.52984 1 0 ˆ F ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.41908 -1 ˆ G

[

0.924896

]

ˆ = Σ

Model State Space direpresentasikan sebagai berikut: zt+1 = F zt + G et+1 ] 1 , 1 [ | 1 1 | 2 1 | 1 + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + + t e G t t x t x F t t x t t x + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + + t t x t x t t x t t x | 1 0.09101 -0.52984 1 0 1 | 2 1 | 1 ₁_, ₁ 0.41908 -1 + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ t e dan var[e₁_,_t₊₁]=

[

0.924896

]

Persamaan dalam bentuk matriks di atas dapat dijabarkan sebagai berikut:

xt+1|t+1 = xt+1|t + e1,t+1

xt+2|t+1 = 0.52984xt - 0.09101xt+1|t - 0.41908

e1,t+1

Peramalan

Setelah diperoleh model State Space yang fitted, tahap berikutnya adalah peramalan

dengan menggunakan teknik Kalman filter. Hasil ramalan untuk lima periode ke depan dapat dilihat pada plot berikut:

In d e x 2 0 0 1 8 0 1 6 0 1 4 0 1 2 0 1 0 0 8 0 6 0 4 0 2 0 1 4 3 2 1 0 - 1 - 2 - 3 - 4 T im e S e r ie s P l o t o f P e r a m a la n Gambar 4 Plot ramalan untuk lima periode ke depan dengan menggunakan model State Space

Nilai AIC pada model AR 2 diperoleh sebesar 559.0803 dan pada model State Space sebesar -12.6769 (Lampiran 17). In d e x Da ta 2 4 2 2 2 0 1 8 1 6 1 4 1 2 1 0 8 6 4 2 3 2 1 0 - 1 - 2 V ar iab le S tateS p ac e A k tu al A R 2 T i m e S e r i e s P l o t o f A k tua l , A R 2 , S ta te S p a c e

Gambar 5 Plot aktual, model AR 2, dan model

State Space

2. MA 1 : Xt= et - 0.8et-1

Tahapan yang digunakan untuk memodelkan model State Space sama dengan tahapan yang dilakukan di atas. Output pada SAS dapat dilihat pada Lampiran 7 sampai Lampiran 11. sehingga diperoleh penduga parameternya sebagai berikut:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.0487 0.19952 -1 0 ˆ F ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.72407 -1 ˆ G

[

0.965547

]

ˆ = Σ

Maka model yang diperoleh adalah:

+ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + + t t x t x t t x t t x | 1 0.0487 0.19952 -1 0 1 | 2 1 | 1 ₁_, ₁ 0.72407 -1 + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ t e dan var[e₁_,_t₊₁]=

[

0.965547

]

(16)

Persamaan dalam bentuk matriks di atas dapat dijabarkan sebagai berikut :

xt+1|t+1 = xt+1|t + e1,t+1

xt+2|t+1 = -0.19952 xt + 0.0487 xt+1|t - 0.72407 e1,t+1

Peramalan

Setelah diperoleh model State Space yang

fitted, tahap berikutnya adalah peramalan

dengan menggunakan teknik Kalman filter. Hasil ramalan untuk lima periode ke depan dapat dilihat pada plot berikut:

In d e x 2 0 0 1 8 0 1 6 0 1 4 0 1 2 0 1 0 0 8 0 6 0 4 0 2 0 1 3 2 1 0 - 1 - 2 - 3 - 4 T i m e S e r i e s P l o t o f P e r a m a l a n

Gambar 6 Plot ramalan untuk lima periode ke depan dengan menggunakan model State Space

Nilai AIC pada model MA 1 diperoleh sebesar 574.0239 dan pada model State Space sebesar -4.93261 (Lampiran 18). In d e x Da ta 2 4 2 2 2 0 1 8 1 6 1 4 1 2 1 0 8 6 4 2 3 2 1 0 - 1 - 2 - 3 - 4 V ar iab le S tateS p ac e ak tu al M A 1 T im e S e r ie s P lo t o f a k tu a l, M A 1 , S ta te S p a c e

Gambar 7 Plot aktual, model MA1, dan model

State Space

3. ARMA2,1: Xt= -0.3Xt-1 -0.6Xt-2+et -0.8et-1

Tahapan yang digunakan untuk memodelkan model State Space sama dengan tahapan yang dilakukan di atas. Output pada SAS dapat dilihat pada Lampiran 12 sampai Lampiran 16. sehingga diperoleh penduga parameternya sebagai berikut:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.2188 -0.45937 -1 0 ˆ F ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 0.95772 -1 ˆ G

[

8.270716

]

ˆ = Σ

Maka model yang diperoleh adalah:

+ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + + t t x t x t t x t t x | 1 0.2188 -0.45937 -1 0 1 | 2 1 | 1 ₁_, ₁ 0.95772 -1 + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ t e dan var[e₁_,_t₊₁]=

[

8.270716

]

Persamaan dalam bentuk matriks di atas dapat dijabarkan sebagai berikut:

xt+1|t+1 = xt+1|t + e1,t+1

xt+2|t+1 = -0.45937xt - 0.2188xt+1|t - 0.95772 e1,t+1

Peramalan

Setelah diperoleh model State Space yang fitted, tahap berikutnya adalah peramalan

dengan menggunakan teknik Kalman filter. Hasil ramalan untuk lima periode ke depan dapat dilihat pada plot berikut :

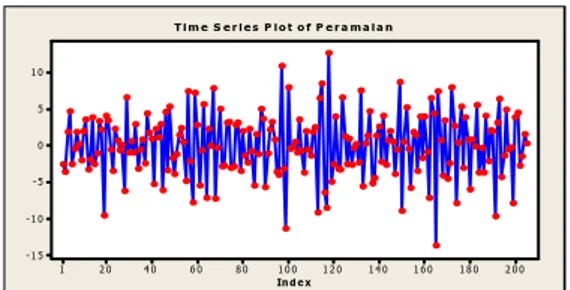
In d e x1 2 0 1 4 0 1 6 0 1 8 0 2 0 0 1 0 0 8 0 6 0 4 0 2 0 1 1 0 5 0 - 5 - 1 0 - 1 5 T im e S e r ie s P lo t o f P e r a m a l a n

Gambar 8 Plot ramalan untuk lima periode ke depan dengan menggunakan model State Space

Nilai AIC pada model ARMA 2,1 diperoleh sebesar 989.519 dan pada model

State Space sebesar 421.203 (Lampiran 19).

In d e x Da ta 2 4 2 2 2 0 1 8 1 6 1 4 1 2 1 0 8 6 4 2 5 .0 2 .5 0 .0 - 2 .5 - 5 .0 - 7 .5 - 1 0 .0 V ar iab le S tateS p ac e ak tu al A R M A 2,1 T im e S e r ie s P lo t o f a k tu a l, A R M A 2 ,1 , S ta te S p a c e

Gambar 9 Plot aktual, model ARMA 2,1 dan model State Space

KESIMPULAN

Pendugaan parameter model State Space

dilakukan dengan menggunakan pendekatan

maximum likelihood dengan proses iterasi.

Pada model AR (2), proses iterasi dilakukan sebanyak tujuh kali.

(17)

Model State Space yang diperoleh adalah:

xt+2|t+1 = 0.52984xt - 0.09101xt+1|t - 0.41908

e1,t+1

Untuk model MA (1), proses iterasi dilakukan sebanyak delapan kali, model State

Space yang diperoleh adalah:

xt+2|t+1 = -0.19952 xt + 0.0487 xt+1|t - 0.72407 e1,t+1

Sedangkan pada model ARMA (2,1), proses iterasi yang dilakukan sebanyak lima kali, model State Space yang diperoleh adalah:

xt+2|t+1 = -0.45937xt - 0.2188xt+1|t - 0.95772 e1,t+1

Model State Space yang diperoleh dari

hasil iterasi tersebut dapat digunakan untuk peramalan.

SARAN

Pada penelitian selanjutnya dapat mengkaji lebih lanjut analisis data deret waktu peubah tunggal melalui pendekatan model

State Space dengan menggunakan data real

dan tidak menutup kemungkinan untuk melakukan analisis data deret waktu peubah ganda melalui pendekatan model State Space.

DAFTAR PUSTAKA

Montgomery, D. C., L. A. Johnson, & J. S. Gardiner. 1990. Forecasting and time Series Analysis. Mc Graw Hill, Singapore.

SAS Institute Inc. 2002. SAS User’s Guide. Version 9.1 SAS Institute Inc., Cary, NC, USA.

Wei, W.W.S. 1989. Time Series Analysis:

Univariate and Multivariate. Addison

Wesley Publishing Company. Canada. Zivot, Eric. 2006. State Space Models and the

Kalman Filter.

http://faculty.washington.edu/ezivot/econ5 84/notes/statespacemodels.pdf

(18)

(19)

Lampiran 1 Hubungan antara ARMA dan State Space Model AR 2 t e t X t X t X =μ+φ₁ ₋₁+φ₂ ₋₂+ ~ t e iid N(0,σ2)

Definisikan z_t =(X_t,X_t₋₁)', maka persamaan transisi untuk z_tadalah

t e t X t X t X t X ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − 0 1 0 2 1 0 1 2 1 1 μ φ φ

Persamaan pengukurannya adalah

t z t x =(1,0) Yang menyiratkan Ht = (1, 0) Model MA (1) : 1 − + =a_t a_t t Z θ

dapat disajikan dalam bentuk State Space dengan beberapa cara. Ditetapkan α_t =(y_t −μ,θa_t), kemudian dapat ditulis

μ α + = _t t y (1 0) t a t t ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = θ α α ₁ 1 0 0 1 0

Elemen pertama dari α adalah t θat−1+atyang nilainya sama dengan yt −μ.

Model ARMA (p,q) q t e q t e t e p t X p t X t X =φ₁ ₋₁+...+φ ₋ + +θ₁ ₋₁+...+θ ₋

Jika m = max(p,q+1), maka bentuk ARMA (p,q) dapat ditulis

1 1 ... 1 1 ... 1 1 − + + − + + − + + − − + = X_t _pX_t _m e_t e_t _m e_t _m t X φ φ θ θ

Dimana beberapa koefisien AR atau MA dapat menjadi nol kalau p=q+1.

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + − + − − + + + + + − + + − = t e m t X m m t e m t e t e m t X p t X t X t z θ φ θ θ φ φ 1 2 1 ... 1 1 ... 1 2 M set t X =(1 0’m-1) zt t e m m t z m m t z ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − + − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = 1 2 1 1 1 0 0 0 1 0 0 1 0 1 0 2 0 0 1 1 θ θ θ φ φ φ φ M L L M O M M M L L

(20)

Model ARMA (2,1) : 1 1 2 2 1 1 − +Φ − + − − Φ = Z_t Z_t a_t a_t t Z θ (1)

Jika ditulis ke dalam bentuk moving average

t a B B B t Z =(1−Φ₁ −Φ₂ 2)−1(1−θ₁ )

∑∞ = Ψ − = 0 j t j a j Dimana Ψ0 =1,Ψ1=Φ1−θ1

Maka, penyajian State Space dari bentuk (1) adalah :

1 1 1 | 1 1 2 1 0 1 | 2 1 | 1 + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Ψ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Φ Φ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + + t a t t Z t Z t t Z t t Z

Bentuk persamaan linier-nya:

1 | 1 1 | 1 + = + + + + t Zt t at t Z

(2) 1 1 2 1 1 1 | 2 + =Φ ₊ +Φ +Ψ + + t Z_t Zt at t Z (3)

Dari persamaan (2), dapat diperoleh :

2 1 | 2 2 | 2 + = + + + + + t Zt t at t Z (4)

Z_t₊₂_|_t₊₂−a_t₊₂ =φ₁Z_t₊₁_|_t₊₁−φ₁a_t₊₁+φ₂Z_t +Ψ₁a_t₊₁

Z_t₊₂_|_t₊₂ =φ₁Z_t₊₁_|_t₊₁+φ₂Z_t+(Ψ₁−φ₁)a_t₊₁+a_t₊₂

Z_t =φ₁Z_t₋₁+φ₂Z_t₋₂+a_t−θ₁a_t₋₁

(21)

Output SAS untuk model AR (2) : Xt= -0.3Xt-1 + 0.4Xt-2+et

Lampiran 2 Penyeleksian Orde VAR Berdasarkan IC Terkecil

The STATESPACE Procedure

Information Criterion for Autoregressive Models

Lag=0 Lag=1 Lag=2 Lag=3 Lag=4 Lag=5 Lag=6 Lag=7 Lag=8 Lag=9 Lag=10 100.0829 18.35745 -9.31294 -8.91916-7.38727 -7.26778 -5.26931 -3.61021-2.11773-0.79299 0.86489 Yule-Walker Estimates

for Minimum AIC

--Lag=1- --Lag=2- x x x -0.36769 0.371312

Lampiran 3 Analisis Korelasi Kanonik

The STATESPACE Procedure Canonical Correlations Analysis Information Chi x(T;T) x(T+1;T) Criterion Square DF 1 0.380484 27.2766 31.12022 2 Information Chi x(T;T) x(T+1;T) x(T+2;T) Criterion Square DF 1 0.391229 0.025077 -1.87419 0.125495 1 Keterangan: DF = r (p+1) – q + 1 = 1 (2+1) – 2 + 1 = 2 DF = r (p+1) – q + 1 = 1 (2+1) – 3 + 1 = 1

Lampiran 4 Dugaan Awal Model State Space

Selected Statespace Form and Preliminary Estimates State Vector

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 0.501557 -0.14499 Input Matrix for Innovation 1

-0.36769

Variance Matrix for Innovation 0.935602

(22)

Lampiran 5 Proses Iterasi Pendugaan Maksimum Likelihood

Iterative Fitting: Maximum Likelihood Estimation

Iter Half Determinant Lambda F(2,1) F(2,2) G(2,1) Sigma(1,1) 0 0 0.927321 0.1 0.50155694 -0.1449908 -0.367689 0.92732064 1 0 0.92526 0.01 0.50648616 -0.1310761 -0.4049297 0.92526034 2 0 0.924935 0.001 0.52239116 -0.1052014 -0.4155773 0.92493456 3 0 0.924899 0.0001 0.52797052 -0.0947861 -0.4180693 0.92489882 4 0 0.924896 0.00001 0.52935548 -0.091995 -0.4188133 0.92489616 5 0 0.924896 1E-6 0.52971877 -0.0912562 -0.4190133 0.92489598 6 0 0.924896 1E-7 0.52981452 -0.0910611 -0.4190663 0.92489596 7 0 0.924896 1E-8 0.52983977 -0.0910097 -0.4190803 0.92489596 Maximum likelihood estimation has converged.

Lampiran 6 Model State Space yang disesuaikan (fitted)

Selected Statespace Form and Fitted Model State Vector

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 0.52984 -0.09101 Input Matrix for Innovation 1

-0.41908

(23)

Output SAS untuk model MA (1) : Xt= et - 0.8et-1

Lampiran 7 Penyeleksian Orde VAR Berdasarkan IC Terkecil

Lag=0 Lag=1 Lag=2 Lag=3 Lag=4 Lag=5 Lag=6 Lag=7 Lag=8 Lag=9 87.54265 61.14247 33.18255 16.16742 8.836911 2.390563 4.283737 5.77197 7.087625 9.0752

Lag=10 8.142032

Yule-Walker Estimates for Minimum AIC

--Lag=1- --Lag=2- --Lag=3- --Lag=4- --Lag=5- x x x x x x -0.71959 -0.72299 -0.56096 -0.351 -0.20335

The STATESPACE Procedure Canonical Correlations Analysis Information Chi x(T;T) x(T+1;T) Criterion Square DF 1 0.533063 56.85873 66.023 5 Information Chi x(T;T) x(T+1;T) x(T+2;T) Criterion Square DF 1 0.630165 0.123341 -4.93402 3.03532 4 Keterangan: DF = r (p+1) – q + 1 = 5 = 1 (5+1) – 2 + 1 DF = r (p+1) – q + 1 = 1 (5+1) – 3 + 1 = 4

Lampiran 9 Dugaan Awal Model State-space

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 -0.15421 0.101746 Input Matrix for Innovation 1

-0.71959

(24)

Iter Half Determinant Lambda F(2,1) F(2,2) G(2,1) Sigma(1,1) 0 0 0.968991 0.1 -0.1542128 0.10174557 -0.7195872 0.96899077 1 0 0.965769 0.01 -0.1856491 0.07159899 -0.7142361 0.96576919 2 0 0.965549 0.001 -0.1994832 0.04961986 -0.722961 0.96554893 3 1 0.965549 0.01 -0.1995282 0.04885771 -0.723766 0.96554854 4 2 0.965549 0.1 -0.1995165 0.04903814 -0.7235736 0.96554852 5 0 0.965548 0.01 -0.1995405 0.04850388 -0.7242335 0.96554809 6 2 0.965548 0.1 -0.1995289 0.0486031 -0.7241541 0.96554776 7 2 0.965548 1 -0.1995212 0.04868135 -0.7240897 0.96554753 8 2 0.965547 10 -0.19952 0.04870011 -0.7240722 0.96554749 Maximum likelihood estimation has converged.

Lampiran 11 Model State Space yang disesuaikan (fitted)

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 -0.19952 0.0487 Input Matrix for Innovation 1

-0.72407

(25)

Output SAS untuk model ARMA (2,1) : Xt= -0.3Xt-1 - 0.6Xt-2+et - 0.8et-1

Lampiran 12 Penyeleksian Orde VAR Berdasarkan IC Terkecil

Lag=0 Lag=1 Lag=2 Lag=3 Lag=4 Lag=5 Lag=6 Lag=7 Lag=8 Lag=9 586.2296 558.3838 467.8288 450.1532 444.7467 435.8104 437.6083 437.0992 437.671 437.6859

Lag=10 433.7754

Yule-Walker Estimates for Minimum AIC

--Lag=1- --Lag=2- --Lag=3- --Lag=4- --Lag=5- --Lag=6- --Lag=7- --Lag=8- --Lag=9- --Lag=10- x x x x x x x x x x -0.93324 -1.14883 -0.84618 -0.63299 -0.57748 -0.39971 -0.43256 -0.36554 -0.25574 -0.17065

The STATESPACE Procedure Canonical Correlations Analysis Information Chi x(T;T) x(T+1;T) Criterion Square DF 1 0.714966 123.1508 139.5721 10 Information Chi x(T;T) x(T+1;T) x(T+2;T) Criterion Square DF 1 0.77353 0.239203 -6.21594 11.51892 9 Keterangan: DF = r (p +1) – q + 1 = 1 (10+1) – 2 + 1 = 10 DF = r (p +1) – q + 1 = 1 (10+1) – 3 + 1 = 9

Lampiran 14 Dugaan Awal Model State Space

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 -0.47921 -0.25126 Input Matrix for Innovation 1

-0.93324

(26)

Iter Half Determinant Lambda F(2,1) F(2,2) G(2,1) Sigma(1,1) 0 0 8.308588 0.1 -0.4792057 -0.2512609 -0.9332425 8.30858776 1 0 8.274034 0.01 -0.4521501 -0.2099237 -0.9644939 8.2740344 2 2 8.271093 0.1 -0.4561565 -0.2151117 -0.9605667 8.27109332 3 2 8.270876 1 -0.4598123 -0.2202446 -0.9563226 8.27087622 4 3 8.270717 10 -0.4593692 -0.2188592 -0.9576641 8.27071677 5 5 8.270716 100 -0.4593657 -0.2187984 -0.9577242 8.27071628 Maximum likelihood estimation has converged.

Lampiran 16 Model State-space yang disesuaikan (fitted)

x(T;T) x(T+1;T) Estimate of Transition Matrix 0 1 -0.45937 -0.2188 Input Matrix for Innovation 1

-0.95772

(27)

Lampiran 17 Nilai pendugaan parameter dan nilai AIC pada model AR 2 Conditional Least Squares Estimation

Standard Approx

Parameter Estimate Error t Value Pr > |t| Lag AR1,1 -0.35342 0.06562 -5.39 <.0001 1 AR1,2 0.38601 0.06567 5.88 <.0001 2 Variance Estimate 0.948925 Std Error Estimate 0.974128 AIC 559.0803 SBC 565.6769 Number of Residuals 200 Lampiran 18 Nilai pendugaan parameter dan nilai AIC pada model MA 1

Conditional Least Squares Estimation

Standard Approx

Parameter Estimate Error t Value Pr > |t| Lag MA1,1 0.77730 0.04465 17.41 <.0001 1 Variance Estimate 1.02763 Std Error Estimate 1.013721 AIC 574.0239 SBC 577.3222 Number of Residuals 200

Lampiran 19 Nilai pendugaan parameter dan nilai AIC pada model ARMA 2,1 Conditional Least Squares Estimation

Standard Approx

Parameter Estimate Error t Value Pr > |t| Lag MA1,1 0.83261 0.04510 18.46 <.0001 1 AR1,1 -0.17012 0.07066 -2.41 0.0170 1 AR1,2 -0.42862 0.06986 -6.14 <.0001 2 Variance Estimate 8.124073 Std Error Estimate 2.850276 AIC 989.519 SBC 999.414 Number of Residuals 200

(28)

Lampiran 20 Program SAS Model State Space data coba; input x ; cards; 0.83950 -0.98375 2.53223 . . . ;

proc statespace data=coba cancorr out=out itprint lead=5;

var x ;

proc print data=out;