KAJIAN MATEMATIS DAN ASPEK PENDIDIKAN DALAM
PENYELESAIAN DERET TAYLOR UNTUK MASALAH
NILAI BATAS ORDE TIGA
TESIS
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Magister Pendidikan Program Studi Magister Pendidikan Matematika
Disusun oleh: Auxilia Maria Aroran
NIM: 161442027
PROGRAM STUDI MAGISTER PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA
YOGYAKARTA 2020
i
KAJIAN MATEMATIS DAN ASPEK PENDIDIKAN DALAM
PENYELESAIAN DERET TAYLOR UNTUK MASALAH
NILAI BATAS ORDE TIGA
TESIS
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Magister Pendidikan Program Studi Magister Pendidikan Matematika
Disusun oleh: Auxilia Maria Aroran
NIM: 161442027
PROGRAM STUDI MAGISTER PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA
YOGYAKARTA 2020
ii
MATHEMATICAL STUDY AND EDUCATIONAL ASPECTS
IN TAYLOR SERIES SOLUTION FOR A THIRD ORDER
BOUNDARY VALUE PROBLEM
THESIS
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Master Education in Mathematics Education Study Program
Written by: Auxilia Maria Aroran Student ID: 161442027
MAGISTER OF MATHEMATICS EDUCATION STUDY PROGRAM DEPARTMENT OF MATHEMATICS AND SCIENCE EDUCATION
FACULTY OF TEACHER TRAINING AND EDUCATION SANATA DHARMA UNIVERSITY
YOGYAKARTA 2020
v
HALAMAN PERSEMBAHAN
Tesis ini saya persembahkan untuk Tuhan Yesus dan Bunda Maria Kedua Orang Tua, Nixon Aroran dan Maryke Pontoan Adik Lafio Aroran & Adik ipar Cyprianus Warouw Keponakan Karlen Junno Aquinas Warouw dan Kialen Jino Aquino Warouw Kakek, Nenek, Keluarga Besar dan Sanak Saudara Pastor Yong Ohoitimur dan keluarga besar Yayasan Pendidikan Lokon Almamater tercinta, Universitas Sanata Dharma
viii
ABSTRAK
Auxilia Maria Aroran, 2020. Kajian Matematis dan Aspek Pendidikan dalam Penyelesaian Deret Taylor untuk Masalah Nilai Batas.
Tesis.
Program Studi Magister Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Berbagai fenomena dalam kehidupan sehari-hari bisa dimodelkan secara matematis. Terdapat bermacam-macam cara untuk menyelesaikan model yang telah diperoleh. Solusi deret Taylor menawarkan penyelesaian yang relatif lebih mudah dan lebih akurat.
Tesis ini bertujuan untuk memperoleh solusi deret Taylor untuk masalah nilai batas orde tiga. Hasil penelitian juga menunjukkan bahwa solusi deret Taylor untuk masalah nilai batas orde tiga bisa digunakan untuk mengolah keterampilan berpikir tingkat tinggi siswa SMA.
Kata kunci: deret Taylor, deret Maclaurin, masalah nilai batas, keterampilan berpikir tingkat tinggi.
ix
ABSTRACT
Auxilia Maria Aroran, 2020. Mathematical Study and Educational Aspects on Taylor Series Solution for a Third Order Boundary Value Problem.
Thesis.
Magister of Mathematics Education Study Program, Department of Mathematics and Science Education, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Real world phenomenon could be described in a mathematical model. There are many ways to solve the obtained model. Taylor series solution suggests a relatively easier solution that is more accurate.
This thesis aims to achieve a Taylor series solution for a third order boundary value problem. The result of this research also shows that Taylor series solution for a third order boundary value problem is useful to explore high school students’ higher order thinking skills.
Keywords: Taylor series, Maclaurin series, boundary value problem, higher order thinking skills.
x
KATA PENGANTAR
Puji dan syukur kepada Tuhan atas berkat dan penyertaannya sampai pada saat penulis dapat menyelesaikan tugas akhir ini. Tesis yang berjudul “Kajian Matematis dan Aspek Pendidikan dalam Penyelesaian Deret Taylor untuk Masalah Nilai Batas Orde Tiga” ini disusun sebagai salah satu syarat untuk memperoleh gelar Magister Pendidikan pada Program Studi Magister Pendidikan Matematika Universitas Sanata Dharma. Selama proses penyusunan, tentu saja penulis menemui berbagai macam hambatan sampai akhirnya bisa selesai berkat penyertaan Tuhan dan dukungan dari berbagai pihak. Ucapan terima kasih atas berbagai dukungan yang diterima ingin disampaikan oleh penulis kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dosen pembimbing tesis atas semua bentuk bimbingan, arahan dan saran yang diberikan baik selama proses penyusunan tesis, maupun sejak penulis berada di Program Studi Magister Pendidikan Matematika ini.
2. Bapak Dr. M. Andy Rudhito, S.Pd., selaku Ketua Program Studi Magister Pendidikan Matematika atas semua bentuk saran dan dukungan yang diberikan selama penulis menempu pendidikan di Program Studi Magister Pendidikan Matematika ini.
3. Para Dosen yang telah membagikan ilmu pengetahuannya selama penulis menjalani perkuliahan di Universitas Sanata Dharma, sejak menempuh pendidikan sarjana sampai pendidikan magister.
4. Keluarga dan sanak saudara di Manado atas segala bentuk doa, dukungan, dan dorongan sehingga penulis bisa menyelesaikan tesis ini.
5. Yayasan Pendidikan Lokon yang telah memberikan kesempatan kepada penulis untuk menempuh pendidikan di USD, serta dorongan dan semangat yang telah diberikan sampai penulis bisa menyelesaikan tesis.
6. Bapak/Ibu/Saudara/i rekan-rekan mahasiswa seangkatan yang juga menempuh pendidikan magister di Prodi S2PMat USD atas semangat dan dorongan selama penulisan, khususnya buat Kak Olive, Wike, Dian, Archa,
xi
Tya. Terima kasih juga atas waktu berdinamika bersama sebagai bagian dari keluarga Prodi S2PMat USD.
7. Keluarga Besar Program Studi Magister Pendidikan Matematika Universitas Sanata Dharma, kakak-kakak dan adik-adik angkatan, juga keluarga besar JPMIPA, FKIP USD, khususnya karyawan dan staf sekretariat yang baik secara langsung maupun secara tidak langsung memberikan bantuan kepada penulis.
8. Clarisa, Valen, Vena, Cia, Rini, dan juga teman-teman Goldenness yang memberikan semangat dan menjadi teman diskusi selama penulis mengerjakan tesis.
9. Serta Bofie, Golcha, dan juga semua pihak yang tidak sempat disebutkan di atas, yang secara tidak langsung telah menyemangati penulis sehingga bisa menyelesaikan tesis ini.
Penulis menyadari, bahkan dengan bantuan dan keterlibatan dari berbagai pihak, tulisan ini adalah karya dari penulis, manusia biasa yang tak luput dari kesalahan. Oleh karena itu, penulis dengan tangan terbuka menerima segala bentuk kritik dan saran dari pembaca sekalian. Semoga kiranya tulisan ini dapat bermanfaat bagi para pembaca.
Yogyakarta, Juli 2020 Penulis
xii
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR GAMBAR ... xiv
DAFTAR TABEL ... xv
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah... 1
B. Tinjauan Pustaka ... 4 C. Rumusan Masalah ... 5 D. Tujuan Penulisan ... 5 E. Manfaat Penulisan ... 5 F. Metode Penelitian ... 5 G. Kebaruan Penelitian ... 6 H. Sistematika Penulisan ... 6
BAB II LANDASAN TEORI ... 8
A. Deret Pangkat ... 8
B. Deret Taylor dan Deret Maclaurin ... 12
C. Teorema-Teorema Pendukung ... 20
D. Higher Order Thinking Skill (HOTS)... 21
BAB III PENYELESAIAN MASALAH NILAI BATAS ... 24
xiii
B. Contoh Masalah ... 25
BAB IV ASPEK KEPENDIDIKAN MATERI DERET TAYLOR ... 29
A. Deret Taylor untuk Mengolah Keterampilan Berpikir Tingkat Tinggi Siswa SMA ... 29 B. Refleksi ... 30 BAB V PENUTUP ... 34 A. Kesimpulan ... 34 B. Saran ... 35 DAFTAR PUSTAKA ... 36
xiv
DAFTAR GAMBAR
Gambar 1.1 Proses Pemodelan ... 1 Gambar 2.1 Perbandingan fungsi eksponensial dengan polinomial Taylor
untuk , , ... 16 Gambar 3.1 Perbandingan solusi pendekatan dengan solusi eksak ... 27
xv
DAFTAR TABEL
1
BAB I PENDAHULUAN
A. Latar Belakang Masalah
Bermacam-macam permasalahan dalam kehidupan sehari-hari dapat melahirkan berbagai konsep matematika. Model matematika adalah deskripsi matematis (sering kali dalam bentuk fungsi atau persamaan) dari fenomena dalam kehidupan sehari-hari seperti permintaan konsumen untuk suatu produk, kecepatan jatuhnya sebuah objek, konsentrasi dari suatu unsur dalam reaksi kimia, atau biaya pengurangan emisi. Tujuan dari model matematika adalah untuk memahami suatu fenomena, bahkan mungkin untuk membuat perkiraan tentang bagaimana perilaku dari fenomena yang dimodelkan di masa yang akan datang.
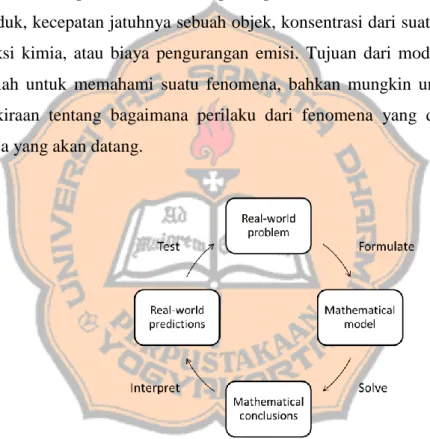
Gambar 1.1. Proses pemodelan
Gambar 1.1 menjelaskan proses dari pemodelan matematika. Misalkan terdapat suatu masalah nyata, hal pertama yang perlu dilakukan yaitu merumuskan model matematika dengan mengidentifikasi dan menamai variabel-variabel bebas dan tak bebas, dan membuat asumsi yang menyederhanakan fenomena terkait sehingga bisa membuatnya mudah dikerjakan secara matematis. Selanjutnya dengan pengetahuan tentang hukum-hukum fisika dan matematika yang ada, variabel-variabel dan
asumsi-asumsi yang telah dikemukakan kemudian disatukan untuk memperoleh suatu persamaan. Jika tidak ada hukum-hukum yang bisa dijadikan acuan, maka yang bisa dilakukan yaitu dengan mengumpulkan data dari mana saja, kemudian mengolah data tersebut dalam bentuk tabel untuk memperoleh suatu pola. Selain mendapatkan representasi numeris untuk pola yang diperoleh, data-data yang dikumpulkan juga bisa diolah dalam bentuk grafik. Grafik yang diperoleh bisa mengacu pada suatu fungsi atau rumus aljabar yang cocok.
Tahap kedua yaitu menerapkan teori matematika (seperti kalkulus) ke dalam model yang telah diperoleh untuk mengambil kesimpulan matematis. Selanjutnya pada tahap ketiga, kesimpulan tersebut diinterpretasikan sebagai informasi tentang fenomena nyata yang dimodelkan, bisa sebagai suatu penjelasan tentang fenomena itu, maupun berupa sebuah prediksi. Langkah akhir yaitu menguji prediksi yang telah diperoleh dengan data-data baru. Jika prediksi tersebut tidak cocok dengan data-data baru dari fenomena yang sama, atau dengan kata lain tidak cocok dengan realitas, maka model yang diperoleh perlu diperbaiki, dengan demikian mengulang kembali prosesnya.
Tidak ada model matematika yang merupakan representasi akurat dari situasi nyata, karena model merupakan suatu idealisasi. Model yang baik menyederhanakan kenyataan, cukup untuk memungkinkan perhitungan matematis, tetapi juga cukup akurat untuk memberikan kesimpulan yang berarti.
Terdapat banyak masalah dalam bidang teknik (engineering) yang bisa dimodelkan dengan persamaan diferensial orde tinggi, yang bisa dituliskan secara umum dalam bentuk
( )( ) ( ( )) dimana adalah fungsi nonlinear dari dan turunannya.
Untuk suatu syarat batas yang ditentukan, persamaan di atas dapat diselesaikan secara numerik atau analitik. Sebagai contoh, perhatikan gerak dinamik dari suatu batang meruncing (tapered beam). Persamaan pengaturnya yaitu
( )
dengan melambangkan perpindahan, melambangkan kekakuan, melambangkan masa jenis, dan melambangkan luasan bagiannya.
Dengan pemisahan variabel, asumsikan ( )
Subsitusikan ke persamaan pengatur, dengan mempertimbangkan bahwa dan adalah fungsi koordinat, diperoleh persamaan diferensial orde empat yaitu
( )( ) ( )
Persamaan di atas bisa mendeskripsikan bermacam-macam masalah nilai batas yang muncul dalam bidang teknik arsitektur, dari pembelokan balok sampai getaran struktur berskala nano. Terdapat berbagai metode analitik untuk menyelesaikan persamaan ini, misalnya metode perturbasi homotopi, metode iterasi variasional, dan lain-lain.
Dalam penelitian ini, yang menjadi pokok bahasan yaitu persamaan diferensial biasa orde tiga yaitu
( ) ( ) ( ) ( ) , - dengan , , dan merupakan konstanta.
Tesis ini membahas pendekatan analitis dengan deret Taylor untuk persamaan di atas. Lebih jauh lagi, tesis ini membahas penyelesaian deret Taylor untuk masalah nilai batas orde tiga berkaitan dengan persamaan diferensial biasa orde tiga di atas.
Selain membahas penyelesaian deret Taylor untuk masalah nilai batas orde tiga, tesis ini juga memuat eksplorasi aspek pendidikan dari deret Taylor bagi keterampilan berpikir tingkat tinggi siswa SMA. Konsep berpikir tingkat tinggi ini berdasar pada Taksonomi Bloom, yang membagi kemampuan dalam ranah kognitif menjadi enam aspek. Keenam aspek kemampuan tersebut mencakup aspek mengingat, memahami, menerapkan, menganalisa, mengevaluasi, dan mencipta. Aspek-aspek yang menjadi bagian dari kemampuan berpikir tingkat tinggi yaitu aspek menganalisa, mengevaluasi,
dan mencipta. Akan dilihat bagaimana deret Taylor bisa digunakan untuk mengolah kemampuan berpikir tingkat tinggi siswa SMA.
B. Tinjauan Pustaka
Pada bagian ini dituliskan beberapa hasil penelitian yang berkaitan dengan topik penelitian tesis ini, baik yang berkaitan dengan solusi deret Taylor, masalah nilai batas, maupun yang berkaitan dengan meningkatkan keterampilan berpikir tingkat tinggi.
Ji-Huan He dalam tulisannya Taylor Series Solution for a Third Order Boundary Value Problem Arising in Architectural Engineering berhasil menerapkan solusi deret Taylor untuk masalah nilai batas orde tiga dengan proses penyelesaian yang relatif sederhana dan hasil yang lebih akurat. Hasil penelitian ini mengatakan bahwa metode ini dapat dikembangkan juga untuk masalah nilai batas lainnya, dan untuk masalah nilai awal. Diperoleh juga beberapa keuntungan metode ini yaitu selain prosedurnya yang sederhana dan bisa diterapkan untuk masalah nilai batas dan masalah nilai awal, metode ini bisa dikembangkan untuk syarat batas yang lebih kompleks. Keuntungan lainnya yaitu solusi deret Taylor konvergen ke solusi eksaknya, dan bisa dicari untuk berbagai tingkat akurasi.
Selain solusi deret Taylor, terdapat penelitian yang menggunakan metode yang lain. Misalnya penelitian oleh Arora dkk. yang dipublikasikan pada tahun 2018 menggunakan metode hibrid untuk menemukan solusi masalah nilai batas dengan orde yang lebih tinggi. Tahun 2019, El-Kalla dkk. menggunakan metode dekomposisi Adomian. Sementara Abdelrahim mengemukakan solusi numeris dari masalah nilai batas orde tiga menggunakan metode blok hibrid satu langkah. Solusi deret Taylor juga pernah digunakan oleh Ji-Huan He dkk. untuk menyelesaikan fractal Bratu-type equation.
Untuk penelitian yang berkaitan dengan bidang pendidikan, pada tahun 2009 Lewy dkk. mengembangkan soal untuk mengukur kemampuan berpikir tingkat tinggi siswa SMP dalam pokok bahasan Barisan dan Deret. Penelitian
ini memberikan indikator kemampuan berpikir tingkat tinggi untuk aspek menganalisis, mengevaluasi, dan mencipta.
C. Rumusan Masalah
Berdasarkan latar belakang yang telah dipaparkan, masalah-masalah yang akan dibahas dalam tulisan ini antara lain:
1. Bagaimana menerapkan turunan ke dalam deret Taylor untuk menyelesaikan masalah nilai batas orde tiga?
2. Bagaimana eksplorasi aspek pendidikan dari turunan dan deret Taylor bagi keterampilan berpikir tingkat tinggi siswa SMA?
D. Tujuan Penulisan
Tujuan yang ingin dicapai oleh penulis selain untuk memenuhi syarat tugas akhir dalam program studi Magister Pendidikan Matematika Universitas Sanata Dharma, yaitu sebagai berikut:
1. Menerapkan konsep turunan ke dalam deret Taylor untuk menyelesaikan masalah nilai batas orde tiga.
2. Mengeksplorasi aspek pendidikan dari turunan dan deret Taylor bagi keterampilan berpikir tingkat tinggi siswa SMA.
E. Manfaat Penulisan
Manfaat dari penulisan tugas akhir ini adalah sebagai berikut:
1. Dari sisi keilmuan, penerapan konsep turunan ke dalam deret Taylor untuk menyelesaikan masalah nilai batas orde tiga dapat dipelajari penggunaannya untuk menyelesaikan masalah-masalah di bidang lain. 2. Dari sisi kependidikan, hasil eksplorasi bisa digunakan untuk
mengembangkan keterampilan berpikir tingkat tinggi siswa SMA.
F. Metode Penelitian
Metode yang digunakan penulis dalam penyusunan tugas akhir yaitu studi pustaka, yaitu dengan mempelajari buku dan/atau jurnal yang
membahas tentang deret Taylor dan masalah nilai batas, serta buku-buku SMA yang memuat materi turunan fungsi.
G. Kebaruan Penelitian
Kebaruan penelitian ini yaitu mengimplementasikan hasil dan pembahasan pada bab ketiga dalam pembelajaran di SMA untuk mengolah keterampilan berpikir tingkat tinggi siswa.
H. Sistematika Penulisan
Tesis ini disusun dalam lima bab utama yang sistematika sebagai berikut. 1. BAB I PENDAHULUAN
Bab ini memuat latar belakang penelitian, tujuan penulisan, manfaat penulisan, tinjauan pustaka, kebaruan penelitian, dan sistematika penulisan. Dalam bab ini, dijelaskan bagaimana masalah sehari-hari dimodelkan ke dalam model matematika yang bisa diselesaikan untuk mempelajari perilaku suatu fenomena, lebih lanjut lagi untuk memprediksi bagaimana perilaku fenomena tersebut di masa yang akan datang. Model matematika ini yang biasanya berupa fungsi atau persamaan akan diselesaikan menurut aturan-aturan matematis untuk mencapai suatu kesimpulan. Penyelesaian model matematika bisa dengan cara analitis maupun numeris. Dalam tesis ini, model matematika yang dibahas yaitu masalah nilai batas, dengan penyelesaian melalui deret Tayor. Tesis ini juga akan membahas eksplorasi aspek pendidikan deret Taylor untuk mengolah keterampilan berpikir tingkat tinggi siswa SMA. 2. BAB II LANDASAN TEORI
Bab ini memuat dasar-dasar teori yang berkaitan dengan pembahasan pada bab selanjutnya. Bab ini mencakup teori tentang deret pangkat, konvergensi dari deret pangkat, serta deret Taylor dan deret Maclaurin. Juga terdapat landasan teori untuk aspek pendidikan yaitu teori tentang keterampilan berpikir tingkat tinggi.
3. BAB III. HASIL PENELITIAN DAN PEMBAHASAN
Bab ini memuat hasil penelitian tentang solusi deret Taylor untuk masalah nilai batas orde tiga. Selain itu terdapat juga contoh masalah yang menggunakan deret Taylor.
4. BAB IV. ASPEK KEPENDIDIKAN
Bagian pertama bab ini mengeksplorasi aspek pendidikan dari deret Taylor yang bisa diterapkan untuk mengolah keterampilan berpikir tingkat tinggi dari siswa SMA. Deret Taylor dari suatu fungsi berhubungan erat dengan turunan-turunan dari fungsi bersangkutan. Konsep turunan fungsi merupakan salah satu pokok bahasan di SMA.
Satu hal yang perlu diperhatikan dalam proses pembelajaran yaitu keterampilan berpikir tingkat tinggi dari siswa. Keterampilan berpikir tingkat tinggi mencakup tiga aspek yaitu analisis, evaluasi, dan mencipta. Bagian pertama bab ini mengkaji bagaimana ketiga aspek tersebut bisa dicapai selama mempelajari deret Taylor. Siswa akan melakukan analisis tentang deret Taylor berkaitan dengan akurasi dari deret Taylor. Selanjutnya siswa akan mengevaluasi apakah deret Taylor yang diperoleh sungguh-sungguh mendekati fungsi yang dituju. Hasil dari proses ini yaitu siswa bisa menciptakan suatu fungsi hampiran dalam bentuk deret Taylor yang menghampiri fungsi asli. Hasil pendekatan inilah yang kemudian bisa digunakan untuk menyelesaikan masalah-masalah nilai batas untuk orde berapapun.
Bagian kedua memuat refleksi dari penulis selama berkuliah di Program Studi S2 Pendidikan Matematika USD, terutama selama penyusunan tesis yang sampai beberapakali mengalami perubahan topik dan judul.
5. BAB V. PENUTUP
Bab terakhir merangkum apa saja yang telah dibahas pada bab-bab sebelumnya, khususnya bab III dan bab IV. Ada juga saran yang dikemukakan penulis bagi para pembaca.
8
BAB II
LANDASAN TEORI
Dalam bab ini, terdapat subbab-subbab yang merupakan landasan teori yang mendasari pembahasan pada bab selanjutnya. Bagian pertama membahas tentang deret pangkat, bagian kedua tentang deret Taylor dan deret Maclaurin (kasus khusus dari deret Taylor), dan bagian ketiga memuat teorema-teorema yang sempat disebutkan pada bagian pertama dan kedua, tetapi tidak dibahas lebih mendalam.
A. Deret Pangkat
Pada bagian ini akan dibahas tentang deret pangkat dan konvergensinya. Deret pangkat yaitu deret yang berbentuk
∑
(2.1)
dengan merupakan variabel dan melambangkan koefisien suku ke- dari deret tersebut. Deret pangkat dapat diuji apakah konvergen atau divergen. Deret pangkat bisa konvergen untuk beberapa nilai dan divergen untuk nilai lainnya.
Konvergensi dari suatu deret didefinisikan sebagai berikut.
Definisi 2.1
Diberikan deret tak berhingga ∑ , misalkan menotasikan jumlahan parsial deret tersebut, yaitu
∑
Jika barisan * + konvergen dan ada dan merupakan bilangan real, maka deret ∑ disebut konvergen dan ditulis
atau
∑
Dalam hal ini, disebut jumlahan dari deret. Jika barisan * + divergen, maka deret yang bersangkutan juga divergen.
(2.2)
Dengan demikian, jumlahan dari suatu deret merupakan limit dari barisan jumlahan parsialnya. Atau bisa ditulis
∑
∑
Sebagai contoh sederhana, tinjau kembali deret geometri yang berbentuk
∑
Jika , maka yang hasilnya menuju ketika menuju . Karena tidak ada, maka dikatakan bahwa deret geometri dalam kasus ini divergen.
Jika , maka
dan
Dengan mengurangkan kedua ruas, diperoleh
( ) ( )
( )
Sedangkan bisa dicari bahwa jika , ketika , sehingga
( )
Jadi, ketika | | , deret geometri akan konvergen dan jumlahannya adalah . Sedangkan jika atau , bisa dibuktikan bahwa * + divergen sehingga tidak ada. Dengan demikian deret geometri menjadi divergen untuk kasus ini.
Meninjau kembali deret pangkat pada persamaan (1), misalkan untuk semua , deret pangkat ini menjadi deret geometri yang berbentuk
∑
(2.3)
Seperti pada contoh deret geometri, deret (2.3) akan konvergen ketika dan divergen ketika | | .
Lebih umum, deret yang berbentuk
∑ ( )
( ) ( )
disebut deret pangkat di ( ) atau deret pangkat yang berpusat pada atau deret pangkat di sekitar .
Selanjutnya untuk mengetahui nilai yang mana yang membuat deret konvergen, bisa digunakan berbagai cara, salah satunya dengan tes rasio. Berkaitan dengan konvergensi dari deret pangkat, terdapat teorema yang mengemukakan tentang hal ini.
Teorema 1
Untuk suatu deret pangkat ∑ ( ) , hanya terdapat tiga kemungkinan:
1. Deret konvergen hanya ketika . 2. Deret konvergen untuk semua .
3. Terdapat bilangan positif sedemikian hingga deret konvergen ketika | | dan divergen ketika | | .
Lambang pada kasus ketiga disebut radius konvergensi dari deret pangkat. Sering juga dikatakan untuk kasus pertama dan untuk kasus kedua. Sedangkan selang konvergensi dari suatu deret pangkat adalah selang yang memuat semua nilai yang membuat deret konvergen. Pada kasus pertama, selang konvergensi hanya memuat satu titik yakni . Pada kasus kedua, selang konvergensinya adalah ( ). Sedangkan pada kasus ketiga, perhatikan bahwa | | dapat juga ditulis sebagai . Ketika merupakan titik ujung dari selang, yakni , deret bisa konvergen pada satu titik ujung atau keduanya, atau bisa juga divergen pada kedua titik ujung. Dengan demikian, terdapat empat kemungkinan untuk selang konvergensi pada kasus ketiga, yaitu
( ) ( - , ) , - Setelah membahas konvergensi dari deret pangkat, selanjutnya akan dibahas bagaimana menurunkan dan mengintegralkan deret pangkat.
Jumlahan dari deret pangkat merupakan sebuah fungsi ( ) yaitu ( ) ( ) ( ) ( )
∑ ( )
(2.5)
yang domainnya merupakan selang konvergensi dari deret pangkat. Teorema berikut mengatakan bahwa penurunan dan pengintegralan deret pangkat dapat dilakukan dengan menurunkan atau mengintegralkan masing-masing suku pada deret pangkat seperti halnya pada polinomial. Hal ini disebut penurunan dan pengintegralan suku demi suku.
Teorema 2
Jika suatu deret pangkat ∑ ( ) memiliki radius konvergensi , maka fungsi yang didefinisikan dengan
( ) ( ) ( ) ∑ ( )
dapat diturunkan (dan karena itu fungsi kontinu) pada selang ( ) dan bahwa
(i) ( ) ( ) ( ) ∑( ) (ii) ∫ ( ) ( ) ( ) ( ) ∑ ( )
Radius konvergensi deret pangkat pada persamaan (i) dan (ii) adalah . (2.6)
Dengan catatan, persamaan (i) dan (ii) pada teorema di atas bisa juga ditulis (iii) [∑ ( ) ] ∑ , ( ) (iv) ∫ [∑ ( ) ] ∑ ∫ ( )
Juga walaupun Teorema 2 mengatakan bahwa radius konvergensi deret tetap sama ketika deret pangkat diturunkan atau diintegralkan, bukan berarti selang konvergensinya juga tetap sama. Hal ini bisa terjadi ketika deret awal konvergen pada titik ujung, tetapi setelah diturunkan deret menjadi divergen di titik tersebut.
B. Deret Taylor dan Deret Maclaurin
Sub-bab ini akan membahas mengenai deret Taylor dan deret Maclaurin. Misalkan sembarang fungsi yang bisa dinyatakan sebagai deret pangkat ( ) ( ) ( ) ( ) ( )
dimana | | . (2.7)
Akan dicari koefisien dinyatakan dalam . Perhatikan bahwa jika , maka semua suku kecuali suku pertama pada persamaan (2.7) akan menjadi 0, sehingga
Berdasarkan Teorema 2, turunan dari persamaan (2.7) adalah
( ) ( ) ( ) ( ) (2.8) Substitusi pada persamaan (2.8) diperoleh
( )
Selanjutnya dengan menurunkan kedua sisi pada persamaan (2.8), diperoleh
( ) ( ) ( ) (2.9) Substitusi lagi ke persamaan (2.9) diperoleh
( )
Proses ini dilakukan sekali lagi dengan menurunkan persamaan (2.9), diperoleh
( ) ( ) ( ) (10) Substitusi ke persamaan (2.10) diperoleh
( )
Bisa dilihat polanya, jika persamaannya diturunkan terus kemudian substitusi , akan diperoleh
( )( )
sehingga koefisien ke- yakni bisa diperoleh dengan menyelesaikan persamaan tersebut, yaitu
( )( )
Bentuk ini tetap berlaku untuk , mengingat dan ( ) . Hal ini membuktikan teorema berikut.
Teorema 3
Jika dapat dinyatakan dalam deret pangkat dengan perluasan di sekitar , yaitu jika
( ) ∑ ( )
| |
( )( )
(2.11)
Dengan substitusi kembali ke deret semula, terlihat bahwa jika dapat dinyatakan dalam deret pangkat dengan perluasan di sekitar maka
bentuknya akan menjadi
( ) ∑ ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (2.12) Deret pada persamaan 6 ini disebut deret Taylor dari fungsi di sekitar . Untuk kasus khusus , deret Taylor tersebut menjadi
( ) ∑ ( )( ) ( ) ( ) ( ) (2.13) Kasus khusus ini diberi nama Deret Maclaurin.
Perlu diingat bahwa jika dapat dinyatakan dalam deret pangkat di sekitar , maka nilai fungsi akan sama dengan jumlah dari deret Taylornya. Contoh 1
Tentukan Deret Maclaurin dari fungsi ( ) dan radius kovergensinya.
Penyelesaian
Jika ( ) , maka ( )( ) sehingga ( )( ) untuk setiap . Diperoleh deret Taylor untuk di sekitar 0 (dengan kata lain deret Maclaurin) yaitu
∑ ( )( )
∑
Untuk mencari radius konvergensinya, misalkan . Maka | | | ( ) | | |
Dengan uji rasio, deret ini konvergen untuk semua maka radius konvergensinya yaitu .
Kesimpulan yang bisa diambil dari Teorema 1 dan Contoh 1 yaitu jika bisa dinyatakan dalam deret pangkat di sekitar 0, maka
∑
Selanjutnya akan dilihat apakah benar-benar bisa dinyatakan dalam deret pangkat.
Ada baiknya untuk mencari tahu terlebih dahulu dalam keadaan yang bagaimana suatu fungsi akan bernilai sama dengan jumlahan deret Taylornya. Dengan kata lain, jika bisa diturunkan tak hingga banyak kali, akan dilihat kapan
( ) ∑
( )( )
( )
berlaku. Untuk deret konvergen, ( ) merupakan limit dari barisan jumlahan parsialnya. Atau dalam kasus deret Taylor, jumlahan parsialnya yaitu
( ) ∑ ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) Perhatikan bahwa merupakan polinoial berderajat yang disebut dengan polinomial Taylor derajat ke- dari di sekitar . Sebagai contoh, untuk fungsi eksponensial ( ) , hasil pada Contoh 1 menunjukkan polinomial Taylor di sekitar 0 (atau polinomial Maclaurin) dengan , , dan yakni
( ) ( )
( )
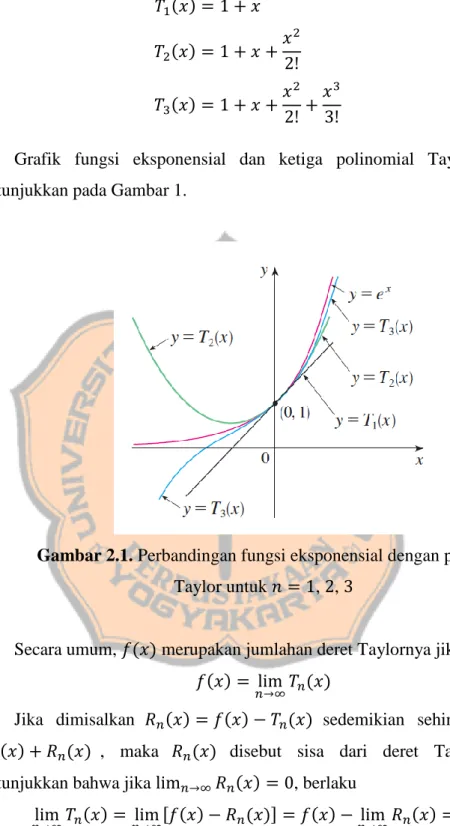
Grafik fungsi eksponensial dan ketiga polinomial Taylor di atas ditunjukkan pada Gambar 1.
Gambar 2.1. Perbandingan fungsi eksponensial dengan polinomial Taylor untuk , ,
Secara umum, ( ) merupakan jumlahan deret Taylornya jika ( )
( )
Jika dimisalkan ( ) ( ) ( ) sedemikian sehingga ( ) ( ) ( ) , maka ( ) disebut sisa dari deret Taylor. Dapat ditunjukkan bahwa jika ( ) , berlaku
( ) , ( ) ( )- ( ) ( ) ( ) Dengan demikian, teorema berikut terbukti.
Teorema 4
Jika ( ) ( ) ( ) , dengan ( ) adalah polinomial Taylor derajat ke- dari di sekitar dan ( ) untuk | | , maka sama dengan jumlahan dari deret Taylor pada interval | |
(2.14) Untuk menunjukkan bahwa ( ) untuk fungsi tertentu, digunakan teorema berikut.
Teorema 5. Ketaksamaan Taylor
Jika | ( )( )| untuk | | , maka sisa ( ) dari deret Taylor memenuhi ketaksamaan
| ( )|
( ) | | untuk | |
(2.15)
Untuk melihat bahwa teorema ini berlaku untuk , asumsikan | ( )| . Secara khusus, ( ) , sehingga untuk diperoleh
∫ ( ) ∫
Anti turunan dari adalah , sehingga dengan teorema fundamental kalkulus diperoleh ( ) ( ) ( ) atau ( ) ( ) ( ) sehingga ∫ ( ) ∫ , ( ) ( )- ( ) ( ) ( )( ) ( ) ( ) ( ) ( )( ) ( ) Tetapi karena ( ) ( ) ( ) ( ) ( ) ( )( ) , maka
( )
Menggunakan argumen serupa, dengan ( ) , bisa dicek bahwa ( ) ( )
sehingga
| ( )| | |
Meskipun asumsi awalnya , perhitungan yang sama akan menunjukkan bahwa pertidaksamaan ini juga berlaku untuk .
Hal ini membuktikan ketaksamaan Taylor untuk kasus ketika . Hasil untuk sembarang dapat diperoleh dengan cara yang sama, dengan mengintegral kali.
Dalam menerapkan Teorema 2 dan 3, lebih sering digunakan fakta berikut.
untuk setiap bilangan real (2.16) Fakta ini berlaku karena berdasarkan Contoh 1, deret ∑ konvergen untuk semua sehingga suku ke- deretnya mendekati 0.
Contoh 2
Buktikan bahwa sama dengan jumlahan dari deret Maclaurinnya. Penyelesaian
Jika ( ) , maka ( )( ) untuk setiap . Jika sebarang bilangan positif dan | | , maka | ( )( )| . Ketaksamaan Taylor dengan dan mengatakan bahwa
| ( )|
( ) | | untuk | |
Perhatikan bahwa konstata berlaku untuk setiap nilai . Dari persamaan (2.10),
( ) | | | | ( ) ( ) | | | | ( )
Berdasarkan teorema apit (Squeeze Theorem), karena | ( )| maka ( ) untuk semua . Dengan Teorema 2, sama dengan jumlahan deret Maclaurinnya, yaitu
∑
untuk semua (2.17)
Secara khusus, substitusi ke persamaan (11), diperoleh nilai untuk sebagai penjumlahan dari deret tak berhingga yang berbentuk
∑ (2.18) Contoh 3
Tentukan deret Taylor untuk ( ) di sekitar . Penyelesaian
Diketahui ( )( ) , sehingga substitusi ke persamaan (2.6) menghasilkan ∑ ( )( ) ( ) ∑ ( )
Bisa diperiksa bahwa seperti Contoh 1, radius konvergensinya yaitu . Di Contoh 2 telah diperiksa bahwa ( ) sehingga diperoleh ∑ ( ) untuk semua (2.19) Dari Contoh 2 dan 3, diperoleh dua deret pangkat untuk , yaitu deret Maclaurin pada persamaan (2.11) dan deret Taylor pada persamaan (2.13).
Deret pertama lebih baik digunakan jika yang diamati yaitu ketika nilai yang dekat dengan 0, sementara deret kedua lebih baik digunakan untuk nilai yang dekat dengan 2.
C. Teorema-Teorema Pendukung
Pada bagian ini akan dipaparkan beberapa teorema yang sempat disebutkan pada bagian sebelumnya.
1. Teorema Apit
Jika ( ) ( ) ( ) ketika dekat dengan (kecuali mungkin pada ) dan ( ) ( ) maka ( ) 2. Teorema Fundamental Kalkulus
Misalkan kontinu pada selang , -. 1. Jika ( ) ∫ ( ) , maka ( ) ( )
2. ∫ ( ) ( ) ( ), dengan sebarang anti turunan dari , yaitu .
Bagian 1 bisa ditulis dengan
∫ ( ) ( )
yang sekaligus mengatakan bahwa jika punya integral dan integralnya bisa diturunkan, maka hasilnya akan kembali lagi ke fungsi awal yaitu . Dan karena ( ) ( ), bagian 2 bisa juga ditulis dengan
∫ ( ) ( ) ( )
yang sekaligus mengatakan jika terdapat suatu fungsi yang diturunkan kemudian diintegralkan kembali, maka hasilnya adalah fungsi itu
sendiri, tetapi dalam bentuk ( ) ( ). Dengan menyatukan keduanya, bagian pertama bersama dengan bagian kedua menegaskan bahwa penurunan dan pengintegralan merupakan proses yang berkebalikan.
D. Keterampilan Berpikir Tingkat Tinggi
Salah satu keterampilan berpikir adalah berpikir tingkat tinggi (higher order thinking) atau HOT. Kemampuan berpikir tingkat tinggi merupakan suatu kemampuan berpikir yang tidak hanya membutuhkan kemampuan mengingat saja, namun membutuhkan kemampuan lain yang lebih tinggi, seperti kemampuan berpikir kreatif dan kritis. Berpikir Tingkat Tinggi terjadi ketika seseorang mengambil informasi baru dan informasi yang tersimpan dalam memori dan saling terhubungkan atau menata kembali dan memperluas informasi ini untuk mencapai tujuan atau menemukan jawaban yang mungkin dalam situasi membingungkan. Tugas guru selanjutnya adalah bagaimana mengajarkan keterampilan berpikir secara eksplisit dan memadukannya dengan materi pembelajaran khususnya mata pelajaran matematika yang dapat membantu para siswa untuk mengembangkan kemapuan berpikir tingkat tingginya atau dengan kata lain guru harus bisa mengintegrasikan level berpikir ini dalam proses belajar dan evaluasi.
Taksonomi Bloom dianggap merupakan dasar bagi berpikir tingkat tinggi. Bloom membagi kemampuan dalam ranah kognitif menjadi enam aspek. Tiga aspek diantaranya menjadi bagian dari kemampuan berpikir tingkat tinggi atau higher-Level thinking. Ketiga aspek itu adalah aspek analisa (C4), aspek evaluasi (C5) dan aspek mencipta (C6). Sedang tiga aspek lain dalam ranah yang sama, yaitu aspek mengingat (C1), aspek memahami (C2), dan aspek aplikasi (C3), masuk dalam bagian intilektual berpikir tingkat rendah atau lower order thinking (LOT).
Stein dan Lane (dalam Thomson 2008) mendefinisikan berpikir tingkat tinggi adalah menggunakan pemikiran yang kompleks, non algorithmic untuk menyelesaikan suatu tugas, ada yang tidak dapat diprediksi, menggunakan pendekatan yang berbeda dengan tugas yang telah ada dan berbeda dengan
contoh. Senk, et al (dalam Thomson 2008) menjelaskan karakteristik berpikir tingkat tinggi adalah kemampuan untuk menyelesaikan tugas-tugas dimana tidak ada algoritma yang telah diajarkan, yang membutuhkan justifikasi atau penjelasan dan mungkin mempunyai lebih dari satu solusi yang mungkin (Lewy, 2009). Dari definisi-definisi diatas disimpulkan bahwa pengukuran kemampuan berpikir tingkat tinggi dalam penelitian ini mempunyai indikator non algorithmic, cenderung kompleks, memiliki solusi yang mungkin lebih dari satu (open ended approach), membutuhkan usaha untuk menemukan struktur dalam ketidakteraturan.
Menurut Krathworl (dalam Lewy, 2009) dalam A revision of Bloom’s Taxonomy: an overview – theory Into Practice, indikator untuk mengukur kemampuan berpikir tingkat tinggi meliputi:
1. Menganalisis
a. Menganalisis informasi yang masuk dan membagi-bagi atau menstrukturkan informasi kedalam bagian yang lebih kecil untuk mengenali pola atau hubungannya.
b. Mampu mengenali serta membedakan faktor penyebab dan akibat dari sebuah skenario yang rumit.
c. Mengidentifikasi/merumuskan pertanyaan. 2. Mengevaluasi
a. Memberikan penilaian terhadap solusi, gagasan, dan metodologi dengan menggunakan kriteria yang cocok atau standar yang ada untuk memastikan nilai efektivitas atau manfaatnya.
b. Membuat hipotesis, mengkritik dan melakukan pengujian.
c. Menerima atau menolak suatu pernyataan berdasarkan kriteria yang telah ditetapkan.
3. Mencipta
a. Membuat generalisasi suatu ide atau cara pandang terhadap sesuatu. b. Merancang suatu cara untuk menyelesaikan masalah.
c. Mengorganisasikan unsur-unsur atau bagian-bagian menjadi struktur baru yang belum pernah ada sebelumnya.
Hasil penelitian Thompson (dalam Hobri, 2015:6-7) tentang interpretasi guru di USA menunjukkan bahwa guru-guru Matematika mendefinisikan HOT sebagai discoverinng pattern, solving word problems, interpreting information, complex information, conceptual understanding, critical thinking or analyzing. Dengan demikian, HOT dapat dipandang sebagai: (1) menemukan pola/rumus, bukan langsung diberikan dan digunakan, (2) menyelesaikan pemecahan masalah terutama pada soal cerita, (3) menginterpretasi informasi dengan bahasanya sendiri atau menggunakan bahasa/kalimat lain, (3) memahami informasi yang kompleks, (4) pemahaman konseptual, bukan sekedar prosedural, (5) berfikir kritis, dapat menganalisis secara detail unsur-unsur yang harus dikaji.
24
BAB III
PENYELESAIAN MASALAH NILAI BATAS
Bab ini dibagi dalam dua subbab yang akan membahas bagaimana solusi deret Taylor untuk masalah nilai batas orde tiga beserta contohnya.
A. Deret Taylor untuk Masalah Nilai Batas Orde Tiga
Pada sub-bab ini, akan dicari solusi deret Taylor untuk masalah nilai batas.
Perhatikan persamaan diferensial biasa orde tiga berikut.
( ) ( ) ( ) ( ) , - (3.1) dengan , , dan adalah konstan.
Dengan menurunkan persamaan (1) kali terhadap , diperoleh
, ( )- (3.2)
kemudian dengan mengatur pada persamaan (2), bisa diperoleh nilai dari ( )( ).
Asumsikan
( ) (3.3)
dengan suatu konstanta tidak diketahui. Solusi deret Taylornya adalah ( ) ∑
( )( )( )
(3.4)
Dengan syarat batas ( ) , dari persamaan (3.4), dapat ditentukan, dan diperoleh solusi perkiraan. Solusi deret konvergen ke solusi eksak ketika menuju tak hingga. Solusi deret dengan orde lebih tinggi memperkirakan akurasi lebih tinggi dari solusi perkiraan, sehingga akurasi berapapun dapat diperoleh.
Untuk menunjukkan proses penyelesaian, perhatikan contoh sederhana
(3.5)
( ) (3.6) Menurunkan persamaan (3.5) sebanyak dua kali, diperoleh
(3.7)
(3.8)
Dengan menetapkan pada persamaan (3.5), (3.7), dan (3.8), diperoleh
( ) ( ) (3.9)
( ) ( ) ( ) (3.10) ( ) ( ) ( ) ( ) (3.11) Solusi deret Taylor orde ketiganya yaitu
( ) ( ) ( )
( ) ( )
(3.12)
Penyelesaian bisa diteruskan untuk memperoleh solusi perkiraan orde , yaitu
( ) ( ) (3.13)
Ketika menuju tak hingga, diperoleh
( ) (3.14)
yang merupakan solusi eksak.
Solusi deret Taylor konvergen ke solusi eksak, dimana solusi orde yang lebih tinggi memperkirakan akurasi yang lebih tinggi, sehingga dapat diperoleh solusi perkiraan untuk sembarang akurasi.
B. Contoh Masalah
Perhatikan persamaan berikut.
( ) ( ) ( ) (3.15) Bentuk tersebut diberikan oleh Abdelrahim dalam artikelnya Maret 2019, dan hasil akurat diperoleh dengan metode blok hibrid satu langkah.
Menurunkan persamaan (3.15) terhadap diperoleh
( ) (3.17)
( ) (3.18)
( ) ( ) (3.19)
Asumsikan
( ) (3.20)
dimana konstanta tak diketahui yang nilainya akan dicari kemudian. Dengan mengatur pada persamaan (3.15)-(3.19), dengan syarat awal ( ) , ( ) , dan ( ) , diperoleh
( ) (3.21)
( )( ) (3.22)
( )( ) (3.23)
( )( ) (3.24)
( )( ) (3.25)
Solusi deret Taylor dapat dituliskan sebagai berikut
( ) ( ) ( ) ( ) ( ) ( )( ) ( )( ) ( )( ) ( )( ) ( ) (3.26) Menggunakan syarat batas ( ) , diperoleh
( )| { ( )
}|
( ) (3.27) Dari persamaan tersebut, diperoleh nilai , yaitu
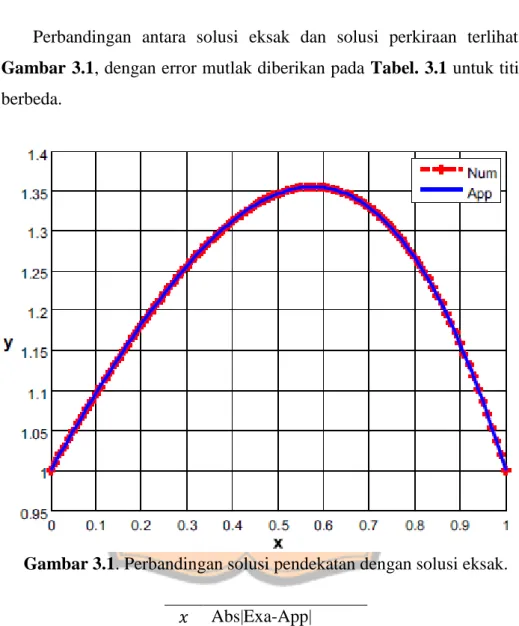
Solusi perkiraannya menjadi ( ) (3.29) Perbandingan antara solusi eksak dan solusi perkiraan terlihat pada Gambar 3.1, dengan error mutlak diberikan pada Tabel. 3.1 untuk titik-titik berbeda.
Gambar 3.1. Perbandingan solusi pendekatan dengan solusi eksak. Abs|Exa-App| 0 0.000000000000002 0.1 0.001549000715525 0.2 0.002135816866002 0.3 0.001973919783068 0.4 0.001284477260845 0.5 0.000296559425368 0.6 0.000750773107341 0.7 0.001603524000466 0.8 0.001983735685903 0.9 0.001574895753898 1 0.000000000000000
Seperti pada Gambar 3.1, solusi numeris dan solusi perkiraan mencapai maksimum pada dengan error relatif , yang menunjukkan bahwa metode ini terpercaya dan efektif, dan akurasinya bisa ditingkatkan lagi jika solusi deret dengan orde lebih tinggi diselesaikan.
Untuk memperjelas keuntungan metode diatas, akan dibandingkan dengan metode iterasi variasional. Algoritma dari iterasi tersebut dapat dituliskan dalam bentuk
∫ ( ) ( ( ) ) (3.30) Misalkan dugaan awal bentuknya
(3.31)
dengan konstata tidak diketahui. Dengan menggunakan rumus
∫ ( )
( )( ) (3.32)
diperoleh solusi pendekatan orde satu
∫ ( ) (( ) ) ( ) (3.33) Iterasi dapat dilanjutkan tanpa kesulitan, tetapi penghitungan menjadi lebih kompleks untuk solusi pendekatan dengan orde lebih tinggi. Jika iterasi dihentikan sebelum iterasi kedua, dapat ditentukan dari ( ) , yang menghasilkan
Jelas bahwa solusi pendekatan orde satu dengan cara ini memiliki akurasi yang lebih rendah.
29
BAB IV
ASPEK KEPENDIDIKAN MATERI DERET TAYLOR
Materi pada bab sebelumnya telah menjabarkan bagaimana memperoleh solusi deret Taylor untuk masalah nilai batas orde tiga dan juga contohnya. Pada bab ini akan dibahas mengenai aspek pendidikan yang bisa dikembangkan dari deret Taylor. Bab ini dibagi menjadi dua bagian yaitu bagian pertama yang memuat eksplorasi aspek pendidikan turunan dan deret Taylor
A. Deret Taylor untuk Mengolah Keterampilan Berpikir Tingkat Tinggi Deret Taylor berkaitan erat dengan turunan, karena deret Taylor memuat hampiran suatu fungsi yang nilainya merupakan penjumlahan dari tak hingga banyak suku-suku yang terdiri dari turunan-turunan fungsi yang bersangkutan. Dalam pembelajaran di SMA, pembahasan mengenai turunan fungsi dimulai dari gradien garis singgung.
Sesuai kurikulum 2013 yang menekankan pada pengalaman belajar siswa untuk berpikir kritis dan kreatif dalam mempelajari suatu konsep, siswa dituntut untuk menemukan dan mengembangkan konsep-konsep yang berkaitan dengan hal yang menjadi pokok bahasan. Langkah awal bagi siswa untuk mempelajari turunan yaitu dengan memahami bahwa dalam suatu grafik fungsi, turunan fungsi pada suatu titik merupakan gradien garis singgung kurva fungsi di titik terkait. Langkah selanjutnya yaitu memahami turunan sebagai limit fungsi. Kemudian siswa akan mempelajari bagaimana menentukan turunan dari bermacam-macam fungsi, sampai berlanjut pada aplikasi konsep turunan untuk masalah maksimum dan minimum, juga masalah sehari-hari lainnya.
Salah satu yang penting dibahas yaitu tentang turunan fungsi polinomial. Penurunan deret Taylor sendiri mirip dengan teknik penurunan fungsi polinomial, yaitu dengan menurunkan suku demi suku. Hal ini tentu bisa dikerjakan siswa SMA, jika para siswa bisa mengerjakan soal-soal tentang turunan fungsi polinomial.
Lebih lanjut lagi, jika diberi nilai batas, maka nilai dari fungsi hampiran bisa dicari. Hasil ini kemudian bisa dibandingkan dengan nilai dari fungsi yang asli. Pembelajaran ini bisa diawali dengan mengambil contoh-contoh sederhana seperti fungsi eksponensial sebagai fungsi asli yang akan dihampiri. Dalam praktek pembelajaran ini, bisa diteliti bahwa aspek-aspek keterampilan berpikir tingkat tinggi berperan selama proses memperoleh fungsi hampiran dengan deret Taylor. Aspek-aspek tersebut antara lain:
1. Menganalisis
Tahap analisis muncul ketika siswa memperoleh nilai hasil perhitungan dari fungsi hampiran misalnya dengan berbagai orde, kemudian membandingkannya dengan nilai dari fungsi yang asli. Dari sini siswa akan menganalisis bahwa setiap orde memiliki tingkat akurasi yang berbeda-beda, dimana semakin tinggi orde dari fungsi hampiran, maka akan semakin akurat nilai yang diperoleh, dengan kata lain semakin dekat nilainya dengan nilai dari fungsi aslinya.
2. Mengevaluasi
Dengan membandingkan hasil yang diperoleh masing-masing, para siswa bisa melihat, dalam hal ini mengevaluasi apakah deret yang mereka dapatkan benar-benar mendekati fungsi aslinya.
3. Mencipta
Dengan menemukan deret untuk menghampiri suatu fungsi, para siswa sudah mengembangkan atau menciptakan rumusan baru untuk menyelesaikan masalah, yang salah satunya jika dikaitkan dengan tesis ini, yaitu masalah nilai batas.
Melalui pemaparan di atas, nampak bahwa pembelajaran deret Taylor bisa mengolah keterampilan berpikir tingkat tinggi siswa, yakni mengasah kemampuan menganalisis, mengevaluasi, dan mencipta.
B. Refleksi
Sejak awal, pilihan untuk kuliah di Program Studi S2 Pendidikan matematika merupakan suatu tantangan tersendiri bagi saya. Melanjutkan
kuliah S2 hanya dalam kurun waktu sekitar 2 minggu setelah dinyatakan lulus dari program s1 termasuk salah satu hal yang membuat saya kepayahan. Mungkin bisa dikatakan juga kalau saat itu saya sebenarnya belum siap untuk langsung meneruskan kuliah, apalagi dengan situasi yang membuat saya 'pindah jalur', karena harus mempelajari ilmu pendidikan. Bermodalkan tekad untuk mengenali sekaligus mempelajari dunia pendidikan, saya menguatkan diri untuk melanjutkan pendidikan saya di Program Studi S2 Pendidikan Matematika ini.
Dengan tekad yang sama, saya mengambil mata kuliah pilihan yang berkaitan dengan pendidikan, juga memutuskan untuk menyusun tesis untuk bidang pendidikan. Ketika mulai menentukan topik penelitian di awal semester, saya mengalami banyak kendala. Hambatan yang paling besar yaitu untuk menentukan topik tesis berkaitan dengan pendidikan, sementara waktu itu saya tidak tahu apa-apa soal teori-teori pembelajaran, atau ilmu pendidikan secara umum. Mengatasi hambatan tersebut, saya berhasil menentukan topik untuk menyusun tesis. Sayangnya, karena kurang inisiatif untuk bertanya kepada dosen maupun teman-teman, topik yang saya ajukan kurang matang. Karenanya, saya mencari topik lain untuk diteliti. Tidak jauh berbeda dari saat mengerjakan topik yang pertama, saya masih kurang inisiatif untuk konsultasi, bahkan kepada dosen pembimbing saya waktu itu. Selama berbulan-bulan, proposal tesis saya tidak mengalami perkembangan yang signifikan karena memang jarang konsultasi. Ditambah lagi, mencari tempat untuk penelitian lapangan merupakan hambatan tersendiri bagi saya. Sebelumnya ketika praktek untuk tugas mata kuliah, saya memiliki rekan satu kelompok yang membuat hal-hal berkaitan dengan praktek menjadi tak berkendala. Terjadinya masalah yaitu ketika saya harus memikirkan sendiri segala hal yang berkaitan dengan penelitian, sementara saya belum pernah melakukan penelitian sendiri, dan masih merasa belum berpengalaman untuk bisa melakukan semuanya sendirian. Alhasil, sampai tahun 2018 berakhir, saya belum mendapat data apapun sebagai hasil penelitian.
Pada awal tahun 2019, saya akhirnya bisa melakukan penelitian lapangan, walaupun dipenuhi dengan macam-macam keterbatasan. Mulai dari perizinan ke sekolah yang seadanya. Saya akhirnya melakukan penelitian di SMA Lokon St. Nikolaus Tomohon, bukan di salah satu sekolah yang terletak di daerah Yogyakarta. Dengan HLT (Hypothetical Learning Trajectory) yang telah disusun sebelumnya, saya memulai penelitian awal di bulan Februari. Karena satu dan lain hal, siswa kelas X yang menjadi subjek penelitian harus mengalami perombakan kelas, jadi penelitian saya tertunda. Hal ini tentu saja menjadi hambatan, tetapi di lain pihak justru menjadi kesempatan untuk memperbaiki HLT dari hasil uji coba. Dari penelitian itu, saya merombak HLT awal, yang menjadi salah satu keterbatasan penelitian. HLT yang baru tidak dikonsultasikan ke dosen, jadi penelitian yang akhirnya terlaksana dilakukan berdasarkan HLT seadanya. Pun ketika penelitian, kelas uji coba dan kelas penelitian yang harusnya berselang beberapa waktu agar bisa dilakukan perbaikan HLT, terpaksa dilakukan dengan jeda satu jam istirahat, sehingga revisi HLT untuk kelas penelitian hanya punya waktu selama jam istirahat.
Penelitian lapangan sudah terlaksana, tinggal mewawancarai siswa untuk melengkapi data penelitian. Akan tetapi karena waktu itu sudah mulai banyak libur, sedangkan pertemuan dengan siswa sulit diatur, data wawancara yang penting menjadi tidak ada. Dengan dorongan dari dosen pembimbing, saya akhirnya mulai menganalisis data seadanya, walaupun dengan berat hati karena data tidak lengkap. Masalah lain muncul ketika data rekaman diskusi di kelas yang tersimpan di SD card hilang. Niat untuk meneruskan analisis menjadi semakin mengecil. Saya sempat berniat untuk menganti topik lagi menjadi topik yang sempat saya presentasikan dalam sebuah seminar, tapi saya sadar, dalam topik itu juga terdapat banyak kekurangan, sehingga saya tetap bertahan dengan untuk melanjutkan analisis pada penelitian lapangan yang saya lakukan.
Berbulan-bulan terlewatkan, saya masih belum bisa menyelesaikan analisis untuk bab keempat tesis saya, sampai akhirnya Pak Sudi
menghubungi saya dan menawarkan topik untuk dijadikan tesis. Mengikuti saran dan arahan Pak Sudi, saya akhirnya bisa menyusun tesis saya sampai sejauh ini. Saya sungguh berterima kasih karena Pak Sudi bersedia membatu saya menyelesaikan tesis. Secara garis besar penyusunan tesis ini memberikan pelajaran bagi saya untuk lebih berinisiatif untuk bertanya kalau kesulitan, tidak hanya diam saja dan akhirnya malah membuang-buang waktu.
34
BAB V PENUTUP
A. KESIMPULAN
Kesimpulan dari penelitian ini adalah sebagai berikut. 1. Bentuk umum dari deret Taylor yaitu
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Untuk kasus khusus , deret Taylor di atas menjadi
( ) ∑ ( )( ) ( ) ( ) ( )
dan disebut deret Maclaurin.
2. Solusi deret Taylor untuk persamaan diferensial biasa orde tiga berbentuk ( ) ( ) ( ) ( ) , - dengan , , dan adalah konstan yaitu
( ) ∑
( )( )( )
3. Solusi deret Taylor konvergen ke solusi eksak, dimana solusi orde yang lebih tinggi memberikan akurasi yang lebih tinggi.
4. Dibandingkan dengan metode iterasi variasional, untuk hasil dengan orde yang lebih tinggi, perhitungan dengan metode iterasi variasional menjadi lebih kompleks sehinggi solusi deret Taylor yang bisa dihitung sampai orde yang lebih tinggi akan memiliki akurasi yang lebih tinggi.
5. Materi deret Taylor bisa digunakan untuk mengolah keterampilan berpikir tingkat tinggi siswa SMA, yakni untuk menggali aspek-aspek berpikir tingkat tinggi, antara lain:
Menganalisis
Semakin tinggi orde deret Taylor, semakin tinggi akurasi. Mengevaluasi
Membandingkan fungsi hampiran dengan fungsi asli. Mencipta
Menggunakan hasil yang diperoleh untuk menyelesaikan masalah, salah satunya masalah nilai batas.
B. SARAN
Hal-hal yang bisa penulis kemukakan sebagai saran untuk penelitian lanjutan yaitu untuk membuat suatu rancangan pembelajaran agar siswa bisa memahami deret Taylor dan menggunakan deret Taylor untuk menghampiri nilai suatu fungsi. Rancangan ini bisa dalam bentuk Hypothetical Learning Trajectory (HLT) atau lintasan belajar, kemudian dikaji lebih dalam bagaimana pencapaian siswa dalam tiap-tiap aspek keterampilan berpikir tingkat tinggi.
36
DAFTAR PUSTAKA
Abdelrahim, R., 2019, Numerical Solution of Third Order Boundary Value Problems Using One-Step Hybrid Block Method, Ain Shams Engineering Journal, 10(1):179-83.
Arora, G., Kumar, R., & Kaur, H., 2018, A Novel Wavelet Based Hybrid Method for Finding the Solution of Higher Order Boundary Value Problems, Ain Shams Engineering Journal, 9(4):3015-31.
El-Kalla, I.L., El Mhlawy, A.M., & Botros, M., 2019, A Continuous Solution of Solving a Class of Nonlinear Two Point Boundari Value Problems, Ain Shams Engineering Journal, 10(1):211-6.
He, C.H., Shen, Y., Ji, F.Y., et al., 2019, Taylor Series Solution for Fractal Bratu-Type Equation Arising in Electrospinning Process, Fractals, DOI:
https://doi.org/10.1142/S0218348X20500115
He, J.H., 2020, Taylor Series Solution for a Third Order Boundary Value Problem Arising in Architectural Engineering, Ain Shams Engineering Journal, DOI:
https://doi.org/10.1016/j.asej.2020.01.016
He, J.H., Ji, F.Y., 2019, Taylor Series Solution for Lane-Emden Equation, Journal of Mathematical Chemistry, 57(8):1932-4.
Hobri, 2015, Mengintegrasikan Higher Order Thinking (HOT) Dalam Scientific Approach. Seminar Nasional Pendidikan, Jember.
Lewy. 2009, Pengembangan Soal untuk Mengukur Kemampuan Berpikir Tingkat Tinggi Pokok Bahasan Barisan dan Deret Bilangan di Kelas IX Akselerasi SMP Xaverius Maria palembang, Jurnal Pendidikan Matematika, volume 3.no.2, Desember 2009.
Lodhi, R.K., Mishra, H.K., 2018, Septic B-spline Method for Second Order Self-Adjoint Singularly Perturbed Boundary Value Problems, Ain Shams Engineering Journal, 9(4):2153-61.
Stewart, J., 2016, Calculus: Early Transcendentals, Eight Edition. Boston: Cengage Learning.
Thomas, G.B. Weir, M.D., & Hass, J., 2010, Thomas’ Calculus: Early Transcendentals, Twelfth Edition. Boston: Pearson.
Thomson, T., 2008, Mathematics Teachers’ Interpretation of Higher-Order Thinking in Bloom’s Taxonomy, International Electronic Journal of Mathematics Education, Volume 3, No. 2, July 2008.
Varberg, D., Purcell., E.J., & Rigdon, S.E., 2007, Kalkulus, Edisi Kesembilan Jilid I, diterjemahkan oleh: I Nyoman Susila, Ph.D., Jakarta: Erlangga