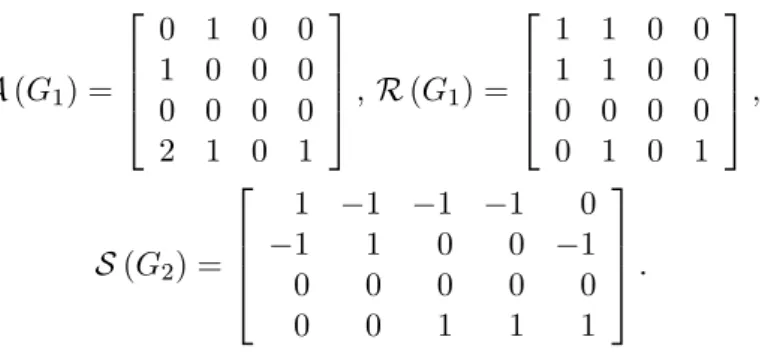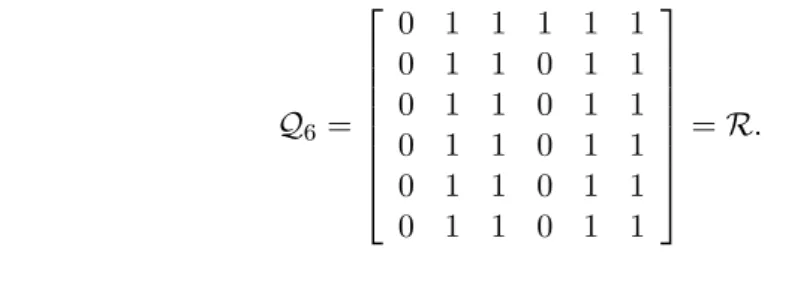MX 324 Pengantar Teori Graf
(Draft Versi Desember 2008 )Oleh:
Didit Budi Nugroho, M.Si.
DAFTAR GAMBAR ii
DAFTAR TABEL iii
KATA PENGANTAR iv
1 De…nisi dan Konsep Fundamental 1
1.1 De…nisi-de…nisi Dasar . . . 1
1.2 Operasi Graf . . . 5
1.3 Lintasan dan Lingkaran . . . 7
1.4 Lingkaran Hamilton dan Jalan Euler . . . 9
1.5 Pohon dan Hutan . . . 10
1.6 Pohon dan Hutan Rentangan . . . 12
1.7 Soal-soal untuk Bab 1 . . . 14
2 Pohon Rentangan Minimal 17 2.1 Pengantar . . . 17
2.2 Pohon Rentangan Minimal . . . 18
2.3 Soal-soal untuk Bab 2 . . . 22
3 Algoritma Pencarian 24 3.1 Pengantar . . . 24
3.2 Depth-First Search . . . 24
3.3 Breadth-First Search . . . 27
3.4 Masalah Lintasan Terpendek . . . 29
3.5 Soal-soal untuk Bab 3 . . . 31
4 Graf Berarah 33 4.1 Pengantar . . . 33
4.2 Jaringan dan Arus . . . 38
4.3 Teorema Max-Flow-Min-Cut . . . 40
4.4 Soal-soal untuk Bab 4 . . . 45
DAFTAR PUSTAKA 47
1.1 Graf dengan sisi ganda dan gelang. . . 1
1.2 Dua graf yang isomor…k. . . 5
1.3 Suatu lintasan P6 di graf G. . . 8
1.4 (a) Graf tidak terhubung G1; dan (b) graf terhubung G2. . . 9
1.5 (a) T1 bukan pohon; (b) T2 adalah pohon. . . 10
1.6 Pohon-pohon yang tidak isomor…k sampai dengan enam titik. . . 10
1.7 Subpohon T1 dan T2 yang diperoleh dari T dengan menghapus satu sisi x. 12 1.8 (a) Graf tangga; (b) pohon rentangan; (c) hutan rentangan. . . 13
2.1 Suatu graf terhubung berbobot dengan 6 titik dan 7 sisi. . . 17
2.2 Suatu graf terhubung berbobot dengan 9 titik dan 16 sisi. . . 19
3.1 Suatu graf tidak terhubung dengan 7 titik dan 6 sisi. . . 24
3.2 Suatu graf terhubung dengan 10 titik dan 11 sisi. . . 26
3.3 Suatu graf berbobot dengan 8 titik dan 15 sisi. . . 30
4.1 Graf berarah dengan 5 titik. . . 33
4.2 Suatu graf berarah tanpa sisi ganda dan loop. . . 35
4.3 Jaringan dengan sumber a dan target akhir z. . . 38
1.1 Pembentukan pohon rentangan dari graf dalam Gambar 1.8(a) menggu-nakan Algoritma Greedy. . . 14 2.1 Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2
menggunakan Algoritma Prim. . . 19 2.2 Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2
menggunakan Algoritma Kruskal. . . 21 3.1 Pembentukan pohon berakar (T; v1) dari graf dalam Gambar 3.2 berdasarkan
Algoritma Depth-First Search. . . 26 3.2 Pembentukan pohon berakar (T; v1) dari graf dalam Gambar 3.2 berdasarkan
Algoritma Breadth-First Search. . . 28 3.3 Pencarian lintasan terpendek dari titik u untuk graf dalam Gambar 3.3
berdasarkan Algoritma Lintasan Terpendek Dijkstra. . . 31
Naskah ini ditulis selama satu semester ketika penulis mengajar Pengantar Teori Graf di Program Studi Matematika dan Pendidikan Matematika, Universitas Kristen Satya Wacana, Salatiga, pada Semester I tahun 2008-2009. Catatan ini membentuk naskah dasar untuk kuliah MX 324 Pengantar Teori Graf.
Teori Graf adalah suatu bidang dari Matematika Diskrit yang mempelajari ben-tuk (dinamakan graf) yang terdiri dari suatu himpunan titik-titik yang dihubungkan oleh garis (dinamakan sisi). Teori Graf dan aplikasinya tidak hanya dijumpai dalam cabang-cabang matematika, tetapi juga dalam disiplin-disiplin ilmiah seperti teknik, ilmu komputer, riset operasi, dan manajemen sains.
Naskah ini difokuskan pada beberapa aplikasi dari teori graf dan menyajikan al-goritma-algoritma graf yang biasanya digunakan untuk menyelesaikan masalah dalam aplikasi. Keseluruhan dari naskah ini berkaitan dengan algoritma graf, seperti Algo-ritma Greedy untuk pencarian pohon, AlgoAlgo-ritma Prim dan Kruskal untuk pencarian pohon rentangan minimal, Algoritma Dijkstra untuk masalah lintasan terpendek, dan terakhir adalah Algoritma Ford-Fulkerson untuk mencari arus maksimum dari suatu jaringan.
Salatiga, Desember 2008 Didit B. Nugroho
De…nisi dan Konsep Fundamental
Tujuan Pembelajaran:
Mengetahui sifat-sifat dasar dari teori graf. Mengetahui operasi-operasi graf.
Mengetahui tentang jalan, trail, lintasan, lingkaran, pohon, dan hutan dalam suatu graf. Mengetahui tentang lingkaran Hamilton dan jalan Euler.
Mengaplikasikan Algoritma Greedy untuk mencari pohon rentangan dari suatu graf.
1.1
De…nisi-de…nisi Dasar
Di [7], de…nisi non-formal dari graf (graph) dalam kamus Webster (1913) diberikan seperti berikut ini.
De…nisi 1.1 Graf mempunyai dua pengertian:
1. Suatu kurva atau permukaan, letak (locus) dari suatu titik dimana koordinat-koordinatnya merupakan variabel-variabel dalam persamaan letak.
2. Suatu diagram yang melambangkan suatu sistem keterhubungan berdasarkan titik (spot), semua dapat saling dibedakan dan beberapa dihubungkan oleh garis sejenis.
De…nisi non-formal dari graf pada poin 2 adalah pengertian yang digunakan dalam naskah ini. Secara sederhana, suatu graf merupakan suatu koleksi titik-titik (vertices), bersama-sama dengan beberapa sisi (edges) yang menghubungkan beberapa titik terse-but.
Gambar 1.1: Graf dengan sisi ganda dan gelang.
Sebagai contoh, graf G dalam Gambar 1.1 mempunyai titik-titik v1; v2; v3; v4; v5,
sedangkan sisi-sisinya dinyatakan oleh e1 = fv1; v2g, e2 = fv2; v3g, e3 = fv3; v4g,
e4 = fv1; v4g, e5 = fv1; v4g, e6 = fv4; v5g, e7=fv5; v5g. Secara khusus, sembarang
sisi dapat dinyatakan sebagai 2-himpunan bagian dari himpunan semua titik; dengan kata lain, suatu himpunan bagian yang terdiri dari anggota (tidak perlu berbeda) dari himpunan semua titik. Secara formal, graf G pada himpunan V dan E dapat dide…nisikan seperti berikut ini.
De…nisi 1.2 (formal) Suatu graf G adalah pasangan himpunan V dan E, dituliskan G = (V; E), dimana V adalah suatu himpunan berhingga dan E adalah koleksi dari 2-himpunan bagian dari V .
Anggota-anggota V dikenal sebagai titik dan anggota-anggota dari E dikenal seba-gai sisi. Jadi, dalam contoh sebelumnya dipunyai V = V (G) = fv1; v2; v3; v4; v5g dan
E = E (G) = fe1; e2; e3; e4; e5; e6; e7g. Banyaknya titik dalam graf dinamakan order
dan dituliskan sebagai jV j, sedangkan banyaknya sisi dituliskan sebagai jEj. Suatu graf berorder 0 dinamakan graf kosong (empty graph), dan yang berorder 1 dinamakan graf trivial.
De…nisi 1.3 Graf G1= (V1; E1) adalah suatu subgraf dari G2 = (V2; E2) jika V1 V2
dan E1 E2.
Graf berikut ini:
mempunyai subgraf antara lain
Diperhatikan kembali graf G dalam Gambar 1.1. Sisi-sisi yang mempunyai titik-titik ujung sama, e4 dan e5 dinamakan sisi ganda (parallel edges atau multiple edges).
Jika suatu sisi menghubungkan titik yang sama, sisi tersebut dinamakan gelang (loop), seperti e7.
De…nisi 1.4 Suatu graf yang mempunyai sisi ganda dan atau gelang dinamakan multi-graf.
Suatu graf yang tidak mempunyai sisi ganda dan gelang disebut graf sederhana (simple graph).
De…nisi 1.6 Dua sisi, misalnya e1 dan e2, dikatakan bertetangga jika keduanya
mempunyai suatu titik ujung yang sama, misalnya z, artinya e1 = fu; zg dan e2 =
fv; zg.
De…nisi 1.7 Untuk sembarang sisi e = fx; yg, sisi e dikatakan bersisian (incidency) dengan titik x dan y. Bisa juga dikatakan bahwa titik x dan y bersisian dengan e.
Sebagai contoh, pada graf G dalam Gambar 1.1, v3 dan v2 bertetangga karena
dihubungkan oleh sisi e2, sedangkan v2 dan v4 tidak bertetangga karena tidak ada sisi
fv2; v4g. Sisi e2 bertetangga dengan sisi e3karena keduanya mempunyai titik v3sebagai
ujung yang sama. Jika semua titik pada graf G adalah bertetangga, maka G dinamakan graf lengkap. Suatu graf lengkap dengan n titik dituliskan sebagai Kn. Lima graf
lengkap pertama diberikan seperti berikut:
De…nisi 1.8 Diambil G = (V; E) adalah suatu multigraf dengan himpunan titik V = fv1, v2, :::, vng dan himpunan sisi E = fe1, e2, :::, epg. Matriks ketetanggaan
(adjacency matrix) dari G adalah suatu matriks A (G) = [aij] berukuran n n dimana
masukan-(i; j) diberikan oleh
aij = banyaknya sisi yang menghubungkan vi dan vj;
dan matriks kebersisian (incidence matrix) dari G adalah suatu matriks S (G) = [sij]
berukuran n p dimana masukan-(i; j) diberikan oleh sij =
1 jika vi bersisian dengan ej
0 jika vi tidak bersisian dengan ej
. Dicatat bahwa matriks A (G) adalah simetris, artinya At= A.
dapat dinyatakan oleh matriks ketetanggaan dan matriks kebersisian berturut-turut: A = 2 6 6 6 6 4 0 2 1 0 0 2 1 0 1 0 1 0 3 0 0 0 1 0 0 0 0 0 0 0 0 3 7 7 7 7 5, S = 2 6 6 6 6 4 1 1 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 3 7 7 7 7 5
De…nisi 1.9 Derajat (degree atau valency) dari suatu titik v, dituliskan (v), adalah banyaknya sisi yang bersisian dengan titik v.
Secara khusus, titik berderajat nol dikatakan terasing (isolated ) dan titik berder-ajat 1 dinamakan titik pendant. Dicatat bahwa dalam De…nisi 1.9 setiap gelang pada suatu titik berkontribusi 2 untuk (v). Sebagai contoh, pada graf dalam Gambar 1.1 dipunyai (v3) = 2, (v4) = 4, (v5) = 3, dan seterusnya.
Teorema 1.10 Jumlah dari semua derajat titik pada sembarang graf G = (V; E) adalah dua kali banyaknya sisi, artinya
X
v2V
(v) = 2 jEj dengan jEj menyatakan banyaknya sisi.
Bukti. Hasil secara langsung mengikuti seperti berikut ini. Jika kita menjumlahkan semua derajat titik dalam G, kita menghitung setiap sisi tepat dua kali: sekali dari setiap ujung-ujungnya.
Akibat 1.11 Jumlah dari semua derajat titik pada sembarang graf adalah bilangan bulat positif genap.
Bukti. Jelas.
Akibat 1.12 Banyaknya titik berderajat ganjil dalam suatu graf adalah genap.
Bukti. Diambil Vedan Vo yang berturut-turut menyatakan koleksi titik-titik
berdera-jat genap dan ganjil untuk graf G. Berdasarkan Teorema 1.10 diperoleh X
v2Ve
(v) +X
v2Vo
(v) = 2 jEj : Untuk setiap v 2 Ve, derajat (v) adalah genap. Akibatnya
X
v2Ve
(v) adalah genap. Karena (v) ganjil untuk setiap v 2 V0, maka jV0j haruslah genap.
Gambar 1.2: Dua graf yang isomor…k.
De…nisi 1.13 Dua graf G1 = (V1; E1) dan G2 = (V2; E2) dikatakan isomor…k,
di-tuliskan G1 ' G2, jika terdapat suatu fungsi bijektif (1-1 dan pada) : V1 ! V2
sedemikian sehingga untuk setiap u; v 2 V1 berlaku fu; vg 2 E1 jika dan hanya jika
f (u) ; (v)g 2 E2. Suatu fungsi yang demikian dinamakan suatu isomor…sma
(isomorphism).
Secara cepat, dua graf dalam Gambar 1.2 adalah isomor…k, dan suatu isomor…sma diberikan oleh
(a) = v2; (b) = v1; (c) = v3; (d) = v4: (1.1)
Ini bisa ditunjukkan seperti berikut. Diambil fungsi yang dide…nisikan oleh (1.1). Di G1 dipunyai himpunan sisi
E1 = ffa; bg ; fa; cg ; fa; dg ; fb; dg ; fc; dgg ;
sehingga menggunakan fungsi diperoleh sisi-sisi
f (a) ; (b)g = fv2; v1g ; f (a) ; (c)g = fv2; v3g ; f (a) ; (d)g = fv2; v4g ;
f (b) ; (d)g = fv1; v4g ; f (c) ; (d)g = fv3; v4g :
Karena gabungan dari semua sisi yang diperoleh melalui sama dengan himpunan sisi E2 di G2, maka disimpulkan bahwa fungsi yang dide…nisikan oleh (1.1) adalah
isomor…sma dari G1 ke G2.
1.2
Operasi Graf
De…nisi 1.14 Komplemen (complement) dari suatu graf sederhana G = (V; E) adalah graf sederhana G = V; E dimana sisi-sisi di E secara tepat adalah sisi-sisi yang tidak ada di G.
De…nisi 1.15 Diberikan graf-graf sederhana G1 = (V1; E1) dan G2 = (V2; E2) dimana
V2 V1.
1. Jumlahan kedua graf adalah G1+ G2 = (V1[ V2; E1[ E2[ E) dimana E adalah
himpunan sisi-sisi baru yang menghubungkan setiap titik di G1 dengan setiap titik
di G2.
2. Jika V2 V1, dide…nisikan suatu graf beda (di¤ erence graph) G1 G2= (V1; E3)
(graf sederhana) dimana E3 adalah himpunan sisi-sisi dari G1 yang tidak ada di
G2.
Contoh dari selisih dan jumlahan dua graf diberikan seperti berikut:
Terdapat beberapa operasi biner antara dua graf sederhana G1 = (V1; E1) dan
G2= (V2; E2) :
(i) Gabungan: G1[ G2 = (V1[ V2; E1[ V2) (graf sederhana).
(ii) Irisan: G1\ G2 = (V1\ V2; E1\ V2) (graf sederhana).
(iii) Jumlahan ring: G1 G2 adalah subgraf dari G1[ G2 dimana himpunan sisinya
E1 E2 = (E1 E2) [ (E2 E1)
dan himpunan titiknya terdiri dari setiap titik-titik ujung dari sisi-sisi di E1 E2.
dipunyai
Dicatat bahwa untuk suatu bilangan asli n dan sembarang graf G dipunyai nG = G [ G [ [ G
| {z }
nkali
.
1.3
Lintasan dan Lingkaran
Diambil G = (V; E) sebagai suatu graf dengan himpunan V = fv1; v2; :::g dan E =
fe1; e2; :::g.
De…nisi 1.16 Suatu jalan (walk) dalam graf G adalah suatu barisan bergantian (titik dan sisi) tak kosong berhingga
v0; e1; v1; :::; vk 1; ek; vk
sedemikian sehingga ei = fvi 1; vig 2 E, untuk setiap i = 1; :::; k. Secara khusus,
apabila graf G adalah sederhana, jalan dapat dinyatakan sebagai suatu barisan titik-titik
v0; v1; :::; vk 1; vk
sedemikian sehingga fvi 1; vig 2 E, untuk setiap i = 1; :::; k.
Dicatat bahwa suatu jalan bisa melalui sembarang titik atau sisi lebih dari satu kali. Jika v0 = vk, maka jalan dikatakan tertutup, jika tidak dikatakan terbuka. Untuk
graf dalam Gambar 1.1, barisan v3, e3, v4, e4, v1, e4, v4, e5, v1, e4, v4, e6, v5 adalah
jalan terbuka dan barisan v3, e2, v2, e1, v1, e5, v4, e4, v1, e5, v4, e3, v3 adalah jalan
tertutup.
De…nisi 1.17 Suatu jalan adalah trail jika semua sisi-sisinya berbeda.
Suatu trail adalah tertutup jika titik-titik ujungnya sama, jika tidak maka dikatakan terbuka. Sebagai contoh, pada graf dalam Gambar 1.1 jalan v2, e2, v3, e3, v4, e4, v1,
e5, v4, e6, v5 adalah suatu trail meskipun titik v4 muncul dua kali.
De…nisi 1.18 Suatu lintasan (path) adalah suatu trail dengan semua titiknya berbeda. De…nisi 1.19 Banyaknya sisi dalam lintasan dinamakan panjang lintasan.
Lintasan dengan panjang n dinotasikan dengan Pn. Suatu contoh untuk lintasan
Gambar 1.3: Suatu lintasan P6 di graf G.
De…nisi 1.20 Lingkaran (cycle) adalah suatu trail tertutup dengan semua titik-titik-nya, kecuali titik-titik ujung, berbeda.
Lingkaran dinyatakan oleh barisan berputar titik-titik seperti C = v0; v1; :::; vk; v0.
Panjang suatu lingkaran adalah banyaknya sisi atau titik. Lingkaran dengan panjang n dinotasikan dengan Cn. Tiga lingkaran pertama diberikan seperti berikut:
De…nisi 1.21 Jarak antara dua titik u dan v di graf G, dinotasikan dengan d (u; v), adalah panjang dari lintasan terpendek antara kedua titik tersebut.
De…nisi 1.22 Diameter dari graf G, dinotasikan diam(G), adalah lintasan terpan-jang antara sembarang dua titik di G.
Pada graf G dalam Gambar 1.3, jarak antara titik v1dan v5adalah 2 karena lintasan
terpendeknya v1; v4; v5 atau v1; v6; v5. Untuk diameter dari graf G yaitu diam (G) = 7
yang bisa diperoleh dari lintasan terpanjang v1; v4; v2; v3; v5; v6; v7; v8.
Berdasarkan bahasan di atas, sifat-sifat dari lintasan dan lingkaran:
1. dalam lintasan, derajat dari setiap titik adalah 2, kecuali untuk titik-titik ujung yang berderajat 1,
2. dalam lingkaran, derajat dari setiap titik adalah 2,
3. banyak sisi pada lintasan adalah kurang satu dari banyaknya titik, sedangkan banyak sisi pada lingkaran sama dengan banyak titik.
De…nisi 1.23 Dua titik u dan v dalam graf G dikatakan terhubung jika terdapat suatu lintasan dari u ke v.
Gambar 1.4: (a) Graf tidak terhubung G1; dan (b) graf terhubung G2.
Dalam Gambar 1.4, graf G1 adalah tidak terhubung karena terdapat dua titik
(mi-salnya v1 dan v7) yang tidak dihubungkan oleh suatu lintasan. Dalam kasus ini graf
G1 dikatakan mempunyai dua komponen, karena dapat dinyatakan
1. V = V1[ V2 dimana V1\ V2 = ? ; dan
2. E = E1[ E2 dimana E1\ E2 = ?;
untuk V1 = fv1; v2; v3; v4g dan V2 = fv5; v6; v7g.
1.4
Lingkaran Hamilton dan Jalan Euler
Pada suatu waktu, matematikawan Hamilton dan Euler pergi berlibur. Mereka me-ngunjungi negara dengan 7 kota (titik) yang dihubungkan oleh suatu sistem jalan (sisi) yang digambarkan oleh graf di bawah ini.
Hamilton hanya ingin mengunjungi setiap kota sekali dan kembali ke kota awal dia berangkat. Berbeda dengan Hamilton, Euler tertarik dalam hal melewati setiap jalan tepat sekali dan tidak memikirkan apakah akhir perjalanannya pada kota yang berbeda atau tidak dari kota awal dia berangkat.
De…nisi 1.25 Suatu lingkaran Hamilton dalam suatu graf G = (V; E) adalah suatu lingkaran yang memuat semua titik di V .
De…nisi 1.26 Suatu jalan Euler dalam suatu graf G = (V; E) adalah suatu jalan yang menggunakan setiap sisi di E tepat satu kali.
Bisa diperiksa bahwa graf di atas mempunyai lingkaran Hamilton, misalnya v1, v2,
Berikut ini diberikan teorema (tanpa bukti) untuk menentukan apakah suatu graf mempunyai lingkaran Hamilton atau jalan Euler.
Teorema 1.27 (Dirac 1952) Setiap graf G = (V; E) dengan titik n 3 dan (G) = min f (v) : v 2 V g n2 mempunyai lingkaran Hamilton.
Teorema 1.28 Suatu graf terhubung adalah Euler jika dan hanya jika setiap titik mempunyai derajat genap.
Akibat 1.29 Suatu graf terhubung adalah Euler jika dan hanya jika setiap titik mem-punyai derajat genap atau terdapat tepat dua titik berderajat ganjil.
1.5
Pohon dan Hutan
De…nisi 1.30 Suatu graf T = (V; E) dinamakan pohon jika memenuhi kondisi berikut: 1. T adalah terhubung; dan
2. T tidak mempunyai lingkaran.
Gambar 1.5: (a) T1 bukan pohon; (b) T2 adalah pohon.
Dalam Gambar 1.5, graf T1 bukan pohon karena terdapat lingkaran C3 = v3; v4; v5,
sedangkan T2 adalah pohon berdasarkan De…nisi 1.30. Lebih lanjut, pohon-pohon yang
tidak isomor…k sampai dengan enam titik diberikan dalam Gambar 1.6.
Dua sifat sederhana berikut ini diperoleh berdasarkan de…nisi yang sudah diberikan. Teorema 1.31 Jika graf T = (V; E) adalah pohon dengan minimal dua titik, maka untuk setiap pasang titik berbeda x; y 2 V terdapat lintasan tunggal dari x ke y. Bukti. Diandaikan terdapat dua lintasan berbeda dari x ke y:
x = v0; v1; v2; :::; vr= y, dan
x = u0; u1; u2; :::; us= y,
maka terdapat i 2 N sehingga
v0 = u0; v1 = u1; :::; vi = ui, tapi vi+16= ui+1:
Sekarang diperhatikan titik-titik vi+1, vi+2, ..., vr. Karena kedua lintasan berakhir di
y, maka terdapat nilai terkecil j 2 fi + 1, i + 2, ..., rg sedemikian sehingga vj = ul
untuk suatu l 2 fi + 1, i + 2, ..., sg.
Jadi dua lintasan tersebut memberikan suatu lingkaran vi; vi+1; :::; vj 1; ul; ul 1; :::; ui+1; vi
yang kontradiksi dengan hipotesis bahwa T adalah pohon.
Teorema 1.32 Jika T = (V; E) adalah suatu pohon dengan n titik, maka pohon mem-punyai n 1 sisi.
Bukti. Digunakan induksi pada banyaknya titik dari T = (V; E). (i) Jelas bahwa hasil adalah benar untuk jV j = 1.
(ii) Diandaikan bahwa hasil benar untuk jV j k. Diambil T = (V; E) dengan jV j = k + 1. Jika satu sisi dari T dihapus, maka graf mempunyai dua komponen:
T1= (V1; E1) dan T2 = (V2; E2) :
Jelas bahwa jV1j k dan jV2j k, sehingga dari hipotesis induksi diperoleh
jE1j = jV1j 1 dan jE2j = jV2j 1:
Gambar 1.7: Subpohon T1 dan T2 yang diperoleh dari T dengan menghapus satu sisi x.
De…nisi 1.33 Suatu hutan (forest) F = fT1; :::; TNg adalah suatu himpunan dari
pohon-pohon Tk = (Vk; Ek) dimana N
\
k=1
Vk = ?, atau dengan kata lain komponen dari
F adalah pohon.
Sebagai contoh, empat pohon berikut ini bersama-sama akan membentuk hutan.
1.6
Pohon dan Hutan Rentangan
De…nisi 1.34 Diberikan graf terhubung G = V (V; E).
1. Pohon rentangan (spanning tree) dari graf G adalah suatu pohon dari G yang memuat semua titik di G.
2. Hutan rentangan (spanning forest) dari graf G adalah suatu hutan dari G yang memuat semua titik di G.
Diperhatikan graf yang dinyatakan oleh Gambar 1.8. Setiap graf di bagian (b) dan (c) berturut-turut menyatakan suatu pohon dan hutan rentangan dari graf di bagian (a). Dari contoh ini jelas bahwa pohon dan hutan rentangan dari suatu graf belum tentu tunggal.
Teorema 1.35 Jika graf terhubung G = (V; E) memenuhi jEj = jV j 1, maka graf G adalah pohon.
Bukti. Diambil G adalah sembarang pohon terhubung dengan n titik dan n 1 sisi. Dimisalkan G0 adalah suatu pohon rentangan dalam G, maka G0 juga mempunyai n titik dan n 1 sisi. Karena itu G0 = G.
Gambar 1.8: (a) Graf tangga; (b) pohon rentangan; (c) hutan rentangan.
sebagian demi sebagian dan selalu memilih bagian berikutnya yang memberikan man-faat segera dan paling jelas [3].
Algoritma Greedy untuk pohon rentangan. Input: Graf terhubung G = (V; E) dimana jV j = n. Output: Pohon rentangan T dari G.
(1) Diambil sembarang titik u di V (G) dan dimasukkan u ke V (T ).
(2) Dibentuk V (G) V (T ). Dipilih suatu titik y 2 V (G) V (T ) dan y bertetangga dengan suatu titik x 2 V (T ). Selanjutnya dimasukkan sisi fx; yg ke E (T ). (3) Diulangi langkah (2) sebanyak (n 2) kali sampai semua titik di V (G) termuat
dalam pohon.
Tabel 1.1: Pembentukan pohon rentangan dari graf dalam Gambar 1.8(a) menggunakan Algoritma Greedy.
sisi yang ditam-Langkah V (G) nV (T ) y V (T ) bahkan pada T
1 u = v5 fv5g 2 fv1; v2; v3; v4; v6g v4 fv5; v4g fv5; v4g 3 fv1; v2; v3; v6g v6 fv5; v4; v6g fv5; v6g 4 fv1; v2; v3g v2 fv5; v4; v6; v2g fv5; v2g 5 fv1; v3g v1 fv5; v4; v6; v2; v1g fv4; v1g 6 fv3g v3 fv5; v4; v6; v2; v1; v3g fv6; v3g
Proposisi 1.36 Algoritma Greedy selalu bisa mengkonstruksi suatu pohon rentangan. Bukti. Perlu ditunjukkan bahwa di sembarang tingkat, suatu titik baru di V selalu dapat dihubungkan ke pohon parsial menggunakan suatu sisi di E. Untuk melihat ini, diambil S yang menyatakan himpunan titik-titik dalam pohon parsial di sembarang tingkat. Diasumsikan bahwa S 6= ? agar selalu bisa dipilih suatu titik awal. Diandaikan bahwa S 6= V . Dibuktikan sebaliknya bahwa suatu titik tambahan di V tidak bisa dihubungkan ke pohon parsial. Karena itu tidak ada sisi di E mempunyai satu titik di S dan titik lainnya di V nS. Akibatnya tidak ada lintasan dari sembarang titik di S ke sembarang titik di V nS, yang berarti G tidak terhubung. Ini kontradiksi dengan kenyataan bahwa G adalah terhubung.
1.7
Soal-soal untuk Bab 1
1. Gambarkan suatu graf yang dinyatakan oleh matriks ketetanggaan berikut ini. 2 6 6 6 6 6 6 6 6 6 6 6 6 6 6 4 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 5
2. Gambarkan suatu graf sederhana dengan 6 titik dan 10 sisi.
3. Konstruksi suatu graf dengan 5 titik dan 6 sisi yang tidak memuat lingkaran C3.
4. Berapa banyak sisi dari graf lengkap Kn? Berikan penjelasan.
(a) 2, 2, 2, 3 (b) 2, 2, 4, 4, 4 (c) 1, 2, 2, 3, 4 (d) 1, 2, 3, 4 (e) 5; 2; 3; 2; 4 (f) 4; 4; 3; 2; 3 (g) 3; 3; 2; 3; 2 (h) 4; 4; 1; 3; 2 6. Tentukan 11 graf (sederhana) berbeda dengan 4 titik?
7. Tentukan semua graf (sederhana) berbeda dengan 5 titik dan 2 sisi? Bagaimana dengan 3 sisi? Berapa banyak sisi maksimum pada suatu graf sederhana dengan 5 titik yang dapat dibuat?
8. Buktikan bahwa pasangan graf berikut ini adalah isomor…k.
9. Periksa apakah pasangan graf di bawah isomor…k? Jika ya, tentukan isomor…s-manya.
10. Berapa banyak sisi yang dipunyai oleh komplemen dari suatu graf dengan n titik dan m sisi?
11. Untuk setiap operasi graf di bawah ini, gambarkan graf dari hasil operasinya. (a) K4 K2 (b) C5+ K1 (c) 5K1+ P2
(d) K3[ K1 (e) K3[ K1 (f) (K3[ K1) K3[ K1
(g) K4[ 2K2 (h) K4[ 2K2 (i) (K4[ 2K2) K4[ 2K2
12. Tentukan rumus untuk diameter dari graf Kn.
13. Untuk nilai n 2 N yang mana sedemikian sehingga graf lengkap Kn mempunyai
suatu jalan Euler?
14. Berapa banyak pohon rentangan dari graf Cn?
16. Apakah pada graf K5 dan W5 terdapat lingkaran Hamilton atau jalan Euler?
17. Pada graf K5, tentukan suatu lingkaran Hamilton yang juga merupakan jalan
Euler.
18. Periksa apakah ada lingkaran Hamilton atau jalan Euler dalam graf yang dinya-takan oleh matriks ketetanggaan berikut ini.
2 6 6 6 6 6 6 6 6 6 6 6 6 4 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 3 7 7 7 7 7 7 7 7 7 7 7 7 5
19. Gambarkan semua pohon dengan tujuh titik yang tidak isomor…s.
Pohon Rentangan Minimal
Tujuan Pembelajaran:
Mengetahui tentang graf berbobot.
Mengetahui tentang pohon rentangan minimal. Mengetahui aplikasi-aplikasi dari pohon.
Mengaplikasikan Algoritma Prim dan Kruskal untuk pencarian pohon rentangan minimal.
2.1
Pengantar
Pada bab ini akan diperhatikan masalah pohon rentangan ketika sisi-sisi dari suatu graf terhubung mempunyai bobot.
De…nisi 2.1 Diandaikan bahwa G = (V; E) adalah suatu graf. Sembarang fungsi bertipe w : E ! N dinamakan fungsi bobot. Graf G, bersama-sama dengan fungsi w : E ! N, dinamakan graf berbobot (weighted graph).
Gambar 2.1: Suatu graf terhubung berbobot dengan 6 titik dan 7 sisi.
Sebagai contoh, diperhatikan graf berbobot dalam Gambar 2.1. Graf mempunyai fungsi bobot w : E ! N, dimana
E = ffv1; v2g ; fv1; v4g ; fv2; v3g ; fv2; v5g ; fv3; v6g ; fv4; v5g ; fv5; v6gg
dan
w (fv1; v2g) = 3; w (fv1; v4g) = 2; w (fv2; v3g) = 5; w (fv2; v5g) = 1;
w (fv3; v6g) = 4; w (fv4; v5g) = 6; w (fv5; v6g) = 7:
De…nisi 2.2 Diandaikan bahwa G = (V; E), bersama-sama dengan fungsi w : E ! N, membentuk suatu graf berbobot. Lebih lanjut diandaikan bahwa G adalah terhubung dan T adalah suatu pohon rentangan dari G. Nilai
w (T ) =X
e2T
w (e) ;
jumlahan bobot dari sisi-sisi di T , dinamakan bobot dari pohon rentangan T .
2.2
Pohon Rentangan Minimal
Secara jelas, untuk sembarang pohon rentangan T dari G dipunyai w (T ) 2 N. Jelas juga bahwa hanya terdapat berhingga pohon rentangan T dari G. Karena itu pasti ada satu pohon rentangan T dimana nilai w (T ) adalah terkecil diantara semua pohon rentangan dari G.
De…nisi 2.3 Diandaikan bahwa G = (V; E) adalah terhubung dan bersama-sama de-ngan fungsi w : E ! N membentuk suatu graf berbobot. Suatu pohon rentade-ngan T dari G, untuk yang mana bobot w (T ) adalah terkecil diantara semua pohon rentangan dari G, dinamakan suatu pohon rentangan minimal (minimal spanning tree) dari G.
Dicatat bahwa pohon rentangan minimal dari suatu graf terhubung berbobot mung-kin tidak tunggal. Diperhatikan, sebagai contoh, suatu graf terhubung dimana semua sisinya mempunyai bobot sama, maka jelas bahwa setiap pohon rentangan adalah mi-nimal.
Sekarang pertanyaannya adalah bagaimana membangun suatu pohon rentangan minimal dari sembarang graf terhubung berbobot. Jawaban diperoleh dengan memo-di…kasi Algoritma Greedy di Subbab 1.6. Dalam hal ini ada dua algoritma, yaitu Algoritma Prim dan Algoritma Kruskal.
Menurut [12], Algoritma Prim ditemukan pada tahun 1930 oleh matematikawan Vojt¼ech Jarník (1887 1970) dan kemudian secara terpisah oleh ilmuwan komputer Robert C. Prim pada tahun 1957 dan ditemukan kembali oleh Dijkstra pada tahun 1959. Karena itu algoritma ini sering dinamakan Algoritma DJP atau Algoritma Jarník. Algoritma Prim membentuk suatu pohon rentangan minimal dengan cara mengambil satu sisi pada setiap langkah pembentukan. Ketentuannya adalah bahwa satu sisi yang diambil harus bersisian dengan suatu titik di pohon pada langkah sebelumnya, memiliki bobot minimal, dan tidak membentuk lingkaran di pohon. Berikut ini adalah algoritmanya.
Algoritma Prim untuk suatu pohon rentangan minimal.
Input: Graf terhubung G = (V; E) dengan jV j = n, dan dilengkapi fungsi bobot w : E ! N.
Output: Pohon rentangan minimal T dari G.
(1) Dibuat T dengan mengambil satu sisi di E (G) yang berbobot mimimal.
(3) Diulangi langkah (2) sebanyak (n 3) kali sampai semua titik di V (G) termuat dalam pohon.
Gambar 2.2: Suatu graf terhubung berbobot dengan 9 titik dan 16 sisi.
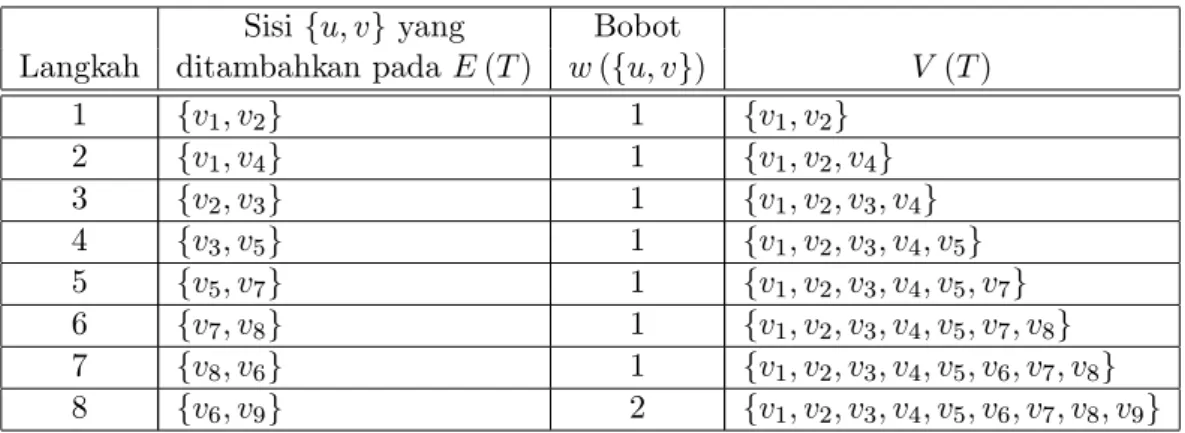
Tabel 2.1: Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggu-nakan Algoritma Prim.
Sisi fu; vg yang Bobot
Langkah ditambahkan pada E (T ) w (fu; vg) V (T ) 1 fv1; v2g 1 fv1; v2g 2 fv1; v4g 1 fv1; v2; v4g 3 fv2; v3g 1 fv1; v2; v3; v4g 4 fv3; v5g 1 fv1; v2; v3; v4; v5g 5 fv5; v7g 1 fv1; v2; v3; v4; v5; v7g 6 fv7; v8g 1 fv1; v2; v3; v4; v5; v7; v8g 7 fv8; v6g 1 fv1; v2; v3; v4; v5; v6; v7; v8g 8 fv6; v9g 2 fv1; v2; v3; v4; v5; v6; v7; v8; v9g
Sebagai contoh, diperhatikan graf terhubung berbobot dalam Gambar 2.2. Pemben-tukan pohon rentangan minimal menggunakan Algoritma Prim disajikan dalam Tabel 2.1, dengan pohon rentangan minimalnya seperti di bawah ini.
Bukti. Diandaikan bahwa T adalah suatu pohon rentangan dari G yang dibangun oleh algoritma Prim. Akan ditunjukkan bahwa w (T ) w (U ) untuk sembarang pohon rentangan U dari G. Diandaikan bahwa sisi-sisi dari T dalam urutan konstruksi adalah e1; e2; :::; en 1, dimana jV j = n. Jika U = T , maka jelas bahwa hasil adalah benar dan
bukti selesai. Sekarang, tanpa kehilangan keumuman, diandaikan bahwa U 6= T , yang berarti T memuat suatu sisi yang tidak ada di U . Diandaikan bahwa
e1; e2; :::; ek 12 U dan ek2 U.=
Dinotasikan S adalah himpunan titik-titik dari pohon parsial yang membentuk sisi-sisi e1; e2; :::; ek 1, dan diambil ek = fx; yg, dimana x 2 S dan y 2 V nS. Karena U
adalah suatu pohon rentangan dari G, berarti terdapat suatu lintasan di U dari x ke y yang pasti memuat suatu sisi e dengan satu titik di S dan titik lainnya di V nS. Dalam pandangan algoritma haruslah dipunyai w (ek) w (e), jika tidak maka sisi e
akan dipilih lebih dulu daripada ek dalam konstruksi dari T berdasarkan algoritma.
Sekarang dihapus sisi e dari U dan diganti dengan ek. Selanjutnya diperoleh suatu
pohon rentangan baru U1 dari G, dimana
w (U1) = w (U ) w (e) + w (ek) w (U ) .
Lebih jauh,
e1; e2; :::; ek 1; ek 2 U1:
Jika U1 6= T , maka proses di atas diulang dan diperoleh suatu barisan dari pohon
rentangan U1; U2; ::: dari G, yang masing-masing memuat suatu bagian dari barisan
e1; e2; :::; en 1 dan lebih panjang daripada yang mendahului. Karena itu proses pasti
berhenti dengan suatu pohon rentangan Um= T . Secara jelas
w (U ) w (U1) w (U2) w (Um) = T
seperti yang diinginkan.
Algoritma kedua, yaitu Algoritma Kruskal, pertama kali muncul pada tahun 1956 dalam sebuah tulisan yang ditulis oleh Joseph Kruskal [5]. Algoritma ini membangun suatu pohon rentangan minimal dimana pada setiap langkah pembentukan mungkin tidak terbentuk pohon tetapi hutan. Berikut ini adalah algoritmanya.
Algoritma Kruskal untuk suatu pohon rentangan minimal.
Input: Graf terhubung G = (V; E) dengan jV j = n, dan dilengkapi fungsi bobot w : E ! N.
Output: Pohon rentangan minimal T dari G.
(1) Dibuat T dengan mengambil satu sisi di E (G) yang berbobot mimimal.
(2) Dipilih satu sisi fu; vg 2 E (G) nE (T ) yang memiliki bobot minimal dan tidak membentuk lingkaran di T . Selanjutnya dimasukkan fu; vg ke dalam E (T ). (3) Diulangi langkah (2) sebanyak (n 3) kali sampai semua titik di V (G) termuat
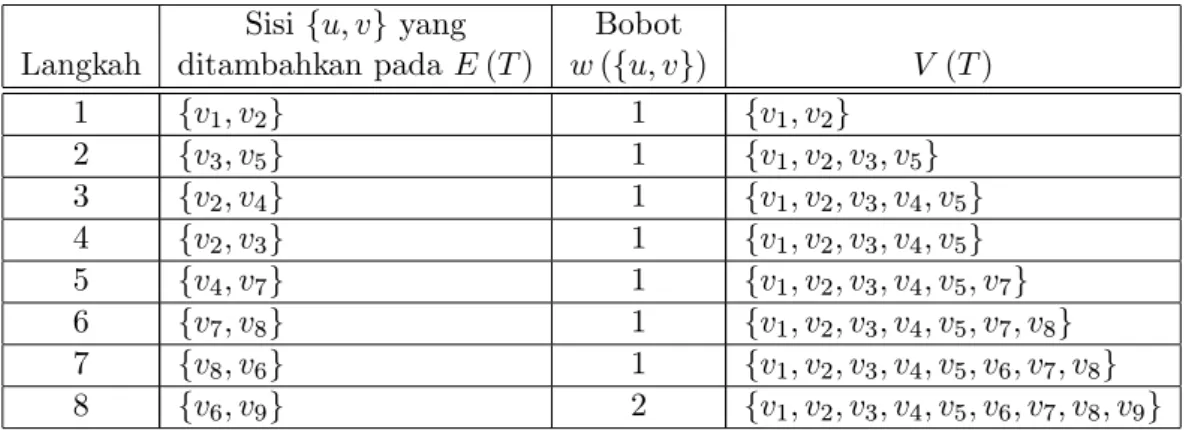
Tabel 2.2: Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggu-nakan Algoritma Kruskal.
Sisi fu; vg yang Bobot
Langkah ditambahkan pada E (T ) w (fu; vg) V (T ) 1 fv1; v2g 1 fv1; v2g 2 fv3; v5g 1 fv1; v2; v3; v5g 3 fv2; v4g 1 fv1; v2; v3; v4; v5g 4 fv2; v3g 1 fv1; v2; v3; v4; v5g 5 fv4; v7g 1 fv1; v2; v3; v4; v5; v7g 6 fv7; v8g 1 fv1; v2; v3; v4; v5; v7; v8g 7 fv8; v6g 1 fv1; v2; v3; v4; v5; v6; v7; v8g 8 fv6; v9g 2 fv1; v2; v3; v4; v5; v6; v7; v8; v9g
Diperhatikan kembali graf dalam Gambar 2.2. Pohon rentangan minimalnya dapat dibentuk menggunakan Algoritma Kruskal seperti pada Tabel 2.2 dengan hasil akhirnya seperti di bawah ini.
Dicatat bahwa pohon rentangan minimal yang diperoleh dari dua algoritma di atas adalah tidak identik, tetapi bobot minimal dari kedua pohon rentangan yang dihasilkan adalah sama.
Proposisi 2.5 Algoritma Kruskal selalu bisa mengkonstruksi suatu pohon rentangan minimal.
Bukti. Diandaikan bahwa T adalah suatu pohon rentangan dari G yang dibangun oleh algoritma Kruskal, dan sisi-sisi dari T dalam urutan konstruksi adalah e1; e2; :::; en 1,
dimana jV j = n. Diambil U adalah sembarang pohon rentangan minimal dari G. Jika U = T , maka jelas bahwa hasil adalah benar dan bukti selesai. Sekarang, tanpa kehilangan keumuman, diandaikan bahwa U 6= T , yang berarti T memuat suatu sisi yang tidak ada di U . Diandaikan bahwa
e1; e2; :::; ek 12 U dan ek2 U.=
Ditambahkan suatu sisi ek ke U , maka ini akan menghasilkan suatu lingkaran. Jika
w (e), jika tidak maka sisi e akan dipilih lebih dulu daripada ek dalam konstruksi dari
T berdasarkan algoritma. Ini berarti bahwa pohon rentangan baru U1 memenuhi
w (U1) = w (U ) w (e) + w (ek) w (U ) .
Karena U adalah suatu pohon rentangan minimal dari G, maka w (U1) = w (U ),
se-hingga U1 juga merupakan suatu pohon rentangan minimal dari G. Lebih jauh,
e1; e2; :::; ek 1; ek 2 U1:
Jika U1 6= T , maka proses di atas diulang dan diperoleh suatu barisan dari pohon
rentangan minimal U1; U2; ::: dari G, yang masing-masing memuat suatu bagian dari
barisan e1; e2; :::; en 1dan lebih panjang daripada yang mendahului. Karena itu proses
pasti berhenti dengan suatu pohon rentangan Um= T .
2.3
Soal-soal untuk Bab 2
1. Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini.
2. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal 1.
3. Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini.
5. Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini.
6. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal 5.
7. Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini.
Algoritma Pencarian
Tujuan Pembelajaran:
Mengaplikasikan strategi-strategi pencarian pohon dari satu titik khusus untuk graf terhubung. Mengaplikasikan Algoritma Dijkstra untuk memecahkan masalah lintasan terpendek.
3.1
Pengantar
Dalam banyak kejadian kita ingin mengunjungi setiap titik tepat satu kali dalam suatu urutan yang khusus. Proses mengunjungi titik-titik dari suatu pohon dalam suatu urutan khusus dinamakan dinamakan pencarian (searching) atau melakukan suatu pencarian pohon. Seringkali proses ini dinamakan pelintasan (traversal ). Dalam bab ini diberikan strategi-strategi dalam mencari suatu lintasan dari satu titik tertentu ke titik-titik lainnya untuk suatu graf terhubung dan graf terhubung berbobot.
3.2
Depth-First Search
Gambar 3.1: Suatu graf tidak terhubung dengan 7 titik dan 6 sisi.
Diperhatikan graf yang direpresentasikan dalam Gambar 3.1. Diandaikan bahwa ingin dicari semua titik u di graf sedemikian sehingga ada suatu lintasan dari titik v1
ke titik u. Ini bisa didapatkan seperti berikut ini.
(1) Dimulai dari titik v1, bergerak ke suatu titik tetangga v2 dan dengan segera
bergerak ke titik tetangga v3. Dari sini disimpulkan bahwa ada suatu lintasan
dari titik v1ke titik v2atau v3. Dalam kasus ini v1dinamakan orang tua (parent )
dari v2 atau sebaliknya v2adalah anak (child ) dari v1, sedangkan v2 dinamakan
orang tua (parent ) dari v3
(2) Karena tidak ada titik tetangga baru dari titik v3, maka kembali ke titik v2.
Karena tidak ada tetanga baru dari titik v2, maka kembali ke titik v1.
(3) Dimulai dari titik v1 lagi, bergerak ke titik tetangga v5 dan segera bergerak ke
titik tetangga v4. Dari sini disimpulkan bahwa ada suatu lintasan dari titik v1 ke
titik v2, v3, v4, atau v5.
(4) Karena tidak ada titik tetangga baru dari titik v4, maka kembali ke titik v5.
(5) Dimulai dari titik v5 dan bergerak ke titik tetangga v6. Dari sini disimpulkan
bahwa ada suatu lintasan dari titik v1 ke titik v2, v3, v4, v5 atau v6.
(6) Karena tidak ada titik tetangga baru dari titik v6, maka kembali ke titik v5.
Karena tidak ada titik tetangga baru dari titik v5, maka kembali ke titik v1.
Karena tidak ada titik tetangga baru dari titik v1, maka proses berhenti.
Disim-pulkan bahwa ada suatu lintasan dari titik v1 ke titik v2, v3, v4, v5 atau v6.
Dicatat bahwa hasil dari proses di atas adalah suatu pohon rentangan dari graf yang direpresentasikan oleh graf di bawah ini.
Proses di atas merupakan suatu contoh dari strategi yang dikenal sebagai Depth-First Search, yang dapat dipandang sebagai suatu metode pertumbuhan-pohon khusus (spe-cial tree-growing method ). Diaplikasikan dari suatu titik u di suatu graf G, proses tersebut akan memberikan suatu pohon rentangan dari komponen graf G yang memuat titik u. Dalam hal ini titik u tersebut biasanya dinamakan akar dari pohon rentangan.
Algoritma Depth-First Search.
Input: Graf terhubung G = (V; E), V = fv1, v2, ..., vng.
Output: Pohon rentangan berakar (T; u) untuk G, dengan u 2 V (G). (1) Ditetapkan titik u sebagai v.
(2) Dipilih vi, dengan i adalah indeks terkecil, sedemikian sehingga fv; vig 2 V dan vi
belum pernah dipilih sebelumnya. Jika tidak ditemukan vi, lanjut ke langkah (3).
Jika vi ada, dimasukkan sisi fv; vig ke T dan ditetapkan vi sebagai v, selanjutnya
kembali ke langkah (2).
Gambar 3.2: Suatu graf terhubung dengan 10 titik dan 11 sisi.
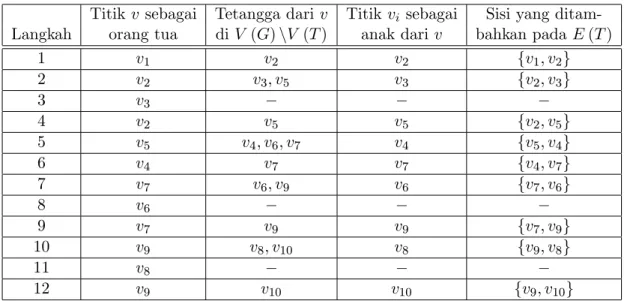
Tabel 3.1: Pembentukan pohon berakar (T; v1) dari graf dalam Gambar 3.2 berdasarkan
Algoritma Depth-First Search.
Titik v sebagai Tetangga dari v Titik vi sebagai Sisi yang
ditam-Langkah orang tua di V (G) nV (T ) anak dari v bahkan pada E (T )
1 v1 v2 v2 fv1; v2g 2 v2 v3; v5 v3 fv2; v3g 3 v3 4 v2 v5 v5 fv2; v5g 5 v5 v4; v6; v7 v4 fv5; v4g 6 v4 v7 v7 fv4; v7g 7 v7 v6; v9 v6 fv7; v6g 8 v6 9 v7 v9 v9 fv7; v9g 10 v9 v8; v10 v8 fv9; v8g 11 v8 12 v9 v10 v10 fv9; v10g
Sebagai contoh, Algoritma Depth-First Search untuk mencari pohon berakar v1
3.3
Breadth-First Search
Diperhatikan kembali graf dalam Gambar 3.1. Diandaikan lagi bahwa kita ingin men-cari semua titik u sedemikian sehingga ada suatu lintasan dari titik v1 ke titik u. Kita
bisa mendapatkannya seperti berikut ini.
(1) Dimulai dari titik v1, dan berjalan ke semua titik baru yang bertetangga dengan
v1, yaitu v2, v5, dan v6.
(2) Berikutnya dimulai dari v2, dan berjalan ke semua titik baru yang bertetangga
dengan v2, yaitu hanya v3.
(3) Berikutnya dimulai dari v5, dan berjalan ke semua titik baru yang bertetangga
dengan v5, yaitu hanya v4.
(4) Berikutnya dimulai dari v6, dan berjalan ke semua titik baru yang bertetangga
dengan v6, yaitu tidak ada.
(5) Berikutnya dimulai dari v3, dan berjalan ke semua titik baru yang bertetangga
dengan v3, yaitu tidak ada.
(6) Berikutnya dimulai dari v4, dan berjalan ke semua titik baru yang bertetangga
dengan v4, yaitu tidak ada.
(7) Karena titik v4merupakan titik terakhir dalam daftar v1, v2, v5, v6, v3, v4(dalam
urutan pencapaian), maka proses berhenti.
Dicatat bahwa hasil dari proses di atas adalah suatu pohon rentangan dari graf yang direpresentasikan oleh garf di bawah ini.
Proses di atas merupakan suatu contoh dari strategi yang dikenal sebagai Breadth-First Search, yang dapat dipandang sebagai suatu metode pertumbuhan-pohon khusus. Diaplikasikan dari suatu titik u di graf G, strategi tersebut juga akan memberikan suatu pohon rentangan dari komponen graf G yang memuat titik u.
Algoritma Breadth-First Search.
Input: Graf terhubung G = (V; E), V = fv1, v2, ..., vng.
Output: Pohon rentangan berakar (T; u) untuk G, dengan u 2 V (G). (1) Dimulai dengan barisan titik Q = u 2 V .
(3) Jika terdapat titik w bertetangga dengan v dan w belum pernah masuk barisan, maka masukkan semua sisi fv; wg ke T , tambahkan semua titik w ke bagian akhir dari Q, dan kembali ke langkah (2). Jika tidak ada titik yang bertetangga dengan v yang belum pernah masuk barisan, maka kembali ke langkah (2).
Tabel 3.2: Pembentukan pohon berakar (T; v1) dari graf dalam Gambar 3.2 berdasarkan
Algoritma Breadth-First Search.
v (titik terdepan w (tetangga v Sisi yang ditam-Langkah dari Q) dan tidak di V (T )) Q bahkan pada E (T )
1 v1 2 v1 v2 v2 fv1; v2g 3 v2 v3; v5 v3; v5 fv2; v3g ; fv2; v5g 4 v3 v5 5 v5 v4; v6; v7 v4; v6; v7 fv5; v4g ; fv5; v6g ; fv5; v7g 6 v4 v6; v7 7 v6 v7 8 v7 v9 v9 fv7; v9g 9 v9 v8; v10 v8; v10 fv9; v8g ; fv9; v10g 10 v8 v10 11 v10
Sebagai contoh, akan digunakan Algoritma Breadth-First Search untuk mencari pohon rentangan dari graf dalam Gambar 3.2. Dimulai dari titik v1, dan dalam kasus
ini digunakan ketentuan bahwa ketika kita mempunyai suatu pilihan dari titik-titik maka kita mengambil titik yang mempunyai penomoran lebih rendah. Proses pencarian disajikan dalam Tabel 3.2 dan pohon rentangan yang dihasilkan adalah seperti di bawah ini.
3.4
Masalah Lintasan Terpendek
Diperhatikan suatu graf terhubung G = (V; E), dengan fungsi bobot w : E ! N. Untuk sembarang pasangan titik berbeda x; y 2 V dan untuk sembarang lintasan
v0(= x) ; v1; :::; vr(= y)
dari x ke y, diperhatikan nilai dari
r
X
i=1
w (fvi 1; vig) ; (3.1)
yaitu jumlahan dari bobot-bobot sisi yang membentuk lintasan. Kita tertarik untuk dalam meminimalkan nilai dari (3.1) atas semua lintasan dari x ke y.
Diperhatikan bahwa jika kita memikirkan bobot dari suatu sisi sebagai panjang, maka kita mencoba mencari suatu lintasan terpendek dari x ke y. Algoritma yang di-gunakan untuk menyelesaikan masalah tersebut adalah variasi dari Algoritma Breadth-First Search. Untuk memahami ide pokok dari algoritma yang akan digunakan, diper-hatikan analogi berikut ini.
Diperhatikan tiga kota A, B, dan C. Diandaikan bahwa informasi berikut ini mengenai waktu perjalanan antara kota-kota tersebut:
AB BC AC
x y z
Informasi tersebut dapat direpresentasikan dengan gambar berikut ini.
Jelas bahwa waktu perjalanan antara A dan C tidak bisa melebih minfz; x + yg. Sekarang diandaikan bahwa u adalah suatu titik di graf terhubung berbobot G = (V; E). Untuk setiap titik x 2 V , diandaikan bahwa lintasan terpendek dari u ke x tidak melebihi l (x). Jika diambil y sebagai suatu titik di graf, dan p sebagai suatu titik yang bertetangga dengan y, maka jelas bahwa lintasan terpendek dari u ke y tidak melebihi
Oleh karena itu kita dapat mengganti informasi l (y) dengan minimum (3.2).
Berikut ini diberikan Algoritma Dijkstra untuk memecahkan masalah lintasan ter-pendek untuk suatu graf terhubung berbobot. Algoritma Dijkstra pertama kali muncul pada tahun 1959 dalam sebuah tulisan yang ditulis oleh Edsger Dijkstra [12].
Algoritma Lintasan Terpendek Dijkstra.
Input: Graf terhubung G = (V; E) yang dilengkapi suatu fungsi bobot w : E ! N. Suatu titik khusus u 2 V (G).
Output: Panjang semua lintasan terpendek dari u ke titik-titik lain: l : V (G) n fug ! N.
(1) Diambil l (u) = 0, dan dituliskan l (x) = 1 untuk setiap titik x 2 V dan x 6= u. Selanjutnya dimasukkan u ke V (T ).
(2) Diperhatikan semua titik y 2 V (G) n V (T ) dan bertetangga dengan u. Diganti nilai dari l (y) dengan minfl (y), l (u) + w (fu; yg)g. Diamati pada nilai baru dari l (y) untuk setiap titik y 2 V (G) n V (T ), dan dipilih suatu titik v dimana l (v) l (y) untuk semua titik y. Selanjutnya ditambahkan sisi yang muncul untuk nilai baru dari l (v) ke E (T ).
(3) Jika V (T ) = V (G), maka proses berhenti. Lintasan tunggal dari u ke sembarang titik x 6= u menyatakan lintasan terpendek dari u ke x. Jika V (T ) 6= V (G), maka ditetapkan v = u dan kembali ke langkah (2).
Gambar 3.3: Suatu graf berbobot dengan 8 titik dan 15 sisi.
Sebagai contoh, diperhatikan diperhatikan graf berbobot dalam Gambar 3.3. Di-misalkan titik awalnya adalah u, maka dipunyai proses Dijkstra seperti dalam Tabel 3.3. Nilai-nilai l (v) menyatakan panjang lintasan terpendek dari u ke titik v yang diperhatikan. Dari proses ini juga diperoleh pohon rentangan seperti di bawah ini.
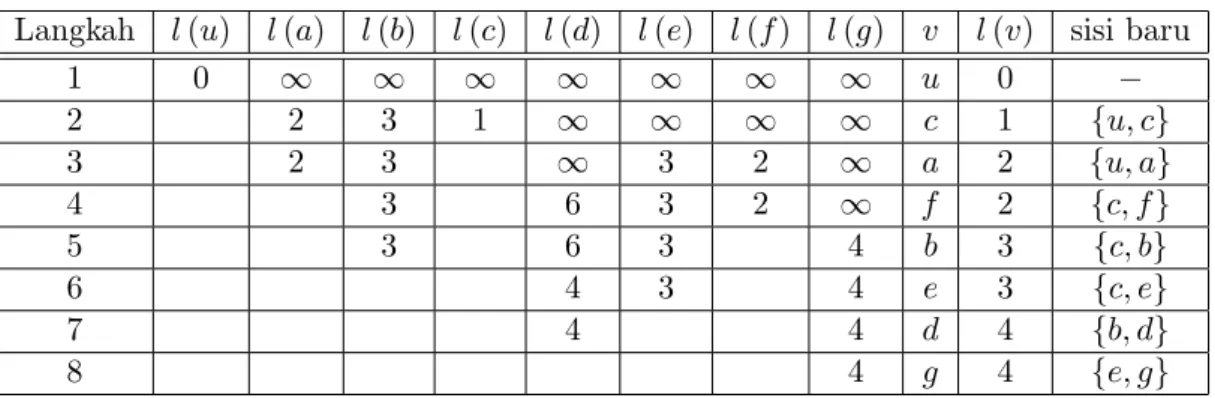
Tabel 3.3: Pencarian lintasan terpendek dari titik u untuk graf dalam Gambar 3.3 berdasarkan Algoritma Lintasan Terpendek Dijkstra.
Langkah l (u) l (a) l (b) l (c) l (d) l (e) l (f ) l (g) v l (v) sisi baru
1 0 1 1 1 1 1 1 1 u 0 2 2 3 1 1 1 1 1 c 1 fu; cg 3 2 3 1 3 2 1 a 2 fu; ag 4 3 6 3 2 1 f 2 fc; fg 5 3 6 3 4 b 3 fc; bg 6 4 3 4 e 3 fc; eg 7 4 4 d 4 fb; dg 8 4 g 4 fe; gg
pada langkah 2: Diperhatikan tetangga dari u, yaitu a, b, dan c. Dihitung nilai baru untuk:
l (a) : min fl (a) ; l (u) + w (fu; ag)g = min f1; 0 + 2g = 2; l (b) : min fl (b) ; l (u) + w (fu; bg)g = min f1; 0 + 3g = 3; l (c) : min fl (c) ; l (u) + w (fu; cg)g = min f1; 0 + 1g = 1: Diperoleh titik c dimana l (c) l (a) ; l (b).
pada langkah 3: Diperhatikan tetangga dari c selain u, yaitu b, e, dan f . Dihitung nilai baru untuk:
l (b) : min fl (b) ; l (c) + w (fc; bg)g = min f3; 1 + 2g = 3; l (e) : min fl (e) ; l (c) + w (fc; eg)g = min f1; 1 + 2g = 3; l (f ) : min fl (f) ; l (c) + w (fc; fg)g = min f1; 1 + 1g = 2: Diperoleh titik f dimana l (f ) l (a) ; l (b) ; l (e).
3.5
Soal-soal untuk Bab 3
1. Aplikasikan Algoritma Depth-First Search untuk graf pada Soal 1 dalam Bab 1. 2. Diperhatikan graf G yang dide…nisikan oleh matriks ketetanggaan berikut ini.
Aplikasikan Algoritma Depth-First Search, dimulai dengan titik v7 dan
meng-gunakan kesepakatan bahwa ketika dipunyai suatu pilihan dari titik-titik maka dipilih titik dengan penomoran lebih rendah.
3. Aplikasikan Algoritma Breadth-First Search untuk graf pada Soal 1 dalam Bab 1.
4. Diperhatikan graf G yang dide…nisikan oleh matriks ketetanggaan berikut ini. 2 6 6 6 6 6 6 6 6 6 6 6 6 4 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 3 7 7 7 7 7 7 7 7 7 7 7 7 5
Aplikasikan Algoritma Breadth-First Search, dimulai dengan titik v1 dan
meng-gunakan kesepakatan bahwa ketika dipunyai suatu pilihan dari titik-titik maka dipilih titik dengan penomoran lebih rendah.
Graf Berarah
Tujuan Pembelajaran:
Mengetahui tentang graf berarah.
Mengetahui representasi matriks dari suatu graf berarah. Mengetahui tentang jaringan dan arus.
Mengaplikasikan Algoritma Ford-Fulkerson untuk mencari arus maksimum dalam suatu jaringan.
4.1
Pengantar
Suatu graf berarah secara sederhana adalah suatu koleksi dari titik-titik, bersama-sama dengan beberapa busur yang menghubungkan beberapa titik. Dicatat bahwa busur mempunyai arah, sehingga (u; v) 6= (v; u) kecuali u = v. Sebagai contoh, graf dalam Gambar 4.1 mempunyai titik-titik v1, v2, v3, v4, v5, sedangkan busur-busurnya
dinyatakan oleh (v1; v2), (v1; v3), (v4; v5), (v5; v5).
Gambar 4.1: Graf berarah dengan 5 titik.
Selanjutnya, de…nisi formal dari graf berarah diberikut seperti di bawah ini.
De…nisi 4.1 Suatu graf berarah (directed graph atau disingkat digraph) D adalah suatu pasangan (V; E), dimana V adalah suatu himpunan berhingga dan E adalah suatu himpunan bagian dari hasil kali kartesius V V . Elemen-elemen dari V dikenal sebagai titik dan elemen-elemen dari E dikenal sebagai busur (arc).
Jadi, pada graf berarah D = (V; E) elemen-elemen dari E adalah pasangan-pasangan terurut: busur dari titik u ke titik v dituliskan seperti (u; v) dan pasangan (v; u) adalah
busur dalam arah sebaliknya. Untuk busur (u; v), titik u adalah titik awal (initial ver-tex ) dan titik v adalah titik akhir (terminal verver-tex ). Selain itu dikatakan juga busur bersisian luar dari u dan bersisian dalam ke v. Dicatat bahwa suatu graf berarah mungkin mempunyai beberapa sisi diantara dua titik x; y. Jika sisi-sisi tersebut mem-punyai arah yang sama (katakan dari x ke y), sisi-sisi tersebut dikatakan paralel.
Selanjutnya de…nisi dari jalan, lintasan, dan lingkaran diberikan dengan cara seperti berikut.
De…nisi 4.2 Suatu jalan berarah dalam graf berarah D = (V; E) adalah suatu barisan titik-titik
v0; v1; :::; vk 2 V
sedemikian sehingga (vi 1; vi) 2 E, untuk setiap i = 1; :::; k. Jika semua titiknya
berbeda, maka jalan berarah tersebut dinamakan suatu lintasan berarah. Di sisi lain, jika semua titiknya berbeda kecuali bahwa v0 = vk, maka jalan berarah tersebut
dina-makan suatu lingkaran berarah.
De…nisi 4.3 Suatu titik v dalam graf berarah D = (V; E) dikatakan dapat dijangkau dari suatu titik u jika terdapat suatu jalan berarah dari u ke v.
Dicatat bahwa suatu titik mungkin tidak dapat dijangkau dari dirinya sendiri. Se-bagai contoh, dalam Gambar 4.1 titik v2dan v3dapat dijangkau dari titik v1, sedangkan
titik v5 dapat dijangkau dari titik v4 dan v5.
De…nisi 4.4 Diambil D = (V; E) adalah suatu graf berarah, dimana V = fv1, v2, ...,
vng dan E = fe1, e2, ..., epg. Matriks ketetanggaan dari graf berarah D adalah
suatu matriks A = [aij] berukuran n n, dimana masukan-(i; j) diberikan oleh
aij = banyaknya busur (vi; vj) :
Matriks keterjangkauan dari graf berarah D adalah suatu matriks R = [rij]
beruku-ran n n, dimana masukan-(i; j) diberikan oleh
rij = 1 jika vj dapat dijangkau dari vi
0 jika vj tidak dapat dijangkau dari vi
:
Matriks kebersisian dari graf berarah D tanpa loop adalah suatu matriks S = [sij]
berukuran n p dimana
sij =
8 < :
1 jika vi adalah titik awal dari ej
1 jika vi adalah titik akhir dari ej
0 untuk lainnya
Sebagai contoh, diperhatikan kedua graf berarah di bawah ini.
Dari kedua graf diperoleh
A (G1) = 2 6 6 4 0 1 0 0 1 0 0 0 0 0 0 0 2 1 0 1 3 7 7 5 , R (G1) = 2 6 6 4 1 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 3 7 7 5 , S (G2) = 2 6 6 4 1 1 1 1 0 1 1 0 0 1 0 0 0 0 0 0 0 1 1 1 3 7 7 5 :
Gambar 4.2: Suatu graf berarah tanpa sisi ganda dan loop.
Keterjangkauan dalam graf berarah sederhana (tanpa sisi ganda dan loop) dapat ditentukan oleh breadth-…rst search dengan cara seperti berikut ini. Diperhatikan graf berarah dalam Gambar 4.2. Dimulai dengan titik v1. Pertama kali dicari semua titik
v sedemikian sehingga (v1; v) 2 E. Titik-titik tersebut adalah v2 dan v4, sehingga
dipunyai daftar v2, v4. Di sini dipunyai informasi bahwa titik v2dan v4dapat dijangkau
dari titik v1. Titik v1 tidak dimasukkan dalam daftar karena v1 tidak dapat dijangkau
dari dirinya sendiri. Selanjutnya dicari semua titik v sedemikian sehingga (v2; v) 2 E.
Titik-titik tersebut adalah v3dan v5, sehingga dipunyai daftar v2, v4, v3, v5. Berikutnya
dicari semua titik v sedemikian sehingga (v4; v) 2 E. Titik tersebut hanyalah titik v5,
sehingga tetap dipunyai daftar v2, v4, v3, v5. Berikutnya dicari semua titik v sedemikian
sehingga (v3; v) 2 E. Titik tersebut hanyalah v6, sehingga dipunyai daftar v2, v4, v3,
v5, v6. Berikutnya dicari semua titik v sedemikian sehingga (v5; v) 2 E. Titik-titik
tersebut adalah v2 dan v6, sehingga tetap dipunyai daftar v2, v4, v3, v5, v6. Berikutnya
dicari semua titik v sedemikian sehingga (v6; v) 2 E. Titik tersebut hanyalah v5,
sehingga tetap dipunyai daftar v2, v4, v3, v5, v6 dan proses berhenti. Disimpulkan
dijangkau dari dirinya sendiri. Metode diulang dengan awalan dari setiap titik lain yang berbeda.
Metode yang lebih baik diberikan oleh Stephen Warshall (1935 2006) dan dikenal sebagai Algoritma Warshall. Sebelum dinyatakan algoritma tersebut, diperhatikan ide pokok dari algoritma. Diandaikan bahwa vi, vj, vk adalah tiga titik dari suatu graf
berarah. Jika diketahui bahwa vj dapat dijangkau dari vi dan vk dapat dijangkau dari
vj, maka vk dapat dijangkau dari vi.
Diambil V = fv1, v2, ..., vng. Diandaikan bahwa Q = [qij] adalah matriks berukuran
n n, dimana masukan-(i; j) dide…nisikan oleh qij =
1 jika sudah diperlihatkan vj dapat dijangkau dari vi
0 jika belum diketahui vj dapat dijangkau dari vi :
Diambil suatu titik vj.
(1) Diperiksa baris ke-j dari Q. Jika sudah diperlihatkan vk dapat dijangkau dari
vj, maka qjk = 1. Jika belum diketahui apakah vk dapat dijangkau dari vj, maka
qjk = 0.
(2) Diperiksa kolom ke-j dari Q. Jika sudah diperlihatkan vj dapat dijangkau dari
vi, maka qij = 1. Jika belum diketahui apakah vj dapat dijangkau dari vi, maka
qij = 0.
(3) Akibatnya, jika qij = 1 dan qjk = 1, maka vj dapat dijangkau dari vidan vkdapat
dijangkau dari vj. Karena itu telah diperlihatkan bahwa vk dapat dijangkau dari
vi. Jadi, nilai dari qik dapat diganti oleh 1.
(4) Dilakukan beberapa manipulasi tersebut secara serempak, maka pada pokoknya ini sedang "menjumlahkan" baris ke-j dari Q ke baris ke-i dari Q dimana qij =
1. Di sini, penjumlahan mempunyai arti penjumlahan Boole; dengan kata lain 0 + 0 = 0 dan 1 + 0 = 0 + 1 = 1 + 1 = 1. Untuk memahami penjumlahan ini, diandaikan bahwa qik = 1, maka penggantian qik oleh qik+ qjk (hasil dari
jumlahan baris ke-j ke baris ke-i) tidak akan mengubah nilai 1. Di sisi lain, jika qik = 0, maka qik diganti oleh qik+ qjk = qjk. Ini akan mempunyai nilai 1 jika
qjk = 1, yaitu telah diperlihatkan bahwa vk dapat dijangkau dari vj. Tetapi
karena qij = 1, yaitu telah diperlihatkan bahwa vj dapat dijangkau dari vi, ini
membenarkan penggantian dari qik = 0 oleh qik+ qjk = 1.
Algoritma Warshall.
Input: Graf berarah sederhana D = (V; E), dimana jV j = n. Output: Matriks keterjangkauan R untuk D.
(1) Diambil Q0 = A.
(2) Diperhatikan masukan-masukan dalam Q0. Baris pertama dari Q0 dijumlahkan
dengan setiap baris dari Q0 yang mempunyai masukan 1 pada kolom pertama.
(3) Diperhatikan masukan-masukan dalam Q1. Baris kedua dari Q1 dijumlahkan
dengan setiap baris dari Q1 yang mempunyai masukan 1 pada kolom kedua.
Diperoleh matriks baru Q2.
(4) Untuk setiap j = 3; 4; :::; n, diperhatikan masukan-masukan pada Qj 1. Baris
ke-j dari Qj 1dijumlahkan dengan setiap baris dari Qj 1yang mempunyai masukan
1 pada kolom ke-j. Diperoleh matriks baru Qj.
(5) Dituliskan R = Qn.
Sebagai contoh, diperhatikan kembali graf dalam Gambar 4.2, dimana dipunyai
A = 2 6 6 6 6 6 6 4 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 3 7 7 7 7 7 7 5 :
Dituliskan Q0 = A. Karena tidak ada baris yang mempunyai masukan 1 pada kolom
pertama dari Q0, disimpulkan bahwa Q1 = Q0 = A. Berikutnya dijumlahkan baris
dua dengan setiap baris satu dan lima untuk memperoleh
Q2 = 2 6 6 6 6 6 6 4 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 0 1 1 0 0 0 0 1 0 3 7 7 7 7 7 7 5 :
Berikutnya dijumlahkan baris tiga dengan setiap baris satu, dua, dan lima untuk mem-peroleh Q3 = 2 6 6 6 6 6 6 4 0 1 1 1 1 1 0 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 0 1 1 0 0 0 0 1 0 3 7 7 7 7 7 7 5 :
Berikutnya dijumlahkan baris empat dengan baris satu untuk memperoleh Q4 = Q3.
Berikutnya dijumlahkan baris lima dengan setiap baris satu, dua, empat, lima, dan enam untuk memperoleh
Terakhir dijumlahkan baris enam dengan setiap baris lainnya untuk memperoleh Q6 = 2 6 6 6 6 6 6 4 0 1 1 1 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 3 7 7 7 7 7 7 5 = R:
4.2
Jaringan dan Arus
Sekarang dibayangkan suatu graf berarah dan busur dianggap sebagai pipa, dimana beberapa komoditas (air, lalu-lintas, dan lain-lain) akan mengalir sepanjang pipa terse-but . Terdapat bobot yang akan disertakan pada setiap busur, untuk diinterpretasikan sebagai kapasitas, yang memberikan batasan-batasan untuk ukuran komoditas yang dapat mengalir sepanjang pipa. Di sini juga dipunyai suatu sumber a dan suatu target akhir z; atau dengan kata lain, semua busur yang memuat a diarahkan dari a dan semua busur yang memuat z diarahkan ke z.
De…nisi 4.5 Suatu jaringan (network) adalah suatu digraf D = (V; E) yang dileng-kapi dengan suatu fungsi kapasitas c : E ! N, suatu titik sumber a 2 V dan suatu titik target akhir z 2 V .
Sebagai contoh, Gambar 4.3 dapat diinterpretasikan sebagai suatu jaringan dengan titik a sebagai sumber dan titik z sebagai target akhir.
Gambar 4.3: Jaringan dengan sumber a dan target akhir z.
Sekarang diandaikan bahwa suatu komoditas sedang mengalir sepanjang busur dari suatu jaringan. Untuk setiap (x; y) 2 E, diambil f (x; y) menyatakan ukuran yang mengalir sepanjang busur (x; y). Digunakan kesepakatan, dengan pengecualian titik sumber a dan titik target akhir z, bahwa ukuran yang mengalir ke titik v sama dengan ukuran yang keluar dari titik v. Selain itu, ukuran yang mengalir sepanjang sembarang busur tidak bisa melebihi kapasitas dari busur.
(F1) (Pengawetan) Untuk setiap titik v 6= a; z, dipunyai I (v) = O (v), dimana arus masuk I (v) dan arus keluar O (v) di titik v dide…nisikan oleh
I (v) = X
(x;v)2E
f (x; v) dan O (v) = X
(v;y)2E
f (v; y) :
(F2) (Batasan) Untuk setiap (x; y) 2 E, dipunyai f (x; v) c (x; v).
Dicatat bahwa di sini fungsi f mempunyai batasan pada nilai-nilai bilangan bulat tak negatif. Tetapi secara umum, fungsi kapasitas c atau fungsi arus f tidak perlu dibatasi pada bilangan-bilangan bulat. Batasan yang dibuat di sini untuk mengabaikan kesulitan tentang eksistensi dari penyelesaian optimal.
Berikut ini diberikan suatu proposisi tanpa bukti.
Proposisi 4.7 Pada sembarang jaringan dengan titik sumber a dan titik target akhir z, pasti dipunyai O (a) = I (z).
De…nisi 4.8 Nilai O (a) = I (z) dari suatu jaringan dinamakan nilai dari arus f , dan dinotasikan dengan V (f).
Diperhatikan suatu jaringan D = (V; E) dengan titik sumber a dan titik target akhir z. Himpunan titik V dipartisi menjadi suatu gabungan terpisah S [T sedemikian sehingga a 2 S dan z 2 T , maka arus dari S ke T , dalam pandangan (F1), sama dengan arus dari a ke z. Dengan kata lain, dipunyai
V (f) = X x2S; y2T (x;y)2E f (x; y) X x2T; y2S (x;y)2E f (x; y) :
Secara jelas, kedua jumlahan pada ruas kanan adalah tak negatif. Ini berakibat bahwa V (f) X x2S; y2T (x;y)2E f (x; y) X x2T; y2S (x;y)2E f (x; y) ; (4.1) dalam pandangan (F2).
De…nisi 4.9 Diberikan V = S [ T , dimana S dan T terpisah serta a 2 S dan z 2 T . Dalam kasus ini, (S; T ) dinamakan suatu potongan (cut) dari jaringan D = (V; E). Nilai
c (S; T ) = X
x2S; y2T (x;y)2E
c (x; y)
Dari (F2) dan (4.1) diperoleh proposisi berikut ini.
Proposisi 4.10 Jika D = (V; E) adalah suatu jaringan dengan fungsi kapasitas c : E ! N, maka untuk setiap arus f : A ! N [ f0g dan setiap potongan (S; T ) dipunyai
V (f) c (S; T ) :
Diandaikan bahwa f0 adalah suatu arus dimana V (f0) V (f) untuk setiap arus
f , dan juga (S0; T0) adalah suatu potongan sedemikian sehingga c (S0; T0) c (S; T )
untuk setiap potongan (S; T ). Secara jelas dipunyai V (f0) c (S0; T0). Dengan kata
lain, arus maksimum tidak pernah melebihi potongan minimum.
4.3
Teorema Max-Flow-Min-Cut
Pada bagian ini akan dinyatakan suatu algoritma praktis yang akan memungkinkan kita untuk menaikkan nilai dari suatu arus dalam suatu jaringan yang diberikan, dimana ditetapkan bahwa arus belum mencapai nilai maksimum.
Akan digunakan notasi berikut ini. Diandaikan (x; y) 2 E, c (x; y) = dan f (x; y) = , maka informasi ini digambarkan seperti:
(4.2) Dicatat bahwa selalu berlaku .
De…nisi 4.11 Dalam notasi pada Gambar (4:2), dapat dilakukan pelabelan maju dari titik x ke titik y jika < , yaitu f (x; y) < c (x; y).
De…nisi 4.12 Dalam notasi pada Gambar (4:2), dapat dilakukan pelabelan mundur dari titik y ke titik x jika > 0, yaitu f (x; y) > 0.
De…nisi 4.13 Diketahui bahwa barisan titik-titik
v0(= a) ; v1; :::; vk(= z) (4.3)
memenuhi sifat bahwa untuk setiap i = 1, 2, ..., k dapat dilabelkan maju atau mundur dari vi 1 ke vi. Dalam kasus ini, barisan titik-titik (4:3) dinamakan lintasan
arus-tambahan (‡ow-augmenting path).
Di sini, pelabelannya adalah maju dimanapun. Dicatat bahwa busur (a; b), (b; c), (c; f ), (f; z) mempunyai kapasitas berturut-turut 9, 8, 4, 3, dimana arus-arus sepanjang busur berturut-turut adalah 7, 5, 0, 1. Karena itu arus sepanjang setiap busur dapat di-naikkan 2 = minf9 7, 8 5, 4 0, 3 1g tanpa melanggar (F2). Selanjutnya dipunyai kondisi seperti berikut:
Jadi, arus dari a ke z telah dinaikkan 2.
Contoh kedua, diperhatikan lintasan arus-tambahan yang diberikan dalam gambar berikut:
Di sini, pelabelannya adalah maju dimanapun, kecuali bahwa titik g dilabelkan mundur dari c. Sekarang dicatat bahwa 2 = minf9 7, 8 5, 2, 10 8g. Jika arus sepanjang setiap busur (a; b), (b; c), (g; z) dinaikkan 2 dan arus sepanjang busur (g; c) diturunkan 2, maka dipunyai kondisi:
Dicatat bahwa jumlahan arus dari b dan g ke c tetap tidak berubah, dan jumlahan arus dari g ke c dan z juga tetap tidak berubah. Jadi, arus dari a ke z telah dinaikkan 2.
Algoritma Arus-Tambahan. Diperhatikan suatu lintasan arus-tambahan bertipe (4.3). Untuk setiap i = 1; :::; k, dituliskan
i =
c (vi 1; vi) f (vi 1; vi) , jika (vi 1; vi) 2 E (pelabelan maju)
f (vi; vi 1) , jika (vi; vi 1) 2 E (pelabelan mundur) ;
dan diambil
= min f 1; :::; kg :
Dinaikkan arus sepanjang sembarang busur berbentuk (vi 1; vi) (pelabelan maju)
sebe-sar dan diturunkan arus sepanjang sembarang busur berbentuk (vi; vi 1) (pelabelan
mundur) sebesar .
De…nisi 4.14 Diketahui bahwa barisan titik-titik
v0(= a) ; v1; :::; vk (4.4)
memenuhi sifat bahwa untuk setiap i = 1, 2, ..., k dapat dilabelkan maju atau mundur dari vi 1 ke vi. Dalam kasus ini, barisan titik-titik (4:4) dinamakan suatu lintasan
arus-tambahan tak lengkap (incomplete ‡ow-augmenting path).
Proposisi 4.15 Pada sembarang jaringan dengan titik sumber a dan titik target akhir z, nilai maksimum untuk suatu arus dari a ke z adalah sama dengan nilai minimum untuk suatu potongan dari jaringan.
Bukti. Diperhatikan suatu jaringan D = (V; E) dengan fungsi kapasitas c : E ! N. Diambil f : E ! N [ f0g sebagai suatu arus maksimum. Diambil
S = fx 2 V : x = a atau
terdapat suatu lintasan arus-tambahan tak lengkap dari a ke xg ; dan T = V nS. Secara jelas z 2 T karena jika tidak maka akan terdapat suatu lintasan arus-tambahan dari a ke z dan mengakibatkan arus f dapat dinaikkan, yang kontradiksi dengan kenyataan bahwa f adalah suatu arus maksimum. Diandaikan bahwa (x; y) 2 E dengan x 2 S dan y 2 T , maka terdapat suatu lintasan arus-tambahan tak lengkap dari a ke x. Jika c (x; y) > f (x; y), maka dapat dilabelkan maju dari x ke y, sehingga akan terdapat suatu lintasan arus-tambahan tak lengkap dari a ke y, kontradiksi dengan kenyataan bahwa y =2 S. Karena itu haruslah c (x; y) = f (x; y) untuk setiap (x; y) 2 E dengan x 2 S dan y 2 T . Di sisi lain, jika x 2 T dan y 2 S, maka terdapat suatu lintasan arus-tambahan tak lengkap dari a ke y. Jika f (x; y) > 0, maka dapat dilabelkan mundur dari y ke x, sehingga akan terdapat suatu lintasan arus-tambahan tak lengkap dari a ke x, kontradiksi dengan kenyataan bahwa x =2 S. Karena itu haruslah f (x; y) = 0 untuk setiap (x; y) 2 E dengan x 2 T dan y 2 S. Akibatnya
V (f) = X x2S; y2T (x;y)2E f (x; y) X x2T; y2S (x;y)2E f (x; y) = X x2S; y2T (x;y)2E c (x; y) = c (S; T ) :
Untuk sembarang potongan lain (S0; T0), dari Proposisi 4.10 diperoleh c S0; T0 V (f) = c (S; T ) :
Karena itu (S; T ) adalah suatu potongan minimum.
Suatu algoritma untuk memaksimumkan arus dalam suatu jaringan diberikan oleh Lester Randolph Ford, Jr. (matematikawan Amerika) dan Delbert Ray Fulkerson (1924 1976) yang diperkenalkan pada pertengahan tahun 1956: dimulai dengan arus nol, secara berulang ditambahkan arus sepanjang lintasan a z dalam graf sisa, sampai tidak ada lintasan tersebut. Algoritma mereka dikenal dengan nama Algoritma Ford-Fulkerson.
Algoritma Ford-Fulkerson.
Input: Suatu jaringan D = (V; E) dengan fungsi kapasitas c : E ! N, titik sumber a dan titik target akhir z.
Ouput: Arus maksimum untuk jaringan D.
(1) (Inisialisasi) Diambil f sebagai suatu arus …sibel awal (contoh, f (e) = 0 untuk setiap e 2 E dalam suatu jaringan tanpa arus).
X
(a;y)2E
f (a; y). Jika terdapat lintasan arus-tambahan P , aplikasikan Algoritma Arus Tambahan pada P dan selanjutnya kembali ke langkah (2).
Sebagai contoh, diinginkan untuk mencari arus maksimum dan potongan minimum dari jaringan dalam Gambar 4.3.
(L1) Dimulai dengan suatu arus f : E ! N [ f0g yang dide…nisikan oleh f (x; y) = 0 untuk setiap (x; y) 2 E, maka dipunyai keadaan berikut:
Berdasarkan pengamatan, dipunyai lintasan arus-tambahan:
Arus dari a ke z dapat dinaikkan sebesar = minf12 0, 9 0, 14 0, 8 0g = 8, sehingga dipunyai keadaan:
(L2) Berdasarkan pengamatan lagi, dipunyai lintasan arus-tambahan:
sehingga dipunyai keadaan:
(L3) Berdasarkan pengamatan lagi, dipunyai lintasan arus-tambahan:
Arus dari a ke z dapat dinaikkan sebesar = minf10 1, 8, 8 0, 7 1g = 6, sehingga dipunyai keadaan:
Karena tidak ditemukan lagi lintasan arus-tambahan, maka proses berhenti dan diperoleh arus maksimum untuk jaringan yaitu
O (a) = f (a; b) + f (a; d) = 8 + 7 = 15:
Selanjutnya, untuk mencari suatu potongan minimum dikonstruksi suatu pohon dari lintasan arus-tambahan tak lengkap. Ini bisa dalam bentuk
Pohon tersebut tidak mencapai titik target akhir z. Karena itu dapat diambil suatu potongan minimum (S; T ), dimana S = fa, b, c, d, eg dan T = fzg, dengan kapasitas potongan
4.4
Soal-soal untuk Bab 4
1. Diberikan graf berarah yang dinyatakan oleh matriks ketetanggaan berikut ini.
A = 2 6 6 6 6 6 6 4 0 0 0 1 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 3 7 7 7 7 7 7 5
a) Cari suatu lintasan berarah dari titik v3 ke titik v6.
b) Cari suatu lingkaran berarah yang dimulai dan diakhiri di titik v4.
c) Aplikasikan algoritma Warshall untuk mencari matriks keterjangkauan dari graf berarah.
2. Diberikan graf berarah yang dinyatakan oleh matriks ketetanggaan berikut ini.
A = 2 6 6 6 6 6 6 6 6 6 6 4 0 1 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 3 7 7 7 7 7 7 7 7 7 7 5
a) Apakah ada suatu lintasan berarah dari titik v3 ke titik v2?
b) Cari suatu lingkaran berarah dari graf berarah.
c) Aplikasikan algoritma Warshall untuk mencari matriks keterjangkauan dari graf berarah.
3. Diberikan suatu digraf yang dinyatakan oleh matriks ketetanggaan berikut ini.
A = 2 6 6 6 6 6 6 6 6 6 6 4 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 3 7 7 7 7 7 7 7 7 7 7 5
a) Apakah ada suatu lintasan berarah dari titik v1 ke titik v8?
b) Cari semua lingkaran berarah pada graf berarah yang dimulai dari titik v1.
4. Diperhatikan suatu jaringan D = (V; E) yang digambarkan oleh graf berikut ini.
a) Suatu arus f : E ! N [ f0g dide…nisikan oleh f (a; b) = f (b; c) = f (c; z) = 3 dan f (x; y) = 0 untuk sembarang busur (x; y) 2 Enf(a; b), (b; c), (c; z)g. Berapakah nilai V (f) dari arus tersebut?
b) Caris suatu arus maksimum dari jaringan, dimulai dengan arus pada bagian a).
c) Cari suatu potongan minimum yang berkorespondensi.
5. Diperhatikan suatu jaringan D = (V; E) yang digambarkan oleh graf berikut ini.
a) Suatu arus f : E ! N [ f0g dide…nisikan oleh f (a; i) = f (i; j) = f (j; g) = f (g; k) = f (k; h) = f (h; z) = 5 dan f (x; y) = 0 untuk sembarang busur (x; y) 2 Enf(a; i), (i; j), (j; g), (g; k), (k; h), (h; z)g. Berapakah nilai V (f) dari arus tersebut?
b) Caris arus maksimum dari jaringan, dimulai dengan arus pada bagian a). c) Cari suatu potongan minimum yang berkorespondensi.
[1] Bondy, J. A., dan Murty, U. S. R. (1982). Graph Theory with Applications. Elsevier Science Publishing Co., Inc., New York.
[2] Chen, W.W.L. (2008). Discrete Mathematics. Naskah, Bab 17 20, Macquarie University.
[3] Dasgupta, S., C.H. Papadimitriou, dan U.V. Vazirani (2006). Algorithms. Naskah, Bab 4 dan Bab 5, University of California.
[4] Diestel, R. (2005). Graph Theory. Springer-Verlag, New York (Electronic Edition). [5] English Wikipedia, Ensiklopedia Bebas. http://en.wikipedia.org/wiki/. Tanggal
ak-ses: 13 Oktober 2008 pukul 09.42.
[6] Harts…eld, N. dan G. Ringel (1990). Pearls In Graph Theory. Academic Press, San Diego.
[7] Haxhimusa, Y.I.I. (2006). The Structurally Optimal Dual Graph Pyramid and its Application in Image Partitioning. Tesis PhD, Bab 2, Vienna University of Tech-nology.
[8] Kumpulan Bahan Kuliah, Kuis dan Ujian, Makalah Matematika Diskrit. http://www.informatika.org/~rinaldi/Matdis/2008-2009/strukdis08-09.htm. Tanggal akses: 13 Oktober 2008 pukul 09.30.
[9] Munir, R. (2003). Matematika Diskrit. Bandung. Informatika.
[10] Ruohonen, K. (2006). Graph Theory. Naskah, Tampere University of Technology. [11] West, D. B. (1996). An Introduction to Graph Theory. Prentice-Hall.
[12] Wikipedia Bahasa Indonesia, Ensiklopedia Bebas. http://id.wikipedia.org/wiki/. Tanggal akses: 13 Oktober 2008 pukul 13.10.