Modul 9.
PENELITIAN OPERASIONAL
PEMROGRAMAN DINAMIS
Oleh : Eliyani
PROGRAM KELAS KARYAWAN PROGRAM STUDI TEKNIK INDUSTRI
FAKULTAS TEKNOLOGI INDUSTRI UNIVERSITAS MERCU BUANA
http://www.mercubuana.ac.id
JAKARTA 2007
MODUL 9
RISET OPERASIONAL PEMROGRAMAN DINAMIS Pendahuluan
Pemrograman dinamis (dynamic programming/DP) adalah prosedur matematis yang terutama dirancang untuk memperbaiki efisiensi perhitungan masalah pemrograman matematis tertentu dengan menguraikannya menjadi bagian-bagian yang lebih kecil sehingga lebih sederhana dalam perhitungan. Pemrograman dinamis pada umumnya menjawab masalah dalam tahap-tahap dengan setiap tahap memiliki satu variabel optimasi. Perhitungan di tahap yang berbeda dihubungkan
dengan perhitungan rekursif dengan cara yang menghasilkan pemecahan optimal yang mungkin bagi seluruh masalah.
Dikatakan dinamis, karena penggunaan metode ini yang melibatkan pengambilan keputusan yang berkaitan dengan waktu. Namun tidak selalu pentahapan berbasis waktu yang dapat dilakukan dengan DP, sehingga nama yang lebih tepat untuk kondisi yang demikian adalah pemrograman multitahap (multistage programming).
Unsur-unsur model DP
Contoh : masalah penganggaran modal
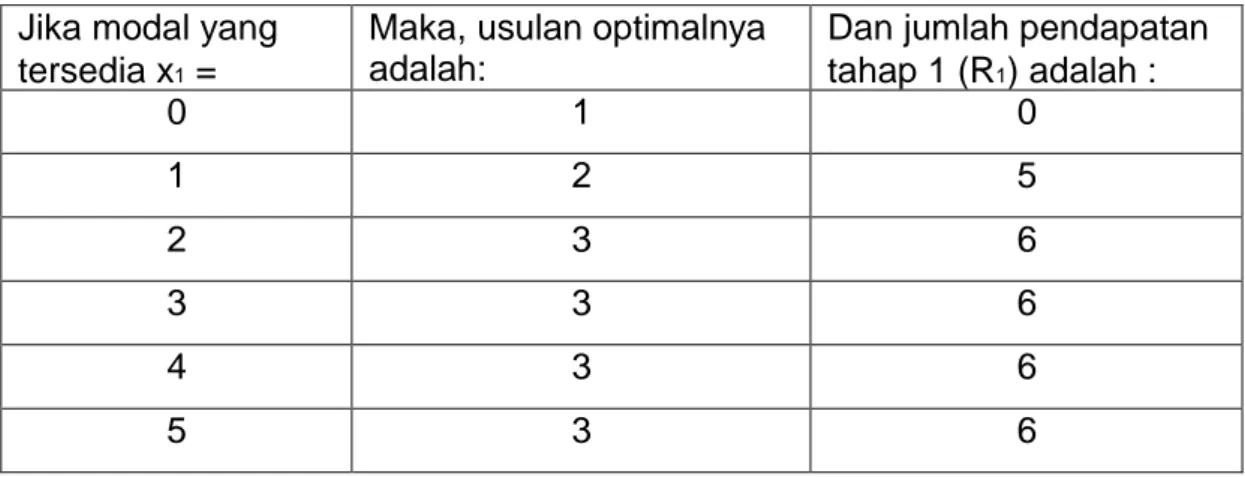
Sebuah perusahaan mempunyai usulan dari ketiga pabriknya untuk kemungkinan mengembangkan sarana produksi. Perusahaan tersebut menyediakan anggaran $5 juta untuk alokasi pada ketiga pabrik. Setiap pabrik diminta untuk menyampaikan usulannya yang memberikan jumlah biaya (c) dan jumlah pendapatan (R) untuk setiap usulan. Tabel 1
meringkaskan biaya dan pendapatan (dalam jutaan dollar). Usulan biaya nol diperkenalkan untuk memungkinkan tidak dialokasikannya dana pada masing-masing pabrik. Sasaran dari perusahaan tersebut adalah untuk memaksimumkan jumlah pendapatan yang dihasilkan dari alokasi $5 juta
1
Usulan Pabrik 1 Pabrik 2 Pabrik 3 c1 R1 c2 R2 c3 R3 1 0 0 0 0 0 0 2 1 5 2 8 1 3 3 2 6 3 9 - - 4 - - 4 12 - - MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS Tabel 1. Usulan Pengembangan Sarana Produksi
Cara yang langsung untuk menjawab masalah ini adalah melalui enumerasi lengkap. Masalah ini memiliki 3 x 4 x 2 = 24 kemungkinan pemecahan, beberapa di antaranya tidak layak karena memerlukan modal yang lebih besar dari $5 juta. Gagasan dari enumerasi yang lengkap adalah menghitung jumlah biaya dari masing-masing kombinasi. Jika tidak melebihi modal yang tersedia, pendapatan total diperhitungkan. Pemecahan optimum adalah kombinasi yang mungkin yang menghasilkan jumlah pendapatan tertinggi. Contoh, usulan 2, 3, dan 1 untuk pabrik 1, 2 dan 3 memerlukan biaya $4 juta (<$5 juta.) dan menghasilkan pendapatan total $14 juta. Sebaliknya, kombinasi yang terdiri dari usulan 3, 4, dan 2 tidak layak karena biayanya adalah $7 juta.
Jadi, kekurangan enumerasi lengkap:
1. mencakup kombinasi dengan kemungkinan tidak layak.
2. penghitungan menjadi tidak efisien karena adanya kombinasi yang tidak layak.
3. kombinasi-kombinasi yang tidak layak yang ditemukan di awal tetap dipertimbangkan pada perhitungan kombinasi berikutnya.
Model DP
Konsep : penyelesaian masalah dibagi dalam beberapa tahap, namun harus ada cara untuk menghubungkan tahap-tahap tersebut. Setiap tahap memiliki penyelesaian optimal.
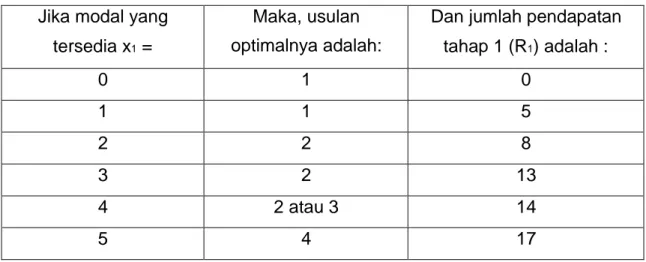
Jika modal yang tersedia x1 =
Maka, usulan optimalnya adalah:
Dan jumlah pendapatan tahap 1 (R1) adalah : 0 1 0 1 2 5 2 3 6 3 3 6 4 3 6 5 3 6 MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS Pada masalah penganggaran modal di atas:
Masalah dapat diselesaikan dalam 3 tahap, sebab kita menginginkan kombinasi biaya dari ketiga pabrik yang memberikan pendapatan atau keuntungan maksimum.
Katakanlah pada tahap 1, kita berusaha mencari usulan terbaik dari pabrik 1, pada tahap 2 kita berusaha mencari usulan terbaik dari
kombinasi antara pabrik 2 dan pabrik 1, dan pada tahap ketiga, kita mencari kombinasi terbaik pabrik 1, 2 dan 3.
Usulan terbaik pada setiap tahap tentu akan menghabiskan sejumlah modal, padahal jumlah modal yang tersedia terbatas yaitu $5 juta. Karena itu, jumlah modal yang telah dialokasikan pada tahap 1 menjadi pertimbangan pada tahap 2 dst. Jadi faktor pembatas kita adalah modal.
Katakanlah :
x1 = jumlah modal yang dialokasikan untuk tahap 1
x2 = jumlah modal yang dialokasikan untuk tahap 1 dan 2
x3 = jumlah modal yang dialokasikan untuk tahap 1, 2 dan 3
Tahap 1.
Pada tahap 1, pengunaan modal yang mungkin adalah dari $0 juta hingga $5 juta
sehingga usulan optimal untuk masing-masing alternatif modal adalah seperti disajikan pada Tabel 1.
http://www.mercubuana.ac.id
MODUL 9
RISET OPERASIONAL PEMROGRAMAN DINAMIS
x1 > 2 mewakili pengeluaran yang berlebihan untuk tahap 1 sebab tidak
terjadi lagi penambahan pendapatan.
Tahap 2. Pengunaan modal yang mungkin adalah dari $0 juta hingga $5 juta. Namun : P e n d a p a t a n t a h a p 2 d e n g a n t a h a p 1 max semua alternatif yan g lay ak pad a 2
pendapa tan dari
alternatif yang
layak untuk tahap
terbesar untuk diketahui x dan 2
untuk tahap 1 dengan
2 diketahui keadaan x1
pendapa tan terbesar
di mana x1 = x2 – modal yang dialokasikan pada alternatif tahap 2.
x2 = 0
Maka usulan yang mungkin adalah usulan 1 baik untuk pabrik 1 maupun 2 dengan total pendapatan 0 + 0 = 0.
x2 = 1
Hanya ada satu kemungkinan yang layak, yaitu usulan 1 untuk pabrik 2 yang bernilai 0 dengan usulan 2 pabrik 1 yang memberikan pendapatan 5, karena kombinasi lain menghasilkan biaya yang paling tidak 2. Sehingga:
Pendapatan terbesar dengan diket. x2 = 1 = 0 + 5 = 5.
x2 = 2
Di sini kita memiliki dua alternatif usulan pabrik 2 yang layak : usulan 1 dan usulan 2 dengan biaya 0 dan 2 yang masing-masing menghasilkan pendapatan sebesar 0 dan 8. Jadi, nilai x1 yang sesuai dengan usulan 1
dan 2 adalah sesuai dengan rumus : x1 = x2 - c2 yaitu x1 = 2 – 0 = 2 dan 2
– 2 = 0. Usulan optimal pabrik 1 yang memberikan x1 = 2 dan x1 = 0
MODUL 9
RISET OPERASIONAL PEMROGRAMAN DINAMIS
berdasarkan Tabel 1 di atas adalah usulan 3 dan usulan 1 dengan pendapatan masing-masing sebesar 6 dan 0, sehingga :
Pendapatan terbesar dengan diket. x2 = 2 = max (0 + 6 = 6, 8 + 0 = 8) = 8
yang bersesuaian dengan usulan 2 untuk pabrik 2.
x2 = 3
Di sini ada dua alternatif yang layak, yaitu usulan 1, 2 dan 3. Nilai x1 yang
sesuai adalah 3 – 0 = 3 dan 3 – 2 = 1, dan 3 – 3 = 0. Jadi kita memperoleh :
Pendapatan terbesar dengan diket. x2 = 3 = max (0 + 6 = 6, 8 + 5 = 13, 9
+ 0 = 9) = 13
yang bersesuaian dengan usulan 2 untuk pabrik 2.
x2 = 4
Alternatif yang layak adalah usulan 1, 2, 3 dan 4. Nilai-nilai x1 yang sesuai
masing-masing adalah 4 – 0 = 4, 4 – 2 = 2, 4 – 3 = 1 dan 4 – 4 = 0, sehingga:
Pendapatan terbesar dengan diket. x2 = 4 = max (0 + 6, 8 + 6, 9 + 5, 12 +
0) = 14
yang bersesuaian dengan usulan 2 atau 3.
x2 = 5
Kita memiliki alternatif layak yang sama seperti dalam x2 = 4. Nilai-nilai x1
yang sesuai masing-masing adalah 5, 3, 2 dan 1. Jadi:
Pendapatan terbesar dengan diket. x2 = 5 = max (0 + 6, 8 + 6, 9 + 6, 12 +
5) = 17
yang bersesuaian dengan usulan 4.
Jika modal yang tersedia x1 =
Maka, usulan optimalnya adalah:
Dan jumlah pendapatan tahap 1 (R1) adalah : 0 1 0 1 1 5 2 2 8 3 2 13 4 2 atau 3 14 5 4 17 MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS Ringkasan perhitungan tahap 2 disajikan pada Tabel 2.
Tabel 2. Alternatif penggunaan modal pada tahap 2.
Tahap 3.
Rumus untuk menghitung pendapatan terbesar sama dengan tahap 2 kecuali bahwa x2 dan x1 digantikan oleh x3 dan x2 dan tahap 2 dan tahap
1 digantikan oleh tahap 3 dan tahap 2. Karena sudah tahap terakhir, maka x3 hanya memiliki satu nilai spesifik, yaitu x3 = 5. Karena x3 memiliki dua
usulan yang biayanya tidak mencapai $5 juta, maka kedua usulan
tersebut layak. Nilai-nilai x2 yang sesuai dengan usulan 1 dan 2 yaitu 5 – 0
= 5 dan 5 – 1 = 4. Dengan menggunakan Tabel 2, kita memperoleh: Pendapatan terbesar dengan diket. x3 = 5 = max (0 + 17, 3 + 14) =
17 yang bersesuaian dengan usulan 1 atau 2.
Definisi Keadaan
Keadaan sistem mungkin merupakan konsep yang paling penting dalam model pemrograman dinamis. Keadaan ini mewakili hubungan antara tahap-tahap sehingga ketika setiap tahap dioptimumkan secara terpisah, keputusan yang dihasilkan dengan sendirinya layak untuk seluruh masalah.
MODUL 9
RISET OPERASIONAL PEMROGRAMAN DINAMIS
Namun keadaan ini seringkali tidak jelas sehingga sulit ditemukan cara menghubungkan tahap-tahap tersebut. Dua pertanyaan berikut dapat menjadi cara untuk menemukan keadaan :
1. Hubungan apa yang mempersatukan tahap-tahap tersebut? 2. Informasi apa yang diperlukan untuk mengambil keputusan yang
layak pada tahap sekarang tanpa memeriksa kelayakan keputusan tahap sebelumnya?
Perhatikan contoh-contoh berikut:
Contoh 1. Pada masalah penganggaran yang sudah dibahas sebelumnya, keadaan yang menghubungkan antar tahap adalah alokasi modal.
Pertimbangannya adalah fakta bahwa semua pabrik (yang menjadi tahap) bersaing untuk bagian modal yang terbatas.
Contoh 2. Pertimbangkan situasi penggantian peralatan di mana pada akhir setiap tahun sebuah keputusan diambil untuk menggunakan mesin pada tahun berikutnya atau menggantinya segera. Jika sebuah mesin disimpan lebih lama, laba yang diperolehnya menurun. Sebaliknya mengganti sebuah mesin mengeluarkan biaya penggantian. Masalahnya adalah memutuskan kapan sebuah mesin harus diganti untuk memaksimumkan jumlah laba bersih.
Dalam masalah ini, tahap j mewakili tahun j. Alternatif pada setiap tahap adalah mempertahankan mesin atau menggantinya. Untuk mendefinisikan keadaan sistem : apa hubungan antara dua tahap berturut-turut?
Informasi apa yang diperlukan dari tahap-tahap sebelumnya untuk mengambil keputusan (mempertahankan atau mengganti) dalam tahap sekarang? Jawabannya adalah : usia mesin. Jadi keadaan sistem pada suatu tahap ditentukan sebagai usia mesin pada awal periode yang berkaitan. Jadi usia mesin akan menjadi x1, x2 dan seterusnya.
f1 ( x1 ) maxR1 (k1 )
f j ( x j ) max
R j (k j ) f j1 x j c j (k j )
, j 2,3 MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS PERSAMAAN REKURSIFPerhitungan yang dilakukan pada pemrograman dinamis bersifat rekursif, perhitungan pada suatu tahap didasarkan pada tahap sebelum atau sesudahnya. Misalnya perhitungan pada tahap 2 tergantung pada perhitungan tahap 1 dan perhitungan pada tahap 3 tergantung pada perhitungan tahap 2. Dengan perkataan lain, perhitungan pada tahap sekarang memanfaatkan ringkasan informasi tahap sebelumnya. Ringkasan ini memberikan pendapatan optimal dari semua tahap dipilih ambil secara optimal tanpa melihat keputusan yang diambil sebelumnya. Sifat ini merupakan prinsip optimalitas yang merupakan daar bagi
keabsahan perhitungan DP.
Persamaan rekursif, secara matematis, dinyatakan dengan simbol- simbol:
Rj(kj) = pendapatan alternatif kj pada tahap j
fj(xj) = keuntungan optimal pada tahap 1, 2,… dan jika j keadaan xj
cj(kj) = harga kj alternatif pada tahapj
Persamaan rekursif dapat ditulis sebagai:
c1k1 x1
c j k j x j
Perhitungan persamaan rekursif dilakukan dalam bentuk tabel standar seperti yang digambarkan pada perhitungan berikut. Tabel standar kasus penganggaran modal adalah:
f1 ( x1 ) maxR1 (k1 ) f 2 ( x2 ) maxR2 (k 2 ) f1
x2 c2 (k 2 )
MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS Tahap 1 c1k1 x1 k11,2,3 R1(k1) Pemecahan Optimal x1 0 1 2 3 4 5 k1=1 0 0 0 0 0 0 k1=2 - 5 5 5 5 5 k1=3 - - 6 6 6 6 f1(x1) 0 5 6 6 6 6 k1* 1 2 3 3 3 3 Tahap 2 c2k 2 x2 k 21, 2,3, 4 R2 (k 2 ) f1
x2 c2 (k 2 )
Solusi Optimal x2 0 1 2 k2=1 0+0=0 0+5=5 0+6=6 k2=2 - - 8+0=8 k2=3 - - - k2=4 - - - f2(x2) 0 5 8 k 2* 1 1 2 3 0+6=6 8+5=13 9+0=9 - 13 2 4 0+6=6 8+6=14 9+5=14 12+0=12 14 2 atau 3 5 0+6=6 8+6=14 9+6=15 12+5=17 17 4 Tahap 3 by Eliyani http://www.mercubuana.ac.id 9f 3 ( x3 ) maxR3 (k 3 ) f 3
x3 c3 (k 3 )
MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMIS c3k3 x3 k31,2 R3 (k 3 ) f 3
x3 c3 (k 3 )
Solusi Optimal x3 k3=1 k3=2 f3(x3) k 3* 5 0+17=17 3+14=17 17 1 atau 2Pemecahan optimum dapat dibaca secara langsung dari tabel di atas dimulai dengan tahap 3. Untuk x3 = 5, usulan optimalnya adalah k 3* =1 atau k 3* =2. Pertimbangkan k 3* =1 terlebih dahulu.Karena c3(1) = 0, hal ini
membuat x2=x3- c3(1)=5 untuk tahap 2 dan tahap 1. Tahap 2 menunjukkan
bahwa x2 = 5 menghasilkan k 2* =4. Karena c2(4) = 4, maka x1= 5-4 = 1.
Dari tahap 1, x1 = 1 memberikan k1* =2. Jadi kombinasi optimal dari usulan untuk tahap 1, 2 dan 3 adalah (2,4,1).
Persamaan Rekursif Mundur
Perhitungan di atas mencerminkan persamaan rekursif maju, dari tahap awal menuju tahap akhir. Yang umum dilakukan adalah rekursif mundur, dari tahap terakhir berlanjut ke belakang ke tahap 1. Perbedaan utama antara kedua prosedur adalah dalam cara mendefinisikan keadaan sistem. Contoh kasus penganggaran modal di atas, dapat diselesaikan dengan metode rekursif mundur sebagai:
Keadaan sistem disimbolkan dengan yj sehingga:
y1 = jumlah modal yang dialokasikan pada tahap 1, 2 dan 3.
y2 = jumlah modal yang dialokasikan pada tahap 2 dan 3.
y3 = jumlah modal yang dialokasikan pada tahap 3.
f3(y3) = pendapatan optimal untuk tahap 3 dengan diketahui y3
f j ( y j ) max
R j (k j ) f j1 y j c j (k j )
, j 1,2 f 3 ( y3 ) maxR3 (k 3 ) f 2 ( y 2 ) maxR2 (k 2 ) f 3
y 2 c2 (k 2 )
MODUL 9 RISET OPERASIONAL PEMROGRAMAN DINAMISf1(y1) = pendapatan optimal untuk tahap 1,2 dan 3 dengan diketahui y1
Persamaan rekursif mundur dengan demikian ditulis sebagai:
f 3 ( y3 ) maxR3 (k 3 ) k 3 c3k3 x3 k j c j k j y j f3 Urutan perhitungan tahap dengan demikian adalah:
Tahap 3. k31, 2 c3k3 x3 f3 f3 R3(k3) Solusi Optimal y3 0 1 2 3 4 5 k3=1 0 0 0 0 0 0 k3=2 - 3 3 3 3 3 f3(y3) 0 3 3 3 3 3 k 3* 1 2 2 2 2 2 Tahap 2. c2k 2 x2 k 21,2,3,4 by Eliyani http://www.mercubuana.ac.id 11
f1 ( y1 ) maxR1 (k1 ) f 2