Aplikasi pengelompokan data penerima kredit sepeda motor PT. Federal International Finance cabang Cilacap dengan menggunakan metode fuzzy c-means - USD Repository

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh:

Irene Widya Ratna Utami NIM : 053114012

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

2010

ii

INTERNATIONAL FINANCE CILACAP

Final Project

Presented as Partial Fulfillment of the Requirements To Obtain the Sarjana Sains Degree

In Mathematics

By:

Irene Widya Ratna Utami Student Number: 053114012

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTEMENT FACULTY OF SCIENCE AND OF TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v

Tidak bisa menciptakan sesuatu yang jenius....

Perlu imajinasi

dan (mungkin) kombinasi keduanya

(Zeth)

Skripsi ini kupersembahkan kepada:

Tuhan Yesus dan Bunda Maria yang selalu memberkatiku,

Papah, Ibu, Eyang Putri dan Kakung yang selalu mendukungku,

Kekasihku tercinta yang selalu memberikan semangat dalam keadaan apapun,

memuat karya atau bagian orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, Maret 2010 Penulis,

Irene widya Ratna Utami

terhadap pusat cluster. Tujuan pengelompokan (cluster) adalah untuk membagi sejumlah data menjadi beberapa kelompok yang memiliki kemiripan. Pada kondisi awal, pusat cluster ditentukan dengan cara membangkitkan bilangan random, kemudian menghitung fungsi objektif untuk memperoleh cluster yang optimum. Tiap-tiap titik data memiliki derajat keanggotaan untuk tiap-tiap cluster. Dengan cara memperbaiki pusat cluster dan derajat keanggotaan tiap-tiap titik data secara berulang, maka akan dapat dilihat bahwa pusat cluster akan bergerak menuju lokasi yang tepat dengan galat yang telah ditentukan.

Output dari Fuzzy C-means (FCM) bukan merupakan fuzzy inference system, namun merupakan deretan pusat cluster dan beberapa derajat keanggotaan untuk tiap-tiap titik data. Informasi ini dapat digunakan untuk membantu dalam melihat profil data dan mempresentasikan kelakuan dari suatu kelompok data

by minimizing the total distance in each cluster of data to the center. The objective of grouping (clustering) is to divide the amount of data into several groups that have similarities. In the initial conditions, the cluster center is determined by generating random numbers, then calculate the objective function to obtain the optimum of clustering. Each data point has a degree of membership for each cluster. By improving the cluster centers and the degree of membership of each data point, again, it will be seen that the cluster center will move to the right location with a predetermined error.

The output of the Fuzzy C-means (FCM) is not a fuzzy inference system, but a row series of cluster centers and some degree of membership for each data point. This information can be used to assist in viewing the data profile and present the behavior of a group of data

x

berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi ini.

Berkat dukungan dan bantuan dari banyak pihak, akhirnya skripsi ini dapat

terselesaikan. Oleh karena itu, penulis mengucapkan terima kasih kepada:

1. Bapak Yosef Agung Cahyanta S.T., M.T., selaku Dekan Fakultas Sains dan

Teknologi Universitas Sanata Dharma Yogyakarta.

2. Bapak Eko Hari Parmadi, S.Si, M.Kom., selaku dosen pembimbing yang

telah memberikan pengarahan dan bimbingan selama penyusunan skripsi ini.

3. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Kaprodi Matematika

yang selalu memberikan semangat kepada penulis.

4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku Dosen Penguji tugas akhir yang

telah memberikan masukan dan saran.

5. Ibu Ch. Enny Murwaningtyas, S.Si, M.Si., selaku Dosen Penguji tugas akhir

yang telah memberikan masukan dan saran.

6. Romo Prof. Dr. Frans Susilo, SJ., selaku Dosen Pembimbing akademik

angkatan 2005 yang telah membimbing dan memberikan semangat selama

menjalani proses akademik.

7. Bapak dan Ibu dosen yang telah memberikan bekal ilmu kepada penulis.

8. Bapak Zaerilus Tukija dan Ibu Erma Linda Santyas Rahayu yang telah

memberikan pelayanan administrasi kepada penulis selama masa

xi

fasilitas dan memberikan kemudahan kepada penulis selama masa

perkuliahan.

11. Kedua orang tuaku tercinta: Bapak Agus Slamet dan Ibu Theresia

Ruminingsih yang dengan penuh cinta kasih telah memberikan semangat,

saran dan dukungan kepada penulis dalam segala hal.

12. Eyang Putri dan Eyang Kakungku terkasih dan tercinta: T.S Sukirman dan

Lucia Roestinah yang sudah mau merawat penulis selama 18 tahun dengan

penuh cinta kasih dan selalu memberikan semangat, dukungan, serta

kepercayaan diri dalam segala hal.

13. Arie Wibowo tercinta yang selalu mendampingi penulis dalam segala hal.

14. Kakakku, Wiwit, Ratih, Mekar, adikku Sari, Fani, dan keponakanku Aurel

serta keluarga besar T.S Sukirman yang telah memberikan doa dan dukungan

kepada penulis.

15. Teman-teman angkatan 2005 yang selalu memberikan kebahagian selama

proses akademik, khususnya Dedi ”si guru privat”, Zetho ”si Jenius”, Sisiria

”si perempuan Cina” yang selalu sabar dengan segala tingkah penulis, serta

teman kos Benteng Lt 1, Siska, Mayan, Rani, Novi, Nila dan Wingga yang

telah memberikan kehangatan dan dukungan kepada penulis.

xii sebutkan satu-persatu di sini.

Yogyakarta, Maret 2010

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

HALAMAN PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... ix

KATA PENGANTAR ... x

DAFTAR ISI... xiii

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 3

C. Pembatasan Masalah ... 3

D. Tujuan Penulisan ... 3

E. Manfaat Penulisan ... 4

F. Metode Penulisan ... 4

G. Sistematika Penulisan ... 4

BAB II HIMPUNAN KABUR DAN ANALISIS CLUSTER... 7

2. Fungsi Keanggotaan ... 11

3. Operasi Baku pada Himpunan Kabur ... 13

4. Relasi Kabur... 17

5. Ukuran Kabur... 20

6. Indeks Kekeburan... 21

B. Analisis Cluster... 22

1. Metode-metode dalam Analisis Cluster ... 26

BAB III PENGELOMPOKAN KABUR DENGAN METODE FUZZY C-MEANS 34 A. Pembangkit Bilangan Random... 34

B. Partisi Kabur ... 37.

C. Konsep Pengelompokan Kabur (Fuzzy Clustering)... 38

D. Pengelompokan Kabur Dengan Metode C-Means ... 40

E. Algoritma Fuzzy C-Means... 47

BAB IV APLIKASI DAN ANALISIS………... 61

A. Gambaran Umum Dan Sejarah Singkat Perusahaan... 61

B. Pengelompokan Kabur dengan Metode Fuzzy C-Means ... 62

1. Aplikasi Fuzzy C-Means ... 63

2. Contoh Kasus ... ... 69

BAB V PENUTUP ... 76

A. Kesimpulan ... 76

B. Saran ... 78

A. Latar Belakang Masalah

informasi yang didapatkan dari hasil pengelompokkan dapat digunakan dalam pemodelan kabur (fuzzy).

Pada ilustrasi di atas dapat diidentifikasi dengan aturan-aturan fuzzy. Salah satu cara untuk menentukan pengelompokan kabur adalah menggunakan metode fuzzy c-means. Dengan metode ini suatu himpunan dikelompokkan menjadi c buah himpunan bagian kabur, masing-masing disebut cluster, yang membentuk

suatu partisi kabur sedemikian sehingga 1 untuk setiap k = 1,2,…,n, 1

=

∑

=

c i

ik μ

dan 0 <

∑

< n untuk setiap i = 1,2,…,c. Misalkan

=

c k

ik 1

μ X =

{

x1,x2,...,xn

}

adalah

himpunan data yang diselidiki, konsep dasar fuzzy c-means, menentukan pusat

cluster yang akan menandai lokasi rata-rata untuk tiap-tiap cluster. Pada kondisi awal, pusat cluster ini masih belum akurat. Tiap-tiap titik data memiliki derajat keanggotaan untuk tiap-tiap cluster. Dengan cara memperbaiki pusat cluster dan derajat keanggotaan tiap-tiap titik data secara berulang, maka akan dapat dilihat bahwa pusat cluster akan bergerak menuju lokasi yang tepat.

Perulangan ini didasarkan pada minimisasi fungsi objektif yang

menggambarkan jarak dari titik data yang diberikan ke pusat cluster yang terbobot oleh derajat keanggotaan titik data tersebut.

i v

t P

B. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi ini adalah :

2. Bagaimana menerapkan pengelompokan kabur dengan metode Fuzzy C-Means pada masalah nyata studi kasus pada PT. FIF Cabang Cilacap?

C. Pembatasan Masalah

Dalam skripsi ini, penulis membahas tentang pengelompokan kabur dengan metode Fuzzy C-Means dan penggunaannya. Data penelitian yang digunakan hanya untuk kelompok data kreditor sepeda motor bermerk Honda D Supra X dengan sample berjumlah 100 kreditor, variabel yang dijadikan acuan pengelompokan menurut analisis Capital, yaitu pendapatan bulanan, pengeluaran bulanan, harga barang, uang muka, besarnya angsuran bulanan, dan lama angsuran bulanan. Dalam skripsi ini tidak membahas fuzzy inference system sebagai outputnya.

D. Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah :

1. Menghasilkan pengelompokan kabur dengan metode fuzzy c-means. 2. Mengerti penggunaan pengelompokan kabur dengan metode Fuzzy

C-Means

3. Menerapkan pengelompokan kabur dengan metode Fuzzy C-Means pada data penerima kredit sepeda motor PT. FIF Cabang Cilacap.

E. Manfaat Penulisan

1. Membantu menghasilkan penerapan pengelompokan kabur dengan metode Fuzzy C-Means.

2. Membantu berbagai pihak khususnya PT. FIF Cabang Cilacap dalam menyelesaikan suatu masalah yang berkaitan dengan pengelompokan kabur dengan metode Fuzzy C-Means.

F. Metode Penulisan

Metode penulisan yang digunakan adalah metode studi pustaka, yaitu dengan mempelajari beberapa bagian dari buku acuan yang berkaitan dengan topik tugas akhir dan bantuan komputer dalam pengaplikasiannya dengan menggunakan program Matlab 7.0.1.

G. Sistematika Penulisan BAB I PENDAHULUAN

A. Latar Belakang Masalah B. Rumusan Masalah C. Pembatasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan

A. Himpunan Kabur

1. Definisi Himpunan Kabur 2. Fungsi Keanggotaan

3. Operasi Baku pada Himpunan Kabur 4. Relasi Kabur

5. Ukuran Kabur 6. Indeks Kekaburan B. Analisis Cluster

BAB III PENGELOMPOKAN KABUR DENGAN METODE FUZZY

C-MEANS

A. Pembangkitan Bilangan Random B. Partisi Kabur

C. Konsep Pengelompokan Kabur (Fuzzy Clustering) D. Pengelompokan Kabur dengan Metode Fuzzy C-Means E. Algoritma Fuzzy C-means

BAB IV APLIKASI DAN ANALISIS

A. Gambaran Umum dan Sejarah Singkat Perusahaan B. Pengelompokan Kabur dengan Metode Fuzzy C-Means

A. Himpunan Kabur

1. Definisi Himpunan Kabur

nilai fungsi itu disebut derajat keanggotaan suatu unsur dalam himpunan itu, yang selanjutnya disebut himpunan kabur. Derajat keanggotaan dinyatakan dengan suatu bilangan real dalam selang tertutup [0, 1]. Dengan perkataan lain, fungsi keanggotaan

dari suatu himpunan kabur A~ dalam semesta X adalah pemetaan μ_A~ dari X ke selang

[0, 1], yaitu ~:X →[0,1] A

μ . Nilai fungsi μ_A~(x) menyatakan derajat keanggotaan

unsur x ∈ X dalam himpunan kabur A~.

Definisi 2.1

Secara matematis suatu himpunan kabur A~ dalam semesta X dapat dinyatakan sebagai himpunan pasangan terurut

} |

)) ( , {( ~

~ x x X

x A

A ∈

= μ

(2.1)

di mana μ_A~ adalah fungsi keanggotaan dari himpunan kabur A~, yang merupakan suatu pemetaan dari himpunan semesta X ke selang tertutup [0, 1]. Apabila semesta

X adalah himpunan yang kontinu, maka himpunan kabur A~ seringkali dinyatakan dengan

∫

∈

= X x

A x x A~ μ~( )/

(2.2)

di mana lambang di sini bukan lambang integral seperti yang dikenal dalam

kalkulus, tetapi melambangkan keseluruhan unsur-unsur

∫

X

derajat keanggotaannya dalam himpunan kabur A~. Apabila semesta X adalah

himpunan yang diskret, maka himpunan kabur A~ seringkali dinyatakan dengan

∑

∈

= X x

A x x A~ μ~( )/

(2.3)

di mana lambang di sini tidak melambangkan operasi penjumlahan seperti yang

dikenal dalam aritmatika, tetapi melambangkan keseluruhan unsur-unsur

∑

X x∈ bersama dengan derajat keanggotaannya dalam himpunan kabur A~.

Contoh 2.1

Dalam semesta X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}, misalkan himpunan kabur

A~ adalah himpunan bilangan real yang dekat dengan nol. Maka

∑

∈

= X x

A x x A~ μ~( )/

= 0.1 / -4 + 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.7 / 1 + 0.5 / 2 + 0.3 / 3 + 0.1 / 4.

Dua buah himpunan kabur A~ dan B~ dalam semesta X dikatakan sama, dengan

lambang A~ = B~, bila dan hanya bila

μ~A(x)=μB~(x) (2.4) untuk setiap x ∈ X. Himpunan kabur A~ dikatakan merupakan himpunan bagian dari

μ~A(x)≤μB~(x) _(2.5) untuk setiap x ∈ X. Jadi A~ = B~ bila dan hanya bila A~ ⊆ B~ dan B~ ⊇ A~.

Definisi 2.2

Pendukung (support) dari suatu himpunan kabur A~, yang dilambangkan

Pend(A~) adalah himpunan tegas yang memuat semua unsur dari semesta yang

mempunyai derajat keanggotaan taknol dalam A~, yaitu

Pend(A~) = {x ∈ X | ~(x) A

μ > 0}. (2.6)

Definisi 2.3

Tinggi (height) dari suatu himpunan kabur A~, yang dilambangkan dengan

Tinggi(A~), didefinisikan sebagai

Tinggi(A~) = sup{ ~(x)}. A X x

μ

∈ _(2.7)

Definisi 2.4

Untuk suatu bilangan α∈[0,1], potongan-α lemah dari suatu himpunan kabur

A~, yang dilambangkan dengan , adalah himpunan tegas yang memuat semua

elemen dari semesta dengan derajat keanggotaan dalam

α

A

A~ yang lebih besar atau sama dengan α , yaitu

}. ) ( |

{ μ~ α

α = x∈X x ≥

A _A

(2.8)

Sedangkan potongan-α kuat dari himpunan kabur A~ adalah himpunan tegas

Aα′ ={x∈X |μA~(x)>α}. _(2.9) Suatu himpunan kabur dalam semesta ℝn disebut konveks bila untuk setiap α ∈(0,1]

potongan-α dari himpunan kabur itu adalah himpunan (tegas) yang konveks.

2. Fungsi Keanggotaan

Setiap himpunan kabur dapat dinyatakan dengan suatu fungsi keanggotaan. Ada beberapa cara untuk menyatakan himpunan kabur dengan fungsi keanggotaannya. Untuk semesta hingga diskret biasanya dipakai cara daftar, yaitu daftar angota-anggota semesta bersama derajat keangota-anggotaannya, seperti misalnya diberikan dalam Contoh 2.1.

bersangkutan dalam bentuk suatu formula matematis yang dapat disajikan dalam bentuk grafik.

Contoh 2.2

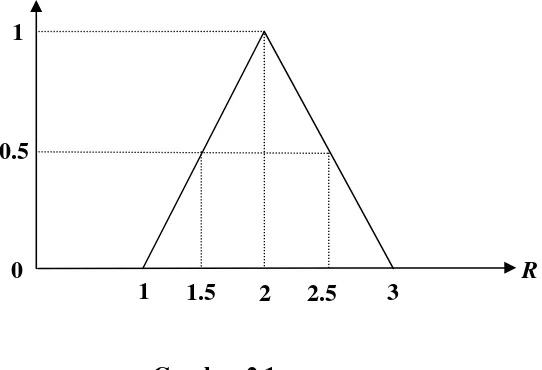
Himpunan kabur A~ adalah bilangan real yang dekat dengan 2 dapat dinyatakan dengan menggunakan fungsi keanggotaan sebagai berikut:

x – 1 untuk 1 ≤ x ≤ 2 3 – x untuk 2 ≤ x ≤ 3 0 untuk lainnya

yang grafiknya adalah sebagai berikut =

) ( ~ x A μ

0 0.5

1

1 1.5 2 2.5 3

R

Gambar 2.1

Kebanyakan himpunan kabur berada dalam semesta himpunan semua

bilangan real dengan fungsi keanggotaan yang dinyatakan dalam bentuk suatu formula yang matematis.

Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan

segitiga jika memilikai tiga buah parameter, yaitu a,b.c∈ℝ dengan a<b<c

dan dinyatakan dengan Segitiga (x,a,b,c) dengan aturan :

untuk a≤x≤b

untuk b≤x≤c

untuk x lainnya ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ − −− − = 0 ) , , ; ( b c x c a b a x c b a x Segitiga

Fungsi keanggotaan ini dapat juga dinyatakan dengan formula sebagai berikut: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − −

=max min , ,0

) , , ; ( b c x c a b a x c b a x Segitiga

3. Operasi Baku pada Himpunan Kabur

Operasi baku pada himpunan kabur yang akan didefinisikan adalah operasi biner “komplemen” dan operasi-operasi biner “gabungan” dan “irisan”.

Definisi 2.5

Komplemen dari suatu himpunan kabur A~ adalah himpunan kabur dengan fungsi keanggotaan ) ( 1 ) ( ~

~ x x A

A

μ

μ

_′ = −

Definisi 2.6

Gabungan dua buah himpunan kabur A~ dan B~ adalah himpunan kabur A~∪B~

dengan fungsi keanggotaan

=

∪~( )

~ x

B A

μ max { ~(x), ~(x)} B

A μ

μ

untuk setiap x ∈ X.

Definisi 2.7

Irisan dua buah himpunan kabur A~ dan B~ adalah himpunan kabur A~∩B~

dengan fungsi keanggotaan

=

∩~( )

~ x

B A

μ min { ~(x), ~(x)} B

A μ

μ

untuk setiap x ∈ X.

Contoh 2.3

Misalkan dalam semesta X = {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6} diketahui

himpunan-himpunan kabur A~ = 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.7 / 1 + 0.5 / 2

+ 0.3 / 3 dan B~ = 0.1 / -1 + 0.3 / 0 + 0.8 / 1 + 1 / 2 + 0. 7 / 3 + 0.4 / 4 + 0.2 / 5, maka

A~′ = 1 / -4 + 0.7 / -3 + 0.5 / -2 + 0.3 / -1 + 0.3 / 1 + 0.5 / 2 + 0.7 / 3 + 1 / 4 + 1 / 5 + 1 / 6

B

A~∪ ~ = 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.8 / 1 + 1 / 2 + 0.7 / 3 + 0.4 / 4 + 0.2 / 5

B

Definisi 2.8

Suatu pemetaan k:[0,1]×[0,1]→[0,1] disebut komplemen kabur jika memenuhi

aksioma-aksioma sebagai berikut:

a. k (0) = 1 dan k(1) = 0 (syarat batas)

b. Jika x< y maka k(x)≥k(y) untuk semua x,y∈[0,1](syarat taknaik)

Definisi 2.9

Suatu pemetaan s:[0,1]×[0,1]→[0,1] disebut gabungan kabur (norma-s) jika

memenuhi aksioma-aksioma sebagai berikut:

a. s(0,x)= s(0,x)= x dan s(1, 1) = 1 (syarat batas)

b. s(x,y)= s(y,x) (syarat komutatif)

c. Jika x≤x′ dan y≤ y′, maka s(x,y)≤s(x′,y′) (syarat takturun)

d. s(s(x,y),z)=s(x,s(y,z)) (syarat asosiatif)

Operasi max{x, y} untuk x,y∈[0,1] merupakan suatu contoh dari norma-t:

a. max{0, x} = max{x,0} = x dan max{1, 1} = 1 (syarat batas)

b. max{x, y} = max{y, x} (syarat komutatif)

c. Jika x≤x′ dan y≤ y′, maka max{x, y} ≤ max{x′,y′} (syarat takturun)

Contoh norma-s lainnya misalnya adalah

a. Jumlah Einstein :

xy y x y x sje

+ + =

1 ) , (

b. Jumlah drastis :

⎪ ⎩ ⎪ ⎨ ⎧

= = =

lainnya jika

1

0 x jika y

0 jika x )

, (

y y

x sjd

Definisi 2.10

Suatu pemetaan t:[0,1]×[0,1]→[0,1] disebut irisan kabur (norma-t) jika

memenuhi aksioma-aksioma sebagai berikut:

a. t(x,1)=t(1,x)= x dan t(0, 0) = 0 (syarat batas)

b. t(x,y)=t(y,x) (syarat komutatif)

c. Jika x≤x′ dan y≤ y′, maka t(x,y)≤t(x′,y′) (syarat takturun)

d. t(t(x,y),z)=t(x,t(y,z)) (syarat asosiatif)

Operasi min{x, y} untuk x,y∈[0,1] merupakan suatu contoh dari norma-t:

a. min{x, 1} = min{1, x} = x dan min{0, 0} = 0 (syarat batas)

b. min{x, y} = min{y, x} (syarat komutatif)

c. Jika x≤x′ dan y≤ y′, maka min{x, y} ≤ min{x′,y′} (syarat takturun)

d. min{min{x, y}, z} = min{x, min{y, z}} (syarat asosiatif)

a. Darab aljabar : tda(x,y)=xy.

b. Darab Einstein :

) ( 2 ) , ( xy y x xy y x t_de − + − =

c. Darab drastis :

⎪ ⎩ ⎪ ⎨ ⎧ = = = lainnya jika 0 1 x jika y 1 jika x ) , ( y y x t_dd

4. Relasi Kabur

Relasi kabur R~ antara elemen-elemen dalam himpunan X dengan elemen-elemen

dalam himpunan Y didefinisikan sebagai himpunan bagian kabur dari darab Cartesius X × Y, yaitu himpunan kabur

}. ) , ( | )) , ( ), , {(( ~

~ x y x y X Y

y x

R= μ_R ∈ ×

(2.10)

Relasi kabur R~ itu juga disebut relasi kabur pada himpunan (semesta) X × Y. jika

X = Y, maka R~ disebut relasi kabur pada himpunan X.

Contoh 2.4

Misalkan X = {31, 78, 205}, Y = {1, 27, 119}, dan R~ adalah relasi kabur “jauh

lebih besar” antara elemen-elemen dalam X dengan elemen-elemen dalam Y. Maka

relasi R~ tersebut dapat disajikan sebagai

Bila himpunan X dan Y keduanya berhingga, misalnya X ={x1,x2,L,xm} dan , maka relasi kabur

} , , ,

{y1 y2 yn

Y = L R~ antara elemen-elemen dalam himpunan X dengan elemen-elemen dalam himpunan Y dapat dinyatakan dalam bentuk suatu matriks berukuran m×n sebagai berikut

⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = mi a a a R M 21 11 ~ 2 22 12 m a a a M L L L ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ mn n n a a a M 2 1

di mana ~( _i, _j) R

ij x y

a =μ untuk i=1,2,L,m dan j =1,2,L,n.Bila X = Y, maka relasi

kabur R~ pada himpunan X itu dapat disajikan dengan suatu matriks bujur-sangkar.

Contoh 2.5

Relasi kabur “jauh lebih besar” antara elemen dalam X dengan elemen-elemen dalam Y dalam Contoh 2.3.1 di atas dapat disajikan dalam bentuk matriks bujur-sangkar sebagai berikut:

⎜ ⎜ ⎜ ⎝ ⎛ = 9 . 0 5 . 0 3 . 0 ~ R 7 . 0 3 . 0 1 . 0 ⎟ ⎟ ⎟ ⎠ ⎞ 4 . 0 0 . 0 0 . 0

dengan elemen baris ke-i kolom ke-j dalam matriks tersebut menyatakan derajat

keanggotaan(xi,yj) dalam relasi R ~

itu, yaitu ~( _i, _j), R x y

μ di mana x_i ∈X dan

.

Definisi 2.11

Himpunan semua himpunan bagian dari A disebut himpunan kuasa dari A, dan dinotasikan dengan P(A)={X | X ⊆ A}.

Definisi 2.12

Suatu fungsi tegas dikatakan dikaburkan bila fungsi tersebut diperluas

menjadi fungsi , di mana F(X) dan F(Y) berturut-turut adalah

himpunan kuasa kabur dari semesta X dan Y, yaitu himpunan semua himpunan kabur dalam X dan dalam Y.

Y X

f : →

) ( ) (

:F X F Y

f →

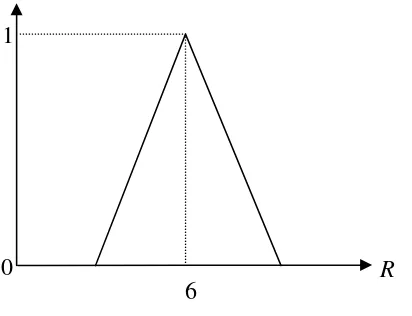
Contoh 2.6

Bilangan kabur “kurang lebih 6” dapat dinyatakan sebagai himpunan kabur 6~ dengan fungsi keanggotaan segitiga sebagai berikut:

0 1

6 R

Definisi 2.13

Misalkan A~ dan B~ adalah dua buah bilangan kabur dalam ℝ. Dengan Prinsip

Perluasan dapat didefinisikan penjumlahan A~ dan B~, yaitu A~+B~, sebagai bilangan

kabur dalam ℝ dengan fungsi keanggotaan

) , ( sup ) ( ~ ~ ~

~ z x y

B A z y x B A × = + + = μ μ

= sup min{ ~(x), ~(y)} B A z y x μ μ = + .

Demikian pula operasi perkalian bilangan kabur A~ dan B~, yaitu A~⋅B~, adalah

bilangan kabur dalam ℝ dengan fungsi keanggotaan

)} ( ), ( min{ sup ) ( ~ ~ ~

~ z _A x _B y

z xy B

A μ μ

μ

=

⋅ = .

5. Ukuran Kabur (Fuzzy Measure)

Ukuran kabur menunjukkan derajat kekaburan dari himpunan kabur. Secara umum ukuran kekaburan dapat dinyatakan sebagai suatu pemetaan :

R X f :Ρ( )→

dengan adalah himpunan kuasa dari X. adalah suatu fungsi yang

memetakan himpunan bagian )

(X

Ρ f(A~)

A~ ke karakteristik derajat kekaburannya.

Dalam mengukur nilai kekaburan, fungsi f harus mengikuti hal-hal sebagai berikut :

2. f(A~)=1jika dan hanya jika A~ adalah himpunan yang paling kabur, yaitu

5 , 0 ) ( ~ x = A

μ untuk setiap x∈X

3. Jika A~<B~ maka f(A~)≤ f(B~) yang berarti

) ( )

(x _B x

A μ

μ ≤ , jika μ_B(x)≤0,5 dan

) ( )

(x _B x

A μ

μ ≥ , jika μ_B(x)≥0,5

4. f(A~)= f(A~') untuk setiap A~∈P(X)

Contoh 2.7

Misalkan pada semesta X = {1,2,3,4,5,6,7} diketahui himpunan kabur A~= 0.3/1 + 0.6/2 + 0.8/3 + 0.9/4 + 0.8/5 + 0.4/6 + 0.2/7. Dengan definisi ukuran kekaburan f di

atas ,derajat kekaburan dari himpunan kabur A~ adalah = 0.2. jika diketahui

pula himpunan kabur

) ~ (A f

B~= 0.3/1 + 0.5/2 + 0.7/3 + 0.8/4 + 0.8/5 + 0.4/6 + 0.3/7, maka

jelas bahwa A~ kurang kabur dari B~ dan f(B~)= 0.4, yaitu f(A~)≤ f(B~)

6. Indeks Kekaburan

Indeks kekaburan adalah jarak antara suatu himpunan kabur A~ dengan himpunan

tegas C yang terdekat. Himpunan tegas C terdekat dari himpunan kabur A~

dinotasikan sebagai berikut :

1. 0μ_C(x)= jika ~(x)≤0,5 A

2. 1μC(x)= jika μ_A~(x)≥0,5

Ada 3 kelas yang paling sering digunakan dalam mencari indeks kekaburan, yaitu : a. Jarak Hamming

∑

−

= | ( ) ( )|

)

(A x x

f μ_A μ_C atau

∑

−

= min| ( ),1 ( )| )

(A x x

f μ_A μ_A

b. Jarak Euclidean

{

₂

}

1/2

)) ( ) ( ( )

(A =

∑

x − x

f μ_A μ_C

c. Jarak Minkowski

(

)

{

_w

}

w

C

A x x

A

f( )=

∑

μ ( )−μ ( ) 1/ dengan w∈

[ ]

1,∞

B. Analisis Cluster

Analisis cluster merupakan suatu alat analisis yang berguna untuk meringkas data yang dapat dilakukan dengan jalan mengelompokkan objek-objek berdasarkan kesamaan karakteristik tertentu di antara objek-objek yang hendak diteliti. Kesamaan tersebut dinyatakan dalam ukuran similaritas atau disimilaritas.

kelompok tersebut akan diikuti dengan terjadinya pengelompokan yang menunjukkan kedekatan kesamaan antar objek.

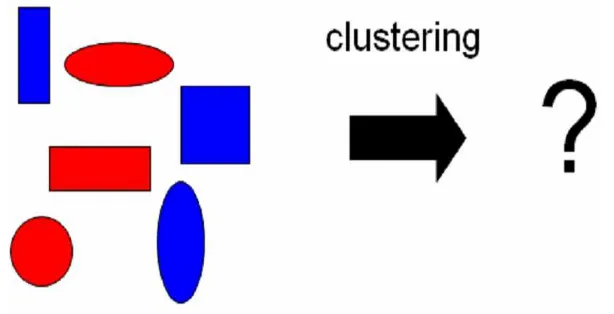
Berikut ini contoh kasus sederhana yang dapat dipakai sebagai ilustrasi bagaimana analisis cluster bekerja. Gambar berikut menunjukkan contoh data yang akan dilakukan klasterisasi

Gambar 2.3. Data sebelum dicluster

Jika data dilakukan clustering (pengelompokkan) berdasarkan warna, maka pengelompokkannya seperti yang terlihat pada gambar berikut

Jika data dilakukan clustering (pengelompokkan) berdasarkan bentuk, maka pengelompokkannya dapat dilihat seperti gambar berikut

Gambar 2.4. Cluster berdasarkan similaritas (kesamaan) bentuk

Analisis cluster akan mengelompokkan objek penelitian ke dalam kelompok-kelompok berdasarkan variabel-variabel tersebut sedemikian hingga kelompok-kelompok yang terbentuk akan memuat objek-objek yang seragam di dalamnya, sedangkan antar kelompok akan dapat dilihat karakteristik (variabel) apa yang membedakannya.

Data objek yang akan diteliti dapat ditampilkan dalam bentuk matriks dengan n banyaknya objek dan d banyaknya variabel.

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = nd n n d d x x x x x x x x x d L M M M L L L 2 1 2 22 21 1 12 11 2 1 variabel X n M obyek 2 1

Kemiripan antara objek-objek yang diteliti dapat dideskripsikan sebagai

matriks . nxnD ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = nn n n n d d d d d d d K K K M O M M M O M M M O M M M M K K K 2 1 22 1 12 11 D

Matriks D berisi ukuran similaritas atau disimilaritas antara n objek. Ukuran disimilaritas yang paling umum untuk mengukur dekatnya dua titik adalah metrik dengan pemetaan RΔ d x Rd onto R1 dan memenuhi aksioma berikut :

a. Δ(x,y)≥0, untuk semua x dan y di Rd.

b. Δ(x,y)=0 jika dan hanya jika x=y.

c. Δ(x,y)=Δ(y,x) untuk semua x dan y di Rd.

Ukuran tersebut dinyatakan dalam jarak dua objek yang pengukurannya dapat menggunakan norma berikut

Norma L2 yang terkenal dengan nama jarak Euclidean

2 1

1

2

2 _⎭⎬

⎫ ⎩

⎨

⎧ ₋

= −

=

∑

=

p k

jk ik j

i

ij x x x x

d (2.11)

1. Metode-Metode Dalam Analisis Cluster

Diagram 2.1. Hubungan antara metode-metode dalam analisis cluster

Metode Nonhierarchical

Tujuan yang akan dicapai dalam metode ini adalah untuk meminimalkan total variansi antar cluster (minimize total intra-cluster variance) atau fungsi kuadrat kesalahan (squared error function), yaitu

(

2

1

∑ ∑

= ∈

− = k

i x C

i j i j

x

E μ

)

(2.12)

di mana μi merupakan centroid dari semua objek xj∈Ci.

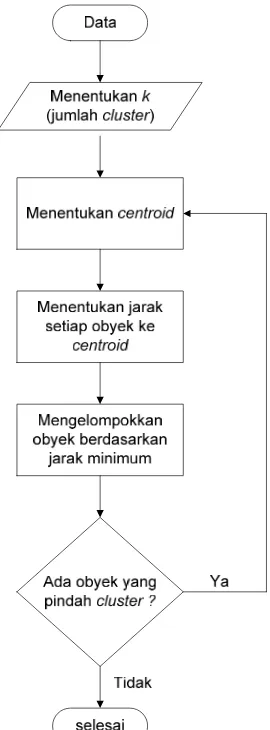
Objek manapun dapat dipilih secara acak sebagai centroid awal atau objek pada urutan pertama juga bisa dipakai sebagai centroid awal, kemudian algoritma k-means akan melalui tiga tahap yang diulang-ulang secara berurutan sampai stabil (tidak ada objek yang berpindah-pindah cluster). Tiga tahap tersebut adalah :

1). Menentukan centroid.

2). Menentukan jarak dari setiap objek ke centroid. 3). Mengelompokkan objek berdasarkan jarak minimum.

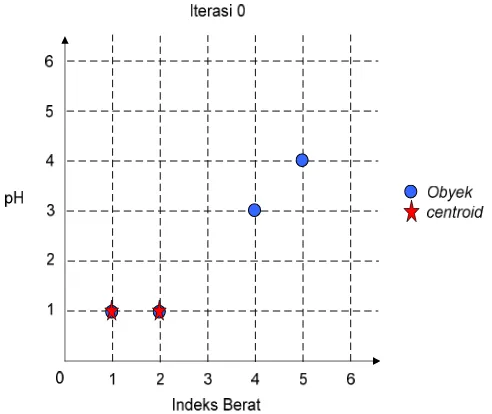
Contoh 2.10

Diketahui empat macam obat yang mempunyai dua variabel, yaitu indeks berat dan pH. Empat macam obat tersebut akan dikelompokkan

menjadi 2 (k =2) berdasarkan indeks berat dan pH.

Obat Indeks Berat Ph A 1 1 B 2 1 C 4 3 D 5 4 Data yang akan dikelompokkan

Dari tabel di atas, diperoleh matriks jarak dengan menggunakan jarak Euclidean (2.11), yaitu

⎥ ⎦ ⎤ ⎢

⎣ ⎡ =

24 . 4 83 . 2 0 1

Matriks tersebut digunakan pada iterasi 0. Misal, obat A dan obat B

sebagai centroid yang pertama, yaitu c₁ =

( )

1,1 dan c₂ =

( )

2,1 .

Gambar 2.11. Koordinat objek dari Tabel

Gambar 2.12. Iterasi 0 pada proses K-means

Setiap kolom di dalam matriks jarak merupakan objek. Baris pertama dari matriks jarak dapat disamakan dengan jarak dari setiap objek ke centroid yang pertama dan baris kedua adalah jarak dari setiap objek ke centroid

adalah

(

4−1

) (

2 + 3−1

)

2 =3.61 dan jarak ke centroid kedua c₂ =

( )

2,1 adalah

(

4−2

) (

2 + 3−1

)

2 =2.83.

Langkah selanjutnya, setiap objek dikelompokkan berdasarkan jarak minimum, maka obat A ditempatkan ke dalam cluster pertama, obat B, C dan D pada cluster kedua.

Iterasi 0 selesai, lanjut ke iterasi 1. Setelah mengetahui mengetahui anggota-anggota dari setiap cluster, centroid baru dapat dihitung berdasarkan keanggotaan yang baru tersebut. Cluster pertama hanya

mempunyai satu anggota, maka centroid-nya tetap berada pada c₁ =

( )

1,1 . Cluster kedua mempunyai 3 anggota, maka centroid-nya berubah, yaitu

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + + + = 3 8 , 3 11 3 4 3 1 , 3 5 4 2 2

c . Langkah selanjutnya adalah

menghitung jarak dari semua objek ke centroid yang baru. Caranya mirip menghitung matriks D11, diperoleh

0 1 2 3 4 5 6 1 2 3 4 5 6 pH Indeks Berat Obyek centroid

Garis pemisah cluster

Gambar2.13. Iterasi 0 pada proses K-means

Lalu mengelompokkan setiap objek berdasarkan jarak minimum pada matriks D12. Berdasarkan matriks tersebut, obat B dipindahkan ke dalam cluster pertama, sementara objek yang lain tetap berada pada cluster yang sudah ditentukan pada iterasi 0.

Iterasi 1 selesai, lanjut ke iterasi 2. Centroid yang baru dihitung kembali berdasarkan pengelompokkan dari iterasi 1. Cluster pertama dan kedua, masing-masing mempunyai dua anggota, maka centroid-centroid-nya

berubah, yaitu ⎟

⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + +

= ,1

2 1 1 2 1 1 , 2 2 1 1 c dan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = 2 1 3 , 2 1 4 2 4 3 , 2 5 4 2

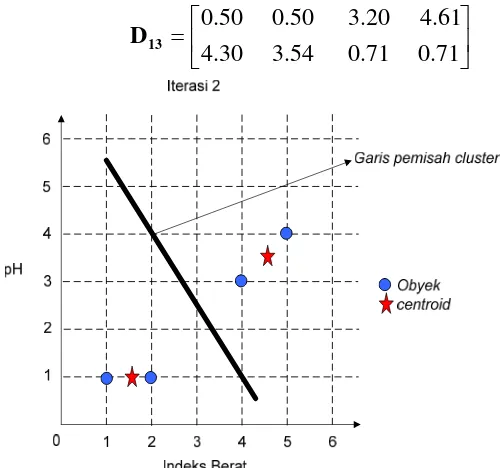
c dan diperoleh matriks jarak yang baru

⎥ ⎦ ⎤ ⎢

⎣ ⎡ =

71 . 0 71 . 0 54 . 3 30 . 4

61 . 4 20 . 3 50 . 0 50 . 0

13

D

Gambar 2.14. Iterasi 2 pada proses K-means

Berdasarkan matriks D13, hasil pengelompokkan sama pada iterasi 1, sehingga pada iterasi 2 objek-obj ek tidak ada yang berpindah cluster. Oleh karena itu, perhitungan pengelompokkan k-means telah mencapai kestabilan dan berhenti pada iterasi 2. Hasil akhir pengelompokkan dari data tabel di atas adalah

Tabel 2.3. Data hasil pengelompokan Obat Indeks Berat pH Cluster

A 1 1 1

B 2 1 1

C 4 3 2

BAB III

PENGELOMPOKAN KABUR DENGAN METODE FUZZY C-MEANS

A. Pembangkit Bilangan Random

Bilangan random adalah suatu bilangan yang diambil dari sekumpulan

bilangan, dimana tiap-tiap elemen dari kumpulan bilangan ini mempunyai peluang

yang sama untuk terambil. Berdasarkan pada tingkat kesulitan untuk memprediksi

bilangan yang akan dibangkitkan selanjutnya maka bilangan random dibagi

menjadi dua yaitu bilangan random sepenuhnya (Trully Random) dan bilangan

random semu (Pseudo-Random). Didalam skripsi ini hanya akan digunakan

bilangan random pseudo.

Dalam sistem nyata, adanya faktor keacakan menyebabkan sesuatu tidak

dapat sepenuhnya dapat diramalkan. Dalam metode Monte Carlo faktor keacakan dimasukkan kedalam model dengan melibatkan satu atau lebih variabel random.

Sebuah metode untuk membangkitkan bilangan random dikatakan baik

jika bilangan random yang dihasilkan memenuhi sifat keacakan, saling bebas,

memenuhi distribusi statistik yang diharapkan, dan dapat direproduksi. Selain itu

pembangkit tersebut harus mampu bekerja dengan cepat dan hanya memerlukan

sedikit kapasitas memori.

Banyak metode yang telah dikembangkan untuk menghasilkan bilangan

random yang baik. Metode yang digunakan saat ini adalah metode yang

melibatkan prosedur deterministik. Walaupun barisan bilangan random yang

tersebut tidaklah sepenuhnya acak, sehingga seringkali disebut sebagai bilangan

random semu (pseudorandom number).

Bilangan random pseudo adalah kumpulan bilangan yang dihasilkan

menggunakan algoritma yang menerapkan rumus matematika untuk menghasilkan

bilangan yang terlihat acak. Salah satu algoritma untuk pembangkitan bilangan

random pseudo adalah pembangkit kesebangunan (Congruential generator).

Metode ini diperkenalkan oleh lehmer (1951) yaitu dengan menggunakan formula

rekursif berdasarkan perhitungan sisa modulo suatu bilangan bulat dari

transformasi linear. Metode ini memerlukan penentuan awal empat bilangan non

negatif a, b, x0, dan m. dalam hal ini x0 berfungsi sebagai nilai awal (seed). Kemudian nilai x1 dapat dicari secara iteasif melalui formula:

) (ax ₁ b

xn = n− + mod m

Dengan,

n

x =bilangan random ke n

1

−

n

x =bilangan random ke n−1

m = angka modulo

a dan b merupakan konstanta , dengan a adalah faktor pengali dan b

adalah increment factor.

Bentuk alternatif metode ini adalah dengan mengambil b=0 sehingga

formula yang digunakan adalah

1

−

= _n

n ax

Walaupun metode ini secara lengkap deterministik, namun dengan

pemilihan nilai yang tepat untuk parameter-parameter yang dibutuhkan dapat

menghasilkan rangkaian bilangan acak dengan sifat acak yang baik.

Contoh 3.1.

Membangkitkan bilangan random sebanyak 8 kali dengan a = 2, b = 7, m = 10 dan

x(0) = 2.

Jawab :

X(1) = (2(2) + 7) mod 10 = 1

X(2) = (2(1) + 7) mod 10 = 9

X(3) = (2(9) + 7) mod 10 = 5

X(4) = (2(5) + 7) mod 10 = 7

X(5) = (2(7) + 7) mod 10 = 1

X(6) = (2(1) + 7) mod 10 = 9

X(7) = (2(9) + 7) mod 10 = 5

X(8) = (2(5) + 7) mod 10 = 7

Bilangan yang dibangkitkan adalah : 1, 9, 5, 7, 1, 9, 5, 7

Didalam komputer bilangan random yang dibangkitkan adalah bilangan

random pseudo. Disini akan digunakan program Matlab untuk membangkitkan

bilangan random pseudo berdistribusi tertentu. Pada Tabel 3.1 berikut akan

ditunjukkan dua himpunan yang terdiri dari sepuluh bilangan. Bilangan-bilangan

menggunakan fungsi rand dan randn pada Matlab untuk memperoleh sampel

U(0,1) dan N(0,1).

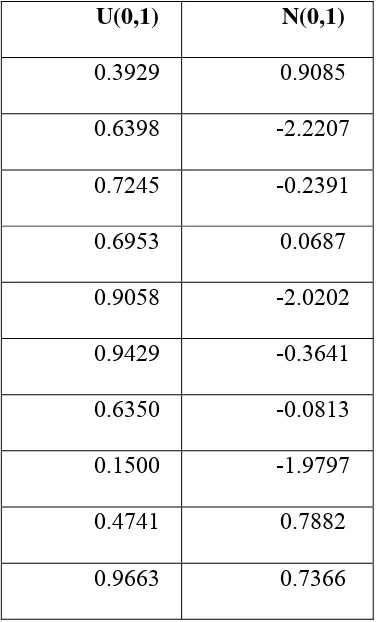
Tabel 3.1 sepuluh bilangan random pseudo berdistribusi U(0,1) dan N(0,1)

U(0,1) N(0,1)

0.3929 0.9085

0.6398 -2.2207

0.7245 -0.2391

0.6953 0.0687

0.9058 -2.0202

0.9429 -0.3641

0.6350 -0.0813

0.1500 -1.9797

0.4741 0.7882

0.9663 0.7366

Dapat dilihat pada Tabel 3.1 bahwa dugaan sampel U(0,1) tersebar dalam

interval (0,1), sedangkan dugaan sampel N(0,1) berada disekitar nol.

B. Partisi Kabur (Fuzzy Partition)

Konsep partisi kabur (fuzzy partition) sangatlah penting untuk analisis cluster

dan digunakan juga untuk mengidentifikasi teknik yang didasarkan pada

Jika pada matriks, suatu data secara eksklusif menjadi anggota hanya pada

satu cluster saja, tidak demikian halnya dengan partisi kabur. Pada partisi kabur,

nilai keanggotaan suatu data pada suatu cluster μ_ik, dengan ;

dimana n banyaknya data, terletak pada interval

n i =1,2,3,...,

c

k =1,2,3,....,

[ ]

0,1.

Definisi 3.1

Misalkan himpunan berhingga, adalah himpunan semua

matriks berukuran adalah bilangan bulat. Matriks

{

x xn

X = ₁,...,

}

V_cn

n

c× U~=

[ ]

μ_ik ∈V_cn disebut

partisi-c kabur. Matriks partisi pada partisi kabur memenuhi kondisi sebagai berikut :

[ ]

i c k n ik ∈ 0,1,1≤ ≤ ,1≤ ≤

μ (3.1)

; 1≤k≤n (3.2)

∑

=

= c i

ik

1

1

μ

0 <

∑

< n; 1≤i ≤c (3.3)

=

N k

ik

1

μ

Baris ke-i pada matriks partisi U~ berisi nilai keanggotaan data dari himpunan bagian kabur Ai. Jumlah derajat keanggotaan setiap data pada semua cluster (jumlah setiap kolom) bernilai 1

C. Konsep Pengelompokan Kabur (Fuzzy Clustering)

Tujuan pengelompokan (cluster) adalah untuk membagi bermacam-macam

kelompok ke sejumlah sub kelompok yang memiliki kemiripan. Objek yang

terkecil antar kelas. Clustering data merupakan jalan yang sangat bagus untuk memulai suatu analisis data apa saja. Kemiripan cluster itu sendiri dapat memberikan titik awal untuk mengetahui apa yang ada dalam data dan

mengggambarkan bagaimana baiknya menggunakan hasil clustering tersebut.

Pembentukan kelompok-kelompok observasi berdasarkan jarak, objek yang

mirip seharusnya berada dalam kelompok yang sama dan sebaliknya objek yang

mempunyai banyak perbedaan berada dalam kelompok yang berbeda.

Pembentukan kelompok tersebut akan diikuti dengan terjadinya pengelompokan

yang menunjukkan kedekatan kesamaan antar objek.

Metode hard clustering didasarkan pada teori himpunan klasik dan

memerlukan suatu objek yang termasuk atau tidak dalam suatu kelompok

(cluster). Hard clustering berarti mempartisi data ke dalam jumlah tertentu dari subset saling asing, sedangkan metode pengelompokan kabur (fuzzy clustering) dapat secara bersamaan mengelompokkan objek-objek ke dalam beberapa

kelompok (cluster) dalam derajat keanggotaan yang berbeda. Dalam banyak

situasi, pengelompokan kabur (fuzzy clustering) lebih alami daripada hard clustering. Pada pengelompokan kabur (fuzzy clustering) objek yang berada pada batas-batas di antara beberapa kelompok tidak sepenuhnya menjadi milik salah

satu cluster, tetapi diberikan derajat keanggotaan antara 0 dan 1 yang

menunjukkan bagian keanggotaanya.

Pengelompokan kabur merupakan salah satu pokok persoalan mendasar dalam

penentuan pola dan memegang peranan penting untuk mencari struktur di dalam

permasalahan pengelompokan dalam X adalah mencari beberapa pusat kelompok

yang dapat memberikan ciri kepada masing-masing kelompok dalam X. Dalam

pengelompokan klasik, kelas-kelas ini dibutuhkan untuk membentuk partisi dari X

sedemikian sehingga derajat kesamaan bernilai tinggi untuk data yang berada di

dalam kelompok yang sama dan bernilai rendah untuk data yang berada pada

kelompok yang berlainan. Akibatnya, pengelompokan klasik ini digantikan

dengan pengelompokan fuzzy, yaitu pengelompokan dengan konsep partisi fuzzy

(fuzzy partition) atau pseudopartisi fuzzy (fuzzy pseudopartition). fuzzy pseudopartition disebut juga fuzzy c-partition, dengan c mewakili jumlah kelas-kelas fuzzy di dalam partisi.

Pengelompokan kabur (Fuzzy Clustering) adalah salah satu teknik untuk

menentukan kelompok (cluster) optimal dalam suatu ruang vektor yang

didasarkan pada bentuk normal Euclidian untuk jarak antar vektor. Misalnya X

adalah himpunan data-data yang diselidiki, maka kelas-kelas dari data-data itu

biasanya membentuk suatu partisi atau sekurang-kurangnya suatu partisi kabur

dari X. Pengelompokan data-data dalam bentuk suatu partisi kabur disebut

pengelompokan kabur (fuzzy clustering).

D. Pengelompokan Kabur dengan Metode C-Means

Metode pengelompokan Fuzzy C-means (FCM) adalah mengelompokan

data dengan meminimalkan total jarak pada masing-masing data terhadap pusat

cluster, yang membentuk suatu partisi kabur sedemikian sehingga

untuk setiap k = 1,2,…,n, dan 0 < < n untuk setiap i = 1,2,…,n . Misalkan

himpunan data

1

1

=

∑

=

c i

ik μ

∑

=

c k

ik

1

μ

{

}

<

= x xn

X ₁,..., ℝp adalah sebuah himpunan bagian dari ruang

vektor real berdimensi-p ℝp. Setiapx_k =(x_ki,...,x_kp)∈ ℝp disebut vektor ciri.

adalah ciri ke-j dari observasi . Biasanya mendefinisikan “ketaksamaan” atau

“jarak” dari 2 objek dan menjadi sebuah fungsi bernilai real

dimana memenuhi

kj x

k x

k

x x_l

+

→ ×X R X

d:

0 )

,

(x_k x_l =d_kl ≥

d (3.4)

l k

kl x x

d =0⇔ = (3.5)

(3.6)

lk kl d d =

Jika sifat penjumlahan d memenuhi ketaksamaan segitiga, yaitu

jl kj kl d d

d ≤ + (3.7)

maka ketaksamaan dari 2 titik dan dapat ditafsirkan sebagai jarak

antara titik-titik ini.

kl

d xk xl

Setiap partisi dari himpunan X =

{

x1,...,xn

}

ke dalam himpunan bagian

kabur Si

~

dengan terminologi dari bagian sebelumnya yang kita gunakan untuk metode

clustering tegas adalah

{ }

0,1

:X →

u_Si (3.8)

dan untuk metode clustering kabur

[ ]

0,1 :

~ X →

i S

μ (3.9)

dimana u_ikdan μ_ikadalah derajat keanggotaan dari objek x_k ke himpunan bagian

i

S~ yaitu

) ( : Si k ik u x

u (3.10)

) (

: _{Si k}

ik μ x

μ (3.11)

Lokasi dari sebuah cluster dinyatakan oleh pusat clusternya

ℝ

∈ =( _i1,..., _ip)

i v v

v p , i=1,…,c dimana objek-objeknya terpusat disekitarnya.

Misalkan v =(v₁,...,v_c)∈ℝcp adalah vektor dari semua pusat cluster dimana

pada umumnya tidak dapat disamakan dengan elemen-elemen dari X.

i v

Ukuran yang sering digunakan untuk memperbaiki partisi awal disebut

ukuran variansi. Ukuran ini digunakan untuk mengukur ketaksamaan antara

titik-titik pada sebuah cluster dan pusat clusternya menggunakan jarak Eulcidean. Jarak ini,d_ik , adalah

) ,

( _{k i}

Ukuran variansi untuk partisi tegas dapat disamakan dengan

meminimalkan jumlahan dari variansi dari semua variable j dalam setiap cluster i

dengan Si =n menghasilkan

∑ ∑ ∑

∑∑ ∑

= ∈ = = = ∈ − ⇔ − c

i x S p j ij kj c i p

j x S

ij kj

i k i k i

v x n

v x

S 1 1

2 1 1 2 ) ( 1 min ) ( 1

min (3.13)

sebagai akibat dari transformasi di atas, ukuran variansi sama halnya (kecuali

untuk factor 1/ n) dengan meminimalkan jumlahan dari kuadrat jarak Euclidean. Jumlahan ukuran dengan dirinya sendiri digunakan untuk menyelesaikan

permasalahan di bawah ini

∑ ∑

= ∈

− = c

i x S

i k c i k v x v S S z 1 2 1,..., ; )

(

min (3.14)

dimana

∑

∈ = i k S x k i i x S

v 1 (3.15)

untuk c-partisi kabur dengan menggunakan definisi partisi kabur jumlahan ukuran

variansi untuk menyelesaikan masalah di bawah ini

∑∑

= = − = c i n k i k w ik x v v U z 1 1 2 ) ( ) , (

min μ (3.16)

dimana pusat cluster

Disini (pusat cluster) adalah rata-rata dari pembobot –w, dengan derajat keanggotaanya. Itu berarti bahwa dengan derajat keanggotaan tinggi

memiliki pengaruh tinggi pada dan sebaliknya. Tendensi ini diperkuat oleh w.

Hal ini menunjukan bahwa apabila diberikan sebuah partisi U i

v x_k

k x

i v

~

maka dinyatakan

dengan cluster

i v

i

S~ seperti yang dijelaskan di atas.

Generalisasi ukuran yang digunakan untuk masalah norma clustering tegas adalah sebagai berikut. Misalkan G adalah sebuah matriks berukuran

yang simetrik dan positif. Maka kita dapat mendefinisikan sebuah norma umum

sebagai berikut

) (p×p

) ( ) ( 2 i k T i k G i

k v x v G x v

x − = − − (3.18)

Pengaruh yang mungkin dari pemilihan norma ditentukan oleh pemilihan dari G. hal ini menghasilkan rumus sebagai berikut

∑∑

= = − = n k c i G i k ik x v v U z 1 1 2 ) , (

min μ (3.19)

Dimana cp c R v M U ∈ ∈

Ini adalah sebuah masalah optimasi kombinasi dimana susah untuk

diselesaikan,bahkan untuk nilai yang agak kecil dari c dan n. Pada kenyataannya,

banyaknya cara berbeda untuk mempartisi x ke dalam himpunan bagian tak

( )

( )

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =

∑

= − c j w j c c j

c c j

M 1 1 ) ! / 1 ( (3.20)

Dimana untuk c=10 n= 25 sudah 10^18 partisi-10 berbeda dari 25 titik. Definisi dasar dari masalah partisi kabur untuk w>1

∑∑

= = − = n k c i G i k w ik

w U v x v

z 1 1 2 ) ( ) ; ~ (

min μ (3.21)

) (P_m

dimana cp fc R v M U ∈ ∈ ~ )

(P_m adalah sebuah masalah analitik, dimana mempunyai manfaat untuk

menentukan fungsi objektif

Dengan menurunkan fungsi objektif dengan berpegang pada sebagai pusat

cluster ( untuk U

i v

~

konstan) dan untuk μ_ik ( untuk v konstan ) dan

mengaplikasikan kondisi

∑

∑

= = = n k k w ik n k w ik i x v 1 1 ) ( ) ( 1 _μ μ

i=1,...,c (3.22)

Diperoleh matriks partisi baru

∑

= − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = c j w G i k w G i k ik v x v x 1 ) 1 /( 1 2 ) 1 /( 1 2 1 1

Sistem yang dijelaskan pada persamaan (3.22) dan (3.23) tidak dapat

diselesaikan secara analitik. Ada algoritma iterative (non hierarchial) dimana

minimum rata-rata dari fungsi objektif dimulai dari posisi yang diberikan. Salah

satu algoritma terbaik untuk masalah clustering tegas adalah algoritma c-means

atau algoritma ISODATA.

Sama halnya masalah clustering kabur dapat diselesaikan dengan

menggunakan algoritma c-means kabur. Dimana akan dijelaskan lebih detail menggunakan Algoritma c-means kabur.

Untuk setiap w∈

( )

0,∞ algoritma c-means kabur dapat digambarkan dengan secara iterative menyelesaikan kondisi (3.1) dan (3.2) di atas dan

mengkonvergenkan pada sebuah fungsi objektif.

Pada kondisi awal, pusat cluster ini masih belum akurat. Tiap-tiap titik

data memiliki derajat keanggotaan untuk tiap-tiap cluster. Dengan cara

memperbaiki pusat cluster dan derajat keanggotaan tiap-tiap titik data secara berulang, maka akan dapat dilihat bahwa pusat cluster akan bergerak menuju lokasi yang tepat. Perulangan ini didasarkan pada minimisasi fungsi objektif yang

menggambarkan jarak dari titik data yang diberikan ke pusat cluster yang terbobot oleh derajat keanggotaan titik data tersebut. Semakin kecil jarak, semakin kecil

pula fungsi objektif partisi kaburnya yang berarti semakin baik partisi kabur itu.

Dua permasalahan utama yang muncul dalam fuzzy c-means, pertama,

bagaimana menentukan inisial pusat cluster. Kedua, bagaimana menentukan

Sedangkan, untuk masalah kedua, Bezdek (1981) menyarankan menggunakan

partititon coefficient (PC) sebagai pengakuan jumlah cluster yang sesuai. Rumus

partititon coefficient (PC) sebagai berikut :

n x u

PC

n j

c i

j ij

∑∑

= =

= 1 1 2

) (

) (

μ

Dimana n adalah banyaknya data, c adalah jumlah cluster, μ adalah matriks random dan x adalah data. Jumlah cluster ditentukan oleh nilai maksimum

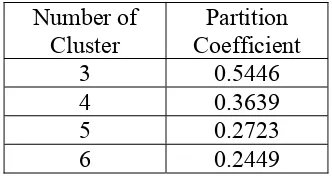
partititon coefficient (PC). Misalnya diketahui hasil perhitungan PC dalam tabel 3.1 yang diperoleh dari perhitungan data penelitian kreditor sepeda motor. Dapat

diketahui, karena nilai maksimum PC didapat ketika jumlah cluster adalah 3, maka jumlah cluster yang digunakan adalah 3.

Output dari FCM bukan merupakan fuzzy inference system, namun merupakan deretan pusat cluster dan beberapa derajat keanggotaan untuk tiap-tiap titik data. Informasi ini dapat digunakan untuk membangun suatu fuzzy inference system

(Kusumadewi,2002).

Tabel 3.1 Contoh hasil Partition Coefficient suatu permasalahan

Number of Cluster

Partition Coefficient

3 0.5446 4 0.3639 5 0.2723 6 0.2449

E. Algoritma Fuzzy C-means

1. Input data yang akan di cluster X, berupa matriks berukuran n x m ( n = jumlah sampel data, m = atribut setiap data). x_kj =data sampel ke- k

(k =1,2,3,...,n) dan atribut j =1,2,3,...,m

2. Tentukan

Jumlah cluster = c ;

Pangkat = w ;

Maksimum Iterasi = MaxIter ;

Eror terkecil yang diharapkan = ξ ;

Fungsi objektif awal = P₀ =0 ;

Iterasi awal = t = 1;

3. Bangkitkan bilangan random μ_ik , k =1,2,3,...,n; i=1,2,3,....,csebagai elemen-elemen matriks partisi awal U. Hitung jumlah setiap kolom

(atribut) :

∑

=

= c k

ik j

Q

1

μ (3.24)

dengan j =1,2,3,...,m

4. Hitung pusat cluster ke-i : v_i dengan i=1,2,3,....,c, j =1,2,3,...,m

1 , ) ( 1

1 1

>

=

∑

∑

=

=

w x v

n k

k w ik n

k ik

ij μ

μ

(3.25)

(

)

( )

∑∑ ∑

= = = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = n k c i w ik m j ij kj

t x v

P

1 1 1

2 _μ

(3.26)

6. Hitung perubahan matriks partisi :

(

)

(

)

∑ ∑

∑

= − − = − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = c k w m j ij kj w m j ij kj ik v x v x 1 1 1 1 2 1 1 1 2

μ (3.27)

dengan : i=1,2,3,...,c; dan k =1,2,3,....,n

7. Cek kondisi berhenti

Gambar 3.1. Flowchart Algoritma Fuzzy C-Means

E. Contoh Kasus

Tabel 3.2 Tabel data Xij

1

X X₂

12 150

25 155

17 126

20 132

18 145

15 135

26 122

25 127

10 130

14 145

Akan dilakukan pengelompokan data dengan input data variabel awal sebagai

berikut :

Jumlah cluster = 3

Pangkat = 2

Maksimum Iterasi = 100

Eror terkecil yang diharapkan = 5

10−

Fungsi objektif awal = 0

Iterasi awal = 1

ik

Bangkitkan bilangan random μ , i=1,2,3,...,c; k =1,2,3,....,nsebagai

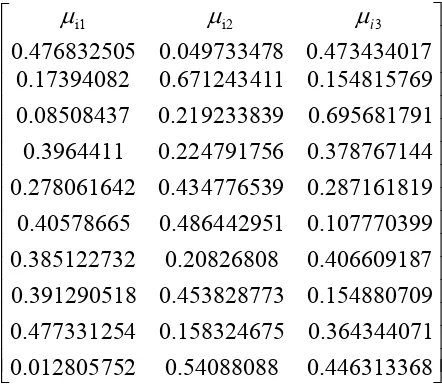
elemen-elemen matriks partisi awal U. Matriks partisi U dapat dilihat

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 8 0.44631336 0.54088088 2 0.01280575 1 0.36434407 5 0.15832467 4 0.47733125 9 0.15488070 3 0.45382877 8 0.39129051 7 0.40660918 0.20826808 2 0.38512273 9 0.10777039 1 0.48644295 0.40578665 9 0.28716181 9 0.43477653 2 0.27806164 4 0.37876714 6 0.22479175 0.3964411 1 0.69568179 9 0.21923383 0.08508437 9 0.15481576 1 0.67124341 0.17394082 7 0.47343401 8 0.04973347 5 0.47683250 3 i2

i1 μ μi μ =

∑

= 10 1 k ik Q μ = =

∑

= 10 1 2 k ik Q μ = =

∑

= 10 1 3 k ik Q μ ij

v 1,2,3,....,c

Hitung jumlah setiap kolom (atribut) dengan persamaan 3.24,didapat hasil sebagai

berikut :

=

1 3.07

3.4007

3.464

Hitung pusat cluster ke-k : dengan i= dan

digunakan persamaan 3.25. Proses perhitungan persamaan 3.25 dapat dilihat pada

tabel 3.2 berikut

2 1

i

μ 2

2

i

μ 2

3

i

μ 1

2 1 k i ×x

μ 1

2 2 k i ×x

μ 1

2 3 k i ×x

μ 2

2 1 k i ×x

μ 2

2 2 k i ×x

μ 2

2 3 k i ×x μ

0.227369 0.002473 0.22413977 2.728430854 0.029681026 2.689677221 34.10538567 0.371012825 33.62096527

0.030255 0.450568 0.02396792 0.756385222 11.26419292 0.599198058 4.689588374 69.83799611 3.715027961

0.007239 0.048063 0.48397315 0.12306895 0.817079095 8.227543624 0.912158102 6.055997996 60.98061745

0.157166 0.050531 0.14346455 3.143310915 1.010626671 2.869290987 20.74585204 6.670136031 18.93732052

0.077318 0.189031 0.08246191 1.391728982 3.4025515 1.484314385 11.21115013 27.40944264 11.95697699

0.164663 0.236627 0.01161446 2.46994208 3.549401169 0.174216884 22.22947872 31.94461052 1.567951952

0.14832 0.043376 0.16533103 3.856307486 1.127765422 4.298606805 18.09498128 5.291822364 20.17038578

0.153108 0.205961 0.02398803 3.827706737 5.14901388 0.599700851 19.44475022 26.15699051 3.046480321

0.227845 0.025067 0.1327466 2.27845126 0.250667027 1.327466021 29.61986639 3.258671353 17.25705827

0.000164 0.292552 0.19919562 0.002295822 4.095729769 2.788738714 0.023778156 42.42005832 28.88336526

∑

=

1.193448

∑

=

1.544248

∑

=

1.49088305

∑

=

20.57762831

∑

=

30.69670848

∑

=

25.05875355

∑

=

161.0769891

∑

=

cluster

(

)

( )

1.193448 17.24217

1 20.5776283 * ) ( 6 1 2 1 10 1 1 2 1

11 = = =

∑

∑

= = i i k k i x v μ μ

Untuk pusat cluster kedua pada atribut ke-1

(

)

( )

1.544248 19.87809

8 30.6967084 * ) ( 6 1 2 2 6 1 1 2 2

21 = = =

∑

∑

= = i i i k i x v μ μ

Untuk pusat cluster ketiga pada atribut ke-1

(

)

( )

1.49088305 16.80799

5 25.0587535 * ) ( 6 1 2 3 6 1 1 2 3

31 = = =

∑

∑

= = i i i k i x v μ μ

Untuk pusat cluster pertama pada atribut ke-2

(

)

( )

1.193448 134.9678

1 161.076989 * ) ( 6 1 2 1 6 1 2 2 1

12 = = =

∑

∑

= = i i i k i x v μ μ

Untuk pusat cluster kedua pada atribut ke-2

(

)

( )

1.544248 142.0864

7 219.416738 * ) ( 6 1 2 2 6 1 2 2 2

22 = = =

∑

∑

= = i i i k i x v μ μ

Untuk pusat cluster ketiga pada atribut ke-2

(

)

( )

1.49088305 134.24

8 200.136149 * ) ( 6 1 2 3 6 1 2 2 3

32 = = =

∑

∑

= = i i i k i x v μ μ

3 2 1

134.24 16.80799

142.0864 19.87809

134.9678 17.24217

cluster cluster cluster ⎥

⎥ ⎥ ⎦ ⎤

⎢ ⎢ ⎢ ⎣ ⎡

Setelah di dapat pusat cluster ( ), akan dicari Fungsi Objektif yang dapat dihitung dengan persamaan 3.26. Detil perhitungan fungsi objektif dapat dilihat pada tabel 3.3;3.4;3.5

berikut

Tabel 3.4. (Tabel perhitungan data x_k1 dengan pusat cluster v_1j)

11 1 v

x_k − x_k2 −v₁₂ (x_k1−v₁₁)2 (x_k2 −v₁₂)2 ⎥⎥_⎦

⎤ ⎢

⎢ ⎣ ⎡

−

∑

=

2 2

1 1

j

j kj v

x

( )

12

2 2

1

1 i j

j kj v

x μ

⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣ ⎡

−

∑

=

-5.24217 15.0322 27.4803742 225.9669845 253.4473587 57.62613278

7.757827 20.0322 60.183885 401.2889671 461.4728521 13.96204982

-0.24217 -8.9678 0.0586476 80.42146808 80.48011568 0.582623727

2.757827 -2.9678 7.60561162 8.807847178 16.4134588 2.57963021

0.757827 10.0322 0.57430227 100.6450019 101.2193042 7.826102172

-2.24217 0.032198 5.02733825 0.001036728 5.028374977 0.82798633

8.757827 -12.9678 76.6995397 168.163882 244.8634217 36.31802485

7.757827 -7.9678 60.183885 63.4858646 123.6697496 18.93486135

-7.24217 -4.9678 52.4490649 24.67905415 77.12811902 17.573266

-3.24217 10.0322 10.5116836 100.6450019 111.1566855 0.018228283

∑

21 1 v

x_k − x_k2 −v₂₂ (x_k1 −v₂₁)2 (x_k2 −v₂₂)2 ⎥⎥_⎦

⎤ ⎢ ⎢ ⎣ ⎡ −

∑

= 2 2 1 2 j j kj v

x

( )

₁2

2 2 1 2 i j j kj v x μ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ −

∑

=

-7.87809 7.913564 62.064319 62.62448977 124.6888088 0.308407648

5.121909 12.91356 26.233951 166.7601263 192.9940773 86.95690079

-2.87809 -16.0864 8.28340825 258.7734342 267.0568424 12.83568018

0.121909 -10.0864 0.01486179 101.7361981 101.7510599 5.141616747

-1.87809 2.913564 3.5272261 8.488853188 12.01607929 2.271407144

-4.87809 -7.08644 23.7957726 50.21758003 74.0133526 17.51353868

6.121909 -20.0864 37.4777688 403.4649249 440.9426938 19.12615089

5.121909 -15.0864 26.233951 227.6005615 253.8345125 52.27989713

-9.87809 -12.0864 97.5766833 146.0819435 243.6586268 6.107718362

-5.87809 2.913564 34.5519547 8.488853188 43.04080791 12.59167987

∑

215.1329974

Tabel 3.6. (Tabel perhitungan data xkj dengan pusat cluster v3j)

31 1 v

x_k − x_k2 −v₃₂ (x_k1 −v₃₁)2 (x_k2 −v₃₂)2 ⎥⎥_⎦

⎤ ⎢ ⎢ ⎣ ⎡ −

∑

= 2 2 1 3 j j kj v

x

( )

₁2

2 2 1 3 i j j kj v x μ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ −

∑

=

-4.80799 15.75999 23.1168072 248.3774161 271.4942233 60.85265234

8.19