Abstrak- Angka putus sekolah menjadi permasalahan yang saat ini dihadapi oleh pemerintah. Jawa Timur merupakan salah satu provinsi yang berpotensi dalam menyumbang tingginya angka putus sekolah di Indonesia khususnya untuk usia SMA. Angka putus sekolah usia SMA lebih tinggi dibandingkan dengan angka putus sekolah jenjang pendidikan lain. Dalam upaya menggalakkan wajib belajar 12 tahun, maka perlu dilakukan pemodelan angka putus sekolah usia SMA untuk mengetahui faktor-faktor yang mempengaruhi angka putus sekolah usia SMA tersebut. Pendekatan regresi yang digunakan adalah regresi nonparametrik spline multivariabel dikarenakan data memiliki pola hubungan yang tidak diketahui bentuk pola datanya. Penentuan model regresi spline terbaik berdasarkan pemilihan titik knot optimal. Titik knot optimal ditentukan menggunakan metode Generalized Cross Validation (GCV). Hasil penelitian menunjukkan bahwa model regresi spline terbaik adalah model regresi spline dengan kombinasi titik knot. Variabel yang berpengaruh signifikan terhadap angka putus sekolah usia SMA di Jawa Timur adalah persentase penduduk miskin, laju pertumbuhan ekonomi, persentase jumlah sekolah, dan persentase tenaga pengajar.
Kata Kunci- Angka Putus Sekolah Usia SMA, Regresi Nonparametrik Spline, Titik Knot
I.
PENDAHULUANPendidikan merupakan salah satu faktor penting dalam upaya mengembangkan Sumber Daya Manusia (SDM). Peran pendidikan dalam pembangunan SDM akan berdampak terhadap peningkatan kualitas hidup masyarakat. Mengingat hal tersebut, peningkatan mutu pendidikan sebagai upaya pengembangan SDM tentu sangat penting dilakukan. Namun, pada kenyataannya masih banyak anak yang mengalami putus sekolah.
Jawa Timur merupakan salah satu provinsi yang berpotensi dalam menyumbang tingginya angka putus sekolah di Indonesia. Angka putus sekolah di Jawa Timur sampai saat ini masih tinggi, khususnya untuk jenjang usia SMA. Angka putus sekolah atau persentase yang tidak bersekolah pada usia SMA yaitu kelompok umur 16-18 tahun adalah sebesar 0.84 persen. Angka ini cukup tinggi bila dibandingkan dengan kelompok umur lainnya. Angka putus sekolah kelompok umur 7-12 tahun yaitu sebesar 0,14 persen. Sedangkan untuk usia 13-15 tahun adalah sebesar 0.4 persen. Hal ini juga dapat dilihat pada persentase yang bersekolah. Tahun 2011 jumlah anak usia SMA ada 1.808.731 anak. Sementara angka partisipasi untuk usia SMA adalah 54,97 persen. Artinya hanya 55 persen saja anak usia SMA yang bisa sekolah, sementara sisanya 45 persen tidak bisa sekolah di jenjang tersebut. Jadi ada 813.929 anak usia SMA tidak bisa sekolah di jenjang SMA.
Salah satu metode yang dapat digunakan untuk mengenalisis faktor-faktor yang mempengaruhi angka putus sekolah adalah analisis regresi.. Dalam banyak hal, sering kali suatu data dipaksakan mengikuti pola tertentu sehingga
menyebabkan model yang didapatkan tidak cukup baik. Untuk mengatasi hal tersebut dapat digunakan metode regresi nonparametrik di mana metode regresi nonparametrik dapat digunakan untuk memodelkan pola data di mana bentuk kurva regresi tidak diketahui.
Penelitian sebelumnya mengenai putus sekolah dilakukan oleh [1] pada penelitian pemodelan remaja putus sekolah usia SMA di Provinsi Jawa Timur dengan menggunakan metode regresi spasial. Pada penelitian tersebut nilai R2 yang didapat cukup rendah yaitu kurang dari 50 persen. Oleh karena itu, diperlukan metode yang dapat menghasilkan nilai R2 yang lebih baik. Pada penelitian ini digunakan metode regresi nonparametrik spline yang lebih dapat menyesuaikan terhadap pola data. Kelebihan dari spline adalah dapat mengatasi pola data yang menunjukkan adanya perubahan perilaku pada sub – sub interval tertentu dengan bantuan titik–titik knot.
Berdasarkan latar belakang di atas, maka didapatkan rumusan masalah, yaitu bagaimana karakteristik angka putus sekolah usia SMA di Jawa Timur dan faktor-faktor yang mempengaruhinya secara deskriptif dan bagaimana memodelkan faktor-faktor yang mempengaruhi angka putus sekolah usia SMA di Jawa Timur menggunakan regresi spline multivariabel.
II. TINJAUAN PUSTAKA A. Analisis Regresi
Analisis regresi merupakan salah satu analisis dalam statistika yang digunakan untuk menyelidiki pola hubungan fungsional antara variabel respon dan variabel prediktor.
Pada umumnya terdapat tiga pendekatan dalam mengestimasi kurva regresi, yaitu pendekatan parametrik, nonparametrik, dan semiparametrik [2]. Apabila dalam analisis regresi bentuk kurva pola hubungan variabel respon dan prediktor diketahui, maka pendekatan regresi yang digunakan adalah regresi parametrik. Sedangkan jika pola hubungan kurva regresi tidak diketahui maka model regresi yang digunakan adalah model regresi nonparametrik. Pendekatan regresi semiparametrik digunakan untuk pola hubungan variabel respon dan prediktor yang sebagian diketahui kurva regresinya dan sebagian lagi tidak.
B. Regresi Nonparametrik Spline
Regresi nonparametrik merupakan metode pendekatan regresi yang sesuai untuk pola data yang tidak diketahui bentuk kurva regresinya atau tidak terdapat informasi masa lalu yang lengkap tentang bentuk pola data [3]. Bentuk model regresi nonparametrik secara umum adalah sebagai berikut.
(1) Pendekatan regresi nonparametrik memiliki fleksibilitas yang tinggi, karena data diharapkan mencari sendiri bentuk estimasi kurva regresinya tanpa dipengaruhi oleh faktor subyektifitas peneliti.
Dalam fungsi spline terdapat titik knot yang merupakan titik perpaduan yang menunjukkan perubahan perilaku kurva
PEMODELAN ANGKA PUTUS SEKOLAH USIA SMA DI JAWA TIMUR
DENGAN PENDEKATAN REGRESI SPLINE MULTIVARIABEL
Mega Pradipta, Madu Ratna, I Nyoman Budiantara
Jurusan Statistika Fakultas MIPA Institut Teknologi Sepuluh Nopember (ITS) Jl. Arif Rahman Hakim, Surabaya 60111
pada selang yang berbeda [4]. Bentuk umum model regresi Spline disajikan pada persamaan berikut
J j m j i j m m j j i j ix
x
K
x
F
1 0)
(
)
(
(2) dengan
j i j i m j i m j iK
x
K
x
K
x
K
x
;
0
;
di mana
j merupakan parameter model dan m merupakan orde spline. K adalah titik knot merupakan titik perpaduan bersama dimana terdapat perubahan pola perilaku pada interval yang berbeda.C. Pemilihan Titik Knot Optimal dan Model Terbaik
Titik knot merupakan titik perpaduan bersama dimana terdapat perubahan pola perilaku pada interval yang berbeda Model spline dengan titik knot yang optimal merupakan model spline yang terbaik. Salah satu metode pemilihan titik knot optimal yang paling banyak dipakai adalah Generalized Cross Validation (GCV). Titik knot yang optimal diperoleh dari nilai GCV yang paling minimum [5]. Metode GCV secara umum adalah sebagai berikut.
2 2 1 1 2 1 2 1 ) , , , ( ) , , , ( ) , , , ( J J J K K K A I tr n K K K MSE K K K GCV (3)dimana
D. Pengujian Signifikansi Parameter
Pengujian signifikansi parameter digunakan untuk menentukan variabel prediktor yang berpengaruh terhadap variabel respon pada model yang telah didapat. Uji yang dilakukan antara lain:
1. Uji Serentak
Untuk mengetahui signifikansi parameter secara bersama-sama maka dilakukanlah uji serentak. Statistik uji yang digunakan adalah statistic uji F.
2. Uji Individu
Untuk mengetahui parameter yang berpengaruh signifikan secara individu terhadap model maka dilakukanlah uji individu. Statistik uji yang digunakan adalah statistik uji t.
E. Uji Asumsi Residual
Asumsi residual digunakan untuk mengetahui kelayakan suatu model dalam menggambatkan data yang sebenarnya. Asumsi yang perlu dipenuhi adalah residual identik, independen, dan berdistribusi normal.
a. Residual identik
Residual dikatakan identik apabila residual tersebut memiliki varians yang sama (homogen). Uji yang dapat digunakan untuk mengetahui apakah residual memilki varians yag homogen adalah uji Glejser [6].
b. Residual independen
Tujuan dilakukan pengujian residual independen adalah untuk mengetahui apakah korelasi antar residual bernilai 0 atau tidak. Adanya korelasi antar residual disebut dengan istilah autokorelasi. Pengujian asumsi residual independen dapat menggunakan Auto Correlation Function (ACF). Residual dikatakan independen apabila tidak ada lag yang keluar dari batas atas maupun batas bawah pada plot ACF.
c. Residual berdistribusi Normal
Pengujian residual berdistribusi normal untuk mengetahui apakah distribusi residual telah memenuhi asumsi berdistribusi normal atau tidak. Salah satu uji yang dapat digunakan adalah uji Kolmogorov Smirnov.
F. Kebaikan Model
Penentuan titik Model yang sudah diperoleh dapat diketahui kehandalan modelnya. Kehandalan model diwakili oleh nilai koefisien deterninasi atau R2. Nilai R2 menyatakan seberapa besar variabel respon dijelaskan atau diakibatkan oleh hubungan dengan variabel prediktor dalam model.
G. Putus Sekolah
Putus sekolah adalah proses berhentinya siswa secara terpaksa dari suatu lembaga pendidikan tempat dia belajar atau terlantarnya anak dari sebuah lembaga pendidikan formal, yang disebabkan oleh berbagai faktor. Faktor-faktor yang mempengaruhi angka putus sekolah antara lain faktor ekonomi, demografi, dan geografi.
III. METODOLOGI PENELITIAN
Data yang digunakan pada penelitian ini adalah data sekunder yang diperoleh dari data Badan Pusat Statistik Jawa Timur dan data Dinas Pendidikan dan Kebudayaan Jawa Timur pada tahun 2011. Data tersebuat mencakup data angka putus sekolah usia jenjang pendidikan SMA dan faktor-faktor yang diduga mempengaruhinya di Provinsi Jawa Timur yang terdiri dari 38 kota/kabupaten.
Tabel 1. Variabel Penelitian
Variabel Keterangan Tipe
Y
Persentase angka putus sekolah usia SMA Kab/Kota di Jawa Timur
Kontinu X1 Persentase penduduk miskin Kontinu
X2 Laju pertumbuhan ekonomi Kontinu
X3 Persentase sekolah Kontinu
X4 Persentase tenaga pengajar Kontinu
Langkah-langkah analisis yang dilakukan pada penelitian ini adalah sebagai berikut
1. Melakukan analisis deskriptif karakteristik angka putus sekolah usia SMA di Jawa Timur, persentase keluarga miskin, laju pertumbuhan ekonomi, persentase sekolah, dan persentase tenaga pengajar.
2. Memodelkan faktor-faktor yang mempengaruhi angka putus sekolah usia SMA di Jawa Timur dengan regresi spline multivariabel
a. Membuat scatterplot variabel respon dengan masing-masing variabel prediktor untuk mengetahui pola hubungan antara variabel respon dan variabel prediktor
b. Memodelkan variabel respon dengan berbagai model Spline dan berbagai titik knot
c. Menetukan titik knot optimal berdasarkan nilai GCV minimum
d. Menentukan model Spline terbaik.
e. Menguji signifikansi parameter secara serentak dan individu.
f. Melakukan uji IIDN pada residual
g. Menghitung koefisien determinasi dan MSE h. Menginterpretasikan hasil yang diperoleh dan
IV. ANALISIS DAN PEMBAHASAN
A. Karakteristik Angka Putus Sekolah Usia SMA di Jawa Timur beserta Faktor yang Diduga Mempengaruhinya Berikut merupakan deskripsi angka putus sekolah usia SMA dan faktor-faktor yang diduga mempengaruhi di 38 kabupaten/kota di Jawa Timur.
Tabel 2. Statistika Deskriptif
Variabel Rata-rata Varians Minimum Maksimum
Y 0.9820 0.4610 0.2000 3.0300
X1 13.8160 34.6390 4.7400 30.2100
X2 6.8560 0.4160 6.1400 9.2000
X3 0.2453 0.0069 0.1530 0.5038
X4 7.558 13.7120 3.5660 18.6630
Rata-rata angka putus sekolah usia SMA di Jawa Timur tahun 2011 adalah sebesar 0.9820 dengan varians 0.4610. Angka putus sekolah usia SMA terendah sebesar 0.2000 yaitu berada di Kabupaten Mojokerto dan angka putus sekolah usia SMA tertinggi sebesar 3.0300 berada di . Kota Blitar.
Persentase penduduk miskin menunjukkan bahwa rata-rata persentase penduduk miskin sebesar 13.8160 dengan varians 34.6390. Persentase penduduk miskin terendah pada tahun 2011 sebesar 4.7400 berada di Kota Batu dan persentase penduduk miskin tertinggi mencapai angka 30.2100 berada di Kabupaten Sampang.. Karakteristik variabel laju pertumbuhan ekonomi dengan rata-rata sebesar 6.8560 dan varians sebesar 0.4160. Laju pertumbuhan ekonomi terendah sebesar 6.1400 dan laju pertumbuhan ekonomi tertinggi mencapai 9.2000. Laju pertumbuhan ekonomi terendah terjadi di Kabupaten Sampang sedangkan laju pertumbuhan ekonomi tertinggi terjadi di Kabupaten Bojonegoro.
Persentase sekolah SMA memiliki rata-rata sebesar 0.2453 dengan varians yang kecil yaitu sebesar 0.0069. Persentase sekolah terendah adalah sebesar 0.1530 sedangkan persentase sekolah tertinggi sebesar 0.5038. Variabel persentase tenaga pengajar (X4) pada tahun 2011 memiliki
rata-rata sebesar 7.5580 dengan varians sebesar 13.712. Persentase tenaga pengajar terendah berada di Kediri yakni sebesar 3.5660. Sedangkan persentase tenaga pengajar tertinggi berada di Kota Madiun yakni sebesar 18.6630.
B. Scatterplot Variabel Respon dan Variabel Prediktor
Berikut merupakan pemaparan pola hubungan angka putus sekolah usia SMA dengan variabel yang diduga berpengaruh.
Gambar 1. Scatterplot antara Angka Putus Sekolah dengan Keempat Variabel yang Diduga berpengaruh Berdasarkan scatterplot yang diperoleh dari keempat variabel prediktor terhadap angka putus sekolah diperoleh bahwa semua pola hubungan yang terbentuk tidak membentuk pola tertentu.
C. Pemilihan Titik Knot Optimal dan Model Regresi Spline Terbaik
Selanjutnya dilakukan pemilihan titik knot optimal dengan 1 knot, 2 knot, 3 knot, 4 knot dan kombinasi knot untuk memperoleh model regresi nonparametrik spline multivariabel terbaik. Generelized Cross Validation (GCV) merupakan salah satu metode yang digunakan pada pemilihan titik knot optimal. Semakin kecil GCV maka akan menghasilkan titik knot yang optimal.
Berikut merupakan hasil nilai GCV dari beberapa pilihan titik knot.
1. Pemilihan Titik Knot Optimal dengan Satu Knot
Nilai GCV regresi spline multivariabel dengan satu titik knot adalah sebagai berikut
Tabel 3. Nilai GCV dengan Satu Titik Knot
No X1 X2 X3 X4 GCV
1 15.1359 7.3890 0.2962 9.7283 0.4110 2 16.1755 7.5139 0.3105 10.3445 0.4001 3 17.2151 7.6388 0.3248 10.9607 0.4065
Berdasarkan hasil pemilihan titik knot optimal dengan satu titik knot diperoleh nilai GCV terkecil sebesar 0.4001. 2. Pemilihan Titik Knot Optimal dengan Dua Knot
Nilai GCV regresi spline multivariabel dengan dua titik knot adalah sebagai berikut
Tabel 4. Nilai GCV dengan Dua Titik Knot
No X1 X2 X3 X4 GCV 1 10.9776 6.8894 0.2389 7.2635 0.3959 13.5765 7.2016 0.2747 8.8040 2 10.9776 6.8894 0.2389 7.2635 0.3988 15.6557 7.4514 0.3033 10.0364 3 12.0171 7.0143 0.2532 7.8797 0.3815 12.5369 7.0767 0.2604 8.1878
Berdasarkan hasil pemilihan titik knot optimal dengan dua titik knot diperoleh nilai GCV terkecil sebesar 0.3815. 3. Pemilihan Titik Knot Optimal dengan Tiga Knot
Nilai GCV regresi spline multivariabel dengan tiga titik knot adalah sebagai berikut
Tabel 5. Nilai GCV dengan Tiga Titik Knot
No X1 X2 X3 X4 GCV 1 10.4578 6.8269 0.2318 6.9554 0.3125 10.9776 6.8894 0.2389 7.2635 12.0171 7.0143 0.2532 7.8797 2 10.4578 6.8269 0.2318 6.9554 0.3474 11.4973 6.9518 0.2461 7.5716 12.0171 7.0143 0.2532 7.8797
Berdasarkan hasil pemilihan titik knot optimal dengan tiga titik knot diperoleh nilai GCV terkecil sebesar 0.3125. 4. Pemilihan Titik Knot Optimal dengan Empat Knot
Nilai GCV regresi spline multivariabel dengan empat titik knot adalah sebagai berikut
Tabel 6. Nilai GCV dengan Empat Titik Knot
No X1 X2 X3 X4 GCV 1 9.1314 6.6676 0.2135 6.1693 0.2810 10.0097 6.7731 0.2256 6.6898 10.8879 6.8786 0.2377 7.2104 12.6445 7.0897 0.2619 8.2516 2 9.1314 6.6676 0.2135 6.1693 0.2968 10.0097 6.7731 0.2256 6.6898 10.8879 6.8786 0.2377 7.2104 15.2793 7.4062 0.2982 9.8133 30 20 10 6 7 8 9 3 2 1 0 0.5 0.4 0.3 0.2 3 2 1 0 20 15 10 5 persentase penduduk miskin
a n g ka p u tu s se ko la h
laju pertumbuhan ekonomi
Berdasarkan hasil pemilihan titik knot optimal dengan tiga titik knot diperoleh nilai GCV terkecil sebesar 0.2810 5. Pemilihan Titik Knot Optimal dengan Kombinasi Knot
Nilai GCV regresi spline multivariabel dengan kombinasi titik knot adalah sebagai berikut
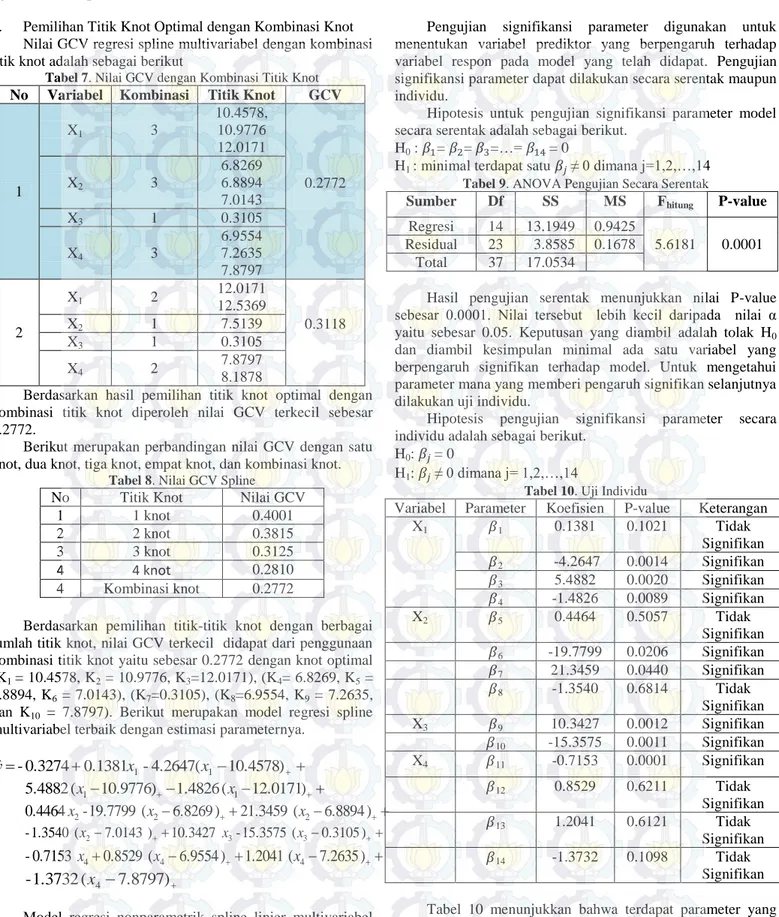
Tabel 7. Nilai GCV dengan Kombinasi Titik Knot
No Variabel Kombinasi Titik Knot GCV
1 X1 3 10.4578, 10.9776 12.0171 0.2772 X2 3 6.8269 6.8894 7.0143 X3 1 0. 0.3105 X4 3 6.9554 7.2635 7.8797 2 X1 2 12.0171 12.5369 0.3118 X2 1 7.5139 X3 1 0.3105 X4 2 7.8797 8.1878
Berdasarkan hasil pemilihan titik knot optimal dengan kombinasi titik knot diperoleh nilai GCV terkecil sebesar 0.2772.
Berikut merupakan perbandingan nilai GCV dengan satu knot, dua knot, tiga knot, empat knot, dan kombinasi knot.
Tabel 8. Nilai GCV Spline
No Titik Knot Nilai GCV
1 1 knot 0.4001
2 2 knot 0.3815
3 3 knot 0.3125
4 4 knot 0.2810
4 Kombinasi knot 0.2772
Berdasarkan pemilihan titik-titik knot dengan berbagai jumlah titik knot, nilai GCV terkecil didapat dari penggunaan kombinasi titik knot yaitu sebesar 0.2772 dengan knot optimal (K1 = 10.4578, K2 = 10.9776, K3=12.0171), (K4= 6.8269, K5 =
6.8894, K6 = 7.0143), (K7=0.3105), (K8=6.9554, K9 = 7.2635,
dan K10 = 7.8797). Berikut merupakan model regresi spline
multivariabel terbaik dengan estimasi parameternya.
-
0.3274
0.1381
-
4.2647
(
10.4578
)
ˆ
x
1x
1y
10.9776
)
1.4826
(
12.0171
)
(
5.4882
x
1x
1
6.8269
)
21.3459
(
6.8894
)
(
19.7799
-0.4464
x
2x
2x
2 7.0143 ) 10.3427 -15.3575 ( 0.3105) ( 1.3540 - x2 x3 x3
0.8529
(
6.9554
)
1.2041
(
7.2635
)
0.7153
-
x
4x
4x
4
7.8797
)
(
1.3732
-
x
4Model regresi nonparametrik spline linier multivariabel dengan kombinasi knot tersebut menghasilkan koefisien determinasi sebesar 77.3740 persen dan MSE sebesar 0.1678. Hal tersebut mempunyai arti bahwa variabel prediktor mampu menjelaskan variabilitas variabel respon sebesar 77.3740 persen. Tahap selanjutnya adalah melakukan uji signifikansi parameter.
D. Pengujian Signifikansi Parameter Model Regresi Spline Terbaik
Pengujian signifikansi parameter digunakan untuk menentukan variabel prediktor yang berpengaruh terhadap variabel respon pada model yang telah didapat. Pengujian signifikansi parameter dapat dilakukan secara serentak maupun individu.
Hipotesis untuk pengujian signifikansi parameter model secara serentak adalah sebagai berikut.
H0 : = = =…= = 0
H1 : minimal terdapat satu ≠ 0 dimana j=1,2,…,14
Tabel 9. ANOVA Pengujian Secara Serentak
Sumber Df SS MS Fhitung P-value
Regresi 14 13.1949 0.9425
5.6181 0.0001 Residual 23 3.8585 0.1678
Total 37 17.0534
Hasil pengujian serentak menunjukkan nilai P-value sebesar 0.0001. Nilai tersebut lebih kecil daripada nilai α yaitu sebesar 0.05. Keputusan yang diambil adalah tolak H0
dan diambil kesimpulan minimal ada satu variabel yang berpengaruh signifikan terhadap model. Untuk mengetahui parameter mana yang memberi pengaruh signifikan selanjutnya dilakukan uji individu.
Hipotesis pengujian signifikansi parameter secara individu adalah sebagai berikut.
H0: = 0
H1: ≠ 0 dimana j= 1,2,…,14
Tabel 10. Uji Individu
Variabel Parameter Koefisien P-value Keterangan
X1 1 0.1381 0.1021 Tidak Signifikan 2 -4.2647 0.0014 Signifikan 3 5.4882 0.0020 Signifikan 4 -1.4826 0.0089 Signifikan X2 5 0.4464 0.5057 Tidak Signifikan 6 -19.7799 0.0206 Signifikan 7 21.3459 0.0440 Signifikan 8 -1.3540 0.6814 Tidak Signifikan X3 9 10.3427 0.0012 Signifikan 10 -15.3575 0.0011 Signifikan X4 11 -0.7153 0.0001 Signifikan 12 0.8529 0.6211 Tidak Signifikan 13 1.2041 0.6121 Tidak Signifikan 14 -1.3732 0.1098 Tidak Signifikan Tabel 10 menunjukkan bahwa terdapat parameter yang tidak signifikan yaitu 1, 5 8, 12, 13,, dan 14 dikarenakan
mempunyai nilai P-value yang lebih dari α=0.05. Meskipun begitu, didapatkan kesimpulan bahwa semua variabel berpengaruh signifikan terhadap model. Setelah didapatkan model regresi spline terbaik maka dilakukan uji asumsi residual.
E. Pengujian Asumsi Residual Model Regresi Spline Terbaik Uji asumsi residual bertujuan untuk mengetahui apakah residual yang dihasilkan model sudah memenuhi asumsi
residual. Residual harus memenuhi asumsi identik, independen, dan berdistribusi normal.
Residual dikatakan memenuhi asumsi identik apabila residual tersebut memiliki varians yang sama (homogen). Untuk mengetahui apakah residual memilki varians yang homogen dapat dijui menggunakan uji Glejser.
Hipotesis untuk mengetahui apakah varians dari residual sudah identik atau belum adalah sebagai berikut.
Tabel 11. Uji Glejser
Sumber df SS MS Fhitung P-value
Regresi 14 0.62292 0.04450 1.97 0.061 Residual 23 0.52064 0.02264
Total 37 1.34356
Hasil pengujian Glejser tersebut menghasilkan nilai P-value sebesar 0.061. Nilai tersebut lebih besar dari alpha yang ditetapkan yaitu 0.05 sehingga diambil keputusan gagal tolak H0. Dapat disimpulkan bahwa residual telah identik.
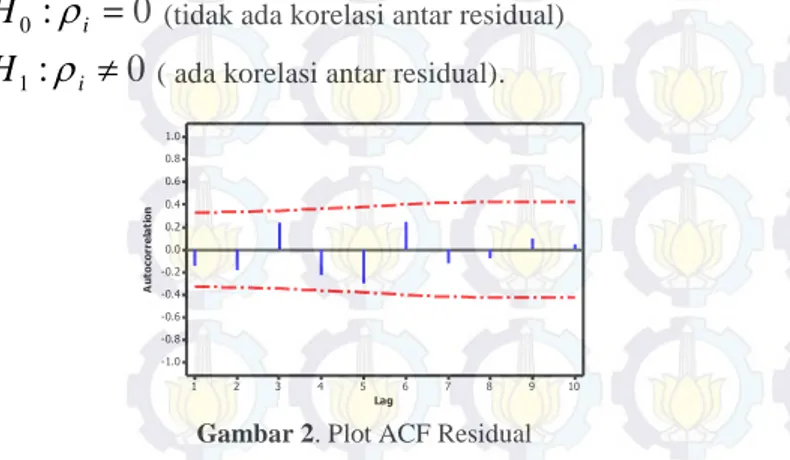
Tujuan dilakukan pengujian residual independen adalah untuk mengetahui apakah antar residual independen atau tidak. Asumsi residual independen dapat dilihat menggunakan Auto Correlation Function (ACF). Berikut adalah hipotesis untuk mengetahui apakah residual sudah memenuhi asumsi indepen
0
:
0 i
H
(tidak ada korelasi antar residual)0
:
1 i
H
( ada korelasi antar residual).Gambar 2. Plot ACF Residual
Hasil menunjukkan bahwa tidak ada lag yang keluar atau melewati dari garis batas. Oleh karena dapat disimpulkan bahwa tidak ada korelasi antar residual atau dengan kata lain asumsi residual independen telah terpenuhi.
Pengujian residual berdistribusi normal untuk mengetahui apakah distribusi residual telah memenuhi asumsi berdistribusi normal atau tidak. Uji yang dapat digunakan adalah uji Kolmogorov Smirnov. Hipotesis yang digunakan untuk menguji residual berdistribusi normal adalah sebagai berikut.
:
0
H
residual berdistribusi normal:
1
H
residual tidak berdistribusi normalGambar 3. Uji Normalitas Residual
Dengan menggunakan Kolmogorov Smirnov didapatkan nilai P-value sebesar 0.150. Nilai tersebut lebih besar daripada α. Keputusan yang diambil adalah gagal tolak H0. Dengan
demikian diambil kesimpulan bahwa asumsi residual berdistribusi normal telah terpenuhi.
F. Interpretasi Model
Interpretasi model spline terbaik dicontohkan untuk hubungan angka putus sekolah usia SMA dengan salah satu variabel prediktor yaitu persentase sekolah (X3) .
Hubungan persentase sekolah (X3) terhadap angka putus
sekolah usia SMA (Y) dengan asumsi variabel X1, X2, dan X4
konstan adalah pada saat persentase sekolah kurang dari 0.3105 persen, apabila persentase sekolah naik sebesar satu persen maka angka putus sekolah usia SMA cenderung akan naik sebesar 10.3427 persen. Pada saat persentase sekolah lebih dari 0.3105 persen, apabila persentase sekolah mengalami kenaikan sebesar satu persen maka angka putus sekolah usia SMA akan cenderung turun sebesar 5.0148 persen.
Pengelompokan kabupaten/kota berdasarkan model yang didapat sebagai berikut.
- kabupaten/kota dengan persentase sekolah kurang dari 0.3105 persen yaitu Kota Surabaya, Kota Malang, Kota Pasuruan, Kota Probolinggo, Kota Gresik, Kabupaten Gresik, Kabupeten Sidoarjo, Kabupaten Mojokerto, Kabupaten Jombang, Kabupaten Bojonegoro, Kabupaten Tuban, Kabupaten Madiun, Kabupaten Ngawi, Kabupaten Magetan, Kabupaten Ponorogo, Kabupaten Pacitan, Kabupaten Kedir, Kabupaten Nganjuk, Kabupaten Blitar, Kabupaten Tulungagung, Kabupaten Trenggalek, Kabupaten Malang, Kabupaten Pasuruan, Kabupaten Probolinggo, Kabupaten Lumajang, Kabupaten Bondowoso, Kabupaten Situbondo, Kabupaten Jember, Kabupaten Banyuwangi, Kabupaten Sampang, dan Kabupaten Bangkalan.
- kabupaten/kota dengan persentase sekolah lebih dari 0.3105 persen yaitu Kota Madiun, Kota Kediri, Kota Mojokerto, Kota Blitar, Kabupaten Jombang, Kabupaten Lamongan, Kabupaten Pamekasan, dan kabupaten Sumenep.
Bedasarkan model yang diperoleh diharapkan persentase sekolah di tiap kabupaten/kota dapat melebihi angka 0.3105 karena dengan demikian angka putus sekolah dapat diturunkan.
V KESIMPULAN DAN SARAN
Kesimpulan yang dapat diambil dari penelitian ini adalah sebagai berikut.
1. Rata-rata angka putus sekolah usia SMA di Jawa Timur pada tahun 2011 adalah sebesar 0.9820 dengan varians sebesar 0.4610. Angka putus sekolah usia SMA terendah sebesar 0.2000 yaitu berada di Kabupaten Mojokerto. Kota Blitar menyumbang angka putus sekolah usia SMA tertinggi sebesar 3.0300.
2. Model regresi nonparametrik spline multivariabel terbaik yang terbentuk adalah model regresi spline linier dengan kombinasi knot. Nilai GCV yang diperoleh sebesar 0.2772 dengan Rsquare yaitu sebesar 77.3740 persen, sedangkan nilai MSEnya adalah 0.1678. Persamaan modelnya adalah sebagai berikut
-
0.3274
0.1381
-
4.2647
(
10.4578
)
ˆ
x
1x
1y
10.9776
)
1.4826
(
12.0171
)
(
5.4882
x
1x
1
6.8269
)
21.3459
(
6.8894
)
(
19.7799
-0.4464
x
2x
2x
2 10 9 8 7 6 5 4 3 2 1 1.0 0.8 0.6 0.4 0.2 0.0 -0.2 -0.4 -0.6 -0.8 -1.0 Lag A u to co rr e la ti o n 0.8 0.6 0.4 0.2 0.0 -0.2 -0.4 -0.6 -0.8 99 95 90 80 70 60 50 40 30 20 10 5 1 res P e rc e n t Mean -2.74936E-12 StDev 0.3229 N 38 KS 0.107 P-Value >0.150 7.0143 ) 10.3427 -15.3575 ( 0.3105 ) ( 1.3540 - x2 x3 x3
0.8529
(
6.9554
)
1.2041
(
7.2635
)
0.7153
-
x
4x
4x
4
7.8797
)
(
1.3732
-
x
4Variabel-variabel yang berpengaruh terhadap angka putus sekolah usia SMA adalah persentase penduduk miskin, laju pertumbuhan ekonomi, persentase sekolah, dan persentase tenaga pengajar.
Saran yang dapat diberikan penulis adalah pada penelitian selanjutnya dapat dilakukan penambahan variabel prediktor yang mempengaruhi angka putus sekolah usia SMA di Jawa Timur. Selain itu penelitian pada penelitian selanjutnya dapat mencoba menggunakan regresi spline orde dua atau orde tiga.
DAFTAR PUSTAKA
[1] Septiana, L. (2011). Pemodelan Remaja Putus Sekolah Usia SMA di Provinsi Jawa Timur dengan Menggunakan Metode Regresi Spasial, Tugas Akhir, Statistika FMIPA ITS, Surabaya
[2] Budiantara, I.N. (2005). Model Spline Multivariabel dalam Regresi Nonparametrik. Makalah Seminar Nasional Matematika, Jurusan Matematika ITS Surabaya. [3] Eubank, R. L. (1988). Spline Smoothing and
Nonparametric Regression, Marcel Deker: New York. [4] Hardle, W. (1990). Applied Nonparametric Regression.
New York: Cambridge University Press.
[5] Wahba G. (1990). Spline Models for Observational Data. Philadelphia: SIAM.
[6] Gujarati, D. N. (2006). Dasar-Dasar Ekonometrika Edisi Pertama, Jakarta: Erlangga.