Informasi Dokumen
- Penulis:
- Kana Hidayati
- Sari Dewi
- Adityo Suksmono
- Pengajar:
- Tim Visindo Media Persada
- Sekolah: SMAN 8 Batam
- Mata Pelajaran: Matematika
- Topik: Aktif Menggunakan Matematika untuk SMK/MAK Kelas XI Rumpun Sosial, Administrasi Perkantoran, dan Akuntansi
- Tipe: buku teks
- Tahun: 2008
- Kota: Jakarta
Ringkasan Dokumen
I. Logika Matematika
Bab ini membahas tentang logika matematika yang merupakan dasar dari pemikiran matematis. Dalam konteks pendidikan, logika matematika membantu siswa untuk memahami cara berpikir yang sistematis dan kritis. Pembelajaran logika dimulai dengan pernyataan dan kalimat terbuka yang menjadi landasan dalam membangun argumen dan penalaran. Melalui pemahaman logika, siswa dapat mengembangkan kemampuan analisis yang diperlukan dalam berbagai disiplin ilmu, termasuk sains dan teknologi.
1.1. Pernyataan dan Kalimat Terbuka
Pernyataan adalah kalimat yang memiliki nilai kebenaran, sedangkan kalimat terbuka mengandung variabel yang belum memiliki nilai kebenaran tertentu. Pemahaman ini penting untuk membedakan antara kalimat yang dapat dinilai benar atau salah dan yang tidak. Dengan mempelajari pernyataan dan kalimat terbuka, siswa dilatih untuk berpikir kritis dan analitis, yang sangat berharga dalam pendidikan matematika dan ilmu pengetahuan lainnya.
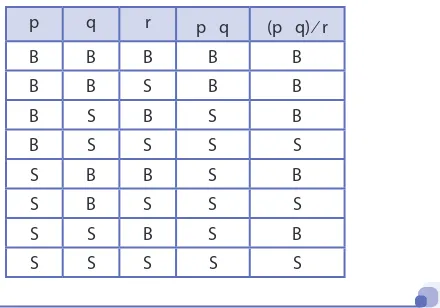
1.2. Pernyataan Majemuk
Pernyataan majemuk terbentuk dari penggabungan beberapa pernyataan tunggal menggunakan kata penghubung. Terdapat beberapa jenis pernyataan majemuk, seperti konjungsi dan disjungsi, yang masing-masing memiliki aturan nilai kebenaran tersendiri. Dengan memahami pernyataan majemuk, siswa dapat meningkatkan kemampuan logika dan pemecahan masalah yang sangat dibutuhkan dalam berbagai situasi akademik.
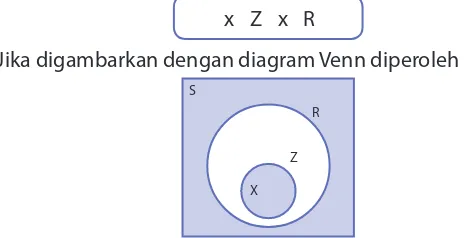
II. Relasi dan Fungsi
Materi ini membahas tentang relasi dan fungsi yang merupakan konsep dasar dalam matematika. Relasi menggambarkan hubungan antara dua himpunan, sedangkan fungsi adalah relasi khusus yang setiap elemen di domain berpasangan dengan tepat satu elemen di kodomain. Pemahaman tentang relasi dan fungsi sangat penting karena menjadi dasar bagi konsep yang lebih kompleks dalam matematika dan aplikasinya di bidang lain, seperti ekonomi dan ilmu komputer.
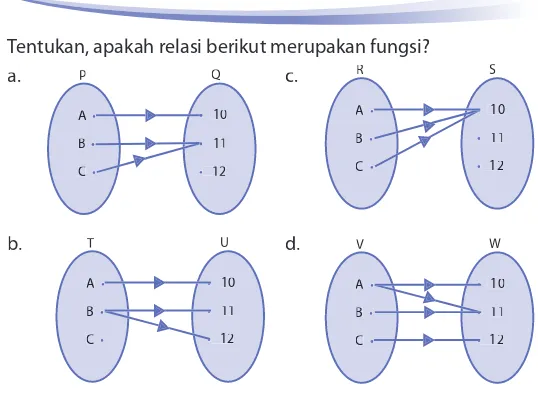
2.1. Pengertian Relasi dan Fungsi
Relasi adalah cara untuk menghubungkan elemen dari dua himpunan, sedangkan fungsi adalah relasi yang memenuhi syarat tertentu. Memahami relasi dan fungsi membantu siswa dalam menganalisis data dan menyelesaikan masalah yang melibatkan hubungan antar variabel. Ini juga merupakan langkah awal untuk memahami grafik dan analisis data.
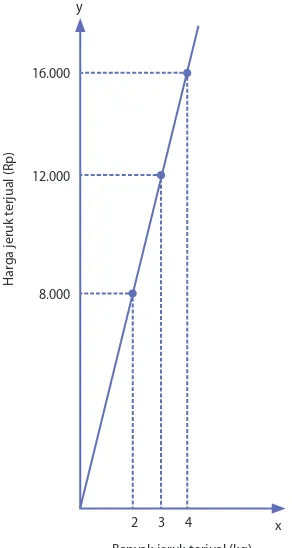
2.2. Fungsi Linear
Fungsi linear adalah fungsi yang dapat digambarkan dengan persamaan linear. Fungsi ini memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam perhitungan keuangan dan analisis tren. Memahami fungsi linear membantu siswa untuk mengembangkan keterampilan pemecahan masalah dan aplikasi praktis dalam berbagai bidang.
III. Barisan dan Deret Bilangan
Bab ini menjelaskan tentang barisan dan deret bilangan, yang merupakan konsep penting dalam matematika. Barisan adalah urutan angka yang mengikuti aturan tertentu, sedangkan deret adalah jumlah dari elemen-elemen barisan. Pemahaman tentang barisan dan deret sangat penting dalam analisis matematis dan dapat diterapkan dalam berbagai konteks, termasuk dalam statistik dan probabilitas.
3.1. Pengertian Barisan dan Deret Bilangan
Barisan adalah urutan angka yang mengikuti pola tertentu. Deret adalah jumlah dari elemen-elemen dalam barisan. Dengan memahami konsep ini, siswa dapat belajar bagaimana menganalisis pola dan membuat prediksi berdasarkan data yang ada. Ini adalah keterampilan penting dalam ilmu pengetahuan dan teknologi.
3.2. Barisan dan Deret Aritmetika
Barisan aritmetika adalah barisan angka yang memiliki selisih tetap antara suku-sukunya. Memahami barisan aritmetika memungkinkan siswa untuk menyelesaikan masalah yang melibatkan perhitungan dan estimasi. Ini juga membantu dalam pengembangan keterampilan pemecahan masalah yang lebih kompleks.
IV. Geometri Dimensi Dua
Geometri dimensi dua membahas tentang bentuk dan ukuran objek dalam dua dimensi. Pemahaman geometri sangat penting dalam berbagai aplikasi, seperti arsitektur, desain, dan teknik. Melalui pembelajaran geometri, siswa diajarkan untuk berpikir spasial dan mengembangkan keterampilan visual yang diperlukan dalam banyak bidang.
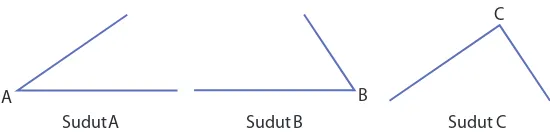
4.1. Sudut
Sudut adalah dua garis yang bertemu di satu titik. Pemahaman tentang sudut sangat penting dalam geometri, karena sudut mempengaruhi banyak aspek desain dan analisis. Siswa belajar untuk mengukur dan menggambar sudut, yang merupakan keterampilan dasar dalam geometri.
4.2. Bangun Datar
Bangun datar adalah bentuk geometris yang memiliki dua dimensi. Memahami bangun datar membantu siswa dalam menghitung luas dan keliling, serta memahami sifat-sifat geometris. Ini adalah dasar untuk banyak aplikasi praktis dalam kehidupan sehari-hari.
V. Transformasi Bidang Datar
Transformasi bidang datar mencakup perubahan posisi atau bentuk objek dalam bidang datar. Pemahaman tentang transformasi sangat penting dalam seni, desain, dan teknik. Melalui pembelajaran ini, siswa dapat memahami bagaimana objek dapat dimanipulasi dan diterapkan dalam berbagai konteks.
5.1. Translasi
Translasi adalah pergeseran objek tanpa mengubah bentuk atau ukurannya. Memahami translasi membantu siswa dalam menggambar dan memvisualisasikan objek dalam ruang. Ini adalah keterampilan penting dalam seni dan desain.
5.2. Releksi
Releksi adalah pencerminan objek terhadap garis tertentu. Memahami releksi membantu siswa dalam memahami simetri dan keseimbangan dalam desain. Ini juga merupakan konsep dasar dalam geometri yang dapat diterapkan dalam berbagai bidang.