ALGORITMA GOOGLE PAGERANK DAN APLIKASINYA PADA TWITTER

i

ALGORITMA GOOGLE PAGERANK DAN

APLIKASINYA PADA TWITTER

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Felicia Angela Saputra NIM: 163114007

PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

GOOGLE PAGERANK ALGORITHM AND

ITS APPLICATION ON TWITTER

Thesis

Presented as a Requirement to Obtain a Bachelor of Science Degree

Mathematics Study Program

By:

Felicia Angela Saputra NIM: 163114007

MATHEMATICS STUDY PROGRAM, DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

vi

MOTTO

“Always be a little kinder than necessary.” (James M. Barrie)

vii

HALAMAN PERSEMBAHAN

Skripsi ini saya persembahkan kepada:

Allah Subhaanahu Wa Ta‟ala, tanpa rahmat-Nya saya tidak bisa menyelesaikan skripsi ini.

Kedua orang tua saya Andy Saputra dan Ida Zuchriana, kakak dan adik saya Florentina Melani dan Ferdinand Fahriansyah S. yang selalu membuat saya

viii

ABSTRAK

Internet adalah suatu sistem global dari jaringan-jaringan komputer tanpa kabel yang saling terhubung dan dapat digunakan untuk mencari informasi dari berbagai sumber yang dapat diakses dari seluruh dunia. Untuk memudahkan

pengguna internet dalam mencari informasi tersebut diperlukan suatu alat, yaitu mesin pencarian. Mesin pencarian adalah sebuah situs web yang digunakan untuk mencari informasi di internet. Salah satu algoritma pada mesin pencarian adalah algoritma Google PageRank yang memberikan setiap halaman pada situs web sebuah peringkat berdasarkan tingkat kepentingan halaman tersebut. Algoritma ini juga dapat mengurutkan peringkat halaman web tersebut sesuai dengan kata kunci pencarian. Peringkat atau skor halaman web diperoleh dari koefisien pada nilai stasioner rantai Markov sehingga akan dibahas tentang bagaimana penggunaan matriks transisi peluang, sifat-sifat rantai Markov, pencarian nilai eigen dan nilai stasioner yang bersesuaian.

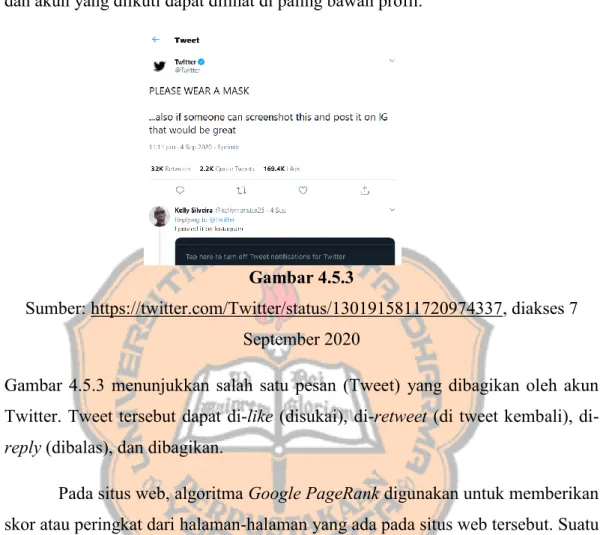
Selain digunakan untuk menentukan peringkat halaman-halaman pada situs web, algoritma Google PageRank juga dapat digunakan untuk mencari tingkat popularitas suatu akun pada Twitter dengan hubungan mengikuti dan diikuti. Dapat disimpulkan bahwa pada situs web, halaman yang penting adalah halaman yang memiliki banyak tautan dari halaman yang penting juga, sama halnya dengan Twitter yaitu akun yang tingkat popularitasnya tinggi adalah akun yang banyak diikuti oleh akun yang populer atau akun yang memiliki banyak pengikut juga.

Kata kunci: algoritma Google PageRank, rantai Markov, Teorema Frobenius, popularitas akun Twitter.

ix

ABSTRACT

Internet is a global system of wireless computer networks that are connected and can be used to look for information from various sources that accessible from all over the world. A tool that can help internet users when they are looking for information is a search engine. A search engine is a website which used to look for information on the internet. One of the algorithms used in the search engine is the Google PageRank algorithm that gives every page on the website a rank or score based on the importance of the page. The ranking or the score of every page on the web is the corresponding coefficient of the Markov chain stationary regime. To obtain the stationary regime, first, we must discuss the probability transition matrix, the properties of Markov chains, how to calculate eigenvalue, and the associated eigenvector.

Besides being used to find a rank of the website pages, the Google PageRank algorithm also can be used to find the popularity ranking of a Twitter account with the following and followed relation. In conclusion, on the website, the important page is a page that has a lot of links from important pages also, as well as Twitter, a high popularity account is an account that is followed by another popular account or an account that has a lot of followers.

Keywords: Google PageRank algorithm, Markov chain, Frobenius Theorem, popularity of Twitter account.

xiii

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN DOSEN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

MOTTO ... vi

HALAMAN PERSEMBAHAN ... vii

ABSTRAK ... viii

ABSTRACT ... ix

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... x

KATA PENGANTAR ... xi

DAFTAR ISI ... xiii

BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 3 C. Batasan Masalah... 3 D. Tujuan Penulisan ... 3 E. Manfaat Penulisan ... 4 F. Metode Penulisan ... 4 G. Sistematika Penulisan ... 4

BAB II LANDASAN TEORI ... 6

A. Graf ... 6

B. Probabilitas ... 8

C. Probabilitas Bersyarat ... 9

D. Situs Web ... 12

E. Nilai Eigen dan Vektor Eigen ... 16

F. Rantai Markov ... 18

G. Matriks Transisi Peluang... 20

xiv

BAB III TEOREMA FROBENIUS ... 30

A. Pendahuluan ... 30

B. Teorema Frobenius... 32

BAB IV ALGORITMA GOOGLE PAGERANK ... 37

A. Hipotesis ... 37

B. Nilai Stasioner ... 37

C. Peringkat Halaman Web ... 41

D. Algoritma PageRank yang Ditingkatkan ... 45

E. Penerapan Algoritma Google PageRank pada Twitter ... 50

BAB V PENUTUP ... 62

A. Kesimpulan ... 62

B. Saran ... 63

DAFTAR PUSTAKA ... 64

1

BAB I PENDAHULUAN

A. Latar Belakang

Internet adalah suatu sistem global dari jaringan-jaringan komputer tanpa kabel yang saling terhubung. Internet membawa informasi yang sangat luas dari berbagai sumber dan dapat diakses dari seluruh dunia, sehingga penggunaan internet saat ini sangatlah populer di masyarakat. Dengan internet, kita dapat berkomunikasi jarak jauh dengan sangat mudah dan mendapatkan semua informasi yang kita inginkan. Untuk mencari informasi tersebut, diperlukan suatu alat yang dapat membantu kita untuk menemukan informasi yang tepat dari internet, yaitu mesin pencarian. Mesin pencarian adalah sebuah program pada web yang digunakan untuk mencari informasi di internet. Teknologi mesin pencarian ini mulai muncul pada tahun 1990.

Alat pertama yang digunakan untuk pencarian di internet adalah Archie. Archie dibuat oleh Allan Emtage, Bill Heelan, dan J. Peter Deustch, mahasiswa di Universitas McGill pada tahun 1990. Program Archie berisi daftar semua file yang berada pada suatu situs FTP (File Transfer Protocol), sehingga membentuk basis data yang dapat dicari dari nama-nama file tersebut. Archie tidak mendaftar isi atau konten dari situs-situsnya karena jumlah datanya masih terbatas.

Pada tahun 1991, Mark McCahill menciptakan Gopher, yang terdiri dari dua program pencarian, Veronica dan Jughead. Veronica (Very Easy Rodent-Oriented Net-wide Index to Computerized Archives) menyediakan kata kunci pencarian dari judul-judul file Gopher. Jughead (Jonzy’s Universal Gopher Hierarchy Excavation and Display) adalah alat untuk mendapatkan informasi dari server tertentu saja pada Gopher.

Pada tahun 1993, Oscar Nierstrasz menciptakan W3Catalog. W3Catalog adalah mesin pencarian pertama yang dapat menyediakan pencarian pada suatu katalog yang berisi sumber-sumber WWW. Pada Juni 1993, Matthew Gray, menciptakan situs web robot pertama, yaitu Wanderer yang digunakan untuk

mengukur ukuran dari WWW. Selain itu juga digunakan untuk menghasilkan sebuah daftar yang disebut „Wandex‟. Lalu pada November 1993, mesin pencarian kedua muncul, yaitu Aliweb. Aliweb bukan situs web robot, tetapi bisa mencantumkan halaman web, deskripsi halaman dan kata kunci pada mesin pencarian.

Setelah itu, banyak mesin pencarian internet yang muncul dan menjadi populer. Seperti Jump Station, Magellan, Excite, Lycos, Infoseek, Inktomi, Northern Light, Alta Vista, dan lain-lain.

Lalu pada tahun 1998, Google menjadi sangat populer karena telah me-matenkan algoritma yang disebut Google PageRank yang ditemukan oleh Sergey Brin and Larry Page. Algoritma ini memberikan setiap halaman pada sebuah situs web suatu peringkat berdasarkan tingkat kepentingan web tersebut. Selain itu, algoritma ini dapat mengurutkan peringkat halaman web tersebut sesuai dengan kata pencarian sehingga sangat memudahkan pengguna internet. Peringkat suatu halaman web adalah probabilitas pengguna internet akan berada pada suatu halaman tertentu. Jika ada tautan dari suatu halaman ke halaman , maka tautan itu akan meningkatkan peringkat halaman . Semakin banyak tautan menuju ke suatu halaman web, semakin tinggi juga probabilitas untuk berada di halaman tersebut, sehingga peringkat halaman tersebut akan menjadi lebih tinggi. Misalkan ada seorang pengguna internet yang mengikuti secara acak tautan dari satu halaman ke halaman lain pada situs web, perjalanan acak oleh pengguna internet ini dapat dimodelkan dengan Rantai Markov.

Misalkan ( ) ( ) adalah proses stokastik yang nilainya berada pada himpunan halaman situs web * +. Kita menye-but ( ) adalah rantai Markov jika peluang ( ) , hanya bergantung pada nilai dari halaman web sebelumnya, yaitu , dan tidak bergantung pada nilai halaman situs web sebelumnya . Kita definisikan sebagai jumlah halaman situs web pada Rantai Markov pada sistem ini direpresentasikan oleh Matriks Transisi Peluang (MTP).

Dari MTP tersebut dapat ditemukan minimal satu nilai eigen bernilai satu. Dari nilai eigen itu, dapat ditemukan vektor eigen yang entri-entrinya tak negatif.

Sifat ini adalah sebuah akibat dari Teorema Frobenius. Vektor eigen ini disebut juga nilai stasioner dari rantai Markov. Koefisien pada nilai stasioner tersebut adalah skor atau nilai peringkat dari halaman situs web.

Pada tugas akhir ini, akan dibahas tentang algoritma yang dipakai untuk menentukan peringkat pada mesin pencarian pada Google yaitu algoritma Google PageRank. Selain itu, juga akan dibahas tentang bagaimana penggunaan matriks transisi peluang, penggunaan sifat-sifat rantai Markov, pencarian nilai eigen dan nilai stasioner yang bersesuaian untuk mendapatkan nilai peringkat suatu halaman. Setelah itu, algoritma Google PageRank akan diaplikasikan untuk mencari nilai atau peringkat popularitas suatu akun Twitter dengan menggunakan hubungan/relasi follower.

B. Rumusan Masalah

Rumusan masalah dalam tugas akhir ini adalah:

1. Bagaimana cara kerja algoritma Google PageRank dalam menentukan peringkat suatu halaman web?

2. Bagaimana penerapan algoritma Google PageRank pada pencarian popularitas suatu akun pada Twitter?

C. Batasan Masalah

Penulisan tugas akhir ini hanya berfokus pada algoritma Google PageRank yang paling dasar saja.

D. Tujuan Penulisan

Tujuan penulisan tugas akhir ini adalah:

1. Mengetahui bagaimana cara kerja algoritma Google PageRank untuk menentukan peringkat suatu halaman web.

2. Mengetahui penerapan algoritma Google PageRank pada pencarian peringkat popularitas suatu akun pada Twitter.

E. Manfaat Penulisan

Manfaat penulisan tugas akhir ini adalah agar dapat memahami cara kerja algoritma Google PageRank untuk mencari peringkat suatu halaman web dan aplikasinya pada peringkat popularitas suatu akun pada Twitter.

F. Metode Penulisan

Metode penulisan yang digunakan dalam menyusun tugas akhir ini adalah studi pustaka dengan membaca buku-buku, jurnal, dan skripsi, dan menggunakan program MATLAB. G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II LANDASAN TEORI

A. Graf

B. Probabilitas

C. Probabilitas Bersyarat D. Situs Web

E. Nilai Eigen dan Vektor Eigen F. Rantai Markov

G. Matriks Transisi Peluang

BAB III TEOREMA FROBENIUS A. Pendahuluan

B. Teorema Frobenius

BAB IV ALGORITMA GOOGLE PAGERANK A. Hipotesis

B. Nilai Stasioner

C. Peringkat Halaman Web

D. Algoritma PageRank yang Ditingkatkan

E. Penerapan Algoritma Google PageRank pada Twitter BAB V PENUTUP

A. Kesimpulan B. Saran Daftar Pustaka Lampiran

6

BAB II

LANDASAN TEORI A. Graf

Secara umum, sebuah graf terdiri dari himpunan simpul-simpul dan himpunan sisi-sisi yang menghubungkan berbagai pasangan simpul-simpul. Graf dapat digunakan untuk memodelkan bermacam-macam relasi dan proses pada bidang fisika, biologi, ilmu sosial, dan sistem informasi.

Definisi 2.1.1

Sebuah graf terdiri dari 2 himpunan hingga: himpunan tak kosong ( ) berisi simpul-simpul dan himpunan ( ) berisi sisi-sisi, dimana setiap sisi bersesuaian dengan sebuah himpunan yang berisi satu atau dua simpul yang disebut endpoint.

Contoh 2.1.1

Gambar 2.1

Gambar 2.1 merepresentasikan sebuah graf dengan himpunan simpul

* +, dan himpunan sisi * +, dan korespondensi dari sisi dan endpoint diberikan oleh tabel berikut

Sisi Endpoint * + * + * + * + * +

Definisi 2.1.2

Sebuah graf berarah terdiri dari 2 himpunan hingga: himpunan tak kosong ( )

berisi simpul-simpul dan sebuah himpunan ( ) berisi sisi-sisi berarah, yang bersesuaian dengan pasangan terurut dari simpul-simpul yang disebut endpoint. Jika sisi bersesuaian dengan pasangan simpul-simpul ( ), maka disebut sebagai sisi (berarah) dari ke .

Contoh 2.1.2

Gambar 2.2

Gambar 2.2 merepresentasikan sebuah graf berarah dengan himpunan sisi berarah

* + yang bersesuaian dengan pasangan terurut simpul-simpul dari himpunan simpul * +. Korespondensi dari sisi dan endpoint diberikan oleh tabel berikut Sisi Endpoint * + * + * + * +

Perhatikan bahwa setiap graf berarah bersesuaian dengan sebuah graf (tidak berarah) yang diperoleh dengan mengabaikan arah dari sisi-sisinya.

B. Probabilitas

Dalam kehidupan sehari-hari, probabilitas sering kita temui untuk mencoba memprediksi nilai kemungkinan sebuah kejadian dalam percobaan acak. Kita memerlukan teori probabilitas untuk bisa melakukan prediksi dari hasil pengamatan sebuah kejadian. Sebelum membahas teori probabilitas, kita perlu mengetahui notasi dasar yang akan digunakan. Himpunan semua kemungkinan hasil dari suatu eksperimen disebut ruang sampel, dilambangkan dengan . Himpunan bagian dari ruang sampel disebut kejadian, dilambangkan dengan huruf kapital: , , ... . Jika elemen-elemen pada kejadian adalah , , dan , kita dapat menuliskannya

* +.

Misalkan adalah ruang sampel pada suatu percobaan adalah himpunan hingga dengan banyaknya anggota pada adalah ( ), dan kejadian di dalam memiliki ( ) anggota. Probabilitas terjadinya kejadian adalah

( ) ( ) ( )

Untuk setiap kejadian , probabilitas ( ) dari selalu memenuhi: Aksioma 1: ( )

Aksioma 2: ( )

Aksioma 3: Jika , , , adalah sebuah barisan kejadian yang saling asing di (yakni jika ), maka

(⋃

) ∑ ( )

Contoh 2.2

Sebuah dadu seimbang dilambungkan sebanyak satu kali. Kita memperoleh ruang sampel * + dengan ( ) Apabila adalah kejadian munculnya bilangan prima, maka * + dengan ( ) . Probabilitas kejadian adalah

( ) ( ) ( )

C. Probabilitas Bersyarat

Probabilitas dari suatu kejadian terkadang akan bergantung pada kejadian lain yang telah terjadi. Misalkan, nelayan di Semarang ingin mengetahui probabilitas hari hujan dengan mempertimbangkan kejadian atau cuaca hari-hari yang telah terjadi. Sekarang kita ingin menghitung probabilitas besok hujan, dengan mempertimbangkan kejadian di mana sudah 2 hari berturut-turut hujan. Nelayan tersebut dapat menyimpulkan bahwa probabilitas bersyarat hari hujan akan lebih besar dari pada probabilitas tak bersyarat hari hujan.

Definisi 2.3.1

Probabilitas bersyarat dari suatu kejadian dengan syarat kejadian adalah

( | ) ( ) ( )

asalkan ( ) .

Contoh 2.3.1

Sebuah dadu seimbang dilambungkan sebanyak satu kali. Misalkan adalah kejadian munculnya angka 1 dan adalah kejadian munculnya angka ganjil. Kita akan mencari probabilitas dari jika diketahui sebelumnya kejadian terjadi dari ruang sampel * + Kejadian memerlukan pengamatan pada munculnya angka 1 dan angka ganjil. Karena , maka , dan

( ) ( ) ( ) ( )⁄ Kita hitung probabilitas kejadian ,

( ) ( ) ( )⁄ , dan menggunakan Definisi 2.3.1,

( | ) ( ) ( )

⁄ ⁄

Definisi 2.3.2

Kejadian dan dikatakan saling bebas (independent) jika dan hanya jika memenuhi salah satu dari:

( | ) ( ) atau

( | ) ( ) atau

Contoh 2.3.2

Dalam percobaan melambungkan sebuah dadu seimbang satu kali diketahui: : Kejadian munculnya angka ganjil,

: Kejadian munculnya angka genap, dan : Kejadian munculnya angka 1 atau 2. Tentukan:

a. Apakah dan adalah kejadian yang saling bebas? b. Apakah dan adalah kejadian yang saling bebas? Jawaban:

a. Untuk menentukan apakah dan saling bebas, kita perlu mengetahui apakah mereka memenuhi kondisi pertama pada Definisi 2.3.2. Pada contoh ini, ( ) ⁄ , ( ) ⁄ , ( ) ⁄ ⁄ Karena

, maka ( ) , dan jelas bahwa

( | ) ( )

( ) ⁄ ( )

Karena memenuhi ( | ) ( ), maka kejadian dan adalah kejadian tidak saling bebas.

b. Untuk menentukan apakah dan saling bebas, kita perlu mengetahui apakah mereka memenuhi kondisi pertama pada Definisi 2.3.2. Karena

* +, maka ( ) ⁄ ,

( | ) ( ) ( )

⁄

⁄ ( )

Karena ( | ) ( ), maka kejadian dan adalah kejadian saling bebas.

Definisi 2.3.3

Variabel random adalah sebuah fungsi yang memetakan setiap anggota dalam ruang sampel ke himpunan bilangan real.

Terdapat 2 jenis variabel random, yaitu variabel random diskret dan variabel random kontinu. Sebagai contoh, kejadian hasil pemilihan dari voting, dengan variabel random banyaknya pemilih yang memilih kandidat tertentu.

Banyaknya pemilih yang memilih kandidat tertentu ini pasti nol atau bilangan bulat antara 1 dan total sampelnya. Sebuah variabel random disebut diskret jika anggotanya berhingga atau tak berhingga yang terbilang dan nilainya berbeda. Contoh lain dari variabel random ini adalah jumlah dari televisi yang rusak pada pengiriman 100 televisi. Suatu variabel random juga dapat digunakan untuk mengidentifikasi kejadian-kejadian numerik.

Contoh 2.3.3

Sebuah koin dilemparkan sebanyak 2 kali.

Misalkan adalah variabel random diskret yang mengidentifikasi kejadian-kejadian munculnya gambar dari 2 kali pelemparan koin. Dari dua kali pelemparan koin, kemungkinan kejadiannya adalah kejadian tidak muncul gambar, kejadian muncul 1 gambar, dan kejadian munculnya 2 gambar. Kita misalkan adalah banyaknya gambar yang muncul. adalah variabel random, tetapi nilai spesifik tidak random. ( ) adalah himpunan ruang sampel saat nilainya dari variabel random . ( ) adalah probabilitas saat bernilai . Sehingga

kita peroleh:

0 1 2

( )

Sekarang kita amati curah hujan setiap hari pada titik geografis yang sudah ditentukan. Dengan alat pengukuran dengan akurasi yang tinggi, nilai curah hujan berada di antara 0 dan 5 inci. Hasilnya, setiap bilangan yang tak terbilang pada interval ( ) merepresentasikan kemungkinan nilai curah hujan yang berbeda setiap harinya. Sebuah variabel random yang dapat merepresentasikan nilai pada suatu interval dikatakan kontinu. Contoh lainnya adalah ketika seseorang ingin

G A G A A G ⁄ ⁄ ⁄ ⁄ ⁄ ⁄

mengetahui kedalaman danau pada posisi tertentu, sehingga variabel random adalah level kedalaman danau pada suatu posisi acak. adalah variabel random kontinu dengan interval kemungkinan kedalaman minimum sampai kedalaman maksimum danau tersebut. Variabel random lain seperti tinggi, berat, besar suhu juga merupakan variabel random kontinu.

D. Situs Web

Situs web (website) adalah sistem untuk menciptakan, mengatur, dan mentautkan dokumen-dokumen agar dapat diakses dengan mudah. Situs web diciptakan oleh Tim Berners-Lee pada tahun 1990. Situs web juga merupakan salah satu perkembangan yang luar biasa selama beberapa dekade terakhir yang akan terus menjadi pengaruh pada pemberi dan penerima informasi di masa yang akan datang.

Situs web terdiri dari jutaan halaman-halaman yang berbeda, dan juga terdapat banyak tautan di antara mereka. Situs web dapat kita modelkan sebagai graf berarah, dimana halamannya adalah simpul, dan tautan di antara halaman tersebut adalah sisi berarah yang menghubungkan simpul-simpul tersebut.

Gambar 2.3 adalah sebuah ilustrasi situs web memiliki lima halaman ( , , , , dan ).

Gambar 2.3

Sebuah situs web dengan lima halaman dan tautannya Garis berarah di antara titik-titiknya memiliki arti bahwa:

 satu-satunya tautan dari halaman adalah menuju ke halaman ,

 halaman memiliki tautan ke halaman dan , A

B

D

 halaman memiliki tautan ke halaman , , dan ,

 satu-satunya tautan dari halaman adalah menuju ke halaman , dan

 halaman memiliki tautan ke halaman , , dan .

Peringkat dari suatu halaman adalah suatu nilai tingkat kepentingan halaman tersebut, yakni suatu halaman akan menjadi semakin penting apabila terdapat banyak tautan dari halaman-halaman yang memiliki banyak tautan. Semakin banyak tautan menuju ke suatu halaman, semakin tinggi juga probabilitas untuk berada di halaman tersebut, sehingga peringkat halaman tersebut akan menjadi lebih tinggi. Untuk menentukan peringkat dari kelima halaman, kita akan menggunakan versi sederhana dari algoritma PageRank. Pada tahun 1998, Google pertama kali diciptakan oleh Larry Page dan Sergey Brin. Sekitar tahun 2000, mesin pencarian Google menjadi terkenal karena perusahaannya mencapai hasil yang lebih baik setelah menerapkan inovasi yang dinamakan algoritma PageRank. Algoritma PageRank adalah algoritma yang digunakan untuk memberi peringkat pada halaman-halaman pada situs web berdasarkan tingkat kepentingan halaman tersebut. Algoritma ini mengurutkan halaman-halaman pada suatu web berdasarkan skor PageRank dan tautan dari halaman-halaman yang lain. Misalkan, seorang pengguna internet menjelajahi situs web tersebut dengan cara memilih tautan-tautannya secara acak. Ketika dia hanya memiliki satu pilihan halaman (sebagai contoh, jika dia berada di halaman ), maka dia akan mengikuti tautan tersebut (menuju ke halaman pada contoh ini). Jika dia berada pada halaman , dia akan mengikuti tautan ke halaman , , atau . Jika dia berada di suatu halaman tertentu dengan tiga tautan yang tersedia, maka dia akan memilih secara acak dari ketiga tautan yang ada.

Jika pengguna internet mulai dari halaman , maka halamannya memiliki tiga tautan ke luar; sehingga pengguna internet hanya bisa menuju ke salah satu dari tiga halaman , , .

( ) _{( )} ( ) ( ) _{( ) ( )} ( ) ( ) _{( )} ( ) ( ) _{( )} ( ) _{( )} ( )

Mulai langkah 1 langkah 2

Gambar 2.4

Dua langkah pertama dari pengguna internet yang berawal dari halaman . Gambar 2.4 mengilustrasikan dua langkah yang dapat diambil seorang pengguna internet bila memulai dari halaman . Jadi, pada langkah pertama, dia bisa menuju ke halaman dengan probabilitas , ke halaman dengan probabilitas , dan ke halaman dengan probabilitas . Ini ditunjukkan pada kolom tengah pada Gambar 2.4, yang mengindikasikan tiga hubungan berikut

( ) ( ) ( )

Demikian pula,

( ) dan ( )

yang berarti setelah langkah pertama, pengguna internet tidak akan bisa berada pada halaman atau , karena tidak ada tautan yang dapat membawanya ke sana. Selanjutnya, karena dia harus berada dalam situs web tersebut, mereka memenuhi

( ) ( ) ( ) ( ) ( )

Hasil dari langkah pertama cukup sederhana dan dapat diprediksi. Namun, setelah dua langkah, hubungan dari tautan-tautannya mulai kompleks. Kolom ketiga dari gambar 2.4 menunjukkan kemungkinan lintasan setelah dua langkah. Jika pengguna internet berada pada setelah langkah pertama, maka pada langkah ke dua dia pasti menuju ke halaman . Karena dia sebelumnya berada pada halaman dengan probabilitas , maka lintasan ini memiliki probabilitas untuk menuju ke halaman pada langkah kedua. Namun, ( ) tidak bernilai , karena ada lintasan independen lain yang dapat menuju ke halaman : . Jika pengguna internet berada pada halaman setelah langkah pertama, dia dapat memilih (dengan probabilitas sama) dari tiga tautan yang menuju ke halaman , , dan . Setiap lintasan tersebut memberikan nilai ke setiap probabilitas

( ), ( ), dan ( ) setelah langkah kedua. Walaupun ada lebih banyak kemungkinan dan probabilitasnya semakin rumit, tetapi hasil akhirnya termasuk sederhana. Setelah dua langkah, pengguna internet sampai pada sebuah halaman dengan probabilitas sebagai berikut:

( ) ( ) ( )

( ) ( )

Kita dapat lihat bahwa nilai-nilai probabilitas tersebut memenuhi:

( ) ( ) ( ) ( ) ( )

E. Nilai Eigen dan Vektor Eigen Definisi 2.5.1

Jika adalah matriks berukuran , maka vektor tak nol disebut vektor eigen dari jika adalah adalah kelipatan skalar dari , yakni

untuk suatu . Skalar disebut nilai eigen dari dan disebut vektor eigen yang bersesuaian dengan .

Contoh 2.5.1

Diberikan matriks 0

1. Vektor 0 1 adalah vektor eigen dari

matriks , karena

0

1 0 1 0 1

dengan adalah nilai eigen dari matriks .

Untuk menentukan nilai eigen dari matriks berukuran , kita dapat tulis kembali persamaan sebagai

atau

( ) (2.1)

Agar menjadi suatu nilai eigen, harus terdapat solusi tak nol dari persamaan (2.1). Persamaan (2.1) memiliki solusi tak nol jika dan hanya jika

( )

Definisi 2.5.2

Persamaan ( ) disebut persamaan karakteristik dari dengan skalar yang memenuhi persamaan tersebut adalah nilai eigen dari . Ketika dijabarkan, determinan dari ( ) selalu berupa polinomial dalam variabel yang disebut polinomial karakteristik dari .

Dapat dilihat bahwa jika adalah matriks berukuran , maka polinomial karakteristik dari memiliki derajat dan koefisien dari adalah 1, yaitu bentuk dari polinomial karakteristik ( ) dari matriks adalah

( ) ( ) Dari teorema fundamental aljabar, persamaan karakteristik

memiliki paling banyak solusi yang berbeda. Jadi, sebuah matriks

memiliki paling banyak nilai eigen yang berbeda.

Contoh 2.5.2

Diberikan matriks

[

]

Polinomial karakteristik dari adalah

( ) [ ] ( )

Nilai eigen dari memenuhi persamaan karakteristik

dan penyelesaian dari persamaan tersebut adalah

( )( )

Jadi nilai eigen dari adalah

F. Rantai Markov

Sebuah proses stokastik waktu diskret ( ) adalah keluarga variabel random dengan indeks * +. Kita asumsikan setiap nilai dari variabel random berada di suatu himpunan hingga . Pada Gambar 2.3, adalah himpunan dari halaman-halaman pada situs web: * +. Untuk setiap langkah * +, posisi dari pengguna internet adalah . Dalam proses stokastik ini, kita telah menentukan kemungkinan probabilitas dari dan dengan asumsi bahwa titik awalnya dari halaman . Ini dapat disebut probabilitas bersyarat ( | ), yang memberikan probabilitas kejadian terjadi dengan diketahuinya kejadian terjadi. Contohnya, ( | ) adalah probabilitas bahwa pengguna internet berada pada halaman pada langkah pertama apabila mula-mula (langkah 0) berada di halaman . Jadi

( | ) ( | ) ( | ) ( | ) ( | ) dan ( | ) ( | ) ( | ) ( | ) ( | ) .

Perjalanan acak oleh pengguna internet ini mendefinisikan sifat dari sebuah proses stokastik khusus yang disebut rantai Markov.

Definisi 2.6.1

Misalkan ( ) ( )adalah proses stokastik waktu diskret yang nilainya berada pada himpunan hingga * +. Kita sebut

( ) adalah rantai Markov jika probabilitas ( ) , hanya bergantung pada probabilitas dari proses sebelumnya, yaitu ( ), dan tidak bergantung pada probabilitas yang lebih lama ( ) ( ) . Dengan kata lain, berlaku

( | ) ( | )

Pada contoh pengguna internet, variabel randomnya adalah posisi setelah langkah ke . Dari perhitungan sebelumnya, kita tahu bahwa saat menghitung probabilitas setelah langkah pertama, ( ) kita hanya menggunakan titik mulainya. Demikian pula untuk menghitung probabilitas setelah langkah kedua ( ), kita hanya menggunakan probabilitas dari langkah pertama. Sifat untuk menghitung ( ) dengan hanya menggunakan informasi dari ( ) adalah sifat utama dari rantai Markov.

Misalkan kita ingin mencegah pengguna internet agar tidak langsung kembali ke halaman sebelumnya. Sebagai contoh, setelah langkah pertama, pengguna internet kita sampai pada halaman , , dan dengan probabilitas yang sama. Dia tidak dapat kembali ke halaman dari halaman , tapi memungkinkan dia untuk ke halaman dari halaman dan . Dari aturan baru ini, pengguna internet hanya memiliki satu pilihan setelah sampai pada halaman dari halaman (dia hanya dapat menuju ke halaman ), dan akan mengurangi pilihan pada saat sampai ke halaman (hanya bisa ke halaman atau ). Dengan mencegah pengguna internet untuk menuju ke tautan yang berhubungan dengan halaman sebelumnya, kita menghilangkan sifat dari Markov, yaitu prosesnya memiliki ingatan (memori). Faktanya, untuk menentukan probabilitas dari ( ) kita tidak hanya perlu mengetahui probabilitas saat langkah pertama tetapi juga halaman dimana pengguna internet tersebut memulai (langkah nol). Aturan yang kita definisikan, bersifat spesial karena rantai Markov tidak memiliki ingatan terhadap keadaan yang lalu, dan keadaan yang akan datang ditentukan dari keadaan sekarang.

G. Matriks Transisi Peluang

Sebuah matriks yang merangkum nilai probabilitas semua perubahan keadaan dari rantai Markov disebut matriks transisi peluang (MTP). Matriks transisi peluang biasa disimbolkan dengan .

Definisi 2.7

Diberikan ( ) adalah rantai Markov yang nilainya berada pada himpunan keadaan hingga * +. Matriks transisi peluang dari rantai Markov adalah matriks yang komponen baris ke- kolom ke- diberikan oleh

( | ) untuk (2.2) Sebuah matriks adalah matriks transisi rantai Markov jika memenuhi

, - untuk semua dan ∑ untuk semua (2.3) Pada matriks transisi peluang kolom pada matriks merepresentasikan keadaan sekarang atau keadaan sedangkan baris pada matriks merepresentasikan keadaan yang dituju atau keadaan Matriks transisi peluang

dapat diilustrasikan sebagai berikut:

(keadaan sekarang)

( ) ⏞

} (keadaan yang dituju)

Jumlahan kolom sama dengan 1

Contoh 2.7.1

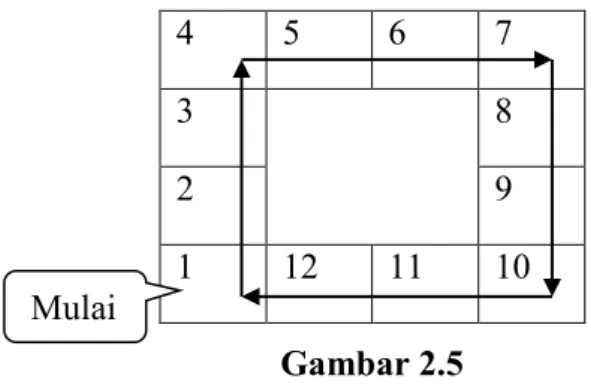
Kita ambil contoh permainan monopoli sederhana dengan aturan pemain bergerak mengelilingi kotak dengan cara melambungkan sebuah dadu seimbang. Kita ilustrasikan sebagai berikut

4 5 6 7

3 8

2 9

1 12 11 10

Gambar 2.5

Kita misalkan terlebih dahulu:

Nomor kotak di mana pemain berada setelah langkah 1

( ) ( ) barisan variabel random dengan dengan

* + adalah ruang sampel yang berasal dari pelambungan sebuah dadu dan ruang keadaan * +. Misalkan

Untuk pelambungan pertama dadu muncul angka 2:

Untuk pelambungan kedua dadu muncul angka 1:

Untuk pelambungan ketiga dadu muncul angka 5:

Dari empat posisi awal pemain, akan ditentukan probabilitas , dengan

* +.

Menggunakan Definisi 2.6.1, hanya dipengaruhi oleh keadaan sebelumnya, yaitu dan tidak dipengaruhi oleh , sehingga

( | ) ( | )

untuk * +. Mulai

Matriks transisi peluang dari permainan monopoli sederhana di atas adalah                                       0 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 6 1 6 1 6 1 6 1 6 1 6 1 6 1 0 0 0 0 0 0 12 11 10 9 8 7 6 5 4 3 2 1 Contoh 2.7.2

Cuaca di suatu kota dapat berupa salah satu dari tiga keadaan, yaitu cerah, berawan, dan hujan. Dari data-data empiris dapat disusun sebuah matriks transisi peluang yang merepresentasikan rantai Markov dari perubahan cuaca di kota tersebut:

Cerah Berawan Hujan

( ) Cerah Berawan Hujan

Dari model di atas, dapat kita lihat bahwa apapun keadaan cuaca pada hari ini, ada kemungkinan sekurang-kurangnya 60% bahwa besok akan hujan.

Contoh 2.7.3

Kita perhatikan kembali Gambar 2.3

Gambar 2.3

Sebuah situs web dengan lima halaman dan tautannya

Untuk menentukan matriks transisi peluangnya, kita tentukan terlebih dahulu variabel random Kita asumsikan setiap nilai dari variabel random berada di suatu himpunan hingga . Pada Gambar 2.3, adalah himpunan dari halaman-halaman pada situs web: * +. Untuk setiap langkah * +, posisi dari pengguna internet adalah Elemen dari matriks transisi menunjukkan probabilitas untuk sampai ke halaman ketika dia berasal dari halaman . Aturan kita mengakibatkan pengguna internet untuk memilih dengan probabilitas yang sama dari semua tautan yang tersedia. Jadi, jika halaman memiliki tautan, maka kolom dari akan berisi pada baris yang sesuai dengan tautan halaman tersebut, dan 0 pada baris sisanya. Matriks transisi untuk rantai Markov yang menggambarkan situs web sederhana pada gambar 2.3 adalah sebagai berikut

⏞                   0 0 3 1 0 0 3 1 0 0 0 0 3 1 0 0 2 1 0 3 1 0 3 1 0 1 0 1 3 1 2 1 0 } A B D C E

Kolom-kolom pada menunjukkan halaman tujuan yang memungkinkan; dari halaman , pengguna internet dapat melanjutkan ke halaman , , dan . Demikian pula dengan entri-entri tak nol pada baris menunjukkan kemungkinan halaman asalnya: satu-satunya entri tak nol pada baris ke empat menunjukkan bahwa kita dapat sampai ke halaman hanya dari halaman .

Apa arti dari kendala pada persamaan (2.3)? Untuk mengklarifikasi, kita dapat tulis kembali matriks transisi pada (2.2):

∑ ∑ ( | )

yang dapat dibaca sebagai berikut: jika pada langkah sistem berada pada keadaan (pada halaman ), maka probabilitas sistem berada pada sebarang kemungkinan keadaan pada langkah adalah 1. Atau lebih sederhananya, ini berarti bahwa seorang pengguna internet pada suatu halaman tertentu pada langkah harus sampai pada halaman yang masih berada di situs web tersebut saat langkah ke .

Seperti sebelumnya kita asumsikan pengguna internet memulai pada halaman . Jadi, kita mempunyai

( ( ) ( ) ( ) ( ) ( )) ( )

Vektor probabilitas setelah langkah pertama diperoleh dari , karena itu ( ( ) ( ) ( ) ( ) ( ))               0 0 3 1 0 0 3 1 0 0 0 0 3 1 0 0 2 1 0 3 1 0 3 1 0 1 0 1 3 1 2 1 0 ( )             3 1 0 0 3 1 3 1

sama seperti yang telah kita hitung sebelumnya. Dengan cara yang sama, terapkan matriks transisi untuk menghasilkan ; maka vektor probabilitas setelah dua langkah adalah

( ( ) ( ) ( ) ( ) ( ))             0 0 3 1 0 0 3 1 0 0 0 0 3 1 0 0 2 1 0 3 1 0 3 1 0 1 0 1 3 1 2 1 0             3 1 0 0 3 13 1               0 9 1 18 5 9 4 6 1

Cara yang sama dapat kita ikuti untuk menghitung vektor probabilitas setelah berapapun langkah yang telah kita tempuh: _{, atau}

( ) ⏟

Contoh 2.7.4

Akan kita temukan matriks transisi yang merepresentasikan situs web berikut

Gambar 2.6

Matriks transisi rantai Markov yang bersesuaian adalah              0 0 0 0 0 0 0 1 0 0 2 1 2 1 2 1 2 1 2 1 2 1 P A A Z B B C C

Asumsikan bahwa pada langkah ke- , probabilitas untuk menuju ke setiap halaman sama: ( ) ( ) ( ) ( ) . Berapa probabilitas untuk berada pada halaman pada langkah ?

( ( ) ( ) ( ) ( ))               4 1 4 1 4 1 4 1

Untuk menemukan vektor probabilitas pada langkah , akan kita hitung                           4 1 4 1 4 1 4 1 2 1 2 1 2 1 2 1 2 1 2 1 1 0 0 0 0 0 0 0 1 0 0 n p ( ( ) ( ) ( ) ( ))              8 3 8 1 8 1 8 3

Jadi, probabilitas untuk berada pada halaman pada langkah ke adalah .

Contoh 2.7.5

Terdapat sebuah web sebagai berikut

Gambar 2.7

A

C

B

Matriks transisi rantai Markov yang bersesuaian dengan situs web tersebut adalah              0 0 0 1 0 0 0 0 0 3 1 3 1 2 1 2 1 2 1 2 1 3 1 P

Jika kita mulai dari halaman , maka berapakah probabilitas kita akan berada pada halaman setelah 2 langkah?

( ( ) ( ) ( ) ( )) ( )

Untuk menemukan vektor probabilitas setelah 2 langkah, akan kita hitung

                                     0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 3 1 3 1 2 1 2 1 2 1 2 1 3 1 3 1 3 1 2 1 2 1 2 1 2 1 3 1 2 p                          0 0 1 0 0 0 0 6 1 6 1 125 6 3 6 1 2 1 4 1 6 2 4 1 2 1 6 1 3 1 125              0 6 3 6 2 6 1

H. Sifat-Sifat Matriks Transisi Peluang

Sifat pertama yang akan dibahas dapat dilihat dari mengambil beberapa pangkat dari matriks transisi : , , , dan _{(dihitung menggunakan} MATLAB) adalah ( ₎ ( ₎ ( ₎ ( ₎ dan ( ₎

Kita amati bahwa konvergen ke sebuah matriks yang vektor kolomnya identik saat semakin besar.

Ini adalah salah satu sifat dari matriks transisi rantai Markov, yaitu suatu perpangkatan matriks transisi rantai Markov sebanyak akan konvergen ke sebuah matriks yang kolom-kolomnya identik saat .

Sifat 2.8.1

Matriks transisi dari rantai Markov mempunyai paling sedikit satu nilai eigen yang bernilai satu.

Bukti:

Kita ingat kembali bahwa nilai eigen dari sebuah matriks selalu sama dengan nilai eigen dari transpose matriks tersebut. Ini adalah hasil dari fakta bahwa kedua matriks tersebut memiliki karakteristik polinomial yang sama

( ) det( ) det( ) det( ) = ( ),

dan determinan dari suatu matriks sama dengan determinan transposenya. Cukup sederhana untuk menemukan vektor eigen dari . Misalkan ( ) . Maka, . Dengan menjabarkan perkalian matriksnya ternyata kita dapat lihat bahwa ( ) ∑, - ∑ Sifat 2.8.2

Jika adalah sebuah nilai eigen dari sebuah matriks transisi peluang berukuran

maka | | Selanjutnya, ada sebuah vektor eigen yang berkorespondensi dengan nilai eigen dengan semua elemennya non negatif.

Sifat ini adalah hasil langsung dari Teorema Frobenius. Walaupun bukti teorema ini berdasarkan dari aljabar linear elementer dan analisis, tetapi buktinya tidaklah sederhana. Kita akan membahasnya pada bab III.

30

BAB III

TEOREMA FROBENIUS A. Pendahuluan

Diberikan himpunan . Sebuah relasi pada suatu himpunan dikatakan:

 refleksif jika ( )  simetrik jika ( )  asimetrik jika ( )  antisimetrik jika (( dan ) )  transitif jika (( dan ) )

 preorder jika refleksif dan transitif;

 terurut parsial jika adalah preorder antisimetrik.

Jika terurut parsial pada suatu himpunan , kita sebut pasangan ( ) sebuah himpunan terurut parsial.

Definisi 3.1.1

Misalkan adalah subhimpunan tak kosong dari himpunan terurut parsial

Elemen kita sebut batas atas dari , jika untuk semua . Jika terdapat batas atas dari S, maka kita sebut S terbatas ke atas. Elemen kita sebut batas atas terkecil atau supremum dari jika dua kondisi berikut terpenuhi:

 adalah batas atas dari , dan

 jika adalah batas atas dari , maka .

Perhatikan bahwa S paling sedikit memiliki satu supremum. Jika terdapat suatu supremum dari S, kita notasikan dengan sup S atau dapat kita notasikan juga dengan

jika * + adalah himpunan berhingga, dan dengan

⋁

jika * + adalah himpunan terhitung.

Teorema 3.1.2 (Heine Borel)

Subhimpunan di dalam dikatakan kompak jika dan hanya jika tertutup dan terbatas di dalam .

Definisi 3.1.3

Simpleks- atau simpleks berdimensi adalah sebuah objek berdimensi yang terbentuk dari proyeksi titik-titik ( ) tak negatif dari suatu vektor yang saling bebas pada suatu oktan. Dapat ditulis sebagai berikut

Simpleks- * ( ) +

Contoh 3.1

Simpleks-1 atau simpleks berdimensi 1 berupa garis. Simpleks-2 atau simpleks berdimensi 2 berupa segitiga. Simpleks-3 berupa piramida segitiga.

(a) (b) (c)

Gambar 3.1

B. Teorema Frobenius

Untuk menggambarkan dan mendemonstrasikan teorema Frobenius, kita perlu memahami matriks dengan elemen tak negatif (positif atau nol). Kita bagi menjadi 3 kasus. Jika adalah matriks , maka kita notasikan

 jika untuk semua ;

 jika dan ada setidaknya satu dari positif;

 jika untuk semua .

Kita akan gunakan notasi yang sama untuk vektor-vektor . Notasi

berarti . Kita akan tunjukkan beberapa contoh penggunaan pertidaksamaan tersebut. Yang pertama, jika dan , maka , yang berdasarkan fakta bahwa karena dan , maka perkalian matriks ( ) hanya terdiri dari jumlahan elemen-elemen tak negatif. Karena itu, entri-entri dari vektor ( ) adalah tak negatif, sehingga

. Contoh yang kedua adalah jika dan , maka . Karena dan , maka perkalian matriks ( ) hanya terdiri dari jumlahan elemen-elemen positif. Karena itu entri-entri dari vektor ( ) adalah positif, sehingga .

Gambar 3.2 Tiga sudut pandang dari simpleks dari vektor ( ) Bidang

direpresentasikan dengan persegi putih, sedangkan simpleks berdimensi 2 ( ) direpresentasikan dengan segitiga abu-abu.

c b a c b a a b c

Untuk menotasikan himpunan titik-titik yang memenuhi sifat berikut: terdapat sebuah vektor ( ) sedemikian sehingga

∑

(3.1)

Sebagai contoh, jika , dengan kondisi , maka titik ( ) berada di oktan dimana titik-titiknya memiliki koordinat tak negatif. Pada saat yang sama, kendala menggambarkan sebuah bidang datar. Jadi, titik dibatasi pada perpotongan antara dua himpunan ini, seperti yang ditunjukkan pada Gambar 3.2. Pada gambar ini, oktannya digambarkan dengan 3 sumbu, dan bidangnya digambarkan dengan persegi putih. Titik potong dari keduanya digambarkan dengan segitiga abu-abu. Pada kasus dimensi berhingga , objek yang terbentuk disebut simpleks- . Sifat yang paling penting dari simpleks yaitu himpunan kompak, yakni tertutup dan terbatas. Untuk setiap titik pada simpleks, kita dapat menghitung yang memenuhi . Jadi, kita dapat menemukan

, sehingga . ( juga dapat terjadi, sebagai contoh jika . / dan . /, maka . / . /dapat terpenuhi hanya ketika .)

Proposisi 3.2.1

Apabila , maka . Lebih lanjut, jika , maka . Bukti:

Kita misalkan bahwa , adalah elemen terbesar dari matriks . Maka untuk setiap yang memenuhi ∑ dan , berlaku

( ) ∑ ∑

Karena setidaknya harus ada satu entri dari , kita sebut , harus memenuhi , maka dari kondisi mengharuskan ( ) . Karena berlaku untuk semua , maka . Misalkan bahwa

. / , berlaku ( ) ∑ ( ) ( ) , sehingga

( ) dan .

Teorema 3.2.1 (Frobenius)

Misalkan dan .

(a) adalah nilai eigen dari dan memungkinkan kita untuk memilih vektor eigen yang bersesuaian sehingga ;

(b) Jika adalah nilai eigen lain dari , maka | | . Bukti:

Akan kita buktikan pernyataan (a) dalam dua tahap, (a1) dan (a2).

(a1) Jika , maka terdapat sedemikian sehingga . Untuk membuktikan pernyataan pertama, kita misalkan sebuah baris

* + dari elemen-elemen yang konvergen ke , dan vektor-vektor ( ) _{yang bersesuaian memenuhi (3.1):}

∑ ( )

( ) ( ) ( )

Karena himpunan titik-titik ( ) _{adalah simpleks kompak, maka terdiri dari} titik akumulasi, dan dapat kita pilih sebuah subbarisan { ( )} dengan

, yang konvergen ke titik ini. Misalkan adalah limit dari subbarisan:

( )

Perhatikan bahwa sendiri berada pada simpleks sehingga memenuhi

∑ dan . Akhirnya, karena ( ( ) ( )) , maka

. Selanjutnya, kita akan tunjukkan bahwa .

Misalkan bahwa . Karena , dengan mengalikan kedua bagian dari dengan dan mendefinisikan , kita mendapatkan . Karena pertidaksamaan ini berlaku untuk semua elemen, terdapat sebuah sedemikian sehingga ( ) . Dengan menormalisasi , sehingga kita peroleh ∑ , kita dapat

menyimpulkan bahwa dan bahwa tidak dapat menjadi supremum. Kontradiksi dengan Proposisi 3.1. Jadi, terbukti bahwa

. Karena dan , maka . Dengan kata lain,

, dan akhirnya karena .

(a2) Jika , maka terdapat sedemikian sehingga .

Misalkan sebuah matriks berukuran yang semua elemen-elemennya adalah 1. Kita amati bahwa jika , maka ( ) ∑ untuk semua , sehingga . Jika , maka ( ) untuk semua

, dan (a1) bisa diaplikasikan kepada matriks ini. Misalkan

dan akan menjadi dan ∑ . Jika ( ) , maka berlaku

( ) ( ) ( ) ( )

sehingga fungsi ( ) yang diprediksi dengan mengaplikasikan (a1) ke matriks ( ) adalah fungsi naik dari . Lebih jelasnya, ( ) adalah yang bersesuaian dengan matriks . Bentuk sebuah barisan positif * + yang konvergen ke 0. Dengan (a1), kita dapat mencari ( ) yang memenuhi ( ) ( ) ( ) ( ) , dimana ( ) dan

∑ ( ) . Karena semua vektor-vektor tersebut berada pada simpleks, terdapat sebuah subbarisan { }, dimana ( ) konvergen ke sebuah akumulasi titik . Vektor ini harus memenuhi dan ∑ . Misalkan adalah limit dari ( ). Karena baris menurun dan ( )

adalah fungsi naik, maka ( ) . Karena dan

( ) ( ) ( ) ( ), kita ambil limit dari kedua bagian dan menghasilkan , dan dari definisi , maka menjadi . Karena , memenuhi bukti (a).

(b) Misalkan adalah nilai eigen lain dari dan adalah vektor eigen tak nol yang bersesuaian dengan nilai eigen . Maka , dengan kata lain

( ) ∑

Dengan menentukan panjang dari kedua sisi, kita peroleh | || | | ∑ | ∑ | | sehingga | | | || | ketika | | (| | | | | |).

Vektor eigen | | harus dinormalisasi terlebih dahulu. Normalisasi berfungsi untuk mengatur atau mengontrol elemen-elemen pada | | Ada banyak cara untuk menormalisasi | | cara yang digunakan adalah dengan menormalisasi

| | sehingga ∑ . Setelah itu dapat pastikan bahwa | | yang telah dinormalisasi berada pada simpleks, sedemikian sehingga | | . Karena itu, dari definisi , dapat kita simpulkan bahwa | | .

Akibat 3.2.3

Jika adalah matriks transisi rantai Markov, maka . Bukti:

Kita misalkan . Maka ∑ untuk semua . Karena , kita dapat katakan bahwa . Dari bagian (a) teorema Frobenius, terdapat nilai eigen dan vektor eigen yang bersesuaian (dimana dan ∑ ) sehingga

. Karena , elemen terbesar dari , kita sebut yang bernilai positif dan memenuhi

( ) ∑

∑

Dapat kita simpulkan bahwa . Sifat 2.8.1 menunjukkan bahwa 1 adalah nilai eigen dari (dan juga dari ) maka , sehingga terbukti bahwa . Sifat 2.8.2 muncul dari teorema 3.2.2 (Frobenius) dan akibat 3.2.3.

37

BAB IV

ALGORITMA GOOGLE PAGERANK

A. Hipotesis

Sebelum kita melanjutkan, kita nyatakan tiga hipotesis yang akan kita asumsikan dari sekarang.

i. Ada tepat satu nilai eigen di mana | | , dan karena itu dari Sifat 2.8.1, nilai eigennya 1.

ii. Subruang eigen yang bersangkutan dengan nilai eigen pada hipotesis i berdimensi 1.

iii. Matriks transisi adalah matriks yang dapat didiagonalisasi, yang berarti vektor eigennya membentuk basis.

Hipotesis pertama dan kedua tidak selalu benar untuk semua matriks transisi peluang. Namun, hipotesis tersebut masih masuk akal untuk matriks transisi peluang yang dihasilkan dari situs web yang luas.

B. Nilai Stasioner

Nilai stasioner akan kita gunakan untuk menentukan peringkat suatu halaman pada situs web.

Teorema 4.2

1. Jika matriks transisi peluang dari rantai Markov memenuhi tiga hipotesis di atas, maka ada vektor dimana ( ) , memenuhi

∑ ∑

Kita akan sebut vektor sebagai nilai stasioner dari rantai Markov. Dengan kata lain, nilai stasioner dari rantai Markov adalah vektor probabilitas sehingga .

2. Terlepas dari titik awal ( ) (dimana ∑ ), distribusi probabilitas ( ) akan konvergen ke nilai stasioner untuk .

Bukti:

Poin pertama hanya mengulangi fakta bahwa memiliki sebuah vektor eigen dengan nilai eigen 1 yang penjumlahan komponennya sama dengan 1. Persamaan yang mendefinisikan nilai stasioner adalah . Dengan kata lain, adalah vektor eigen dari yang bersesuaian dengan nilai eigen 1. Sifat dari poin kedua memberitahu kita bahwa terdiri dari entri-entri tak negatif. Karena vektor eigen selalu tak nol, jumlahan dari entri-entrinya pasti juga tak nol. Dengan menormalisasi vektor ini, kita dapat memastikan bahwa ∑ .

Untuk menunjukkan poin kedua, kita tulis kembali vektor keadaan awal dalam bentuk basis yang dibentuk dari vektor eigen-vektor eigen dari P. Kita urutkan nilai eigen dari P sebagai berikut: | | | | | |. Hipotesis i dan ii menunjukkan bahwa pertidaksamaan pertama pada urutan tersebut benar (yaitu nilai mutlak dari pasti lebih besar dari ), sementara hipotesis iii memastikan kita bahwa vektor eigen dari membentuk suatu basis untuk ruang dimensi . Misalkan adalah vektor eigen yang bersesuaian dengan nilai eigen . Selanjutnya, asumsikan bahwa telah dinormalisasi sehingga . Himpunan * + membentuk sebuah basis, sehingga kita dapat tulis

∑

dimana adalah koefisien dari pada basis ini.

Kita akan tunjukkan bahwa koefisien selalu bernilai 1. Untuk ini, kita akan menggunakan vektor (1, 1, …, 1) . Jika adalah eigen vektor dari dengan nilai eigen (yaitu ), maka perkalian matriks dapat disederhanakan menjadi 2 bentuk, yaitu

( )

dan yang kedua,

Kedua persamaan tersebut haruslah sama dari sifat asosiatif perkalian matriks. Untuk , nilai eigen tidak bernilai 1, dan persamaan tersebut hanya berlaku bila , yang dijabarkan sebagai

∑( )

dengan ( ) merepresentasikan koordinat ke- dari vektor . Kondisi ini menunjukkan bahwa jumlahan dari vektor koordinat , pasti nol. Jika kita jumlahkan komponen dari , hasilnya adalah 1 dari hipotesis (∑ ). Jadi

∑ ∑ ∑ ( ) ∑ ∑( ) ∑( ) ∑( ) ∑( )

Jumlahan dari vektor koordinat bernilai kecuali untuk , sehingga

∑( )

∑( )

Dengan asumsi vektor eigen telah dinormalisasi menjadi , sehinga

∑

Menggunakan sifat 4.2 (1) sehingga

Untuk mendapatkan perilaku setelah langkah ke- , terapkan perkalian matriks transisi peluang sebanyak kali, dimulai dari keadaan awal

∑ ∑ ∑ Karena , sehingga ∑ Karena , sehingga ∑ sudah dinormalisasi, sehingga menjadi ∑

Jumlahan pada sisi sebelah kanan adalah jumlahan dari vektor-vektor yang koefisiennya berkurang atau mengecil secara eksponensial seperti . (Ingat bahwa semua memiliki norma yang kurang dari 1). Jumlahan ini berhingga, sehingga barisan akan konvergen ke 0 apabila . Jadi,

, ketika .

Sifat-sifat dari rantai Markov bisa diinterpretasikan dengan mengatakan bahwa jika pengguna internet melanjutkan untuk menjelajahi situs web tersebut lebih

∑

∑

Jadi, jarak Euclid antara keadaan langkah ke- , , dan adalah

‖ ‖ ‖∑

lama, maka dia akan berada pada suatu halaman dengan probabilitas yang mendekati nilai stasioner di mana adalah eigen vektor yang sudah dinormalisasi dan bersesuaian dengan nilai eigen 1.

C. Peringkat Halaman Web

Sekarang kita dapat membuat hubungan antara vektor nilai stasioner dan urutan peringkat PageRank untuk halaman-halaman pada web.

Definisi 4.3

Skor untuk halaman ke pada algoritma PageRank (yang disederhanakan) adalah koefisien yang bersesuaian dengan vektor Kita dapat mengurutkan halaman tersebut berdasarkan skor PageRank-nya, dari yang terbesar ke yang terkecil.

Contoh 4.3.1

Sekarang dari situs web dengan lima halaman (Contoh 2.7.3, halaman 23) dapat kita peroleh hasil skor untuk setiap halamannya. Dari Hipotesis (i), kita asumsikan bahwa matriks transisi peluang rantai Markov memiliki tepat satu nilai eigen yaitu

. Sekarang kita harus mencari vektor eigen yang bersesuaian dengan nilai eigen dan memenuhi persamaan . Kita peroleh sistem persamaan linear berikut _}

Dengan menyelesaikan sistem persamaan linear di atas, dapat kita peroleh vektor eigen yang bersesuaian dengan nilai eigen , yaitu ( ). Ketika dinormalisasi, akan kita peroleh nilai stasioner

. 3 1 9 16 12                

Ini menunjukkan bahwa dalam perjalanan yang cukup lama, pengguna internet akan paling sering mengunjungi halaman , dengan 16 dari 41 langkah untuk menuju ke sana. Dengan cara yang sama, pengguna internet akan mengabaikan halaman karena hanya dapat mengunjungi halaman sebanyak satu kali dari 41 langkah rata-rata.

Bagaimana urutan peringkat akhir untuk halaman-halaman tersebut? Halaman memiliki peringkat 1, yang berarti halaman adalah halaman yang paling penting. Halaman memiliki peringkat 2, diikuti oleh halaman , , dan yang terakhir, yang paling tidak penting, yaitu halaman .

Ada cara lain untuk menginterpretasikan skor PageRank, yaitu setiap halaman memberikan skor PageRank ke semua halaman yang bertautan. Perhatikan kembali vektor .

/. Halaman hanya memiliki satu tautan dari halaman . Karena memiliki skor

dan ketiga tautan tersebut harus membagi rata nilai skor tersebut, maka skor akhir halaman adalah sepertiga skor , yaitu

. Tiga halaman memiliki tautan ke halaman , yaitu halaman , , dan , yang masing-masing memiliki skor

. Halaman hanya memiliki satu tautan keluar, sedangkan halaman dan memiliki tiga tautan keluar. Jadi, skor untuk halaman adalah

( )

Contoh 4.3.2

Akan kita tentukan nilai stasioner dari rantai Markov dengan MTP di bawah ini . 0 ₄1 6 1 2 1 2 1 2 1 4 1 2 1 3 1            P

Dari hipotesis, sudah kita asumsikan bahwa matriks transisi rantai Markov memiliki satu nilai eigen bernilai 1. Sehingga akan kita cari vektor eigen yang bersesuaian dengan nilai eigen dan memenuhi persamaan .

Kita peroleh sistem persamaan linear sebagai berikut

_}

Dengan menyelesaikan sistem persamaan linear di atas, kita memperoleh vektor eigen yang memenuhi nilai eigen , yaitu ( ) . Jadi, nilai stasionernya adalah _         4 22 18 Contoh 4.3.3

Dari Contoh 2.7.4 (halaman 24) telah kita peroleh matriks transisi rantai Markov sebagai berikut



























0

0

0

0

0

0

0

1

0

0

2 1 2 1 2 1 2 1 2 1 2 1

P

Sudah diasumsikan bahwa matriks transisi rantai Markov memiliki tepat satu nilai eigen bernilai 1. Sehingga akan kita cari vektor eigen yang bersesuaian dengan nilai eigen dan memenuhi .

Kita peroleh sistem persamaan linear sebagai berikut

_}

Dapat kita selesaikan sistem persamaan linear di atas, sehingga kita memperoleh vektor eigen yang bersesuaian dengan nilai eigen 1 adalah ( ). Jadi nilai stasionernya adalah             10 6 2 12

Jadi, peringkat pertama adalah halaman dengan skor

, dilanjutkan halaman dengan skor

, halaman dengan skor , dan yang terakhir adalah halaman dengan skor

. Pengguna internet akan paling sering mengunjungi halaman dan jarang mengunjungi halaman .

Contoh 4.3.4

Dari rantai Markov pada Contoh 2.7.5, kita mempunyai matriks transisi peluang

             0 0 0 1 0 0 0 0 0 3 1 3 1 2 1 2 1 2 1 2 1 3 1 P

Karena adalah matriks transisi rantai Markov, maka memiliki satu nilai eigen

. Akan kita cari vektor eigen yang bersesuaian dengan nilai eigen

_}

Kita selesaikan persamaan linear di atas, dan diperoleh vektor eigen yang bersesuaian dengan adalah ( ). Jadi nilai stasionernya adalah

            3 10 9 8

Jadi, peringkat pertama adalah halaman dengan skor

, dilanjutkan peringkat kedua yaitu halaman dengan skor

, lalu halaman dengan skor , dan yang terakhir adalah halaman dengan skor

.

Mengapa urutan yang diperoleh dari skor PageRank memiliki urutan yang masuk akal untuk halaman yang ada di situs web? Sebagian besar karena urutan tersebut mempercayakan pengguna itu sendiri untuk membuat keputusan tentang halaman mana yang lebih baik. Sebuah halaman penting yang memiliki tautan ke beberapa halaman lain dapat “menyebarkan” kepentingannya kepada halaman lain. Jadi, pengguna menunjukkan kepercayaan diri mereka dengan mentautkan halamannya ke halaman tertentu, sehingga mereka dapat menyebarkan bagian dari skor mereka ke halaman-halaman tersebut pada algoritma PageRank. Fenomena ini disebut “kepercayaan kolaboratif” oleh penemu PageRank.

D. Algoritma PageRank yang Ditingkatkan

Algoritma sebelumnya tidak dapat digunakan apa adanya. Terdapat dua kesulitan yang harus kita selesaikan.

Yang pertama adalah keberadaan halaman-halaman yang tidak memiliki tautan keluar. Ketiadaan tautan tersebut mungkin dikarenakan web Google belum

mengindeks tujuan dari tautan-tautan tersebut, atau karena memang halaman tersebut tidak memiliki tautan. Jadi, pengguna internet yang sampai pada halaman ini akan selamanya berada di sana. Satu cara untuk menghindari masalah ini adalah dengan mengabaikan dan menghapus halaman-halaman ini (dan semua tautan-tautan yang menuju ke halaman-halaman ini) dari situs web. Dengan begitu nilai stasionernya dapat dihitung. Setelah diperoleh, dapat ditemukan skor untuk halaman-halaman ini dengan “menyebarkan” kepentingan dari semua halaman yang memiliki tautan ke mereka, seperti yang telah dibahas sebelumnya:

∑

dimana adalah jumlah dari tautan yang dikeluarkan oleh halaman ke- yang menuju ke halaman buntu, dan adalah tingkat kepentingan halaman ke- yang sudah dihitung. Masalah selanjutnya menunjukkan bahwa pendekatan dengan mengabaikan atau menghapus halaman-halaman ini hanya memberikan solusi parsial. Solusi parsial di sini berarti solusi yang hanya mengandung beberapa halaman saja atau solusi yang tidak mengandung semua halaman-halaman pada situs web. Kesulitan yang kedua menyerupai kesulitan yang pertama, tetapi kesulitan kedua tidak terlalu mudah untuk diperbaiki.

Contoh 4.4.1

Sebuah contoh digambarkan sebagai berikut.

Gambar 4.1

Sebuah situs web dengan tujuh halaman. A

B

D

C E

Web ini mempunyai lima halaman dari contoh awal, ditambah dengan dua halaman yang terhubung ke web awal dengan tautan tunggal dari halaman . Kita tahu bahwa kita hanya dapat menuju ke halaman hanya dari halaman

sehingga pengguna internet tidak menghabiskan banyak waktu pada halaman

namun tetap mengunjungi halaman tersebut dengan menghabiskan

waktunya di sana. Pada situs web dengan tujuh halaman ini, setiap kali pengguna internet mengunjungi halaman , dia dapat memilih untuk menuju ke halaman atau ke halaman . Jika dia memilih untuk menuju ke halaman , maka dia tidak akan pernah bisa kembali ke halaman , , , , atau . Matriks transisi rantai Markov untuk situs web di atas adalah

                      0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 2 1 3 1 3 1 3 1 2 1 3 1 3 1 2 1 3 1 2 1

Dengan cara yang sama, dapat diperoleh nilai stasioner untuk web baru ini, yaitu

                      1 1 0 0 0 0 0

Dengan kata lain, halaman dan “menyerap” seluruh kepentingan yang harusnya dibagi di antara halaman lain. (Perhatikan bahwa pada contoh ini, (-1) juga adalah nilai eigen dari , yang berarti bahwa tidak lagi mendekati matriks kolom saat .) Dalam konteks rantai Markov secara umum, dan