Dalam sistem pengendalian berhirarki 2 level, maka optimasi dapat. dilakukan pada level pertama yaitu pengambil keputusan level pertama yang

(1)

BAB V

OPTIMASI SISTEM

Dalam sistem pengendalian berhirarki 2 level, maka optimasi dapat dilakukan pada level pertama yaitu pengambil keputusan level pertama yang langsung berhubungan dengan proses dan level kedua yang mengkoordinasikan beberapa pengambil keputusan pada level pertama. Pada sistem pengendalian berhirarki optimasi level pertama menggunakan Linear Quadratic Regulator (LQR), sedangkan pada level kedua digunakan metode interaction prediction untuk memberikan nilai baru pada α dan m sehingga error interaksi semakin kecil sampai batas yang diinginkan. Metode penyelesaian LQR diberikan oleh Davison, dan Maki (1973) dan Jamshidi (1980), sedangkan metode interaction prediction diberikan oleh Takahara (1965).

V.1. OPTIMASI LEVEL PERTAMA

Jika diketahui suatu sistem dinamik:

x& =Ax+ Bu (5.1)

di mana A dan B adalah kontinyu dan mempunyai indeks performansi (cost function):

(2)

( ) ( )

[

]

=

_∫

[

( )

+

( )

]

+

( ) ( )

tf to f f T T T 0 0 0 ,u t ,t u R t u x Q t xdt x t Fx t t x J (5.2)

di mana matriks Q(t) dan R(t) kontinyu, simetrik dan definit non negatif atau definit positif dan F adalah matriks definit non negatif. Permasalahan pengendalian optimal adalah menemukan fungsi pengendalian u*(t), di mana t0 < t

< tf, yang memenuhi sistem dinamik di atas dengan meminimasi indeks

performansi.

Jika diasumsikan tf finite, maka indeks performansi J*(x(t),t) menjadi

J*[x(t),t] = xT(t) K(t) x(t) (5.3)

di mana K(t) adalah matriks simetrik. Jika K(t) tidak simetrik, dapat diganti dengan matriks simetrik ½ [K(t) + KT(t)] tanpa mengubah indeks performansi.

Persamaan Hamilton-Jacobi digunakan untuk memperoleh aksi pengendalian optimal. Bentuk pertama dari persamaan Hamilton-Jacobi adalah sebagai berikut:

( )

[

]

[

( ) ( )

]

[

( )

]

[

( ) ( )

]

              ∂ ∂ + − = ∂ ∂ t , t u , t x f t , t x x J t , t u , t x L min t , t x t J * T ) t ( u * (5.4)

Dengan mensubstitusi persamaan-persamaan di atas diperoleh:

(

u Ru x Qx 2x KAx 2x KBu

)

min x

K

xT _& ₌₋ T ₊ T ₊ T ₊ T _(5.5)

Dengan menggunakan identitas:

(

Q KBR B K KA A K

)

x x KBu x 2 KAx x 2 Qx x Ru uT + T + T + T = T − −1 T + + T (5.6) diperoleh

(

Q KBR B K KA A K

)

x x x K xT & =− T − −1 T + + T (5.7)

(3)

) t ( Q ) t ( K ) t ( B ) t ( R ) t ( B ) t ( K ) t ( K ) t ( A ) t ( A ) t ( K ) t ( K& = + T − −1 T + (5.8)

Persamaan ini dikenal sebagai Differential Matriks Riccati Equation (DMRE).

Jika K&

( )

t = 0, diperoleh Algebraic Matriks Riccati Equation (AMRE).

Dari pembahasan di atas, dapat disimpulkan:

1. Aksi pengendalian optimal diberikan oleh Kalman (1960), yaitu: ) t ( x ) t ( K ) t ( B ) t ( R ) t ( * u =− −1 T = -G(t)x(t) (5.9)

di mana K(t) adalah solusi AMRE dan ) t ( K ) t ( B ) t ( R ) t ( G = −1 T (5.10)

Dari persamaan di atas, diperoleh sistem pengendalian optimal loop tertutup adalah:

( )

[

( )

( ) ( ) ( ) ( )

]

( )

( ) ( ) ( )

[

]

( )

( ) ( )

[

A t B t G t

]

x

( )

t t x t K t S t A t x t K t B t R t B t A t x 1 T − = − = − = − & (5.11)

2. Dengan menggunakan solusi AMRE, nilai sub optimal dari indeks performansi diberikan oleh

( ) ( )

[

]

( ) ( ) ( )

0 0 T 0 0 , t x t K t x t t x * J = (5.12)

K(t) adalah matriks simetrik positif definit.

Contoh 5.1.:

Dari sistem pada contoh 3.1., tentukan aksi kendali optimal level pertama dengan menggunakan LQR dan nilai sub optimalnya jika diketahui t0 = 0 dan tf = 10, dan

diberikan Q=diag(1,2,1,1,1,2,1,2,1) dan R=diag(1,1,1,1,1,1,1,1,1,1), sedangkan state awalnya adalah x(0) = (1 1 1 1 1 1 1 1 1)T

(4)

Penyelesaian:

Mengacu pada persamaan 5.2 dan dengan t0 = 0 dan tf = 10, maka indeks

performansi sistem adalah:

( ) ( )

[

]

( ) ( )

∫

+ + = 10 0 f f T T T t Fx t x dt t Qx t x t Ru t u J (5.14)

Permasalahan pengendalian optimal adalah mencari aksi kendali optimal u*(t) dan nilai optimal indeks performansi sistem dengan meminimasi indeks performansi. Penyelesaian permasalahan ini dilakukan dengan langkah-langkah sebagai berikut:

1. Sesuai dengan persamaan 5.9. – 5.10., maka aksi kendali optimal adalah ) t ( x ) t ( K ) t ( B ) t ( R ) t ( * u =− −1 T (5.15)

Mengacu pada persamaan 5.11, sistem optimal loop tertutup adalah

( )

[

A t B t R (t)B (t)K(t)

]

x(t) ) t ( x& = − −1 T

( )

[

A t B t G(t)

]

x(t) ) t ( x& = − (5.18)

2. K(tf) dan G(tf) diperoleh dengan menggunakan fungsi LQR pada Matlab.

Dari perhitungan menggunakan Matlab, diperoleh K(tf) dan G(tf), yaitu

                              − − − − − − − − − − − − − − − − = 5482 . 0 3460 . 0 2093 . 0 0137 . 0 0010 . 0 0011 . 0 0003 . 0 0001 . 0 0 3460 . 0 8249 . 0 2458 . 0 0143 . 0 0013 . 0 0013 . 0 0004 . 0 0001 . 0 0 2093 . 0 2458 . 0 3874 . 0 2103 . 0 0252 . 0 0253 . 0 0021 . 0 0001 . 0 0 0137 . 0 0143 . 0 2103 . 0 7812 . 0 0943 . 0 0948 . 0 0085 . 0 0008 . 0 0 0010 . 0 0013 . 0 0252 . 0 0943 . 0 0949 . 0 0121 . 0 0011 . 0 0001 . 0 0 0011 . 0 0013 . 0 0253 . 0 0948 . 0 0121 . 0 0964 . 0 0129 . 0 0018 . 0 0002 . 0 0003 . 0 0004 . 0 0021 . 0 0085 . 0 0011 . 0 0129 . 0 0843 . 0 0081 . 0 0007 . 0 0001 . 0 0001 . 0 0001 . 0 0008 . 0 0001 . 0 0018 . 0 0081 . 0 3673 . 0 0746 . 0 0 0 0 0 0 0002 . 0 0007 . 0 0746 . 0 4584 . 0 K (5.19) dan

(5)

                              − − − − − − − − − − − − − − − − = 5482 . 0 3460 . 0 2093 . 0 0137 . 0 0010 . 0 0011 . 0 0003 . 0 0001 . 0 0 3460 . 0 8249 . 0 2458 . 0 0143 . 0 0013 . 0 0013 . 0 0004 . 0 0001 . 0 0 4186 . 0 4915 . 0 7749 . 0 4206 . 0 0504 . 0 0506 . 0 0042 . 0 0003 . 0 0 0137 . 0 0143 . 0 2103 . 0 7812 . 0 0943 . 0 0948 . 0 0085 . 0 0008 . 0 0 0052 . 0 0066 . 0 1260 . 0 4716 . 0 4743 . 0 0603 . 0 0054 . 0 0005 . 0 0 0053 . 0 0067 . 0 1264 . 0 4739 . 0 0603 . 0 4819 . 0 0647 . 0 0088 . 0 0010 . 0 0016 . 0 0018 . 0 0106 . 0 0427 . 0 0054 . 0 0647 . 0 4217 . 0 0404 . 0 0034 . 0 0002 . 0 0002 . 0 0003 . 0 0016 . 0 0002 . 0 0035 . 0 0162 . 0 7346 . 0 1493 . 0 0 0 0 0 0 0002 . 0 0007 . 0 0746 . 0 4584 . 0 G (5.20)

Jika elemen matriks G yang terlalu kecil diabaikan, maka diperoleh matriks struktur dari matriks G, yaitu:

                              = 99 98 97 89 88 87 79 78 77 76 75 74 67 66 65 64 57 56 55 47 46 44 43 34 33 23 32 22 21 12 11 G g g g 0 0 0 0 0 0 g g g 0 0 0 0 0 0 g g g g g g 0 0 0 0 0 g g g g 0 0 0 0 0 g g g 0 0 0 0 0 0 g g 0 g g 0 0 0 0 0 0 0 g g g 0 0 0 0 0 0 0 g g g 0 0 0 0 0 0 0 g g S (5.21)

Dari matriks struktur SG di atas, terlihat adanya empat kelompok. Empat

kelompok tersebut sama dengan dekomposisi berdasarkan strongly coupled system yang telah dibahas pada bagian pertama.

3. Indeks performansi sub optimal diperoleh dengan menggunakan persamaan 5.12., yaitu J*= ½ x0T K x0 (5.22) Jika x0= (1 1 1 1 1 1 1 1 1)T (5.23) maka ( )                                                             − − − − − − − − − − − − − − − − = 1 1 1 1 1 1 1 1 1 5482 . 0 3460 . 0 2093 . 0 0137 . 0 0010 . 0 0011 . 0 0003 . 0 0001 . 0 0 3460 . 0 8249 . 0 2458 . 0 0143 . 0 0013 . 0 0013 . 0 0004 . 0 0001 . 0 0 2093 . 0 2458 . 0 3874 . 0 2103 . 0 0252 . 0 0253 . 0 0021 . 0 0001 . 0 0 0137 . 0 0143 . 0 2103 . 0 7812 . 0 0943 . 0 0948 . 0 0085 . 0 0008 . 0 0 0010 . 0 0013 . 0 0252 . 0 0943 . 0 0949 . 0 0121 . 0 0011 . 0 0001 . 0 0 0011 . 0 0013 . 0 0253 . 0 0948 . 0 0121 . 0 0964 . 0 0129 . 0 0018 . 0 0002 . 0 0003 . 0 0004 . 0 0021 . 0 0085 . 0 0011 . 0 0129 . 0 0843 . 0 0081 . 0 0007 . 0 0001 . 0 0001 . 0 0001 . 0 0008 . 0 0001 . 0 0018 . 0 0081 . 0 3673 . 0 0746 . 0 0 0 0 0 0 0002 . 0 0007 . 0 0746 . 0 4584 . 0 . 1 1 1 1 1 1 1 1 1 2 1 * J

(6)

J* = 3.2180 (5.24) Dari hasil perhitungan di atas, diperoleh aksi kendali optimal yang meminimasi indeks performansi pada persamaan 5.14, di mana G(t) = G(tf) pada

persamaan 5.20 dan nilai sub optimal indeks performansi adalah 3.2180.

Jadi, dengan memberikan aksi kendali optimal, di mana aksi kendali optimal ini merupakan umpan balik state yang diperoleh dengan meminimasi indeks performansi, maka level pertama sistem menjadi optimal.

II.5.2. OPTIMASI LEVEL KEDUA

Dalam pengendalian sistem pengendalian berhirarki, maka pencapaian

feasible optimal control diantara subsistem hasil dekomposisi adalah hal yang

teramat penting. Untuk sistem dengan dua level pengendalian, maka optimasi level pertama berpengaruh terhadap level kedua.

Jika diberikan sistem:

( )

t

Ax

( )

t

Bu

( )

t

,

x

( )

t

0

x

0

x

&

=

+

=

(5.25)

dan quadratic cost function yang akan diminimasi,

( ) ( )

+

_∫

(

+

)

= f 0 t t T T f f T dt Ru u Qx x 2 1 t Fx t x 2 1 J (5.26)

di mana F > 0, Q > 0, R > 0, to,tf adalah waktu awal dan waktu akhir dan xo adalah

state awal.

Sistem disederhanakan menjadi N sub sistem, sehingga:

( )

t Ax

( )

t Bu

( )

t , m

( )

t x

( )

t x , i 1,...,N

x&_i = _i _i + _i _i + _i _i ₀ = _i₀ = (5.27)

(7)

( )

_∑

( )

≠ = = N i j 1 j j ij i t A x t m (5.28)

yang menggambarkan interaksi dari subsistem ke-i dengan N-1 subsistem yang lainnya.

Matriks Qi dan Ri adalah blok diagonal dan dengan matriks Si yang

antiblok-diagonal, maka akan terbentuk indeks performansi sistem yang terdekomposisi adalah:

( )

[

( )

]

∑

_∫

=         + + + = N 1 i t t i i T i i i T i i i T i f i i f T i x t Q x t u t R u t m t Sm t dt 2 1 t x F t x 2 1 J f 0 (5.29) Dalam dekomposisi sistem linear terinterkoneksi secara luas ini, faktor

coupling antar subsistem merupakan interaksi variabel-variabel mi(t). Interaksi ini

akan digantikan oleh vektor parameter α = (αi ,…,αN)T yang disebut juga vektor

koordinasi dan dinyatakan oleh Si(α), di mana i = 1,…,N.

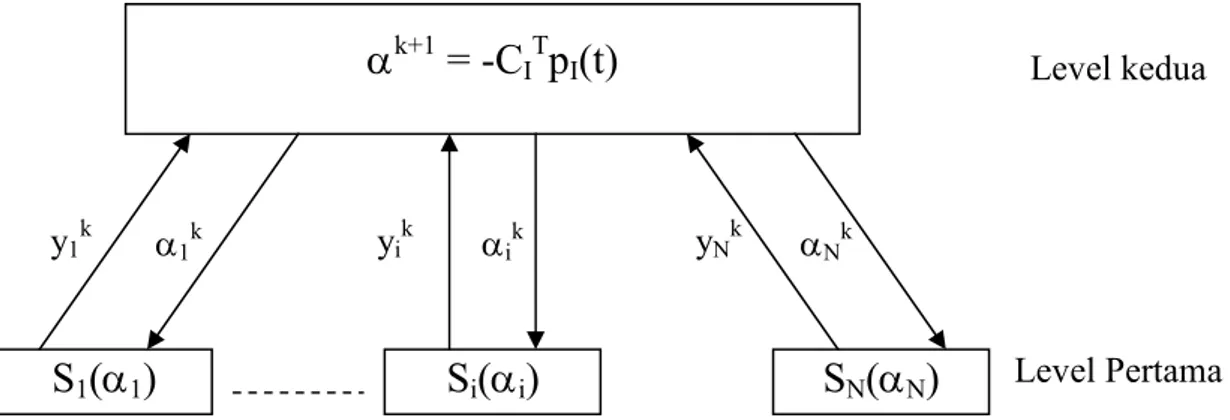
Gambar 5.1. memperlihatkan struktur pengendalian dua level suatu sistem skala besar. Dengan cara ini, pada iterasi ke-k (atau langkah pertukaran informasi), tiap pengendali lokal i menerima αik dari koordinator (hirarki level

dua) untuk mendapatkan solusi Si(αik), dan mengirimkankan yik dari solusi

tersebut ke koordinator.

Minimasi fungsi dari beberapa variabel terdapat dalam area umum dari optimasi sehingga dibutuhkan metode minimasi yang tepat. Beberapa metode optimasi yang terkenal berdasar pada gradien fungsional f(x) dari vektor x = (x1,x2,.., xN)T yang tidak diketahui. Diantara metode-metode gradien yang ada,

(8)

metode steepest descent merupakan satu skema yang banyak dipakai. Dalam

metode ini, arah pencarian optimum (minimum atau maximum) diberikan oleh s(k) = - g(k), di mana s(k) adalah arah yang dicari selama k iterasi dan g(k)=∂f(x(k)/∂x(k)) adalah vektor gradien. Di sini, pencarian metode dalam arah steepest descent, objective function akan berkurang untuk secepatnya menuju x(k). Dalam metode

steepest descent x(k) biasanya jatuh di nilai yang terlalu jauh dari solusi hasil pembulatan error. Maka, metode ini sering tidak reliable dan tidak efisien.

Metode Interaction prediction adalah metode lain yang dapat digunakan

untuk menyelesaikan permasalahan level kedua. Metode ini menggunakan fungsi Hamiltonian pada permasalahan level pertama untuk mendapatkan parameter sistem yang akan digunakan untuk menyelesaikan permasalahan level kedua. Fungsi Hamilton dari sistem terdekomposisi di atas adalah:

( )

_∑

(

)

(

)

≠ = + + + α − α + + = N 1 j 1 j i i i i i i T i i ji T j i T i i i T i i i T i i u t R u t m A x p A x Bu C z 2 1 t x Q t x 2 1 H (5.30)

α

k+1

= -C

IT

p

I

(t)

S

1

(α

1

)

S

i

(α

i

)

S

N

(α

N

)

y1k α1k yik αik yNk αNk Level kedua Level Pertama

(9)

dan mempunyai syarat perlu optimalitas,

( )

t K

( ) ( )

t x t g

( )

t

p_i = _i _i + _i (5.31)

dan dengan penyederhanaan penyelesaian permasalahan TPBV (Two Point Boundary Value), diperoleh,

( )

i

( )

i

( )

i i

( )

i T i i i i t K t A A K t K t SK t Q K& =− − + − (5.32)

( )

(

( )

) ( )

( ) ( )

_∑

( )

≠ = α + − − − = N i j 1 j T j T ji i i i T i i i i t A SK t g t K t m t A t g& (5.33)

di mana nilai akhir dari Ki(tf) dan gi(tf) dari persamaan 5.29, sehingga

( )

_{( )}

( )

_i _i

( )

_f f i f i i f T i i Fx t t x t x F t x 2 1 t p = ∂     ∂ = (5.34)

dan dengan menggunakan persamaan 5.31 diperoleh:

Ki(tf) = F dan gi(tf) = 0 (5.35)

Dari formulasi ini, aksi pengendalian u(t) pada optimasi level pertama adalah:

( )

t R B K

( ) ( )

t x t R B g

( )

t

u_i =− _i−1 _iT _i _i − _i−1 _iT _i (5.36)

Pada permasalahan level kedua, bagian yang penting adalah meng-update

vektor kordinasi (α) yang baru. Untuk tujuan ini, dengan memperhatikan fungsi Hamiltonian pada persamaan 5.30, persamaan-persamaan berikut adalah penyelesaian dari permasalahan level kedua:

0 p C m H i T i i i i ₌_α ₊ ₌ ∂ ∂

(10)

0 x A m H N i j1 j j ij i i i ₌ ₋ ₌ α ∂ ∂

∑

≠ = (5.37) sehingga diperoleh:

( )

_∑

≠ = = − = α N i j 1 j j ij i i T i i t C p t , m t A x (5.38)

Maka, prosedur koordinasi level kedua pada iterasi ke-(k+1) adalah sebagai berikut:

( )

k N i j1 j j ij i T i 1 k i i x A t p C t m t          − =      α

∑

≠ = + (5.39)

Dari pembahasan di atas, maka metode Interaction prediction dapat

diformulasikan sebagai berikut:

1. Persamaan differensial matriks riccati orde N dengan kondisi akhir pada persamaan 5.35 dapat diselesaikan dan mendapatkan serta menyimpan Ki(t),

di mana i=1,2, . . . , N dan to < t < tf.

2. Dengan nilai awal αio(t) dan mio(t) ditentukan, maka persamaan 5.33 dapat

diselesaikan dengan kondisi akhir pada persamaan 5.35. Dari langkah ini gi(t)

diperoleh dan nilainya disimpan.

3. Dengan hasil yang diperoleh pada langkah 1 dan 2, maka persamaan state berikut dapat diselesaikan.

( )

(

_i _i _i

( )

) ( )

_i _i

( ) ( )

_i _i

( )

_i

( )

_i

i t A SK t x t S t g t m t , x 0 x

(11)

4. Permasalahan level kedua adalah meng-update error interaksi dengan

menggunakan hasil pada langkah 3 dan persamaan 5.39 sampai error interaksi menjadi cukup kecil. Dan perhitungan error interaksi adalah:

( )

t dt t x A t m t x A t m Error N 1 i t t N i j 1 j j ij i T N i j 1 j j ij i f 0 ∆                       −           − =

∑ ∫

∑

= ≠ = ≠ = (5.41)

di mana ∆t_{adalah step size integrasi.}

Dari formulasi ini, setelah beberapa kali iterasi dan diperoleh error interaksi yang cukup kecil, maka diperoleh vektor koordinasi αi, state xi, aksi

pengendalian ui di mana i=1..N optimal.

Contoh 5.2.:

Dari sistem pada contoh 3.1., dapatkan optimasi level kedua sistem jika diberikan nilai awal sebagai berikut:

- waktu awal (t0) = 0 dan waktu akhir (tf) = 10

- nilai awal xi(0) yang menyatakan x pada t=0, mi0 yang menyatakan m pada

iterasi ke-0 dan αi0 yang menyatakan α pada iterasi ke-0.

Nilai awal xi(0), mi0 dan αi0 diberikan sebagai berikut:

x1[0] = 1 x2[0] = 1 x3[0] = 1 x4[0] = 1 α10 = 1 α20 = 1 α30 = 1 α40 = 1 m10 = 0 m20 = 1/12 m30 = 1/12 m40 = 2/12

(12)

x5[0] = 1 x6[0] = 1 x7[0] = 1 x8[0] = 1 x9[0] = 1 α50 = 1 α60 = 1 α70 = 1 α80 = 1 α90 = 1 m50 = 1/12 m60 = 3/12 m70 = 1/12 m80 = 2/12 m90 = 2/12

- Ki(t) diperoleh dari hasil perhitungan pada optimasi level pertama.

- langkah integrasi (∆t_{) yang digunakan untuk mencari error interaksi adalah}

0.1

- langkah iterasi (h) yang digunakan untuk menghitung persamaan differensial adalah 0.1, sehingga dilakukan 100 iterasi karena tf=10

Penyelesaian:

Penyelesaian permasalahan tersebut dilakukan dengan langkah-langkah sebagai berikut:

1. Mencari g(t)

Jika persamaan 5.33 diaplikasikan pada model sistem dengan harga awal awal α dan m(t) ditentukan serta matriks A yang diperoleh dari model sistem, maka diperoleh persamaan g(t) sebagai berikut:

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t g&₁ =− ₁₁ − ₁₁ T ₁ − ₁ ₁

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t g&₂ =− ₂₂ − ₂₂ T ₂ − ₂ ₂ + ₂₁α₁

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t a

( )

t g&₃ =− ₃₃ − ₃₃ T ₃ − ₃ ₃ + ₃₂α₂ + ₃₄α₄

(13)

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t a

( )

t g&₄ =− ₄₄ − ₄₄ T ₄ − ₄ ₄ + ₄₃α₃ + ₄₆α₆

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t g&₅ =− ₅₅ − ₅₅ T ₅ − ₅ ₅ + ₅₆α₆

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t a

( )

t a

( )

t g&₆ =− ₆₆ − ₆₆ T ₆ − ₆ ₆ + ₆₄α₄ + ₆₅α₅ + ₆₇α₇

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t g&₇ =− ₇₇ − ₇₇ T ₇ − ₇ ₇ + ₇₆α₆

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t a

( )

t g&₈ =− ₈₈ − ₈₈ T ₈ − ₈ ₈ + ₈₇α₇ + ₈₉α₉

( )

t

[

a k

( )

t

]

g

( )

t k

( ) ( )

t z t a

( )

t a

( )

t g&₉ =− ₉₉ − ₉₉ T ₉ − ₉ ₉ + ₉₇α₇ + ₉₈α₈ (5.42) 2. Mencari State

Dengan menggunakan informasi g(t) di atas dan persamaan 5.40, diperoleh persamaan x(t) sebagai berikut:

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₁ = ₁₁ − ₁₁ ₁ − ₁ + ₁

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₂ = ₂₂ − ₂₂ ₂ − ₂ + ₂

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₃ = ₃₃ − ₃₃ ₃ − ₃ + ₃

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₄ = ₄₄ − ₄₄ ₄ − ₄ + ₄

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₅ = ₅₅ − ₅₅ ₅ − ₅ + ₅

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₆ = ₆₆ − ₆₆ ₆ − ₆ + ₆

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₇ = ₇₇ − ₇₇ ₇ − ₇ + ₇

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₈ = ₈₈ − ₈₈ ₈ − ₈ + ₈

( )

t

[

a k

( )

t

]

x

( )

t g

( )

t m

( )

t x&₉ = ₉₉ − ₉₉ ₉ − ₉ + ₉ (5.43)

(14)

3. Memberikan nilai baru vektor koordinasi α dan m(t)

Untuk memberikan nilai baru pada vektor koordinasi α dan m(t) setelah iterasi, maka p(t) perlu dicari sesuai dengan persamaan 5.31. Dengan menggunakan x(t) dan g(t) yang diperoleh dari iterasi sebelumnya, pada iterasi sebelumnya, diperoleh persamaan p(t) sebagai berikut:

( )

t K

( ) ( )

t x t g

( )

t p₁ = ₁₁ ₁ + ₁

( )

t K

( ) ( )

t x t g

( )

t p₂ = ₂₂ ₂ + ₂

( )

t K

( ) ( )

t x t g

( )

t p₃ = ₃₃ ₃ + ₃

( )

t K

( ) ( )

t x t g

( )

t p₄ = ₄₄ ₄ + ₄

( )

t K

( ) ( )

t x t g

( )

t p₅ = ₅₅ ₅ + ₅

( )

t K

( ) ( )

t x t g

( )

t p₆ = ₆₆ ₆ + ₆

( )

t K

( ) ( )

t x t g

( )

t p₇ = ₇₇ ₇ + ₇

( )

t K

( ) ( )

t x t g

( )

t p₈ = ₈₈ ₈ + ₈

( )

t K

( ) ( )

t x t g

( )

t p₉ = ₉₉ ₉ + ₉ (5.44) Dengan p(t) yang dihasilkan di atas, maka vektor koordinasi α diberi nilai baru sesuai dengan persamaan 5.39. Persamaan α yang diperoleh adalah sebagai berikut:

( )

t k 1 c₁₁p₁

( )

t 1 =− α +

( )

t k 1 c₂₂p₂

( )

t 2 =− α +

( )

t k 1 c₃₃p₃

( )

t 3 =− α +

(15)

( )

t k 1 c₄₄p₄

( )

t 4 =− α +

( )

t k 1 c₅₅p₅

( )

t 5 =− α +

( )

t k 1 c₆₆p₆

( )

t 6 =− α +

( )

t k 1 c₇₇p₇

( )

t 7 =− α +

( )

t k 1 c₈₈p₈

( )

t 8 =− α +

( )

t k 1 c₉₉p₉

( )

t 9 =− α + (5.45) Dengan menggunakan x(t) pada iterasi sebelumnya diperoleh m(t) yang baru, yaitu:

( )

t 0 m₁ =

( )

21 2 2 t A x m =

( )

32 2 34 4 3 t A x A x m = +

( )

₄₃ ₃ ₄₆ ₆ 4 t A x A x m = +

( )

56 6 5 t A x m =

( )

64 4 65 5 67 7 6 t A x A x A x m = + +

( )

76 6 7 t A x m =

( )

₈₇ ₇ ₈₉ ₉ 8 t A x A x m = +

( )

97 7 98 8 9 t A x A x m = + (5.46)

(16)

Error interaksi dicari dengan menggunakan persamaan 5.41. Pada sistem pengendalian proses pembuatan semen menggunakan DCS di atas, diperoleh persamaan error interaksi:

( )

_

( )

₊

[

( )

₋

( )

]

₊

[

( )

₋

( )

₋

( )

]

∆ =

_∫

f 0 f 0 f 0 t t 3 32 2 34 4 t t 2 21 1 t t m1 t dt m t A x t dt m t A x t A x t dt t 1 t e

( )

[

]

_∫

[

( )

]

∫

− − ++ − + f 0 f 0 t t 5 56 6 t t m4 t A43x3 t A46x6 t dt M t A x t dt

( )

[

]

_∫

[

( )

]

∫

− − − + − + f 0 f 0 t t 7 76 7 t t m6 t A64x4 t A65x5 t A67x7 t dt m t A x t dt

( )

[

]

_∫

[

( )

]

∫

− − + − − + f 0 f 0 t t 9 97 7 98 8 t t m8 t A87x7 t A89x9 t dt m t A x t A x t dt (5.47) Dengan menggunakan bahasa pemrograman Turbo Pascal 7.0, maka permasalahan di atas dapat diselesaikan. Program melakukan iterasi sampai error interaksi menjadi cukup kecil. Saat error interaksi cukup kecil, program menyimpan nilai xi(t), mi(t), αi, ui(t) dan error interaksi.

Saat running program, iterasi dihentikan setelah diperoleh error

interaksi yang cukup kecil (0.0134). Error interaksi yang cukup kecil ini diperoleh pada iterasi ke-25. Karena error interaksi tersebut diperoleh pada iterasi ke-25 maka α dan m(t) yang digunakan adalah αi dan mi(t) pada iterasi ke-24,

sedangkan xi(t) dan ui(t) yang digunakan adalah xi(t) dan ui(t) pada iterasi ke-25.

Pada iterasi ke-24, nilai vektor koordinasi α adalah sebagai berikut: α1 = 0.000031

α2 = 0.000023

(17)

α4 = 0.000023 α5 = 0.000026 α6 = -0.000228 α7 = -0.000013 α8 = -0.000183 α9 = -0.000123 (5.48) Nilai mi(t) iterasi ke-24 adalah sebagai berikut:

m1 = 0.000000 m2 = 0.000032 m3 = 0.000289 m4 = 0.000551 m5 = 0.000351 m6 = 0.000579 m7 = 0.000351 m8 = 0.000455 m9 = 0.000425 (5.49) Error interaksi iterasi ke-1 sampai iterasi ke-25 terdapat pada Gambar 5.2. State (xi(t)) iterasi ke-25 terdapat pada Gambar 5.3., dan aksi kendali (ui(t)) iterasi

ke-25 terdapat pada Gambar 5.4.

Pada iterasi ke-25, state x1 sampai dengan x9 menunjukkan perilaku yang

(18)

awal (xi(0)) mendekati 0. Hal ini terjadi, karena tidak ada referensi yang menjadi

tujuan xi. State x1 sampai dengan x9 berhasil mencapai steady state. State pada

iterasi ke-25 ini menggunakan vektor koordinasi αi dan mi hasil iterasi ke-24.

Vektor koordinasi ini dipengaruhi oleh state (persamaan 5.31 dan 5.39), sehingga apabila xi mendekati nol, maka αi mendekati nol juga. Demikian juga mi yang

merupakan pengaruh dari sub sistem lain ke sub sistem i, sehingga apabila state sub sistem lain mendekati nol, maka mi mendekati nol.

Aksi kendali ui pada iterasi ke-25 nilainya naik dari nilai negatif menuju

ke nol. Hal ini terjadi karena aksi kendali dipengaruhi state. Jadi pada iterasi ke-25, ui mendekati nol karena xi mendekati nol.

Error interaksi menjadi semakin kecil seiring dengan bertambahnya iterasi. Pada iterasi pertama, error interaksi = 6.0668, dan nilainya semakin turun sampai pada iterasi ke-5 nilainya dibawah 1 (0.6973) dan pada iterasi ke-25 nilainya = 0.0134. Karena nilai ini sudah cukup kecil, maka iterasi diberhentikan.

Dengan metode interaction prediction, level kedua sistem tersebut dapat

dioptimasi. Error interaksi yang dihasilkan dari metode ini menggambarkan besarnya error yang terjadi pada interaksi antara satu sub sistem dengan sub sistem lain. Apabila error interaksinya cukup kecil, maka sistem tersebut optimal. Dari hasil perhitungan yang dilakukan, error interaksi yang cukup kecil terjadi pada iterasi ke-25 sehingga sistem tersebut optimal pada iterasi ke-25. Vektor koordinasi yang digunakan adalah vektor koordinasi iterasi ke-24 (persamaan 6.16). Hal ini terlihat juga pada perilaku state yang mencapai steady state pada