TUGAS AKHIR MODUL 5 PROFESIONAL.docx

(1)

TUGAS AKHIR MODUL 5 PROFESIONAL TUGAS AKHIR MODUL 5 PROFESIONAL

TEORI PELUANG DAN STATISTIKA TEORI PELUANG DAN STATISTIKA

1.

1. Pertama kita buat terlebih dahulu sketsa tempat duduPertama kita buat terlebih dahulu sketsa tempat dudu k di mobil. Kemudian diisi dengank di mobil. Kemudian diisi dengan banyak cara yang mungkin orang dapat menduduki kursi tersebut sesuai dengan cerita. banyak cara yang mungkin orang dapat menduduki kursi tersebut sesuai dengan cerita.

“

“ Lima orang pemuda pergi berekreasi menggunakan mobil. Mobil yang digunakan memiliki Lima orang pemuda pergi berekreasi menggunakan mobil. Mobil yang digunakan memiliki

dua tempat duduk di depan (termasuk untuk pengemudi) dan tiga d ibelakang. Dari kelima dua tempat duduk di depan (termasuk untuk pengemudi) dan tiga d ibelakang. Dari kelima pemuda tersebut hanya dua orang yang bisa mengemudi

pemuda tersebut hanya dua orang yang bisa mengemudi””

2 4 3 2 1



 Tempat duduk sopir hanya dapat diisi dengan 2 caraTempat duduk sopir hanya dapat diisi dengan 2 cara 

 Tempat duduk berTempat duduk berikutnya ikutnya kemungkinan dapat diisi kemungkinan dapat diisi dengan (5dengan (5 – – 1) cara = 4 cara 1) cara = 4 cara



 Tempat duduk berikutnya kemungkinan dapat diisi dengan (4Tempat duduk berikutnya kemungkinan dapat diisi dengan (4 – – 1) cara = 3 cara 1) cara = 3 cara 

 Tempat duduk berikutnya kemungkinan dapat diisi dengan (3Tempat duduk berikutnya kemungkinan dapat diisi dengan (3 – – 1) = 2 cara 1) = 2 cara 

 Tempat duduk berikutnya kemungkinan dapat diisi (2Tempat duduk berikutnya kemungkinan dapat diisi (2 – – 1) cara = 1 cara 1) cara = 1 cara

Jadi, banyaknya cara mereka duduk di mobil adalah 2

Jadi, banyaknya cara mereka duduk di mobil adalah 2xx44xx33xx22 xx1 = 48 cara.1 = 48 cara.

2.

2. Diketahui :: Diketahui sebuah kotak berisi 4 lembar uang Rp.5000,00, 3 lembar uang Rp.10,000,00, dan 3sebuah kotak berisi 4 lembar uang Rp.5000,00, 3 lembar uang Rp.10,000,00, dan 3

lembar uang Rp.20.000,00. Secara acak diambil 4 lembar uang, lembar uang Rp.20.000,00. Secara acak diambil 4 lembar uang, Ditanyakan

Ditanyakan : : peluang peluang terambil uang terambil uang sejumlah Rp. 30.000,00.sejumlah Rp. 30.000,00. Penyelesaian

Penyelesaian::

Jumlah uang Rp. 30.000,00 antara lain: Jumlah uang Rp. 30.000,00 antara lain:



 (4 lembar (4 lembar x Rp 5.000,00) x Rp 5.000,00) + (1 + (1 lembar x lembar x Rp 10.000,00) Rp 10.000,00) = Rp = Rp 30.000,0030.000,00 

 (3 (3 lembar lembar x x Rp Rp 10.000,00) 10.000,00) = = Rp Rp 30.000,0030.000,00 

 (1 lembar x Rp 10.000,00) + (1 lembar x Rp 20.000,00) = Rp30.000,00(1 lembar x Rp 10.000,00) + (1 lembar x Rp 20.000,00) = Rp30.000,00

Maka : n(S) = 5 Maka : n(S) = 5

Jadi peluang terambil 4 lembar uang sejumlah Rp 30.000,00 adalah Jadi peluang terambil 4 lembar uang sejumlah Rp 30.000,00 adalah





3.

3. Diketahui : Diketahui : Pelajar Pelajar puta puta = = 4 4 orangorang Pelajar Putri = 3 orang Pelajar Putri = 3 orang

Ditanyakan

Ditanyakan : peluang terjadi susunan duduk putra mengumpul dengan putra dan putri : peluang terjadi susunan duduk putra mengumpul dengan putra dan putri mengumpul dengan putri.

mengumpul dengan putri. Tempat duduk di depan

(2)

Penyelesaian

Pelajar putra duduk mengumpul dan pelajar putrid duduk mengumpul maka: Pelajar putra + pelajar putri = 2! cara

Pelajar Putra posisi duduknya yaitu ada = 4! cara Pelajar Putri posisi duduknya yaitu ada = 3! cara

Jadi, peluang terjadi susunan duduk putra mengumpul dengn putra dan putri mengumpul dengan putri adalah =

2!×4!×3!

 (2×1)×(4×3×2×1)×(3×2×1)

 2×24×12

 2

88 cara 4. Diketahui : Bola Putih = 2 buah

Bola Merah = 6 buah Total Bola = 8 buah

Ditanyakan : peluang terambilnya dua bola berlainan warna Penyelesaian:

Peluang terambil bola putih pada pengambilan pertama dan bola merah pada pengambilan kedua.

Peluang =





×









_



_



Peluang terambil bola merah pada pengambilan pertama dan bola putih pada pengambilan kedua

Peluang =



_

×



_





_



_



Jadi, peluang terambilnya dua bola berlainan warna adalah

















5. Mengurutkan data dan menyajikan dalam bentuk table

Nilai 43 56 72 73 74 75 89 90 92 98 100 Frekuensi 1 1 1 1 2 1 1 1 1 1 1  Rata-rata (

Mean

)



(×)+(×)+(×)+(×)+(×)+(×)+(×)+(×)+(×)







_

 78

 Modus adalah data yang sering muncul.

Modus data tersebut adalah 74. Artinya bahwa nilai terbanyak tes kemampuan bahasa adalah 74.

(3)

 Median adalah data tengah setelah diurutkan.

Karena data genap maka median terletak pada data ke-6 dan data ke-7 Median

 74,5

 Kuartil

Kuartil terdiri dari tiga yaitu kuartil bawah, kuartil tengah dan ku artil atas. Kuartil Bawah (Q1 )

Lokasi Q1 = ¼

×(121)  3,25

(data ke-3 dan ke-4)

Jadi, kuartil bawah dari data tersebut adalah 72,5 Kuartil Tengah (Q2 ) = Median = 74,5

Kuartil Atas (Q3 )

Lokasi kuartil atas = ¾

×(121)  9,75

(data ke-9 dan data ke-10) Jadi, kuartil atas dari data tersebut adalah 91

 Simpangan Baku

Data nilai tes kemampuan bahasa dari 12 siswa yang mengikuti ujian





̅

|



 ̅|

|



  ̅ |



43 56 72 73 74 74 75 89 90 92 98 100 78 35 22 6 5 4 4 3 11 12 14 20 22 1225 484 36 25 16 16 9 121 144 196 400 484 158 3156 Variansi :

 286,91





 7273

_{2  72,5}

 7475

₂





 9092

_{2  91}





_{ 1}

  1|



  ̅ |





=

 1

_121(3156)

 3156

₁₁

(4)

Simpangan baku:

  √



 √ 286,91

 16,94

Jadi, simpangan baku data tersebut adalah 16,94

6. Data tes kemampuan akademik (TPA) terhadap nilai matematika dari 12 anak yang hasilnya berikut Nomor Siswa Skor TPA (X) Nilai Matematika (Y) X2 _Y2 _XY 1 65 85 4225 7225 5525 2 50 74 2500 5476 3700 3 55 76 3025 5776 4180 4 65 90 4225 8100 5850 5 55 85 3025 7225 4675 6 70 87 4900 7569 6090 7 65 94 4225 8836 6110 8 70 98 4900 9604 6860 9 55 81 3025 6561 4455 10 70 91 4900 8281 6370 11 50 76 2500 5776 3800 12 55 74 3025 5476 4070 725 1011 44475 85905 61685

Selanjutnya, memasukkan angka-angka statistik dan membuat persamaan regresi. Menghitung rumus a

 30,043

Menghitung rumus b

  (∑)(∑ 

_(∑ 



_

)(∑ )(∑ )

_{) (∑ )}

_

 (

1011

)(

_{12(44475)(725)}

44475

)



(

725

)

(61685)

_

 44964225

_{533700525625}

44721625

 242600

₈₀₇₅

  (∑ ) (∑

_(∑

_

₂

_)(

)(

_∑

_)

∑

₂

)



12

(61685)(725)(1011)

_{12(44475)(725)}

_

740220732975

(5)



0,898

Menulis persamaan regresi dengan rumus

̂   

 30,0430,898

Uji Independensi

H0 = Tidak ada pengaruh skor TPA terhadap Nilai Matematika

H1 = Ada pengaruh skor TPA terhadap Nilai Matematika Menguji signifikansi

Menghitung jumlah kuadrat XY

 61685

61081,25

 603,75

Menghitung jumlah kuadrat total

 85905

_85176,75

 728,25

Menghtiung jumlah kuadrat regresi





 ()

 (0,898)(603,75)

 542,17

Menghitung jumlah kuadrat residu





   



 728,25542,17

 186,08



7245

₈₀₇₅

    ∑ ∑

_

 61685(725)(1011)

₁₂

 61685732975

₁₂

   



_

(

∑)





 85905

(

1011)

₁₂



(6)

Mencari



_{ℎ}

 29,13

Ternyata Ftable > Fhitung = 29,13 > Ftabel = 4,96 sehingga kita tolak H0 atau terima H1,

dengan kata lainada pengaruh Skor TPA terhadap hasil belajar matematika. Uji linieritas

H0 : garis regrsinya linier H1 : garis liniernya tak linier.

Untuk memudahkan perhitungan uji linieritas dipakai bantuan table berikut.

No X Y 1 50 74 2 50 76 3 55 74 4 55 85 5 55 81 6 55 76 7 65 94 8 65 90 9 65 85 10 70 91 11 70 98 12 70 87 k = 4 dan n = 12

()  {74



_{ 76}



_

(+)





}{74



 85



 81



 76





(+++)





}

{94



_{ 90}



_{ 85}



_

(++)





}{91



 98



 87





(++)





}

 (1125211250)  (25038 24964)  (24161 24120,33)

(25454 25392)

 27440,6762

 178,67



ℎ



_

_



_{/(  1)}



/

 542,14/1

_{186,08/(1211)}

 542,14

_18,608

(7)

()  



()

 186,08178,67

 7,41





_{ }

()

−



,

_−

 3,705





_{ }

()

−



,

_−

 22,33

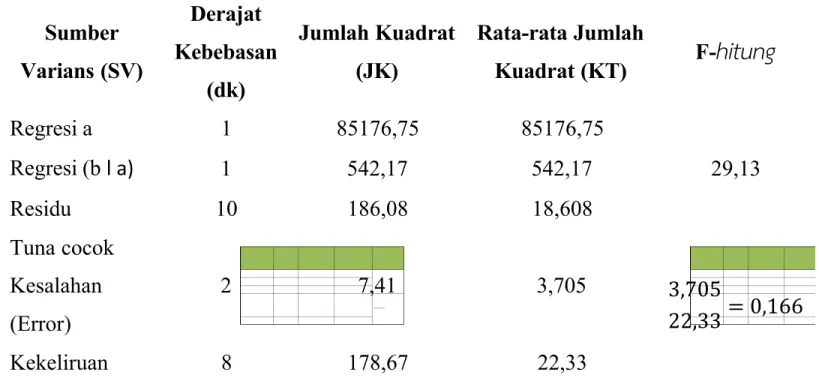
Table analisi varians untuk uji independent dan linieritas

Sumber Varians (SV) Derajat Kebebasan (dk) Jumlah Kuadrat (JK) Rata-rata Jumlah Kuadrat (KT) F-

hitung

Regresi a 1 85176,75 85176,75 29,13 Regresi (bl a) 1 542,17 542,17 Residu 10 186,08 18,608 Tuna cocok Kesalahan (Error) 2 7,41 3,705

3,705

22,33  0,166

Kekeliruan 8 178,67 22,33

Dengan taraf signifikan 5% dan dk pembilang 2, penyebut 8 didapat Ftable= 4,46. Fhitung =

0,1769 < Ftabel = 4,46. Ho diterima maka regresi linear

Untuk meramalan nilai matematika jika skor TPA sebesar 72, nilai X=72 disubstitusikan ke persamaan

̂   

 30,0430,898

 30,0430,898(72)

 94,70

Jadi ramalan nilai matematika jika skor TPA sebesar 72 adalah 94,70

Perhatikan kembali Data pertama. Akan ditentukan korelasinya dan menguji apakah ada pengaruh dengan skor TPA terhadap Nilai Matematika

 

(∑ ) (∑

)(

∑

)

(8)

 0,9966 ≅ 1

Uji Independensi

H0 = tidak ada pengaruh skor TPA terhadap hasil belajar matematika H1 = ada pengaruh skor TPA terhadap hasil belajar matematika

Berdasarkan F table dengan taraf signifikan 5% dengan dk(1,10) didapat nilai Ftable

sebesar 4,96. Fhitung = 29,13 >Ftabel = 4,96 sehingga kita tolak H0 atau terima H1, dengan

kata lain ada pengaruh Skor TPA terhadap hasil belajar matematika. Misalkan dipunyai data X dan Y berikut

X -3 -2 -1 0 1 2 3 Y 11 6 3 2 3 6 11 koefisien korelasi No X Y XY X2 Y2 1 -3 11 -33 9 121 2 -2 6 -12 4 36 3 -1 3 -3 1 9 4 0 2 0 0 4 5 1 3 3 1 9 6 2 6 12 4 36 7 3 11 33 9 121

∑

0 42 0 28 336

Karena korelasi adalah 0 , ini berarti bahwa tidak ada hubungan antara X dan Y

 

(30)(61685)(725)(1011)

 [(30)(44475725



][

(

30

)(

85905

)

 (1011)

2

]

 

(∑ )(∑

)(

∑

)

 [(∑



2

_)(

_∑

_)

2

_][((

_∑

_

2

_{) (}

_∑

_)

2

_]