E
very year, plants produce 180 billion tons of cellulose1, which has enor-mous commercial value as wood, paper and cotton. Cellulose is produced in the form of cellulose microfibrils, (semi)-crystalline aggregates of linear polymers of D-glucopyranosyl residues2–4, linked in the b-(1→4) conformation. The pattern formed by these cellulose microfibrils in the walls is cell type- and developmental stage-specific, and is a major determinant of wall properties.Cellulose synthases in the plasma membrane
Golgi vesicles carrying wall matrix material as cargo and cellulose synthases in their mem-branes, deposit these into the wall and the plasma membrane, respectively, as a result of exocytosis. Freeze-fractured plasma mem-branes show these cellulose synthases, which consist of six particles arranged in a ring5 (Fig. 1), a so-called particle rosette. These rosettes spin out the cellulose polymers6,7, which crystallize as bundles, the cellulose microfibrils. The polymerization forces cause the synthases to move in the plasma membrane. A functional model for cellulose synthase has been hypothesized (Fig. 1), in which the particles of the rosette spin out the cellulose polymers.
Types of cell wall textures
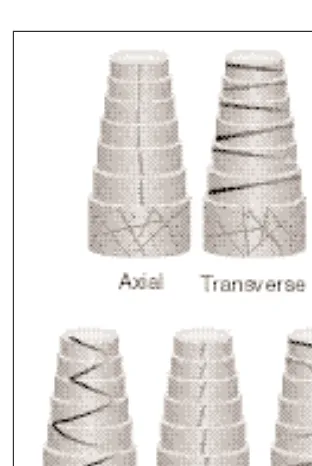
The following cell wall textures are known: axial, transverse, crossed, helical, helicoidal and random (Fig. 2). Other types of texture are de-rived from these basic types by the successive deposition of different textures.
Hypotheses for cell wall texture formation
Cortical microtubules direct the individual cellulose microfibrils during their synthesis: the textbook hypothesis
In elongating plant cells, the cortical micro-tubules, as well as the cellulose microfibrils that are being deposited, are both transverse to the elongation direction of the cells8. This cor-relation has led to the hypothesis that cortical microtubules determine the orientation of the cellulose microfibrils9by stiffening the
plasma membrane, forming corridors for the cellulose synthases locally10. The credibility of this hypothesis is based on experiments in which microtubule drugs change the orien-tation of the cellulose microfibrils11 (reviewed in Ref. 12). However, at most of the concen-trations tested, these drugs also stop unidirec-tional cell elongation. The conclusion of the drug experiments should be that cortical microtubules determine the elongation orien-tation of anisotropically expanding cells. The microtubule depolymerizing drugs in many12 (but not all13) cases also change the deposition orientation of the cellulose microfibrils. From such data it was concluded that the cortical microtubule orientation determines the depo-sition orientation of the cellulose microfibrils. However, because a second parameter appears to be changed by the drug application, it could be concluded that cell elongation orientation determines microfibril deposition orientation. Therefore the effect that cortical microtubules have on nascent cellulose microfibrils should be studied in fully expanded cells. In the fully expanded cells that have been studied, corti-cal microtubules and the most recently deposited cellulose microfibrils are not gener-ally in parallel alignment14. Mutants disturbed in either cortical microtubule alignment or cel-lulose microfibril alignment during deposition are important for determining the role that the microtubules play in microfibril deposition.
Membrane flow determines cellulose microfibril deposition orientation
Plant scientists often take the microtubule– microfibril paradigm for granted, without even studying the cellulose microfibrils properly14.
How the deposition of
cellulose microfibrils builds
cell wall architecture
Anne Mie C. Emons and Bela M. Mulder
Fig. 1. (a) Particle rosette, the cellulose synthase, in the plasma membrane of an
Equisetum hyemale root hair. The rosette has a diameter of 25 nm and consists of six particles.
In this cell type, the rosette density is relatively low, 5–15 rosettes/mm22, which agrees with the large distance between individual microfibrils in the last deposited lamella6. (b) Hypothesis for a functional model of a particle rosette (adapted from Ref. 6 ). The six pro-teins constituting the particle rosette (PR) [seen in the plasmatic-fracture (PF) face] form channels in the plasma membrane. Through these channels UDP-glucose passes while being polymerized into cellulose molecules. The terminal globule (TG) (sometimes seen in the exoplasmic (EF)-fracture face) could be the still uncrystallized cellulose polymers. Cell walls, the extracytoplasmic matrices of plant cells, consist of an ordered
However, scientists studying the cell wall have come up with several alternative hypotheses for the orientation mechanism of cellulose mirofibrils. One such alternative is the membrane flow hypothesis15. According to this hypothesis the particle rosettes are free to move in the plane of the viscous medium of the plasma membrane, and are pushed forward by synthesis and crystallization forces of the cellulose microfibril. The first part of this hypothesis is generally accepted and is also used by us. But the hypothesis also suggests that the rotation of the protoplast relative to the cell wall is the orienting principle. However, this rotation has never been observed in plants.
Cell wall texture formation is a self-assembly process like liquid crystal formation
Scientists faced with helicoidal cell walls in which the microtubules and the cellulose microfibrils did not match, realized that the helicoidal walls resemble cholesteric liquid crystals, which are known to self-assemble spontaneously16,17. However, this type of equi-librium assembly can only take place when a sufficient amount of bulk material is present. There is no evidence that this condition is ever met because we now know that cellulose microfibrils are made by plasma membrane-embedded synthase complexes in a sequential growth process18 (reviewed in Ref. 7). Moreover, from a physics point of view, there
are strong counter-arguments against this hypothesis:
• The cellulose microfibrils have dimensions (both in linear size and mass) that put them outside the colloidal domain, thus pre-cluding their equilibration on reasonable timescales19,20.
• The available space between the plasma membrane and the already extant primary cell wall is so limited that this sys-tem would be dominated by boundary effects. In most cases these effects would disturb the equilibrium configuration of the particles involved, either by promo-ting boundary layers of different structure, or anchoring defects or the imposition of antagonistic geometrical constraints21.
• The wall matrix material is probably more like a dense gel than a thermal sol-vent and would thus also be an obstacle to equlibration22.
The geometrical theory
We have proposed a geometrical model for cellulose microfibril deposition23–26 . The model quantitatively relates the deposition angle of the cellulose microfibrils (with respect to the cell axis) to:
• The density of active synthases in the plasma membrane.
• The distance between individual micro-fibrils within a wall lamella.
• The geometry of the cell.
The helicoidal wall texture of root hairs Inspiration for the geometrical model came from observations on the secondary wall of root hairs of Equisetum hyemale. A secondary wall is deposited in a cell or part of a cell that does not expand. Thus, at any stage of
Fig. 2. Basic wall textures: axial,
trans-verse, crossed, helical, helicoidal and random. Successive wall lamellae have been peeled off from top to bottom showing the random wall texture of the outermost wall at the base.
Fig. 4. (a) Shadowcast preparation of the helicoidal cell wall texture of an Equisetum hyemale root
hair showing the cellulose microfibrils in three subsequent orientations of the helicoid. A cellulose microfibril with platinum/carbon shadow deposit is 7–8 nm wide. Scale bar 5500 nm. (b) Thin sec-tion through the cell wall of a root hair of E. hyemale showing the arcs, which are visual artifacts of the helicoidal texture. A negatively stained cellulose microfibril is 3–4 nm wide. Scale bar 5500 nm
Fig. 3. Schematic showing a section
its deposition, the secondary wall is a record of the wall deposition process. The root hair is a tip-growing cell with primary wall depo-sition at the growing hair tip and secondary wall deposition in the shank of the hair. Root hairs, including those from E. hyemale, have particle rosettes, the cellulose synthases (Fig. 1), in the plasma membrane27. The E. hyemale root hairs have helicoidal cell walls and the cortical microtubules do not align with the nascent cellulose micro-fibrils28–30. A helicoidal cell wall texture (Fig. 2) consists of one microfibril thick lamellae. The orientation of the cellulose micro-fibrils in a lamella makes a constant angle with the orientation in the subsequent lamella (Fig. 3). In sections, this gives rise to the opti-cal illusion of arcs (Fig. 4).
Facts and assumptions of the geometrical model
Cellulose microfibrils are long structures. No reliable estimate of their length is available to date because microfibril ends are seen rarely in wall preparations. An individual cellulose microfibril can, therefore, con-tribute to several wall lamellae. Freeze-frac-ture images show that the cell wall is appressed against the plasma membrane. Therefore, wall deposition occurs under space-limiting conditions.
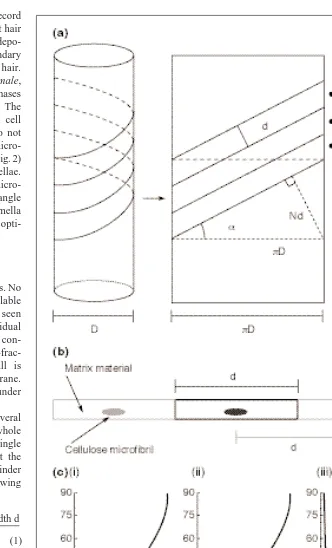
Consider a cylinder around which several tapes are being wound, such that the whole cylinder surface is covered with one single layer of tape (Fig. 5). The angle that the tape makes with the long axis of the cylinder is completely described by the following formula:
where ais the fibril angle with the cell’s long axis, D denotes the cell diameter, N the number of active synthases in the plasma membrane and d is the distance between indi-vidual microfibrils within a lamella in a plant cell (Fig. 5). Therefore, d depends on the quantity of matrix between cellulose microfibrils31and, thus, on the ratio of cellu-lose to matrix. In an E. hyemale root hair plasma membrane, this distance is ~150 nm (Ref. 6).
Because a texture can be described fully by describing the angle every cellulose micro-fibril makes with the cell axis during its depo-sition, the dependencies described in Equation 1 give us the basis of the geometrical theory of cell wall texture formation.
Now that we can describe how a synthase moves, we need to consider these questions: where and at what rate are these synthases activated? The important assumption of our model is that this activation takes place in
Fig. 5. (a) The geometrical rule for cellulose microfibril deposition follows from the notion
of winding tapes densely around a cylinder, as is illustrated by unrolling the cylinder into a planar figure, where D denotes the cell diameter, N the number of active synthases in the plasma membrane and d is the distance between individual microfibrils within a lamella in a plant cell. (b) Schematic of a cellulose microfibril surrounded by a wall matrix. The distance between two microfibrils is the width of one tape, d, used in the model. In Equisetum
hyemale, root hair plasma membrane width is ~150 nm. (c) The influence of changing
cellular parameters on the microfibril winding-angle as predicted by the geometrical theory. (i) Changing the relative number of microfibrils expressed as a fraction of the maximum Nmax5 pD/d; (ii) changing the relative effective width of the microfibrils expressed as a fraction of the maximum possible width dmax 5 pD/N; (iii) changing the relative diameter of the cell expressed in units of the minimum diameter Dmin 5 Nd/p.
number of tapes N 3tape width d p 3cell diameter D
localized mobile insertion domains. An in-sertion domain consists of a plasma membrane area in which Golgi vesicles, containing the synthases in their membranes32, are inserted into the plasma membrane (i.e. a domain where exocytosis occurs; Fig. 6). For inser-tion domain mobility, at least two experi-mentally verifiable scenarios are possible: • The Golgi bodies that produce the Golgi
vesicle-containing synthases move along the plasma membrane while inserting the vesicles.
• The Golgi bodies themselves are station-ary, but exocytosis of their vesicles is locally controlled by a time-varying concentration of an activating–inhibiting substance.
It is possible that calcium ions fulfil this role. We believe that the activation of exocytosis in root hairs involves calcium33,34, and calcium ion concentration oscillations have been observed in root hairs upon stimulation35.
Fig. 6. (a) Insertion domain. The assumption of the geometrical model is that synthase activation
takes place in localized mobile insertion domains. An insertion domain consists of a plasma mem-brane area in which Golgi vesicles, containing the synthases in their memmem-branes, are inserted into the plasma membrane. (b) This insertion domain itself, or the activation of the synthases in the domain, moves with a velocity v, while the microfibrils are spun from the synthases in the oppo-site direction. t5time; t†
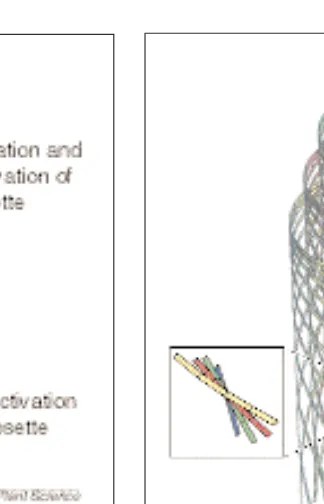
5time interval; w5the speed with which the synthase moves. Fig. 7. Visualization of the solution of our geometrical model in a helicoidal example. For clarity, only a small num-ber of cellulose microfibrils are shown, and have been drawn at a highly expanded scale. Four ‘generations’ of cellulose microfibrils are spun by syn-thases that were activated at the tip of an insertion domain at four equally spaced moments in time. The displacement of the starting points along the cell is a consequence of the motion of the inser-tion domain. Each of these generainser-tions contributes locally to a single lamella. The inset shows how the angle of depo-sition between adjacent lamellae is nearly constant, the hallmark of heli-coidal texture.
The equation that describes the evolution of active cellulose microfibril synthase density on a perfectly cylindrical cell of radius R, is given by
where w is the speed with which the synthase moves, d is the effective width of a cellulose microfibril plus adherent matrix material and N(z,t) is synthase density. wis the local rate of synthase production for which we choose the following form
if N (z,t),N* and z is
located inside an insertion domain. In all other cases w 5 0. The param-eter gcontrols the shape of the synthase production curve and lies between 0 and 1. Synthase production stops when the maximum density
is reached, which for stationary insertion domains would happen after time t*. The insertion domains are assumed to have a length l and travel at a speed v. Finally, the local rate of rosette de-activation w✝needs to be determined. This rate depends on the full evolution of the density in a time interval of length t✝(the synthase lifetime). Fortunately, the resultant equa-tions are of a type that can be readily solved with entirely classical techniques. At first sight the model appears to have many parameters, but dimensional analysis reveals that there are only four relevant ones:
• Length of the insertion domain
• Speed of the insertion domain
• Synthase lifetime ∂
∂ −
∂
∂ = −
N z t t
wd RN z t
N z t
z N z t N z t
( , )
( , ) ( , ) ( , , ) ( , , )
2p w w
†
w( , , )
( )
( , )
N z t N
t
N z t N =
− −
∗
∗1 g 1 ∗
g
N R
d ∗ = 2p
l
b n
t
g =
=
= ∗
∗ l wt
w t t
† †
The mathematical model
We can formulate a model that describes the whole process of cell wall texture formation using the elements described for the geomet-rical model. The theory describes the evolu-tion of active synthase density in the plasma membrane in space and time. If the number of active synthases present at a given location in the plasma membrane is known, the geomet-rical rule predicts the orientation of the cellu-lose microfibrils that are deposited. In a sense, each microfibril ‘records’ the motion of its synthase. The totality of all these ‘recordings’ creates the cell wall texture. To formulate such a model, attention needs to be focused on a small segment of the plasma membrane. How does the number of active synthases in the por-tion of plasma membrane belonging to this segment change in a small interval of time? There are three sources of change:
• Movement of synthases into and out of the segment.
• Activation of new synthases by an insertion domain.
• De-activation of synthases after a finite life span.
Mathematically, this yields a partial differen-tial equation for synthase density N (z,t ), which can be solved as a function of position z along the cell and time t (Box 1).
The Helicoidal solution
The solution for a helicoidal cell wall demon-strates what the geometrical model can do (Fig. 7). In such a wall, the microfibril orien-tation changes by a constant angle from one lamella to another (Fig. 2), producing a stair-case-like structure (hence the name helicoid). To obtain such a structure in which the depo-sition angle progresses from transversal (a 5 08), through axial (a 5 908) and back to trans-versal (a 5 1808), after which the cycle can repeat itself, the parameters of the model need to be precisely tuned. In our view, the geo-metrical model is sufficient to explain the most complicated cell wall texture. However, its general utility is its ability to describe the various other wall textures also seen in plant cells (Fig. 2).
Utility of the model
Numerous cell wall examples that support the geometrical model have been discussed before23–26. The important assumption to be verified is the movement or activation of the insertion domains. We have proposed two sce-narios for local, sequential exocytosis: the movement of the Golgi vesicle-producing Golgi bodies along the plasma membrane while inserting the vesicles, and the local cal-cium-induced exocytosis of vesicles along the plasma membrane. Other properties of the insertion domain that need to be determined and manipulated include its length and speed.
Furthermore, to date we know nothing about the synthase life-time. The use of mutants, GFP-technology and calcium measurements of high sensitivity along the plasma membrane of cells with known wall deposition patterns, should provide an appropriate series of experi-ments for studying the exocytosis machinery in living cells in relation to wall deposition.
Acknowledgements
We thank Allex Haasdijk for the artwork in Figures 1(b), 2, 3 and 6(a), and Ton Bisseling for critically reading the manuscript.
References
1 Englehardt, J. (1995) Sources, industrial derivatives, and commercial applications of cellulose. Carbohydr. Eur. 12, 5–14 2 Bacic, A. and Stone, B.A. (1988) Structure and
function of plant cell walls. In The Biochemistry
of Plants: A Comprehensive Treatise (Vol. 14)
(Stumpf, P.K. and Conn, E.E., eds), pp. 297–371, Academic Press
3 Reiter, W-D. (1998) The molecular analysis of cell wall components. Trends Plant Sci. 3, 27–32
4 Carpita, N.C. and Gibeaut, D.M. (1993) Structural models of primary cell walls in flowering plants: consistency of molecular structure with the physical properties of the walls during growth. Plant J. 3, 1–30 5 Mueller, S.C and Brown, R.M., Jr (1980)
Evidence for an intramembranous component associated with a cellulose microfibril-synthesizing complex in higher plants. J. Cell
Biol. 84, 315–326
6 Emons, A.M.C. (1991) The role of rosettes and terminal globules in cellulose synthesis. In Biosynthesis and Biodegradation of
Cellulose and Cellulosic Material (Weimer P.
and Haigler C.H., eds), pp. 71–98, Marcel Dekker
7 Delmer, D.P. (1999) Cellulose biosynthesis: exciting times for a difficult field of study.
Annu. Rev. Plant Physiol. Plant Mol. Biol. 50,
245–276
8 Cyr, R.J. (1994) Microtubules in plant morphogenesis: role of the cortical array. Annu.
Rev. Cell Biol. 10, 153–180
9 Heath, I.B. (1974) A unified hypothesis for the role of membrane-bound enzyme complexes and microtubules in plant cell wall synthesis.
J. Theor. Biol. 48, 445–449
10 Staehelin, L.A. and Giddings, T.H., Jr (1982) Membrane-mediated control of cell wall microfibrillar order. In Developmental Order: Its
Origin and Regulation (Subtelny, S. and Green,
P.B., eds), pp. 133–147, Alan Liss, New York, USA
11 Green, P. (1962) Mechanism for plant cellular morphogenesis. Science 138, 1404–1405 12 Wymer, C. and Lloyd, C. (1996) Dynamic
microtubules: implications for cell wall patterns.
Trends Plant Sci. 7, 222–228
13 Emons, A.M.C. et al. (1990) The effect of colchicine on microtubules and microfibrils in root hairs. Acta Bot. Neerl. 39, 19–27
14 Emons, A.M.C. et al. (1992) Do microtubules control plant cell wall microfibrils? Physiol.
Plant. 84, 486–493
15 Mueller, S.C. and Brown, R.M., Jr (1982) The control of microfibril deposition in the cell wall of higher plants. I. Can directed membrane flow orient cellulose microfibrils? Indirect evidence from freeze-fractured plasma membranes of maize and pine seedlings. Planta 154, 501–515
16 Neville, A.C. (1985) Molecular and mechanical aspects of helicoid development in plant cell walls. BioEssays 3, 4–8
17 Vian, B. et al. (1994) Cholesteric-like crystal analogs in glucuronoxylan-rich cell wall composites: experimental approach to a cellular re-asssembly from native cellulosic suspension.
Protoplasma 180, 70–81
18 Arioli, T. et al. (1998) Molecular analysis of cellulose synthesis in Arabidopsis. Science 279, 717–720
19 Fennell Evans, D. and Wennerstrom, H. (1999)
The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet (Advances in Interfacial Engineering Series),
John Wiley & Sons
20 de Gennes , P.G. (1979) Scaling Concepts in
Polymer Physics, Cornell University Press,
Ithaca, NY, USA
21 Crawford, G.P. and Zumer, S., eds (1996) Liquid
Crystals in Complex Geometries, Taylor &
Francis
22 Tong, P. et al. (1997) Sedimentation of colloidal particles through a polymer solution. Phys. Rev.
Lett. 79, 2363–2366
23 Emons, A.M.C. (1994) Winding threads around plant cells: a geometrical model for microfibril deposition. Plant Cell Eviron. 17, 3–14
24 Emons, A.M.C. and Kieft, H. (1994) Winding cells around plant cells: applications of the geometrical model for microfibril deposition.
Protoplasma 180, 59–69
25 Emons, A.M.C. and Mulder, B.M. (1997) Plant cell wall architecture. Comments Theor. Biol. 4, 115–131
26 Emons, A.M.C. and Mulder, B.M. (1998) The making of the architecture of the plant cell wall: how cells exploit geometry.
Proc. Natl. Acad. Sci. U. S. A. 95,
7215–7219
27 Emons, A.M.C. (1985) Plasma-membrane rosettes in root hairs of Equisetum hyemale.
Planta 163, 350–359
28 Emons, A.M.C. (1982) Microtubules do not control microfibril orientation in a helicoidal cell wall. Protoplasma 113, 85–87
Equisetum hyemale. Protoplasma 117,
68–81
30 Emons, A.M.C. (1989) Helicoidal microfibril deposition in a tip-growing cell and microtubules alignment during tip morphogenesis: a dry-cleaving and freeze-substitution study. Can. J. Bot. 67, 2401–2408
31 McCann, M.C. and Roberts, K. (1991) Architecture of the primary cell wall. In
The Cytoskeletal Basis of Plant Growth and Form (Lloyd, C.W., ed.), pp. 109–129, Academic
Press
32 Haigler, C.H. and Brown, R.M. (1986) Transport of rosettes from the Golgi apparatus to plasma membrane in isolated mesophyll cells of
Zinnia elegans during differentiation to tracheary
elements in suspension culture. Protoplasma 134, 111–120
33 Felle, H.H. and Hepler, P.K. (1997) The cytosolic Ca21concentration gradient of Sinapis alba root hairs as revealed by Ca21-selective
microelectrode tests and fura-dextran ratio imaging. Plant Phys. 114, 39–45 34 De Ruijter, C.A. et al. (1998)
Lipochito-oligosaccharides re-initiate root hair tip growth in Vicia sativa with high calcium and spectrin-like antigen at the tip. Plant J. 13, 341–350
35 Ehrhardt, D.W. et al. (1996) Calcium spiking in plant root hairs responding to Rhizobium nodulation signals. Cell 85, 573–681
Anne Mie C. Emons is at the Laboratory of Experimental Plant Morphology and Cell Biology, Dept of Plant Sciences, Wageningen University, Arboretumlaan 4, 6703 BD Wageningen, The Netherlands (tel 131 317 484329;
fax 131 317 485005;
e-mail [email protected]); Bela M. Mulder is at the Condensed Matter Division of the FOM Institute for Atomic and Molecular Physics, Kruislaan 407, 1098 SJ Amsterdam, The Netherlands
(tel 131 20 6081231; fax 131 20 6684106; e-mail [email protected]).
L
ight profoundly influences plant development and allows photosyn-thesis to occur, but it also represents a tremendous risk. Photo-oxidative damage initiated by excited state photosensitizing molecules, such as chlorophylls and their biosynthetic precursors, can be lethal. Angiosperms that germinate in darkness in the soil enter the seedling developmental pro-gram known as skotomorphogenesis (Fig. 1). However, such seedlings must be prepared for a subsequent light-triggered switch to photomorphogenesis. Upon illumination, the leaves of etiolated angiosperms synthesize and accumulate large quantities ofchloro-phylls a and b. Seedlings are particularly sus-ceptible to photo-oxidative damage during this transition to photoautotrophy.
The presence or absence of light dramatically influences plastid development. Dark-grown angiosperm seedlings contain an achlorophyl-lous plastid type known as the etioplast, which is transformed into a photosynthetically com-petent chloroplast during photomorphogenesis1. The etioplast is defined by the presence of two types of internal membranes, the lattice-like prolamellar body, which is composed of inter-connected tubules, and the unstacked prothyl-akoids. Etioplasts characteristically accumulate the chlorophyll precursor protochlorophyllide
(Pchlide), more specifically protochlorophyllide a (Pchlide a)2–4. Illumination of etioplasts initi-ates the dispersal of the prolamellar body and the formation of thylakoid membranes con-taining the pigment–protein complexes of the photosynthetic apparatus.
In this context, recent in vitro reconstitution experiments have been interpreted as providing evidence for a novel light-harvesting Pchlide a/b-binding protein complex5, termed LHPP by analogy to the ubiquitous light-harvesting chlorophyll a/b-binding proteins (LHCP) of green plants. LHPP is speculated to: • Serve as the central structural determinant
of the prolamellar body in etioplasts. • Be essential for the establishment of the
photosynthetic apparatus.
• Confer photoprotection on greening seedlings by dissipating excess light energy, thereby minimizing Pchlide-induced photo-oxidative damage. On the one hand, if they are correct, these hypotheses would have a major impact on our understanding of the seedling transition from skotomorphogenesis to photomorphogenesis. On the other hand, to date there are no in vivo data that directly support the existence of an LHPP complex6. Here, we critically analyse the LHPP model in light of the current litera-ture on the properties of etioplast membranes, pigment–protein complexes and pigments.
Roles of the light-dependent PORA and PORB proteins in etioplast formation and photo-oxidative protection
The presence of the prolamellar body and the accumulation of Pchlide a in etioplasts are known to correlate with large quantities of the strictly light-dependent NADPH:protochloro-phyllide oxidoreductase (POR; 1.3.1.33)1,7–9. This nuclear-encoded but plastid-localized protein is unusual in that it mediates the only