Module 7 Algoritma & Struktur Data (Binary Tree)

Binary Tree

Teknik Informatika - Universitas Muhammadiyah Malang (UMM) Tahun Akademik 2010-2011

Sub Topik

• _{Penjelasan Tree}

• _{Istilah pada tree}

• _{Binary Tree}

• _{Jenis Binary Tree}

Real World

root

branches

Computer Scientist’s View

branches

leaves

root

Definisi

• _{Kumpulan node yang saling terhubung}

secara hirarki.

• _{Hirarki = bertingkat.}

• _{Tiap node dapat berisi data dan link}

(penghubung) ke node lainnya

• _{Tiap node memiliki satu induk, kecuali}

node root (akar) yang tidak memiliki induk.

• _{Tiap node dapat memiliki anak dalam}

Linked list dan Tree

• _{Linked list}  linear/serial data

– _{Contoh : nama-nama mahasiswa dalam}

satu kelas.

• _Tree  non linear/hierachically data

– _{Contoh : tingkatan pegawai dalam}

Contoh Tree

• _{Mis. : Struktur organisasi sebuah}

Contoh Tree

Contoh Tree

Tree (Pohon)

• _{Root adalah node yang memiliki}

hirarki tertinggi.

• _{Subtree (pohon anak) adalah}

Root and Subtrees

Object

Number Throwable OutputStream

Integer Double Exception FileOutputStream

RuntimeException

Tree (Pohon)

• _{Level adalah posisi hirarki dari}

sebuah node. Untuk root bisa diberikan level 0 atau 1.

• _{Leaf (Daun) adalah node yang tidak}

memiliki anak atau node yang

berada pada hirarki paling bawah.

• _{Height (tinggi)/depth adalah jumlah}

Leaves

Object

Number Throwable OutputStream

Integer Double Exception FileOutputStream

Node Degree

Object

Number Throwable OutputStream

Integer Double Exception FileOutputStream

RuntimeException

3

2 1 1

0 0 1 0

Level

Level 3

Object

Number Throwable OutputStream

Integer Double Exception FileOutputStream

RuntimeException

Level 4

Level 2 Level

1

Level 3

Level 4

17

Contoh Tree (Pohon)

Level 0

Level 1

Level 2

Level 3

Latihan

Ancestor (F)?

Descendant (B)? Parent (I)?

Child (C)? Sibling (G)? Size?

Height? Root? Leaf?

Tree (Pohon)

• _Dimana,

Ancestor (F) = C,A

Descendant (B) = D,E Parent (I) = H

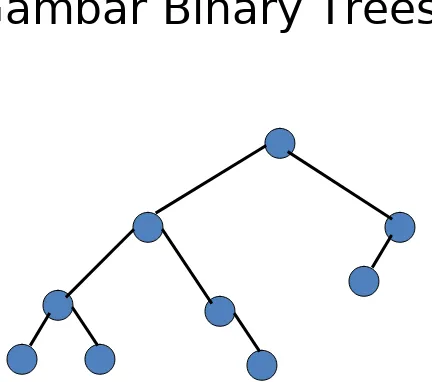
Binary Tree

• _{Tiap node pada binary tree hanya}

boleh memiliki paling banyak dua child.

• _{Sehingga hanya ada dua subtree pada}

Tree dan Binary Tree

• _{Pada binary tree nilai degree tidak}

lebih dari 2, sedangkan pada tree tidak terbatas.

• _{Sub tree pada binary harus terurut}

Jenis Binary Tree

• _{Berdasarkan subtree binary tree}

dibedakan menjadi 4 jenis:

– _{Full Binary Tree}

– _{Complete Binary Tree}

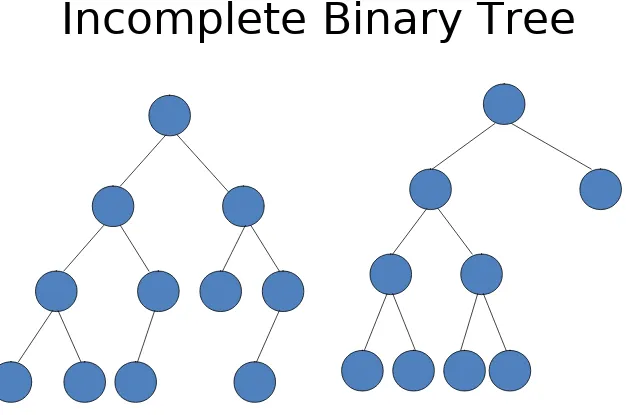
– _{Incomplete Binary Tree (Unbalanced}

Tree)

Jenis Tree

(Full Binary Tree)

• _{Semua node (kecuali leaf) memiliki nol}

atau 2 anak dan tiap subtree memiliki panjang path yang sama.

Jenis Tree

(Complete Binary Tree)

• _{Seluruh node sebelah kiri terisi}

Complete Binary Tree

H

D K

B F J L

Incomplete Binary Tree

Jenis Tree

(Skewed Binary Tree)

• _{Binary tree yang semua nodenya}

(kecuali leaf) hanya memiliki satu anak.

• _{Disebut juga minimum binary tree.}

Binary Tree

Representation

• _{Array representation}

ADT BinaryTree

public interface BinaryTree {

public boolean isEmpty(); public Object root();

public void makeTree(Object root, Object left, Object right);

public BinaryTree removeLeftSubtree(); public BinaryTree removeRightSubtree(); public void preOrder(Method visit);

Struktur Data - Tree 36

Akses Elemen

• _{Posisi node dapat ditentukan}

berdasarkan rumus berikut :

– _{Anak kiri dari node i berada pada indeks}

: 2*i+1

– _{Anak kanan dari node i berada pada}

Class BinaryTreeNode

class BinaryTreeNode {

Object element;

BinaryTreeNode leftChild; // left subtree

BinaryTreeNode rightChild;// right subtree

// constructors and any other methods come here

Definisi

• _{Penelusuran seluruh node pada}

binary tree.

• _{Metode :}

– _Preorder

– _Inorder

– _Postorder

Preorder Traversal

PreOrder Traversal

• _{Preorder traversal}

1. Cetak data pada root

2. Secara rekursif mencetak seluruh data pada subpohon kiri

Preorder Example (visit =

print)

Preorder Example (visit =

print)

Preorder Of Expression Tree

Gives prefix form of expression!

Inorder Traversal

InOrder Traversal

• _{Inorder traversal}

1.Secara rekursif mencetak seluruh data pada subpohon kiri

2.Cetak data pada root

Inorder Example (visit =

print)

a

b c

Inorder Example (visit =

print)

Inorder Of Expression Tree

Gives infix form of expression (sans parentheses)!

e

Postorder Traversal

Postorder Traversal

• _{Postorder traversal}

1.Secara rekursif mencetak seluruh data pada subpohon kiri

2.Secara rekursif mencetak seluruh data pada subpohon kanan

Postorder Example (visit =

print)

a

b c

Postorder Example (visit =

print)

Postorder Of Expression

Tree

Gives postfix form of expression!

Traversal Applications

• Determine height.

Latihan

• _{Telusuri pohon biner berikut dengan}

PreOrder, PostOrder,

InOrder

• Pre-order :

– _{Node, left, right}

– _{Ekspresi Prefix : ++a*bc*+*defg}

• _{Post-order :}

– _{Node, left, right}

– _{Ekspresi Postfix : abc*+de*f+g*+}

• _{In-order :}

– _{Node, left, right}

Pustaka

• _{Sartaj Sahni , “Data Structures &}

Algorithms”, Presentation L20-24.

• _{Mitchell Waite, “Data Structures &}