MATEMATIKA DASAR 2A
Modul 11: Bidang Singgung, Nilai Hampiran, Nilai Maksimum dan Nilai Minimum Fungsi Dua Variabel
Tim Matematika
TAHAP PERSIAPAN BERSAMA
INSTITUT TEKNOLOGI SUMATERA - LAMPUNG SELATAN
16 JANUARI 2019
PENDAHULUAN 1
Pada modul ini akan dijelaskan mengenai Bidang Singgung, Nilai Hampiran, Nilai Ekstrim (Nilai Maksimum dan Nilai Minimum). Suatu bidang yang menyinggung suatu permukaan 𝑧 = 𝑓(𝑥, 𝑦) di titik (𝑥0, 𝑦0, 𝑧0) dengan 𝑧0 = 𝑓(𝑥0, 𝑦0) dinamakan sebagai bidang singgung. Dengan menggunakan
bidang singgung ini dapat ditentukan nilai hampiran dari suatu nilai fungsi 𝑓(𝑥, 𝑦) di suatu titik (𝑥0, 𝑦0). Selain itu, dengan menggunakan bidang singgung dapat ditentukan nilai ekstrim (nilai maksimum atau nilai minimum) dari suatu fungsi dua variabel.
Setelah mempelajari modul ini diharapkan mahasiswa mampu 1. Menentukan bidang singgung dari suatu fungsi dua variabel 2. Menentukan nilai hampiran dari suatu fungsi dua variabel
3. Menentukan nilai ekstrim dari suatu fungsi dua variabel dan menentukan jenisnya
MATERI PERKULIAHAN 2
Bidang Singgung
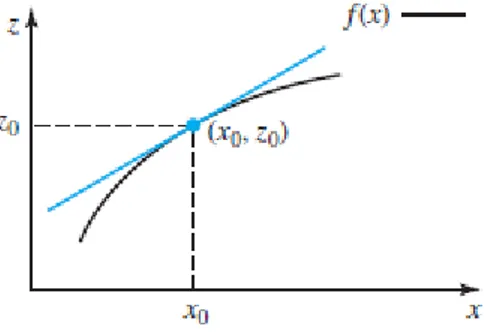
Misal fungsi 𝑓(𝑥) mempunyai turunan di titik 𝑥 = 𝑥0, maka persamaan garis singgung dari kurva 𝑧 = 𝑓(𝑥) di titik (𝑥0, 𝑧0) dengan 𝑧0 = 𝑓(𝑥0) adalah sebagai berikut, 𝑧 − 𝑧0 = 𝑓′(𝑥0)(𝑥 − 𝑥0). Sebagai ilustrasi dapat dilihat pada Gambar 1.
Gambar 1 Kurva dari 𝑧 = 𝑓(𝑥) dan garis singgungnya di titik (𝑥0, 𝑧0)
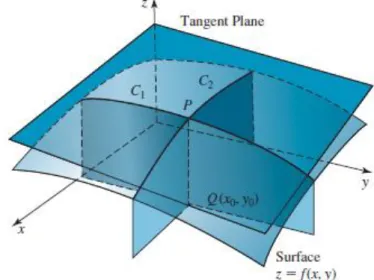
Konsep ini dapat diperluas pada fungsi dua variabel, dan didapatkan suatu bidang singgung. Sebagai ilustrasi dapat dilihat pada Gambar 2. Misal 𝑧 = 𝑓(𝑥, 𝑦) merupakan fungsi dua variabel, pada modul sebelumnya
dijelaskan bahwa turunan parsial 𝜕𝑓
𝜕𝑥 dan 𝜕𝑓
𝜕𝑦 yang dihitung pada titik (𝑥0, 𝑦0) merupakan kemiringan garis singgung dari kurva perpotongan permukaan 𝑧 = 𝑓(𝑥, 𝑦) dan bidang 𝑦 = 𝑦0 (kemiringan garis singgung dalam arah sumbu- 𝑥) atau bidang 𝑥 = 𝑥0 (kemiringan garis singgung dalam arah sumbu-𝑦) di titik tersebut.
Persamaan bidang singgung di titik (𝑥0, 𝑦0, 𝑧0) pada permukaan 𝑧 = 𝑓(𝑥, 𝑦) dapat ditentukan berdasarkan dua garis singgung dalam arah sumbu- 𝑥 dan garis singgung dalam arah sumbu-𝑦. Misal suatu kurva yang diperoleh dari perpotongan antara permukaan 𝑧 = 𝑓(𝑥, 𝑦) dan bidang yang sejajar dengan bidang-𝑦𝑧 dan melalui titik (𝑥0, 𝑦0, 𝑧0) yaitu, bidang 𝑥 = 𝑥0, kita notasikan sebagai 𝐶1. Garis singgung di titik (𝑥0, 𝑦0, 𝑧0) termuat di dalam
bidang singgung (Perhatikan Gambar 2). Demikian juga, jika dimisalkan suatu kurva yang diperoleh dari perpotongan antara permukaan 𝑧 = 𝑓(𝑥, 𝑦) dan
3
bidang yang sejajar dengan bidang-𝑥𝑧 dan melalui titik (𝑥0, 𝑦0, 𝑧0) yaitu, bidang 𝑦 = 𝑦0, kita notasikan sebagai 𝐶2. Garis singgung di titik (𝑥0, 𝑦0, 𝑧0) ini juga termuat di dalam bidang singgung (Perhatikan Gambar 2).
Gambar 2 Permukaan dari 𝑧 = 𝑓(𝑥, 𝑦) dengan bidang singgungnya di titik 𝑃 = (𝑥0, 𝑦0, 𝑧0)
Bidang singgung ini merupakan bidang dengan persamaan sebagai berikut
𝑧 − 𝑧0 = 𝐴(𝑥 − 𝑥0) + 𝐵(𝑦 − 𝑦0) (1)
Dengan menggunakan kurva 𝐶1 dan 𝐶2, dapat ditentukan nilai konstan dari 𝐴 dan 𝐵. Kurva 𝐶1 memenuhi persamaan 𝑧 = 𝑓(𝑥0, 𝑦), dan garis singgung dari 𝐶1 di titik (𝑥0, 𝑦0, 𝑧0) memenuhi persamaan sebagai berikut,
𝑧 − 𝑧0 = 𝜕𝑓(𝑥0,𝑦0)
𝜕𝑦 (𝑦 − 𝑦0) (2)
Garis singgung di titik (𝑥0, 𝑦0, 𝑧0) termuat dalam bidang singgung di titik
(𝑥0, 𝑦0, 𝑧0). Sehingga persamaan garis singgung dari 𝐶1 di titik (𝑥0, 𝑦0, 𝑧0) dapat juga diperoleh dengan menetapkan 𝑥 = 𝑥0 pada Persamaan (1), dan
didapatkan bahwa,
𝑧 − 𝑧0 = 𝐴(0) + 𝐵(𝑦 − 𝑦0) = 𝐵(𝑦 − 𝑦0)
Bandingkan dengan yang didapat pada Persamaan (2) diperoleh 𝐵 =𝜕𝑓(𝑥0,𝑦0)
𝜕𝑦
Dengan cara yang sama jika digunakan kurva 𝐶2, maka akan didapatkan bahwa
𝐴 =𝜕𝑓(𝑥0,𝑦0)
4
𝜕𝑥
Berdasarkan penjelasan di atas didapatkan suatu hasil yaitu persamaan bidang singgung sebagai berikut,
Jika bidang singgung pada permukaan 𝑧 = 𝑓(𝑥, 𝑦) di titik (𝑥0, 𝑦0, 𝑧0) dengan 𝑧0 = 𝑓(𝑥0, 𝑦0) ada, maka bidang singgung tersebut mempunyai persamaan
𝑧 − 𝑧0 = 𝜕𝑓(𝑥0,𝑦0)
𝜕𝑥 (𝑥 − 𝑥0) +𝜕𝑓(𝑥𝜕𝑦0,𝑦0)(𝑦 − 𝑦0)
Contoh:
Tentukanlah persamaan bidang singgung dari 𝑧 = 𝑓(𝑥, 𝑦) = 4𝑥2+ 𝑦2 di titik (1,2,8).
Jawab:
Pertama-tama periksa terlebih dahulu apakah titik (1,2,8) termuat pada permukaan 𝑧 = 𝑓(𝑥, 𝑦).
Karena 8 = 𝑓(1,2), maka titik (1,2,8) termuat pada permukaan 𝑧 = 𝑓(𝑥, 𝑦).
Kemudian tentukan turunan parsial terhadap 𝑥 dan turunan parsial terhadap 𝑦, yaitu didapatkan bahwa 𝜕𝑓
𝜕𝑥 = 8𝑥 dan 𝜕𝑓
𝜕𝑦= 2𝑦. sehingga didapatkan 𝜕𝑓(1,2)
𝜕𝑥 = 8(1) = 8 dan 𝜕𝑓(1,2)
𝜕𝑦 = 2(2) = 4. Dengan demikian didapatkan persamaan bidang singgung dari 𝑓(𝑥, 𝑦) di titik (1,2,8) sebagai berikut,
𝑧 − 8 = 8(𝑥 − 1) + 4(𝑦 − 2)
Atau dapat ditulis menjadi sebagai berikut, 𝑧 − 8 = 8𝑥 − 8 + 4𝑦 − 8
8𝑥 + 4𝑦 − 𝑧 = 8
Nilai Hampiran
Dengan menggunakan persamaan bidang singgung, dapat ditentukan suatu hampiran dari nilai fungsi 𝑓(𝑥, 𝑦) di suatu titik (𝑥0, 𝑦0).
5
Definisi:
Misal fungsi 𝑓(𝑥, 𝑦) mempunyai turunan parsial di titik (𝑥0, 𝑦0), pelinieran dari 𝑓(𝑥, 𝑦) di titik (𝑥0, 𝑦0) adalah fungsi
𝐿(𝑥, 𝑦) = 𝑓(𝑥0, 𝑦0) +𝜕𝑓(𝑥𝜕𝑥0,𝑦0)(𝑥 − 𝑥0) +𝜕𝑓(𝑥𝜕𝑦0,𝑦0)(𝑦 − 𝑦0)
𝐿(𝑥, 𝑦) merupakan nilai hampiran dari 𝑓(𝑥, 𝑦) di sekitaran titik (𝑥0, 𝑦0), atau ditulis sebagai 𝑓(𝑥, 𝑦) ≈ 𝐿(𝑥, 𝑦) yaitu fungsi hampiran linier standar atau hampiran bidang singgung dari 𝑓(𝑥, 𝑦) di titik (𝑥0, 𝑦0)
Contoh:
Tentukan bentuk pelinieran dari 𝑓(𝑥, 𝑦) = ln(𝑥 − 2𝑦2) di titik (3,1).
Kemudian gunakan bentuk pelinieran tersebut untuk menghitung nilai hampiran dari 𝑓(3.05,0.95).
Jawab:
Bentuk pelinieran dari 𝑓(𝑥, 𝑦) di titik (3,1) adalah sebagai berikut, 𝐿(𝑥, 𝑦) = 𝑓(3,1) +𝜕𝑓(3,1)
𝜕𝑥 (𝑥 − 3) +𝜕𝑓(3,1)
𝜕𝑦 (𝑦 − 1) Didapatkan bahwa 𝑓(3,1) = ln((3) − 2(1)2) = ln(1) = 0.
Dan 𝜕𝑓(𝑥,𝑦)
𝜕𝑥 = 1
𝑥−2𝑦2 dan 𝜕𝑓(𝑥,𝑦)
𝜕𝑦 = −4𝑦
𝑥−2𝑦2, sehingga didapatkan 𝜕𝑓(3,1)
𝜕𝑥 =
1
(3)−2(1)2 = 1 dan 𝜕𝑓(3,1)
𝜕𝑦 = −4(1)
(3)−2(1)2 = −4. Dengan demikian
𝐿(𝑥, 𝑦) = 0 + (1)(𝑥 − 3) + (−4)(𝑦 − 1) = 𝑥 − 3 − 4𝑦 + 4 = 𝑥 − 4𝑦 + 1 dan didapatkan bahwa 𝑓(3.05,0.95) ≈ 𝐿(3.05,0.95) = (3.05) − 4(0.95) + 1 = 0.25.
Nilai Maksimum dan Minimum
Pada Matematika Dasar 1A dijelaskan mengenai nilai ekstrim
(maksimum dan miminum) lokal pada fungsi satu variabel. Nilai ekstrim dapat diperluas juga ke dalam fungsi dua variabel. Berikut diberikan definisi formal dari nilai ekstrim lokal pada fungsi dua variabel.
Definisi:
Fungsi 𝑓(𝑥, 𝑦) yang terdefinisi pada domain 𝐷𝑓 mempunyai nilai maksimum lokal di titik (𝑥0, 𝑦0) jika ada 𝛿 > 0 sehingga berlaku
6
𝑓(𝑥, 𝑦) ≤ 𝑓(𝑥0, 𝑦0) untuk setiap (𝑥, 𝑦) ∈ 𝐵𝛿(𝑥0, 𝑦0) ∩ 𝐷𝑓
Fungsi 𝑓(𝑥, 𝑦) yang terdefinisi pada domain 𝐷𝑓 mempunyai nilai minimum lokal di titik (𝑥0, 𝑦0) jika ada 𝛿 > 0 sehingga berlaku
𝑓(𝑥, 𝑦) ≥ 𝑓(𝑥0, 𝑦0) untuk setiap (𝑥, 𝑦) ∈ 𝐵𝛿(𝑥0, 𝑦0) ∩ 𝐷𝑓
𝐵𝛿(𝑥0, 𝑦0) merupakan cakram buka dengan jari-jari 𝛿 dan titik pusat (𝑥0, 𝑦0), yaitu himpunan semua titik (𝑥, 𝑦) pada cakram buka tersebut, dalam notasi himpunan dapat ditulis sebagai berikut
𝐵𝛿(𝑥0, 𝑦0) = {(𝑥, 𝑦)|√(𝑥 − 𝑥0)2 + (𝑦 − 𝑦0)2 < 𝛿}
Nilai maksimum lokal merupakan nilai dari 𝑧 = 𝑓(𝑥, 𝑦) yang tertinggi dari semua titik di sekitarannya, dan nilai minimum lokal merupakan nilai dari 𝑧 = 𝑓(𝑥, 𝑦) yang terendah dari semua titik di sekitarannya. Jika pertidaksamaan di atas berlaku untuk semua (𝑥, 𝑦) ∈ 𝐷𝑓 maka 𝑧 = 𝑓(𝑥, 𝑦) merupakan nilai
maksimum global (minimum global). Gambar 3 memperlihatkan bahwa 𝑓(𝑥, 𝑦) memiliki nilai maksimum lokal di titik (0,0).
Gambar 3
Pertanyaannya sekarang, bagaimana cara menentukan eksrim lokal?
Perhatikan bahwa bidang singgung pada ekstrim lokal adalah bidang yang sejajar dengan bidang-𝑥𝑦. Sehingga persamaan dari bidang singgung pada
7
ekstrim lokal tersebut adalah 𝑧 = 𝑓(𝑥0, 𝑦0). Jika disubstitusikan ke persamaan bidang singgungnya, yaitu
𝑧 − 𝑧0 = 𝜕𝑓(𝑥0,𝑦0)
𝜕𝑥 (𝑥 − 𝑥0) +𝜕𝑓(𝑥𝜕𝑥0,𝑦0)(𝑦 − 𝑦0) maka didapatkan bahwa 𝜕𝑓(𝑥0,𝑦0)
𝜕𝑥 = 0 dan 𝜕𝑓(𝑥0,𝑦0)
𝜕𝑥 = 0. Dengan kata lain
∇𝑓(𝑥0, 𝑦0) = [0
0]. Dengan demikian dapat disimpulkan bahwa
jika 𝑓(𝑥, 𝑦) mempunyai nilai ekstrim lokal di titik (𝑥0, 𝑦0) dan 𝑓(𝑥, 𝑦) mempunyai turunan parsial di titik (𝑥0, 𝑦0), maka ∇𝑓(𝑥0, 𝑦0) = [0
0].
Titik (𝑥0, 𝑦0) tersebut dinamakan sebagai titik kritis. Titik dimana 𝑓(𝑥, 𝑦) tidak mempunyai turunan parsial juga merupakan titik kritis. Titik-titik kritis ini merupakan titik kemungkinan tejadinya nilai ekstrim. Untuk selanjutnya perlu pemeriksaan lebih lanjut apakah titik kritis tersebut merupakan titik terjadinya ekstrim lokal atau bukan.
Contoh:
Tentukan semua titik kritis dari 𝑓(𝑥, 𝑦) = 𝑥2+ 𝑦2+ 𝑥𝑦 Jawab:
Karena 𝑓(𝑥, 𝑦) mempunyai turunan parsial di 𝑅2, maka titik kritis hanya terjadi pada titik (𝑥, 𝑦) sehingga berlaku ∇𝑓(𝑥, 𝑦) = [0
0].
∇𝑓(𝑥, 𝑦) = [2𝑥 + 𝑦 2𝑦 + 𝑥] = [0
0]
Atau dapat ditulis dalam bentuk sistem persamaan linier sebagai berikut 2𝑥 + 𝑦 = 0
2𝑦 + 𝑥 = 0
Berdasarkan persamaan yang pertama didapatkan bahwa 𝑦 = −2𝑥, jika kita substitusikan pada persamaan kedua didapatkan bahwa
2(−2𝑥) + 𝑥 = 0 atau −4𝑥 + 𝑥 = 0 atau −3𝑥 = 0 atau 𝑥 = 0.
Jika disubstitusikan ke persamaan pertama maka didapatkan bahwa 2(0) + 𝑦 = 0 atau 𝑦 = 0. Dengan demikian sistem persamaa tersebut mempunyai solusi (0,0). Sehingga dapat disimpulkan bahwa titik kritis dari 𝑓(𝑥, 𝑦) yaitu titik (0,0).
8
Misal turunan parsial kedua dari 𝑓(𝑥, 𝑦) kontinu pada suatu cakram dengan pusat (𝑥0, 𝑦0) dan ∇𝑓(𝑥0, 𝑦0) = [0
0]. Didefinisikan 𝐷 = 𝑓𝑥𝑥(𝑥0, 𝑦0)𝑓𝑦𝑦(𝑥0, 𝑦0) − (𝑓𝑥𝑦(𝑥0, 𝑦0))2
1. Jika 𝐷 > 0 dan 𝑓𝑥𝑥(𝑥0, 𝑦0) > 0, maka 𝑓 memiliki nilai minimum lokal di titik (𝑥0, 𝑦0).
2. Jika 𝐷 > 0 dan 𝑓𝑥𝑥(𝑥0, 𝑦0) < 0, maka 𝑓 memiliki nilai maksimum lokal di titik (𝑥0, 𝑦0).
3. Jika 𝐷 < 0, maka 𝑓 tidak memiliki nilai ekstrim lokal di titik (𝑥0, 𝑦0). Titik (𝑥0, 𝑦0) yang demikian disebut sebagai titik pelana.
Contoh:
Tentukan apakah titik kritis (0,0) dari 𝑓(𝑥, 𝑦) = 𝑥2+ 𝑦2+ 𝑥𝑦 merupakan titik terjadinya nilai maksimum lokal atau nilai minimum lokal.
Jawab:
Diketahui bahwa 𝑓(𝑥, 𝑦) = 𝑥2+ 𝑦2+ 𝑥𝑦, sehingga didapatkan bahwa 𝑓𝑥(𝑥, 𝑦) = 2𝑥 + 𝑦, 𝑓𝑦(𝑥, 𝑦) = 2𝑦 + 𝑥, 𝑓𝑥𝑥(𝑥, 𝑦) = 2, 𝑓𝑦𝑦(𝑥, 𝑦) = 2, dan 𝑓𝑥𝑦(𝑥, 𝑦) = 1. Dengan demikian didapatkan bahwa
𝑓𝑥𝑥(0,0) = 2, 𝑓𝑦𝑦(0,0) = 2, dan 𝑓𝑥𝑦(0,0) = 1 𝐷 = (2)(2) − (1)2 = 3 > 0
Karena 𝐷 > 0 dan 𝑓𝑥𝑥(0,0) > 0 dapat disimpulkan bahwa (0,0) merupakan titik terjadinya nilai minimum lokal.
Contoh:
Tentukan semua nilai ekstrim dari 𝑓(𝑥, 𝑦) = 3𝑥𝑦 − 𝑥3− 𝑦3 dan tentukan jenisnya apakah nilai maksimum lokal atau nilai minimum lokal.
Jawab:
Diketahui bahwa 𝑓(𝑥, 𝑦) = 3𝑥𝑦 − 𝑥3 − 𝑦3 mempunyai turunan parsial pada domain naturalnya. Maka titik kritis hanya terjadi pada titik (𝑥, 𝑦) sehingga berlaku ∇𝑓(𝑥, 𝑦) = [0
0].
∇𝑓(𝑥, 𝑦) = [3𝑦 − 3𝑥2
9
3𝑥 − 3𝑦2] = [0 0]
Atau dapat ditulis dalam bentuk sistem persamaan linier sebagai berikut 3𝑦 − 3𝑥2 = 0
3𝑥 − 3𝑦2 = 0
Sistem persamaan tersebut mempunyai solusi (0,0) dan (1,1).
Selain itu didapatkan bahwa,
𝑓𝑥𝑥(𝑥, 𝑦) = −6𝑥, 𝑓𝑦𝑦(𝑥, 𝑦) = −6𝑦, dan 𝑓𝑥𝑦(𝑥, 𝑦) = 3. Dengan demikian untuk (𝑥, 𝑦) = (0,0) didapatkan bahwa
𝐷 = (0)(0) − (9)2 = −9 < 0
Karena 𝐷 < 0, maka dapat disimpulkan bahwa (0,0) merupakan titik pelana.
Dan untuk (𝑥, 𝑦) = (1,1) didapatkan bahwa
𝑓𝑥𝑥(1,1) = −6, 𝑓𝑦𝑦(1,1) = −6, 𝑓𝑥𝑦(1,1) = 3, dan 𝐷 = (−6)(−6) − (9)2 = 36 − 9 = 27 > 0
Karena 𝐷 > 0 dan 𝑓𝑥𝑥(1,1) = −6 < 0, maka dapat disimpulkan bahwa (1,1) merupakan titik terjadinya nilai maksimum lokal, yaitu 𝑓(1,1) = 3(1)(1) − (1)3− (1)3 = 1 merupakan nilai maksimum lokal.
SOAL LATIHAN 10
1. Tentukan bidang singgung dari fungsi berikut di titik (𝑥0, 𝑦0, 𝑧0) yang diberikan.
a. 𝑓(𝑥, 𝑦) = 2𝑥3+ 𝑦2; (1,2,6) b. 𝑓(𝑥, 𝑦) = 𝑥𝑦; (−1, −2,2) c. 𝑓(𝑥, 𝑦) = sin(𝑥𝑦); (1,0,0)
2. Tentukan bentuk pelinieran dari fungsi berikut di titik yang diberikan.
a. 𝑓(𝑥, 𝑦) = 𝑦2𝑥 + 𝑥2𝑦; (1,1) b. 𝑓(𝑥, 𝑦) = cos(𝑥 + 𝑦); (0,0) c. 𝑓(𝑥, 𝑧) = 𝑥 + 𝑦2− 2𝑥𝑦; (−1,2)
3. Tentukan bentuk pelinieran dari 𝑓(𝑥, 𝑦) = 𝑒𝑥+𝑦 di titik (0,0). Kemudian
gunakan bentuk pelinieran tersebut untuk menghitung nilai hampiran dari 𝑓(0.1,0.05).
4. Tentukan bentuk pelinieran dari 𝑓(𝑥, 𝑦) = ln(𝑥2− 3𝑦) di titik (1,0). Kemudian gunakan bentuk pelinieran tersebut untuk menghitung nilai hampiran dari 𝑓(1.1,0.1).
5. Tentukan semua nilai ekstrim dari fungsi yang diberikan dan tentukan jenisnya apakah nilai maksimum lokal atau nilai minimum lokal.
a. 𝑓(𝑥, 𝑦) = 𝑥2+ 𝑦2− 2𝑥 b. 𝑓(𝑥, 𝑦) = 𝑥2𝑦 − 4𝑥2− 4𝑦 c. 𝑓(𝑥, 𝑦) = −2𝑥2 + 𝑦2− 6𝑦
DAFTAR PUSTAKA 11
Neuhauser, C. 2011. Calculus for Biology and Medicine 3rd Ed. Prentice Hall.
Varberg, D. Purcell, E. and Rigdon, S. 2006. Calculus 9th Ed. Prentice Hall.