UNTUK MENGOPTIMALKAN KEUNTUNGAN PERUSAHAAN
DI PT. VARIA USAHA BETON WARU - SIDOARJO
S K R I P S I
O l e h :
BAYU SAGITA ( 05 32010 127 )
JURUSAN TEKNIK INDUSTRI
FAKULTAS TEKNOLOGI INDUSTRI
UNIVERSITAS PEMBANGUNAN NASIONAL “VETERAN”
JAWA TIMUR
Dengan mengucapkan syukur kehadirat Allah SWT, penulis dapat
menyelesaikan Tugas Akhir (Skripsi) dengan judul “PERENCANAAN
PRODUKSI DENGAN METODE DE NOVO PROGRAMMING UNTUK
MENGOPTIMALKAN KEUNTUNGAN PERUSAHAAN DI PT. VARIA
USAHA BETON WARU – SIDOARJO”. Penelitian dilakukan pada bulan Juli
2009 sampai selesai.
Laporan ini disusun berdasarkan pengamatan dan data informasi yang
kami peroleh dari lapangan dan pembimbing di PT. Varia Usaha Beton Waru -
Sidoarjo serta literatur yang tersedia. Oleh karena itu kami mengucapkan Terima
Kasih yang sebesar-besarnya kepada :
1. Bapak Ir. Sutiyono, MT sebagai Dekan Fakultas Teknologi Industri UPN
“Veteran” Jawa Timur.
2. Ir. M. Tutuk Safirin, MT selaku Ketua Jurusan Teknik Industri FTI UPN
“Veteran” Jawa Timur.
3. Ir. Iriani, MMT selaku dosen pembimbing I dan Enny Aryani, ST. MT selaku
dosen pembimbing II Tugas Akhir.
4. Bapak Abdillah Tejo, bapak Eko Marhaendro, bapak Kholik dan bapak
suwondo selaku pembimbing lapangan di PT. Varia Usaha Beton Waru -
Sidoarjo.
5. Segenap staf dan karyawan PT. Varia Usaha Beton Waru - Sidoarjo yang telah
membantu pelaksanaan penelitian ini.
6. My Family ; Bapak & Ibu serta Kakek & Nenek yg slalu Mendo’akan Q,
Smua My Brother’s & My Sister’s Yg Slalu Ingin aQ agar Cpet Luluz,
keCewa”.
7. Maz^Maz Pembimbing Pribadi_Q
=> Koko Wedhol (Yudha ’03) Yg sdh pinjami Buku, mmbantu Mngajari
Sofware WinQSB, & mmberikn bimbingan bwt aQ.
=> Om Pipit ’03 Yg mWariskan Buku2nya pd Q, & mnJadi pembimbing Q.
8. BuaT Sodara2Q TI pGi aNgKtAn 2005 Yg d Paralel C kan ;
Dwi ‘Rombenk’, TegUh ‘Fukimay’, Bulek Ririn Ojok Kbnykan Facebook
ndang DimarekNo Skripsine Ndang iso Touring2 lg. Genk Warkop
(Andri_Ludruk,Rizal_Sex,SUGAB_Darmo,Sabta_Quntul,Murtafi_Gembrot,
and Andi_Kupink) Kmbalilah k Jln Yg benar ! [Skripsi_Only]. Farid_BrenX,
Umatul_Bebe’X, AnanG, InDah_BaTam, & Onta, Ngenteni Opo! ‘05 wez
punah Ojo MBUleeD ae!. Poppie_Ponity & Catur_NyetNyet yg Uda Jd
SeLirQ. TitiN, Ve_Qchool, & Ieke SilahKan Pacaran’x d Lanjut!. Trio Kwek2
(Yuztian, Prima, & Yuni_Krisit) ‘Skandal’ boleh Tp Jgn Gontok2an truuz!.
Ibu2 PKK HMTI (Fara, CutreX, Niken_ManchunK, & Ria_Cancheel) Msh
adakah Waktu utk Qta Blajar bareng Lg!?!. Om Indra (Mat_Buah) ’Jangan
sering2 Tinggalkan Anak & Istri mu!’. Om Brahma & Om Fuad “Q akan
Mnyusulmu!”. Ruly ’06, Galeh ’06 & Rini ’07 Jgn Pacaran teruuz ae…!.
maupun Adik-Adik moga tambah Sukse aja “Hidup TI !!!!”. Bang Jazzy (’01)
n Om Surya Agunk (’03) Trima Ksih MotivasiX. MySpecial Friends 2004
Dwi_GrandoNG, Taufik_Lambe, Aryo_Kuro, Tante_LidyA, Bude_Frida, dkk
YanG SelaLu MendukunG PerjuanganQ. Genk Kos2an (Maz Eko, Maz
Aak’Tria, & Pendik) Jgn bosen2 klo tak ReCoKin truuuz!. Erna Chryzna
(FE_Ek.Pembangunan ’05) Thanx Bgt KalKuLatorNya. Deco Perdana putra
(FE_Manajemen’05) Thanx uda pinjemi Kostum, serta Temen2Q SMA &
SMP yg dukung lwt Facebook ThanK SupportX “Q Rindu Kalian”. Semua
penghuni Teknik Industri tanpa terKecuali…. ‘Trima Kasih Banyak !’
CoRi bUat yG bLuM dIsButIn g’dA mKZud NgLupaAiN Klian smua....,
U’Re aLwAyZZ mY bEZzZt FriEnDs!, I Lup YoU Pull Pokok’e....!!!!!!
[ KUN FAYAKUN => MaKa JadiLah SKRIPSI ! ]
Berakhirnya Tulisan ini, Bukan Berarti Berakhirnya Kebersamaan KITA.
Suatu saat nanti, ketika Ku buka Buku ini Kembali, Aku hanya Ingin Bilang :
”AKU PENGEN SEMUA MBALEEK!!!”
Semoga Allah SWT melimpahkan berkat dan rahmat-Nya kepada
mereka, atas segala bantuan dan jasa yang telah diberikan kepada Saya selama ini.
Saya menyadari bahwa ada kekurangan dan kesalahan yang tak luput dari diri
saya, jadi mohon dimaklumi. Saya juga mengharapkan kritik dan saran yang
bersifat membangun demi penyempurnaan laporan penelitian ini. Akhir kata,
semoga laporan penelitian tugas akhir ini berguna bagi para pembaca.
Surabaya, 10 April 2010
HALAMAN JUDUL... i
LEMBAR PENGESAHAN ... ii
KATA PENGANTAR... iii
DAFTAR ISI ... iv
DAFTAR TABEL... v
DAFTAR GAMBAR... vi
DAFTAR LAMPIRAN... vii
ABSTRAKSI ... viii
BAB I PENDAHULUAN 1.1 Latar Belakang…………..………. 1
1.2 Perumusan Masalah……..………. 2
1.3 Tujuan Penelitian ...………. 2
1.4 Batasan Masalah ………... 3
1.5 Asumsi ………. …… 3
1.6 Manfaat Penelitian………. 3
1.7 Sistematika Penulisan…..………. 4
BAB II TINJAUAN PUSTAKA 2.1 Perencanaan Produksi………...……… 6
2.1.1 Arti Perencanaan Produksi ……….... 6
2.1.2 Jenis – Jenis Perencanaan Produksi ……… 9
2.1.3 Faktor – Faktor yang perlu Dipertimbangkan dalam Perencanaan produksi………..………...…… 10
2.2 Linier Programming ……… 12
2.2.2 Asumsi – Asumsi Dasar Linier Programming ………... 23
2.3 De Novo Programming……….……… 24
2.3.1 Penyelesaian De Novo Programming ……… 28
2.4 Pengertian Biaya ..……….……… 32
2.4.1 Klasifikasi Biaya………...………. …………. 33
2.4.2 Penggunaan dari Data Biaya……...……… 38
2.4.3 Penggolongan dari Biaya………… ……... 38
2.4.4 Biaya dalam Hubungannya dengan Volume Produksi….…... 39
2.5 Penelitian Terdahulu ..………..………... 42
BAB III METODOLOGI PENENLITIAN 3.1 Lokasi dan Waktu Penelitian……… 43
3.2 Identifikasi Variabel ……….... 43
3.3 Flow Chart Pemecahan Masalah ……… 45
3.4 Metode Pengumpulan Data………..……… 49
3.5 Metode Pengolahan Data ……… 50
3.5.1 Penetapan Variabel Keputusan……… 50
3.5.2 Penetapan Fungsi Tujuan………….……… 51
3.5.3 Penetapan Fungsi Kendala ……… 51
3.5.4 Penetapan Model Rencana Produksi ……….. 54
BAB IV HASIL DAN PEMBAHASAN 4.1 Pengumpulan Data……… 56
4.1.1 Data Jenis Produk……… 56
4.1.5 Data Ketersediaan Bahan Baku…...……… 59
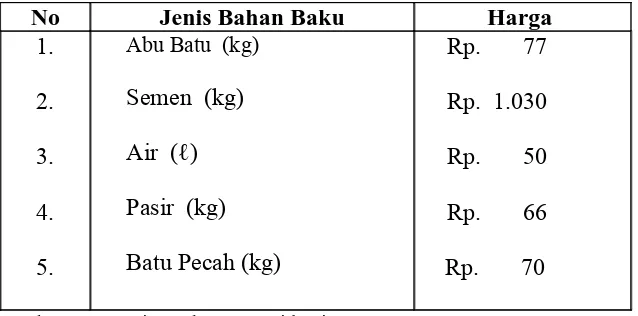
4.1.6 Data Harga Bahan Baku…………..……… 59
4.2 Pengolahan Data………...……… 60
4.2.1 Perencanaan Produksi dengan Keadaan Riil Perusahaan …... 60
4.2.2.1 Perhitungan Laba..………..……… 60
4.2.1.2 Produksi Riil dan Total Keuntungan Perusahaan...… 61
4.2.2 Perencanaan Produksi dengan Metode De Novo
Programming………..……… 62 4.2.2.1 Formulasi Model De Novo Programming ……….. 62
4.2.2.1.1 Penentuan Variabel Keputusan ……….... 62
4.2.2.1.2 Penentuan Fungsi Tujuan ...….…………. 62
4.2.2.1.3 Penetapan Fungsi Kendala ……… 63
4.2.2.1.4 Penetapan Rencana Produksi model De
Novo Programming ………. 67 4.2.2.2 Penyelesaian Model De Novo Programming ……. 68
4.2.2.3 Validasi Model De Novo programming …………. 69
4.2.2.4 Perbandingan Hasil Profit……… 73
4.3 Analisa dan Pembahasan…………..……… 73
BAB V KESIMPULAN DAN SARAN
5.1 Kesimpulan……….……….. 75
5.2 Saran………. 75
DAFTAR PUSTAKA
Tabel 2.1 Data untuk Model Linier Programming ……… 15
Tabel 2.2 Table Simpleks dalam Bentuk Simbol ……… 20
Tabel 2.3 Perbedaan Formulasi Linier
Programming dengan De Novo
Programming
……… 28
Tabel 2.4 Perbedaan Model Linier Programming dengan Model De Novo Programming ditinjau dari Masalah Mix Produk
……… 32
Tabel 2.5 Klasifikasi Biaya dalam Hubungannya dengan Produk
……… 35
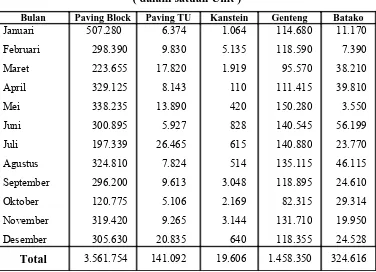
Tabel 4.1 Data Hasil Produksi Bulan Januari – Desember 2008 Dalam Satuan Unit
……… 57
Tabel 4.4 Data ketersediaan Bahan Baku Bulan Januari – Desember 2008
……… 59
Tabel 4.5 Daftar Harga Bahan Baku ……… 60
Tabel 4.6 Keuntungan Masing – Masing Produk ……… 61
Tabel 4.7 Perbandingan Profit Riil Perusahaan dan Metode De Novo Programming
……… 73
Tabel 4.8 Profit Riil Perusahaan dan Metode De Novo Programming
……… 74
Programming
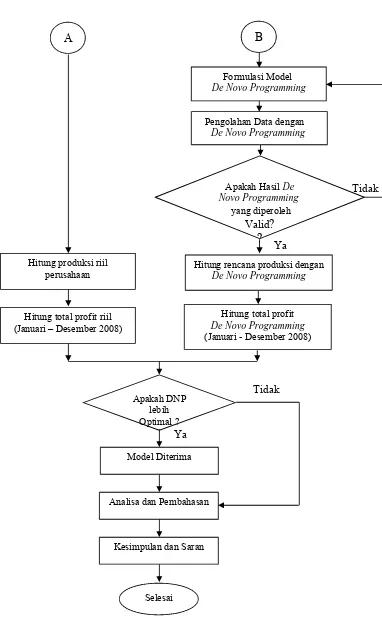
Gambar 3.1 Langkah – langkah Pemecahan
Masalah
……… 45
DAFTAR LAMPIRAN
Lampiran I Gambaran Umum Perusahaan PT. VARIA USAHA BETON WARU
Ketersediaan Bahan baku, Harga Bahan Baku dan Kapasitas Mesin
Lampiran IV Perhitungan Biaya Bahan Baku dan Biaya Produksi
Lampiran V Penghitungan Jumlah Pemakaian Bahan Baku dan Sisa Bahan Baku
Dalam Rupiah
Lampiran VI Perhitungan Rencana Produksi dan Keuntungan dengan Software
Dalam industri manufactur sering dihadapkan pada masalah–masalah yang kompleks dalam mengambil suatu keputusan untuk mencapai tujuan perusahaan. Salah satu tujuan tersebut adalah meminimalkan biaya produksi dan memaksimalkan keuntungan atau profit yang diperoleh guna menjamin kelangsungan hidup perusahaan
PT. Varia Usaha Beton Sidoarjo adalah perusahaan yang berdiri pada tahun 1988 dan bergerak dibidang Industri manufaktur dengan produk yang dihasilkan berupa beton cetak maupun beton cair siap pakai. Dalam memproduksi beton cetak di PT. Varia Usaha Beton selalu terdapat sisa bahan baku karena bahan baku yang digunakan tidak habis. Hal ini dianggap suatu pemborosan bagi perusahaan, karena diperkirakan penyebabnya adalah pada masalah perencanaan produksi yaitu menentukan jumlah tiap–tiap produk yang harus diproduksi dengan memperhatikan jumlah bahan baku yang dibutuhkan tanpa terjadi kelebihan atau sisa.
Berdasarkan latar belakang diatas, maka peneliti melakukan penelitian dengan menggunakan metode De Novo Programming untuk menentukan jumlah beton cetak yang harus diproduksi oleh perusahaan sehingga diperoleh keuntungan yang maksimal.
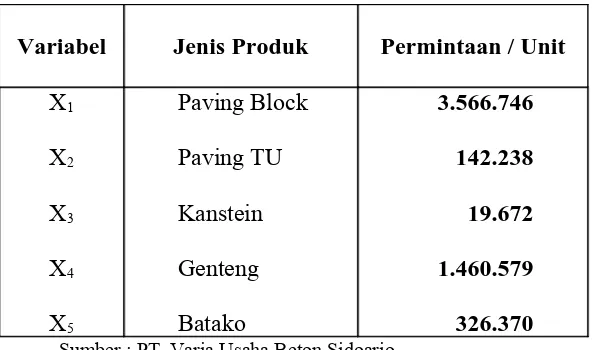
Dalam pengolahannya diperoleh hasil dari metode De Novo Programming adalah profit rill perusahaan sebesar Rp. 2.742.079.900,- sedangkan profit DeNovo sebesar Rp. 2.747.634.000,- maka memperoleh selisih sebesar Rp. 5.554.100,- atau dapat mengalami kenaikan sebesar 0,2 % dari profit rill perusahaan. Dan rencana hasil produksi beton cetak yaitu Paving Block sebanyak 3.566.746 unit, Paving TU sebanyak 142.238 unit, Kanstein sebanyak 19.672 unit, Genteng sebanyak 1.460.579 unit, dan Batako sebanyak 326.370 unit.
Kata Kunci : Profit, De Novo Programming
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Dalam memasuki era pasar bebas, industri sebagai tempat untuk
memberikan informasi produksi input/ masukan menjadi output/ keluaran
(meliputi barang/ jasa) yang sesuai dengan kebutuhan dan keinginan konsumen,
sering dihadapkan pada masalah–masalah yang kompleks dalam mengambil suatu
keputusan untuk mencapai tujuan perusahan. Salah satu tujuan tersebut adalah
meminimalkan biaya produksi dan memaksimalkan laba yang diperoleh guna
menjamin kelangsungan hidup perusahaan. Selain itu, metode yang digunakan
dalam pengambilan keputusan biasanya menyeleksi berbagai alternatif yang ada
untuk dipilih alternatif yang terbaik dengan berdasarkan suatu kriteria yang
bersifat tunggal atau ganda.
Dalam persaingan usaha, tujuan untuk mendapatkan laba adalah faktor yang
utama. Dengan semakin meningkatnya permintaan pasar, maka PT. Varia Usaha
Beton yang merupakan salah satu perusahaan yang bergerak dibidang
manufacturing industry yang menghasilkan produk berupa berbagai jenis beton cetak (paving, batako, genteng, kanstein) maupun beton cair siap pakai, berusaha
meningkatkan hasil produksinya agar mampu bersaing dalam memenuhi
permintaan pasar tersebut.
Dalam memproduksi beton, di PT. Varia Usaha Beton selalu terdapat sisa
bahan baku karena bahan baku yang digunakan selalu berlebih. Hal ini dianggap
masalah perencanaan produksi yaitu menentukan jumlah tiap – tiap produk yang
harus diproduksi dengan memperhatikan jumlah bahan baku yang dibutuhkan
tanpa terjadi kelebihan atau sisa.
Dengan adanya masalah tersebut maka dilakukan penelitian dengan metode
De Novo Programming dengan harapan dapat dilakukan perencanaan produksi sehingga diperoleh keuntungan yang maksimal. Pendekatan De Novo
Programming dalam menyelesaikan masalah optimasi dilakukan dengan pendekatan sistem secara total, artinya selain menentukan kombinasi yang terbaik
terhadap outputnya, juga dapat memberikan suatu usulan penggunaan sumber
daya yang terintegrasi melalui anggaran yang tersedia. Pada metode De Novo
Programming kendala sumber daya (bahan baku) akan disusun seefisien mungkin sehingga tidak menghasilkan sisa.
1.2 Perumusan Masalah
Setelah diketahui mengenai latar belakang permasalahan maka dapat
dirumuskan sebagai berikut :
“Berapa jumlah produk beton cetak yang harus diproduksi sehingga diperoleh keuntungan yang maksimal ?”.
1.3. Tujuan Penelitian
Berdasarkan perumusan masalah diatas, maka tujuan yang ingin dicapai
pada penelitian Tugas Akhir ini adalah :
1. Mencari keuntungan perusahaan yang optimal.
1.4. Batasan Masalah
Untuk penyederhanaan penelitian agar lebih terfokus pada inti permasalahan
dan sesuai dengan metode yang diterapkan, maka perlu pemberian batasan -
batasan sebagai berikut :
1.
Penelitian dilakukan pada lima jenis produk beton cetak yaitu Paving Block, Paving TU, Batako, Genteng, dan Kanstein.2.
Data yang digunakan adalah data produksi dan penjualan selama bulan Januari sampai Desember 2008.1.5. Asumsi
Asumsi–asumsi yang digunakan dalam penelitian ini :
1. Tidak ada perubahan harga jual tiap produk dan harga bahan baku selama
penelitian berjalan.
2. Setiap produk yang dihasilkan terjual habis.
3. Kondisi lingkungan kerja baik operator maupun fasilitas produksi lainnya
dalam keadaan baik.
4. Biaya Produksi untuk tahun berikutnya dianggap tidak mengalami perubahan.
5. Tenaga kerja dianggap mempunyai kemampuan yang standard.
1.6. Manfaat Penelitian
Manfaat dari hasil penelitian tugas akhir yang akan dilakukan ini adalah
1. Bagi Perusahaan
Memberikan informasi dan sebagai bahan pertimbangan pada perusahaan
untuk mengadakan perbaikan–perbaikan yang dianggap perlu dalam
perencanaan produksinya.
2. Bagi Universitas
Untuk menambah perbendaharaan perpustakaan yang berguna dalam
pengembangan ilmu pengetahuan dan sebagai perbandingan bagi mahasiswa
di masa yang akan datang.
3. Bagi Mahasiswa
Menambah wawasan dan kemampuan dalam mengaplikasikan ilmu–ilmu
teknik industri, khususnya dalam bidang perencanaan produksi untuk
memaksimalkan keuntungan perusahaan.
1.7. Sistematika Penulisan
Uraian tentang sistematika penulisan dimaksudkan untuk mempermudah
usaha pemahaman keseluruhan materi dan permasalahan pokok dalam skripsi ini.
Sistematika penulisan tersebut dibuat dalam lima pokok bahasan sebagai
berikut :
BAB I : PENDAHULUAN
Bab ini menggambarkan secara garis besar isi skripsi, meliputi Latar
Belakang, Perumusan Masalah, Tujuan Penelitian, Batasan Masalah,
BAB II : TINJAUAN PUSTAKA
Bab ini berisikan mengenai teori-teori yang relevan dan metode yang
digunakan sebagai landasan teori dalam penelitian dan untuk
memecahkan permasalahan yang dibahas dalam tugas akhir ini.
BAB III : METODE PENELITIAN
Bab ini menjelaskan tentang langkah–langkah dalam penelitian yang
berbentuk kerangka penelitian beserta penjelasannya. Dalam bab ini
diuraikan tentang lokasi dan waktu penelitian, langkah-langkah
pemecahan masalah (Flow Chart), identifikasi variabel, metode
pengambilan data dan pengolahan data.
BAB IV : HASIL DAN PEMBAHASAN
Bab ini berisikan mengenai analisa dan pembahasan dari hasil
perhitungan dan pengolahan data yang telah dilakukan sebelumnya,
termasuk mengenai alternatif solusi-solusi yang diharapkan dapat
menjawab permasalahan yang dikaji.
BAB V : KESIMPULAN DAN SARAN
Pada bab ini berisikan kesimpulan yang diperoleh dari hasil
pemecahan masalah yang mencakup hal-hal penting pada hasil yang
didapat dari penelitian dan saran–saran yang diajukan kepada pihak
Perusahaan sebagai bahan pertimbangan selanjutnya.
DAFTAR PUSTAKA
BAB II
TINJAUAN PUSTAKA
2.1. Perencanaan Produksi
2.1.1. Arti Perencanaan Produksi
PPC dapat diartikan sebagai proses untuk merencanakan dan
mengendalikan aliran material yang masuk, mengalir dan keluar dari sistem
produksi/operasi sehingga permintaan pasar dapat dipenuhi dengan jumlah yang
tepat, waktu penyerahan yang tepat, dan biaya produksi yang minimum. Dari
definisi di atas, maka pekerjaan yang terkandung dalam PPC secara garis besar
dapat kita bedakan menjadi dua hal yang saling berkaitan yaitu : Perencanaan
Produksi dan Pengendalian Produksi.
Perencanaan merupakan salah satu fungsi managemen. Dalam
perencanaan ditentukan usaha-usaha atau tindakan-tindakan yang akan atau perlu
diambil oleh pimpinan perusahaan untuk mencapai tujuan perusahaan, dengan
mempertimbangkan masalah-masalah yang mungkin timbul di masa yang akan
datang. Untuk dapat membuat perencanaan yang baik, maka perlu diperhatikan
masalah intern dan ekstern. Masalah intern adalah masalah yang datangnya dari
dalam perusahaan (masih dalam kekuasaan pimpinan perusahaan), seperti mesin
yang digunakan, buruh yang dikaryakan, bahan yang diperlukan dan sebagainya.
Sedangkan masalah ekstern adalah masalah yang datangnya dari luar perusahaan,
seperti inflasi, kebijaksanaan, keadaan politik dan sebagainya. (Sofjan Assauri,
Barang yang direncanakan akan diproduksi pada suatu periode di masa
depan harus memenuhi beberapa syarat yaitu : (Sofjan Assauri, Manajemen
Produksi dan Operasi, 2004)
a. Bahwa barang tersebut harus dapat diprodusir atau dibuat pada waktu itu.
b. Bahwa barang tersebut harus dapat dikerjakan dengan/oleh pabrik ini.
c. Bahwa barang tersebut harus sesuai atau dapat memenuhi/ dicocokkan dengan
keinginan pembeli sesuai dengan ramalan baik mengenai harga, kuantitas,
kualitas dan waktu yang dibutuhkan.
Perencanaan produksi membutuhkan pertimbangan dan ketelitian yang
terinci dalam menganalisis kebijaksanaan, karena perencanaan ini merupakan
dasar penentuan bagi manajer dalam rangka mencapai tujuan perusahaan.
Perencanaan produksi ini merupakan suatu fungsi yang menentukan batas - batas
(level) dari kegiatan perusahaan pabrik di masa yang akan datang. Perencanaan dapat dibedakan antara lain :
1. Perencanaan usaha yang bersifat umum (general business planning) adalah
perencanaan kegiatan yang dijalankan oleh setiap perusahaan, baik perusahaan
besar maupun kecil, untuk berhasil (sukses) nya perusahaan mencapai tujuan.
Dalam perencanaan ini ditentukan tujuan jangka panjang yang merupakan
masa depan perusahaan yang diharapkan. Oleh karena itu perlu diperhatikan
dan dipertimbangkan keadaan atau situasi faktor-faktor yang dapat
mempengaruhi perkembangan perusahaan di masa depan seperti situasi pasar,
keperluan-keperluan pabrik (plant requirement) dan pengaruh saingan serta
2. Perencanaan produksi (production planning) adalah perencanaan dan pengorganisasian sebelumnya mengenai orang-orang, bahan-bahan,
mesin-mesin dan peralatan lain serta modal yang diperlukan untuk memprodusir
barang-barang pada suatu periode tertentu di masa depan sesuai dengan yang
diperkirakan atau diramalkan.
Berdasarkan rencana-rencana produksi yang telah disusun, pimpinan
perusahaan dapat menentukan langkah-langkah sebagai berikut : (Sofjan Assauri,
Manajemen Produksi dan Operasi, 2004)
a. Bilamana kegiatan produksi dimulai dan berapa banyak buruh/ pekerja yang
dibutuhkan dalam kegiatan produksi tersebut
b. Menentukan alat-alat dan perlengkapan/ peralatan yang diperlukan dalam
proses produksi
c. Tingkat persediaan yang dibutuhkan
Tujuan Perencanaan Produksi ini adalah : (Sofjan Assauri, Manajemen
Produksi dan Operasi, 2004)
1. Untuk mencapai tingkat/ level keuntungan (profit) yang tertentu. Misalnya
berapa hasil (output) yang diprodusir supaya dapat dicapai tingkat/level profit
yang diinginkan dan tingkat persentase tertentu dari keuntungan (profit)
setahun terhadap penjualan (sales) yang diinginkan.
2. Untuk menguasai pasar tertentu, sehingga hasil atau output perusahaan ini tetap
mempunyai pangsa pasar (market share) tertentu.
3. Untuk mengusahakan supaya perusahaan pabrik ini dapat bekerja pada tingkat
4. Untuk mengusahakan dan mempertahankan supaya pekerjaan dan kesempatan
kerja yang sudah ada tetap pada tingkatnya dan berkembang
5. Untuk menggunakan sebaik-baiknya (efisien) fasilitas yang sudah ada pada
perusahaan yang bersangkutan.
2.1.2. Jenis-jenis Perencanaan Produksi
Perencanaan produksi yang terdapat dalam suatu perusahaan dapat
dibedakan menurut jangka waktu yang tercakup, yaitu:
1. Perencanaan Produksi Jangka Pendek (Perencanaan Operasional) adalah
penentuan kegiatan produksi yang akan dilakukan dalam jangka waktu satu
tahun mendatang atau kurang, dengan tujuan untuk mengatur penggunaan
tenaga kerja, persediaan bahan dan fasilitas produksi yang dimiliki perusahaan
pabrik. Oleh karena perencanaan produksi jangka pendek berhubungan dengan
pengaturan operasi produksi, maka perencanaan ini disebut juga dengan
perencanaan operasional.
2. Perencanaan Produksi Jangka Panjang adalah penentuan tingkat kegiatan
produksi lebih daripada satu tahun, dan biasanya sampai dengan lima tahun
mendatang, dengan tujuan untuk mengatur pertambahan kapasitas peralatan
atau mesin-mesin, ekspansi pabrik dan pengembangan produk (product
development). (Sofjan Assauri, Manajemen Produksi dan Operasi, 2004) Dari kedua jenis perencanaan produksi diatas dapatlah kita ketahui bahwa
setiap perencanaan produksi mempunyai ciri-ciri sebagai berikut :
1. Perencanaan produksi yang menyangkut kegiatan pada masa yang akan datang,
dibuat berdasarkan panaksiran atau ramalan kegiatan yang ditentukan oleh
2. Perencanaan produksi mempunyai jangka waktu tertentu
3. Perencanaan produksi mempersiapkan tenaga kerja, bahan-bahan,
mesin-mesin, dan peralatan lain pada waktu yang diperlukan
4. Perencanaan produksi harus menentukan jumlah dan jenis serta kualitas dari
produk yang akan diproduksi
5. Perencanaan produksi harus dapat mengkoordinir kegiatan produksi dengan
mengkoordinir bagian-bagian yang mempunyai hubungan langsung ataupun
tidak dengan kegiatan produksi.
(Sofjan Assauri, Manajemen Produksi dan Operasi, 2004)
2.1.3. Faktor-faktor yang perlu Dipertimbangkan dalam Perencanaan
Produksi
Adapun faktor-faktor yang perlu dipertimbangkan dalam perencanaan
produksi , antara lain : (Sofjan Assauri, Manajemen Produksi dan Operasi, 2004)
1. Sifat proses produksi
Proses produksi dapat dibedakan atas :
a. Proses produksi yang terputus-putus (intermittent process/manufacturing)
Perencanaan produksi dalam perusahaan pabrik yang mempunyai proses
produksi yang terputus-putus, dilakukan berdasarkan jumlah pesanan
(order) yang diterima. Oleh karena kegiatan produksi yang dilakukan
berdasarkan pesanan (order), maka jumlah produknya biasanya sedikit atau
relatif kecil, sehingga perencanaan produksi yang dibuat semata-mata tidak
berdasarkan ramalan penjualan (sales forecasting), tetapi terutama
didasarkan atas pesanan yang masuk. Perencanaan produksi dibuat untuk
pesanan yang masuk. Ramalan penjualan ini membantu untuk dapat
memperkirakan order yang akan diterima, sehingga dapat diperkirakan dan
ditentukan bagaimana penggunaan mesin dan peralatan yang ada agar
mendekati optimum pada masa yang akan datang, dan tindakan-tindakan
apa yang perlu diambil untuk menutupi kekurangan-kekurangan.
Perencanaan produksi yang disusun haruslah fleksibel, agar peralatan
produksi dapat dipergunakan secara optimal.
b. Proses produksi yang terus-menerus (continuous process)
Perencanaan produksi pada perusahaan yang mempunyai proses produksi
yang terus - menerus, dilakukan berdasarkan ramalan penjualan. Hal ini
karena kegiatan produksi tidak dilakukan berdasarkan pesanan akan tetapi
untuk memenuhi pasar dan jumlah yang besar serta berulang-ulang dan
telah mempunyai blueprint selama jangka waktu yang tertentu.
Langkah-langkah perencanaan produksi yang dilakukan dalam perusahaan yang
mempunyai proses produksi yang terus-menerus adalah :
1). Membuat ramalan penjualan (sales forecasting)
2). Membuat master schedule yang didasarkan atas ramalan penjualan
3). Setelah master schedule dibuat, dilakukan perencanaan yang lebih teliti.
2. Jenis dan Mutu dari barang yang diproduksi
Untuk menyusun suatu perencanaan produksi, ada beberapa hal mengenai
jenis dan sifat produk yang perlu diketahui dan diperlihatkan, yaitu : (Sofjan
Assauri, Manajemen Produksi dan Operasi, 2004)
b. Apakah produk yang akan diproduksi itu merupakan costumer’s goods
(barang-barang yang langsung dikonsumsi oleh konsumen) atau producer’s
goods (barang yang akan dipergunakan untuk memproduksi barang lain)
c. Sifat dari produk yang akan dihasilkan, apakah merupakan barang yang
tahan lama atau tidak
d. Sifat dari permintaan barang yang akan dihasilkan, apakah mempunyai sifat
permintaan yang musiman (seasonal) yang permintaannya hanya pada
musim-musim tertentu saja ataukah sifat permintaannya sepanjang masa
e. Mutu dari barang yang akan diproduksi, yang akan tergantung pada biaya
persatuan yang diinginkan, dan permintaan atau keinginan konsumen
terhadap barang hasil produksi tersebut.
f. Sifat dari barang yang diproduksi apakah barang baru ataukah barang lama.
Hal ini perlu kita perhatikan, karena untuk barang yang baru maka perlu
diadakan penelitian (research) pendahuluan mengenai : (Sofjan Assauri,
Manajemen Produksi dan Operasi, 2004)
1. Lokasi perusahaan, apakah perusahaan perlu diletakkan berdekatan dengan
sumber bahan mentah ataukah dekat dengan pasir
2. Jumlah barang yang akan diproduksi
3. Sifat permintaan barang ini, apakah musiman atau sepanjang masa, dan
4. Hal-hal lain yang dibutuhkan untuk memulai produksi tersebut.
2.2. Linier Programming
Pokok pikiran yang utama dalam menggunakan linier programming
ialah merumuskan masalah dengan jelas menggunakan sejumlah informasi yang
tersedia. Merumuskan masalah dengan baik dan menterjemahkan masalah ke
programming merupakan suatu model umum yang dapat digunakan dalam pemecahan masalah pengalokasian sumber–sumber yang terbatas secara optimal.
Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau
menentukan tingkat setiap kegiatan yang akan dilakukannya, dimana masing–
masing kegiatan membutuhkan sumber daya yang sama sedangkan jumlahnya
terbatas. (Pangestu Subagyo, T.H Handoko, Dasar – dasar Operation Research, :
1995).
Jadi Linier Programming mencakup perencanaan kegiatan–kegiatan
untuk mencapai suatu hasil yang ”optimal”, yaitu suatu hasil yang mencerminkan
tercapainya sasaran tertentu yang paling baik (menurut model matematis) diantara
alternatif – alternatif yang mungkin, dengan menggunakan fungsi linier.
Kegunaan Linier Programming adalah lebih luas pada aplikasinya
semata–mata. Pada kenyataannya linier programming harus dipandang sebagai
dasar penting untuk pengembangan teknik–teknik riset operasi lainnya, termasuk
pemrograman integer, stokhastik, arus jaringan dan kuadratik. Dalam hal ini,
pemahaman akan linier programming adalah penting untuk implementasi teknik–
teknik tambahan ini.
2.2.1. Model Linier Programming
Metode analisis yang paling bagus untuk menyelesaikan persoalan
alokasi sumber ialah metode Linier Programming. Dalam model Linier
Programming dikenal dua macam ”fungsi”, yaitu fungsi tujuan (objective function) dan fungsi–fungsi batasan (constraint function). Fungsi tujuan adalah
fungsi yang menggambarkan tujuan/ sasaran di dalam permasalahan Linier
sumber daya, untuk memperoleh keuntungan maksimal atau biaya minimal. Pada
umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z. Sedangkan fungsi
batasan merupakan bentuk penyajian secara matematis batasan–batasan kapasitas
yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.
(Pangestu Subagyo, T.H Handoko, Dasar – dasar Operation Research, : 1995).
Agar memudahkan pembahasan model Linier Programming ini,
digunakan simbol–simbol sebagai berikut :
m = macam batasan–batasan sumber atau fasilitas yang tersedia
n = macam kegiatan–kegiatan yang menggunakan sumber atau fasilitas
tersebut
i = nomor setiap macam sumber atau fasilitas yang tersedia (I = 1, 2,
3, ...., m)
j = nomor setiap macam kegiatan yang menggunakan sumber atau
fasilitas yang tersedia (j = 1, 2, 3, ...., n)
Xj = tingkat kegiatan ke – j (j = 1, 2, 3, ...., n)
aij = banyaknya sumber i yang diperlukan untuk menghasilkan setiap unit
keluaran (output) kegiatan j (j = 1, 2, 3, ..., m, dan j = 1, 2, 3, ...,n)
bij = banyaknya sumber (fasilitas) i yang tersedia untuk dialokasikan ke
setiap unit kegiatan (i = 1, 2, 3, ....,n)
Z = nilai yang dioptimalkan (maksimum atau minimum)
Cj = kenaikan nilai Zz apabila ada pertambahan tingkat kegiatan (Xj)
dengan satuan (unit).
Keseluruhan simbol–simbol di atas selanjutnya disusun ke dalam bentuk
Tabel 2.1 Data Untuk Model Linier Programming
Kegiatan Pemakaian Sumber per unit Kegiatan (Keluaran)
1 2 3 ... n
Sumber : Dasar – dasar Operation Research, Handoko, T.H., Pangestu Subagyo, 1995.
Atas dasar tabel diatas kemudian dapat disusun suatu model matematis
yang digunakan untuk mengemukakan suatu permasalahan Linier Programming
sebagai berikut :
Bentuk atau model Linier Programming diatas merupakan bentuk standart
Dengan kata lain, bila setiap masalah dapat diformulasikan secara matematis
mengikuti model diatas, maka masalah tersebut dapat dipecahkan dengan teknik
Linier Programming.
Terminologi umum untuk model Linier Programming yang diuraikan
diatas dapat diringkas sebagai berikut :
1. Fungsi yang akan dimaksimumkan : C1X1 + C2X2 + ...
+ CnXn disebut fungsi tujuan (objective function).
2. Fungsi–fungsi batasan dapat dikelompokkan menjadi 2
macam, yaitu :
a. Fungsi batasan fungsional, yaitu fungsi – fungsi batasan sebanyak m (yaitu
ai1X1 + ai2X2 + ai3X3 + ... + aimXm).
b. Fungsi batasan non–negatif (non–negatif - constraints) yaitu
fungsi–fungsi batasan yang dinyatakan dengan Xi≥ 0.
3. Variabel – variabel Xj disebut sebagai decision variables.
4. aij, bi, dan cj, yaitu masukan–masukan (input) konstan; disebut sebagai
parameter model.
Himpunan feasible dari variabel–variabel X1, X2, ...,Xn yang memenuhi
semua kendala disebut feasible point atau feasible vector. Sedangkan himpunan
semua titik yang memenuhi bentuk suatu daerah penyelesaian yang disebut
feasible region atau feasible space.
Dalam praktek, tidak semua masalah linier programming dapat persis
1. Masalah minimasi, dimana seseorang dituntut untuk menentukan kombinasi
(output) yang dapat meminimumkan pengorbanan (misal : biaya). Dalam hal ini, fungsi tujuan dinyatakan sebagai berikut :
Minimumkan : Z = C1X1 + C2X2 + C3X3 + ... + CnXn
2. Masalah dengan fungsi batasan fungsional yang memiliki tanda matematis ≥;
sehingga apabila dirumuskan terlihat sebagai berikut :
ai1X1 + ai2X2 + ai3X3 + ... + ainXn ≥ bi
3. Masalah dengan fungsi batasan fungsional yang memiliki tanda matematis
= ; sehingga bila dirumuskan sebagai berikut :
ai1X1 + ai2X2 + ai3X3 + ... + ainXn = bi
4. Masalah tertentu, dimana fungsi batasan non – negatif tidak diperlukan;
atau dengan kata lain Xj tidak terbatas.
Dalam menyelesaikan model linier programming, kita mengenal dua
metode yaitu : metode grafik dan metode simpleks.
2.2.1.1. Metode Grafik
Seorang manajer kadang–kadang menganggap tidak perlu memahami
proses penyelesaian suatu terapan program linier dalam proses pengambilan
keputusan, karena proses ini dalam praktek, umumnya dilaksanakan melalui
pelayanan komputer. Anggapan ini sama sekali adalah keliru, karena dengan
memahami teknik program linier, ini benar–benar sangat berguna untuk
mengetahui sifat–sifat dari masalah keputusan sendiri. (Siagian, Penelitian
Operasional, 2006 ).
Metode grafik hanya dapat digunakan dalam pemecahan masalah Linier
kemampuan suatu grafik dalam ”menyampaikan” sesuatu. (Pangestu Subagyo,
T.H Handoko, Dasar – dasar Operation Research, : 1995).
Bentuk umum metode grafik :
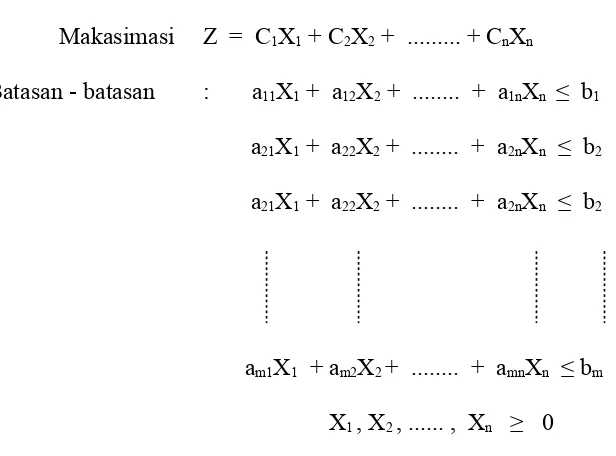
Maksimasi : Z = C1X1 + C2X2 + ... + CnXn
Kendala : a11X1 + a12X2 + ... + a1nXn ≤ b1
a21X1 + a22X2 + ... + a2nXn ≤ b2
am1X1 + am2X2 + ... + amnXn ≤ bm
X1 , X2 , ... , Xn ≥ 0
Langkah–langkah penggunaan metode garfik dapat ditunjukkan secara
ringkas sebagai berikut : (Pangestu Subagyo, T.H Handoko, Dasar – dasar
Operation Research, 1995 )
a. Menentukan fungsi tujuan dan memformulasikannya dalam bentuk matematis.
b. Mengidentifikasi batasan–batasan yang berlaku dan memformulasikannya
dalam bentuk matematis.
c. Menggambarkan masing–masing garis fungsi batasan dalam satu sistem salib
sumbu.
d. Mencari titik yang paling menguntungkan (optimal) dihubungkan dengan
fungsi tujuan.
Sebelum mempraktekkan setiap langkah diatas, sebaiknya terlebih
dahulu diuraikan masalah yang biasanya paling kritis, yaitu menggambarkan
garis–garis dan fungsi–fungsi batasan. Fungsi–fungsi batasan ini dinyatakan
≤ kurang dari atau sama dengan
≥ lebih besar dari atau sama dengan
= sama dengan
2.2.1.2. Metode Simpleks
Apabila suatu masalah Linier Programming hanya mengandung dua
kegiatan (atau variabel–variabel keputusan) saja, maka akan dapat diselesaikan
dengan metode grafik. Tetapi bila melibatkan lebih dari dua kegiatan maka
metode grafik tidak dapat digunakan lagi, sehingga diperlukan metode simpleks.
Metode simpleks merupakan suatu cara yang lazim dipakai untuk menentukan
kombinasi optimal dari tiga variabel atau lebih. (Pangestu Subagyo, T.H
Handoko, Dasar – dasar Operation Research, 1995)
Metode simpleks adalah suatu metode yang merupakan prosedur umum
untuk memecahkan problem linier programming. Proses pemecahan problem
linier programming dengan menggunakan metode simpleks terjadi melalui algoritma, yaitu suatu urutan kerja secara teratur dan berulang sehingga tercapai
hasil optimal yang dikehendaki. Metode ini paling efisien karena proses
pemecahan dapat digunakan program komputer yang sudah tentu akan
menghabiskan waktu singkat bila dibandingkan secara manual. Proses algoritma
ini mencakup prosedur kapan mulai pemecahan dan kapan berakhirnya proses
iterasi. Secara umum struktur algoritma tersbut adalah sebagai berikut :
a. Tahap awal, yaitu menyusun tabel dasar sebagai pangkal tolak
proses iterasi.
b. Proses iterasi yang dilakukan secara berulang hingga mencapai
c. Proses akan berhenti apabila hasil optimal yang dikehendaki
tercapai atau bahkan hasil optimal tidak dapat dicapai sama sekali.
Bentuk Umum Tabel Simpleks
Misal masalah linier programming mempunyai tujuan maksimasi dan
beberapa kendala, maka bentuk umum standart formulasi tersebut adalah sebagai
berikut :
Apabila bentuk standart tersebut dimasukkan dalam tabel, akan diperoleh
bentuk umum tabel simpleks atau juga initial table seperti dalam Tabel 2.2.
Tabel 2.2. Tabel Simpleks Dalam Bentuk Simbol
Variebel Z X1 X2 ... Xn Sn+1 Sn+2 .... Sn+m RHS
Sumber : Dasar – dasar Operation Research, Handoko, T.H., Pangestu Subagyo, 1995.
Right Hand Side (RHS) adalah nilai disebelah kanan persamaan atau dibelakang tanda (=) dan Sn+1, Sn+2, ... Sn+m adalah variabel slack yang
Langkah–langkah pembuatan metode simpleks dapat dijelaskan sebagai
berikut : (Pangestu Subagyo, T.H Handoko, Dasar – dasar Operation Research,
1995).
1. Merubah fungsi tujuan dan fungsi kendala.
Dalam hal ini fungsi tujuan diubah menjadi fungsi implisit, artinya semua
CjXij kita geser ke kiri.
2. Menyusun persamaan–persamaan di dalam tabel
Setelah mengubah formulasi kemudian memasukkan variabel atau bilangan ke
dalam sebuah tabel dan nilai variabel slack =, seperti pada tabel 2.2.
3. Memilih kolom kunci yang mempunyai nilai pada garis fungsi tujuan yang
bernilai negatif dengan angka terbesar.
4. Memilih baris kunci, yaitu dengan mencari indeks tiap–tiap baris dengan
cara membagi nilai–nilai pada kolom RHS dengan nilai yang sebaris pada
5. Mengubah nilai–nilai baris kunci, yaitu dengan cara membaginya dengan
angka kunci
6. Mengubah nilai–nilai selain pada baris kunci
Baris baru = (Lawan koefisien pada kolom kunci x Nilai baru pada garis
pivot) + baris lama.
7. Melanjutkan perbaikan–perbaikan/ perubahan–perubahan. Ulangilah
langkah–langkah perbaikan mulai langkah 3 sampai langkah 6 untuk
memperbaiki tabel–tabel yang telah diubah. Perubahan berhenti bila pada
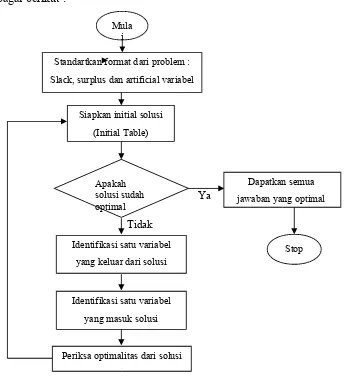
Proses penyelesaian metode simpleks dapat dibuat suatu program alir adalah sebagai berikut :
Gambar 2.1. Diagram Alir Metode Simpleks Sumber : Landasan Operation Research, Efraim Turban, 1981.
2.2.2. Asumsi–Asumsi Dasar Linier Programming
Seharusnya semua asumsi–asumsi (anggapan-anggapan) dasar Linier
Programming telah tersirat pada model yang telah dibahas diatas. Tetapi ada baiknya untuk menguraikan asumsi–asumsi dasar tersebut agar penggunaan teknik
Mula i
Standartkan format dari problem :
Slack, surplus dan artificial variabel
Stop Siapkan initial solusi
(Initial Table)
Apakah solusi sudah optimal
Dapatkan semua
jawaban yang optimal
Identifikasi satu variabel
yang keluar dari solusi
Identifikasi satu variabel
yang masuk solusi
Periksa optimalitas dari solusi
Ya
Linier Programming ini dapat memuaskan tanpa terbentur pada berbagai hal.
Asumsi–asumsi dasar Linier Programming dapat diperinci sebagai berikut :
(Pangestu Subagyo, T.H Handoko, Dasar – dasar Operation Research, 1995)
1. Proportionality
Asumsi ini berarti bahwa naik turunnya nilai Z dan penggunaan sumber atau
fasilitas yang tersedia akan berubah secara sebanding (proportional) dengan
perubahan tingkat kegiatan.
Misal :
Z = C1X1 + C2X2 + C3X3 + ... + CnXn
Artinya : Setiap pertambahan 1 unit X1 akan menaikkan Z dengan C1. Setiap
perubahan 1 unit X2 akan menaikkan nilai Z dengan C2, dan seterusnya.
2. Additivity
Asumsi ini berarti bahwa nilai tujuan tiap kegiatan tidak saling mempengaruhi
atau dalam Linier Programming dianggap bahwa kenaikkan dari nilai tujuan
(Z) yang diakibatkan oleh kenaikkan suatu kegiatan dapat ditambahkan tanpa
mempengaruhi bagian nilai Z yang diperoleh dari kegiatan lain.
Misal :
Z = 3 X1 + 5 X2
dimana : X1 = 10 ; X2 = 2 ;
Sehingga Z = 30 + 10 = 40
Andai kata X1 bertambah 1 unit, maka sesuai dengan asumsi pertama nilai Z
Jadi nilai 3 karena kenaikkan X1 dapat langsung ditambahkan pada nilai Z
mula–mula tanpa mengurangi bagian Z yang diperoleh dari kegiatan 2 (X2).
Dengan kata lain, tidak ada korelasi antara X1 dan X2.
3. Divisibility
Asumsi ini dinyatakan bahwa keluaran (output) yang dihasilkan oleh setiap
kegiatan dapat berupa bilangan pecahan. Demikian pula dengan nilai Z yang
dihasilkan.
4. Deterministik (Certainty)
Asumsi ini menyatakan bahwa semua parameter yang terdapat dalam model
Linier Programming (aij, bi, cj) dapat diperkirakan dengan pasti, meskipun
jarang dengan tepat.
2.3. De Novo Programming
Zeleny (1976, 1982, 1986) mengemukakan suatu cara untuk melihat
sistem dimana selain mengoptimalkan sistem yang telah ada, Beliau juga
menyarankan perancangan suatu sistem yang optimal. Yang dititikberatkan pada
membuat suatu desain yang optimal terhadap sistem dengan produktivitas tinggi
yang memiliki beberapa kriteria (multiple criteria).
(Mario T. Tabucanon, Multiple Criteria Making in Industry, 1988).
Terdapat perbedaan mendasar antara pendekatan mengoptimalkan suatu
sistem dengan pendekatan mendesain sistem yang optimum.
1. Pada pendekatan pertama yaitu antara pendekatan Linier Programming,
setiap batasan sumber daya dianggap sudah diberikan atau ditetapkan
sepenuhnya (terdapat sisa), dianggap tidak mempengaruhi produktivitas
sistem.
2. Pada pendekatan kedua, kendala sumber daya akan disusun sedemikian
rupa sehingga tidak menghasilkan sisa. Pendekatan kedua ini dikenal dengan
nama De Novo Programming.
Model Linier Programming digunakan untuk optimasi jenis produk mix
yang terdiri dari satu fungsi tujuan (objective function) dan beberapa batasan
sumber daya (constrain). Formulasi dari Linier Programming adalah sebagai
berikut :
Fungsi Tujuan :
Maksimasi Z = C1X1 + C2X2 + ... + CnXn
Batasan – batasan :
Subject to : a11X1 + a12X2 + ... + a1nXn≤ b1
a21X1 + a22X2 + ... + a2nXn≤ b2
am1X1 + am2X2 + .... + amnXn≤ bm
X1, X2, ..., Xn≥ 0
Pendekatan De Novo Programming dalam menyelesaikan masalah
optimasi dilakukan pendekatan sistem secara total, artinya selain menentukan
kombinasi terbaik yang optimal terhadap outputnya. Pendekatan ini dapat
memberikan suatu usulan penggunaan sumber daya yang terintegrasi melalui
anggaran yang tersedia karena adanya keterbatasan anggaran yang merupakan
Perbedaan dari dua model optimasi antara Linier Programming dan De Novo Programming, ditinjau dari penggunaan sumber daya yang ada yaitu
konstanta bm pada kendala model Linier Programming yang besarnya telah
ditetapkan sebelumnya, sedangkan pada model De Novo Programming dinyatakan
sebagai Xn+1. Ditinjau dari penggunaan tanda kanonik, pada model linier
programming tanda ≤ sebagai batasan bahwa kombinasi variabel keputusan tidak
boleh melebihi dari jumlah sumber (bm) yang telah ditetapkan sebelumnya,
sedangkan pada model De Novo Programming tanda ≤ diganti dengan tanda =
untuk menetukan jumlah sumber (Xn+1) yang diperlukan dengan pasti. Dalam
formulasi pendekatan De Novo Programming (DNP) adalah sebagai berikut :
Fungsi Tujuan :
Maksimasi atau Minimasi : Z = C1X1 + C2X2 + ... + CnXn (2.1)
Batasan – batasan :
Kendala : a11X1 + a12X2 + ... + a1nXn = Xn+1
a21X1 + a22X2 + ... + a2nXn = Xn+2
am1X1 + am2X2 + ...+ amnXn = Xn+m (2.2)
p1Xn+1 + p2Xn+2 + ... + pmXn+m≤ B (2.3)
Xn , Xn+1 , ..., Xn+m ≥ 0
Dimana :
Xn+1 = variabel- variabel keputusan yang menggambarkan jumlah dari sumber i
yang harus dibeli
Pi = harga per unit dari sumber i
Dari formulasi De Novo Programming di atas dapat disederhanakan menjadi suatu persamaan sebagai berikut :
P1a1j + p2a2j + pmamj = vj untuk semua j (2.4)
Dimana :
vj = variabel cost untuk membuat 1 unit produk j, (j = 1, 2, 3, ..., n) aij = koefisien teknologis untuk i = 1, 2, 3, ..., m dan j = 1, 2, 3, ..., m
Dari persamaan (2.4) dapat diuraikan sebagai berikut :
Untuk : v1 = p1a11 + p2a21 + ... + pmam1
v2 = p1a12 + p2a22 + ... + pmam2
vn = p1a1n + p2a2n + ... + pmamn
Apabila dari persamaan (2.2) disubtitusikan ke persamaan (2.3) maka
diperoleh :
p1 (a11X1 + a12X2 + ... + a1nXn) + p2 (a21X1 + a22X2 + ... + a2nXn) + ... + pm
(am1X1 + am2X2 + ... + amnXn) ≤ B (2.5)
Dengan mensubtitusikan persamaan (2.4) dengan persamaan (2.5) di atas
maka didapat persamaan sebagai berikut :
v1X1 + v2X2 + ... + vnXn ≤ B (2.6)
Sehingga formulasi De Novo Programming menjadi :
Maksimasi Z = C1X1 + C2X2 + ... + CnXn
Kendala : v1X1 + v2X2 + ... + vnXn ≤ B
a21X1 + a22X2 + ... + a2nXn ≤ b2
Untuk lebih jelas lagi mengenai perbedaan formulasi dari Linier programming dengan formulasi De Novo Programming dapat dilihat pada Tabel
2.3. (Mario T. Tabucanon, Multiple Criteria Making in Industry :1988)
Tabel 2.3.
Perbedaan Formulasi Linier Programming dengan De Novo Programming
No Model
2. Kendala Sumber Daya :
a11X1 + a12X2 + ... + a1nXn ≤ b1
3. Non Negative Constraint : X1, X2, ..., Xn ≥ 0
Non Negative Constraint :
Xn , Xn+1 , ..., Xn+m ≥ 0
Sumber : Multiple Criteria Making In Industri, Tabucanon, Mario.T., 1988.
2.3.1. Penyelesaian De Novo Programming
Apabila dalam formulasi model De Novo Programming tidak ada
kendala–kendala yang lain, hanya terdiri dari satu fungsi tujuan dan satu kendala
(kendala keterbatasan anggaran), maka penyelesaiannya dengan langkah–langkah
sebagai berikut : (Mario T. Tabucanon, Multiple Criteria Making in Industry,
1988).
Perbandingan (Cj / vj) menggambarkan keuntungan dari produk j (bila fungsi
tujuan adalah memaksimumkan profit) atau nilai tujuan biaya per unit yang
tercapai dari kombinasi sumber – sumber yang digunakan untuk memproduksi
produk j. Tujuan dari langkah ini adalah untuk mencari produk mana yang
paling menguntungkan untuk diproduksi.
2. Untuk Max (Cj / vj) yang diperoleh, katakanlah (Ck / vk) yang
berhubungan dengan variabel Xk, maka jumlah dari Xk yang harus diproduksi
adalah Xk = B / vj, dan Xk merupakan jumlah produk yang paling optimal
yang harus diproduksi.
Dimana :
vj = variabel cost untuk membuat i unit produk j (j = 1, 2, 3, ..., n)
Cj = koefisien biaya yang terdapat pada semua fungsi tujuan
Hal ini menunjukkan bahwa sumber–sumber yang dimiliki akan
digunakan untuk memproduksi produk Xk sebagai produk yang paling
menguntungkan dengan jumlah yang sesuai dengan anggaran (budget), apabila
tidak ada kendala – kendala lain.
Apabila terdapat jumlah permintaan yang terbatas pada setiap produk,
maka formulasi De Novo Programming dapat diselesaikan dengan langkah –
langkah sebagai berikut :
1. Cari Max j (Cj / vj)
2. Untuk Max j (Cj / vj) katakanlah sebagai contoh (Ck / vk) untuk produksi
Xk sedemikian rupa sehingga tidak melampui batas dari permintaan atau batas
3. Jika anggaran tidak digunakan sepenuhnya pada saat memproduksi Xk,
maka cari produk lain yang menguntungkan, selanjutnya dengan
menggunakan Max j (Cj / vj), dimana j ≠ k.
4. Kembali ke langkah (2) sampai anggaran yang ada sudah digunakan
sepenuhnya.
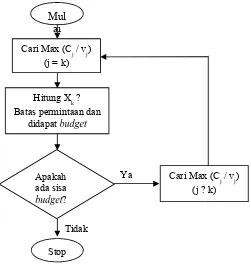
Dari langkah-langkah di atas dapat dibuat suatu diagram alir sebagai berikut :
Gambar 2.2. Diagram Alir Metode De Novo Programming
Sumber : Multiple Criteria Making In Industri, Tabucanon, Mario.T., 1988.
Dengan prosedur penyelesaian di atas, model De Novo Programming akan
memberikan jawaban berupa satu variabel yang paling menguntungkan untuk
diproduksi. Sehingga variabel–variabel keputusan lainnya (produk lain) tidak
akan diproduksi. Apabila model tersebut hanya diketahui kendala–kendala
komposisi sumber (bahan baku) yang kemudian diubah menjadi satu kendala
berupa konstanta anggaran. Hal ini tentu saja kurang memuaskan, karena apabila
perusahaan hanya memproduksi stu produk yang paling menguntungkan saja dan
tidak memproduksi produk–produk yang lain, tentunya usaha perusahaan untuk
memenuhi market share tidak optimal. Hal ini dapat diatasi dengan menambah
kendala batas–batas permintaan tiap produk (demand limits) ataupun kendala lain
yang dianggap perusahaan sudah baku, misalnya kendala kapasitas kemampuan
mesin.
Apabila dalam penyelesaian model De Novo Programming terdapat
adanya kendala–kendala selain kendala bahan baku dan anggaran, yaitu kendala
yang dianggap baku bagi perusahaan, maka dapat diselesaikan dengan
menggunakan metode–metode penyelesaian dalam Linier Programming seperti
dengan metode grafik, apabila hanya memiliki dua variabel keputusan atau
dengan metode simpleks apabila memiliki variabel keputusan lebih dari dua.
Dapat juga diselesaikan dengan menggunakan program komputer.
Model De Novo Programming tidak dapat digunakan untuk menyelesikan
masalah dengan fungsi tujuan berupa minimasi biaya produksi, karena salah satu
kendala dari model tersebut adalah kendala keterbatasan anggaran (budget),
sehingga rencana produksi yang dioptimalkan sudah sesuai dengan biaya yang
disediakan perusahaan.
Perbedaan model De Novo Programming dan model Linier Programming
Tabel 2.4.
Perbedaan Model Linier Programming Dengan Model De Novo Programming
Ditinjau Dari Masalah Mix Produk
No Model
Linier Programming
Model
De Novo Programming 1.
2.
3.
4.
5.
Asumsi bahwa sumber daya terbatas pada
jumlah yang telah ditetapkan sebelumnya.
Analisa sumber telah ditentukan dan
sumber tidak dapat dikendalikan
perolehannya, karena bahan baku tersebut
harus dibeli sesuai dengan ukuran
minimum yang telah ditentukan
sebelumnya.
Tidak sesensitif terhadap faktor harga dari
sumber. Pemberian harga terjadi selama
analisa sensitivitas.
Tidak selalu memiliki kendala
keterbatasan bugdet.
Pada beberapa kasus masih terdapat sisa
penggunaan sumber daya.
Asumsi bahwa sumber daya menjadi
terbatas karena adanya jumlah maksimum
dari bugdet (anggaran).
Analisa dilakukan sebelum sumber dibeli,
belum dapat ditetapkan dan sumber dapat
dikendalikan serta dapat diperoleh atau
dibeli pada tiap satuan.
Sensitif terhadap faktor harga. Sumber telah
diberi harga berdasarkan penetapan harga
aktual.
Faktor keterbatasan bugdet merupakan
elemen penting karena hal ini dijadikan
ukuran dari sumber yang dibutuhkan.
Solusi dari model ini dengan utilitas sumber
yang penuh tanpa adanya sisa.
Sumber : Dasar – dasar Operation Research, Handoko, T.H., Pangestu Subagyo, 1995 dan Multiple Criteria Making In Industri, Tabucanon, Mario.T., 1988.
2.4. Pengertian Biaya
Perkembangan akuntansi sekarang ini banyak konsep–konsep yang
timbul untuk mengartikan dan merumuskan arti biaya walaupun pada dasarnya
sama.
Menurut Mulyadi (1992), “Biaya adalah pengorbanan sumber ekonomi
yang diukur dalam satuan uang yang telah terjadi atau yang kemungkinan terjadi
untuk mencapai tujuan tertentu”.
Menurut Supriyono (1995), “Biaya adalah hanya perolehan yang
pengurang penghasilan”. Sedangkan menurut Usry / Hammer (1993), biaya
didefinisikan sebagai “suatu tukar prasyarat, pengorbanan yang dilakukan guna
memperoleh manfaat”.
2.4.1. Klasifikasi Biaya
Dalam perusahaan pabrikasi, total biaya operasi terdiri dari :
1. Biaya Pabrikasi
Biaya pabrikasi sering disebut juga biaya produksi atau biaya pabrik (factory
cost) adalah jumlah dari unsur biaya yaitu bahan langsung, pekerja langsung
dan overhead pabrik. Bahan langsung dan pekerja langsung dapat
digabungkan ke dalam kelompok biaya utama (primer cost). Upah pekerja
langsung dan overhead pabrik dapat digabungkan ke dalam kelompok biaya
konversi (conversion cost), yang mencerminkan biaya pengubahan bahan
langsung menjadi barang jadi.
a. Bahan langsung
(direct material) adalah semua bahan yang membentuk bagian material dari barang jadi dan yang dimasukkan langsung dalam kalkulasi biaya
produk. Contoh bahan langsung adalah kayu untuk membuat peralatan
mebel, minyak mentah untuk membuat bensin dan kain untuk membuat
pakaian.
b. Pekerja atau tenaga
kerja langsung (direct labour) adalah karyawan yang dikerahkan untuk
mengubah bahan langsung menjadi barang jadi. Biaya untuk ini meliputi
c. Overhead pabrik
(factory overhead) yang juga disebut sebagai overhead pabrikasi, beban pabrikasi atau “beban” pabrik dapat didefinisikan sebagai bahan tidak
langsung, pekerja tidak langsung dan semua biaya pabrikasi lainnya yang
tidak dapat dibebankan langsung ke produk tertentu. Secara sederhana
dapat dinyatakan bahwa overhead pabrik mencakup semua biaya pabrikasi
kecuali yang dicatat sebagai biaya langsung, yaitu bahan langsung dan
pekerja langsung.
d. Bahan tidak langsung
(indirect material) adalah bahan–bahan yang dibutuhkan guna menyelesaikan suatu produk, tetapi pemakainya sedemikian kecil atau
sedemikian rumit, sehingga tidak dianggap sebagai bahan langsung yang
tidak berguna atau tidak ekonomis. Contohnya sekrup, paku, perekat, dan
lain–lain. Bahan–bahan seperti minyak pelumas, minyak gemuk, lap
pembersih dan sikat termasuk dalam perlengkapan pabrik (factory
supplies) yang merupakan bahan tidak langsung yang diperlukan untuk menjaga lokasi kerja dan mesin–mesin tetap dalam kondisi siap pakai dan
aman.
e. Pekerja tidak
langsung (indirect labour) dapat didefinisikan sebagai para karyawan yang
dikerahkan dan tidak secara langsung mempengaruhi pembuatan atau
pembentukan barang jadi Pekerja tidak langsung mencakup gaji penyelia,
pelayan stook, pembantu umum, pekerja bagian pemeliharaan dan
mencakup gaji resepsionis, karyawan bagian arsip, karyawan bagian
pemasok dan seketaris.
2. Beban Komersial
Beban komersial dibagi dalam dua kelompok, yaitu :
a. Beban Pemasaran (Distribusi dan Penjualan)
Beban pemasaran dimulai pada saat biaya pabrik berakhir, yaitu pada saat
proses pabrikasi diselesaikan dan barang–barang sudah dalam kondisi siap
dijual. Beban ini meliputi beban penjualan dan beban pengiriman.
b. Beban Administrasi
Beban administrasi meliputi beban yang dikeluarkan dalam mengatur dan
mengendalikan organisasi. Beberapa dari beban tersebut, seperti gaji
direktur yang ditugaskan bekerja di pabrik, mungkin dialokasikan sebagai
biaya pabrikasi dan gaji direktur yang ditugaskan di bagian pemasaran
mungkin dialokasikan sebagai beban pemasaran. (Milton F. Usry,
Lawrence H. Hammer, Akuntansi Biaya Perencanaan dan Pengawasan
(Cost Accounting) : 1993).
Di bawah ini klasifikasi biaya dalam hubungannya dengan produk pabrik :
Bahan langsung + pekerja langsung =
Bahan tidak langsung + pekerja tidak langsung +
biaya tidak langsung lainnya =
Beban pemasaran + beban administrasi =
Biaya utama
+
Overhead pabrik
=
Biaya pabrikasi
+
Beban komersial
=
Total biaya produksi
Sumber : Akuntansi Biaya Perencanaan dan Pengawasan, Milton F. Usry, Lawrence H. Hammer, 1993.
Keterangan :
a. Bahan tidak langsung, meliputi :
Perlengkapan pabrik
Minyak pelumas
b. Pekerja tidak langsung, meliputi :
Pengawasan
Pemeriksaan
Gaji buruh pabrik
Hasil kerja yang cacat
c. Biaya tidak langsung lainnya, meliputi :
Sewa
Asuransi kebakaran dan kewajiban
Pajak bumi dan bangunan
Penyusutan
Sumber tenaga
Penerangan
Pajak penghasilan pimpinan
Perkakas kecil
Overhead pabrik lainnya
d. Beban pemasaran, meliputi :
Gaji penjualan
Komisi staf penjualan
Pajak penghasilan kerja
Iklan
Contoh barang gratis
Hiburan
Ongkos perjalanan
Sewa
Penyusutan
Pajak bumi dan bangunan
Telepon dan telegraf
Alat tulis menulis dan cetak
Benda–benda pos
Ongkos transportasi/ angkut
Beban penjualan rupa-rupa
e. Beban administrasi, meliputi :
Pajak penghasilan pekerja
Beban pemeriksaan akuntansi
Beban urusan hukum
Piutang yang tidak tertagih
Sewa
Penyusutan
Pajak bumi dan bangunan
Telepon dan telegraf
Alat tulis menulis dan cetak
Benda–benda pos
2.4.2. Penggunaan dari Data Biaya
Pengumpulan, penyajian dan analisa dari data biaya harus dapat memenuhi
kegunaan dan tujuan utama antara lain : (Milton F. Usry, Lawrence H. Hammer,
Akuntansi Biaya Perencanaan dan Pengawasan (Cost Accounting) : 1993).
1. Perencanaan laba melalui penganggaran
2. Pengawasan biaya melalui akunting tanggung jawab
3. Penilaian laba tahunan atau berkala termasuk penilaian persediaan
4. Membantu dalam menetapkan harga jual dan kebijaksanaan harga
5. Menyediakan data biaya yang relevan untuk proses analisis bagi pengambilan
keputusan.
2.4.3. Penggolongan dari Biaya
Penggolongan dari biaya diperlukan untuk pengembangan dari suatu data
biaya, maka biaya digolongkan menjadi : (Milton F. Usry, Lawrence H. Hammer,
Akuntansi Biaya Perencanaan dan Pengawasan (Cost Accounting) : 1993).
1. Menurut sifat dari unsur yang bersangkutan (penggolongan dasar)
2. Menurut masa akunting yang dilaluinya
3. Menurut kecenderungannya untuk berubah sesuai dengan kegiatan produksi.
4. Menurut hubungannya dengan hasil produksi
5. Menurut hubungannya dengan bagian produksi
6. Menurut sifatnya sebagai biaya bersama atau gabungan
7. Untuk perencanaan dan pengawasan
8. Untuk proses anlisis.
2.4.4. Biaya dalam Hubungannya dengan Volume Produksi
Beberapa jenis biaya bervariasi langsung dengan perubahan volume
produksi keluaran, sedang biaya lainnya relative tidak berubah (fixed).
Manajemen harus memperhatikan kecenderungan biaya yang bervariasi dengan
keluaran jika mereka ingin merencanakan suatu strategi perencanaan yang baik
dan mengendalikan biaya dengan berhasil.
1. Biaya Variabel
Secara umum yang dimaksud dengan biaya variabel adalah biaya yang
totalnya berubah secara proporsional dengan perubahan total kegiatan atau
volume yang berkaitan dengan biaya variabel tersebut selama periode tertentu.
Biaya yang mempunyai karakteristik ini umunya meliputi bahan langsung dan
pekerja langsung. Beberapa overhead pabrik dan biaya non pabrikasi juga
termasuk dalam kategori biaya variabel.
a. Biaya yang jumlah totalnya akan berubah secara sebanding
(proporsional) dengan perubahan volume kegiatan, semakin besar volume kegiatan semakin tinggi jumlah total biaya variabel. Semakin rendah
volume kegiatan, semakin rendah jumlah total biaya variabel.
b. Pada biaya variabel, biaya satuan tidak dipengaruhi oleh perubahan
volume kegiatan, jadi biaya satuan konstan.
Yang termasuk overhead pabrik variabel antara lain :
a. Bahan baku
b. Perkakas kecil
c. Upah lembur
d. Pengangkutan dalam pabrik
2. Biaya Tetap
Biaya tetap adalah biaya yang jumlah totalnya tetap selama periode waktu
tertentu meskipun terjadi perubahan besar dalam total kegiatan atau volume
yang berkaitan dengan biaya tetap tersebut.
Karakteristik dari biaya tetap sebagai berikut :
a. Biaya yang jumlah totalnya tetap konstan tidak dipengaruhi oleh
perubahan volume kegiatan atau aktivitas sampai dengan tingkatan
tertentu.
b. Pada biaya tetap, biaya satuan (unit cost) akan berubah berbanding
terbalik dengan perubahan volume kegiatan, semakin tinggi volume
kegiatan semakin rendah biaya satuan. Semakin rendah volume kegiatan
Biaya overhead pabrik berikut ini biasanya diklasifikasikan sebagai
biaya tetap antara lain :
a. Gaji eksekutif produktif
b. Pajak bumi dan bangunan
c. Gaji satpam dan pesuruh pabrik
3. Biaya Semi Variabel
Biaya semi variabel adalah biaya yang mengandung unsur–unsur tetap
dan variabel, yaitu mencakup suatu jumlah yang sebagian tetap dan bagian
lainnya bervariasi sebanding dengan perubahan volume kegiatan selama periode
tertentu. Sebagai contoh biaya listrik yang digunakan untuk penerangan
cenderung lebih tetap, karena berapapun volume produksi penerangan akan tetap
diperlukan. Sebaliknya tenaga listrik yang digunakan untuk pengoperasiannya
akan bervariasi sesuai dengan pemakaian peralatan tersebut.
Karakteristik dari biaya semi variabel sebagai berikut :
a. Biaya yang jumlah totalnya akan berubah sesuai dengan perubahan
volume kegiatan, akan tetapi sifat perubahannya tidak sebanding. Semakin
tinggi volume kegiatan semakin besar jumlah biaya total, semakin rendah
volume kegiatan semakin rendah biaya, tetapi perubahannya tidak sebanding.
b. Pada biaya semi variabel, biaya satuan akan berubah terbalik
dihubungkan dengan perubahan volume kegiatan tetapi sifatnya tidak
sebanding sampai dengan tingkatan kegiatan tertentu. Semakin tinggi volume
kegiatan semakin rendah biaya satuan, semakin rendah volume kegiatan
semakin tinggi biaya satuan.
a. Pemeliharaan dan reparasi mesin
b. Jasa–jasa administrasi pabrik.
Dalam akuntansi tingkah laku biaya dinyatakan dalam persamaan
matematis dalam bentuk garis lurus (linier) yaitu y = a + bx .
dimana :
y = Jumlah total biaya
a = Jumlah total biaya tetap
b = Biaya variabel satuan
x = Volume kegiatan
2.5. Penelitian Terdahulu
Di sini peneliti akan mengemukakan suatu penelitian yang pernah
dilakukan di beberapa perusahaan dengan menggunakan De Novo Programming
antara lain dengan judul :
a. Perencanaan Produksi dengan menggunakan metode De Novo
Programming untuk memperoleh Keuntungan yang Maksimal di PT. Keramik Diamond Industries di Jalan Semeru Desa Bambe Driyorejo Gresik, oleh Dwi
Suhariyanti.
b. Penerapan De Novo Programming pada Perencanaan Produksi dalam
Upaya Meningkatkan Keuntungan di Perusahaan tegel dan Beton Kian Indah
c. Aplikasi De Novo Programming dalam Perencanaan Produksi Pakan Ternak dengan Keuntungan yang Maksimal di PT. Artacitra Terpadu Feedmill
BAB III
METODE PENELITIAN
3.1. Lokasi dan Waktu Penelitian
Lokasi penelitian dilakukan di PT. Varia Usaha Beton yang
memproduksi berbagai jenis beton cetak maupun cair, yang terletak di Jalan
Letjen S. Parman no. 38 Waru - Sidoarjo. Waktu Penelitian dilaksanakan pada
bulan Juli 2009 sampai dengan selesai.
3.2. Identifikasi Variabel
Identifikasi variable adalah dengan memilih konsep–konsep tertentu
yang mempunyai variasi nilai. Agar konsep–konsep dalam pemodelan (metode)
dapat diteliti secara empiris maka harus dioperasionalisasikan dengan
mengubahnya menjadi variabel.
Berdasarkan jenis variabel, maka tujuan dari model program linier yaitu
pencapaian keuntungan yang maksimal, dapat diidentifikasi sebagai variabel
terikat.
Dalam permasalahan yang akan diteliti ini variabel–variabel yang
digunakan adalah :
1. Variabel Terikat
Yang dimaksud variabel terikat adalah variabel yang dipengaruhi oleh
variabel bebas. Variabel tersebut adalah :