PREDIKSI CUACA HARIAN DENGAN BAYESIAN MODEL AVERAGING UNTUK ANTISIPASI BENCANA HIDROMETEOROLOGI

i TUGAS AKHIR – SS141501

PREDIKSI CUACA HARIAN DENGAN BAYESIAN MODEL

AVERAGING UNTUK ANTISIPASI BENCANA

HIDROMETEOROLOGI

MUHAMMAD LUKMAN HAKIM NRP 062114 4000 0038

Dosen Pembimbing Dr. Sutikno, S.Si, M.Si

PROGRAM STUDI SARJANA DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA, KOMPUTASI, DAN SAINS DATA INSTITUT TEKNOLOGI SEPULUH NOPEMBER

ii

iii HALAMAN JUDUL

TUGAS AKHIR – SS141501

PREDIKSI CUACA HARIAN DENGAN BAYESIAN MODEL

AVERAGING UNTUK ANTISIPASI BENCANA

HIDROMETEOROLOGI

MUHAMMAD LUKMAN HAKIM NRP 062114 4000 0038

Dosen Pembimbing Dr. Sutikno, S.Si, M.Si

PROGRAM STUDI SARJANA DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA, KOMPUTASI, DAN SAINS DATA INSTITUT TEKNOLOGI SEPULUH NOPEMBER

iv

v COVER PAGE

FINAL PROJECT – SS141501

DAILY WEATHER PREDICTION USING BAYESIAN

MODEL AVERAGING TO ANTICIPATE

HIDROMETEOROLGY DISASTER

MUHAMMAD LUKMAN HAKIM SN 062114 4000 0038 Supervisor

Dr. Sutikno, S.Si, M.Si

UNDERGRADUATE PROGRAMME DEPARTMENT OF STATISTICS

FACULTY OF MATHEMATICS, COMPUTING, AND DATA SCIENCE INSTITUT TEKNOLOGI SEPULUH NOPEMBER

vi

vii

viii

ix

PREDIKSI CUACA HARIAN DENGAN BAYESIAN MODEL AVERAGING UNTUK ANTISIPASI BENCANA

HIDROMETEOROLOGI

Nama Mahasiswa : Muhammad Lukman Hakim

NRP : 062114 4000 0038

Departemen : Statistika

Dosen Pembimbing : Dr. Sutikno, S.Si, M.Si Abstrak

Indonesia dalam beberapa tahun terakhir mengalami fenomena perubahan iklim. Salah satu dampak darinya yaitu terjadinya bencana hidrometeorologi. Badan Meteorologi, Klimatologi, dan Geofisika atau BMKG dibentuk untuk melaksanakan tugas pemerintahan di bidang Meteorologi, Klimatologi, dan Geofisika. Perlu upaya untuk meningkatkan kualitas dari informasi cuaca yang diberikan. Pada penelitian ini dilakukan kalibrasi prediksi ensemble suhu maksimum, suhu minimum, dan kelembaban menggunakan Bayesian Model Averaging dengan memanfaatkan data observatif stasiun pengamatan BMKG dan data luaran model NWP. Prediksi anggota ensemble yang digunakan berasal dari model PLS, PCR, Regresi Ridge, dan Stepwise Regression. Hasil yang didapatkan prediksi anggota ensemble menghasilkan hasil yang cukup akurat dan masuk kategori sedang-baik. Nilai RMSE yang didapat menujukan bahwa prediksi model PLS dan Regresi Ridge lebih baik daripada dua model lainnya. Sementara hasil BMA menunjukkan bahwa BMA mampu mengatasi kasus underdispersive(nilai prakiraan terpusat pada suatu nilai dengan varians yang rendah) dan ketidakpastian pada prediksi raw ensemble, serta BMA menghasilkan prediksi yang lebih akurat. Selain itu disimpulkan pula bahwa perlu adanya pendekatan statistik dalam memanfaatkan luaran NWP untuk prediksi cuaca.

Kata Kunci : Bayesian Model Averaging, BMKG, Cuaca Harian, Numerical Weather Prediction

x

xi

DAILY WEATHER PREDICTION USING BAYESIAN MODEL AVERAGING TO ANTICIPATE

HIDROMETEOROLOGY DISASTER

Name : Muhammad Lukman Hakim

Student Number : 062114 4000 0038

Department : Statistics

Supervisor : Dr. Sutikno, S.Si, M.Si

Abstract

Indonesia in the last few years has experienced climate change phenomenon. One of the impacts of this is the occurrence of hydrometeorological disaster. BMKG was formed to carry out government duties in the field of Meteorology, Climatology, and Geophysics in accordance with the provisions of applicable legislation. It is necessary to improve the quality of weather information provided. In this research, calibration of ensemble prediction of maximum temperature, minimum temperature, and humidity using Bayesian Model Averaging by using observational data of BMKG observation station and NWP outcomes. The ensemble member predictions used are derived from PLS, PCR, Ridge, and Stepwise Regression models. The results obtained predicted MOS produce results that are quite accurate and into the category of medium-well. The obtained RMSE values indicate that the prediction of PLS and Ridge Regression models is better than the other two models. While the BMA results show that BMA is able to overcome the underdispersive case and uncertainty in predictions of raw ensemble, and BMA produces a more reliable prediction. It is also concluded that statistical approaches in utilizing NWP outcomes for weather prediction are required.

Keyword : Bayesian Model Averaging, BMKG, Daily Weather, Numerical Weather Prediction

xii

xiii

KATA PENGANTAR

Assalamualaikum wr wb. Alhamdulillah segala puji bagi Allah SWT, atas rahmat dan hidayah-Nya penulis dapat menyelesaikan Tugas Akhir yang berjudul Prediksi Cuaca Harian dengan Bayesian Model Averaging untuk Antisipasi Bencana Hidrometeorologi dengan lancar dan tepat waktu.

Tugas Akhir ini dapat diselesaikan tidak lepas dari bimbingan dan dukungan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terimakasih kepada:

1. Kedua orang tua, kakak-kakak, dan keluarga besar penulis yang selalu memberikan doa dan dan dukungan kepada penulis dalam proses penyusunan Tugas Akhir ini.

2. Bapak Dr. Sutikno, S.Si, M.Si selaku dosen pembimbing Tugas Akhir yang telah meluangkan waktu, tenaga dan pikiran untuk membagikan ilmu, saran dan nasehat selama penyusunan Tugas Akhir.

3. Bapak Dr. Bambang Widjanarko O. S.Si, M.Si dan Bapak Prof. Drs. Nur Iriawan MIkom, Ph.D selaku dosen penguji Tugas Akhir yang telah banyak memberikan ilmu, saran, dan masukan kepada penulis untuk kesempurnaan Tugas Akhir ini.

4. Bapak Dr. Suhartono selaku Kepala Departemen Statistika ITS.

5. Bapak Dr. Agus Suharsono, M.S selaku dosen wali penulis, seluruh dosen yang telah memberikan ilmu yang bermanfaat, dan segenap karyawan Departemen Statistika ITS.

6. Semua pihak yang telah memberikan bantuan dan dukungan kepada penulis dalam menyusun Tugas Akhir ini.

Semoga seluruh kebaikan yang diberikan kepada penulis dibalas oleh Allah SWT dengan balasan yang lebih baik. Aamiin.

Penulis menyadari bahwa masih banyak kekurangan dalam Tugas Akhir ini. Penulis mengharapkan kritik dan saran dari

xiv

pembaca. Semoga Tugas Akhir ini dapat memberikan manfaat bagi kita semua.

Surabaya, Juli 2018

Penulis

Muhammad Lukman Hakim

xv

DAFTAR ISI

Halaman

HALAMAN JUDUL... iii

COVER PAGE ...v

LEMBAR PENGESAHAN ... vii

ABSTRAK ... ix

ABSTRACT ... xi

KATA PENGANTAR ... xiii

DAFTAR ISI ...xv

DAFTAR TABEL ... xix

DAFTAR GAMBAR ... xxiii

DAFTAR LAMPIRAN ...xxv BAB I PENDAHULUAN ...1 1.1 Latar Belakang ...1 1.2 Rumusan Masalah ...5 1.3 Tujuan Penelitian ...5 1.4 Manfaat Penelitian ...6 1.5 Batasan Masalah ...6

BAB II TINJAUAN PUSTAKA ...7

2.1 Principal Component Analysis ...7

2.2 Partial Least Square Regression ...9

2.3 Principal Component Regression ...13

2.4 Regresi Ridge ...14

2.5 Stepwise Regression ...15

xvi

2.7 Bayesian Model Averaging ... 17

2.7.1 Bayesian Model Averaging dengan Pendekatan Distribusi Normal ... 19

2.8 Algoritma Expectation Maximization (EM) ... 21

2.8.1 Tahap Expectation pada Algoritma EM ... 22

2.8.2 Tahap Maximization pada Algoritma EM ... 22

2.9 Evaluasi Kebaikan Model ... 23

2.9.1 Root Mean Square Error ... 23

2.9.2 Verification Rank Histogram ... 24

2.9.3 Continuous Ranked Probability Score ... 24

2.9.4 Coverage ... 25

2.10 Numerical Weather Prediction ... 26

2.11 Suhu dan Kelembaban ... 27

BAB III METODOLOGI PENELITIAN ... 29

3.1 Sumber Data ... 29

3.2 Langkah Analisis Data ... 33

BAB IV ANALISIS DAN PEMBAHASAN ... 39

4.1 Deskripsi Suhu Maksimum, Suhu Minimum dan Kelembaban di Lokasi Penelitian ... 39

4.2 Penyusunan Model Prediksi Anggota Ensemble ... 40

4.2.1 Pre-Processing Parameter NWP dengan PCA .... 40

4.2.2 Partial Least Square Regression untuk Prediksi Unsur Cuaca ... 42

4.2.3 Principal Component Regression untuk Prediksi Unsur Cuaca ... 46

xvii

4.2.5 Stepwise Regression untuk Prediksi Unsur

Cuaca ...55

4.3 Kalibrasi Prediksi Unsur Cuaca Dengan Bayesian Model Averaging (BMA) ...60

4.3.1 Penentuan Training Window untuk Analisis BMA ...61

4.3.2 Bayesian Model Averaging untuk Prediksi Unsur Cuaca Stasiun Hasanuddin ...63

4.3.3 Bayesian Model Averaging untuk Prediksi Unsur Cuaca Stasiun Pattimura...70

BAB V KESIMPULAN DAN SARAN ...79

5.1 Kesimpulan ...79

5.2 Saran ...80

DAFTAR PUSTAKA ...83

LAMPIRAN ...87

xviii

xix

DAFTAR TABEL

Halaman

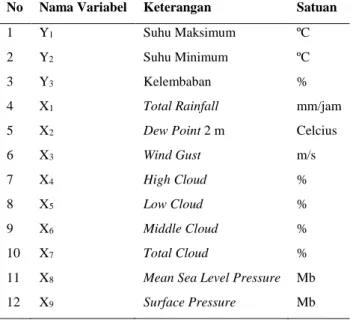
Tabel 3.1 Variabel Penelitian ...29 Tabel 3.2 Struktur Data Penelitian ...31 Tabel 3.3 Struktur Data Estimasi Parameter b0k dan b1k ...35

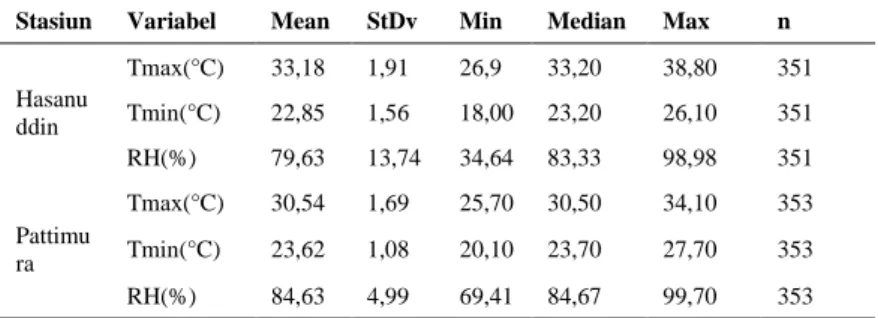
Tabel 4.1 Statistika Deskriptif Suhu Maksimum, Suhu

Mini-mum, dan Kelembaban pada Stasiun Hasanuddin dan Pattimura ...39

Tabel 4.2 Nilai Eigen dan Kum.Varians PCA Parameter

hujan-total ...40

Tabel 4.3 Banyak PC dan Kumulatif Varians Parameter NWP..41 Tabel 4.4 Nilai RMSEP Model PLS Suhu Maksimum, Suhu

Minimum, dan Kelembaban di Stasiun Hasanuddin .42

Tabel 4.5 Nilai RMSEP Model PLS Suhu Maksimum, Suhu

Minimum, dan Kelembaban di Stasiun Pattimura ...43

Tabel 4.6 Model PLS Suhu Maksimum, Suhu Minimum, dan

Kelembaban di Stasiun Hasanuddin ...44

Tabel 4.7 Model PLS Suhu Maksimum, Suhu Minimum, dan

Kelembaban di Stasiun Pattimura ...45

Tabel 4.8 Kumulatif Varians Variabel Prediktor Model PCR di

Stasiun Hasanuddin ...47

Tabel 4.9 Kumulatif Varians Variabel Prediktor Model PCR di

Stasiun Pattimura ...48

Tabel 4.10 Model PCR Suhu Maksimum, Suhu Minimum, dan

Kelembaban di Stasiun Hasanuddin ...49

Tabel 4.11 Model PCR Suhu Maksimum, Suhu Minimum, dan

Kelembaban di Stasiun Pattimura ...50

Tabel 4.12 Nilai Konstanta λ Optimum Hasil Cross Valida-tion

Model Ridge Suhu Maksimum, Suhu Mini-mum, dan Kelembaban ...53

xx

Tabel 4.13 Model Regresi Ridge Suhu Maksimum, Suhu

Mini-mum, dan Kelembaban di Stasiun Hasanuddin ... 53

Tabel 4.14 Model Regresi Ridge Suhu Maksimum, Suhu

Mini-mum, dan Kelembaban di Stasiun Pattimura ... 55

Tabel 4.15 Variabel Prediktor Model Stepwise Regression

Su-hu Maksimum, SuSu-hu Minimum, dan Kelembaban di Stasiun Hasanuddin ... 56

Tabel 4.16 Model Stepwise Regression Suhu Maksimum, Suhu

Minimum, dan Kelembaban Unsur Cuaca di Stasiun Hasanuddin ... 57

Tabel 4.17 Variabel Prediktor Model Stepwise Regression

Suhu Maksimum, Suhu Minimum, dan Kelembaban di Stasiun Pattimura ... 57

Tabel 4.18 Model Stepwise Regression Suhu Maksimum, Suhu

Minimum, dan Kelembaban di Stasiun Pattimura .... 58

Tabel 4.19 RMSE Hasil Predikisi Tmaks, Tmin, dan RH

de-ngan Pendekatan MOS ... 59

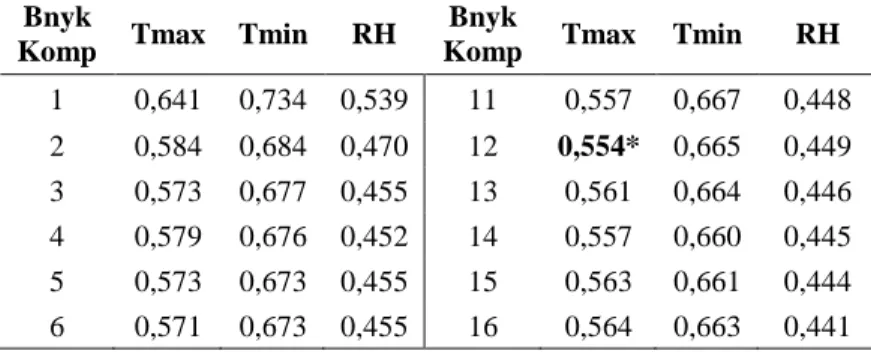
Tabel 4.20 Hasil Penentuan Training Window untuk Kalibrasi

Prediksi Ensemble dengan BMA ... 62

Tabel 4.21 Parameter Koefisien Bias, Bobot, dan Varians Suhu

Maksimum, Suhu Minimum, dan Kelembaban Periode 01 Sep 2016 di Stasiun Hasanuddin ... 63

Tabel 4.22 Nilai Mean dan Varians BMA Suhu Maksimum,

Suhu Minimum, dan Kelembaban Periode 01 Sep 2016 di Stasiun Hasanuddin ... 64

Tabel 4.23 RMSE Hasil Prediksi Model MOS, Raw Ensemble,

dan BMA Suhu Maksimum, Suhu Minimum, dan Kelembaban di Stasiun Hasanuddin Periode Testing ... 68

Tabel 4.24 Coverage dan CRPS Hasil Prediksi Model MOS,

xxi

Minimum, dan Kelembaban di Stasiun Hasanuddin Periode Testing ...68

Tabel 4.25 Parameter Koefisien Bias, Bobot, dan Varians Suhu

Maksimum, Suhu Minimum, dan Kelembaban Periode 01 Sep 2016 di Stasiun Pattimura ...71

Tabel 4.26 Mean dan Varians BMA Suhu Maksimum, Suhu

Minimum, dan Kelembaban Periode 01 Sep 2016 di Stasiun Pattimura ...72

Tabel 4.27 RMSE Hasil Prediksi Suhu Maksimum, Suhu

Mi-nimum, dan Kelembaban di Stasiun Pattimura Periode Testing ...75

Tabel 4.28 Coverage dan CRPS Hasil Prediksi Suhu

Mak-simum, Suhu Minimum, dan Kelembaban di Sta-siun Pattimura Periode Testing ...76

xxii

xxiii

DAFTAR GAMBAR

Halaman

Gambar 2.1 Ilustrasi Penggunaan Training Window ...20 Gambar 2.2 Kriteria Pola Verification Rank Histogram...24 Gambar 2.3 Ilustrasi Perbedaan Kondisi Cuaca (a) Dunia

Nya-ta dan (b) NWP (Linacre & Geerts, 2003) ...27

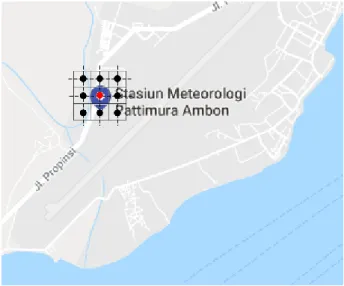
Gambar 3.1 Ilustrasi Pengukuran Parameter NWP pada Grid 3

x 3 ...32

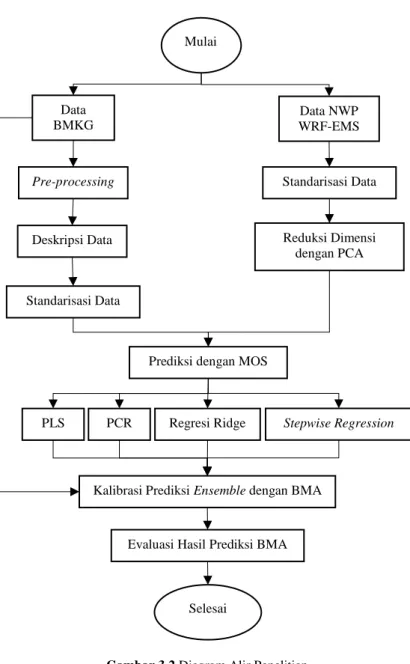
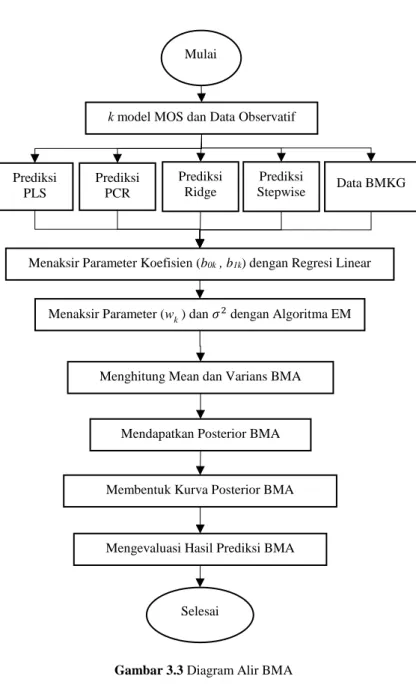
Gambar 3.2 Diagram Alir Penelitian ...37 Gambar 3.3 Diagram Alir BMA ...38 Gambar 4.1 Konvergensi Koefisien Regresi Ridge Stasiun

Ha-sanuddin. (a) Suhu Maksimum, (b) Suhu Mi-nimum, (c) Kelembaban ...51

Gambar 4.2 Konvergensi Koefisien Regresi Ridge Stasiun

Pa-ttimura. (a) Suhu Maksimum, (b) Suhu Mi-nimum, (c) Kelembaban ...52

Gambar 4.3 Verification Rank Histogram Tmaks MOS

Stasi-un Hasanuddin ...60

Gambar 4.4 Perbandingan Nilai CRPS (a), RMSE (b), dan

Co-verage (c) untuk Penentuan Training Window pada Tmaks Stasiun Hasanuddin ...62

Gambar 4.5 Perbandingan Kurva Posterior Prediktif untuk

Su-hu Maksimum 01 Sep 2016 di Stasiun Hasanuddin ...65

Gambar 4.6 Perbandingan Kurva Posterior Prediktif Suhu

Mi-nimum 01 Sep 2016 di Stasiun Hasanuddin ...66

Gambar 4.7 Perbandingan Kurva Posterior Prediktif

xxiv

Gambar 4.8 VRH Prediksi BMA Suhu Maksimum (a), Suhu

Minimum (b), dan Kelembaban (c) di Stasiun Hasanuddin ... 70

Gambar 4.9 Perbandingan Kurva Posterior Prediktif Suhu

Maksimum 01 Sep 2016 di Stasiun Pattimura .... 73

Gambar 4.10 Perbandingan Kurva Posterior Prediktif Suhu

Minimum 01 Sep 2016 di Stasiun Pattimura ... 74

Gambar 4.11 Perbandingan Kurva Posterior Prediktif

Kele-mbaban 01 Sep 2016 di Stasiun Pattimura ... 74

Gambar 4.12 VRH Prediksi BMA Tmaks (a), Tmin (b), dan

xxv

DAFTAR LAMPIRAN

Halaman

Lampiran 1 Data Observasi Suhu Maksimum, Suhu Minimum

Kelembaban Stasiun Hasanuddin ...87

Lampiran 2 Data Observasi Suhu Maksimum, Suhu Minimum

Kelembaban Stasiun Pattimura ...88

Lampiran 3 Data NWP WRF-EMS Stasiun Hasanuddin ...89 Lampiran 4 Data NWP WRF-EMS Stasiun Pattimura ...90 Lampiran 5 Eigen Vektor PC pada Stasiun Hasanuddin ...91 Lampiran 6 Eigen Vektor PC pada Stasiun Pattimura ...92 Lampiran 7 Hasil Prediksi MOS Suhu Maksimum Stasiun

Ha-sanuddin ...94

Lampiran 8 Hasil Prediksi MOS Suhu Minumum Stasiun

Ha-sanuddin ...95

Lampiran 9 Hasil Prediksi MOS Kelembaban Stasiun

Hasa-nuddin ...96

Lampiran 10 Hasil Prediksi MOS Suhu Maksimum Stasiun

Pattimura ...97

Lampiran 11 Hasil Prediksi MOS Suhu Minimum Stasiun

Pa-ttimura ...98

Lampiran 12 Hasil Prediksi MOS Kelembaban Stasiun

Patti-mura...99

Lampiran 13 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Suhu Maksimum Stasiun Hasanuddin ...100

Lampiran 14 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Suhu Minimum Stasiun Hasanuddin ...100

xxvi

Lampiran 15 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Kelembaban Stasiun Hasanuddin ... 101

Lampiran 16 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Suhu Maksimum Stasiun Pattimura ... 102

Lampiran 17 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Suhu Minimum Stasiun Pattimura ... 102

Lampiran 18 Perbandingan CRPS, RMSE, dan Coverage

Un-tuk Penentuan Training Window BMA Kelembaban Stasiun Pattimura... 103

Lampiran 19 Estimasi Koefisien Regresi BMA Suhu

Maksi-mum Stasiun Hasanuddin ... 104

Lampiran 20 Estimasi Bobot, Standar Deviasi dan Prediksi

BMA Suhu Maksimum Stasiun Hasanuddin ... 105

Lampiran 21 Estimasi Koefisien Regresi BMA Suhu

Mini-mum Stasiun Hasanuddin ... 106

Lampiran 22 Estimasi Bobot, Standar Deviasi dan Prediksi

BMA Suhu Minimum Stasiun Hasanuddin ... 107

Lampiran 23 Estimasi Koefisien Regresi BMA Kelembaban

Stasiun Hasanuddin ... 108

Lampiran 24 Estimasi Bobot dan Standar Deviasi BMA

Kele-mbaban Stasiun Hasanuddin ... 109

Lampiran 25 Estimasi Koefisien Regresi BMA Suhu

Mak-simum Stasiun Pattimura ... 110

Lampiran 26 Estimasi Bobot, Standar Deviasi dan Prediksi

BMA Suhu Maksimum Stasiun Pattimura ... 111

Lampiran 27 Estimasi Koefisien Regresi BMA Suhu

xxvii

Lampiran 28 Estimasi Bobot dan Standar Deviasi BMA Suhu

Minimum Stasiun Pattimura...113

Lampiran 29 Estimasi Koefisien Regresi BMA Kelembaban

Stasiun Pattimura ...114

Lampiran 30 Estimasi Bobot dan Standar Deviasi BMA

Ke-lembaban Stasiun Pattimura ...115

Lampiran 31 Program Reduksi Dimensi Parameter NWP

de-ngan PCA ...116

Lampiran 32 Program Pembentukan Model MOS ...117 Lampiran 33 Program Kalibrasi Prediksi Ensemble dengan

BMA ...125

xxviii

1 BAB I PENDAHULUAN

1.1 Latar Belakang

Indonesia merupakan negara yang terletak pada koordinat 6º LU-11º LS dan 95º BT-141º BT. Letaknya yang berada pada garis khatulistiwa menyebabkan Indonesia memiliki iklim tropis. Salah satu ciri wilayah yang memiliki iklim tropis yaitu adanya dua musim yang terjadi pada wilayah tersebut. Indonesia sebagai negara beriklim tropis memiliki dua musim setiap tahunnya, yaitu musim hujan dan kemarau. Menurut Aldrian, Karmini & Budiman (2011) iklim di Indonesia tergolong unik karena lokasinya berada di daerah tropis dan wilayahnya berbentuk kepulauan serta letak geografis yang berada diantara dua samudra. Namun akhir-akhir ini telah terjadi perubahan iklim di Indonesia yang diakibatkan oleh aktivitas manusia yang menyumbang bertambahnya gas rumah kaca. Perubahan iklim di Indonesia ditandai oleh beberapa hal, diantaranya: peningkatan rata-rata suhu tahunan sekitar 0.3ºC sejak 1990, penurunan curah hujan sebesar 2-3% sejak 1990, dan perubahan pola musim hujan dan kemarau (World Bank Group, 2011).

Salah satu dampak adanya perubahan iklim yaitu terjadinya bencana alam meteorologi atau bencana hidrome-teorologi. Bencana hidrometeorologi adalah bencana alam yang berhubungan dengan iklim (Qodriyatun, 2013). Bencana ini juga dikenal sebagai bencana yang diakibatkan oleh faktor-faktor meteorologi, seperti: curah hujan, suhu, angin, dan kelembaban. Beberapa contoh bencana hidrometeorologi adalah kekeringan, banjir, tanah longsor, kebakaran hutan, el nino, la nina, puting beliung, gelombang panas, dan gelombang dingin. Indonesia termasuk salah satu negara yang rentan terjadi bencana hidrometeorologi. Menurut Kepala Pusat Data Informasi dan Humas BNPB dalam CNN Indonesia, pada tahun 2016 dari 2.342 bencana 92% diantaranya adalah bencana hidrometeorologi yang didominasi 1

banjir, longsor, dan puting beliung (Ratnasari & Lumbanrau, 2016).

Badan Meteorologi, Klimatologi, dan Geofisika atau BMKG memiliki tugas melaksanakan tugas pemerintahan di bidang Meteorologi, Klimatologi, dan Geofisika sesuai dengan ketentuan perundang-undangan yang berlaku. Salah satu fungsi untuk melaksanakan tugas tersebut melakukan pelayanan data dan informasi di bidang meteorologi, klimatologi, dan geofisika. Berbagai cara telah dilakukan oleh BMKG untuk melaksanakan tugasnya diantaranya: melakukan pengamatan dan prediksi cuaca berupa curah hujan, suhu, dan kelembaban. Melihat pentingnya hasil kajian BMKG, maka perlu adanya ketepatan hasil prediksi cuaca yang dilakukan oleh BMKG. Salah satu masalah yang dihadapi BMKG dalam pemberian informasi prakiraan cuaca harian adalah belum adanya model prakiraan cuaca objektif yang dapat dioperasionalkan. Dikarenakan BMKG belum memiliki Numerical Weather Prediction (NWP) yang merupakan model prakiraan cuaca numerik, maka metode yang digunakan untuk menyediakan prakiraan cuaca objektif yaitu produk dari negara lain seperti: European Centre for Medium-Range Weather Forecast (ECMWF), Weather Research Forecast (WRF), National Centers for Enviromental Prediction (NCEP), ARPEGE, CCAM, dan lain-lain (Haryoko, 2014).

Dalam melakukan prediksi, model NWP melakukan penyederhanaan dan homogenisasi pada kondisi permukaan sementara atmosfer diperlakukan sebagai media yang terdiri dari bujur sangkar sehingga sulit untuk menangkap kondisi-kondisi spasial seperti keadaan topografi, vegetasi, dan jenis tanah yang merupakan komponen penting dalam prediksi cuaca lokal, sehingga seringkali terjadi kesalahan dalam prediksi cuaca yang berdampak tidak dapat dipercayanya hasil prediksi cuaca dari model NWP (Idowu & Rautenbach, 2008). Salah satu upaya yang dapat dilakukan untuk mendapatkan hasil prediksi cuaca yang lebih akurat yaitu dengan melakukan analisis statistical

post-processing. Pendekatan ini merupakan pendekatan statistika yang diterapkan pada bidang meteorologi dalam menghasilkan model serta prediksi. Sebagaimana disampaikan oleh Wilks (2006) bahwa pendekatan statistika diperlukan dalam mereinterpretasi luaran NWP yang dinamis. Model Output Statistik (MOS) merupakan salah satu metode post-processing yang digunakan untuk melakukan prediksi cuaca objektif melalui hubungan statistik antara variabel prediktor dengan variabel respon oleh model objektif pada beberapa proyeksi waktu (Glahn & Lowry, 1972). Kalnay (2003) juga mengatakan bahwa MOS pada dasarnya adalah regresi linear berganda dengan prediktor adalah model prakiraan cuaca seperti suhu, kelembaban, atau angin pada titik grid baik dekat permukaan atau jauh dari permukaan, serta variabel respon berupa output dari stasiun pengamatan cuaca. Pendekatan ini dapat diterapkan di Indonesia dengan memanfaatkan luaran stasiun pengamatan BMKG sebagai variabel respon serta luaran NWP sebagai variabel prediktor.

Beberapa pendekatan yang dapat digunakan dalam MOS diantaranya yaitu Partial Least Square Regression (PLS), Principal Component Regression (PCR), regresi ridge, dan stepwise regression. Dalam pemodelan berbasis regresi yang melibatkan data NWP sebagai variabel prediktor seringkali ditemukan kasus multikolinearitas. Menurut Narendra (2017), metode PLS, PCR, dan regresi ridge mampu mengatasi permasalahan multikolinearitas antar variabel karena keadaan data NWP yang berdimensi besar (skala global). Namun seringkali penggunaan MOS dalam memprediksi cuaca masih menghasilkan bias yang cukup tinggi. Untuk meningkatkan performansi model, salah satu pendekatan yang dapat dilakukan yaitu melakukan kalibrasi prediksi ensemble. Pendekaatan ini berangkat dari ensemble prediction system (EPS) yang kemudian dikalibrasi untuk mengatasi permasalahan underdispersive dan overdispresive. Sebagaimana dikatakan oleh Schmeits & Kok (2010) bahwa EPS memiliki kemampuan yang tinggi, namun untuk prediksi jangka menengah masih bersifat underdispersive atau

overdispresive. Underdispersive dan overdispresive menyebabkan hasil prediksi menjadi kurang reliabel. Menurut Jolliffe & Stephenson (2003) untuk meningkatkan reliabilitas dari suatu prediksi dapat menggunakan kalibrasi statistik. Salah satu metode kalibrasi prediksi ensemble yang umum digunakan yaitu Bayesian Model Averaging (BMA).

BMA merupakan metode ensemble post processing yang menghasilkan prediksi probabilistik dari rata-rata terboboti distribusi probabilistik model anggota ensemble, dengan bobot yang digunakan merupakan probabilitas posterior dari model anggota ensemble yang mencerminkan kontribusi relatif model tersebut dalam melakukan prediksi selama periode training (Raftery, Gneiting, Balabdaoui & Polakowski , 2005). Dalam penelitiannya Raftery, et al. (2005) menerapkan kalibrasi ensemble menggunakan BMA dalam memprediksi suhu permukaan di Pasific Northwest pada bulan Januari sampai Juni tahun 2000. Hasil yang didapatkan dari penelitian tersebut membuktikan bahwa BMA memberikan hasil kalibrasi yang baik dan mampu mengatasi permasalahan underdispersive dan overdispresive baik pada kasus riil maupun studi simulasi. Putera (2017) melakukan penelitian untuk memprediksi cuaca jangka pendek yang memanfaatkan luaran BMKG sebagai variabel respon serta luaran NWP sebagai variabel prediktor dengan menggunakan metode BMA dan GOP. Hasil yang didapatkan akurasi dan presisi hasil prediksi BMA lebih tinggi daripada GOP, dan BMA mampu mengkalibrasi prakiraan suhu udara dengan coverage yang dihasilkan sudah mendekati standar 50%. Selain itu Anggraeni (2013) dalam penelitiannya juga melakukan kalibrasi peramalan ensemble data curah hujan menggunakan EMOS dan BMA. Dari hasil penelitiannya didapatkan metode yang memberikan hasil prediksi terbaik berdasarkan nilai CRPS yaitu dengan BMA-EM. Sloughter, et al (2006) dalam penelitiannya melakukan prediksi curah hujan harian menggunakan Bayesian Model Averaging dengan pendekatan power-transformed gamma distributions. Hasil penelitiannya menunjukkan bahwa metode BMA mampu mengkalibrasi dengan

baik prediksi curah hujan serta mampu menghasilkan prediksi yang lebih baik daripada dengan anggota ensemble.

Sebagaimana telah disebutkan sebelumnya bahwa penting bagi BMKG untuk memberikan informasi prediksi cuaca sebaik dan seakurat mungkin. Selain itu jika melihat tingginya angka bencana hidrometeorologi di Indonesia, maka dalam penelitian ini dilakukan prediksi cuaca harian yang meliputi variabel suhu maksimum, suhu minimum, dan kelembaban dengan Bayesian Model Averaging. Diharapakan hasil penelitian ini dapat memberikan akurasi prediksi cuaca harian yang akurat dan reliabel sehingga mampu membantu BMKG dalam memberikan informasi prediksi cuaca yang akurat serta membantu pemerintah dalam upaya pencegahan bencana hidrometeorologi.

1.2 Rumusan Masalah

Berdasarkan uraian sebelumnya dikatakan bahwa penting bagi BMKG memberikan hasil prediksi cuaca yang tepat sebagai bentuk antisipasi menghadapi potensi bencana hidrometeorologi. MOS merupakan satu metode yang digunakan untuk menghasilkan prediksi cuaca harian dengan memanfaatkan luaran BMKG dan NWP. Dalam penelitian ini dilakukan prediksi suhu maksimum (Tmax), suhu minimum (Tmin), dan kelembaban (Rh) harian dengan empat pendekatan metode MOS yaitu Partial Least Square Regression (PLS), Principal Component Regression (PCR), regresi ridge, dan stepwise regression. Selanjutnya dilakukan kalibrasi prediksi dari hasil keempat metode tersebut menggunakan Bayesian Model Averaging (BMA). Setelah itu, akan dikaji bagaimana performansi hasil kalibrasi prediksi BMA dengan RMSE, coverage, dan Continuous rank probability score (CRPS).

1.3 Tujuan Penelitian

Berdasarkan rumusan masalah di atas, tujuan yang ingin dicapai oleh peneliti dalam penelitian ini yaitu.

1. Mendapatkan prediksi cuaca harian menggunakan MOS dengan pendekatan metode PLS, PCR, regresi ridge, dan stepwise regression.

2. Mendapatkan hasil prediksi cuaca harian dari hasil kalibrasi ensemble menggunakan BMA.

3. Melakukan evaluasi prediksi dengan RMSE, verification rank histogram, dan Continuous rank probability score (CRPS).

1.4 Manfaat Penelitian

Bagi BMKG diharapkan penelitian ini dapat memberikan model prediksi cuaca harian yang menghasilkan hasil prediksi lebih akurat dan reliabel. Selain itu dalam dunia pendidikan diharapkan penelitian ini dapat memberikan informasi terkait penerapan statistik khususnya metode BMA dalam melakukan prediksi cuaca harian.

1.5 Batasan Masalah

Ruang lingkup yang digunakan dalam penelitian ini dibatasi pada beberapa stasiun meteorologi terpilih yaitu Stasiun Meteorologi Hasanuddin dan Pattimura. Selain itu, dalam kalibrasi prediksi pendekatan metode BMA yang digunakan adalah pendekatan BMA-EM berdistribusi normal.

2 BAB II

TINJAUAN PUSTAKA

2.1 Principal Component Analysis

Sebelum dilakukan pemodelan dengan MOS, terlebih dahulu dilakukan reduksi dimensi sebagai bentuk pre-processing pada data. Principal Component Analysis (PCA) merupakan salah satu metode yang mampu mereduksi dimensi data. Menurut Jolliffe (2002) PCA merupakan salah satu teknik analisis multivariat yang paling tua dan terkenal. Selain itu Jolliffe (2002) juga mengatakan bahwa gagasan utama PCA adalah mereduksi dimensi data ketika terdapat banyak variabel yang saling berkorelasi dengan mengubahnya menjadi principal conponent (PC) yang tidak berkorelasi, namun tetap mempertahankan sebanyak mungkin variasi yang ada pada data. Untuk membentuk komponen utama atau PC, dapa digunakan matriks korelasi atau matriks varians-kovarians. Matriks varians-kovarians biasa digunakan ketika satuan pengukuran data antar variabel sama, sementara matrik korelasi biasa digunakan ketika satuan pengukuran data antar variabel berbeda. Namun matriks varians-kovarians bisa digunakan apabila terlebih dahulu dilakukan standarisasi pada data untuk menghasilkan matriks varians-kovarians yang serupa dengan matriks korelasi dari data sebelum distandarisasi (Jolliffe, 2002). Hasil dari PCA dapat digunakan sebagai input dalam beberapa analisis seperti regresi berganda, analisis klaster, dan analisis faktor (Johnson & Wichern, 2007).

Secara aljabar linear, PC merupakan kombinasi linear dari p variabel random (Johnson & Wichern, 2007). Apabila suatu vektor random 𝐱 = [𝑥1, 𝑥2, … , 𝑥𝑘]′ mempunyai matriks varians-kovarians

𝚺 dengan eigenvalue 𝜆1 ≥ 𝜆2≥ ... ≥ 𝜆𝑝≥ 0, maka kombinasi

linear utama dapat ditunjukkan pada persamaan (2.1)

1 1 11 1 21 2 1 2 2 12 1 22 2 2 1 1 22 2 PC ... PC ... PC ... k k k k k k k kk e x e x e x e x e x e x e x e x e x = = + + + = = + + + = = + + + ' ' ' e x e x e x (2.1) dengan,

PC1 = PC pertama yang memiliki varians terbesar

PC2 = PC kedua yang memiliki varians terbesar kedua

PCk = PC ke-k yang memiliki varians terbesar ke-k

𝑥1 = Variabel random pertama

𝑥2 = Variabel random kedua

𝑥𝑘 = Variabel random ke-k

𝒆𝟏 = Eigenvector PC pertama

𝒆𝟐 = Eigenvector PC kedua

𝒆𝒌 = Eigenvector PC ke-k

Secara umum, model PC ke-i dapat ditulis seperti persamaan (2.2)

PC_i=e x_i' , dengan i = 1,2,...,k (2.2) Varians dan kovarians untuk PC ke-i dituliskan

var(PC )_i =e Σe_i' _i=



_i, dengan i = 1,2,...,k (2.3)

cov(PC ,PC )_{i m} =e Σe'_{i m} =0, dengan i = 1,2,...,k dan i≠k (2.4) PC yang dihasilkan tidak saling berkorelasi dan memiliki varians yang sama dengan eigenvalue dari matriks varians -kovarians 𝚺. Total varians dapat dihitung menggunakan persamaan (2.5).

11 22 1 1 2 1 var( ) ... var(PC ) ... k i kk i k i k i x       = = = + + + = + + +





(2.5)

Dan persentase varians total yang mampu dijelaskan oleh PC ke-i dapat dihitung dengan persamaan (2.6)

Proporsi varians PC ke-i

1 2 ... i k     = + + + (2.6)

Apabila PC yang digunakan sebanyak m, maka total varians yang dapat dijelaskan dapat dihitung dengan persamaan (2.7).

Proporsi varians m PC 1 2 1 2 ... ... m k       + + + = + + + , dengan (m < k) (2.7) Dalam melakukan analisis PCA tidak semua PC harus diambil. Menurut Johnson & Wichern (2007) dan Jolliffe (2002) kriteria yang digunakan sebagai acuan untuk menentukan jumlah PC yang diambil diantaranya yaitu.

1. Memilih berdasarkan banyak eigenvalue dari PC yang lebih besar dari satu. Pemilihan ini dikhususkan apabila PC didapatkan dari matriks korelasi

2. Memilih banyak PC yang memberikan kumulatif persentase varians sebesar 80% - 90%

2.2 Partial Least Square Regression

Partial Least Square Regression (PLS) merupakan metode berbasis regresi yang menghubungkan dua matriks data X dan Y dengan menggunakan model linear multivariat (Wold, Sjostrom, & Eriksson, 2001). PLS mengkombinasikan PCA dengan regresi multivariat untuk memprediksi variabel respon berdasarkan variabel prediktor. Prediksi didapatkan dengan mengeskstraksi sejumlah komponen, yang disebut variabel laten, dari variabel prediktor (Wigena, 2011). Wold, et al (2001) mengatakan bahwa PLS mampu menganalisis data yang berkorelasi kuat dan memiliki banyak variabel prediktor serta mampu memodelkan beberapa variabel respon secara simultan. Menurut Voght (1990) dalam (Wigena & Aunuddin, 1998) proses penentuan model dilakukan

secara iterasi dengan struktur variasi dalam varibel respon mempengaruhi komponen kombinasi linear dalam variabel prediktor dan sebaliknya.

Jika sebanyak q variabel respon Y1,Y2,...,Yq diprediksi

dengan p variabel prediktor X1,X2,...,Xp dengan jumlah sampel

sebanyak n, maka pasangan variabel tersebut dapat dituliskan (𝑥_𝑡′_𝑦

𝑡′), dengan t = 1,2,...,n. Tahap awal dari metode PLS yaitu

melakukan standarisasi pada data. Tujuan standarisasi ini yaitu untuk memperoleh pembobot yang memiliki satuan pengukuran sama antar variabel. Standarisasi dapat dilakukan dengan mengurangi data pengamatan dengan rata-rata dan membagi dengan standar deviasinya, seperti ditunjukkan pada persamaan (2.8). * * tu u tu u tr r tr r x x x s y y y s − = − = (2.8) dengan,

𝑥𝑡𝑢∗ = observasi ke-t untuk variabel prediktor ke-u yang sudah

distandarisasi, dengan u = 1,2,...,p

𝑦𝑡𝑟∗ = observasi ke-t untuk variabel respon ke-r yang sudah

distandarisasi, dengan r = 1,2,...,q u

x = rata-rata variabel prediktor ke-u r

y = rata-rata variabel respon ke-y su = standar deviasi prediktor ke-u sr = standar deviasi respon ke-r

Kemudian 𝒙𝒕 = (𝑥𝑡1, 𝑥𝑡2, … , 𝑥𝑡𝑝) ′

dikumpulkan dalam matriks X (𝑛 × 𝑝), begitu pula 𝒚𝒕= (𝑦𝑡1, 𝑦𝑡2, … , 𝑦𝑡𝑟)′

dikumpulkan dalam matriks Y (𝑛 × 𝑞), yang dapat dituliskan seperti persamaan (2.9).

;         =_{ } =_{ }         ' ' 1 1 ' ' n n x y X Y x y (2.9)

Jika n adalah banyak pengataman, dan p adalah banyak variabel prediktor. Apabila terjadi kondisi 𝑛 < 𝑝, maka metode regresi yang umum digunakan seperti Oridinary Least Square (OLS) tidak dapat digunakan karena akan menghasilkan matriks kovarian

(

X X yang singular. Namun metode PLS mampu '

)

mengatasi kasus kondisi 𝑛 < 𝑝. PLS melakukan reduksi dimensi dan pemodelan regresi secara simultan, T yang dinotasikan sebagai variabel laten atau scores merupakan hasil dari sebuah dekomposisi matriks dari variabel acak observasi, sementara itu, P disebut dengan X-loadings dan Q disebut dengan Y-loadings. Regresi PLS didasarkan pada dekomposisi komponen laten yang ditunjukkan pada persamaan (2.10).

' ' = + = + X TP E Y TQ F (2.10) dengan,

T = matriks komponen laten (scores matrices) untuk n

pengamatan yang berukuran 𝑛 × 𝑐

P = matriks koefisien (loading matrices) variabel X yang

berukuran 𝑝 × 𝑐

Q = matriks koefisien (loading matrices) variabel Y yang

berukuran 𝑞 × 𝑐

E dan F = matriks residual

PLS sama seperti regresi komponen utama merupakan metode yang membentuk matriks komponen laten T sebagai transformasi linier X. Hal tersebut dapat ditunjukkan pada persamaan (2.11).

=

W adalah matriks weight (pembobot) yang berukuran 𝑝 × 𝑐. Dengan c adalah banyak komponen laten. Selanjutnya W dan T dinotasikan sebagai 1 j j pj w w     =       w dan 1 j j nj t t     =       t , untuk j = 1,2,...,c

Komponen laten digunakan untuk melakukan prediksi terhadap Y, menggantikan variabel asalnya yaitu X. Ketika T sudah terbentuk maka Q diperoleh melalui metode kuadrat ' terkecil seperti pada persamaan (2.12).

(

)

1

ˆ '= ' − '

Q T T T Y (2.12)

Dengan demikian matriks B adalah matriks koefisien regresi untuk model Y=XB+F diperoleh melalui persamaan (2.13).

' = + Y TQ F (dari persamaan 2.10) ' ' '  =  =  = XB TQ XB XWQ B WQ (2.13)

Sehingga dapat diperoleh penaksir untuk B adalah

(

)

1

ˆ _' − _'

=

B W T T T Y (2.14)

maka dugaan Y diperoleh berdasarkan persamaan (2.15).

(

)

(

)

(

)

1 1 -1 -1 ˆ ˆ ˆ ˆ − − =   =       =     Y XB Y TW W T'T T'Y Y TI T'T T'Y = T T'T Y (2.15)

2.3 Principal Component Regression

Principal Component Regression (PCR) merupakan suatu metode yang digunakan untuk mengatasi kasus regresi yang dihadapkan pada tingginya korelasi pada variabel-variabel prediktor. PCR melakukan regresi variabel respon terhadap komponen utama yang merupakan kombinasi linear dari variabel prediktor (Draper & Smith, 1992). Pembetukan komponen utama atau PC sebagaimana dijelaskan pada poin 2.1 bahwa terdapat dua cara dalam pembentukannya, yaitu dengan matiks varians-kovarians dan matriks korelasi. Pemilihan keduanya didasarkan pada satuan pengukuran antar variabel. Dalam penelitian ini, pengolahan data akan dilakukan menggunakan matriks varians-kovarians dengan terlebih dahulu melakukan standarisasi pada data. Pembentukan PC dilakukan dengan mereduksi dimensi data. Reduksi dilakukan dengan menghilangkan korelasi antar variabel melalui transformasi variabel asal ke variabel baru (PC). Kemudian penentuan jumlah PC yang diambil dilakukan berdasarkan kriteria-kriteria seperti mengambil banyak PC yang memberikan kumulatif persentase varians sebesar 80% - 90% (Johnson & Wichern, 2007) sebagaimana telah dijelaskan pada poin 2.1. Selanjutnya PC yang didapat sudah tidak saling berkorelasi sehingga dapat dijadikan prediktor pada analisis regresi (Jolliffe, 2002).

Misal 𝐱𝒕= [𝑥1, 𝑥2, … , 𝑥𝑘]′ merupakan vektor prediktor dari

matriks X berukuran 𝑛 × 𝑝. Jika matriks A adalah matriks ortogonal berukuran 𝑝 × 𝑝 dengan kolom ke-k berisikan eigenvector ke-k dari X X dengan asumsi 𝑘 ≤ 𝑝, maka '

' = '

A A AA Nilai-nilai PC untuk tiap observasi ditunjukkan dalam

persamaan (2.16)

=

Z XA (2.16)

dengan elemen ke-(i,k) dari Z adalah skor PC ke-k untuk observasi ke-i. Menurut Jolliffe (2002) karena matriks A bersifat ortogonal, maka regresi berganda dengan prediktor yang saling berkorelasi

dapat dikonversi menjadi PCR sebagaimana ditunjukkan pada persamaan (2.17) ' Y = Xβ + ε Y = XAA β + ε Y = Zγ + ε (2.17)

dengan XA=Z danA β' =γ . Estimasi untuk γ dapat dilakukan dengan metode OLS, lalu mencari estimasi β berdasarkan persamaan (2.18)

ˆ _{= ˆ}

β Aγ (2.18)

2.4 Regresi Ridge

Regresi ridge merupakan suatu metode yang pertama kali dikemukakan oleh A.E Hoerl pada tahun 1962. Metode ini ditujukan untuk mengatasi kondisi buruk yang diakibatkan oleh korelasi yang tinggi antar beberapa variabel prediktor sehingga mengakibatkan matriks X X bersifat hampir singular. Keadaan ' tersebut memberikan dampak pada hasil duggan parameter model yang menjadi tidak stabil (Draper & Smith, 1992). Apabila matriks

Z adalah matriks yang memuat nilai dari variabel prediktor yang

sudah distandarisasi. Persamaan yang biasa digunakan dalam mengestimasi koefisien regresi seperti pada persamaan (2.19)

(

)

1

ˆ _' − _'

=

β Z Z Z Y (2.19)

Regresi ridge akan memodifikasi persamaan (2.19) menggunakan konstanta non-negatif



. Sehingga penduga dari r elemen

(

1 , 2 ,...,

)

' z =  z z rz

β termodifikasi menjadi r elemen



1 2



( ) ( ), b ( ),..., b ( ) '

z  = bz  z  rz 

b . Persamaan yang lazim

digunakan untuk mengestimasi koefisien regresi ridge ditunjukkan pada persamaan (2.20)

(

)

1

ˆ ( )_z  = ' + − '

Jika nilai=0, maka nilai dugaan yang terbentuk adalah nilai dugaan OLS. Jika  dinaikan, maka nilai mutlak dugaan menjadi semakin kecil menuju nol untuk  menuju tak hingga.

2.5 Stepwise Regression

Stepwise Regression merupakan salah satu metode yang bertujuan untuk mendapatkan model regresi berganda terbaik. Proses yang dilkukan yaitu dengan melakukan pemilihan variabel prediktor yang memberikan pengaruh terbaik kepada model regresi. Dalam proses pemilihan variabel, terdapat dua metode yang biasa digunakan, diantaranya yaitu backward elimination dan forward selection.

Forward selection digunakan dengan cara memasukan variabel prediktor satu demi satu sampai diperoleh persamaan regresi yang paling baik. Urutan penyisipan variabel prediktor ditentukan berdasarkan koefisien korelasi parsial sebagai ukuran pentingnya variabel prediktor (Draper & Smith, 1992).

Backward elimination tidak jauh berbeda dengan forward selection, namun dalam pemilihan variabel prediktor, metode ini mengeluarkan variabel prediktor satu demi satu dari model regresi dengan variabel prediktor yang lengkap sampai didapatkan model regresi yang paling baik.

Pemilihan model Stepwise Regression menggunakan kriteria nilai Akaike’s Information Criterion (AIC). Nilai AIC dapat diperoleh melalui persamaan (2.21)

𝐴𝐼𝐶 = −2 ln(𝐿) + 2𝑘 (2.21) dengan L adalah nilai maksimum fungsi likelihood, dan k adalah jumlah parameter. Fungsi likelihood untuk model regresi dapat dituliskan seperti pada persamaan (2.22).

(

₂

)

(

(

)

)

2 0 ₂ 2 0 1 1 1 1 1 ,..., , exp ..., 2 2 n m i m m i L    y  x  x   =   = _− − + + _  



(2.22)

dengan m adalah banyak variabel prediktor, dan n adalah banyak data observasi.

2.6 Ensemble Prediction System

Park (2006) dalam Narendra (2017) mengatakan Ensemble Prediction System (EPS) memiliki arti sebagai model yang terdiri dari kumpulan dua atau lebih model sistem prediksi tunggal yang diverifikasi dalam waktu yang bersamaan. Prediksi ensemble sudah banyak digunakan dalam bidang lingkungan tertentu seperti meteorologi dan hidrologi (Jolliffe & Stephenson, 2003). Menurut Viney, et al. (2005) pemodelan ensemble atau prediksi dari beberapa model yang digabungkan untuk meningkatkan akurasi prediksi sudah sering dilakukan dalam bidang klimatologi dan ilmu atmosfer. Viney et al. (2005) dalam penelitiannya telah membuktikan bahwa model ensemble pada kasus hidrologi menghasilkan prediksi yang lebih baik dibandingkan model individu. Tujuan dari prediksi ensemble diantaranya yaitu untuk memberikan hasil prediksi yang akurat, serta menyediakan prediksi yang lebih reliabel (Kalnay, 2003).

Beberapa otoritas yang menggunakan EPS untuk komponen cuaca diantaranya yaitu National Centers for Enviromental Prediction (NCEP) of US, Meteo-France, European Centre for Medium-Range Weather Forecast (ECMWF), dan Japan Meteorological Agency (Putera, 2017). Prediksi ensemble dapat dibentuk dalam beberapa cara (Viney, et al., 2005) diantaranya yaitu

1. Menggunakan rata-rata kasar dari model prediksi setiap harinya

2. Menggunakan median harian dari seluruh anggota ensemble 3. Menggunakan regresi multi variabel selama periode

kalibrasi dan menerapkannya pada periode validasi

Dalam tahap konstruksi model, terdapat beberapa teknik yang dapat digunakan, antara lain skema pertubasi. Skema ini mengurangi unsur ketidakpastian model melalui modifikasi nilai

antar anggota ensemble (Putera, 2017). Menurut Schmeits & Kok (2010) meskipun ensemble prediction system memiliki kemampuan yang tinggi, namun untuk prediksi jangka menengah masih bersifat underdispersive atau overdispresive sehingga dibutuhkan kalibrasi.

2.7 Bayesian Model Averaging

Sebagaimana telah disebutkan sebelumnya bahwa hasil prediksi jangka menengah dari EPS masih bersifat underdispersive atau overdispresive sehingga dibutuhkan kalibrasi (Schmeits & Kok, 2010). Kasus underdispersive dapat dikatakan sebagai kecenderungan terpusatnya nilai prediksi cuaca pada suatu interval dengan varians yang rendah. Sementara overdispresive yaitu kejadian ketika prediksi cuaca cenderung terpusat pada suatu interval dengan varians tinggi (Putera, 2017). Bayesian Model Averaging (BMA) merupakan salah satu metode yang mampu mengkalibrasi hasil prediksi ensemble. Penggunaan Bayesian Model Averaging (BMA) dibidang meteorologi pertama kali diperkenalkan oleh Raftery, et al (2005), didapatkan bahwa BMA mampu mengatasi permasalahan underdispersive dan overdispersive pada hasil prediksi suhu permukaan di Pasific Northwest.

BMA merupakan metode ensemble post processing yang menghasilkan prediksi probabilistik dari rata-rata terboboti distribusi probabilistik model anggota ensemble. Bobot yang digunakan merupakan probabilitas posterior dari model anggota ensemble yang mencerminkan kontribusi relatif model tersebut dalam melakukan prediksi selama periode training (Raftery, et al., 2005). Hoeting (2002) juga mengatakan bahwa ide dasar dari BMA yaitu membuat inferensi berdasarkan rata-rata terboboti dari model. Kelebihan dari metode ini terletak pada kemampuannya memadukan beberapa model prakiraan ensemble dan mengoreksi bias prakiraan agar mean dan varians semakin mendekati kenyataan, sehingga menghasilkan prakiraan ensemble terkalibrasi yang mendekati nilai observasi sesungguhnya (Putera, 2017).

Jika M =

(

M₁,...,M_K

)

adalah K model yang digunakan sebagai anggota ensemble dan y adalah prediksi ensemble yang ingin dikalibrasi, maka jika mengacu pada teorema probabilitas total didapatkan PDF posterior prediktif dari y dituliskan seperti persamaan (2.23) 1 ( ) ( | ) ( | ) K T k k k p p M p M = =



y y y (2.23)

Probabilitas posterior dari modelM ditunjukkan pada persamaan K (2.24) (Hoeting, 2002)

( )

( | ) ( ) ( | ) k k k p M p M p M p = y y y (2.24)

dengan ( |p y Mk)adalah PDF prediksi dari modelM , K ( | ) T k

p M y

adalah probalitas posterior dari modelM , dan K p M( k)adalah komponen prior (Raftery, et al., 2005).

Menurut Raftery, et al. (2005) persamaan (2.23) dapat dimodifikasi menjadi persamaan (2.25) untuk kasus model dinamis sebagaimana ide dasar dari BMA untuk mendapat model terbaik dan mengatasi ketidakpastian. Jika diberikan f_kadalah prediksi terbaik dari ensemble dan h y fk( | k)merupakan PDF bersyarat dari model f , maka PDF posterior BMA dapat dituliskan _k

1 1 ( | ,..., ) ( | ) K K k k k k p y f f w h y f = =



(2.25)

denganw adalah probabilitas posterior dari prediksi model k yang k dianggap sebagai model terbaik. w juga merupakan bilangan non k negatif dengan 1 1 K k k w = =



.

2.7.1 Bayesian Model Averaging dengan Pendekatan Distribusi Normal

Jikay_tadalah data observasi riil, dan f_t =

(

f_1t,...,f_Kt

)

adalah prediksi dari K anggota ensemble pada T periode training. Dalam menganalisis data suhu dan tekanan, seringkali digunakan BMA dengan pendekatan distribusi normal. Koreksi bias dalam BMA didapatkan dengan meregresikan data observasi (y) dengan masing-masing prediksi model anggota ensemble (fk) selama

periode training, sehingga akan terbentuk persamaan 0 1

t k k kt kt

y =b +b f + (2.26)

untuk k = 1,...,K dan t = 1,...,T, dengan asumsiE

( )

_kt = , 0

( )

2

Var _kt = , dan cov

(

 _kt, _kv

)

= untuk t ≠ v, maka dapat 0 dituliskan bahwa 𝜀𝑘𝑡~𝑁(0, 𝜎2), dan dapat dituliskan pula

𝑦𝑡~𝑁(𝑏0𝑘+ 𝑏1𝑘𝑓𝑘𝑡, 𝜎2).

Oleh karenanya, probabilitas posterior dari y bersyarat fk

atau komponen h y fk( | k)dalam persamaan (2.25) dinyatakan dengan,

(

)

1 1 2 | exp 2 2 k k k y h y f     _{ − }  = _− _{ } _     (2.27)

dengan rata-rata k =b0k +b f1k k dan varians

2

 atau dapat dituliskan sebagai 𝑦|𝑓𝑘~𝑁(𝑏0𝑘+ 𝑏1𝑘𝑓𝑘, 𝜎2). (Raftery, et al.,

2005)

Dalam melakukan estimasi parameter BMA, langkah-langkah yang dilakukan yaitu,

1. Menentukan training window atau jumlah pengamatan yang digunakan untuk mengestimasi parameter. Gambar 2.1 berikut adalah ilustrasi penggunaan training window sebesar 30 pengamatan dalam estimasi parameter BMA

Gambar 2.1 Ilustrasi Penggunaan Training Window

Gambar 2.1 menunjukkan bahwa dalam melakukan estimasi parameter BMA dibutuhkan 30 hari pengamatan. Diilustrasikan untuk mengestimasi parameter periode 31/01/2015, maka digunakan data pengamatan dan prediksi periode 01/01/2015 sampai 30/01/2015 sebagai data training, kemudian untuk estimasi parameter periode 01/02/2015 digunakan data periode 02/01/2015 sampai 31/01/2015 dan seterusnya.

2. Melakukan esitmasi parameter(b₀k,b₁k), parameter ini didapat regresi linear sederhana pada data observasi sebagai variabel respon dan hasil prediksi masing-masing model yang ingin dikalibrasi ensemble sebagai variabel prediktor pada periode training. Nilai (b0k,b1k)dapat disebut juga koefisien bias regresi.

3. Melakukan estimasi parameter (w )k dan

( )

2

 . Estimasi parameter (w )_k dan

( )

2 _{didapat dengan memaksimumkan} fungsi log-likelihood dari persamaan (2.28)

(

2

)

(

)

1 1 ,..., ; log | K K k k t kt t k l w w  w h y f =   = _{ }  





(2.28) Training window 30 hari untuk estimasi parameter periode 31/01/2015

namun persamaan (2.28) tidak dapat diselesaikan secara analitik, sehingga perlu pendekatan numerik yang salah satunya yaitu dengan algoritma Expectation Maximization (EM) sebagaimana Raftery et al. (2005) menerapkannya. Setelah didapatkan parameter-parameter BMA, maka dapat dihitung nilai mean dan varians BMA meggunakan persamaan (2.29).





(

)

(

)

1 0 1 1 2 2 1, , 0 1 0 1 1 1 | ,..., (b ) Var | ,..., K K k k k k k K K t t K t k k k kt i i i it k i E y f f w b f y f f w b b f w b b f  = = = = +     = _ + − + _ +   _{ }







(2.29)

2.8 Algoritma Expectation Maximization (EM)

Algoritma Expectation Maximization (EM) pertama kali diperkenalkan oleh Dempster, et al (1977). Algoritma EM merupakan suatu metode iteratif yang digunakan untuk estimasi parameter dalam fungsi likelihood dengan pendekatan Maximum Likelihood Estimation pada data yang tidak lengkap. Menurut McLachlan & Krishnan (1996) Algoritma EM digunakan untuk melakukan estimasi parameter yang tidak dapat diselesaikan dengan MLE dengan menerapkan konsep likelihood complete-data

(

; ,

)

L θ y z berdasarkan likelihood incomplete-data L θ y yang

( )

; tidak memiliki penyelesaian secara analitik.

Penggunaan Algoritma EM dalam melakukan estimasi parameter (w )_k dan

( )

2 _{pada BMA Normal memanfaatkan suatu} vektor z , dengan kt zkt =



z1t,...,zKt



adalah himpunan variabel laten yang tidak teramati. z = jika anggota ensemble ke-k adalah kt 1 ensemble yang menghasilkan prediksi terbaik pada waktu ke-t, dan

0 kt

tahap pertama adalah tahap expectation (E) dan tahap kedua adalah maximization (M).

2.8.1 Tahap Expectation pada Algoritma EM

Pada tahap expectation nilai

z

_ktdiestimasi secara berulang berdasarkan w dan

( )

2 yang sudah ditentukan pada tahap insiasi sesuai dengan persamaan (2.30)

(

)

(

)

( 1) ( ) ( 1) 1 | , ˆ | , j k t kt j kt K j i t it i w h y f z w h y f   − − = =



(2.30)

dengan j adalah banyak iterasi dan h y

(

_t| f_kt,(j−1)

)

adalah PDF normal seperti persamaan (2.27) dengan rata-rata b0k +b f1k kt dan standar deviasi (j−1)

yang dievaluasi dari y pada iterasi ke-j. _t Persamaan (2.30) merupakan persamaan yang menghasilkan nilai probabilitas posterior dari observasi waktu ke-t untuk anggota ensemble ke-k. Setelah itu nilai zˆ( )j untuk pada waktu ke-t dikategorikan menjadi nilai z = jika anggota ensemble ke-k kt 1 adalah ensemble yang menghasilkan probabilitas terbesar pada waktu ke-t, dan z = untuk selainnya. kt 0

2.8.2 Tahap Maximization pada Algoritma EM

Tahap maximization merupakan tahap untuk melakukan estimasi (w )_k dan

( )

2 _{berdasarkan hasil estimasiˆ}( )j

kt

z seperti ditunjukkan dalam persamaan (2.31)

(

)

( ) ( ) 2 2( ) ( ) 1 1 _ˆ 1 _ˆ j j k kt t K j j kt t kt t k w z n z y f n  = = = −





(2.31)

dengan n adalah jumlah observasi pada tahap training. Nilai (w )k dan

( )

2 _{pada tahap insisasi diperbaharui dengan nilai yang} dihasilkan dari persamaan (2.30). Iterasi dilakukan sampai konvergen atau dapat dikatakan iterasi berhenti ketika perubahan dari parameter yang diestimasi danzˆ( )_ktj tiap iterasi tidak lebih besar dari batas toleransi yang ditentukan.

2.9 Evaluasi Kebaikan Model

Terdapat beberapa teknik dalam melakukan evaluasi model prediksi ensemble. Menurut (Moller, 2014) Root Mean Square Error (RMSE) adalah indikator yang cukup untuk menilai kualitas prakiraan. Sementara koreksi bias dapat dievaluasi melalui Continuous Rank Probability Score (CRPS). Selain itu dapat digunakan juga Verification Rank Histogram (VRH) untuk melihat kebaikan hasil kalibrasi. Hasil VRH yang didapat dari kalibrasi prediksi dengan BMA akan dibandingkan dengan VRH dari prediksi raw ensemble.

2.9.1 Root Mean Square Error

Root Mean Square Error (RMSE) merupakan salah satu indikator untuk mengevaluasi kebaikan hasil prediksi yang umum digunakan. RMSE merupakan akar kuadrat dari Mean Square Error (MSE) atau jumlah kuadrat dari selisih nilai prediksi dengan observasi. Formula dari RMSE ditunjukkan pada persamaan (2.32)

(

)

2 1 1 _ˆ RMSE= n i i i y y n = −



(2.32) dengan, n = banyak observasi i

y = nilai observasi ke-i ˆ_i

2.9.2 Verification Rank Histogram

Verification Rank Histogram (VRH) dikenal juga sebagai PIT Histogram yang digunakan untuk mengevaluasi hasil kalibrasi pada kasus prediksi ensemble (Feldmann, 2012). VRH digunakan untuk melihat sebaran hasil prediksi ensemble. Berikut pada Gambar 2.2 adalah kriteria dari bentuk-bentuk VRH (Moller, 2014),

Gambar 2.2 Kriteria Pola Verification Rank Histogram

Menurut Feldmann (2012) jika VRH menunjukkan bentuk seragam seperti pada Gambar 2.2 (d), maka itu menunjukkan kalibrasi telah berhasil dengan baik. Namun jika VRH membentuk pola huruf “U” atau lonceng seperti pada Gambar (2.2) (a) dan (c), dapat diartikan sebaran hasil prediksi bersifat underdispersive dan overdispersive. Sementara pola seperti Gambar 2.2 (b) dapat diartikan bahwa terdapat bias cukup besar pada hasil prediksi.

2.9.3 Continuous Ranked Probability Score

Continuous Ranked Probability Score (CRPS) merupakan salah satu scoring rule sama seperti RMSE yang sudah dijelaskan pada pembahasan 2.9.1. CRPS mampu melakukan verifikasi model perkiraan baik dari segi tingkat koreksi bias dan ketajaman yang tercapai. Ketajaman dapat diartikan bahwa PDF prediktif model terkalibrasi mampu memperbaiki PDF prediktif model sebelum dikalibrasi dengan mempersempit interval model PDF model prediksi (Putera, 2017). Semakin sempit interval dan semakin banyak nilai observasi masuk dalam interval tersebut, maka hasil prediksi dikatakan semakin reliabel. Menurut (Hersbach, 2000)

mengatakan bahwa CRPS merupakan teknik verifikasi untuk model prediksi probabilistik. Persamaan CRPS ditunjukkan pada persamaan (2.33)

( )

( )

2 1 1 CRPS= n i ia i P y P y dy n  = −  −   

 

(2.33) dengan, n = Banyak observasi

i = Periode waktu yang digunakan

( )

i

P y = CDF prediktif pada waktu ke-i

( )

ia

P y = CDF data observasi pada waktu ke-i

Hasil prediksi dikatakan baik apabila nilai CRPS yang dihasilkan kecil. Atau semakin rendah nilai CRPS, dalam hal ini mendekati nol, maka model yang dihasilkan semakin baik dan reliabel.

2.9.4 Coverage

Coverage merupakan indikator yang digunakan untuk melihat ketajaman dari hasil prediksi ensemble. Coverage digunakan untuk mengetahui persentase nilai observasi yang berada di dalam interval PDF prediktif tertentu untuk prakiraan model terkalibrasi (ensemble range) (Narendra, 2017). Agar memiliki perbandingan antara nilai observasi dengan hasil prediksi m anggota ensemble maka digunakan standar coverage

1 100% 1 m m − _

+ sebagai nilai standar (Moller, 2014). Nilai standar coverage tergantung pada banyaknya jumlah anggota ensemble, artinya semakin banyak anggota ensemble maka nilai coverage yang dicapai harus semakin tinggi.

Coverage umumnya digunakan untuk mengidentifikasi apakah hasil prediksi ensemble bersifat underdispersive atau overdispersive. Kasus underdispersive ditandai jika nilai coverage jauh lebih rendah dari nilai standar coverage. Sementara kasus overdispersive ditandai jika nilai coverage jauh lebih tinggi dari

nilai standar coverage. Nilai coverage yang mendekati nilai standar coverage menunjukkan prediksi sudah terkalibrasi dengan baik (Putera, 2017).

2.10 Numerical Weather Prediction

Numerical Weather Prediction (NWP) merupakan sekumpulan kode komputer yang digunakan untuk merepresentasikan secara numerik persamaan-persamaan atmosfer serta memprediksi kondisi atmosfer yang akan datang dengan menggunakan kemampuan komputer yang tinggi. Dalam melakukan prediksi, model NWP melakukan penyederhanaan dan homogenisasi pada kondisi permukaan sementara atmosfer diperlakukan sebagai media yang terdiri dari bujur sangkar (Idowu & Rautenbach, 2008). Menurut Raible, et al (1998) model NWP baik digunakan untuk prediksi jangka pendek atau sekitar 24 jam kedepan, dan dalam penggunaannya memerlukan teknik komputasi tinggi. Meskipun demikian menurutnya hasil prediksi model ini seringkali masih tidak stabil. Data yang diperoleh dari NWP adalah data cuaca pada lokasi grid berukuran sampai dengan 0,5º × 0,5º (Lintang × Bujur) atau sekitar 55 × 55 km2 _{dan pada beberapa}

ketinggian (Haryoko, 2014)

Beberapa model NWP yang digunakan oleh BMKG dalam menyediakan prakiraan cuaca objektif yaitu produk dari negara lain seperti European Centre for Medium-Range Weather Forecast (ECMWF), Weather Research Forecast (WRF), National Centers for Enviromental Prediction (NCEP), ARPEGE, CCAM, dan lain-lain (Haryoko, 2014). Dalam melakukan prediksi, model NWP melakukan penyederhanaan dan homogenisasi pada kondisi permukaan sementara atmosfer diperlakukan sebagai media yang terdiri dari bujur sangkar. Model NWP juga sulit untuk menangkap kondisi-kondisi spasial seperti keadaan topografi, vegetasi, dan jenis tanah yang merupakan komponen penting dalam prediksi cuaca lokal. Sehingga seringkali terjadi kesalahan dalam prediksi cuaca harian yang berdampak tidak dapat dipercayanya hasil prediksi cuaca dari model NWP (Idowu & Rautenbach, 2008).

Gambar 2.3 Ilustrasi Perbedaan Kondisi Cuaca (a) Dunia Nyata dan (b) NWP

(Linacre & Geerts, 2003)

Gambar 2.3 menunjukkan perbedaan dari kondisi cuaca riil dan model NWP. Model NWP mengasumsikan kondisi rill secara seragam kedalam grid yang mengakibatkan seringnya terjadi kesalahan prediksi. Wilks (2006) mengatakan bahwa pendekatan statistika diperlukan dalam mereinterpretasi luaran NWP yang dinamis. Menurutnya terdapat beberapa alasan pendekatan statistik diperlukan untuk menginterpretasikan model NWP diantaranya yaitu,

1. Terdapat perbedaan siginifikan antara kondisi rill dengan model NWP. Hal ini dikarenakan model NWP menyederhanakan dan menghomogenkan kondisi permukaan kedalam rangkaian titik grid.

2. Model NWP tidak secara lengkap dan tepat merepresentasikan kondisi atmosfer

3. Model NWP bersifat deterministik

2.11 Suhu dan Kelembaban

Suhu udara merupakan salah satu unsur cuaca yang menunjukkan keadaan udara panas atau dingin suatu waktu dari hasil pengukuran harian dan dirata-ratakan setiap bulan. Dalam meteorologi sering dikenal dengan adanya pengukuran suhu maksimum, suhu minimum, dan suhu rata-rata. Suhu maksimum biasanya terjadi pada pukul 14.00-15.00, sementara suhu minimum biasa terjadi pada pukul 06.00-07.00 (Fachrunisah, 2017). Sementara kelembaban adalah banyak kandungan uap air yang ada dalam udara. Salah satu ukuran yang digunakan untuk mengukur

kelembaban yaitu kelembaban udara relatif yang didapatkan berdasarkan persamaan (2.34) (Wirjohamidjojo & Swarinoto, 2007)

RH =_𝑒𝑒

𝑚× 100% (2.34)

dengan,

RH : kelembaban relatif (%)

e : tekanan uap air pada saat pengukuran (mb)

em : tekanan uap air yang dapat dicapai pada suhu dan tekanan

udara saat pengukuran