ANALISIS PENGARUH INISIALISASI NNDSVD PADA METODE NMF DALAM EKSTRAKSI TOPIK UTAMA BERITA ONLINE INDONESIA

ANALISIS PENGARUH INISIALISASI NNDSVD PADA METODE NMF

DALAM EKSTRAKSI TOPIK UTAMA BERITA ONLINE INDONESIA

Tasya Rahmita1, Hendri Murfi2, Dhian Widya3

1_{Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424, Indonesia} 2_{Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424, Indonesia} 3_{Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424, Indonesia}

1

tasya.rahmita@sci.ui.ac.id, 2_{hmurfi@gmail.com,} 3_{dhianwidya@gmail.com}

Abstrak

Berkembangnya portal berita online di Indonesia sangat pesat sehingga menyebabkan meningkatnya arus informasi. Banyaknya informasi yang ada pada portal berita online menimbulkan kesulitan untuk mengetahui topik berita secara garis besar. Untuk itu diperlukan ekstraksi topik berita online yang dapat dilakukan secara otomatis dengan bantuan mesin. Salah satu metode yang dapat digunakan untuk mengekstraksi topik berita online secara otomatis adalah Non-Negative Matrix Factorization (NMF). Pada umumnya algoritma NMF menggunakan inisialisasi random untuk mendekomposisi matriks. Inisialisasi random pada algoritma NMF menghasilkan topik berita yang berbeda setiap kali eksekusi. Pada penelitian ini akan diimplentasikan salah satu metode inisialisasi NMF yaitu Non-Negative Double Singular Value Decomposition (NNDSVD). Metode ini berdasarkan dua proses dari Singular Value Decomposition (SVD). Proses SVD yang pertama untuk pendekatan matriks data dan yang kedua untuk pendekatan bagian positif. NNDSVD tidak mengandung unsur random, sehingga menghasilkan topik berita yang sama setiap kali eksekusi.

An Impact Analysis on NNDSVD Initialization on NMF Method for Extracting Main Topic of Indonesia Online News

Abstract

The rapid development of portal online news in Indonesia causes the increment of information flow. The amount of information contained in these portals makes it difficult to know the outline of news topic. So, it is necessary to extract the topic automatically by using machine. Non-Negative Matrix Factorization (NMF) is a method used to extract news topic automatically. Generally, NMF algorithm uses random initialization to decompose matrix to get different news topic in every execution. In this research, one of NMF initialization, Non-negative Double Singular Value Decomposition (NNDSVD), will be implemented. This method uses two processes from Singular Value Decomposition (SVD), one approximating the data matrix, the other approximating positive section. NNDSVD contains no randomization, so that produce same news topic in every execution.

Keywords : topic extraction, Non-Negative Matrix Factorization, Non-Negative Double Singular Value Decomposition, initialization on NMF.

1. Pendahuluan

Perkembangan teknologi dan informasi saat ini menyebabkan tidak ada lagi batasan ruang dan waktu untuk berinteraksi. Perkembangan teknologi dan informasi yang paling fenomenal adalah internet. Internet menyediakan berbagai macam informasi yang mudah diakses oleh pengguna. Pengguna dapat mengakses informasi yang tersedia di internet dari belahan dunia

manapun pada waktu kapanpun. Karena internet memudahkan pengguna untuk mengakses informasi, menyebabkan pengguna internet semakin lama semakin meningkat.

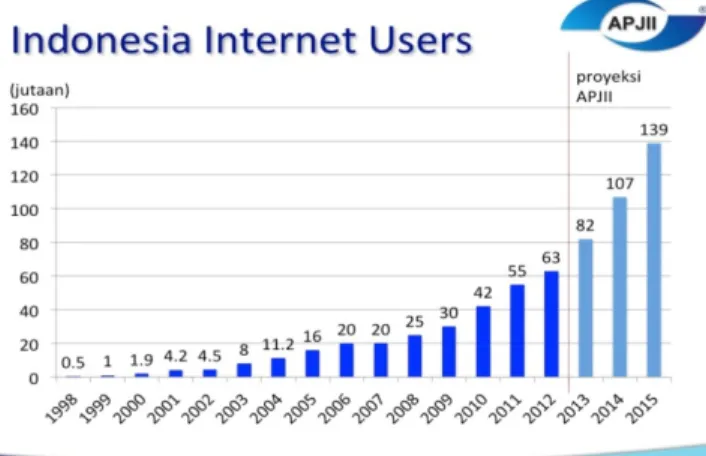
Gambar 1.1 Grafik Pengguna Internet di Indonesia

[Sumber : APJII. Indonesia Internet Users.http://www.apjii.or.id/v2/index.php/read/page/halaman-data/9/statistik.html. diakses pada 15 Januari 2014 pukul 15.00 WIB]

Dari Gambar 1.1 terlihat bahwa banyaknya pengguna internet di Indonesia semakin meningkat setiap tahunnya. Hal itu memicu arus informasi yang diakses oleh pengguna pun semakin meningkat. Dengan meningkatnya arus informasi di internet banyak media berita

online yang bermunculan. Perkembangan portal berita online sangat pesat di Indonesia.

Banyaknya informasi yang ditawarkan dengan sajian-sajian yang berbeda membuat portal berita saat ini begitu eksis dan semakin bisa mengadopsi para pengunjungnya. Hal ini terbukti dengan banyaknya sajian berita yang berupa isu secara cepat dapat ditangkap oleh para pembacanya1. Selain itu juga, pengguna dapat mengakses berita pada portal berita online kapanpun dan dimanapun. Akan tetapi karena adanya keterbatasan akses internet, baik keterbatasan waktu maupun biaya dan juga update berita yang begitu cepat menyebabkan kendala bagi pengguna yang hanya menginginkan topik utama harian saja.

Latent Semantic Analysis (LSA) adalah sebuah teori dan metode untuk ekstraksi dan

representasi topik dari sekumpulan dokumen (Laundauer & Dumais, 1997). LSA mempunyai dua model untuk mengekstraksi topik dari sekumpulan dokumen, yaitu : Singular Value

Decomposition (SVD) dan Non-Negative Matrix Factorization (NMF). SVD mempunyai

kelemahan, yaitu elemen matriks bernilai negatif sehingga sulit untuk diinterpretasikan. Oleh

karena itu, NMF digunakan karena elemen di dalam matriks tidak bernilai negatif sehingga lebih mudah untuk diinterpretasikan.

NMF merupakan metode yang mengekstraksi matriks menjadi dua matriks non-negative. Dengan mengekstraksi matriks tersebut akan didapatkan variabel tersembunyi, dalam hal ini variabel yang tersembunyi adalah topik dari suatu dokumen. Pada algoritma yang memecahkan masalah NMF pada umumnya menggunakan inisialisasi random yang menyebabkan topik yang dihasilkan dari metode NMF berbeda setiap kali eksekusinya.

2. Tinjauan Teoritis

Pada bagian ini, diberikan beberapa teori dasar mengenai Non-Negative Matrix Factorization.

2.1. Non-Negative Matrix Factorization (NMF)

Faktorisasi matriks adalah proses pemecahan atau penguraian suatu matriks menjadi beberapa matriks. Matriks-matriks hasil faktorisasi tersebut biasanya memiliki struktur tertentu dimana membuat beberapa operasi akan menjadi lebih sederhana atau jumlah komponen yang lebih sedikit. Secara umum, metode faktorisasi matriks dibagi menjadi dua kelompok, yaitu metode langsung dan metode aproksimasi. Beberapa jenis metode faktorisasi yang menggunakan metode langsung, yaitu faktorisasi LU, faktorisasi Cholesky, faktorisasi QR. Dan beberapa jenis metode faktorisasi yang menggunakan metode aproksimasi yang sering digunakan yaitu,

Singular Value Decomposition (SVD), Matrix Factorization (MF), Non-Negative Matrix Factorization (NMF).

Pada NMF, matriks ! berukuran !×! dengan !!" ≥ 0, akan diuraikan menjadi dua matriks

non-negative ! ∈ ℝ!×! _{dan ! ∈ ℝ}!×! _{dengan ! < min(!, !) sedemikian sehingga}

! ≈ !". (2.1)

Untuk menyelesaikan masalah aproksimasi (2.1) dan menentukan perkalian matriks ! dan matriks ! yang mendekati matriks !, diperlukan definisi fungsi biaya (cost function). Cost

function dibangun menggunakan jarak antara dua matriks no-negative ! dan !, yaitu : ! − ! ! _{= (!}

!" − !!")!   !,!

. _(2.2)

Berdasarkan persamaan (2.2) cost function pada masalah aproksimasi (2.1) dapat dituliskan menjadi sebagai berikut:

! !, ! = ! − !" ! _{= (!}

!"− (!ℎ)!")!   !,!

. _(2.3)

Jarak antara matriks ! dengan perkalian matriks ! dan ! diminimumkan untuk mencari matriks ! dan ! yang perkaliannya mendekati matriks ! Sehingga, permasalahan aproksimasi (2.1) dapat diformulasikan sebagai masalah optimasi berkendala sebagai berikut:

min !,! ! !, ! = 1 2 (!!"  − !ℎ !")!     ! !!! ! !!! , dengan kendala !_!" ≥ 0, ℎ_!"≥ 0, ∀  !, !, !, !. (2.4)

Berdasarkan Definisi 2.5, persamaan (2.4) dapat dituliskan sebagai berikut: min !,! ! !, ! = 1 2 ! − !" !!, dengan kendala !_!" ≥ 0, ℎ_!"≥ 0, ∀  !, !, !, !. (2.5)

2.1.1. Alternating Non-Negative Least Square (ANLS)

Salah satu metode yang digunakan dalam menyelesaikan model Non-Negative Matrix

Factorization adalah dengan menggunakan algoritma Alternating Non-Negative Least Square.

Metode ini berdasarkan pada metode "Block Coordinate Descent" (Bertsekas, 1999). Fungsi biaya (cost function) pada masalah optimasi NMF merupakan fungsi konveks jika fungsi biaya memiliki satu matriks sebagai variabel bebasnya, sehingga dapat dibentuk sebagai berikut : !!!!_{= !"# min} !!!! !, ! ! _{, (2.6)} !!!!_{= !"# min} !!! ! ! !!!_{, ! . (2.7)} (Lin, 2007)

Pada persamaan (2.6) fungsi biaya hanya memiliki matriks ! sebagai variabel bebasnya, sehingga fungsi biaya (2.6) merupakan fungsi konveks. Pada persamaan (2.7) fungsi biaya hanya memiliki matriks ! sebagai variabel bebasnya, sehingga fungsi biaya (2.7) juga merupakan fungsi konveks. Sehingga algoritma Alternating Non-Negative Least Square untuk mencari matriks ! dan ! yang optimal dari persamaan (2.6) dan (2.7) adalah sebagai berikut:

Tabel 2.1 Algoritma Alternating Non-Negative Least Square Algoritma 1 Alternating Non-Negative Least Square

1. Inisialisasi !_!"!   _{≥ 0, ℎ} !" ! _{≥ 0, ∀  !, !, !, !} 2. for ! = 1, 2, 3, 4, 5, … !!!! _{= !"# min} !!!! !, ! ! !!!! _{= !"# min} !!! !(! !!!_{, !)}

Menurut Paatero (1999) konvergensi Alternating Non-Negative Least Square terjamin berapa pun blok variabelnya. Namun, analisis konvergensi untuk metode Alternating Non-Negative

Least Square (“Block Coordinate Descent”) memerlukan sifat keunikan solusi dari sub

masalah (Bertsekas, 1999). Akan tetapi, sifat tersebut tidak terpenuhi di masalah ini. Karena sub masalah (2.6) dan (2.7) merupakan masalah konveks, bukan tepat konveks. Sehingga, kedua sub masalah mempunyai beberapa solusi optimal (solusi tidak unik). Untungnya, untuk kasus dua blok, Grippo dan Siandrone (2000) menunjukkan bahwa kondisi keunikan solusi tidak diperlukan sehingga konvergensi Alternating Non-Negative Least Square terjamin melalui Teorema 2.1.

Teorema 2.1 (Lin, 2007)

Setiap titik limit dari barisan {!_!, !_!}  yang dihasilkan dari Algoritma (1) adalah titik

stasioner dari 2.8.

Persamaan (2.6) dan (2.7) merupakan sub masalah pada algoritma 1. Ketika salah satu blok variabel (! dan !) konstan, maka sub masalah menjadi masalah non-negative least square. Masing-masing sub masalah tersebut dapat diselesaikan dengan menggunakan metode

Projected Gradient Descent (Lin, 2007).

2.1.2. Projected Gradient Descent

Pada subbab 2.1.1. sub masalah (2.6) dan (2.7) dapat diselesaikan dengan menggunakan

Projected Gradient Descent. Metode ini berdasarkan dari metode Gradient Descent. Sub

min !!!  ! ! ≡ ! ! ! − !" ! !_, dengan kendala !_!" ≥ 0, ∀  !, ! (2.8) Fungsi !(!) diperoleh dari sub masalah (2.6) dimana !! _{matriks konstanta. Jadi, pada} persamaan (2.8) matriks ! dan ! merupakan matriks konstanta.

Asumsikan ! merupakan indeks dari iterasi. Gradient Descent akan mencari solusi dari permasalahan tersebut dengan aturan memperbarui solusi sebagai berikut :

!!!!_{= !}!_{− !∇}

!!(!). (2.9)

Gradient dari masalah NMF didapatkan dari turunan parsial pertama dari fungsi !(!, !) terhadap blok variabel !.

∇_!! !, ! = !" − ! !! (2.10)

Namun, perbaruan solusi dengan aturan (2.9) dapat berupa bilangan negatif maka dengan fungsi projection, solusi akan diproyeksikan. Sehingga, Projected Gradient Descent memperbarui solusi !! _{menjadi !}!!! _{dengan aturan sebagai berikut:}

!!!! _{= ![!}!_{− !∇}

!!(!)] (2.11)

dengan fungsi projection didefinisikan sebagai berikut :

! !_!" =  

!_!" jika !_!" ≥ 0 0 jika !_!" < 0 (Lin, 2007).

Dengan aturan perbaruan solusi pada (2.11), solusi yang didapatkan bernilai non-negative. Dengan memperhatikan sub masalah (2.7), bentuknya dapat dituliskan kembali sebagai berikut: min !!!  ! ! ≡ ! ! ! − !" ! !_, dengan kendala ℎ_!" ≥ 0, ∀  !, ! (2.12) Fungsi !(!) diperoleh dari sub masalah (2.7) dimana !!!! _{matriks konstanta. Jadi, pada} persamaan (2.12) matriks ! dan ! merupakan matriks konstanta.

Dengan cara yang sama diperoleh Projected Gradient Descent yang berdasarkan pada aturan

Gradient Descent memperbarui solusi !! _{menjadi !}!!! _{dengan aturan sebagai berikut:} !!!!_{= ![!}!_{− !∇}

!!(!)] (2.13)

dengan fungsi projection didefinisikan sebagai berikut :

! ℎ_!" =  

ℎ_!" jika ℎ_!" ≥ 0 0 jika ℎ_!" < 0

Gradient dari masalah NMF didapatkan dari turunan parsial pertama dari fungsi !(!, !) terhadap blok variabel !.

∇_!! !, ! = !! _{!" − ! (2.14)}

(Lin, 2007).

Sehingga algoritma Projected Gradient Descent dapat disusun berdasarkan solusi terbaru dari persamaan (2.11) dan (2.13) menjadi sebagai berikut:

Tabel 2.2 Algoritma Projected Gradient Descent Algoritma 2 Projected Gradient Descent

1. Inisialisasi !_!"! _{≥ 0, ℎ} !" ! _{≥ 0, ∀  !, !, !, !} 2. for ! = 1, 2, 3, 4, 5, … !!!! _{= ![!}!_{− !∇} !!(!)] !!!!_{= ![!}!_{− !∇} !!(!)] (Lin, 2007).

Beberapa penelitian menggunakan kriteria berhenti dengan memeriksa perbedaan jarak antara solusi terbaru dengan solusi iterasi sebelumnya. Jika jarak yang dihasilkan cukup kecil, maka prosedur (algoritma) berhenti. Tetapi, pada masalah optimasi kriteria tersebut tidak menunjukkan bahwa solusi yang didapat mendekati titik stasioner atau tidak. Oleh karena itu, dibutuhkan kriteria berhenti yang memeriksa solusi mendekati titik stasioner atau tidak pada setiap iterasi.

Pada Alternating Non-Negative Least Square, setiap sub masalah melibatkan permasalahan optimasi yang membutuhkan kriteria berhenti yang memeriksa solusi pada setiap iterasi mendekati titik stasioner atau tidak. Berdasarkan Lin (2007) kondisi yang umum digunakan untuk memeriksa solusi NMF mendekati titik stasioner atau tidak adalah

∇!_{! !}!_{, !}! _‖

! ≤ ! ∇! !!, !! ‖! (2.15)

dimana ∇!_!(!!_{, !}!_{) adalah projected gradient.}

Persamaan (2.15) dapat digunakan untuk kriteria berhenti pada sub masalah Alternating

Non-Negative Least Square. Dari penyelesaian sub masalah menghasilkan matriks !!!! _{dan !}!!! dari setiap iterasi, sehingga kriteria berhenti untuk setiap sub masalah adalah

∇_!! _{! !}!!!_{, !}!

! ≤ !! dan ∇!!! !!!!, !!!! ! ≤ !! (2.16) dimana

!_! = !_! ≡ max(10!!_{, !) ∇! !}!_{, !}!

! (2.17)

! merupakan batas toleransi dari persamaan (2.15).

Selain kriteria berhenti di atas, kriteria berhenti dengan waktu atau batas iterasi juga sebaiknya digunakan sebagai kriteria berhenti tambahan. Mungkin saja kriteria berhenti sudah terpenuhi tanpa melakukan iterasi maka batas toleransi diperkecil menjadi sebagai berikut :

!! ←!_!"! dan !! ←!_!"! (2.18) (Lin, 2007). Dalam penelitian ini digunakan 10!! _{sebagai batas toleransi dan 2000 iterasi} sebagai batas iterasi.

3. Metode Penelitian 3.1. Studi Literatur

Pada tahap awal ini dilakukan perumusan masalah, dan pengumpulan materi atau literatur yang berhubungan dengan masalah yang diangkat. Materi yang digunakan adalah jurnal, buku, makalah, dan media lainnya yang mendukung untuk menyelesaikan masalah yang diangkat.

3.2. Akuisisi Data

Pengumpulan data secara online dilakukan dengan menggunakan RSS (Rich Site Summary) dari portal berita online Indonesia. RSS merupakan dokumen dalam bentuk XML (Extensible

Markup Language) yang menyimpan atau menampilkan gambar, berita utama, audio, dan lain

1. Detik2 2. Republika3 3. Antara4 4. Inilah5 5. Okezone6 6. RMOL7 7. Tempo8 8. Viva9

Karena arus informasi berita dari portal berita online begitu cepat maka pengumpulan data dilakukan secara online dengan menggunakan perangkat lunak DiscovertText10 sehingga memudahkan untuk mengumpulkan data secara lengkap.

3.3. Implementasi Algoritma

Algoritma yang digunakan dalam metode NMF adalah Projected Gradient Descent. Selanjutnya, inisialisasi NNDSVD akan diterapkan untuk algoritma tersebut. Algoritma

Projected Gradient Descent akan diterapkan menggunakan perangkat lunak python11. Dalam perangkat lunak python akan digunakan package scikit-learn12.

3.4. Simulasi

Pada tahap akhir ini, setelah algoritma diterapkan untuk ekstraksi topik berita maka akan dihasilkan topik-topik berita. Topik-topik yang dihasilkan dengan menggunakan inisialisasi NNDSVD akan dibandingkan setiap eksekusinya. Perbandingan tersebut bertujuan untuk

2_{http://www.detik.com/}   3_{http://www.republika.co.id/} 4_{http://www.antaranews.com/} 5_{http://www.inilah.com/} 6_{http://www.okezone.com/} 7_{http://www.rmol.co/} 8_{http://www.tempo.co/} 9_{http://www.vivanews.com/} 10_{http://www.discovertext.com/} 11_{http://wwww.python.org/} 12_{http://www.scikit-learn.org/}

mengetahui keunikan topik yang dihasilkan setiap eksekusi dengan menerapkan inisialisasi NNDSVD pada algoritma Projected Gradient Descent.

4. Pembahasan

Pada umumnya metode NMF menggunakan inisialisasi pada elemen matriks ! dan ! dengan nilai non-negative secara random. Inisialisasi random yang digunakan memberikan hasil yang berbeda setiap kali eksekusi. Oleh karena itu, dibutuhkan inisialisasi yang tidak random. Metode yang digunakan pada penelitian ini adalah NNDSVD. Inisialisasi dengan menggunakan NNDSVD untuk matriks ! dan ! berdasarkan proses pada metode SVD. Metode ini dipilih karena dapat diterapkan oleh semua algoritma NMF yang ada (Boutsidis & Gallopoulos, 2008).

4.1. Singular Value Decomposition (SVD)

Sebelum membahas tentang SVD diberikan definisi bebas linear dan rank.

Definisi 4.1 (Howard, 1994)

Jika !   =   !!, !!, …  , !! adalah himpunan vektor-vektor tak kosong, dan persamaan  

!_!!_! + !_!!_!+ ⋯ !_!!_!= ! (4.1)

memiliki satu-satunya solusi, yaitu :  

!_! = 0, !_! = 0, … , !_! = 0 (4.2)

maka ! adalah himpunan bebas linear. Jika ada solusi lainnya maka ! adalah himpunan

tidak bebas linear.  

Definisi 4.2 (Burden & Faires, 2011)

Rank dari matriks !, dinotasikan dengan !"#$(!), menunjukkan banyaknya vektor baris

yang bebas linear di !.

 

Selain NMF, Singular Value Decomposition (SVD) merupakan metode faktorisasi matriks secara aproksimasi. SVD memanfaatkan beberapa sifat matriks yang diberikan pada Teorema 4.1.

Misalkan ! matriks berukuran !×!, maka berlaku:   1. matriks !!_{! dan !!}! _simetri,

2. !"#$(!)   =  !"#$(!!_!),

3. nilai eigen dari !!_{!   dan !!}! _{riil dan non-negative,}

4. nilai eigen dari !!_{! dan !!}! _sama.

Definsi 4.3 (Howard, 1994)

Suatu matriks bujur sangkar ! dengan sifat  

!!!   _{=   !}!   _(4.3)

disebut matriks orthogonal.

 

Sebelum dijelaskan faktorisasi matriks SVD, akan diberikan definisi dari nilai singular. Berikut adalah definisi nilai singular:

Definsi 4.4 (Burden & Faires, 2011)

Nilai singular dari matriks ! berukuran !×! adalah akar kuadrat positif dari nilai eigen tak

nol matriks simetris !!_!.  

Selanjutnya dapat dibentuk faktorisasi SVD menggunakan Teorema 4.2.

Teorema 4.2 (Golub & Van Loan, 1996)

Singular Value Decomposition (SVD) jika ! matriks bilangan riil ukuran !×!, maka akan

ada matriks-matriks orthogonal  

! = !_!, … , !_! ∈ ℝ!×! _{dan ! = !} !, … , !! ∈ ℝ!×!   (4.4) sedemikian sehingga   !!_{!  !   =  !"#$ !} !, . . . , !! ∈ ℝ!×! (4.5) dimana !   = !"#(!, !)  dan !_! ≥ !_! ≥  . . . ≥ !_! ≥ 0.  

Pada Teorema 4.2, !_! merupakan nilai singular dari !, dan vektor !_!, !_! merupakan vektor yang berkorespodensi dengan nilai singular.

Berdasarkan Teorema 4.2 SVD akan menguraikan matriks ! berukuran !×!, SVD akan menguraikan matriks ! menjadi sebagai berikut:

dimana ! adalah matriks orthogonal ukuran !×!, ! adalah matriks orthogonal ukuran !×!, dan ! adalah matriks ukuran !×! yang memiliki elemen tak nol tak negatif di diagonal utamanya. Ilustrasi dari faktorisasi Singular Value Decomposition (SVD) dapat dilihat pada Gambar 4.1.  

Gambar 4.1 Ilustrasi Singular Value Decomposition

Secara umum algoritma Singular Value Decomposition adalah sebagai berikut: 1. hitung matriks !!_,

2. hitung matriks simetris !!_{! dan !!}!_,

3. hitung semua nilai eigen dari matriks !!_{! dan !!}!_,

4. bentuk matriks ! dari Definisi 4.4 dengan elemen diagonal utama dari matriks ! adalah nilai singular yang terurut mulai dari yang terbesar dan elemen selain diagonal utama adalah 0,

5. bentuk matriks orthogonal !dari vektor eigen !!_{! yang dinormalisasi,} 6. bentuk matriks orthogonal ! dari vektor eigen !!! _{yang dinormalisasi.}

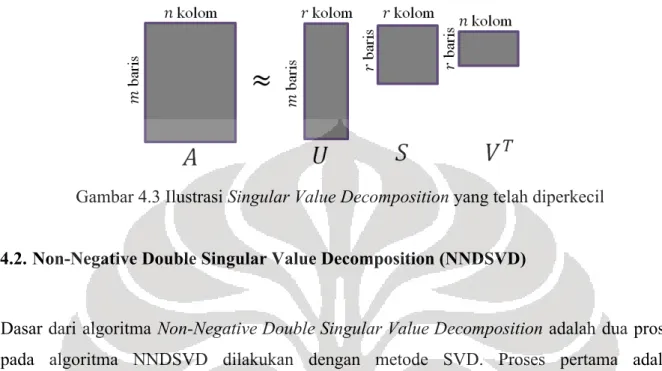
Karena nilai singular pada diagonal matriks ! sudah terurut mulai dari yang terbesar, maka hanya ! baris dan kolom pertama dari ! yang menghasilkan kemungkinan pendekatan terbaik dari matriks ! (Burden & Faires, 2011). Sehingga, matriks pada faktorisasi SVD dapat diperkecil ukuran matriksnya. Dari faktorisasi SVD pada Gambar 4.1 akan ditunjukkan ilustrasi proses pengecilan matriks pada faktorisasi SVD pada Gambar 4.2.

Dari proses pengecilan matriks pada faktorisasi SVD didapatkan matriks-matriks yang ukurannya lebih kecil, ditunjukkan pada Gambar 4.3.

Gambar 4.3 Ilustrasi Singular Value Decomposition yang telah diperkecil

4.2. Non-Negative Double Singular Value Decomposition (NNDSVD)

Dasar dari algoritma Non-Negative Double Singular Value Decomposition adalah dua proses pada algoritma NNDSVD dilakukan dengan metode SVD. Proses pertama adalah menguraikan matriks ! dengan SVD. Selanjutnya, proses kedua adalah menguraikan bagian positif dari matriks ! dan ! pada proses pertama dengan SVD. Sebelum membahas mengenai algoritma NNDSVD akan diberikan definisi mengenai bagian positif dari suatu matriks atau vektor.

Definisi 4.5 (Boutsidis & Gallopoulos, 2008)

Diberikan matriks atau vektor !, bagian positif dari !, dinotasikan dalam !_! ≥ 0, adalah

matriks atau vektor yang berukuran sama dengan ! dengan elemen dari !_! adalah elemen tidak negatif dari ! atau 0. Dan bagian negatif dari ! adalah !_!   =   !_!− ! dimana !_! ≥ 0.  

Singular Value Decomposition yang telah diperkecil akan menguraikan matriks ! ukuran !×! menjadi

!_!×! ≈ !_!×!  !_!×!!_!×!! _{. (4.7)}

Pendekatan 4.7 akan dimodifikasi menjadi   !_!×! ≈ (!_!×!!_!×! ! ! _)(! !×! ! ! _! !×!! ). (4.8) Pada NMF, bagian !_!×!!_!×! !

! _{pada pendekatan 4.8 digunakan untuk menginisialisasi matriks}

! dan bagian !_!×!

!

! _!

Dengan ! ≤ min(!, !) pendekatan 4.7 dapat dinyatakan dalam bentuk penjumlahan dari ! faktor singular sebagai berikut:

!   = !_!!_!!_!! !

!!!

(4.9) dimana !_! ≥  . . . ≥ !_!   >  0 adalah nilai singular tak nol dari ! dan !_!, !_{! !!!}! adalah vektor yang berkorespondensi dengan nilai singular. Untuk setiap ! yang dipilih dengan ! ≤  !, maka persamaan 4.9 akan menjadi:  

!(!) _{=   !} !!(!) ! !!! (4.10) dimana !(!) _{=   !}

!!!!. Untuk mendapatkan matriks yang tidak negatif (non-negative) yang akan menjadi inisialisasi matriks ! dan ! , persamaan 4.10 akan dimodifikasi dengan mencari bagian positif dari !(!) _{yaitu !}

!! . Jika !(!) memiliki rank sama dengan 1, maka !(!) dapat didekatkan dengan menggunakan bagian positifnya, yaitu !_!! .

 

Lemma 4.1 (Boutsidis & Gallopoulos, 2008)

Diberikan matriks ! ∈ ℝ!×! _{sedemikian sehingga rank(!) = 1, dan dapat dituliskan menjadi} !   =   !_!− !_!. Maka rank(!_!), rank(!_!) ≤  2.  

Berdasarkan Lemma 4.1 maka bagian positif dari !(!)_{, yaitu !}

!! dapat diekspansi berdasarkan Teorema 4.3 berikut:

Teorema 4.3 (Boutsidis & Gallopoulos, 2008)

Misalkan ! ∈ ℝ!×! _{memiliki rank sama dengan 1, sedemikian sehingga !   =  !!}!  _untuk ! ∈ ℝ!_{, ! ∈ ℝ}!_{. Misalkan !}

± ≔ !_!±

± , !± ≔

!±

!± adalah normalisasi bagian positif dan negatif dari ! dan !, dan !± = !± ‖!±‖ dan !± = !±  ‖!∓‖. Maka ekspansi tak terurut

nilai singular dari !_! dan !_! adalah  

!_!   = !_!!_!!_!!_{+ !}

!!!!!!, (3.11)

!_!   = !_!!_!!_!!_{+ !}

Maksimum triplet dari !! adalah (!!, !!, !!) jika !! = max( !! !! , !! !! ), selain

itu adalah (!_!, !_!, !_!). Dengan hal yang sama didapatkan maksimum triplet dari !_! adalah (!_!, !_!, !_!) jika !_! = max( !_! !_! , !_! !_! ), selain itu adalah (!_!, !_!, !_!).  

Dengan menggunakan ekspansi pada Teorema 4.3 maka bagian !! dapat didekomposisi dan digunakan untuk menginisialisasi matriks tidak negatif dari ! dan !. Secara umum algoritma NNDVD dapat dituliskan sebagai berikut:

1. hitung ! triplet utama dari !, yaitu:

! = [!_!, !_!, !_!], (4.13)

2. bentuk matriks ! ! !!! !

diperoleh dari pasangan vektor   !(!) _{= !}

!!!!, (4.14)

3. ekstrak bagian positif dari masing-masing triplet  

!_! dari ! dan [!_!, !_!] dari [!, !],

4. dengan ekspansi pada Teorema 4.3 gunakan untuk menginisialisasi (!,!).   (Boutsidis & Gallopoulos, 2008)

Algoritma lengkap dari NNDSVD diberikan pada tabel berikut ini:

Tabel 3.1 Algoritma Non-Negative Double Singular Value Decomposition Algoritma 3 Non-Negative Double Singular Value Decomposition

Input: Matriks non-negative ! ukuran !×!, bilangan bulat ! < min(!, !) Output: Matriks non-negative ! ukuran !×! dan ! ukuran !×!

Hitung ! triplet utama !: [!, !, !]

Inisialisasi !_!! = !_!!×!_!! dan ℎ_!! = !_!!×!_!!! _{untuk ! = 1, … , ! dan} ! = 1, … , ! for j = 2 : ! !   =   !_!", !   =   !_!" untuk !   =  1, 2, … , ! dan !   =  1, 2, …  , ! Cari !_!, !_!, !_!, !_! Cari ‖!!‖, ‖!!‖, ‖!!‖, ‖!!‖ !_!   =   ‖!_!‖‖!_!‖ dan !_!   =   ‖!_!‖‖!_!‖ if !_!   > !_! !   = !! ‖!!‖, ! = !! ‖!!‖,  sigma = !! else !   = !! ‖!!‖, ! = !! ‖!!‖,  sigma = !! end

!!" = !!!×sigma×!   dan ℎ!" = !!!×sigma×!! untuk ! = 1,2, … , ! dan ! = 1,2, … , !

1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

(Boutsidis & Gallopoulos, 2008)  

Hasil dari algoritma NNDSVD adalah matriks non-negative ! dan !. Matriks tersebut digunakan untuk inisialisasi pada algoritma penyelesaian NMF.

5. Hasil Penelitian

Evaluasi dari solusi yang dihasilkan dari kedua inisialisasi dilakukan dari dua aspek, yaitu keunikan solusi yang dihasilkan dan interpretasi topik.

5.1. Keunikan Solusi

Untuk evaluasi keunikan solusi yang dihasilkan diperlukan lebih dari satu kali eksekusi untuk melihat solusi yang dihasilkan pada setiap eksekusi sama atau tidak. Dengan menggunakan algoritma levenshtein13_{, yaitu algoritma perbandingan kata, dapat membandingkan setiap}

topik yang dihasilkan dari setiap eksekusi. Pada penelitian ini, dilakukan 2 kali eksekusi untuk masing-masing inisialisasi dan topik yang diekstrak adalah 50 topik yang sudah terurut, untuk membandingkan per topik diambil 10 topik utama.

Misal ! adalah matriks evaluasi topik, elemen ! adalah !_!" dengan !_!" ∈ [0,1]. Dimana !_!" adalah hubungan kesamaan antar topik. Maka topik ! dikatakan sama dengan topik ! jika !_!" = 1. Diagonal utama pada matriks evaluasi topik merupakan nilai kesamaan setiap topik dengan dirinya sendiri di setiap eksekusinya. Berikut adalah matriks evaluasi untuk inisialisasi random dengan menggunakan algoritma levenshtein untuk menyamakan per topik yang dihasilkan:

13 _{http://www.levenshtein.net/}

10 Topik bulan Agustus 2013 insialisasi

1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

Pada matriks evaluasi topik dengan menggunakan inisialisasi random, elemen-elemen dan diagonal utama yang terdapat di matriks hampir semua bernilai 0 di setiap bulannya. Jadi, setiap kali eksekusi inisialisasi random menghasilkan solusi (topik) yang berbeda.

Evaluasi solusi inisialisasi NNDSVD dilakukan dengan cara yang sama yaitu dengan menggunakan algoritma levenshtein. Berikut adalah hasil dari matriks evaluasi dengan menggunakan inisialsasi NNDSVD:

10 Topik bulan September 2013 insialisasi RANDOM1-RANDOM2 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

10 Topik bulan Desember 2013 insialisasi

RANDOM1-RANDOM2 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ 10 Topik bulan Oktober 2013 insialisasi

RANDOM1-RANDOM2

10 Topik bulan November 2013 insialisasi RANDOM1-RANDOM2

Pada matriks evaluasi dengan menggunakan inisialisasi NNDSVD pada setiap bulannya, dapat dilihat elemen diagonal utama matriks evaluasi setiap bulannya bernilai satu. Hal ini berarti setiap kali eksekusi menghasilkan solusi (topik) yang sama.

1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

10 Topik bulan Agustus 2013 inisialisasi NNDSVD 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

10 Topik bulan September 2013 inisialisasi NNDSVD 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

10 Topik bulan Oktober 2013 inisialisasi NNDSVD 1 2 3 4 5 6 7 8 9 10 topik ke ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞

10 Topik bulan November 2013 inisialisasi NNDSVD

10 Topik bulan Desember 2013 inisialisasi NNDSVD

5.2. Interpretasi Hasil

Pada umumnya, evaluasi dari aspek interpretasi topik dilakukan secara manual. Namun, hal itu sulit dilakukan jika topik yang diekstrak sangat banyak. Oleh karena itu, diperlukan perhitungan otomatis untuk menentukan suatu topik dapat diinterpretasikan atau tidak. Perhitungan otomatis yang digunakan pada penelitian ini adalah dengan menghitung nilai

coherence melalui persamaan 5.1.

!"# ! =   log ! !!, !! ! !! ! !! !!! !!! ! !!! (5.1) (Lau, Newman, & Baldwin, 2014)

!"#(!) merupakan nilai Pointwise Mutual Information (PMI) pada topik ke- ! dimana !(!!, !!) merupakan probabilitas kata !! dan !! muncul bersama, !(!!) probabilitas muncul kata !!, !(!!) probabilitas muncul kata !!.

Evaluasi dari aspek interpretasi hasil penelitian dengan menghitung nilai coherence dari 50 topik setiap bulannya. Semakin tinggi nilai coherence dari sebuah topik berarti semakin dapat diinterpretasikan oleh manusia. Perhitungan nilai coherence menggunakan modul

topic\_interpretability pada python. Pada penelitian ini, dihitung nilai rata-rata coherence dari

topik yang dihasilkan per bulan dengan menggunakan inisialisasi random dan NNDSVD. Berikut adalah grafik dari nilai rata-rata coherence yang dihasilkan:

Pada grafik rata-rata coherence topik yang dihasilkan dengan menggunakan inisialisasi NNDSVD lebih tinggi dibanding dengan inisialisasi random per bulan. Dari aspek interpretasi, inisialisasi NNDSVD jauh lebih mudah diinterpretasikan oleh manusia dibandingkan dengan inisialisasi random.

6. Kesimpulan

Dari percobaan implementasi metode NMF untuk melakukan analisis pengaruh NNDSVD sebagai inisialisasi terhadap topik yang dihasilkan adalah:

1. topik yang dihasilkan dengan menggunakan inisialisasi NNDSVD pada metode NMF menghasilkan solusi yang unik setiap kali eksekusinya,

2. interpretasi topik yang dihasilkan dengan menggunakan inisialisasi NNDSVD pada metode NMF lebih mudah diinterpretasikan oleh manusia dibandingkan dengan topik yang dihasilkan dengan menggunakan inisialisasi random.

7. Daftar Referensi

[1] Akbary, Amir, Dragos Ghioca, & Qiang Wang. (2011). On Constructing Permutations of Finite Fields. Finite Fields and Their Applications, Vol. 17, 51-67.

[2] Gallian, Joseph A. (2010). Contemporary Abstract Algebra. California: Cengage Learning.

[3] Hardy, Darel W., Fred Richman, & Carol L. Walker. (2009). Applied Algebra: Codes, Ciphers, and Discrete Algorithms. Florida: Taylor & Francis Group.

[4] Herstein, I.N. (1996). Abstract Algebra. New Jersey: Prentice Hall, Inc.

[5] Lidl, Rudolf & Harald N. (1997). Finite Fields. Cambridge: Cambridge University Press.

[6] Mullen, Gary L. & Carl Mummert. (2007). Finite Field and Applications. USA: American Mathematical Society.

[7] Patty, C. Wayne. (2009). Foundations of Topology. Massachusetts: Jones & Bartlett Learning.

[8] Zieve, Michael. (2010). Classes of Permutation Polynomials Based on Cyclotomy and An Additive Analogue. Additive Number Theory, pp. 335-361.