ANALISA PERPINDAHAN PADA STRUKTUR DENGAN EXCEL DAN CALCULATOR (Untuk Program Studi Teknik Konstruksi Gedung)

DIKTAT MEKANIKA TEKNIK 5

ANALISA PERPINDAHAN

PADA STRUKTUR DENGAN

EXCEL DAN CALCULATOR

(Untuk Program Studi Teknik Konstruksi Gedung)

PRATIKTO

NIP. 19610725 198903 1 002

JURUSAN TEKNIK SIPIL

Didanai dengan DIPA PNJ Tahun 2010

POLITEKNIK NEGERI JAKARTA

JUNI, 2010

LEMBAR PENGESAHAN

1. Judul : Metode Perpindahan dengan Excel dan Calculator 2. Penulis

a. Nama : PRATIKTO .ST, MsI. b. NIP : 19610725 198903 1 002 c. Jenis kelamin : Laki-Laki

d. Golongan/pangkat : IV a e. Jabatan Fungsional : Lektor f. Mata Kuliah yang diampu

Semester gasal : Mekanika Teknik 5 : Kerja Proyek Perencanaan Semester genap : Kontruksi Beton 1

; Lab Uji Bahan

g. Jurusan/Program Studi : Teknik Sipil/Teknik Konstruksi Gedung h. Alamat rumah : Jl. Kakap3 , P15 ; RT3/8 ; Mampang Indah I

DEPOK 16433

Alamat email : pratikto.tito@gmail.com pratikto@ymail.com 3. Jumlah Anggota : -

4. Lama kegiatan penulisan : 5 (Iima) bulan

5. Biaya yang diperlukan : Rp.3.500.000,- (Tiga Juta Lima Ratus Ribu Rupiah) 6. Sumber dana : DIPA PNJ 2010

Depok, 14 Juni, 2010 Menyetujui, Pelaksana

Ketua Program Studi,

A.Rudi Hermawan, ST,MT PRATIKTO., ST, MSi.

NIP.19660118 199011 1 001 NIP.19610725 198903 1 002

Mengetahui

Ketua Jurusan,

Sidiq Wacono, ST, MT.

Mahasiswa mampu

menggunakan calculator untuk operasi matrik

Mahasiswa mampu menjelaskan lendutan dan putaran sudut balok dengan metode conyugated beam

Mahasiswa mampu

menggunakan lembar kerja dari microsoft excel

Mahasiswa mampu menjelaskan perubahan panjang batang

REVIEW

Mampu menghitung gaya dalam struktur bangunan

gedung bertingkat sistem 2 dimensi

(dengan sistem matrik )

Mahasiswa mampu menjelaskan bidang gaya dalam balok statis tertentu dan statis tak tentu

Mahasiswa mampu menjelaskan langkah langkah metode perpindahan dalam bentuk matrik Mahasiswa mampu

menghitung Atap

bangunan gedung – Gaya Dalam - Rangka Batang

Mahasiswa mampu menghitung – Gaya Dalam - Balok Statis tak tentu dengan sistem matrik

Mahasiswa mampu

menghitung – Gaya Dalam Portal dengan sistem matrik Mahasiswa mampu

menghitung – Gaya Dalam - Portal dengan Kaki Miring

Mahasiswa mampu menjelaskan gaya dalam batang baik statis tertentu dan tak tentu diatas dua tumpuan dengan sistem matrik

Mahasiswa mampu menjelaskan gaya dalam batang statis tertentu

Nama Mata Kuliah : Mekanika Teknik 5 Pengembang : Pratikto ,ST.MSi

Kode Mata Kuliah : TKG Tahun Dikembangkan : 2010

Sistem Kredit Semester : 5 Penelaah Materi : Teori

Deskripsi Matakuliah

Mata Kuliah ini terdiri dari tiga bagian utama yaitu (1).Dasar Teori , (2)Pengoperasian alat bantu dengan format matrik dan Aplikasi pada struktur bangunan gedung bertingkat. Sangat dibutuhkan pemahaman mekanika teknik dari semester yang lalu dan (3)pemahaman operasi matrik. Struktur yang ditinjau adalah : Rangka Batang ( Atap bangunan ) , Balok dan Portal secara dua-dimensi. Beban yang digunakan adalah beban statik Gravitasi dan Lateral. Hasil perhitungan harus dinyatakan dalam gambar bidang gaya dalam Momen, Lintang dan Normal.

Kompetensi Umum

Setelah mengikuti kuliah ini mahasiswa : Mampu menganalisa gaya dalam struktur bangunan gedung bertingkat dengan sistem matrik baik rangka batang ataupun portal 2 dimensi yang berbasis pada perangkat lunak baik Kalkulator ataupun komputer standard seperti microsoft excel .

GARIS-GARIS BESAR PROGRAM PEMBELAJARAN (GBPP)

Nama Mata Kuliah : Mekanika Teknik 5 Pengembang : Pratikto ,ST.MSi Kode Mata Kuliah : TKG 5147 Tahun Dikembangkan : 2010

Sistem Kredit Semester : 5 Pendekatan Materi : Teori dan praktek

No Kompetensi Khusus

Pokok Bahasan

Sub Pokok Bahasan Pengalaman Belajar

Metode Media Estima si Waktu

Kepustak aan

1 _REVIEW Pendahuluan 1. Analisa struktur bangunan 2. Kontrak Perkuliahan

Calculator dan Komputer 3. Review Rangka batang 4. Review bid M,D,N

5. Hubungan mata kuliah dengan MK yang lain

Mahasiswa

mempersiapkan alat bantu hitung dan untuk mengingat kembali pelajaran mekanika teknik semester lalu

Presentasi White board , lcd projector, calculator, komputer 90 menit 2. _Mahasiswa mampu menggunakan calculator untuk operasi matrik Seperti: Casio FX9850GB Operasi pada perhitungan matrik dengan Calculator

1. Definisi matriks ; Sifat matrik 2. Penjumlahan ; Perkalian 3. Invers matrik

4. Input data calculator 5. Transpose

6. Perkalian 7. Invers

8. Solusi Persamaan Linear

Mahasiswa diajarkan bagaimana menggunakan peralatan calculator untuk operasi matrik.

Presentasi , praktek White board , lcd projector, calculator, komputer 90 menit 1

menggunakan komputer untuk operasi matrik Seperti: Lembar Kerja EXCEL perhitungan matrik dengan Lembar Kerja EXCEL 2. Transpose 3. Perkalian 4. Invers

5. Solusi Persamaan Linear

bagaimana menggunakan Komputer untuk operasi matrik. praktek projector, komputer 4 Mahasiswa mampu menjelaskan deformasi elemen struktur Macam-macam Deformasi : Batang dan balok

1. Perubahan Panjang Batang 2. Putaran sudut balok 3. Lendutan Balok

Dosen memberikan pendalaman besaran2 yang akan dipakai untuk matrik Presentasi , kuis, White board , lcd projector, komputer 90 menit 5. Mahasiswa mampu menjelaskan Dasar teori metode perpindahan dalam bentuk matrik Membentuk matrik kekakuan struktur dan menyelesaikan persamaan linear 1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear

Dosen memberikan penjelasan dalam bentuk soal. Presentasi, Conto soal, Latihan mandiri White board , lcd projector, komputer 180 menit 6 Mahasiswa mampu menghitung Rangka Batang dengan bentuk matrik Membentuk matrik kekakuan struktur Rangka Batang dan menyelesaikan persamaan linear 1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear 6. Gaya Dalam Rangka Batang

Dosen memberikan penjelasan dalam bentuk soal dan pemakaian alat hitung Presentasi, Conto soal, Latihan mandiri White board , lcd projector, komputer, calculator 180 menit 6 Mahasiswa mampu menghitung Balok statis tertentu dan tak tentu dengan bentuk matrik Membentuk matrik kekakuan struktur Balok dan menyelesai kan persamaan linear beserta Gambar MDN 1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear 6. Gaya Dalam Balok MDN

Dosen memberikan penjelasan dalam bentuk soal dan pemakaian alat hitung Presentasi, Conto soal, Latihan mandiri White board , lcd projector, komputer, calculator 180 menit

PUSTAKA

1 Supartono F.X. dan Boen T , 1980; Analisa struktur dengan metode matrix,Fakultas Teknik Universitas Indonesia, UI PRESS 2.Wang, C.K: 1999;”Matrix Methods of structural Analysis”, Scrantons International Text Book, Co

3.User guides Casio FXG9850 ; http://world.casio.com/edu-e/ 4.Microsoft office , excel 2007; http://office.microsoft.com/ 7. Mahasiswa mampu menghitung PORTALdengan bentuk matrik Membentuk matrik kekakuan struktur PORTAL dan menyelesai kan persamaan linear beserta Gambar MDN 1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear 6. Gaya Dalam Balok MDN

Dosen memberikan penjelasan dalam bentuk soal dan pemakaian alat hitung Presentasi, Conto soal, Latihan mandiri White board , lcd projector, komputer, calculator 180 menit 8. Mahasiswa mampu menghitung PORTAL dengan kaki Miring dalam bentuk matrik Membentuk matrik kekakuan struktur PORTAL MIRING dan menyelesai kan persamaan linear beserta Gambar MDN 1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear

6. Gaya Dalam Balok MDN

Dosen memberikan penjelasan dalam bentuk soal dan pemakaian alat hitung Presentasi, Conto soal, Latihan mandiri White board , lcd projector, komputer, calculator 180 menit

Kode Mata Kuliah : TKG Tahun Dikembangkan : 2010 Sistem Kredit Semester : 4

Pokok Bahasan (Topik)

Sub Pokok Bahasan (Sub Topik)

Hasil Pembelajaran Daftar Pustaka

1 2 3 4

1.REVIEW 1. Analisa Gaya Dalam balok st tertentu dan rangka batang

2. Dasar teori matrik , operasi matrik, sifat dan jenis matrik dan persamaan linear

1. Memahami mekanika Teknik Statis tertentu balok dan Rangka batang

2. Penggunaan Kalkulator dan Microsoft Excel

2. Metode Matrik - langkah langkah metode perpindahan dalam bentuk matrik

1. Matrik Statis 2. Matrik Deformasi 3. Matrik Kekokohan 4. Matrik Kekakuan 5. Solusi Persamaan Linear

Memahami Dasar teori metode perpindahan

3. Rangka Batang dengan bentuk matrik

1. Beban 2. Kekakuan 3.Perpindahan 4. Gaya Dalam

Menganalisa Rangka Batang dengan metode perpindahan

4. Balok statis tertentu dan tak tentu

1. . Beban 2. Kekakuan 3.Perpindahan 4. Gaya Dalam

Menganalisa Balok dengan metode perpindahan

5. PORTAL 1. . Beban

2. Kekakuan 3.Perpindahan 4. Gaya Dalam

Menganalisa Portal dengan metode perpindahan

6.PORTAL MIRING 1. Beban

2. Kekakuan 3.Perpindahan 4. Gaya Dalam

Menganalisa Portal Miring – Gable dengan metode perpindahan

NO. _KONTRAK ISI URAIAN 1. Manfaat

matakuliah Matakuliah ini membahas masalah gedung  bertingkat  dengan  sistem  matrik  baik  rangka  batang  ataupun analisa gaya dalam struktur bangunan  portal    2  dimensi    yang  berbasis  pada  perangkat  lunak  baik  Kalkulator  ataupun  komputer  standard  seperti  microsoft  excel. Matakuliah ini merupakan penunjang mata kuliah berikutnya yaitu Kerja Proyek Perencanaan yang akan langsung diterapkan pada semester berikutnya. Matakuliah ini juga sangat berguna ketika mahasiswa sudah memasuki di dunia kerja terutama yang bekerja di bidang struktur bangunan gedung bertingkat.

2. Deskripsi

perkuliahan Mata  Kuliah  ini  terdiri  dari  tiga  bagian  utama  yaitu  (1).Dasar  Teori  , (2)Pengoperasian  alat  bantu  dengan  format  matrik  dan  Aplikasi  pada  struktur  bangunan  gedung  bertingkat.  Sangat  dibutuhkan  pemahaman  mekanika  teknik  dari  semester  yang  lalu  dan  (3)pemahaman  operasi  matrik pada struktur yang ditinjau adalah : Rangka Batang ( Atap bangunan  )  ,  Balok  dan  Portal  secara  dua‐dimensi.  Beban  yang  digunakan  adalah  beban  statik  Gravitasi  dan  Lateral.  Hasil  perhitungan  harus  dinyatakan  dalam gambar bidang gaya dalam Momen, Lintang dan Normal.   

3. Tujuan

pembelajaran TIU: Mahasiswa dapat _{bertingkat dengan sistem matrik baik rangka batang ataupun portal}  menghitung gaya dalam struktur bangunan gedung 

2  dimensi    yang  berbasis  pada  perangkat  lunak  baik  Kalkulator  ataupun komputer standard seperti microsoft excel

 

TIK: Mahasiswa dapat menerapkan alat bantu hitung untuk analisa struktur bangunan bertingkat.

Mahasiswa dapat menghitung gaya dalam ataupun lendutan rangka  batang dengan alat bantu hitung 

Mahasiswa dapat menghitung gaya dalam ataupun lendutan Portal  2D atau  PORTAL MIRING dengan alat bantu hitung 

4. Organisasi materi

        

   

       

perkuliahan menyelesaikan kesetimbangan untuk gaya dalam dan mutlak menggunakan alat bantu hitung.

Metode perkuliahan untuk matakuliah ini dilakukan dengan kuliah (ceramah), diskusi, dan praktek langsung dengan alat bantu hitung. Metode kuliah digunakan apabila tujuan dari pembelajaran adalah untuk menjelaskan konsep dasar materi perkuliahan, sedangkan untuk mengetahui tingkat pemahaman mahasiswa dilakukan dengan diskusi atau Latihan soal dengan tujuan untuk mengetahui kemampuan mahasiswa dalam mengaplikasikan alat namtu dan menggunakan rumus-rumus yang telah dijelaskan sebelumnya

6. Referensi 1.Supartono  F.X.  dan  Boen  T  ,  1980;  Analisa  struktur  dengan  metode 

matrix,Fakultas Teknik Universitas Indonesia, UI PRESS 

2.Wang,  C.K:  1999;”Matrix  Methods  of  structural  Analysis”,  Scrantons  International Text Book, Co 

3.User guides Casio FXG9850 ; http://world.casio.com/edu‐e/  4.Microsoft office , excel 2007; http://office.microsoft.com/  

7. Tugas- tugas

• Setiap selesai pokok bahasan diberikan tugas individu mengerjakan soal, dengan waktu 1 minggu. Apabila tidak mengerjakan tugas tidak akan mendapat nilai pada item tersebut. Jika mengumpulkan tetapi terlambat nilai diperhitungkan 50% dari nilai yang diperoleh.

• Kuis/Tugas dilakukan sewaktu-waktu tanpa ada pemberitahuan, selama 1 semester dilakukan sebanyak 2 kali.

• Materi UTS dan UAS menggunakan bentuk essai dan diperbolehkan membuka Ringkasan pada kertas double folio. Tidakdiperkenankan saling meminjam Ringkasan

8. Kriteria

penilaian • Indikator penilaian: ketepatan perhitungan, cara penyelesaian, kebenaran konsep dan ketepatan analisa. • Bobot penilaian: o Tugas 1 : 10% o Kuis/Tugas 2+3 : 20% o UTS : 30% o UAS : 40% • Kategori nilai: A = 100 – 81 A- = 80 – 76 B+ = 75 – 73 B = 72 – 68 B- = 67 – 64 C+ = 63 – 60 C = 59 – 56 D = 55 – 41 E = 40 - 0 9. Jadwal

perkuliahan Minggu Pokok bahasan 1 Pendahuluan elemen struktur bangunan gedung bertingkat 2 – 6 Rangka Batang dan Balok

8 – 10 Portal 2D beraturan

Prakata Daftar Isi

PENDAHULUAN

1.1 Gambaran Umum Mata Kuliah

1.2 Hubungan Mata Kuliah dengan yang lain 1.3 Tujuan Pembelajaran Umum

1.4 Petunjuk Buku Ajar MODUL 1

DASAR METODE PERPINDAHAN

2.1 Pendahuluan

2.2. Tujuan Pembelajaran Khusus 2.3 Kegiatan Belajar

2.3.1 Dasar Teori Perpindahan 2.3.1.1 Pembagian elemen

2.3.1.2 Beban Ekwivalen

2.3.1.3 Pembentukan Matrik Kekakuan 2.3.1.4 Solusi Persamaan Linear

2.3.2 Latihan 2.3.3 Tugas 2.3.4 Evaluasi 2.4 Rangkuman 2.5 Daftar Pustaka MODUL 2 RANGKA BATANG 3.1 Pendahuluan

3.2 Tujuan Pembelajaran Khusus 3.3 Kegiatan Belajar

3.3.1 Perpindahan Batang

3.3.2 Latihan 3.3.3 Tugas 3.3.4 Evaluasi 3.4 Rangkuman 3.5 Daftar Pustaka MODUL 3 BALOK 4.1 Pendahuluan

4.2. Tujuan Pembelajaran Khusus 4.3 Kegiatan Belajar

4.3.1 Deformasi Balok

4.3.1.1 Pembagian elemen

4.3.1.2 Beban Ekwivalen

4.3.1.3 Pembentukan Matrik Kekakuan 4.3.1.4 Solusi Persamaan Linear

4.3.2 Latihan 4.3.3 Tugas 4.3.4 Evaluasi 4.4 Rangkuman 4.5 Daftar Pustaka MODUL 4 PORTAL 5.1 Pendahuluan

5.2. Tujuan Pembelajaran Khusus 5.3 Kegiatan Belajar

5.3.1 Deformasi Lentur Portal 5.3.1.1 Pembagian elemen

5.3.3 Tugas 5.3.4 Evaluasi 5.4 Rangkuman 5.5 Daftar Pustaka MODUL 5 PORTAL MIRING 6.1 Pendahuluan

6.2. Tujuan Pembelajaran Khusus 6.3 Kegiatan Belajar

6.3.1 Deformasi Lentur Portal Miring 6.3.1.1 Pembagian elemen

6.3.1.2 Beban Ekwivalen

6.3.1.3 Pembentukan Matrik Kekakuan 6.3.1.4 Solusi Persamaan Linear

6.3.2 Latihan

6.3.3 Tugas

6.3.4 Evaluasi

6.4 Rangkuman 6.5 Daftar Pustaka

BAB I. PENDAHULUAN

1. 1. Gambaran Umum Mata Kuliah

Ada beberapa hal yang harus dipahami atau disamakan persepsi terhadap analisa struktur dewasa ini. Pemakaian alat bantu hitung seperti calculator ataupun komputer bukan merupakan hal yang aneh dan sulit karena hampir setiap manusia ataupun mahasiswa sudah mempunyai alat tersebut. Hampir disetiap komputer terdapat program microsoft office seperti : word, excel dan juga untuk kalkulator banyak yang menyediakna fungsi2 yang berguna seperti : matrik, trigonometri dan sebagainya. Apakah kita sudah menggunakan se optimal mungkin ? Hal ini juga disertakan dalam peninjauan biaya untuk mendapatkan perangkat lunak tersebut. Mudah2an pernyataan diatas dapat menggugah pembaca untuk dapat memakai alat bantu yang konon sudah dianggap biasa dapat digunakan seoptimal mungkin.

Sebagai tujuan akhir tulisan ini adalah agar supaya pembaca dapat menggunakan alat bantu hitung , seperti kalkulator atau microsoft office untuk menganalisa gaya dalam struktur pada bangunan bertingkat. Hal ini tentu saja dibutuhkan ketrampilan menggunakan Kalkulator dan perangkat lunak untuk lembar kerja microsoft office excel. Lampiran 1

Untuk pemahaman gaya dalam struktur, pembaca dipersilahkan mempersiapkan beberapa hal seperti : deformasi perubahan bentuk sepeti lendutan dan putaran sudut yang umumnya dapat dijelaskan melalui metode moment area

ataupun conyugated beam. Lampiran 2

1. 2. Hubungan Mata Kuliah dengan yang lain

Mata kuliah Mekanika Teknik 5 ini berhubungan erat dengan mata kuliah Mekanika Teknik sebelumnya yang membahas mengenai pengertian Gaya luar, gaya dalam, syarat kesetimbangan dan Bidang gaya dalam MDN. Adapun

deformasi dapat melihat dari mata kuliah Kekuatan Bahan yang membahas

mengenai putaran sudut , lendutan baik aksial ataupun lentur termasuk perpanjangan dan perpendekan. Pada mata kuliah Komputer terapan juga dibahas mengenai pemakaian perangkat lunak microsoft office khususnya adalah excel.

Masalah mengenai teori dasar matrik umumnya dapat dijumpai pada matematik tingkat perguruan tinggi seperti jenis jenis, sifat matrik dan operasi pada matrik termasuk perkalian, penambahan dan invers matrik. Analisa gaya dalam merupakan hal yang harus dilakukan terlebih dahulu sebelum menganalisa pada material yang akan digunakan, seperti Beton, Baja dan sebagainya

1. 3. Tujuan Pembelajaran Umum

Diharapka pembaca dapat melakukan perhitungan dan menganalisa gaya dalam struktur bangunan gedung bertingkat sistem 2 dimensi dengan alat bantu hitung yaitu kalkulator ataupun lembar kerja microsoft office excel.

Struktur bangunan gedung bertingkat adalah sistem 3 dimensi. Struktur ini dapat dipisah dalam beberapa bagian struktur dua 2 dimensi, seperti : Portal, balok, Pelat dan Rangka batang atap.

1. 4. Petunjuk Buku Ajar

Buku ajar ini dimaksudkan tidak hanya sebagai wacana analisa gaya dalam tetapi diharapkan dapat di praktekan langsung dengan alat bantu hitung seperti kalkulator ataupun lembar kerja excel. Dasar teori metode perpindahan akan dibahas pada diktat ini. Untuk teori matrik dan kekuatan bahan pembaca dapat melihat rujukan lain.Pemakaian alat bantu hitung kalkulator dan lembar kerja excel penulis hanya mengambil dari rujukan yang umum dan disajikan pada lampiran.

Dasar teori metode perpindahan akan dibahas pada bab 2 yang akan dilanjutkan aplikasinya pada : Struktur rangka batang bab 3 dan Balok baik statis tertentu ataupun statis tak tentu pada bab 4. Evaluasi akan dilakukan setelah pembaca memahami metode matrik pada rangka batang dan balok. Tahapan ini pembaca diharapkan menguasai proses pembentukan matrik dan operasi pada matrik dengan alat bantu kalkulator.

Pada bab5 pembaca akan diajak untuk mengaplikasikan pada portal bentuk sederhana yang terdiri dari elemen struktur seperti balok dan kolom. Pada tahap ini diberikan tugas untuk menyelesaikan struktur Portal bertingkat dengan

bantuaan lembar kerja excel yang terdapat pada komputer. Disarankan tidak menggunakan kalkulator untuk analisa portal bertingkat ini karena keterbatasan memori yang ada. Untuk bentuk yang tidak beraturan sepeti portal dengan kaki miring dibahas pada bab 6. Masalah ini biasanya digunakan untuk menganalisa struktur tangga 2 dimensi

Tulisan ini membahas metode matrik yang digunakan untuk analisa struktur - framed Structure. Pada umumnya ada 2 metode matrik seperti metode

gaya-force method dan metode kekakuan-displacement method. Metode Gaya adalah

metode untuk analisa gaya dalam struktur yang berdasarkan pada hasil iterasi gaya dalam seperti : metode cross, Kani, Takebaya, Muto, Clapeyron dsbnya. Metode ini sudah banyak ditinggalkan, kenapa? Apakah seperti pengaruh metode elastis dengan kekuatan batas? Tidak seluruh metode dibahas di sini karena menyangkut keterbatasan waktu dan dana yang ada. Methode yang akan dibahas adalah metode perpindahan – displacement methods yang sudah berkembang menjadi metode kekakuan-stiffness method .Metode ini uga merupakan dasar dari pada metode kekakuan langsung – direct stiffness method dan metode elemen

finite element untuk analia benda kontinum.

Beberapa materi dasar akan ditinjau seperti jenis struktur dan deformasi akibat beban. Selain itu juga ditinjau konsep dasar seperti keseimbangan, kesepadanan, derajat ketidaktentuan dan sebagainya.

MODUL 1

BAB II. DASAR TEORI

2. 1. Pendahuluan

Tulisan ini membahas metode matrik yang digunakan untuk analisa struktur

framed Structure. Pada umumnya ada 2 metode matrik seperti metode gaya-force method dan metode kekakuan-displacement method. Metode Gaya adalah metode

untuk analisa gaya dalam struktur yang berdasarkan pada hasil iterasi gaya dalam seperti : metode cross, Kani, Takebaya, Muto, Clapeyron dsbnya. Metode ini sudah banyak ditinggalkan, kenapa? Apakah seperti pengaruh metode elastis dengan kekuatan batas? Tidak seluruh metode dibahas di sini karena menyangkut keterbatasan waktu dan dana yang ada. Methode yang akan dibahas adalah metode perpindahan – displacement methods yang sudah berkembang menjadi metode kekakuan - stiffness method .Metode ini uga merupakan dasar dari pada metode kekakuan langsung – direct stiffness method dan metode elemen finite

element untuk analia benda kontinum.

Beberapa materi dasar akan ditinjau seperti jenis struktur dan deformasi akibat beban. Selain itu juga ditinjau konsep dasar seperti keseimbangan, kesepadanan, derajat ketidaktentuan dan sebagainya.Struktur yang akan dibahas selanjutnya merupakan struktur rangka/ framed structur dan dapat dibagi atas.

1. Rangka batang bidang

2. Balok statis tertentu dan statis tak tentu 3. Portal bidang

4. Portal berkaki miring

Masing-masing jenis struktur mempunyai ciri tersendiri, sehingga perlu dibahas secara terpisah. Tempat titik berkumpulnya elemen-elemen struktur dinamakan titik kumpul (Joints-Nodal) termasuk tumpuan dan ujung elemen yang bebas. Tumpuan dapat merupakan jepit (fixed), sendi (Hinged, Bin), roller dan elastis (springs).

Pada metode ini langkah awal yang harus ditinjau adalah perpindahan yang dinyatakan sebagai derajat kinematis bukan derajat statis. Kinematis adalah perpindahan yang tidak diketahui atau yang dicari. Metode kekakuan ini struktur

dirubah menjadi struktur kinematis tertentu sehingga seluruh perpindahan yang tidak diketahui adalah NOL. Agar perpindahan ini menjadi NOL maka pada titik kumpul diberi pengekangan ( Restraint ) terhadap segala macam perpindahan struktur yang diberi pengekangan dinamakan struktur terkekang / Restrained

structure. Untuk mendapatkan pengaruh seperti pada struktur semula maka dapat

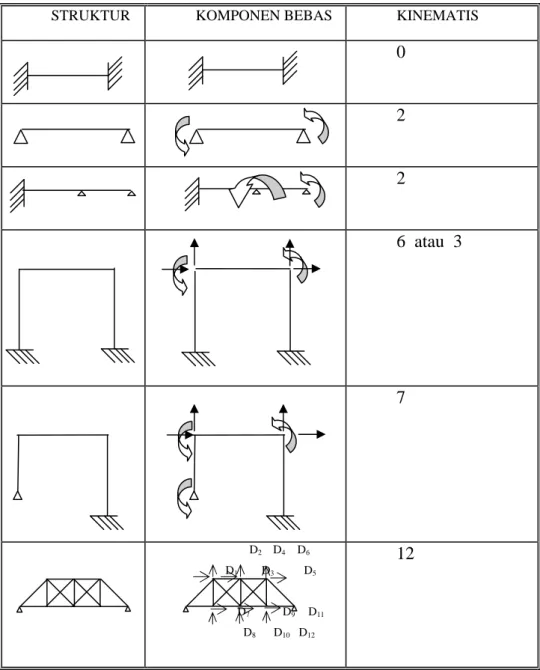
dilakukan super posisi dari stuktur yang terkekang dengan gaya penggantinya. Tabel 2.1 Derajat Kinematis

STRUKTUR KOMPONEN BEBAS KINEMATIS

0 2 2 6 atau 3 7 D2 D4 D6 D1 D3 D5 D7 D9 D11 D8 D10 D12 12

Bagian terpenting dalam penyelesaian superposisi adalah pembentukan persamaan gaya yang menyatakan seperti keadaan struktur semula. Bersamaan superposisi gaya ini dikenal juga sebagai persamaan keseimbangan titik kumpul. Beberapa istilah dalam analisa struktur seperti deformasi, Aksi dan Perpindahan , derajat kebebasan , derajat ketidak tentuan statis atau kinematis , stabilitas, Superposisi , Kekakuan , beban ekivalent dan teori energi, pembaca dapat melihat pada lampiran 1.

2. 2 Tujuan Pembelajaran

Menguasai teori dasar metode perpindahan dalam bentuk matrik dan sekaligus pemakaian dengan alat bantu pada operasi matrik Metode ini sebenarnya adalah mencari hubungan gaya luar dengan lendutan atau pembentukan matrik kekakuan yang merupakan hubungan antara Gaya luar dengan deformasi – lendutan. Selanjutnya penyelesaian persamaan linear untuk mendapatkan deformasi dan diteruskan pada gaya dalam.

Hubungan ini bisa dinyatakan sebagai :

( Q } = [K] { D} (2.1)

{ Q } = matrik gaya2 dalam elemen [K] = matrik kekakuan struktur .

{ D} = matrik lendutan deformasi struktur.

2. 3 Kegiatan Belajar

2.3.1 Dasar Teori Perpindahan

Pada dasarnya metode ini dimulai dengan memisahkan struktur menjadi elemen elemen dan memberikan besaran lendutan “ anu “ yang dalam hal ini merupakan lendutan elemen pada titik diskrit sebagai sasaran yang harus dicari. Untuk mengetahui lendutan titik diskrit , maka harus diketahui derajat kinematis atau derajat kebebasan dari struktur. Derajat Kinematis adalah suatu besaran yang menyatakan jumlah komponen bebas dititik diskrit yang mungkin terjadi. Sehingga urutan kerjanya adalah sebagai berikut :

1. Kompatibiliti; Hubungan antara deformasi dengan lendutan, atau secara tegasnya mencari deformasi yang terjadi pada elemen-elemen dititik-titik diskrit akibat diberikannya lendutan pada struktur dititik-titik tersebut. 2. Persamaan hubungan tegangan dan regangan, yaitu mencari hubungan

mengenai gaya-gaya dalam yang timbul sebagai akibat adanya deformasi pada elemen-elemen struktur tersebut.

3. Kesetimbangan; langkah terakhir untuk menyatakan gaya liuar dititik diskrit dengangaya-gaya dalam, atau mencari berapa besar gaya luar di ujung elemen yang diimbangi oleh gaya dalam dititik diskrit.

Dengan menggabungkan ketiga langkah diatas, akan didapatkan hubungan antara gaya dan lendutan seperti dinyatakan pada persamaan (2.1).

Secara garis besarnya , langkah2 metode ini adalah : 1. Memilih elemen-elemen yang akan digunakan. 2. Menentukan kinematis struktur D ,

3. Menentukan matrik gaya luar Q yang sesuai dengan kinematis D. 4. Memberikan deformasi struktur D = 1 unit dan menghitung deformasi

masing2 elemen (d). Hubungan ini dinyatakan dengan matrik deformasi [A]. 5. Menentukan hubungan gaya dalam dengan deformasi elemen yang

dinyatakan dengan matrik Kekokohan [S].

6. Menentukan hubungan Kesetimbangan antara gaya luar dengan gaya dalam yang dinyatakan sebagai matrik Statis [B].

7. Menghitung matrik K yang berasala dari matrik [A] ; [S] dan [B]. Matrik [K] ini merupakan hubungan antara {Q} dengan {D}

8. Menyelesaikan persamaan linear untuk mendapatkan deformasi struktur {D}. 9. Mencari gaya dalam {H} struktur dari matrik [S] dan [A] .

DIAGRAM :

[K]

{ }

Q

{ }

D

[ ]

B

[ ]

A

{ }

H

{ }

d

[ ]

S

Gambar 2.1 2.3.1.1 Pembagian elemen

Pada struktur 2D bidang dengan Rigid connections pada umumnya struktur terdiri atas beberapa elemen yang dipisahkan oleh titik node diskrit . Perilaku dari elemen ini diwakili oleh titik diskrit dalam bentuk lendutan translasi linear dan rotasi anguler. Lendutan dinyatakan oleh dua komponen yang saling tegak lurus sedangkan rotasi dinyatakan oleh komponen anguler. Sehingga pada titik pertemuan terdapat 3(tiga) komponen lendutan.

Pada Rangka batang 2D dengan sambungan engsel, maka komponen rotasi tidak ada dan hanya komponen traslasi baik vertikal atau mendatar. Titik diskrit merupakan titik pertemuan batang ataun titik kumpul.

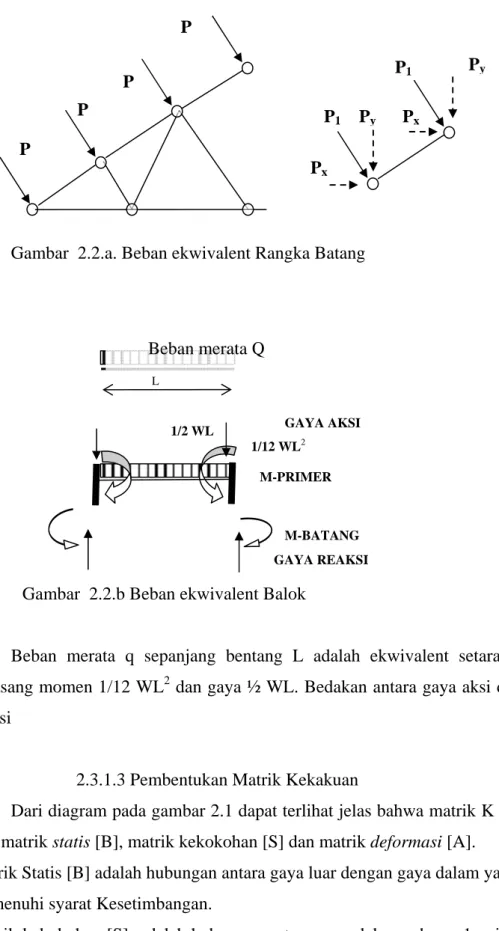
2.3.1.2 Beban Ekwivalen

Beban luar yang bekerja pada elemen harus dipindahkan ke titik disktrit yang berada di ujung elemen. Perlu diperhatikan bahwa beban ini bukan gaya reaksi tetapi merupakan gaya aksi yang bekerja di ujung atau perletakan sebagai pengganti beban luar. Dengan kata lain beban ekwivalen adalah gaya aksi di ujung perletakan elemen. Pembaca dapat melihat pada lampiran 1.

Gambar 2.2.a. Beban ekwivalent Rangka Batang

Gambar 2.2.b Beban ekwivalent Balok

Beban merata q sepanjang bentang L adalah ekwivalent setara dengan sepasang momen 1/12 WL2 dan gaya ½ WL. Bedakan antara gaya aksi dan gaya reaksi

2.3.1.3 Pembentukan Matrik Kekakuan

Dari diagram pada gambar 2.1 dapat terlihat jelas bahwa matrik K dibentuk dari matrik statis [B], matrik kekokohan [S] dan matrik deformasi [A].

Matrik Statis [B] adalah hubungan antara gaya luar dengan gaya dalam yang harus memenuhi syarat Kesetimbangan.

Matrik kekokohan [S] adalah hubungan antara gaya dalam sebesar 1 unit dengan deformasi elemen yang mengikuti Hukum Hooke.

Beban merata Q L 1/12 WL2 1/2 WL GAYA AKSI GAYA REAKSI M-PRIMER M-BATANG P P P P Px Py P1 Px Py P1

Matrik deformasi [A] adalah hubungan compatibility kesesuaian antara deformasi elemen dengan deformasi struktur sebesar 1 unit.

Matrik [K] merupakan penggabungan dari ketiga matrik diatas atau dapat pula ditulis sebagai :

[ ] [ ][ ][ ]

K ≈ B S A

Matrik ini disebut pula sebagai matrik Kekakuan Struktur.

Dilihat dari hasil matrik [B] merupakan transpose dari matrik [A].

2.3.1.4 Solusi Persamaan Linear

Persamaan yang terbentuk dari hubungan gaya luar dengan deformasi adalah persamaan linear dalam bentuk matrik. Persamaan ini dapat diselesaikan dengan operasi matrik untuk mencari besarnya deformasi dari struktur.

{ }

[ ]

{ }

[ ] [ ][ ][ ] [ ] [ ]

{ }

D

[ ]

K

{ }

Q A B A S B K D K Q T 1 − ≈ ≈ ⇔ ≈ ≈

Selanjutnya untuk matrik gaya dalam dapat dihitung setelah deformasi struktur didapatkan. Matrik [H] bukan merupakan gaya dalam struktur karena harus di superposisikan dengan beban aksi

{ }

[ ]

{ }

{ }

H

[ ][ ]

S A

{ }

D d S H ≈ ≈

2.3.1.5 Illustrasi metode

Gambar 2.3

1. Tentukan elemen , Kinematis, buat diagram Q-D dan H-d

Gambar 2.4 ; 3 elemen, Diagram Q-D dan H-d

2. statik Matrik A ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ 6 5 4 3 2 1 d d d d d d = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 X ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ 3 2 1 D D D

{ }

d ≈

[ ]

A

{ }

D ⇒ L EI L L Q1- D1 Q2- D2 Q3- D3 H1-d1 H2-d2 H3-d3 H4-d4 H5-d5 H6-d6 3 elemen 3 kinematis; D1.D2,D3

d1 d3 d5 d2 d4 d6 d5 d4 d6 gambar 2.5 matrik A

3. Gaya Dalam dengan Deformasi ( H-d)

d1 H1 H3 d3 H5d5

d2-H2 d4 -H4 d6-H6

d1 = 1 unit H1=4EI/L ; H2=2EI/L

d1 d2 2EI/L

4EI/L

d2 = 1 unit H1=2EI/L ; H2= 4EI/L

d1 d2 4EI/L

2EI/L

{ }

H =

[ ]

S *

( )

d

gambar 2.6 matrik Kekokohan [S]

⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ 6 5 4 3 2 1 H H H H H H = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ L EI L EI L EI L EI L EI L EI L EI L EI L EI L EI L EI L EI / 4 / 2 0 0 0 0 / 2 / 4 0 0 0 0 0 0 / 4 / 2 0 0 0 0 / 2 / 4 0 0 0 0 0 0 / 4 / 2 0 0 0 0 / 2 / 4 ⎪ ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ 6 5 4 3 2 1 d d d d d d D1=1unit D2=1unit D3=1unit

4. Hubungan Keseimbangan , Gaya Luar = Gaya Dalam H2 H3 H4 H5 H6 Q1 = H2 + H3 Q1 Q2 Q3 Q2 = H4 + H5 Gambar 2.7 matrik B Q3 = H6

∑

P = 0 ; Q1 - H2 - H3 = 0 ⎪ ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ≡ ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ 6 5 4 3 2 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 3 2 1 H H H H H H Q Q Q

{ }

Q ≡

[ ]

B

{ }

H ⇒ 5. Persamaan Linear

{ }

[ ]{ }

[ ] [ ][ ][ ] [ ] [ ]

[ ] [ ] [ ][ ]

{ }

D

[ ] { }

K

Q

A

S

A

K

A

B

A

S

B

K

D

K

Q

T T 1 −

≈

≈

≈

⇔

≈

≈

6. Gaya Dalam

{ }

[ ]

{ }

{ }

H

[ ][ ]

S

A

{ }

D

d

S

H

≈

≈

7. Momen Akhir

Momen akhir adalah superposisi hasil matrik {H} dengan beban ekwivalen yaitu Momen Primer

2.3.2 Latihan

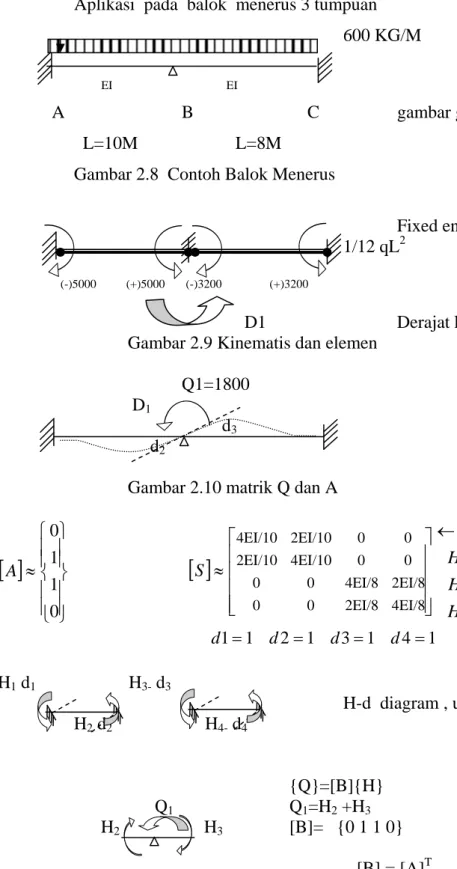
Aplikasi pada balok menerus 3 tumpuan 600 KG/M EI EI

A B C gambar gaya dalam !!

L=10M L=8M

Gambar 2.8 Contoh Balok Menerus

Fixed end momen

1/12 qL2

(-)5000 (+)5000 (-)3200 (+)3200

D1 Derajat kinematis = 1

Gambar 2.9 Kinematis dan elemen Q1=1800 D1

d3

d2

Gambar 2.10 matrik Q dan A

[ ]

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≈ 0 1 1 0 A

[ ]

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ≈ 4EI/8 2EI/8 0 0 2EI/8 4EI/8 0 0 0 0 4EI/10 2EI/10 0 0 2EI/10 4EI/10 S 4 3 2 1 H H H H ← d1=1 d2=1 d3=1 d4=1 H1 d1 H3- d3 H-d diagram , untuk [S] H2 d2 H4- d4 {Q}=[B]{H} Q1 Q1=H2 +H3 H2 H3 [B]= {0 1 1 0} [B] = [A]T Gambar 2.11 Matrik S dan B

[K] = [B][S][A] = 0.9 EI [K]-1 = 1 / (0.9EI) {D} = [K]-1 {Q} = 2000 / EI {H} = [S][A]{D} =

[ ]

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≈ 500 1000 800 400 H

Momen batang ( kebalik 5000 5000 3200 3200 an momen primer) 400 800 1000 500 Momen Akhir 5400 4200 4200 2700 5400 7500 4200 4800 2700 1/8 600 102 _{= 7500} 1/8 600 82 = ₄₈₀₀ GAYA DALAM MOMEN

2700 1350 3000 3000 2400 2400 120 120 187.5 187.5 3120 2587.5 2112.5 GAYADALAM LINTANG 2880 Gambar 2.12 Penyelesaian

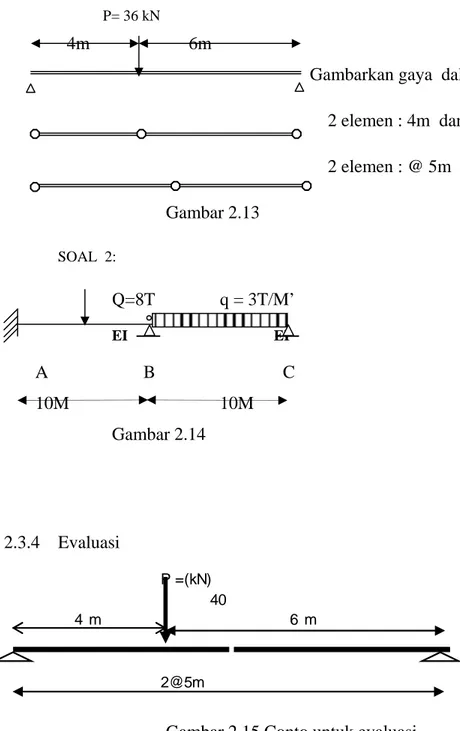
2.3.3 Tugas

SOAL 1: P= 36 kN

4m 6m

Gambarkan gaya dalam , M, D 2 elemen : 4m dan 6m 2 elemen : @ 5m Gambar 2.13 SOAL 2: Q=8T q = 3T/M’ EI EI A B C 10M 10M Gambar 2.14 2.3.4 Evaluasi

Gambar 2.15 Conto untuk evaluasi

P =(kN) 40

4 m 6 m

Tentukan Elemen, Kinematis, Diagram Q-D dan H-d

Beban Ekwivalen

Pembentukan persamaan Linear dan solusi persamaan

Q1-D1 Q2-D2 Q3-D3

Q-D diagram Q4-D4 Degree of kinematic 4 Number of member 2 H1-d1 H2-d2 H3-d3 H4-d4 H-d diagram 40 Q 4 1 -6,4 25,6 6,4 5 -25,6 0 -6,4 25,6 -28,16 -3,84 3,84 11,84 -8 -32 28,16 -11,84 -28,16 40 A S = (EI) SA=(EI) 1 0 0 -0,2 0,8 0,4 0 0 0,8 0,4 0 -0,2 0 1 0 -0,2 0,4 0,8 0 0 0,4 0,8 0 -0,2 0 1 0 0,2 0 0 0,8 0,4 0 0,8 0,4 0,24 0 0 1 0,2 0 0 0,4 0,8 0 0,4 0,8 0,24 A At K=(AE) 1 0 0 -0,2 1 0 0 0 0,8 0,4 0 -0,2 0 1 0 -0,2 0 1 1 0 0,4 1,6 0,4 0 0 1 0 0,2 0 0 0 1 0 0,4 0,8 0,24 0 0 1 0,2 -0,2 -0,2 0,2 0,2 -0,2 0 0,24 0,19 Kinv=(1/EI) D H 3,33 -0,42 -1,67 6,25 -208 -6,4 -0,42 0,83 -0,42 0,00 24 86,4 -1,67 -0,42 3,33 -6,25 176 -60,8 6,25 0,00 -6,25 20,83 -626,667 0 0 M AKHIR 0,00 60,80 -60,80

Hasil Gaya Dalam

2. 4 Rangkuman

Bedakan jenis struktur menurut deformasi yang terjadi Secara garis besarnya , langkah2 metode ini adalah :

1. Menentukan kinematis struktur dan memberikan deformasi struktur D dan deformasi masing2 elemen (d). Hubungan ini dinyatakan dengan matrik [A].

2. Menentukan hubungan gaya dalam dengan deformasi elemen yang dinyatakan dengan matrik [S].

3. Menentukan hubungan Kesetimbangan antara gaya luar dengan gaya dalam yang dinyatakan sebagai matrik [B].

d4 d2 d3 d1 0 60,8 -60,8 0 -48,64 -60,80 -32 -80,64 40x6/10*4 96 -48,64 40x1/5*4 -32 -80,64

4. Menyelesaikan persamaan linear untuk deformasi struktur {D}. 5. Mencari gaya dalam struktur ataupun reaksi.

6. Gambar gaya dalam struktur

DIAGRAM :

[ ]

K

{ }

Q

{ }

D

[ ]

B

[ ]

A

{ }

H

{ }

d

[ ]

S

Gambar 2.1 2.5 Daftar Pustaka

1. Supartono F.X, dan Boen T ; Analisa Struktur dengan Metode Matrix, Fakultas Teknik universitas Indonesia, UI Press, 1984

2. Wang , C.K : “ Matrix methods of Structural Analysisa” Scrantons International Text Book Co., 1986

MODUL 2

BAB III. RANGKA BATANG

3.1 Pendahuluan

Metode ini dimulai dengan memberikan pada struktur ybs beberapa besaran lendutan “ anu “ yang dalam hal ini merupakan lendutan elemen pada titik diskrit sebagai besaran yang harus dicari. Pembagian elemen disesuaikan dengan tempat titik kumpul rangka. Untuk mengetahui lendutan titik diskrit , maka harus diketahui derajat kinematis atau derajat kebebasan perpindahan dari struktur. Derajat kinematis yang merupakan jumlah komponen bebas dititik diskrit baik arah vertikal ataupun horizontal merupakan vektor gaya luar bekerja. Pada rangka batang tidak terdapat lendutan-rotasi dinyatakan oleh komponen anguler – putaran sudut . Sehingga pada Rangka batang 2D dengan sambungan engsel, lendutan dinyatakan oleh dua komponen yang saling tegak lurus.

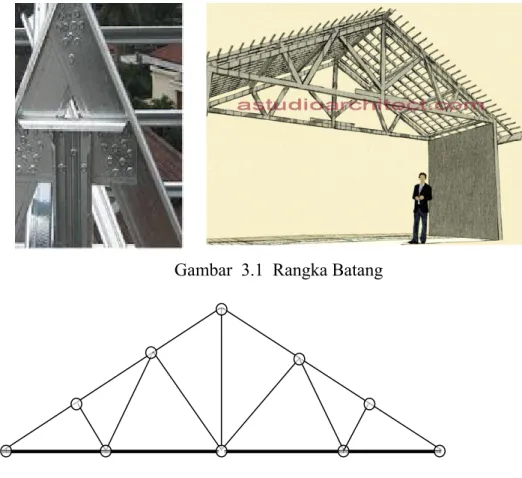
Gambar 3.1 Rangka Batang

3.2 Tujuan Pembelajaran Khusus

Tujuan pada pembahasan ini adalah menghitung gaya dalam dari struktur Rangka Batang. Pada metode ini didahulukan dengan mencari hubungan gaya dengan lendutan. Pembentukan matrik kekakuan untuk hubungan antara Gaya luar dengan deformasi – lendutan akan menghasilkan persamaan linear dalam bentuk matrik. Selanjutnya penyelesaian persamaan linear untuk mendapatkan deformasi dan diteruskan pada gaya dalam harus menggunakan alat bantu baik calculator ataupun komputer.

Hubungan ini bisa dinyatakan ulang dari pers 2.1 sebagai :

{ Q } = [K] { D} (2.1)

{ Q } = matrik gaya2 dalam elemen

[K] = matrik kekakuan struktur Rangka batang. { D} = matrik lendutan deformasi struktur

3.3 Kegiatan Belajar

Pada dasarnya sifat rangka batang berbeda dengan balok didalam analisa gaya dalam. Disetiap sambungan rangka batang umumnya hanya gaya axial yang dipakai dalam perencanaan sambungan. Deformasi axial dapat berupa translasi vertikal dan horizontal. Jadi pada rangka batang setiap titik mempunyai 2 derajat kinematis. Untuk material Hooke yang linear elastis maka berlaku hubungan seperti :

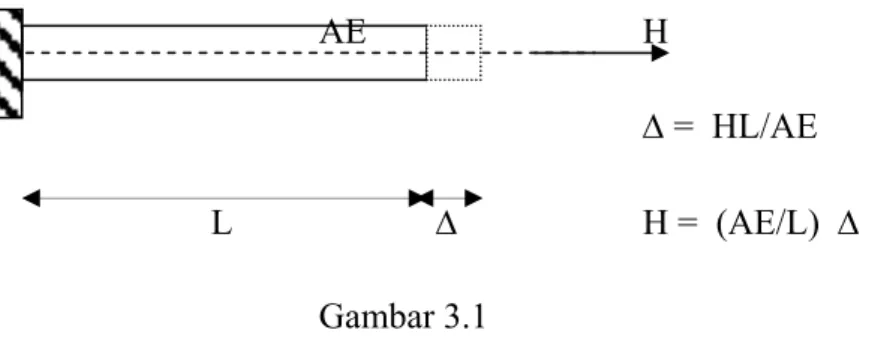
AE H

Δ = HL/AE

L Δ H = (AE/L) Δ

Gambar 3.1

Ilustrasi untuk metode perpindahan pada rangka batang disajikan dalam pembahasan rangka batang berikut ini.

Conto sederhana (1) :

1000 kg

A 1 2 B

C AE for all members

4 3 5 1.5m D 2000 kg 2m 2m

Gambar 3.2 contoh sederhana D1 D2 D4 D3 Gambar 3.3 Kinematis D1=1 D2=1 d1=1 d2=-1 d3=1 α α D3=1 α 4 3 D4=1 5

[ ]

[ ]

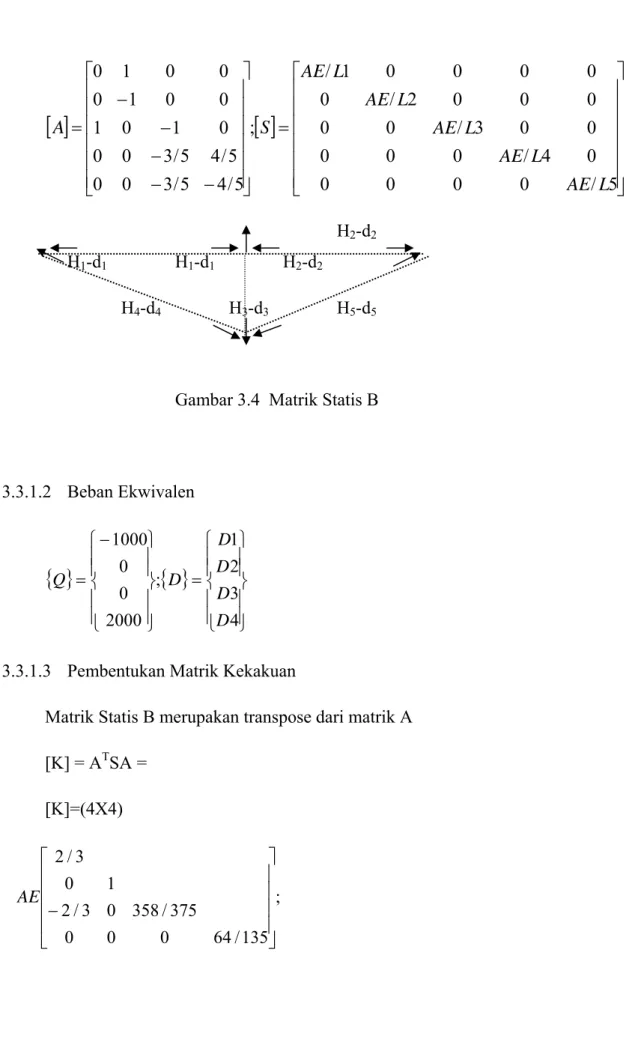
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − = 5 / 0 0 0 0 0 4 / 0 0 0 0 0 3 / 0 0 0 0 0 2 / 0 0 0 0 0 1 / ; 5 / 4 5 / 3 0 0 5 / 4 5 / 3 0 0 0 1 0 1 0 0 1 0 0 0 1 0 L AE L AE L AE L AE L AE S A H2-d2 H1-d1 H1-d1 H2-d2 H4-d4 H3-d3 H5-d5

Gambar 3.4 Matrik Statis B

3.3.1.2 Beban Ekwivalen

{ }

{ }

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧− = 4 3 2 1 ; 2000 0 0 1000 D D D D D Q

3.3.1.3 Pembentukan Matrik Kekakuan

Matrik Statis B merupakan transpose dari matrik A [K] = ATSA = [K]=(4X4) ; 135 / 64 0 0 0 375 / 358 0 3 / 2 1 0 3 / 2 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − AE

3.3.1.4 Solusi Persamaan Linear Dari persamaan 3.1 { Q } = [K] { D} Maka {D} = [K]-1 { D} ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 64 / 125 0 0 0 36 / 125 0 36 / 125 1 0 36 / 179 1 AE Kinv

{ } { } { }

1 ; 25 . 20003906 22 . 3472 0 22 . 4972 4 3 2 1 1 AE D D D D Q K D ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ − − = ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = −

Jadi besarnya Gaya Dalam adalah :

{ } { }{ }{ }

; 67 . 416 33 . 20831000 0 0 5 4 3 2 1 ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ − − = ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = H HH H H D A S H 3.3.2 Latihan 10 T 6m 6m

Gambar 3.5 latihan Rangka Batang (1)

65E /4 65E /4

55E /6

25E /2 _{25E /2}

Es = 20.000 kN/cm2. 80Kn 80Kn 12kN A (20) B (25) (10) (10) (25) 400cm 24kN C (20) D (25) (10) (10) (25) 400cm E F

Gambar 3.6 latihan Rangka Batang (2)

3.3.3 Tugas =(2.4)e-03m2 E=200E+06 Kn/m2 (3.0) (1.2) (1.8) (1.2) (3.0) 6.0m (1.8) (2.4) (2.4) (2.4) 4.5m 4.5m

P

4.5m 50kN Gambar 3.7 Catatan :

Sesuaikan gambar Rangka batang dengan Rangka batang pada kerja Proyek anda. Tanda dalam kurung menyatakan luas penampang propil baja dalam satuana m2 Gunakan fungsi trigonometri yang tepat untuk matrik deformasi.

Pembahasan:

1. Σ batang = 10 , Σ kinematis = 4x2 =8 2. Tiga buah matrik utama

[A] = 10x8 ; [S] = 10x10 ; {Q} = 8x1 ; [K] = 8x8 ; {D} = 8x1 ; [H] = 10x1 ; 3. Perpanjangan (+) dan perpendekan (-)

4. Bila Δ // sumbu batang maka nilainya 1 , bila Δ ⊥ sumbu batang maka nilai nya perubahan batang = 0

5. Gaya batang hanya axial tidak ada momen 6. Perletakan statis tak tentu

3.3.4 Evaluasi

Struktur mempunyai : 8 derajat kinematis, 10 batang

1 2 3 4 5 6 7 8 9 10 1 -1 0 0 -0.6 0 0 0 0 0 0 2 0 1 0 0.8 0 0 0 0 0 0 [ A ]t = 3 1 0 0 0 0.6 0 0 0 0 0 4 0 0 1 0 0.8 0 0 0 0 0 5 0 0 0 0 -0.6 -1 0 0 -0.6 0 6 0 -1 0 0 -0.6 0 1 0 0.6 0 7 0 0 0 0.6 0 1 0 0 0 0.6 8 0 0 -1 -0.8 0 0 0 1 0 0.8 1 -1 0 1 0 0 0 0 0 2 0 1 0 0 0 -1 0 0 3 0 0 0 1 0 0 0 -1 4 -0.6 0.8 0 0 0 0 0.6 -0.8 [ A ] = 5 0 0 0.6 0.8 -0.6 -0.6 0 0 6 0 0 0 0 -1 0 1 0 7 0 0 0 0 0 1 0 0 8 0 0 0 0 0 0 0 1 9 0 0 0 0 -0.6 0.6 0 0 10 0 0 0 0 0 0 0.6 0.8 D 1 2 3 4 5 6 7 8

1 2 3 4 5 6 7 8 9 10 1333.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1250.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 [ S ] = 0.0 0.0 1250.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 400.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 400.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1333.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1250.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1250.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 400.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 400.0 [ SAt ] -1333.333 0 1333.3333 0 0 0 0 0 10x8 0 1250 0 0 0 -1250 0 0 0 0 0 1250 0 0 0 -1250 -240 320 0 0 0 0 240 -320 0 0 240 320 -240 -240 0 0 0 0 0 0 -1333.333 0 1333.3333 0 0 0 0 0 0 1250 0 0 0 0 0 0 0 0 0 1250 0 0 0 0 -240 240 0 0 0 0 0 0 0 0 240 320 [ASAt ] 1477.3333 -192 -1333.333 0 0 0 -144 192 8x8 -192 1506 0 0 0 -1250 192 -256 [K] -1333.333 0 1477.3333 192 -144 -144 0 0 0 0 192 1506 -192 -192 0 -1250 0 0 -144 -192 1621.3333 0 -1333.333 0 0 -1250 -144 -192 0 2788 0 0 -144 192 0 0 -1333.333 0 1621.3333 0 192 -256 0 -1250 0 0 0 3012 [K]inv = 1.32E-02 1.90E-03 1.28E-02 -2.09E-03 5.17E-03 1.37E-03 5.21E-03 -1.55E-03

1.90E-03 1.47E-03 1.84E-03 -1.21E-04 4.47E-04 7.47E-04 3.61E-04 -4.61E-05 1.28E-02 1.84E-03 1.32E-02 -2.13E-03 5.18E-03 1.36E-03 5.18E-03 -1.55E-03 -2.09E-03 -1.21E-04 -2.13E-03 1.48E-03 -4.79E-04 -6.26E-05 -5.65E-04 7.36E-04 5.17E-03 4.47E-04 5.18E-03 -4.79E-04 4.19E-03 4.35E-04 3.85E-03 -4.91E-04 1.37E-03 7.47E-04 1.36E-03 -6.26E-05 4.35E-04 7.59E-04 3.91E-04 -4.98E-05 5.21E-03 3.61E-04 5.18E-03 -5.65E-04 3.85E-03 3.91E-04 4.20E-03 -5.36E-04 -1.55E-03 -4.61E-05 -1.55E-03 7.36E-04 -4.91E-04 -4.98E-05 -5.36E-04 7.32E-04

{Q} = 12 {D} = 1.4623 {H} = 24.75 80 [K]inv*{Q} 0.2987 [ SA ]*D 129.01 80 1.4809 -73.66 0 -0.2167 -61.26 24 0.6129 92.08 0 0.1955 -19.14 0 0.5985 244.35 0 -0.1578 -197.20 H9 dan H10

Hasil ini diambil dari program excel. Check nilai yang terdapat dalam sel. Koreksi untuk perkalian matriks atau matrik A

TUGAS SOAL 2

Beban Angin 25 kg/m2 dari sebelah KANAN ( No absent GANJIL) Beban Angin 25 kg/m2 dari sebelah KIRI ( No absent GENAP)

Tuliskan matrik A,S dan Q !!! saja

☺ AE untuk semua batang sama Jarak kuda-2 diambil 5 m

Gunakan koefisien spt : 0,9 ; 0,02α -0,4 ; -0,4 ; -0,4

3.4 Rangkuman

Bedakan jenis struktur menurut deformasi yang terjadi Secara garis besarnya , langkah2 metode ini adalah :

1. Menentukan kinematis struktur dan memberikan deformasi struktur D dan deformasi masing2 elemen (d). Hubungan ini dinyatakan dengan matrik [A].

2. Menentukan hubungan gaya dalam dengan deformasi elemen yang dinyatakan dengan matrik [S].

3. Menentukan hubungan Kesetimbangan antara gaya luar dengan gaya dalam yang dinyatakan sebagai matrik [B].

4. Menyelesaikan persamaan linear untuk deformasi struktur {D}. 5. Mencari gaya dalam struktur ataupun reaksi.

6. Gambar gaya dalam struktur

DIAGRAM :

[K]

{ }

Q

{ }

D

[ ]

B

[ ]

A

{ }

H

{ }

d

[ ]

S

Gambar 2.1 3.5 Daftar Pustaka

1. Supartono F.X, dan Boen T ; Analisa Struktur dengan Metode Matrix, Fakultas Teknik universitas Indonesia, UI Press, 1984 2. Wang , C.K : “ Matrix methods of Structural Analysisa” Scrantons

ASMAT I - 1

I. 1. Deformasi

Bila suatu struktur diberi beban, maka struktur tersebut (batang) akan mengalami deformasi yaitu perubahan bentuk yang kecil, sehingga setiap titik2 pada struktur akan berpindah ke posisi yang baru perpindahan akan terjadi pada umunya untuk struktur kecuali pada tumpuan yang tidak dapat bergerak. Perpindahan merupakan hal penting dalam analisa struktur.

Gambar L.1

Sebagai contoh diambil suatu potongan elemen dari batang stryktur rangka berbentuk lingkaran panjangnya dx

Gaya2 yang bekerja adalah NX = gaya axsial

Vy & Vz = gaya geser My & Mz = momen lentur T adalah forsi

Deformasi yang terjadi pada penampung dx adalah deformasi axial, geser lentur dan torsi seperti diperlihatkan pada gambar (2).

Adapun material bahan yang digunakan mengikuti Hukum Hooke yang elastis linier.

Perpindahan (displacement) suatu struktur ditimbulkan oleh gabungan pengaruh deformasi seluruh elemen. Dalam menentukan perpindahan suatu struktur

ASMAT I - 2

Untuk jenis struktur rangka batang, maka titik kumpul rangka dianggap sebagai sendi dan semua beban bekerja pada titik kumpul, sehingga analisanya hanya melibatkan deformasi axial batang. Jika terdapat beban di antara titik kumpul, maka beban ini dipindahkan pada titik kumpul seperti analisa balok ber tumpuan sederhana.

Pada portal bidang deformasi yangb berpengaruh adalah akibat lenturan dan gaya axial. Pada balok silang deformasi lentur selalu penting dan deformasi punter kadang kala turut diperhitungkan. Tergantung pada penampung yang digunakan, jika penampung tersebut adalah berdendeng tipis seperti balok I, maka batang akan sangat fleksibel terhadap punter dan tidak mengalami gaya punter yang besar.

Portal ruang merupakan jenis struktur rangka yang paling umum dlm geometrid an pembebanannya. Oleh karena itu deformasi axial, lentur dan punter mungkin seluruhnya perlu diperhitungkan tergantung jenis struktur dan bebannya. Untuk deformasi geser pada struktur rangka biasanya sangat kecil, sehingga jarang ditinjau dalam analisa.

I. 2. Aksi dan Perpindahan

Untuk menerangkan konsep dasar pada analisa struktur ada istilah yang akan digunakan seperti AKSI dan PERPINDAHAN. AKSI atau gaya dapat berupa gaya atau momen kopel ataupun gabungan keduanya. Selain Aksi luar pada struktur Aksi dalam juga perlu ditinjau sebagai contoh adalah resultan distribusi tegangan akibat momen lentur, gaya geser, gaya axial ataupun momen puntir.

Konsep dasar yang lain adalah perpindahan yang umunya berupa translasi atau rotasi di titik struktur. Transaksi menun jukkan adanya pergerakan, sedangkan rotasi menyatakan sudut perputaran antara garis singgung kurva elastis dengan posisi semula.

ASMAT I - 3 L/2 L/2 A1 A B D31 D11 D21 A2 A B D32 D12 D22 A B D33 D13 D23 gambar L.2 Contoh:

Notasi A dipakai untuk aksi gaya dan D untuk perpindahan.

Pada gambar L2 terdapat aksi A1, A2 dan A3

Perpindahan yang terjadi :

A1→ D1 (translasi) D11 D21 D31 A2→ D2 (translasi) D12 D22 D32 A3→ D3 (rotasi) D13 D23 D33 Perhatikan subscript yang dipakai Perpindahan balok atas seluruh beban D1 = D11 + D12 + D13

D2 = D 21 + D22 + D23 D3 = D 31 + D32 + D33

Penjumlahan ini adalah prinsip superposisi yang dibahas lebih lanjut.

I. 3. Keseimbanan dan Kesesuaian

Tujuan analisa struktur di antaranya adalah menentukan berbagai aksi pada struktur seperti reaksi tumpuan dari resultan tegangan, momen lentur, geser dan sebagainya. Penyelesaian ini harus memenuhi syarat keseimbangan statis begitu juga pada bagian struktur yang dianalisa sebagai benda bebas free body.

ASMAT I - 4

ΣMx = 0 ΣMy = 0 ΣMz = 0 momen terhadap sumbu x, y, z

Persamaan ini dapat dideduksi, apabila digunakan pada permasalahan struktur dalam 1 bidang. Dengan menganggap gaya terletak pada bidang x – y maka persamaan menjadi ΣFx = 0 ΣFy = 0 ΣMz = 0

Selain keseimbangan statis maka seluruh syarat kesesuaian harus terpenuhi dalam analisa struktur. Syarat ini juga disebut syarat geometris karena harus menyatakan kontinuitas perpindahan di seluruh bagian struktur.

Sebagai contoh adalah titik tumpuan jepit, harus dipenuhi kesesuaian perpindahan dengan kondisi tumpuan yaitu tidak terjadi tranlasi dan rotasi terhadap sumbu batang. Pada sambungan yang kaku antara dua batang maka perpindahan yang terjadi (tranlasi dan rotasi) harus sama bila ditinjau per batang secara terpisah.

I. 4. Ketidaktentuan Statis dan Kinematis

Ketidaktentuan suatu struktur tergantung pada yang ditinjau aksi atau perpindahan. Ketidaktentuan menunjukkan kelebihan aksi yang tidak diketahui terhadap jumlah persamaan keseimbangan statis.

Jika persamaan keseimbangan cukup untuk menentukan aksi maka struktur bersifat statis tertentu. Sebaliknya bila tidak dapat diselesaikan dengan persamaan keseimbangan maka struktur mempunyai sifat statis tak tentu.

Gambar L3

Ketidaktentuan statis berderajad 3 ada 6 reaksi yang harus dicari

ASMAT I - 5

struktur bidang mempunyai 3 buah persamaan. Apabila lebih di jumlah persamaan keseimbangan statis, maka disebut bersifat statis tak tentu luar.

Ketidaktentuan statis dalam berhubungan dengan perhitungan resultan tegangan dalam struktur dengan anggapan semua reaksi telah ditentukan sebelumnya.

Gambar L4

Ketidaktentuan statis luar adalah bersifat statis tertentu untuk ketidaktentuan statis dalam berdenyut-denyut karena 2j – m = 3 yaitu 2 x 6 – 11 = 1. Ada dua batang yang dipenggal artinya dengan melepas 2 gaya pada rangka batang, maka struktur menjadi statis tertentu.

Jenis ketidaktentuan yang lain adalah ketidaktentuan kenematis yaitu yang bertentangan dengan perpindahan titik kempul yang tidak diketahui. Pada struktur rangka titik kempul dapat berupa perteman dua batang atau lebih, titik tumpuan dan ujung bebas. Titik kumpul dapat mengalami transaksi atau rotasi.

A B Gambar L5

Titik A terjepit tidak mengalami perpindahan, sedangkan titik B memiliki 2 perpindahan ber rotasi dan bergeser.

ASMAT I - 6 ketidaktentuan kenematis. D A E B F C Gambar L6

Rangka batang statis tak tentu berderajat 2 titik A, B, D dan E mempunyai dua derajat kebebasan masing-masing (translasi dalam 2 arah tegak lurus). Titik c dan f masing-masing adalah nol dan satu derajat kebebasan. Jadi rangka batang mempunyai 9 derajat kebebasan untuk translasi titik kempul dan ketidaktentuan kenematisnya berderajat 9.

Untuk menentukan ketidaktentuan statis dan kenematis, maka ada aturan yang dapat dipakai seperti.

I. Tentukan jumlah kelebihan gaya. Hitung jumlah pelepasan yang diperlukan agar struktur menjadi statis tertentu.

II. Tentukan jumlah derajat kebebasan titik kempul. Hitung jumlah pengembangan titik kempul yang diberikan agar struktur menjadi kenematis tertentu tidak ada perpindahan titik kempul.

ASMAT I - 7

sama, maka struktur statis tertentu luar. Hal ini berlaku, bahwa struktur tidak akan bergerak, apabila beban diberikan pada struktur tersebut.

Gambar L7

Pada contoh balok di atas 3 tumpuan roller terdapat 3 reaksi yang sama jumlahnya dengan persamaan keseimbangan statis untuk gaya perbidang.

Akan tetapi jelas bahwa balok akan bergerak ke kiri apabila beban dan yang mirin g diberikan. Jenis struktur ini dikatakan bersifat tidak stabil.

Gambar L8 Struktur pada gambar L8 dikatakan tidak stabil karena garis kerja gaya dan tidak melalui 3 gaya reaksi yang konkuren.

Jadi selain jumlah tumpuan struktur struktur yang cukup, maka tata letaknya harus menjamin agar struktur tidak tidak dapat bergerak.

I. 6. Superposisi

Pada suatu struktur akan terdapat besaran aksi gaya dan perpindahan yang tertentu. Aksi dan perpindahan ini menimbulkan aksi perpindahan lainnya pada struktur. Aksi perpindahan semula merupakan penyebab, sedangkan yang terakhir adalah pengaruh. Secara umum, nahwa pengaruh yang ditimbulkan oleh sejumlah penyebab dapat diperoleh dengan menggabungkan pengaruh setiap penyebabnya.

ASMAT I - 8 Ra Rb A1 M’b R’a D’ R’b M”b R”a D” R”b Gambar L9 RA = RA’ + RA” RB = RB + MB” MD = MB’ + MB” D = D’ + D”

Prinsip superposisi ini hanya berlaku, apabila hubungan antara aksi dan perpindahan pada struktur b ersifat linear. Hal ini terjadi apabila syarat-syarat b erikut terpenuhi: (struktur elstis linear).

1. Bahan struktur mengikuti hokum Hooke 2. Perpindahan struktur kecil (small deflection)

3. Tidak ada interaksi antara pengaruh axial dan lentur. I. 7. Matrik Kekakuan

Hubungan antara aksi dan perpindahan berperan penting dalam analisa struktur dan digunakan dalam metode kekakuan. Untuk menyatakan hubungan aksi dan perpindahan ialah dengan persamaan aksi dan perpindahan.

ASMAT I - 9

A D’ Gambar L10

nimbulkan perpindahan D. Hubungan A dan D ini dapat dengan beban sebagai: A = S D

Di mana S adalah kekakuan yang didefinisikan sebagai aksi yang dikukuhkan untuk menimbulkan perpindahan satu unit. Satuannya adalah gaya persatuan panjang. Untuk keadaan yang lebih umum :

A1 A2 A3 a) b) D1 D2 D3 1 c) S31 S11 S21 d) 1 S12 S22 S32 e) S13 S23 S33 1 Gambar L11

a Dalam gambar diperlihatkan perpindahan balok yang selaras A1,A2 dan A3. Dari superposisi didapatkan :

D1 = D11 + D12 + D13

D11 : perpindahan yang selaras A1 diakibatkan oleh A1

D12 : perpindahan yang selaras A1 diakibatkan oleh A2

D13 : perpindahan yang selaras A1 diakibatkan oleh A3

Analog untuk D2 dan D3

D11 : perpindahan yang selaras A2 diakibatkan oleh A2 dst.

Persamaan aksi:

A1 : S11 D1 + S12 D2 + S13 D3 A2 : S2 D1 + S22 D2 + S23 D3 A3 : S31 D1 + S32 D2 + S23 D3

ASMAT I - 10

S11 : aksi yang selaras dengan A1 bila satu satuan perpindfahan D1 diberikan sementara perpindahan yang lain = 0 dan seterusnya.

Arah setiap koefisien kekakuan yang diperlihatkan dianggap positif, apabila searah dengan aksi yang selaras. Persamaan aksi untuk struktur dengan n buah aksi adalah:

A1 : S11 D1 + S12 D2 + S13 D3 A2 : S21 D1 + S22 D2 + S23 D3

- - -

An : Sn D1 + S31 D2 + S33 D3 Dalam balok matrik

[ ] [ ][ ]

A S D atau Dn D D Snn Sn Sn n S S S n S S S An A A = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ .. 2 1 .. 2 1 .. .. .. .. 2 .. 22 21 1 .. 12 11 .. 2 1

Dimana A = Matrik aksi berukuran n x 1

D = Matrik perpindahan berukuran n x 1 S = Matrik kekakuan berukuran n x n

Koefisien kekakuan Sij didefibnisikan sebagai aksi ke – i akibat satu satuan perpindahan ke- j sementara petrpindahan lainnya adalah nol.

I. 8. Beban Ekivalent

Analisa struktur mengharuskan struktur hanya memikul beban yang bekerja pada titik kempul. Sebenarnya beban yang bekerja pada struktur tidak memenuhi syarat tersebut. Agar supaya syarat terpenuhi beban pada batang harus diganti dengan beban ekivalen pada titik kem pul. Beban ekivalen ini sedemikian rupa, sehingga

ASMAT I - 11 W M1 P1 P2 L L/2 L/2 1/12 WL2 wL/2 P1 PL/8 PL/8 .5P1 .5P1 WL/2 WL/2+.5P1 .5P1+P2 1/12 WL2 M1+1/12WL2-PL/8 Gambar L12

Titik kempul dikekang terhadap semua perpindahan, sehingga menghasilkan 2 balok terjepit (gambar L12).

Di sini gaya ujung ditunjukkan sebagai reaksi pengekangan pada struktur terhekang. Jika reaksi pengekang ini dibalik arahnya akan menjadi beban yang ekivalen dengan beban yang bekerja pada batang.

Beban titik kempul ini digabungkan, sehingga dapat digunakan dalam analisa struktur.

I. 9. Teori Energi

Pembahasan konsep energi ini terbatas pada struktur yang regan gan dan perpindahannya kecil serta energinya tidak hilang selama proses pembebanan statis. Dengan kata kain, kerja luar (external) dari beban yang diberikan secara perlahan-lahan sama dengan energi yang disimpan dalam struktur.

Dari teori elastis, apabila ditinjau pada elemen yang sangat kecil akan terdapat beberapa tegangan seperti pada gambar 17.

ASMAT I - 12 τyz τxy dx τzy σx τzx σz Gambar L13 τyz = τzy τzx = τxz

Jadi hanya 6 komponen tegangan yang perlu ditin jau untuk pegangan berlaku. u,v,w adalah translasi dalam arah x,y,z. Єx = du/ dx

Єy = dv/ dy (b.) Єz = dw/ dz

Untuk regangan geser γxy = γyx = Əu/Əy + Əv/Əx

γyz = γzy = Əv/Əz + Əw/Əy (c.)

γzx = γxz = Əw/Əx + Əu/Əz σ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 6 5 4 3 2 1 σ σ σ σ σ σ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ zx yx xy z y x σ σ σ σ σ σ ε = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 6 5 4 3 2 1 ε ε ε ε ε ε = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ zx yz xy z y x ε ε ε ε ε ε (d.)

Tegangan dan regangan pada sembarang titik untuk benda 3 dimensi

Dari diagram tegangan – regangan untuk bahan linear. Energi regangan didefinisikan sebagai integrasi kerja dalam dari tegangan selama pertambahan regangan untuk pegangan total dan seluruh volume.

U = 2 1

∑

= 5 1 . . n i dV i iσ ε = t dV V . . 2 / 1

∫

σ ε

ASMAT I - 13 U Energi regangan σi dσ dЄ Єi gambar L14

Energi regangan komplementer didefinisikan sebagai integrasi kerja dalam dari regangan pertambahan tegangan untuk tegangan total dan seluruh volume.

U* = 2 1

∑

= 5 1 . . n i dV i iσ ε = t dV V . . 2 / 1

∫

ε σ Dimana : εt _{transpose matirk kolom ε}

Untuk kerja beban dapat dirumuskan sama seperti energi regangan.

Pj dP dΔ Δj Gambar L15 W = 2 1 = Δ

∑

= 5 1 . . n j dV j Pj 1/2 At D W* = 2 1 = Δ

∑

= 5 1 . . n j dV j Pj 1/2 Dt A

Dari prinsip kekuatan energi, bahwa kerja beban W = energi pegangan U yang disimpan dalam struktur, sehingga:

ASMAT I - 14 Dj U ∂ ∂ =

∑

− n k Sjk 1 Dk = Aj ( j = 1, 2, …..n )

Persamaan ini menyatakan n (himpunan) syarat keseimbangan. Apab ila persamaan

ini diturunkan terhadap Dk , maka akan diperoleh suku kekakuan umum Sjk

sebagai: Dj U σ σ Dk Dj U ∂ ∗ ∂ ∂ = Dk Aj ∂ ∂ = Sjk j = 1, 2, ………… n k = 1, 2, …………. N

Hubungan timbal balik (teorema Maxwell), jika untuk differensial dibalik, maka hasilnya harus sama, sehingga: Sjk = Skj

Oleh karena itu semua pasangan kekakuan silang sama besar, sehingga matrik S adalah simetris atau identik transposenya. S = ST

1.10. Rangkuman

• Bandungkan jenis2 struktur rangka seperti Rangka Batang , Balok ataupun Portal. Perbedaan terletak pada gaya dalam dan deformasi • Dasar2 analisa struktur seperti deformasi, Aksi dan Perpindahan ,

derajat kebebasan , derajat ketidak tentuan statis atau kinematis , stabilitas, Superposisi , Kekakuan , beban ekivalent dan teori energi.

ASMAT I - 15

PERINTAH UNTUK CALCULATOR CFX 9850GB Matrix calculations

26 matrix memories (Mat A Through Mat Z) plus a matrix answer memory (MatAns), make it possible to perform the following matrix operations.

y Addition, subtraction, multiplication y Scalar multiplication calculations y Determinant calculations

y Matrix transposition y Matrix inversion y Matrix squaring

y Raising a matrix to a specific power

y Absolute value, integer part extraction, fractional part extraction, maximum integer calculations

y Matrix modification using matrix commands

LII-1 before performing matrix calculations LII-2 matrix cell operations

LII-3 modifying matrices using matrix commands LII-4 matrix calculations

ASMAT I - 16

LII-1 Before Performing Matrix Calaulations

In the Main Menu, select the MAT icon to enter the Matrix Mode and display its initial screen.

{DEL}/{DEL.A} … deletes {a specific matrix}/{all matrices}

The maximum number of rows that can be specifies for a matrix is 255, and the maximum number of columns is 255.

„ About Matrix Answer Memory (MatAns)

The calculator automatically stores matrix Answer Memory. Note the following points about Matrix Answer Memory. Whenever you perform a matrix calculation, the current Matrix Answer Memory contents are replaced by the new result. The previous contents are deleted and cannot be recovered. Inputting values into a matrix does not affect Matrix Answer Memory contents.

„ Creating a Matrix

To create a matrix, you must first define its dimensions (size) in the MATRIX list. Then you can input values into the matrix to specify the dimensions of a matrix

ASMAT I - 17

All of the cells of a new matrix contain the value 0.

All “Mem ERROR” remains next to the matrix area name after you input the dimensions, it means there is not enough free memory to create the matrix you want.

ASMAT I - 18

not displayed.

You can see the entire value assigned to a cell by using the cursor keys to move the highlighting to the cell whose value you want to view.

The amount of memory required for a matrix is ten bytes per cell. This means that 3 x 3 matrix requires 90 bytes of memory ( 3 x 3 x 10 = 90 ).

Deleting Matrices

You can delete either a specific matrix or all matrices in memory. To delete a specific matrix

While the matrix list on the display, use and to highlight the matrix you want to delete.

Press {DEL}

Press {YES} to delete the matrix or {NO} to abort the operation without deleting anything.

The indicator “None” replaces the dimensions of the matrix you delete. To delete all matrices

While the matrix list is on the display, press {DEL A}.

Press {YES} to delete all matrices in memory or {NO} to abort the operation without deleting anything.

ASMAT I - 19

Use the following procedure to prepare a matrix for a cell operations.

While the MATRIX list on the display, use to highlight the name of the matrix you want to use.

And the function menu with the following items appears. {R.OP} …{row calculation menu}

{ROW}/{COL} … {row}/{column} operation menu

Row Calculations

The following menu appears whenever you {R . OP} while a recalled matrix is on the display.

{Swap} … {Row Swap}

{xRw} … {Product of specific row and scalar}

{xRw+} … {Addition of one and the product of a specific row with a scalar}

{Rw+} … {Addition of specific row to another row}

To swap two rows

Example : To swap rows 2 and 3 of the following matrix :