Perancangan Perkuatan Longsoran Badan Jalan Pada Ruas Jalan Sumedang-Cijelag KM Menggunakan Tiang Bor Anna Apriliana

(1)

BAB II

DASAR TEORI

2.1. Teori Lereng

Keruntuhan geser pada tanah/batuan terjadi akibat gerak relatif antar butirnya. Oleh sebab itu kekuatannya tergantung pada gaya yang bekerja antar butirnya. Dengan demikian dapat dikatakan bahwa kekuatan geser terdiri atas :

 Bagian yang bersifat kohesi, tergantung pada macam tanah/batuan dan ikatan butirnya.

 Bagian yang bersifat gesekan, yang sebanding dengan tegangan efektif pada bidang geser.

Kekuatan geser tanah dapat dinyatakan dalam rumus :

(2.1) dimana ;

S = kekuatan geser

 = tegangan total pada bidang geser u = tegangan air pori

c’ = kohesi efektif

’ = sudut geser dalam efektif

Gambar 2.1 Diagram Kekuatan Geser Tanah

Analisis dasar kemantapan lereng didasarkan pada mekanisme gerak suatu benda yang terletak pada bidang seperti terlihat pada gambar dibawah ini :

Persamaan Garis S = c’ + ( - u) tan’

Tegangan Normal Efektif ’ (’ = -u) Ke kuatan Ges er (S) S = c’+ ( - u) tan’

(2)

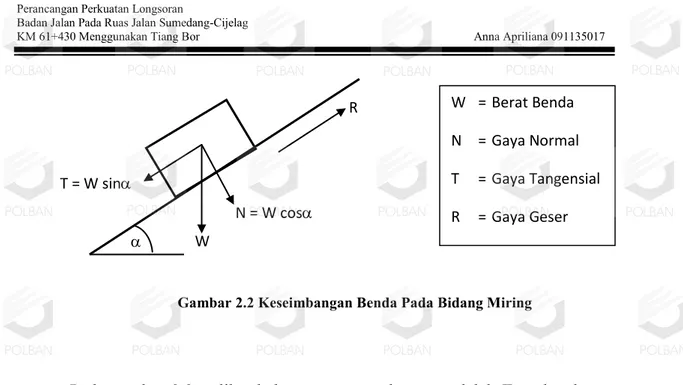
Gambar 2.2 Keseimbangan Benda Pada Bidang Miring

Pada gambar 2.2 terlihat bahwa yang mau longsor adalah T, sedangkan gaya yang melawan longsor adalah R yakni gaya geser yang terjadi antara berat benda W dengan bidang miring, sehingga dengan demikian dapat dikatakan bila ;

R/T < 1 Benda akan bergerak

R/T = 1 Benda dalam keadaan seimbang R/T > 1 Benda akan diam

2.2. Konsep Tegangan Efektif

Untuk mempelajari tegangan-tegangan yang bekerja pada tanah, dan khususnya pada kerangka butir tanah, maka kita dapat menghitung tegangan-tegangan pada kedalaman H dibawah permukaan tanah seperti terlihat pada gambar berikut: h H 1 Muka Tanah T = W sin N = W cos W  R W = Berat Benda N = Gaya Normal T = Gaya Tangensial R = Gaya Geser

(3)

Gambar 2.3 Tegangan dibawah permukaan tanah

Permukaan air tanah disini terletak pada kedalaman ”h”, dan berat isi tanah yang terletak diatas muka air = 1, sedangkan berat isi tanah dibawah muka air = 2. Kita dapat langsung menghitung tegangan-tegangan pada bidang ab pada kedalaman ”H” ini, yaitu dengan :

(2.2)

dimana ;

 = tegangan total

Jadi tegangan total ini adalah tegangan akbiat berat tanah (termasuk air pada porinya) diatas tempat yang bersangkutan. Selain tegangan total ini, besarnya tegangan air didalam pori ini bisa pula kita hitung. Tegangan ini disebut tegangan air pori. Semua pori didalam tanah saling berhubungan satu sama lain, sehingga tegangan air pori adalah sama dengan tegangan hidrostatik, yaitu :

(2.3)

dimana ;

u = tegangan air pori

Tegangan air pori yang bekerja diruang-ruangan antar butir-butir tanah akan mengurangi tegangan yang sebenarnya bekerja pada butir-butir tanah, sehingga tegangan yang bekerja pada kerangka butir tanah ialah selisih antara tegangan total dengan tegangan air pori, yaitu :

(2.4)  = 1 h + 2 (H-h) u = w (H-h) ’ =  - u

(4)

POLITEKNIK NEGERI BANDUNG 2-4 Tegangan ’ disebut tegangan efektif karena memang hanya tegangan inilah yang mempunyai pengaruh pada kerangka tanah.

Tegangan geser tanah sangat tergantung pada tegangan efektif, demikian juga isi (volume) tanah sangat tergantung pada kerangka butir tanah itu sendiri. Tidak dapat terjadi perubahan pada isi tanah kecuali ada perubahan pada tegangan efektif. Jadi kekuatan geser maupun ”compressibility” tanah tergantung pada tegangan efektif dan bukan pada tegangan total.

Persamaan ’ =  - u hanya berlaku bila tanah dalam keadaan jenuh sempurna.

2.3. Analisis Kemantapan Lereng Dengan Metode Irisan

Salah satu perhitungan stabilitas suatu lereng yang sering dilakukan adalah dengan metode irisan, dimana tegangan efektif yang bekerja sepanjang bidang gelincir (slip surface) harus diketahui sebagai syarat untuk kelengkapaan analisis. Hal ini dapat dilakukan dengan membagi-bagi masa tanah yang mengalami keruntuhan ke dalam potongan-potongan (slices) yang representative.

Metode irisan mengasumsikan gaya-gaya geser yang bekerja pada bidang pertemuan antar potongan dapat diabaikan, sehingga hanya gaya-gaya horizontal yang dihitung. Selian itu, pada metode ini bidang gelincir berbentuk silinder lingkaran. Dengan mengambil momen kesetimbangan keseluruhan di sekitar O (lihat gambar 2.4).

7 6 5 3 2 1 X X X X X X X 4 R W R 4 Pk a Zk O

(5)

Gambar 2.4 Suatu Potongan Metode Irisan

Persamaan metode ini adalah:  . 2 4 Zki Zka X W     _(2.5) 4 4 4 W Cos N   _(2.6) 4 4 4 W Sin T   _(2.7) Perhitungan Irisan 4 4 4 2 4 4 4 4 4 4 4 4 W Cos_X Cos XCos W I N           _(2.8) 4 4 4 4 4 4 4 4 4 4 4 W Sin _X Cos Cos X Sin W I T             _(2.9) Bila c’ = 0 maka : 4 4 2 4 4 4 tan tan X Cos W f   _      _(2.10) 4 4 4 4 4 4 4 4 2 4 4 4 4 tan _tan         Sin W Cos W Cos Sin W Cos W FS _ f _ _ (2.11)

(6)

Maka untuk semua Irisan atau Elemen :



 i i i i Sin W Cos W FS _tan (2.12)

Definisi faktor keamanan

d f

FS  

 terhadap kelongsoran sama artinya dengan :



_  M M Ttk.O) Terhadap Kerja (Momen Ttk.O) Terhadap Tahanan Momen ( R FS (2.13)



_      ) . .( tan ). . .( . tan . . . tan . . . . i i i i i i i i i fi Sin W R Cos W R l T R l N R R R R R FS _  _    _  (2.14) Untuk  0 dan c 0 :















    i i i i R Sin W R Cos W l c R M M FS _  . . tan . . . . (2.15) Apabila  X dibuat konstan : l = X / Cos  _i dan W_i/X  p maka :







  i i i i Sin p Cos Cos p c FS     . 1 tan . . 2 (2.16)

Kemudian untuk lebih memudahkan perhitungan secara manual dilakukan dengan membuat tabel seperti terlihat sebagai berikut :

Tabel 2.1 Tabel Perhitungan Cara Manual

N0  W p c _p_._Cos2__._tan_



_c_ _p_._Cos2__._tan_



_/_Cos_ p.Sin

1 2 3

(7)

- - n



Z



N



 N Z FS (2.17) di mana:

c’ = Kohesi tanah ’ = Sudut geser dalam tanah N = Gaya normal pada dasar bidang gelincir W = Berat massa tanah Z = Gaya penahan pada dasar bidang gelincir l = Panjang bidang gelincir R = Jari-jari lingkaran longsoran T₄ = Gaya tangen sial reaksi  = Tegangan normal



= Tegangan geser rata-rata

f

 = Tegangan geser F = Faktor keamanan (FK) p = Gaya horisontal pada sisi irisan

2.4. Tekanan Tanah Lateral Ke Samping

Konstruksi penahan tanah seperti dinding penahan biasanya digunakan untuk menahan massa tanah dengan talud atau lereng vertikal. Agar dapat merencanakan konstruksi penahan dengan benar, maka kita perlu mengetahui gaya horizontal yang bekerja antara konstruksi penahan dan massa tanah yang ditahan. Gaya horizontal ini disebabkan oleh tekanan tanah arah horizontal (tekanan tanah lateral).

2.4.1. Tekanan Tanah Dalam Keadaan Diam (At Rest)

Keadaan diam, yaitu bila dinding penahan tidak bergerak kesalah satu arah baik ke kanan maupun ke kiri dari posisi awalnya, maka massa tanah akan berada dalam keadaan keseimbangan elastis (elastic equilibrium). Rasio tekanan arah horizontal dan tekanan arah vertical dinamakan “koefisien tekanan tanah dalam keadaan diam (coefficient of earth pressure at rest), Ko”.

(8)

H/3

H

Po

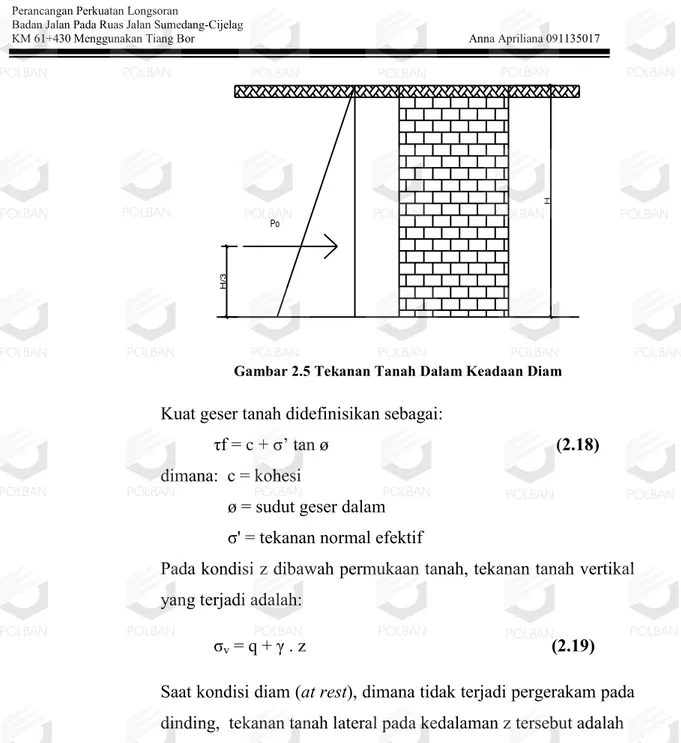
Gambar 2.5 Tekanan Tanah Dalam Keadaan Diam Kuat geser tanah didefinisikan sebagai:

τf = c + σ’ tan ø (2.18)

dimana: c = kohesi

ø = sudut geser dalam σ' = tekanan normal efektif

Pada kondisi z dibawah permukaan tanah, tekanan tanah vertikal yang terjadi adalah:

σv = q + γ . z (2.19)

Saat kondisi diam (at rest), dimana tidak terjadi pergerakam pada dinding, tekanan tanah lateral pada kedalaman z tersebut adalah

σh = Ko . σv + u (2.20)

dimana: u = tekanan air pori

Ko = koefisien tekanan tanah pada kondisi diam (at rest) Untuk pasir: Ko ≈ 1- sin Φ (2.21) Untuk lempung: Ko = 0.4 + 0.007 PI untuk 0<PI<40 (2.22)

(9)

Ko = 0.64 + 0.001 PI untuk 40<PI<40 (2.23) dimana: PI = Plasticity Index

2.4.2. Tekanan Tanah Aktif Menurut Rankine

Dengan cara Rankine, gaya-gaya yang ditinjau dianggap melalui bidang vertikal. Jadi bila dinding miring maka tekanan tanah bekerja pada bidang tegak yang melalui sisi terdalam pihak tanah isian. Kondisi aktif menurut Rankine dapat dijelaskan dengan Gambar 2.6

Ka c Ka z z . . 2. .  (2.24)

Muka tanah datar:

) 2 45 ( tan2 0 _  Ka (2.25)

Muka tanah miring:

       2 2 2 2 cos cos cos cos cos cos cos      Ka (2.26)

Gambar 2.6 Gambar Tekanan Tanah Aktif 2.4.3. Tekanan Tanah Pasif Menurut Rankine

Kondisi pasif menurut Rankine dapat dijelaskan dengan Gambar 2.6

(10)

Kp c Kp z z . . 2. .  (2.27)

Muka tanah datar:

) 2 45 ( tan2 0 _  Kp (2.28)

Muka tanah miring:

       2 2 2 2 cos cos cos cos cos cos cos      Kp (2.29)

Gambar 2.7 Gambar Tekanan Tanah Pasif

2.5. Faktor Keamanan

2.5.1. Aman Terhadap Geser

Faktor keamanan (Safety Factor) untuk geser adalah jumlah gaya penahan horizontal dibagi dengan jumlah gaya pendorong horizontal. Faktor ini perlu diperhitungkan untuk menghindari dinding penahan mengalami geser.

Sebagai acuan angka keamanan terhadap geser diambil 1,5. Bila hasil yang diperoleh dari perhitungan kurang dari 1,5 maka dinding penahan cenderung akan mengalami geser. Sebaliknya bila hasilnya lebih besar dari 1,5 maka dinding penahan dianggap aman terhadap geser .

(11)

Guna memperoleh faktor keamanan diperoleh dengan cara



 tal ongHorison GayaPendor l nHorisonta GayaPenaha SF

SF ≥ 1,5 maka Tekanan Tanah Pasif diabaikan SF ≥ 2,0 maka Tekanan Tanah Pasif diperhitungkan

2.5.2. Aman Terhadap Guling

Faktor keamanan (Safety Factor) terhadap guling adalah perbandingan antara momen penahan (Mp) dengan momen kerja (Mk). Faktor ini diharapkan menjadi acuan dalam perencanaan dinding penahan. Untuk momen kerja (Mk) diperoleh dari hasil perkalian antara total beban lateral (∑ Pa) yang bekerja pada titik tangkap sejauh (y) atau

Mk = ∑Pa y

Sedang momen penahan diperoleh dari Mp = G.e

Dimana :

G = Berat dinding penahan e = Lengan Momen

Biasanya untuk factor keamanan terhadap guling diambil angka sebagai acuan sebesar 1,5. Bila hasil perhitungan yang diperoleh melampaui angka tersebut maka dinding penahan dianggap aman, sedang bila angka keamanan kurang dari nilai patokan maka dinding penahan cenderung akan terjadi guling.



 g MomenGulin an MomenPenah SF

SF ≥ 1,5 untuk Tanah urugan berbutir kasar

(12)

SF ≥ 2,0 untuk Tanah urugan berbutir halus

2.5.3. Aman Terhadap Daya Dukung

Daya dukung adalah tekanan maksimum yang dapat ditahan atau dipikul oleh tanah tanpa terjadi kelongsoran .

Faktor ini perlu diperhitungkan untuk menghindari terjadinya penurunan yang berlebihan tanah pada kaki bangunan dinding penahan tanah sehingga mengakibatkan miringnya bangunan . Kemiringan juga bisa diakibatkan karena tekanan dari berat sendiri dinding penahan yang melebihi kapasitas daya dukung tanah tempat dimana konstruksi dinding penahan tanah itu didirikan.

Secara umum daya dukung menurut Terzaghi (1943) merumuskan sebagai berikut :

- Fondasi Menerus (beban garis): qult = c Nc + q Nq + 0,5 γ B Nγ - Fondasi Setempat (segi empat):

qult = 1,3 c Nc + q Nq + 0,4 γ B Nγ - Fondasi Setempat (lingkaran):

qult = 1,3 c Nc + q Nq + 0,3 γ B Nγ

dimana:

qult : tegangan batas c : kohesi tanah υ : sudut geser dalam B : lebar pondasi γ : berat jenis tanah

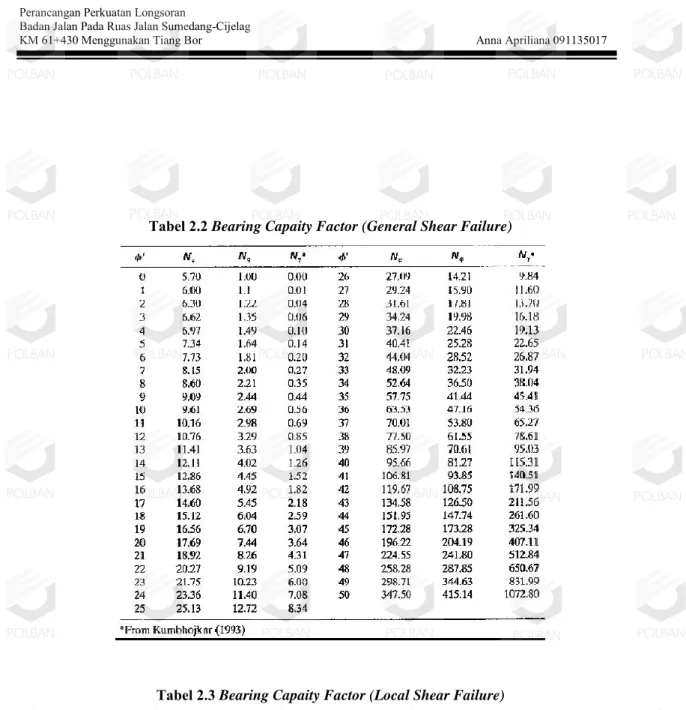
Nc, Nq, Nγ adalah Bearing Capacity Factor

(13)

Tabel 2.2 Bearing Capaity Factor (General Shear Failure)

Tabel 2.3 Bearing Capaity Factor (Local Shear Failure)

(14)

2.6. Pondasi Tiang 2.6.1. Umum

Pondasi tiang adalah suatu konstruksi pondasi yang mampu menahan gaya orthogonal ke sumbu tiag dengan cara menyerap lenturan. Pondasi tiang dibuat menjadi satu kesatuan yang monolit dengan menyatukan pangkal tiang yang terdapat dibawah konstruksi, dengan tumpuan pondasi (K. Nakazawa,1983).

Pondasi tiang digunakan untuk mendukung bangunan bila lapisan yanah kuat terletak sangat dalam. Pondasi jenis ini dapat juga digunakan untuk mendukung bangunan yang menahan gaya angkat ke atas, terutama pada bangunan-bangunan tingkat yang dipengaruhi oleh gaya-gaya penggulingan akibat beban angin. Tiang-tiang juga digunakan untuk mendukung bangunan dermaga. Pada bangunan ini, tiang-tiang dipengaruhi oleh gaya-gaya benturan kapal dan gelombang air (H. C. Hardiyanto, 2002).

Pondasi tiang digunakan untuk beberapa maksud, antara lain:

1. Untuk meneruskan beban bangunan yang terletak di atasa air atau tanah lunak, ketanah pendukung yang kuat.

2. Untuk meneruskan beban ke tanah yang relatif lunak sampai kedalaman tertentu sehingga bangunan mampu memberikan dukungan yang cukup untuk mendukung beban tersebut oleh gesekan dinding tiang dengan tanah disekitarnya.

3. Untuk menangker bangunan yang dipengaruhi oleh gaya angkat keatas akibat tekanan hidrostatis atau momen pemggulingan.

4. Untuk menahan gaya-gaya horizontaldan gaya yang arahnya miring. 5. Untuk memadatkan tanah pasir, sehingga kapasitas dukung tanah

tersebut bertambah.

6. Untuk mendukung pondasi bangunan yang permukaan tanahnya mudah tergerus air (H. C. Hardiyatmo, 2002).

(15)

2.6.2. Penggolongan Pondasi Tiang

Pondasi tiang dapat dibagi menjadi 3 kategori, sebagai berikut: 1. Tiang Perpindahan Besar (Large Displacement Pile).

Tiang perpindahan besar, yaitu tiang pejal atau berlubang dengan ujung tertutup yang dipancang ke dalam tanah sehingga terjadi perpindahan volume tanah yang relatif besar. Yang termasuk dalam tiang perpindahan besar adalah tiang kayu, tiang beton pejal, tiang beton prategang (pejal atau berlubang), tiang baja bulat (tertutup pada ujungnya).

2. Tiang Perpindahan Kecil (Small Displacement Pile).

Tiang perpindahan kecil, yaitu sama seperti tiang kategori pertama hanya volume tanah yang dipindahkan saat pemancangan relatif kecil, contohnya: tiang beton berlubang dengan ujung terbuka, tiang beton prategang berlubang dengan ujung terbuka, tiang baja H, tiang baja bulat ujung terbuka, tiang ulir.

3. Tiang Tanpa Perpindahan (Non Displacement Pile).

Tiang tanpa perpindahan, terdiri dari tiang yang dipasang didalam tanah denga cara menggali atau mengebor tanah. Yang termasuk dalam tiang tanpa perpindahan adalah bored pile, yaitu tiang beton yang pengecorannya langsung didalam lubang hasil pengeboran tanah (pipa baja diletakkan didalam lubang dan dicor beton) (H. C. Hardiyatmo, 2002).

Pondasi tiang dapat digolongkan berdasarkan kualitas materialnya, cara pelaksanaan, pemakaiannya bahan – bahan dan sebagainya:

Penggolongan berdasarkan kualitas material dan cara pembuatannya diperlihatnya dalam tabel 2.4, untuk penggolongan tiang berdasarkan cara pemasangannya seperti diperlihatkan pada table 2.5.

Tabel 2.4 Macam-macam Tipe Pondasi Berdasarkan Kualitas Material dan Cara Pembuatannya

(16)

(K. Nakazawa, 1983)

Tabel 2.5 Pondasi Tiang Berdasarkan Teknik Pemasangannya

(K. Nakazawa, 1983)

Berdasarkan penyaluran beban ke tanah, pondasi tiang dibedakan menjadi tiga, yaitu:

(17)

1. Pondasi tiang dengan tahanan ujung (end bearing pile). Tiang ini meneruskan beban melalui tahanan ujung tiang kelapisan tanah pendukung.

2. Pondasi tiang dengan tahanan geseran (friction pile). Tiang ini meneruskan beban ke tanah melalui tahanan geser selimut tiang. 3. Kombinasi friction dan end bearing capacity.

2.6.3. Pondasi Bored Pile

Bored pile dipasang kedalam tanah dengan cara mengebor tanah terlebih dahulu, baru kemudian diisi tulangan dan dicor beton. Tiang ini biasanya, dipakai pada tanah yang stabil dan kaku, sehingga memungkinkan untuk membentuk lubang yang stabil dengan alat bor. jika tanah mengandung air, pipa besi dibutuhkan untuk menahan dinding lubang dan pipa ini ditarik ke atas pada saat pengecoran beton. Pada tanah keras atau batuan lunak, dasar tiang dapat dibesarkan untuk menambah tahanan dukung ujung tiang (gambar 2.8).

Ada berbagai jeis pondasi bored pile, yaitu: a. Bored pile lurus untuk tanah keras.

b. Bored pile yang ujungnya diperbesar berbentuk bel. c. Bored pile yang ujungnya diperbesar berbentuk trapesium. d. Bored pile lurus untuk tanah berbatu-batuan.

Gambar 2.8 Jenis-jenis Bored Pile (Braja M. Das, 1941)

(18)

Ada beberapa alasan digunakannya pondasi bored pile dalam konstruksi: 1. Bored pile tunggal dapat digunakan pada tiang kelompok atau pile cap. 2. Kedalaman tiang dapat divariasikan.

3. Bored pile dapat didirikan sebelum penyelesaian tahapan selanjutnya.

4. Ketika proses pemancangan dilakukan, getaran tanah akan mengakibatkan kerusakan pada bangunan yang ada didekatnya, tetapi dengan penggunaan pondasi bored pile hal ini dapat dicegah.

5. Pada pondasi tiang pancang, proses pemancangan pada atanah lempung akan memuat tanah bergelombang dan menyebabkan tiang pancang sebelumnya bergerak kesamping. Hal ini tidak terjadi pada konstruksi bored pile.

6. Selama pelaksanaan pondasi bored pile tidak ada suara yang ditimbulkan oleh alat pancang seperti yang terjadi pada pelaksanaan pondasi tiang pancang.

7. Karena dasar dari pondasi bored pile dapat diperbesar, hal ii memberikan ketahanan yang besar untuk gaya keatas.

8. Permukaan diatas dimana dasar bored pile didirikan dapat diperiksa secara langsung.

9. Pondasi bored pile mempunyai ketahanan yang tinggi terhadap beban lateral.

Beberapa kelemahan dari pondasi bored pile:

1. Keadaan cuaca yang buruk dapat mempersulit pengeboran dan pengecoran, dapat diatasi dengan cara menunda pengeboran dan pengecoran sampai kaeadaan cuaca memungkinkan atau memasang tenda sebagai penutup. 2. Pengeboran dapat mengakibatkan gangguan kepadatan, bila tanah berupa

pasir atau tanah berkerikil, maka menggunakan bentonite sebagai penahan longsor.

3. Pengecoran beton sulit bila dipengaruhi air tanah karena mutu beton tidak dapat dikontrol dengan baik, maka diatasi dengan cara ujung pipa tremie berjarak 25-50 cm dari dasar lubang pondasi.

(19)

4. Air yang mengalir ke dalam lubang bor dapat mengakibatkan gangguan tanah, sehingga mengurangi kapasitas dukung tanah terhadap tiang, maka air yang mengalir langsung dihisap dan dibuang kembali kedalam kolam air. 5. Akan terjadi tanah runtuh (ground loss) jika tindakan pencegahan tidak

dilakukan, maka dipasang casing untuk mencegah kelongsoran.

6. Karena diameter tiang cukup besar dan memerlukan banyak beton dan material, untuk pekerjaan kecil mengakibatkan biayanya sangat melonjak maka ukuran tiang bored pile disesuaikan dengan beban yang dibutuhkan.

2.6.4. Daya Dukung

2.6.4.1. Daya Dukung Aksial

Daya dukung tiang dibedakan atas: - daya dukung ujung (Qe) - daya dukung geser (Qs)

Qult = Qe + Qs

Qall = Qult/SF dimana:

Qult : Daya dukung maximum tiang pancang Qe : Daya dukung ujung

Qs : Daya dukung friksi Qall : Daya dukung ijin

SF : Faktor keamanan = 2,5 – 4,0

2.6.4.2. Daya Dukung Ujung

Qe = Ae ( c . Nc + q’ . Nq + 0,3 . γ . D . Nγ )

Karena umumnya D << L maka D bisa diabaikan, sehingga: Qe = Ae ( c . Nc + q’ . Nq) L/D 0 0.5 1.0 1.5 2.0 2.5 3.0 4.0 Nc 6.2 7.1 7.7 8.1 8.4 8.6 8.8 9.0

(20)

2.6.4.3. Daya Dukung Friksi

Tomlinson (tiang pancang):

Tomlinson (sumuran):

C direduksi menjadi 0,30 c (Tomlinson)

C direduksi menjadi 0,45 c (Skempton untuk long pile) C direduksi menjadi 0,30 c (Skempton untuk short pile) K direduksi menjadi 0,70 k

2.6.4.4. Gaya Geser Negatif (Negative Skin Friction)

Gambar 2.9 Kondisi terjadinya Negative Friction

Fn = (ca + σ0 . tanδ ) As

= ( ca + k0 . γ . Dn . tanδ ) Dn . p

dimana:

Fn : negative skin friction

(21)

ca : adhesi tiang-tanah(umumnya diambil 2/3 c sampai c)

γ : berat volume tanah Dn : tebal timbunan

δ : sudut gesek tiang-tanah (≈ 2/3 υ) p : keliling penampang tiang

k0 : koefisien tekanan tanah lateral (= 1 - sin υ) Tanah kohesif:

Fn = ca . Dn . p (υ = 0)

Tanah granular:

Fn = k0 . γ . Dn2 . tanδ . p (c = 0)

Timbunan di atas tanah lunak:

Fn = (ca1+σ01.tanδ1)D1.p +(ca2 + σ02 . tanδ2)D2.P

2.6.4.5. Daya Dukung Lateral

Beban lateral dan momen dapat bekerja pada pondasi tiang akibat gaya gempa, gaya angin pada struktur atas, beban statik seperti misalnya tekanan tanah aktif. Untuk analisis, kondisi kepala tiang dibedakan sebagai kondisi kepala tiang terjepit (fixed head) dan kepala tiang bebas (free head).

(Mc. Nulty, 1956) mendefinisikan tiang ujung jepit (fixed end pile) sebagai tiang yang ujung atasnya terjepit (tertanam) dalam pelat penutup kepala tiang paling sedikit sedalam 60 cm, sedangkan untuk tiang yang bagian atasnya tidak terjepit atau terjepit kedalam pelat penutup kepala tiang kurang dari 60 cm termasuk tiang ujung bebas (free end pile). Untuk lebih jelasnya dapat dilihat pada gambar 2.10

(22)

Gambar 2.10 Model Ikatan Dengan Penutup Kepala Tiang (Mc. Nulty, 1956)

Sedangkan pada tanah lempung yang terkonsolidasi normal dan berbuti kasar, nilai subgrade umumnya meningkat secara linier terhadap kedalaman, sehingga di gunakan kriteria lain, yaitu: h EI T  5  Dimana: E = Modulus tiang (kN.cm2₎ I = Momen Inersia tiang (cm4₎

h

 =Modulus variasi reaksi subgrade (kN/m3₎  Beberapa harga hadalah:

- Tanah lempung lunak terkonsolidasi normal h

 = 350 s/d 700 kN/m3 - Tanah lempung organik

h

 = 150 kN/m3  Kriteria jenis tiang

- Kaku (pendek) tiang ujung bebas L < 2T - Elastis (panjang) tiang ujung bebas L ≥ 4T  Kedalaman titik jepit (zf)

zf = 1,8 T

(23)

 Modulus tanah (kh) kh = h x zf / D

Beban lateral yang diijinkan pada pondasi tiang diperbolehkan berdasarkan dari kriteria sebagai berikut:

 Koefisien defleksi tiang () 4 / 1 . . 4 .          p p h I E D k 

 Untuk tiang bebas (free head)

- Disebut short/rigid pile jika L < 1,5

        L e L D k y H o h / ) 1 5 . . 1 .( 4 . . . 

- Disebut long/infinite pile jika L < 2,5

        ) 1 . ( . 2 . .   e D k y H o h

 Untuk tiang terjepit (fixed head)

- Disebut short/rigid pile jika L < 0,5 L

D k y H  o. h. .

- Disebut long/infinite pile jika L < 1,5

        D k y H o. h. Dimana:

H = gaya lateral izin (kN) yo = defleksi maksimum (cm) D = diameter tiang (cm) L = panjang tiang (cm)

e = jarak beban lateral terhadap muka tanah (cm) 2.7. Pondasi Grup Tiang

2.7.1. Umum

(24)

Pada umumnya, untuk meneruskan beban kolom ke lapisan tanah di bawahnya, fondasi tiang digunakan dalam bentuk kelompok (grup). Masing-masing tiang dalam grupnya selanjutnya diikat bagian atasnya dengan kepala tiang (pile cap/poor). Kepala tiang ini bisa terletak langsung di atas tanah, seperti penggunaan pada umumnya, tetapi juga bisa berada di atas permukaan tanah, seperti biasa dipakai pada bangunan di laut (offshore paltform, dll.).

(a)

Gambar 2.8 Konstruksi Tiang Grup

Daya dukung grup tiang secara keseluruhan sangat tergantung dari jarak antar tiang. Apabila jarak antar tiang sangat dekat satu sama lainnya, maka bisa diasumsikan bahwa tegangan-tegangan yang disalurkan oleh tiang ke tanah di sekitarnya akan overlap (Gambar 4.1c), sehingga akan mengurangi daya dukung grup tiang. Untuk itu sangat disarankan agar antara tiang dalam grup mempunyai jarak sedemikian rupa, sehingga daya dukung grup tiang keseluruhan sama dengan jumlah daya dukung tiang tunggal. Secara praktis jarak antar tiang dalam grup minimum adalah 2.5 d (diameter tiang), tetapi secara umum jarak ini dibuat antara 3 sampai 3.5 kali diameter tiang.

Selain itu jarak antar tiang berdasarkan fungsi tiang disarankan: • Friction pile Smin = 3 d

• End bearing pile Smin = 2.5 d

Konfigurasi pengaturan grup tiang dalam satu kepala tiang bisa dilihat pada Gambar 4.2.

(25)

Gambar 2.9 Konfigurasi Tiang Dalam Grup 2.7.2. Efisiensi Grup Tiang

Apabila jarak antar tiang dalam satu grup (kepala tiang) tidak memenuhi jarak minimum yang disyaratkan, maka daya dukung grup tiang tidak akan sama dengan daya dukung satu tiang dikalikan dengan jumlah tiang dalam grup tersebut, melainkan ada satu faktor pengali yang besarnya kurang dari satu dan biasa disebut dengan efisiensi grup tiang. Dengan demikian daya dukung total grup tiang bisa dituliskan:

Qug = Qut × n × Eg

Qug : daya dukung grup tiang Qut : daya dukung tiang tunggal n : jumlah tiang dalam grup Eg : efisiensi grup tiang (≤ 1)

Gambar 4.3 menjelaskan maksud dari efisiensi grup tiang. Gambar a dan b memperlihatkan diagram tegangan mobilisasi keruntuhan berbentuk

(26)

bulb pressure yang tidak saling berpotongan. Pada kondisi ini daya dukung grup tiang sama dengan daya dukung tiang tunggal dikalikan dengan jumlah tiang dalam satu grup. Hal ini berarti, bahwa efisiensi grup tiang adalah satu.

Berbeda dengan gambar c, dimana terlihat adanya perpotongan antara bulb pressure satu tiang dengan tiang lainnya, yang menyebabkan mobilisasi tegangan pada tanah tidak bisa penuh (100%), karena adanya daerah tegangan yang menjadi milik bersama. Pada kondisi seperti ini efisiensi daya dukung grup tiang menjadi kurag dari satu.

Ada beberapa formula untuk menghitung efisiensi grup tiang, tetapi persamaan di bawah (Labarre) adalah yang paling swering dipakai.

Eg =1-θ n m n m m n . . 90 ) 1 ( ) 1 (   

θ: atan (d/s) dalam derajat d : diameter tiang

s : jarak antar as tiang n : jumlah tiang dalam baris m : jumlah baris

Gambar 2.10 Mobilisasi Keruntuhan (Bulb Pressure)

(27)

2.7.3. Daya Dukung Grup Tiang

Daya dukung tiang dihitung berdasarkan asumsi: • Keruntuhan tiang tunggal (individual pile failure) • Keruntuhan blok (block failure)

Anggapan keruntuhan di atas didsarkan atas klasifikasi tanah dan jarak antar tiang (s) dalam satu grup.

1. Dihitung Berdasarkan Keruntuhan Tiang Tunggal

Pada c-soils, c-υ soils, dan υ soils apabila dipenuhi syarat minimum spacing antar tiang. Formula daya dukung pada anggapan ini adalah:

Qug = Qut × n × Eg

• Untuk c-soils, c-υ soils → Eg = 0,7 (s = 3d) sampai 1 (s ≥ 8d) • Untuk υ soils → Eg = 1

2. Dihitung Berdasarkan Keruntuhan Blok

Pada dua kondisi di bawah keruntuhan yang terjadi tidak lagi sebagai individual pile. Untuk itu perhitungan daya dukung disarankan berdasarkan keruntuhan blok. Kondisi yang dimaksud adalah:

• c-soils lunak atau pasir lepas

• Tanah liat keras dan pasir padat dengan s < 3d

Menurut Coyle dan Sulaiman formula daya dukung berdasakan keruntuhan blok adalah:

Qug = 2D (W+L) f + 1,3 c Nc W L

Friksi Ujung

D : kedalaman tiang W : lebar grup tiang L : panjang grup tiang f = αc

(28)

: friksi antara tanah dengan selimut tiang α : faktor adhesi empiris (Tomlinson) c : kohesi

Gambar 2.11 Definisi W dan L Pada Keruntuhan Blok 2.7.4. Distribusi Gaya Dalam Grup Tiang

Beban luar yang bekerja pada kepala tiang selanjutnya didistribusikan ke semua tiang dalam grup. Perhitungan distribusi gaya ke masing-masing tiang didasarkan atas teori elastisitas, yakni:

Qu = ₂ ₂ . . y y M x x M n V y x     < Qa