Reflektor Gelombang 1 balok

Bab 3

Reflektor Gelombang 1 balok

Setelah diperoleh persamaan yang menggambarkan gerak gelombang air setiap saat yaitu SWE, maka pada bab ini akan dijelaskan mengenai pengaruh 1 balok terendam sebagai reflektor gelombang baik dari hasil analitik maupun numerik.

3.1

Hasil Analitik Reflektor Gelombang Berupa

Satu Balok

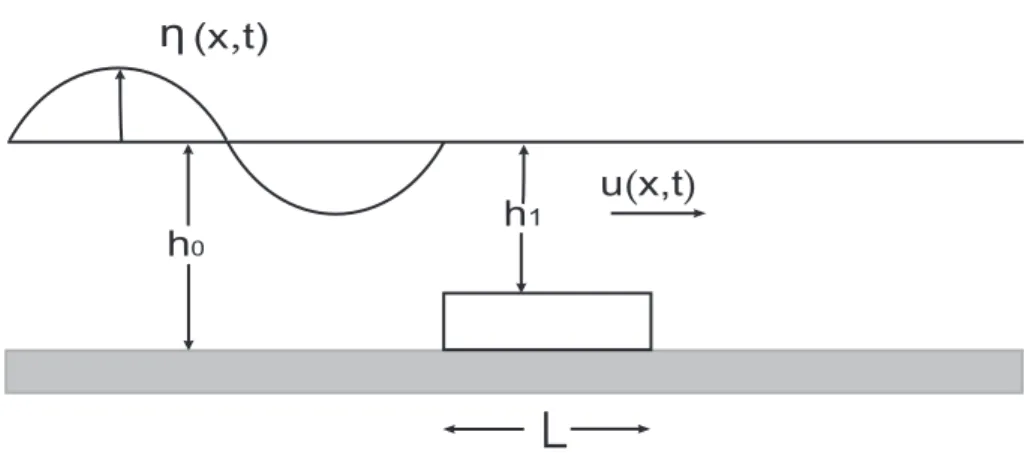
h0 (x t, ) u x,t( ) h1

L

Gambar 3.1: Daerah pengamatan dengan 1 balok terendam selebar L sebagai re-flektor gelombang

Seperti telah dijelaskan pada bab sebelumnya, persamaan SWE linier (2.1.4) dan

(2.1.5) ekivalen dengan persamaan gelombang (2.1.6) dan (2.1.7). Persamaan yang akan digunakan adalah

ηtt= c20ηxx (3.1.1)

dengan c2 _{= gh0 untuk fluida dengan dasar yang rata dan kedalaman sedalam h0.} Berikut ini akan dibahas mengenai relasi dispersi dari (3.1.1). Dimisalkan solusi dari (3.1.1) berbentuk η(x, t) = ei(kx−ωt)_{, maka fungsi ini akan menjadi solusi bagi}

(3.1.1) jika ω dan k memenuhi hubungan

ω k = ±

√ c0 Tulis dalam hj dan cj memberikan

ω kj = ±pghj (3.1.2) dengan cj = p ghj.

Persamaan (3.1.2) dinamakan relasi dispersi, yaitu hubungan yang harus dipenuhi antara bilangan gelombang k dengan frekuensi anguler ω agar η(x, t) = ei(kx−ωt)

merupakan solusi monokromatik bagi (3.1.1). Solusi dari (3.1.1) adalah superpo-sisi dari gelombang yang bergerak ke arah kiri dan kanan dengan kecepatan kon-stan c0. Solusi d’Alembert dari (3.1.1) dengan syarat awal berupa gundukan awal mengatakan bahwa gundukan awal akan terpecah menjadi dua sama besar menjadi gelombang yang bergerak ke kiri dan gelombang yang bergerak ke kanan. Gelom-bang yang telah bergerak ke kanan akan tetap bergerak ke kanan dengan kecepatan dan bentuk yang tetap selama kedalaman fluida tidak berubah. Demikian juga un-tuk gelombang yang bergerak ke kiri.

Perhatikan suatu balok terendam yang lebarnya L dan tingginya (h0 − h1), dile-takkan pada dasar fluida dengan kedalaman h0, lihat Gambar 3.1. Maka kedalaman fluida berupa fungsi h(x) dengan

h(x) =    h1 untuk 0 < x < L, h0 lainnya, (3.1.3)

dengan h1 < h0.

Sebelum dijelaskan mengenai hasil analitik dari pengaruh balok terhadap gelombang datang, maka akan dijelaskan terlebih dahulu sifat-sifat gelombang yaitu gelombang transmisi dan refleksi. Transmisi dan refleksi merupakan suatu gejala fisis dari fenomena gelombang yang terjadi salah satunya sebagai akibat perubahan kedala-man fluida. Bayangkan suatu gelombang air datang dari kiri, bertranslasi di atas dasar rata, dalam perambatannya gelombang tersebut mengalami gangguan (dalam hal ini kedalaman air berubah) maka gelombang akan terpecah dua. Sebagian dari gelombang ini akan direfleksikan dan sebagian lagi ditransmisikan. Istilah gelom-bang transmisi di sini berarti bahwa gelomgelom-bang merambat dengan arah yang sama dengan gelombang semula, sedangkan gelombang refleksi berarti gelombang yang arah rambatnya berbalik arah.

Selanjutnya dimisalkan terdapat gelombang monokromatik datang dari sebelah kiri sebagai A exp i(k0x − ωt) memasuki daerah pengamatan dengan fungsi kedalaman

(3.1.3). Ketika gelombang A exp i(k0x − ωt) memasuki daerah dengan kedalaman air yang lebih dangkal h1 maka gelombang akan terpecah dua, sebagian gelom-bang ditransmisikan menuju daerah di atas balok dan sebagian gelomgelom-bang dire-fleksikan. Gelombang yang merambat ke kanan di atas kedalaman h1 dinyatakan sebagai exp i(k1x − ωt) dan gelombang yang merambat ke kiri di atas kedalaman

h0 sebagai exp −i(k0x + ωt). Ketika gelombang yang merambat ke kanan kembali memasuki daerah dengan kedalaman semula h0, maka gelombang tersebut akan kem-bali terpecah menjadi gelombang ke kiri exp −i(k1x + ωt) dan gelombang ke kanan

exp i(k0x − ωt). Proses ini berulang terus menerus, sehingga profil gelombang setiap saat dapat dituliskan sebagai:

η(x, t) = exp(−iωt)ν(x) (3.1.4) dimana ν(x) =         

A exp ik0x + r exp −ik0x, x < 0

a exp ik1x + b exp −ik1x, 0 ≤ x < L

t exp ik0(x − L), L ≤ x.

dengan r adalah amplitudo superposisi gelombang ke kiri di daerah x < 0 dan t adalah amplitudo superposisi gelombang ke kanan di daerah x > L. Analog untuk

a dan b. Karena η harus kontinu di titik x = 0 dan x = L maka ν(x) haruslah juga

kontinu di titik x = 0 dan x = L. Hal ini merupakan jump condition yang pertama. Subtitusikan η pada (3.1.4) ke dalam persamaan gelombang ηtt = (c2ηx)x dengan

c(x) = gh(x) sehingga diperoleh persamaan −ων(x) = (c2_ν

x)x.

Integralkan persamaan di atas terhadap x dengan batas x dari x = 0− sampai

x = 0+, diperoleh −R0+ 0− ων(x)dx = c 2_ν x|00+− 0 = limx→0+{g(h(x)νx)} − limx→0−{g(h(x)νx)} limx→0−h0νx = limx→0+h1νx

atau dengan kata lain hνx haruslah kontinu pada x = 0. Ini merupakan jump

con-dition yang kedua. Di posisi x = L kondisi ini juga berlaku.

Sehingga profil permukaan air η(x, t) = exp(−iωt)ν(x) dengan kedalaman laut berupa (3.1.3) mempunyai dua jump condition. Dengan menggunakan kekontin-uan ν(x) dan h(x)νx(x) di x = 0 dan x = L dapat dicari hubungan antara r, a, b, t

dengan amplitudo gelombang awal A. Kekontinuan ν(x) dan h(x)νx(x) di x = 0

akan menghasilkan: N0   A r   = N1   a b   , (3.1.6)

sedangkan kekontinuan ν(x) dan h(x)νx(x) di x = L akan menghasilkan persamaan

M0   a b   = t   1 h0k0   , (3.1.7)

dengan Nj =   1 1 hjkj −hjkj   , untuk j = 0, 1 (3.1.8) M0 =   E E−1 h0k0E −h0k0E−1   , (3.1.9)

dan E = exp ik1L. matriks Nj dan M0 mempunyai determinan yang tidak sama dengan 0 sehingga kedua matriks tersebut mempunyai invers.

Perhatikan bahwa pada saat tidak ada balok (h1 = h0), persamaan (3.1.6, 3.1.7) akan memberikan solusi r = 0, t = AE = A exp ik1L, b = 0 dan a = A, yang berarti tidak ada gelombang refleksi dan semua gelombang datang akan ditransmisikan. Hal ini sesuai dengan yang diperkirakan.

Dari persamaan (3.1.6) dan (3.1.7) dapat dicari hubungan antara amplitudo gelom-bang transmisi t dan amplitudo gelomgelom-bang datang A dengan cara mengkombinasikan kedua matriks N dan M.

Karena kedua matriks mempunyai invers maka dari persamaan (3.1.6) diperoleh   a b   = N−1 1 N0   A r  , dengan N−1 1 = 1 2h1k1   h1k1 1 h1k1 1   kemudian subti-tusikan ke persamaan (3.1.7) sehingga diperoleh

t   1 k0h0   = M0N1−1N0   A r   _(3.1.10)

Misalkan S = h1k1+h0k0 dan D = h1k1−h0k0maka M1N1−1N0dapat ditulis menjadi

M0N1−1N0 = 1 2h1k1   ES + E−1D ED + E−1S h1k1(ES − E−1D) (h1k1ED − E−1S)  

Maka r dapat dieliminasi dari kedua persamaan pada (3.1.10) dengan cara menga-likan baris pertama dari matriks dengan ED − SE−1 _{dan mengalikan persamaan}

baris kedua dari matriks dengan ED + SE−1 _{sehingga memberikan} t = A S 2_{− D}2 S2_E−1_{− D}2_E atau _¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ = S 2_{− D}2 |S2_E−1_{− D}2_E| (3.1.11) Dengan cara yang sama dapat diperoleh hubungan antara amplitudo gelombang releksi r dengan amplitudo gelombang datang A yaitu

¯ ¯ ¯r A ¯ ¯ ¯ = SD(E −1_{− E)} |D2_{E − S}2_E−1_| (3.1.12)

Lebih jauh lagi dapat dibuktikan bahwa ¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ 2 + ¯ ¯ ¯r A ¯ ¯ ¯2 = 1. (3.1.13)

Persamaan ini dapat diartikan sebagai kekekalan energi yang berlaku pada gelom-bang air dengan 1 balok sebagai reflektor gelomgelom-bang. Gelomgelom-bang datang dengan amplitudo A setelah melewati balok akan terpecah dua menjadi gelombang transmisi

downstream dengan amplitudo t dan gelombang refleksi upstream dengan amplitudo r sedemikian sehingga (3.1.13) berlaku.

Setelah diketahui hubungan antara amplitudo gelombang transmisi dan gelombang datang maka akan dicari dimensi balok yang akan memberikan |t

A| paling minimum.

Perhatikan bahwa nilai |t

A| bergantung pada h0, h1, k0, k1, E. Karena berlaku relasi

dispersi (3.1.2) maka k0, k1 berturut-turut juga bergantung pada h0, h1, yang artinya juga bergantung pada h0, h1, L. Untuk tinggi balok h0− h1 tertentu, maka nilai |_At| minimum pada saat nilai |S2_E−1_{− D}2_{E| maksimum. Sehingga nilai |}t

A| bergantung

pada nilai L secara periodik. Dengan menggunakan (3.1.13) maka nilai |r A| juga

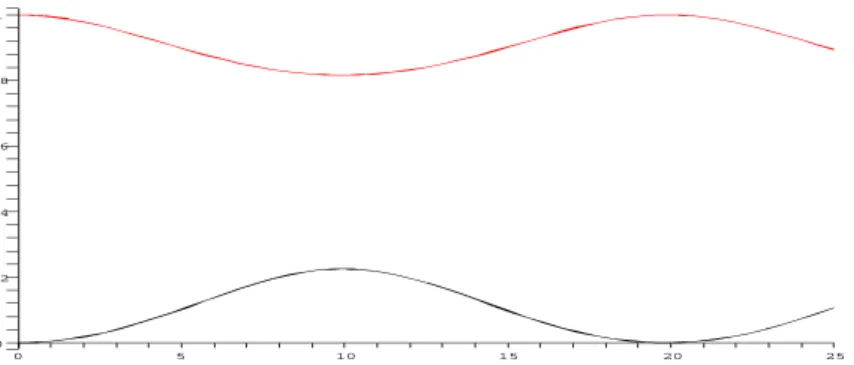
bergantung pada L secara periodik, lihat Gambar 3.2. Sehingga dapat diperoleh lebar balok L yang membuat amplitudo gelombang transmisi minimum

¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ min = S 2_{− D}2 S2_{+ D}2 ketika 2L = (n + 1 2) 2π k1 = (n +1 2)λ1, n = 0, 1, 2, . . . (3.1.14) ¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ max = 1 ketika 2L = n2π k1 = nλ1, n = 0, 1, 2, . . . (3.1.15)

1 0.6 0.8 0.4 0.2 0 L 10 5 25 0 15 20

Gambar 3.2: kurva periodik |t

A|2 (atas) dan | r

A|2 (bawah) sebagai fungsi dari L. Di

sini digunakan h1 = 0.4h0 dengan h0 = 10

Misal Lopt menyatakan nilai minimum dari panjang balok yang memberikan |t/A|

minimum, maka Lopt = 1/4λ1.

Kita dapat menuliskan S = h1k1+ h0k0 = √ω_g(

√ h1+ √ h0) dan D = h1k1 − h0k0 = ω √ g( √ h1 − √

h0) juga menggunakan persamaan (3.1.2), maka persamaan (3.1.11) dapat dituliskan secara eksplisit sebagai fungsi dari h1/h0 dan L yaitu:

¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ = ( √ h1 + √ h0)2− ( √ h1− √ h0)2 (√h1+ √ h0)2E−1+ ( √ h1− √ h0)2E ¯ ¯ ¯ ¯_At ¯ ¯ ¯ ¯ = 2 q h1 h0 r ((h1 h0 + 1) sin( ωL q gh1 h0 ))2_{+ (4}h1 h0)(cos( ωL q gh1 h0 ))2 (3.1.16)

Persamaan (3.1.16) menyatakan bahwa nilai |t

A| bergantung pada h1 dan h0 melalui

perbandingannya, yaitu h1

h0 dan nilai L. Jadi perbandingan amplitudo gelombang

transmisi dengan amplitudo gelombang datang tidak bergantung pada seberapa dalam laut (h0) dan tinggi balok (h0− h1) melainkan pada perbandingan h1

h0. Untuk

lebih jelasnya, dapat dilihat pada Gambar 3.3 dimana dipilih nilai Lopt = 1₄λ1 =

π

2ω

√ gh1.

1 0.8 0.6 0.4 0.2 0 depth 1 0.8 0.4 0.2 0 0.6 Gambar 3.3: Kurva |t

A| sebagai fungsi dari h1

h0. Di sini digunakan lebar optimum

balok L = 1 4λ1

Berikut ini akan dijelaskan interpretasi fisis dari hasil analitik di atas (3.1.14, 3.1.15). Bagian ini penting karena dapat langsung diperumum untuk kasus n-balok. Ketika gelombang mencapai batas kiri dari balok di x = 0 sebagian dari gelombang akan ditransmisikan ke daerah 0 < x < L dan sebagian gelombang akan direflek-sikan. Ketika gelombang yang ditransmisikan mencapai ujung balok kanan di x = L maka gelombang tersebut kembali akan terpecah dua, sebagian ditransmisikan ke daerah x > L dan sebagian direfleksikan ke 0 < x < L. Gelombang yang ke kanan saat mencapai x = L juga akan terpecah dua. Dimisalkan gelombang yang akan terpecah di x = L sebagai ei(k1x−ωt). Sedangkan gelombang yang direfleksikan, saat

mencapai x = 0 akan terpecah dua juga. Gelombang kedua yang mencapai x = L ini rumusannya berupa ei(k1(x+2L)−ωt). Terdapat banyak sekali proses transmisi dan

refleksi, dan gelombang ke-n yang mencapai x = L rumusannya berupa berbentuk

ek1(x+2nL)−ωt dengan n bilangan bulat.

Selanjutnya gelombang-gelombang di x = L akan bersuperposisi saling melemahkan jika beda phase antar gelombangnya sebesar π atau kelipatan bilangan ganjil kali π

yaitu: (k1x − ωt) − (k1(x + 2L) − ωt) = (2n + 1)π 2π λ1(x − x + 2L) = (2n + 1)π 2L = (n + 1 2)λ1

Sebaliknya jika beda phase antara gelombang merupakan kelipatan bilangan genap dari 2π atau sama dengan 2nπ maka gelombang-gelombang yang ada di x = L akan bersuperposisi saling menguatkan atau bersifat destruktif. Hal ini akan terjadi ketika 2L = nλ1 dengan n bilangan bulat.

Jadi total gelombang yang bergerak ke arah kiri di daerah x < 0 adalah superpo-sisi dari semua gelombang yang direfleksikan di x = 0 dan semua gelombang yang ditransmisikan dari daerah 0 < x < L menuju daerah x < 0. Sedangkan total gelombang yang berjalan ke arah kanan di x > L adalah jumlah dari semua gelom-bang yang ditransmisikan dari daerah 0 < x < L menuju x > L. Jika lebar balok

L = (n + 1

4)λ1 maka semua gelombang yang ditransmisikan ke daerah x > L akan bersuperposisi saling melemahkan, sedangkan jika lebar balok L = n

2λ1 maka semua gelombang yang ditransmisikan ke x > L akan bersuperposisi saling menguatkan.

3.2

Diskretisasi SWE Menggunakan Metode Lax

Pada subbab ini persamaan SWE linier akan didiskritisasi menggunakan metode beda hingga (finite difference). Perhatikan persamaan SWE linier pada domain berhingga {(x, t)|a < x < b, 0 < t < T }. Metode yang digunakan untuk meng-hampiri persamaan linear SWE adalah metoda Lax yang merupakan modifikasi dari metode FTCS (Foward Time Centered Space) karena metode FTCS ini meng-hasilkan suatu hampiran yang selalu tidak stabil. Pertama-tama akan dibuktikan bahwa metode FTCS untuk persamaan Linear SWE selalu tidak stabil. Misal

ηn

j = η(j∆x, n∆t) merupakan hampiran bagi η(x, t) dan unj = u(j∆x, n∆t)

menghasilkan persamaan beda: ηn+1 j − ηjn+1 ∆t + h un j+1− unj−1 2∆t = 0 (3.2.1)

Dengan cara yang sama persamaan beda bagi persamaan (2.1.5) juga dapat dicari, yaitu: un+1 j − un+1j ∆t + g ηn j+1− ηj−1n 2∆t = 0 (3.2.2)

Metoda matriks akan digunakan untuk menganalisa kestabilan persamaan beda (3.2.1) dan (3.2.2). Subtitusikan komponen Fourier eji4x _{ke dalam persamaan beda}

(3.2.1) dan (3.2.2) maka diperoleh

ηn+1

j = ηjn−C21unj(eiθ− e−iθ) = ηjn− unjC1i sin θ

un+1_j = un

j − C22ηnj(eiθ− e−iθ) = unj − ηnjC2i sin θ

(3.2.3)

dengan C1 = h4t_4x dan C2 = g4t_4x.

Jika (3.2.3)dituliskan dalam bentuk matriks menjadi   ηn+1j un+1 j   =   1 −iC1sin θ −iC2sin θ 1     ηjn un j   Misalkan G =   1 −iC1sin θ −iC2sin θ 1 

. Maka |G − λI| = 0 memberikan (1 − λ)2_{+ (−i sin θ)}2_C

1C2 = 0

(1 − λ) = ± − i sin θ√C1C2

λ = 1 ± i√C1C2sin θ

|λ| = p1 + C1C2sin2θ

yang bernilai lebih dari 1 untuk setiap C1, C2 > 0. Dengan demikian metode FTCS selalu menghasilkan solusi yang tidak stabil. Metode Lax merupakan modifikasi dari metofe FTCS. Persamaan beda yang diperoleh dapat menghasilkan solusi yang stabil. Metoda Lax mengganti nilai un

j dan ηnj dengan nilai rata-rata dari titik-titik

grid sebelahnya yaitu 1

beda (3.2.1) dan (3.2.2) menjadi η_jn+1= 1 2(η n j+1+ ηj−1n ) − h 4t 24x(u n j+1− unj−1) (3.2.4) un+1_j = 1 2(u n j+1) + unj−1) − g 4t 24x(η n j+1− ηnj−1) (3.2.5)

Persamaan beda di atas mempunyai akurasi O(4t, 4x2_{). Selanjutnya akan diperiksa} syarat kestabilan dari metode Lax ini. Subtitusikan komponen Fourier e(i4x)j_kedalam persamaan (3.2.4) dan (3.2.5) diperoleh

ηn+1

j = ηjn(eiθ + e−iθ) −C21ujn(eiθ− e−iθ) = ηjncos θ − unjC1i sin θ

un+1_j = un

j(eiθ+ e−iθ) − C22ηnj(eiθ− e−iθ) = unj cos θ − ηjnC2i sin θ atau dalam bentuk matriks menjadi

  ηn+1j un+1_j   = 

 cos θ −iC1sin θ

−iC2sin θ cos θ     ηjn un j   Tuliskan G = 

 cos θ −iC1sin θ

−iC2sin θ cos θ  . Maka |G − λI| = 0 memberikan

(cos θ − λ)2_{+ sin}2_θC 1C2 = 0 λ = cos θ ± i√C1C2sin θ |λ| = pcos2_{θ + C} 1C2sin2θ = p1 − sin2_{θ(1 − C} 1C2) Perhatikan bahwap1 − sin2_{θ(1 − C}

1C2) ≤

√

1 sehingga nilai dari sin2_θ(1−C

1C2) ≥ 0. Karena nilai sin2_{θ selalu positif maka C}

1C2 ≤ 1. Oleh sebab itu metode Lax stabil dengan syarat gh(4t

4x)

2 _{≤ 1.}

Maka untuk dasar berupa kedalaman diskontinu sepeti pada (3.1.3), persamaan beda yang sesuai adalah

η_jn+1 = 1

2(ηj+1n + ηj−1n ) − hi_24x4t (unj+1− unj−1)

un+1

j = 12(unj+1+ unj−1) − g24x4t (ηnj+1− ηj−1n ),

dengan hi, i = 0, 1.

Persamaan beda di atas mempunyai akurasi O(4t, 4x2_).

Selain kestabilan juga harus diperhatikan kekonsistenan dari persamaan beda (3.2.4) dan (3.2.5). Kekonsistenan diperiksa dengan cara mensubtitusikan ekspansi deret Taylor dari persamaan (2.4.1) dan persamaan (2.4.2) ke dalam persamaan beda (3.2.4) dan (3.2.5). Diperoleh hasil persamaan beda konsisten. Lebih jauh lagi, jika

ghi(_4x4t)2 < 1 maka pada truncation term muncul suku ηxx. Suku ηxx ini dikenal

se-bagai suku yang memberikan efek difusi. Menyelesaikan persamaan beda ini tak lain adalah menyelesaikan persamaan SWE linier (2.1.4) dan (2.1.5) dengan tambahan suku truncation term. Dengan demikian penggunaan persamaan beda (3.2.6) den-gan ghi(_4x4t)2 < 1 akan memberikan error berupa efek difusi atau disebut juga eror

difusi numerik. Untuk menghindari eror difusi numerik ini maka haruslah dipilih nilai 4x, 4t yang membuat ghi(_4x4t)2 = 1. Eror difusi numerik harus dihindari agar

kita dapat membuat hasil perbandingan kuantitatif yang baik antara hasil analitik dengan numerik. Jadi di sini sumbu x pada domain spatial dipartisi secara tak homogen sebagai berikut. Untuk 4t tertentu, maka 4x1 = √gh14t pada daerah dengan kedalaman h1 yaitu 0 < x < L dan 4x0 =

√

gh04t pada daerah lainnya. Sedangkan pada titik diskontinu, misalkan pada j = J digunakan persamaan beda sebagai berikut: η_Jn+1 = 1 2(ηnJ+1+ ηJ−1n ) − (h0+ h1)/2_4x04t_+4x1(unJ+1− unJ−1) un+1 J = 12(unJ+1+ unJ−1) − g4x04t+4x1(η n J+1− ηJ−1n ) (3.2.7)

Untuk simulasi kita menggunakan syarat awal simpangan permukaan air sebagai berikut :

η(x, 0) = 0 dan u(x, 0) = 0 (3.2.8) Sedangkan untuk syarat batas kiri daerah pengamatan digunakan syarat batas:

η(a, t) = A sin ωt dan u(a, t) = √g gh0

Kedua syarat awal (3.2.8) menyatakan bahwa pada saat awal permukaan air dalam keadaan setimbang dan diam. Syarat batas (3.2.9) menyatakan bahwa gelombang monokromatik A sin ωt masuk dari sebelah kiri domain, sedangkan syarat batas bagi u(a, t) diturunkan dari persamaan linier SWE sebgai berikut. Perhatikan per-samaan SWE linier (2.1.5), gelombang yang berjalan ke kanan dengan dasar rata

h0 dan memenuhi (2.1.5)adalah η(x − λ0t) dan u(x − λ0t). Subtitusikan kembali kedalam persamaan SWE linier (2.1.5)maka akan didapat −λ0u0 = −gη0 sehingga

u = q_hg₀η pada batas kiri. Sehingga dengan syarat batas kiri η(a, t) nilai u(a, t)

diberikan pada (3.2.9). Sedangkan untuk syarat batas kanan diterapkan metode FTBS (Forward Time Backward Space) dengan akurasi O(4x, 4t) bagi η(L, t) dan

u(L, t). Penjelasan untuk ini adalah sebagai berikut. Garis karakteristik bagi

per-samaan gelombang dengan metode FTBS adalah berupa garis x = ct + k dengan

k bilangan real. Garis-garis tersebut mengarah keluar domain. Hal ini

mengaki-batkan gelombang terserap ke kanan seluruhnya. Perhatikan bahwa perbedaan orde akurasi pada metode FTBS tidak akan mempengaruhi akurasi O(4x2_{, 4t) dalam} perhitungan domain, karena perhitungan dengan akurasi rendah ini akan segera meninggalkan domain perhitungan.

3.3

Simulasi Numerik

Setelah diformulasikan skema numerik bagi SWE dengan 1 balok reflektor maka untuk perhitungan digunakan data sebagai berikut: selang spatial [0, 150] dengan waktu pengamatan [0, 22], gravitasi g = 10, frekuensi gelombang ω = 1 dan dasar berupa h(x) =    4, untuk 50 < x < 50 + Lopt = 10 10, untuk lainnya,

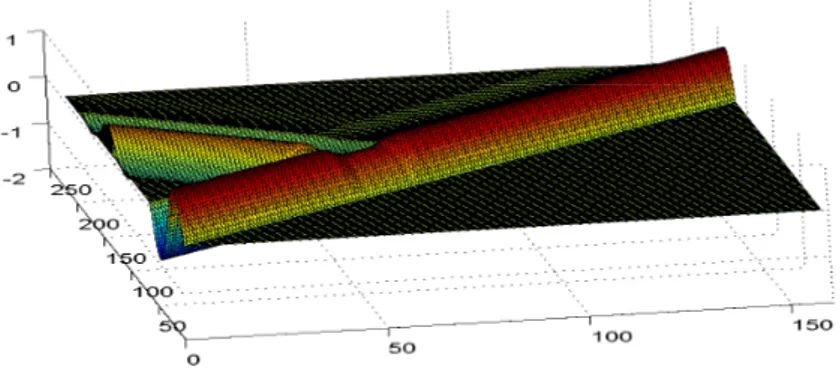
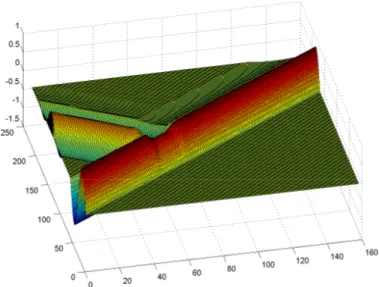
Dengan program MATLAB disimulasikan solusi numerik SWE. Dapat teramati pada Gambar 3.4 bahwa gelombang monokromatik yang masuk dari kiri, setelah melewati balok yang terletak di posisi [50, 60] akan terpecah menjadi gelombang transmisi dan refleksi. Dapat dilihat juga bahwa amplitudo gelombang transmisi lebih kecil

dari-pada amplitudo gelombang awal. Ini berarti bahwa balok dapat berfungsi sebagai pemecah gelombang.

Dari hasil simulasi numerik menggunakan beberapa nilai L, dapat dilihat bahwa

|t

A| juga bergantung pada L secara periodik. Dengan simulasi numerik juga dapat

diuji lebar balok yang paling optimum untuk h1 = 0.4h0. Hasilnya sesuai dengan lebar balok optimum yang diperoleh secara analitik, hal ini akan dijelaskan pada sub bab berikutnya. Dari hasil simulasi numerik dapat diperoleh amplitudo gelombang

Gambar 3.4: Hasil simulasi numerik SWE linier dengan 1 balok terendam, terlihat pada gambar gelombang masuk dari kiri dan setelah melalui balok mengalami proses perpecahan menjadi gelombang refleksi dan transmisi

datang sebelum mencapai balok yaitu di x = [0, 40] jika dibandingkan dengan am-plitudo gelombang setelah balok di x = 120 jauh lebih besar. Hal ini dapat dilihat lebih akurat pada sub bab selanjutnya.

3.4

Perbandingan antara Hasil Analitik dan

Nu-merik

Dari simulasi numerik dengan lebar grid yang diperhalus dan lebar balok L yang berbeda-beda maka diperoleh L yang paling mereduksi amplitudo gelombang datang, nilai yang diperoleh sudah sesuai dengan hasil analitik yaitu Lopt = 1₄λ1 dimana

gelombang yang dibangkitkan dalam program mempunyai panjang gelombang λ1 = 2π k1 = 2π ω √

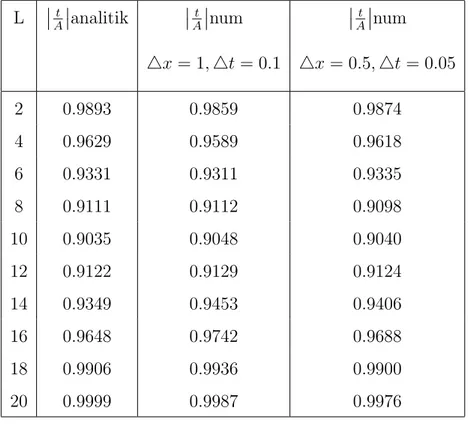
gh1 yaitu sama dengan 9.9435 ≈ 10. Berikut ini adalah tabel per-bandingan antara hasil analitik dan numerik dengan nilai grid yang berbeda yaitu

4x = 1,4t = 0.1 dan grid 4x = 0.5, 4t = 0.05. L ¯¯t A ¯ ¯analitik ¯¯t A ¯ ¯num ¯¯t A ¯ ¯num 4x = 1, 4t = 0.1 4x = 0.5, 4t = 0.05 2 0.9893 0.9859 0.9874 4 0.9629 0.9589 0.9618 6 0.9331 0.9311 0.9335 8 0.9111 0.9112 0.9098 10 0.9035 0.9048 0.9040 12 0.9122 0.9129 0.9124 14 0.9349 0.9453 0.9406 16 0.9648 0.9742 0.9688 18 0.9906 0.9936 0.9900 20 0.9999 0.9987 0.9976

Tabel 3.1: Tabel perbandingan antara hasil analitik dengan numerik menggunakan grid yang berbeda

Dari tabel di atas maka dapat dilihat hasil perbandingan antara¯¯t A

¯

¯ analitik dan numerik menghasilkan Lopt yang sama. Hasil numerik dengan lebar grid yang lebih

kecil akan memberikan hasil yang semakin dekat dengan solusi eksaknya.

3.5

Metode Lax-Wendroff

Perhitungan numerik dengan menggunakan metode Lax akurasinya adalah O(4x2_{, 4t).} Akurasi tersebut sudah cukup baik, tetapi dalam partisi spatial dan partisi waktu metode Lax memberikan akurasi yang berbeda. Hal ini dapat diatasi dengan

men-cari skema numerik yang lebih baik yang memberikan akurasi O(4x2_{, 4t}2_{). Salah} satu metode yang memberikan akurasi O(4x2_{, 4t}2_{) adalah metode Lax-Wendroff.} Persamaan SWE linier (2.1.4) dan (2.1.5) akan dihampiri dengan metode Lax-Wendroff. Perhatikan ekspansi Taylor dari η(x, t) dalam waktu yaitu:

η(x, t + 4t) = η(x, t) + ηt(x, t)4t +

1

2ηtt(x, t)4t

2 _{+ O(4t}3₎

dari persamaan (2.1.4) diketahui bahwa ηt(x, t) = −hux(x, t), sedangkan (2.1.5)

memberikan ηtt(x, t) = (ηt)t = (−hux)t = −h(ut)x = −h(−gηxx). Maka ekspansi

Taylor dari η(x, t + 4t) menjadi:

η(x, t + 4t) = η(x, t) − hux(x, t)4t + gh

2 ηxx(x, t)(4t)

2_{+ O(4t}3₎

Jika ekspansi Taylor ini dihampiri dengan beda pusat untuk ux dan ηxx maka akan

diperoleh persamaan beda bagi persamaan (2.1.4):

ηn+1 j = ηjn− h4t 24x(u n j+1− unj−1) + gh(4t)2 2(4x)2 (η n j+1− 2ηnj + ηj−1n ) (3.5.1)

Dengan cara yang sama maka dapat diperoleh persamaan beda bagi persamaan (2.1.5): un+1 j = unj − g4t 24x(η n j+1− ηnj−1) + gh(4t)2 2(4x)2 (u n j+1− 2unj + unj−1) (3.5.2)

Setelah diperoleh persamaan beda bagi SWE linier maka akan diperiksa kestabilan-nya dengan menggunakan metode matriks. Subtitusikan komponen Fourier e(i4x)j ke dalam persamaan beda sehingga

ηn+1 j = ηjn− h4t 24xu n j(eiθ− e−iθ) + gh(4t)2 2(4x)2 η n j(eiθ− 2 + e−iθ) un+1_j = un_j − g4t 24xη n j(eiθ− e−iθ) + gh(4t)2 2(4x)2 u n j(eiθ − 2 + e−iθ)

Kemudian tuliskan dalam bentuk matriks menjadi   ηjn+1 ηn+1 j   =   1 + gh(4t)2 2(4x)2(cos θ − 1) −h4t_4xi sin θ −g4t_4x 1 + gh(4t)_2(4x)22(cos θ − 1)     ηjn un j   (3.5.3)

Misalkan G =   1 + gh(4t) 2 2(4x)2 (cos θ − 1) −h4t_4xi sin θ −g4t 4x 1 + gh(4t)2 2(4x)2 (cos θ − 1) 

 maka akan dicari nilai eigen dari matriks G.

|G − λI| = 0 memberikan

(1 + c(cos θ − 1) − λ)2₊√_{c sin}2_{θ = 0}

λ − (1 − c) = c cos θ ± i√c sin θ

dengan c = gh(4t)2

(4x)2 . Perhatikan bahwa λ merupakan bilangan kompleks. Tempat kedudukan λ pada bidang kompleks berupa sebuah elips di bidang kompleks dengan pusat (1 − c, 0), dan panjang sumbu horisontal c dan sumbu vertikal √c, lihat

Gambar 3.5. Agar persamaan beda menghasilkan solusi yang stabil maka haruslah

|λ| ≤ 1, hal ini dipenuhi jika √c ≤ 1.

Re Im

1-c √c

Gambar 3.5: Daerah λ pada bidang kompleks

Setelah diperoleh kondisi agar persamaan beda stabil maka akan diperiksa kekon-sistenan dari persamaan beda (3.5.1) dan (3.5.2). Subtitusikan ekspansi Taylor (2.4.1) dan (2.4.2) ke dalam persamaan beda (3.5.1) sehingga diperoleh :

ηn j + ηt|nj4t + ηtt|jn(4t)2+ ηttt|jn(4t)3+ ... = ηn j − h4t 4x(ux| n j4x + uxxx|nj(4x)3+ ...) + gh(4t)2 (4x)2 (ηxx| n j(4x)2+ ηxxxx|nj(4x)4+ ...)

ηt|nj + hux|nj = 1 6(−gh 2_(4t)2_)u xxx|nj + gh4t 24 ηxxxx| n j(4x)2)

Dari persamaan di atas maka diketahui bahwa suku pertama truncation term berupa suku dispersi. Agar persamaan beda konsisten dengan persamaan yang dihampiri maka pilih 4x, 4t yang membuat suku truncation term sama dengan nol. Suku pertama akan nol jika −gh2_(4t)2 _{− h(4x)}2 _{= 0 atau gh(4t)}2 _{= (4x)}2_{. Sehingga} untuk kedalaman fluida yang berbeda seperti pada persamaan (3.1.3) digunakan partisi yang berbeda juga yakni 4x0 = √gh04t untuk daerah dengan kedalaman

h0 dan 4x1 =

√

gh14t untuk daerah dengan kedalaman h1.

Karena persamaan beda stabil dan konsisten menuju persamaan (2.1.4) dan (2.1.5) maka menurut Teorema Ekuivalensi Lax, persamaan beda ini juga akan konvergen menuju persamaan (2.1.4) dan (2.1.5).

Pada titik-titik diskontinu dimana kedalaman fluida berubah, misalkan pada j=J maka skema numerik yang digunakan menjadi:

ηn+1 J = ηJn− (h0+ h1)4t 2(4x0+ 4x1) (un J+1− unJ−1) + g(h0+ h1)(4t)2 2(4x0+ 4x1)2 (ηn J+1− 2ηJn+ ηnJ−1) (3.5.4) un+1 J = unJ− g4t (4x0+ 4x1) (ηn J+1−ηnJ−1)+ g(h0+ h1)(4t)2 2(4x0+ 4x1)2 (un J+1−2unJ+unJ−1) (3.5.5)

3.6

Simulasi Numerik Menggunakan Metode

Lax-Wendroff

Setelah diformulasikan skema numerik Lax-Wendroff maka untuk mensimulasikan pengaruh 1 balok sebagai relektor digunakan data sebagai berikut: selang daerah [0, 150] dengan waktu pengamatan [0, 22], gravitasi g = 10, frekuensi gelombang

ω = 1 dan dasar berbentuk h(x) =    4, untuk 50 < x < 50 + Lopt = 10 10, untuk lainnya,

Dengan program MATLAB disimulasikan solusi numerik SWE linier. Dengan meng-gunakan syarat awal (3.2.8) dan syarat batas (3.2.9) sama seperti pada metode Lax maka dapat disimulasikan gelombang yang masuk domain dari arah sebelah kiri do-main, dan mengalami proses transmisi dan refleksi seperti pada Gambar 3.6. Hasil yang diperoleh sama dengan jika kita menggunakan metode Lax, hanya saja akurasi untuk waktu (4t) lebih besar.

Gambar 3.6: Hasil simulasi numerik menggunakan metode Lax-Wendroff dengan akurasi O(4x2_{, 4t}2₎