0
PELUANG BERTAHAN PERUSAHAAN ASURANSI DARI KEBANGKRUTAN PADA WAKTU KEDATANGAN KLAIM BERDISTRIBUSI GAMMA(2, 𝜷)
Ali Shodiqin alqinok@gmail.com
Dosen Pendidikan Matematika IKIP PGRI Semarang Jl. Sidodadi Timur Semarang
ABSTRAK
Untuk mengantisipasi kemungkinan adanya kerugian keuangan yang mungkin timbul akibat adanya kejadian-kejadian yang tidak diharapkan, maka seseorang biasanya mengikuti program asuransi. Para pemegang polis pada program asuransi di beri berkewajiban membayar sejumlah uang kepada perusahaan asuransi pada tiap periode tertentu yang disebut premi asuransi dan perusahaan asuransi memberikan jaminan terhadap resiko yang terjadi sesuai kesepakatan berupa sejumlah uang yang disebut klaim asuransi. Bila suatu ketika besar modal dan total penerimaan premi lebih kecil dari besar akumulasi dari klaim yang harus dibayarkan, maka perusahaan asuransi mengalami kerugian yang dapat menyebabkan kebangkrutan. Kerugian ini disebabkan jumlah uang klaim yang harus dibayarkan melebihi batas kemampuan dari perusahaan asuransi tersebut. Selanjutnya ingin diketahui peluang bertahan dari kebangkrutan dari proses surplus perusahaan asuransi dengan kedatangan klaim yang berdistribusi gamma (2, 𝛽). Pada perusahaan asuransi, semakin besar modal awal dari perusahaan asuransi maka semakin besar peluang bertahan dan sebaliknya semakin kecil peluang kebangkrutannya. Jika pada prosentase tambahan premi semakin membesar maka peluang bertahan dari kebangkrutan perusahaan asuransi akan semakin besar. Jika laju dari premi semakin mengecil, maka peluang bertahan dari kebangkrutan akan semakin kecil. Suatu perusahaan asuransi akan semakin berkembang baik apabila dimulai dengan modal awal yang cukup.
Kata kunci : proses surplus, klaim, distribusi gamma, peluang bertahan
1. PENDAHULUAN
Untuk mengantisipasi kemungkinan adanya kerugian keuangan yang mungkin timbul akibat adanya kejadian-kejadian yang tidak diharapkan, maka seseorang biasanya mengikuti program asuransi. Hal ini dikarenakan dengan mengikuti program asuransi, kerugian yang diderita oleh orang tersebut akan berkurang dengan adanya jaminan dari perusahaan asuransi berupa uang yang sesuai dengan perjanjian. Perjanjian yang dibuat oleh seseorang yang mengikuti program asuransi dengan perusahaan asuransi disebut polis asuransi, sedangkan orang yang mengikuti program asuransi disebut pemegang polis. Para pemegang polis berkewajiban membayar sejumlah uang kepada perusahaan asuransi pada tiap periode tertentu yang disebut premi asuransi dan perusahaan asuransi memberikan jaminan terhadap resiko yang terjadi sesuai kesepakatan berupa sejumlah uang yang disebut klaim asuransi.
Perusahaan asuransi memperoleh pendapatan dari pembayaran premi para pemegang polis. Di sisi lain, perusahaan harus mengeluarkan biaya untuk pembayaran
1
klaim yang ditagih para pemegang polis. Dengan demikian, pendapatan bersih yang diperoleh perusahaan asuransi akan berubah dari waktu ke waktu, bergantung jumlah penerimaan premi dan jumlah klaim yang dibayarkan.
Bila suatu ketika besar modal dan total penerimaan premi lebih kecil dari besar akumulasi dari klaim yang harus dibayarkan, maka perusahaan asuransi mengalami kerugian yang dapat menyebabkan kebangkrutan. Kerugian ini disebabkan jumlah uang klaim yang harus dibayarkan melebihi batas kemampuan dari perusahaan asuransi tersebut. Selanjutnya ingin diketahui peluang bertahan dari kebangkrutan proses surplus perusahaan asuransi dengan kedatangan klaim yang berdistribusi gamma (2, β).
2. PEMBAHASAN DAN HASIL 2.1 Proses surplus Poisson majemuk
Untuk mempermudah perhitungan matematis, pada penelitian ini digunakan model yang paling sederhana dari proses surplus yaitu model yang mengabaikan investasi
U (t) = u + ct – S (t), t ≥ 0 dan U (0) = u dengan S(t) = 𝑁(𝑡)𝑖=1 𝑋𝑖, 𝑋𝑖> 0 untuk i = 1, 2, 3,……,N(t)
Peubah u adalah modal awal (initial capital), c adalah rata-rata premi yang masuk per satuan waktu, t adalah waktu dan S(t) adalah proses akumulasi klaim (aggregate claims processes). Persamaan terakhir dikenal sebagai model risiko klasik.𝑋𝑖adalah besar klaim ke-i dan N(t) adalah banyaknya klaim yang terjadi dalam interval waktu [0,t]. 𝑋𝑖 dengan i
= 1, 2, 3,……, N(t) adalah peubah acak sebanyak N(t) yang diasumsikan saling bebas dan 𝑋𝑖 juga bebas terhadap N(t). Dengan mengasumsikan bahwa {N(t), t> 0} adalah proses Poisson dengan laju λ, maka 𝑁(𝑡)𝑖=1 𝑋𝑖, t ≥ 0 adalah proses Poisson majemuk, sehingga U (t) merupakan proses stokastik. Buhlmann K [1].
2.2 Peluang Bertahan (Survival)
Berdasarkan definisi peluang bertahan,dimisalkan 𝑈(𝑡) model risiko klasik untuk
waktu kontinu, maka peluang bertahan dalam waktu berhingga adalah ∅ 𝑢 = P(𝑈(𝑡) ≥ 0 𝑈(0) = 𝑢), untuk semua 𝑡 ≥ 0. Klugman et al [5]. Misal peluang
bangkrut dan peluang bertahan (survival) dalam waktu terbatas (finite time) pada suatu perusahaan asuransi sampai waktu 𝑡 dengan modal awal 𝑢 ≥ 0 berturut-turut dinotasikan sebagai 𝜓 𝑢, 𝑡 dan ∅ 𝑢, 𝑡 , maka
2
Jika peluang bangkrut dan peluang bertahan dalam waktu tak terbatas (infinite time) adalah lim𝑡→∞𝜓 𝑢, 𝑡 = 𝜓 𝑢, ∞ = 𝜓 𝑢 dan lim𝑡→∞ ∅ 𝑢, 𝑡 = ∅ 𝑢, ∞ = ∅ 𝑢 , maka
∅ 𝑢 = 1 − 𝜓 𝑢 2.3 Koefisien Penyesuaian (Adjustment Coefficient)
Definisi 2.1
Misal r = 𝜘 solusi positif terkecil untuk persamaan
1 + (1 + 𝜃)µr = E(erx) (2.2) dengan E(erx) adalah fungsi pembangkit momen dari klaim yang berat dengan peubah acak X, jika nilainya ada maka itu dinamakan koefisien penyesuaian. Jika (1+ 𝜃)µ = 𝑐
𝜆,
dengan 𝜃 > 0 maka persamaan (2.2) di atas dapat dinyatakan menjadi 1 + 𝑐
𝜆r = E(e
rx
). Dari persamaan (1+ 𝜃)µ = 𝑐
𝜆 diperoleh nilai c yang merupakan rata-rata premi yang masuk per
satuan waktu yaitu:
c = (1+ 𝜃)𝜆µ (2.3) dengan 𝜃 merupakan prosentase tambahan premi dari nilai harapan klaim.
Dengan f xe( ) 1 F x( ),x 0
sehingga persamaan (2.2) tersebut bisa ditulis sebagai berikut 1 + 𝜃 = 𝑒∞ 𝑟𝑥
0 fe(x)dx
2.4 Batas Atas Peluang Kebangkrutan ( Lundberg’s Inequality) Teorema 2.1
Untuk proses risiko klasik, dimisalkan 𝜓 𝑢 adalah peluang kebangkrutan, dengan u merupakan modal awal, serta r merupakan koefisien penyesuaian, maka untuk r> 0, batas atas peluang kebangkrutan dari proses surplus adalah:
𝜓 𝑢 ≤ 𝑒−𝑟𝑢, 𝑢 ≥ 0 (2.4)
Pertidaksamaan (1.8) dinamakan pertidaksamaan Lundberg’s. Dikson [ 3] 2.5 Premium Loading ( Relative Security Loading)
Sebuah perusahaan asuransi harus mampu menanggung atau membayar semua klaim yang diajukan. Oleh karena itu jumlah premi harus lebih besar dari jumlah klaim. Premium loading (𝜃) adalah prosentase tambahan premi dari nilai harapan klaim. Nilai premium loading (𝜃) ditentukan oleh perusahaan asuransi itu sendiri, seberapa besar nilai tambahan premi yang diperlukan (bisa menanggung semua tuntutan klaim yang terjadi) oleh perusahaan asuransi tersebut. Dari persamaan (2.3) dapat dilihat bahwa semakin besar premium loading (𝜃) maka nilai premi juga akan semakin besar.
3
Misalkan ditentukan batas toleransi maksimal dari peluang kebangkrutan adalah α, berarti: 𝜓 𝑢 ≤ α. Dari persamaan (2.4) dapat ditentukan nilai r sebagai berikut 𝜓 𝑢 ≤ 𝑒−𝑟𝑢, 𝑢 ≥ 0. Dengan 𝑒−𝑟𝑢 = α maka r = −ln α
𝑢 . Dengan menentukan batas toleransi
maksimal dari peluang kebangkrutan (α) dan nilai u diketahui, maka nilai premium loading (𝜃) dapat ditentukan. Dari persamaan (2.2) didapat
1 + (1 + 𝜃)µr = E(erx) 1 + 𝜃 = E(erx) µ 𝑟 − 1 𝜃 = u
{
E(e − ln αu x ) −µ ln 𝛼 − 1}
– 12.5 Persamaan Integral Diferensial Definis 2.2
𝐺 𝑢, 𝑦 adalah peluang terjadinya bangkrut dengan modal awal u dan setelah terjadi bangkrut akan terjadi defisit paling banyak y, di mana 𝑢 ≥ 0 dan 𝑦 ≥ 0. Misalkan akan terjadi surplus setelah terjadi bangkrut antara 0 dan – 𝑦, dengan peluang bangkrut 𝜓 𝑢 . Sehingga dapat ditulis sebagai
𝜓 𝑢 = lim𝑦 →∞𝐺(𝑢, 𝑦) , 𝑢 ≥ 0 (2.5) Teorema 2.2
Misalkan𝑥 besar klaim, dengan sebaran 𝐹(𝑥), maka fungsi 𝐺(𝑢, 𝑦) memenuhi persamaan 𝜕 𝜕𝑢𝐺 𝑢, 𝑦 = 𝜆 𝑐𝐺 𝑢, 𝑦 − 𝜆 𝑐 𝐺 𝑢 − 𝑥, 𝑦 𝑢 0 𝑑𝐹 𝑥 −𝜆 𝑐 𝐹 𝑢 + 𝑦 − 𝐹 𝑢 (2.6) dengan 𝑢 ≥ 0. Teorema 2.3
Jika modal awal 𝑢 = 0, denganbesar klaim𝑥, di mana 𝐹(𝑥)mengikuti sebaran eksponensial, maka fungsi 𝐺(0, 𝑦) memenuhi persamaan
𝐺 0, 𝑦 =𝜆
𝑐 1 − 𝐹(𝑥) 𝑑𝑥 𝑦
0 , dengan 𝑦 ≥ 0 (2.7)
Teorema 2.4
Misalkan ∅(𝑢) peluang bertahan dengan 𝑢 adalah modal awal, maka peluang bertahan (survival) dengan tidak ada modal awal u adalah
𝜙 0 = 𝜃
1 + 𝜃 (2.8) Teorema 2.5
Misalkan ∅(𝑢) peluang bertahan dengan 𝑢 adalah modal awal, maka peluang bertahan terakhir (survival ultimate), yang dinotasikan 𝜙′ 𝑢 adalah
4 𝜙′ 𝑢 =𝜆 𝑐𝜙 𝑢 − 𝜆 𝑐 𝜙 𝑢 − 𝑥 𝑢 0 𝑑𝐹 𝑥 , dengan 𝑢 ≥ 0 (2.9) Klugman et al,[5] 2.6 Menentukan 𝝍 𝟎 dan 𝝓(0)
Dengan menggunakan persamaan (2.5) dan persamaan (2.8) dapat ditentukan nilai 𝜓 0 dan 𝜙(0), yaitu peluang kebangkrutan dengan modal awal 0, dan peluang bertahan dengan modal awal 0. Untuk selanjutnya rataan 𝜙(u) dapat ditentukan.
Teorema 2.6
1 − 𝐹 𝑥 𝑑𝑥 = µ 0∞ Dengan menggunakan persamaan 𝜓 𝑢 = lim
𝑦→∞𝐺(𝑢, 𝑦), jika u = 0 maka: 𝜓 0 = lim 𝑦→∞ G(u,y) = 𝑦→∞lim G(0, y) =𝜆 𝑐 1 − 𝐹 𝑥 𝑑𝑥 = 𝜆µ 𝑐 ∞ 0 = 𝜆µ (1 + 𝜃)𝜆µ= 1 (1 + 𝜃) 𝜙(0) = 1− 𝜓 0 = 1− 1 1+ 𝜃 = 1+ 𝜃−1 1+ 𝜃 = 𝜃 1+ 𝜃 (2.10)
2.7 Menentukan 𝝍′ 𝒖 dan 𝝓′(u)
Misalkan 𝜓 𝑢 dan 𝜙 𝑢 masing-masing merupakan peluang kebangkrutan dan peluang bertahan dengan u adalah modal awal, maka peluang kebangkrutan terakhir dan peluang bertahan terakhir yang masing-masing dinotasikan 𝜓′ 𝑢 dan 𝜙′(u) bisa
ditentukan.
Dari persamaan (2.5) dengan y → ∞ dan persamaan (2.6) didapat persamaan 𝜓′ 𝑢 sebagai berikut: 𝜓′ 𝑢 =𝜆 𝑐𝜓 𝑢 − 𝜆 𝑐 𝜓 𝑢 − 𝑥 𝑑𝐹(𝑥) 𝑢 0 − 𝜆 𝑐 1 − 𝐹 𝑢 (2.11) 𝜓 𝑢 = 1−𝜙 𝑢 𝜓′ 𝑢 = −𝜙′(u) 𝜓′ 𝑢 = 𝜆 𝑐𝜓 𝑢 − 𝜆 𝑐 𝜓 𝑢 − 𝑥 𝑑𝐹 𝑥 𝑢 0 −𝜆 𝑐 [1 − 𝐹( 𝑢 )] 𝜓′ 𝑢 = −𝜆 𝑐𝜙 𝑢 𝜆 𝑐 𝜙 𝑢 − 𝑥 𝑑𝐹(𝑥) 𝑢 0 Jadi 𝑑 𝑑𝑢𝜙 𝑢 = 𝜆 𝑐𝜙 𝑢 − 𝜆 𝑐 𝜙 𝑢 − 𝑥 𝑑𝐹 𝑥 𝑢 0 𝑑 𝑑𝑢𝜙 𝑢 = 𝜆 𝑐𝜙 𝑢 − 𝜆 𝑐 𝑓(𝑥)𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 (2.12) Persamaan 𝜓′ 𝑢 dan 𝜙′(u) disebut persamaan integral-diferensial.
5
2.8 Solusi Analitik Untuk Besar Klaim Menyebar Gamma (2, β)
Selanjutnya akan dicari solusi analitik peluang kebangkrutan dari besar klaim yang diketahui sebarannya. Tidak semua sebaran akan dicari solusi analitiknya. Pada penelitian ini akan dicari solusi analitik dari besar klaim menyebar Gamma (2, β).
Untuk selanjutnya akan dicari solusi analitik peluang kebangkrutan dari besar klaim yang menyebar Gamma (2, β), Sebaran Gamma dengan γ = 2 adalah:
Dengan f(x, γ, β) = 1 𝛤(𝛾)𝛽𝛾 x γ-1 𝑒− 𝑥 𝛽, x > 0 𝛤(2) = 𝑡0∞ 2−1 𝑒 − 𝑡 𝑑𝑡 = 1 Sehingga X~ Gamma(2, β) f(2, β) = β-2𝑥 𝑒− 𝑥 𝛽, x > 0 X~ Gamma (2, β). Dengan fkp f(x) = β-2𝑥𝑒− 𝑥
𝛽 maka nilai harapaanya E(x) = µ = 2β.
Dari persamaan (1+ 𝜃)µ = 𝑐
𝜆 diperoleh nilai c yang merupakan rata-rata premi yang masuk
per satuan waktu dengan sebaran gamma (2, β) maka c = (1+ 𝜃)𝜆µ akan menjadi 𝑐
𝜆 = µ
(1+ 𝜃) = 2β(1+ 𝜃).
Selanjutnya dari persamaan integral-diferensial (2.9) ruas kiri dan ruas kanan dikalikan dengan nilai 𝑐 𝜆 maka didapat : 𝑑 𝑑𝑢𝜙 𝑢 = 𝜆 𝑐𝜙 𝑢 − 𝜆 𝑐 𝑓(𝑥)𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 𝑐 𝜆 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝑓(𝑥)𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 𝑐 𝜆 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝛽 −2 𝑥𝑒− 𝛽𝑥𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 Dengan 𝑐 𝜆 = 2𝛽(1 + 𝜃) di peroleh. 2𝛽 1 + 𝜃 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝛽 −2 𝑥𝑒− 𝑥𝛽𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 (2.13) Selanjutnya dicari nilai 𝜙 𝑢 − 𝑥 0𝑢 𝑥𝑒−
𝑥
𝛽 𝑑𝑥, dengan mensubstitusikan peubah integral di
atas dengan y = u – x, maka didapat:
𝜙 𝑢 − 𝑥 𝑢 0 𝑥 𝑒− 𝑥 𝛽 𝑑𝑥 𝜙 𝑦 𝑢 0 (𝑢 − 𝑦) 𝑒− (𝑢−𝑦) 𝛽 𝑑𝑦
6 𝑒− 𝑢 𝛽 (𝑢 − 𝑦) 𝑢 0 𝜙 𝑦 𝑒 𝑦 𝛽 𝑑𝑦 Misal a = (𝑢 − 𝑦) db = 𝑒 𝑦 𝛽 𝜙 𝑦 𝑑𝑦 da = - dy b = 𝑒 𝑦 𝛽 𝑢 0 𝜙 𝑦 𝑑𝑦 𝑍1 𝛽 (𝑢) = 𝑒 𝑦 𝛽 𝑢 0 𝜙 𝑦 𝑑𝑦 maka persamaan di atas menjadi:
𝜙 𝑢 − 𝑥 𝑢 0 𝑥𝑒− 𝑥 𝛽 𝑑𝑥 = 𝑒− 𝑢 𝛽 𝑢 − 𝑦 𝑍1 𝛽 𝑢 u0 + 𝑍1 𝛽 𝑢 0 (𝑢)𝑑𝑦 = 0 + 𝑒− 𝑢 𝛽 𝑍1 𝛽 𝑢 0 (𝑢)dy = 𝑒− 𝑢 𝛽 𝑍1 𝛽 𝑢 0 (𝑢)dy Persamaan (2.13) menjadi: 2𝛽(1 + 𝜃) 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝛽 −2 𝑥𝑒− 𝛽𝑥𝜙 𝑢 − 𝑥 𝑑 𝑥 𝑢 0 2𝛽 1 + 𝜃 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝛽 −2𝑒− 𝑢𝛽 𝑧1 𝛽 𝑢 0 u dy (2.14) Persamaan (2.14) diturunkan terhadap u:
Misal a = β-2𝑒− 𝑢 𝛽 b = 𝑧1 𝛽 (𝑢) 𝑢 0 𝑑𝑦 a' =− β-3𝑒− 𝑢 𝛽 b' = 𝑧1 𝛽 (𝑢) 2𝛽 1 + 𝜃 𝑑 𝑑𝑢𝜙 𝑢 = 𝜙 𝑢 − 𝛽 −2𝑒− 𝑢𝛽 𝑧1 𝛽 𝑢 0 𝑢 dy Sehingga diturunkan terhadap u:
2𝛽 1 + 𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 = 𝑑 𝑑𝑢𝜙 𝑢 − [−𝛽 −3𝑒− 𝑢𝛽 𝑍1 𝛽 𝑢 0 𝑦 dy + 𝛽−2𝑒− 𝑢𝛽 𝑧1 𝛽 𝑢 ] = 𝑑 𝑑𝑢𝜙 𝑢 − 𝛽 −2𝑒− 𝑢𝛽 𝑧1 𝛽 𝑢 + 𝛽−1 [𝛽−2𝑒− 𝛽𝑢 𝑍1 𝛽 𝑢 0 𝑦 dy] Dari persamaan (2.14) didapat:
2𝛽 1 + 𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 = 𝑑 𝑑𝑢𝜙 𝑢 − 𝛽 −2𝑒− 𝛽𝑢 𝑧1 𝛽 𝑢 +𝛽−1 [𝜙 𝑢 − 2𝛽 1 + 𝜃 𝑑 𝑑𝑢𝜙 𝑢 ]
7 2𝛽 1 + 𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 = − 1 + 2𝜃 𝑑 𝑑𝑢𝜙 𝑢 + 𝛽 −1𝜙 𝑢 −𝛽−2𝑒− 𝑢𝛽 𝑍1 𝛽 𝑢 (2.15) Persamaan (2.15) diturunkan lagi terhadap u:
Misal a = β-2𝑒− 𝑢 𝛽 b= 𝑍1 𝛽 (𝑢)= 𝑒 𝑦 𝛽 𝑢 0 𝜙 𝑢 𝑑𝑦 a' = − β-3𝑒− 𝑢 𝛽 b' = 𝑒 𝑢 𝛽 𝜙 𝑢 maka di dapat: 2𝛽 1 + 𝜃 𝑑 3 𝑑𝑢𝜙 𝑢 = − 1 + 2𝜃 𝑑2 𝑑𝑢𝜙 𝑢 + 𝛽 −1 𝑑 𝑑𝑢𝜙 𝑢 − 𝛽−3𝑒− 𝑢𝛽 𝑍1 𝛽 𝑢 + 𝛽−2𝑒− 𝑢𝛽𝑒 𝑢 𝛽𝜙 𝑢 = − 1 + 2𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 + 𝛽 −1 𝑑 𝑑𝑢𝜙 𝑢 − 𝛽 −2𝜙 𝑢 + 𝛽−1[𝛽−2𝑒− 𝑢𝛽 𝑍1 𝛽 𝑢 ] Dari persamaan (2.15) didapat
2𝛽 1 + 𝜃 𝑑 3 𝑑𝑢𝜙 𝑢 = − 1 + 2𝜃 𝑑2 𝑑𝑢𝜙 𝑢 + 𝛽 −1 𝑑 𝑑𝑢𝜙 𝑢 − 𝛽 −2𝜙 𝑢 +𝛽−1[− 1 + 2𝜃 𝑑 𝑑𝑢𝜙 𝑢 + 𝛽 −1𝜙 𝑢 − 2𝛽 1 + 𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 ] = − 3 + 4𝜃 𝑑 2 𝑑𝑢𝜙 𝑢 − 𝛽 −12𝜃 𝑑 𝑑𝑢𝜙 𝑢 + (𝛽 −2 − 𝛽−2)𝜙 𝑢 2𝛽 1 + 𝜃 𝑑 3 𝑑𝑢𝜙 𝑢 = − 3 + 4𝜃 𝑑2 𝑑𝑢𝜙 𝑢 − 𝛽 −12𝜃 𝑑 𝑑𝑢𝜙 𝑢 Sehingga persamaan terakhir bisa ditulis:
2𝛽 1 + 𝜃 𝑑 3 𝑑𝑢𝜙 𝑢 + 3 + 4𝜃 𝑑2 𝑑𝑢𝜙 𝑢 + 𝛽 −12𝜃 𝑑 𝑑𝑢𝜙 𝑢 = 0 𝑑3 𝑑𝑢𝜙 𝑢 + 3 + 4 𝜃 2𝛽 1 + 𝜃 𝑑2 𝑑𝑢𝜙 𝑢 + 𝜃 𝛽2 1 + 𝜃 𝑑 𝑑𝑢𝜙 𝑢 = 0 Dengan memisalkan 𝑑 2
𝑑𝑢𝜙 𝑢 = 𝑝 sehingga persamaan di atas menjadi
𝑝2+ 3 + 4𝜃
2𝛽 1 + 𝜃 p +
𝜃
𝛽2 1 + 𝜃 = 0
diperoleh nilai p1 dan p2 sebagai berikut:
p1 = −3−4𝜃+ 8𝜃+9 4𝛽 (1+ 𝜃) dan p2 = −3−4𝜃− 8𝜃+9 4𝛽 (1+ 𝜃) jadi 𝑑 𝑑𝑢𝜙 𝑢 = A1𝑒 −(−𝑝1)𝑢 + A2 𝑒−(−𝑝2)𝑢 (2.16)
8 0 20 40 60 80 100 120 140 0.80 0.85 0.90 0.95 1.00 Modal Awal u_ untuk 𝑑 𝑑𝑢𝜙 0 = A1+ A2
dari persamaan (2.10) dan (2.13) didapat: 𝑑
𝑑𝑢𝜙 0 = 𝜙 0 2𝛽 (1+ 𝜃) = 𝜃 (1+ 𝜃 ) 2𝛽 (1+ 𝜃) = 𝜃 2𝛽 (1+ 𝜃)2 jadi diperoleh A1+ A2 = 𝜃 2𝛽 (1+ 𝜃)2 maka A2 = 𝜃 2𝛽 (1+ 𝜃)2 −A1
selanjutnya persamaan (2.16) diintegralkan diperoleh: 𝜙 𝑢 = 𝐴1 p1 𝑒 −(−𝑝1)𝑢+ 𝐴2 p2 𝑒 −(−𝑝2)𝑢+ A 3
karena 𝜙(∞) = 1 maka didapat A3 = 1
untuk u = 0 persamaan tersebut menjadi
𝜙(0)= 𝐴1 p1 + 𝐴2 p2 + 1 𝜃 (1+ 𝜃) = 𝐴1 p1 + 𝐴2 p2 + 1 A1(𝑝1− 𝑝2) = 𝑝1𝑝2 (1+ 𝜃)+ 𝜃𝑝1 2𝛽 (1+ 𝜃)2
Maka didapat nilai A1dan A2 sebagai berikut:
A1 = 1 𝑝1−𝑝2 ( 𝑝1𝑝2 (1+ 𝜃)+ 𝜃𝑝1 2𝛽 (1+ 𝜃)2 ) A2 = 𝜃 2𝛽 (1+ 𝜃)2− 1 𝑝1−𝑝2 ( 𝑝1𝑝2 (1+ 𝜃)+ 𝜃𝑝1 2𝛽 (1+ 𝜃)2 )
maka diperoleh 𝜙(u) = 1 + 𝐴1
p1 𝑒
𝑝1𝑢 + 𝐴2 p2 𝑒
𝑝2𝑢
Jadi solusi analitik peluang bertahan dari kebangkrutan untuk besar klaim menyebar Gamma (2, β) adalah 𝜙(u) = 1 + 𝐴1
p1 𝑒 𝑝1𝑢 + 𝐴2 p2 𝑒 𝑝2𝑢 dengan p1 = −3−4𝜃+ 8𝜃+9 4𝛽 (1+ 𝜃) dan p2 = −3−4𝜃− 8𝜃+9
4𝛽 (1+ 𝜃) dan 𝜃 adalah prosentase tambahan
premi dari nilai harapan klaim.
2.9 Simulasi Peluang Bertahan pada klaim berdistribusi gamma (2, 𝜷) dengan Software Mathematica
A. Simulasi peluang bertahan pada klaim berdistribusi gamma (2, 𝜷) dengan Software Mathematica
1. Simulasi peluang bertahan dengan memilih θ = 1 , 𝛽 = 5
Untuk simulasi peluang bertahan dari kebangkrutan dengan modal awal dari 0 sampai 100 satuan, diperoleh grafik dan tabel sebagai berikut.
9
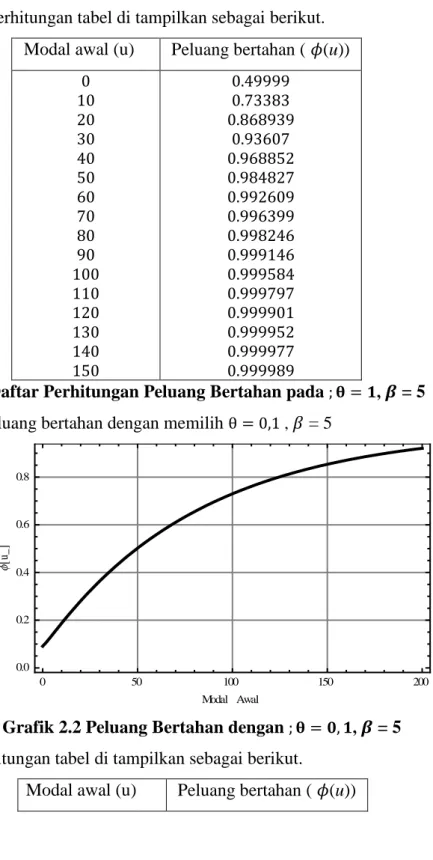
Grafik 2.1 PeluangBertahandengan ; 𝛉 = 𝟏, 𝛽 = 5 Dalam perhitungan tabel di tampilkan sebagai berikut.
Modal awal (u) Peluang bertahan ( 𝜙(u)) 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 0.49999 0.73383 0.868939 0.93607 0.968852 0.984827 0.992609 0.996399 0.998246 0.999146 0.999584 0.999797 0.999901 0.999952 0.999977 0.999989
Tabel 2.1 Daftar Perhitungan Peluang Bertahan pada ; 𝛉 = 𝟏, 𝜷 = 5 2. Simulasi peluang bertahan dengan memilih θ = 0,1 , 𝛽 = 5
Grafik 2.2 Peluang Bertahan dengan ; 𝛉 = 𝟎, 𝟏, 𝜷 = 5 Dalam perhitungan tabel di tampilkan sebagai berikut.
Modal awal (u) Peluang bertahan ( 𝜙(u))
0 50 100 150 200 0.0 0.2 0.4 0.6 0.8 Modal Awal u_
10 0 20 40 60 80 100 120 140 160 180 200 0.090909 0.2805811 0.4368893 0.5592526 0.6550265 0.729989 0.788662 0.834586 0.87053 0.898664 0.920684
Tabel 2.2 Daftar Perhitungan Peluang Bertahan pada 𝛉 = 𝟎, 𝟏, 𝜷 = 5
Dari grafik dan tabel perhitungan diperoleh bahwa semakin modal awal bertambah maka peluang bertahan semakin besar, dan pada peluang bertahan semakin prosentase tambahan premi (𝛉) membesar maka peluang bertahan akan semakin besar. Pada 𝛽 membesar berarti berarti laju premi semakin mengecil sehingga peluang bertahan agak mengecil.
3. SIMPULAN DAN SARAN 3.1 SIMPULAN
1. Solusi analitik dari peluang bertahan dari kebangkrutan pada proses surplus apabila kedatangan klaim berdistribusi gamma (2, 𝛽) yaitu:
𝜙(u) = 1 + 𝐴1 p1 𝑒 𝑝1𝑢 + 𝐴2 p2 𝑒 𝑝2𝑢 , 𝑢 ≥ 0 dengan: A1 = 1 𝑝1−𝑝2 ( 𝑝1𝑝2 (1+ 𝜃)+ 𝜃𝑝1 2𝛽 (1+ 𝜃)2 ) , p1 = −3−4𝜃+ 8𝜃+9 4𝛽 (1+ 𝜃) A2 = 𝜃 2𝛽 (1+ 𝜃)2− 1 𝑝1−𝑝2 ( 𝑝1𝑝2 (1+ 𝜃)+ 𝜃𝑝1 2𝛽 (1+ 𝜃)2 ) , p2 = −3−4𝜃− 8𝜃+9 4𝛽 (1+ 𝜃)
Dimana 𝜃 merupakan prosentase tambahan premi dari nilai harapan klaim. 𝛽 merupakan seperlaju dari premi, u adalah modal awal, dan
𝜙 𝑢 adalah peluang bertahan.
2. Semakin besar modal awal dari perusahaan asuransi maka semakin besar peluang bertahan dari kebangkrutannya, sehingga suatu perusahaan asuransi akan semakin berkembang baik apabila dimulai dengan modal awal yang cukup. 3. Jika pada prosentase tambahan premi (θ) semakin membesar maka peluang
bertahan dari kebangkrutan akan semakin besar.
4. Jika 𝛽 semakin membesar artinya laju dari premi semakin mengecil, maka peluang peluang bertahan perusahaan dari kebangkrutan akan mengecil.
3.2 Saran
Peluang bertahan dari kebangkrutan pada perusahaan asuransi yang dipengaruhi oleh pendapatan dari penerimaan premi serta klaim-klaim yang harus
11
dibayarkan oleh perusahaan asuransi yang menyebar secara gamma (2, 𝛽) . Oleh karena itu selanjutnya dapat dikembangkan pada sebaran klaim yang menyebar yang lain.
DAFTAR PUSTAKA
Shodiqin A, Najmah, Buchori A. 2012. Peluang Kebangkrutan Perusahaan Asuransi Dimana Waktu Antar Kedatangan Klaim Berdistribusi Eksponensial. Semarang : IKIP PGRI Semarang.
Shodiqin A, Purnaba, Retno. 2009. Studi Strategi untuk Mendapatkan Besar Dividen yang Optimal dari Proses Surplus. Bogor : IPB.
Buhlmann K. 1990. Mathematical Method in Risk Theory. Berlin: Spring-Verlag.
Dickson DCM, Howard WR. 2004. Some Optimal Dividends Problems. Astin Bulletin Vol. 34 No. I, 49 - 74.
Dickson DCM. 2005. Insurance Risk and Ruin. Cambridge: Cambridge University Press. Dickson DCM, Hipp C. 2007. On The Time to Ruin for Erlang(2) Risk Processes.
Insurance Mathematics and Ekonomics. Vol. 29, 333-334
Ghahramani S. 2000. Fundamentals of Probability. New Jersey: Prentice Hall, Inc
Grimmett GR, Strizaker DR. 2001. Probability and Random Processes.Ed. ke-3.Oxford: Clarendon Press.
Klugman SA, Panjer HH, Willmot GE. 1998. Loss Models – from data to decisions. New York : John Wiley.