SKRIPSI ESTIMASI PARAMETER DISTRIBUSI WEIBULL 2 PARAMETER MENGGUNAKAN METODE LINEARISASI (METODE DERET TAYLOR)

(1)

SKRIPSI

ESTIMASI PARAMETER

DISTRIBUSI WEIBULL 2 PARAMETER MENGGUNAKAN

METODE LINEARISASI (METODE DERET TAYLOR)

JULISTRIA PUTRI G1D011014

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS MATARAM

(2)

i

SKRIPSI

ESTIMASI PARAMETER

DISTRIBUSI WEIBULL 2 PARAMETER MENGGUNAKAN

METODE LINEARISASI (METODE DERET TAYLOR)

THE ESTIMATION OF

2 PARAMETER WEIBULL DISTRIBUTION PARAMETER

USING LINEARIZATION METHOD

(TAYLOR SERIES METHOD)

Diajukan untuk memenuhi salah satu syarat untuk memperoleh gelar Sarjana Sains dalam Ilmu Matematika

JULISTRIA PUTRI G1D011014

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS MATARAM

(3)

ii

PERNYATAAN

Dengan ini saya menyatakan bahwa didalam skripsi ini tidak terdapat karya yang pernah diajukan untuk memperoleh gelar kesarjanaan di suatu perguruan tinggi dan sepanjang pengetahuan saya juga tidak terdapat karya atau pendapat yang pernah dituliskan atau dipublikasikan oleh orang lain, kecuali yang secara tertulis diacu dalam naskah ini dan disebutkan dalam daftar pustaka.

Mataram, Maret 2015

(4)

iii

HALAMAN PENGESAHAN

SKRIPSI

ESTIMASI PARAMETER DISTRIBUSI WEIBULL 2 PARAMETER MENGGUNAKAN

METODE LINEARISASI (METODE DERET TAYLOR)

Julistria Putri G1D011014

Telah dipertahankan di depan Tim Komisi Penguji pada tanggal 7 April 2015

Susunan KOMISI PENGUJI 1. Mustika Hadijati, M.Si.

(Pembimbing I)

2. Desy Komalasari, M.Si. (Pembimbing II)

3. Lailia Awalushaumi, M.Si. (Penguji)

Mengesahkan, Dekan FMIPA Universitas Mataram,

Prof. Ir. I Made Sudarma, M. Sc., Ph. D. NIP. 19600606 198503 1 032

a.n Ketua Program Studi Matematika, Sekretaris

(5)

iv

PRAKATA

Segala puja dan puji bagi Allah SWT yang telah memberikan limpahan rahmat, hidayah, dan kasih sayang-Nya, sehingga penulis dapat menyelesaikan skripsi dengan judul Estimasi Parameter Distribusi Weibull 2 Parameter Menggunakan Metode Linearisasi (Metode Deret Taylor). Dalam kesempatan ini, penulis juga banyak mengucapkan terima kasih kepada semua pihak yang telah membantu dalam pengerjaan skripsi ini, yaitu kepada :

1. Kedua orang tua tercinta, atas kegigihan, perjuangan, air mata dalam doa, dan kasih sayangnya selama ini.

2. Prof. Ir. I Made Sudarma, M.Sc., Ph.D., selaku Dekan FMIPA Universitas Mataram yang telah memberikan kesempatan untuk melaksanakan skripsi ini. 3. Mamika Ujianita Romdhini, M.Si., selaku Sekretaris Program Studi

Matematika FMIPA Universitas Mataram.

4. Mustika Hadijati, M.Si, selaku Dosen Pembimbing I, yang telah meluangkan banyak waktunya untuk memberikan bimbingan, arahan, dan bantuan tak terhingga kepada penulis, sehingga skripsi ini dapat terselesaikan.

5. Desy Komalasari, M.Si., selaku Dosen Pembimbing II, atas keikhlasan mengarahkan dan membimbing penulis dalam menyusun skripsi ini dari awal hingga akhir.

6. Lailia Awalushaumi, M.Si., selaku Dosen Penguji atas kesediaannya menguji tugas akhir ini dan selaku Dosen Pembimbing Akademik, atas motivasi dan dukungan untuk melaksanakan skripsi ini.

7. Para dosen dan staf tata usaha di Program Studi Matematika, atas ilmu dan bantuannya. Semoga jasa bapak dan ibu tercatat sebagai amal dan pahala di sisi-Nya

(6)

v

9. Sahabat pejuang skripsi My Cebong (Jannah, Asmita, Fauziah, Indi, Aya’, Uyung, Qori’, Puji) dan seluruh teman-teman math’11 unyu’ yang telah banyak membantu dan selalu mendukung serta memberikan nasehat.

10. Buat Dinda Family dan Rajib Maulana, atas bantuan dan dukungannya.

11. Buat seluruh GAMATIKA FMIPA Universitas Mataram yang selalu memberi semangat dan motivasi.

12. Semua pihak yang membantu dan memberikan dukungan dalam proses penyelesaian tugas akhir ini.

Penulis mengharapkan kritik dan saran yang bersifat membangun demi kesempurnaan skripsi ini. Semoga bantuan dan bimbingan yang telah diberikan kepada penulis selama penyelesaian skripsi ini mendapat balasan setimpal dari Allah SWT dan dapat memberi manfaat bagi pembacanya. Amin.

Mataram, Maret 2015 Penulis

(7)

vi

DAFTAR ISI

HALAMAN JUDUL ... i

PERNYATAAN ... ii

HALAMAN PENGESAHAN ... iii

PRAKATA ... iv

DAFTAR ISI ... vi

DAFTAR GAMBAR ... viii

DAFTAR TABEL ... ix

DAFTAR LAMPIRAN ... x

INTI SARI ... xi

ABSTRACT ... xii

BAB I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Rumusan Masalah ... 2

1.3 Tujuan Penelitian ... 2

1.4 Manfaat Penelitian ... 3

1.5 Batasan Masalah ... 3

BAB II TINJAUAN PUSTAKA 2.1 Analisis Regresi ... 4

2.2 Regresi Nonlinear ... 4

2.3 Metode Kuadrat Terkecil dalam Kasus Nonliear ... 5

2.4 Metode Linearisasi (Metode Deret Taylor) ... 6

2.5 Asumsi Regresi Nonlinear ... 8

2.6 Distribusi Weibull ... 10

2.6.1 Uji Mann untuk Distribusi Weibull ... 10

(8)

vii BAB III METODE PENELITIAN

3.1 Alat ... 13

3.2 Sumber Data dan Variabel Penelitian ... 13

3.3 Langkah-Langkah Penelitian ... 13

BAB IV HASIL DAN PEMBAHASAN 4.1 Metode Kuadrat Terkecil Nonlinear ... 17

4.2 Metode Linearisasi (Metode Deret Taylor) ... 20

4.3 Aplikasi pada Data ... 21

4.3.1 Uji Distribusi Data ... 22

4.3.2 Penentuan Nilai Dugaan Parameter Awal ... 22

4.3.3 Estimasi Parameter Distribusi Weibull 2 Parameter dengan Metode Linearisasi (Metode Deret Taylor) ... 24

4.3.4 Perhitungan Mean dan Variansi ... 40

4.4 Interpretasi Model Regresi Nonlinear ... 41

BAB V KESIMPULAN DAN SARAN 5.1 Kesimpulan ... 43

5.2 Saran ... 44

(9)

viii

DAFTAR GAMBAR

Halaman Gambar 3.1 Bagan langkah-langkah penelitian. 14 Gambar 3.2 Bagan aplikasi data pada proses estimasi dengan metode

linearisasi (metode deret Taylor). 15

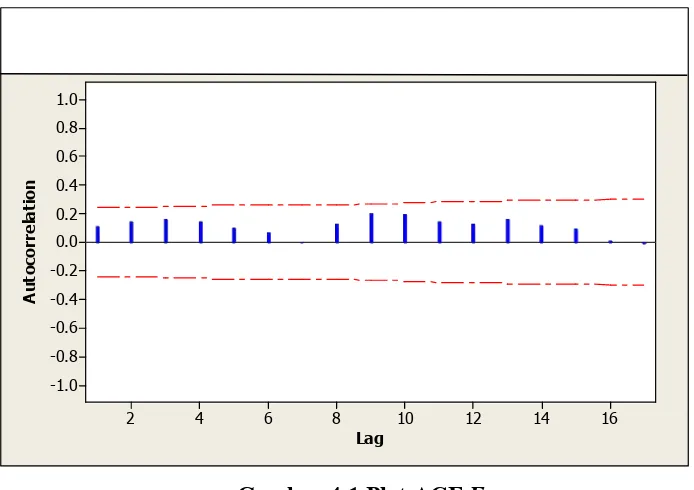
Gambar 4.1 Plot ACF error. 37

Gambar 4.2 Plot kenormalan error. 38 Gambar 4.3 Plot pencaran titik nilai variabel independen dengan

nilai error. 39

Gambar 4.4 Grafik data kecepatan angin terbesar terhadap peluang

(10)

ix

DAFTAR TABEL

Halaman

Tabel 4.1 Ringkasan hasil iterasi. 34

Tabel 4.2 Ringkasan hasil iterasi menggunakan SAS 9. 35

Tabel 4.3 Analisis Varian (ANOVA). 35

(11)

x

DAFTAR LAMPIRAN

Lampiran 1 : Data kecepatan angin terbesar perbulan di wilayah Nusa Tenggara Barat tahun 2009-2014.

Lampiran 2 : Perhitungan uji Mann untuk kecepatan angin. Lampiran 3 : Perhitungan pendugaan nilai awal parameter.

Lampiran 4 : Hasil estimasi parameter menggunakan program SAS 9. Lampiran 5 : Pemeriksaan asumsi regresi nonlinear.

(12)

xi

ESTIMASI PARAMETER DISTRIBUSI WEIBULL 2 PARAMETER

MENGGUNAKAN METODE LINEARISASI (METODE DERET TAYLOR)

JULISTRIA PUTRI

INTISARI

Estimasi parameter adalah sebuah prosedur untuk mencari parameter dari sebuah model yang paling cocok pada suatu data pengamatan yang ada. Dalam mengestimasi parameter distribusi Weibull 2 parameter, probability density function (pdf) dapat dilihat sebagai suatu model persamaan regresi dengan bentuk persamaan nonlinear, sehingga estimasi parameter distribusi sama artinya dengan estimasi parameter regresi nonlinear. Metode yang digunakan untuk mengestimasi parameter model regresi nonlinear adalah metode linearisasi (metode deret Taylor). Tujuan penelitian ini adalah melakukan estimasi dan menerapkannya dalam memodelkan data kecepatan angin terbesar per bulan di wilayah NTB. Berdasarkan hasil analisis yang telah dilakukan, estimasi parameter regresi nonlinear menggunakan metode linearisasi (metode deret Taylor) diperoleh nilai parameter = 4.4779 dan = 17.7524 dengan nilai MSE = 0.00269 dan = 0.99216 . Didapatkan model dengan persamaan regresi nonlinear sebagai berikut

=_17.75244.4779_. . _{− 17.7524} .

(13)

xii

THE ESTIMATION OF 2 PARAMETER WEIBULL DISTRIBUTION PARAMETER

USING LINEARIZATION METHOD (TAYLOR SERIES METHOD)

JULISTRIA PUTRI

ABSTRACT

Parameter estimation is a procedure to find the parameters of a model that is best suited to an existing observational data. In estimating parameters the Weibull distribution 2 parameters, probability density function (pdf) an be seen as a regression model with the form of nonlinear equations, so the distribution parameter estimation synonymous with nonlinear regression parameter estimates. The method used to estimate the parameters of nonlinear regression model is a method of linearization (Taylor series method). The purpose of this study was to estimate and implement them in modeling largest wind speed data per month in NTB. Based on analysis result that have been done, a nonlinear regression parameter estimation using linearization method (Taylor series method) obtained value of the parameter = 4.4779 and = 17.7524 with MSE = 0.00269 and

= 0.99216. Obtained models with nonlinear regression equation as follows

=_17.75244.4779_. . _{− 17.7524}

.

(14)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Estimasi parameter adalah sebuah prosedur untuk mencari parameter dari sebuah model yang paling cocok pada suatu data pengamatan yang ada. Masalah estimasi menjadi hal yang penting yang dikaji dalam suatu distribusi tertentu.

Dalam statistika, distribusi probabilitas dapat dibagi dalam dua jenis distribusi, yaitu distribusi variabel acak kontinu dan distribusi variabel acak diskrit. Salah satu distribusi variabel acak kontinu adalah distribusi Weibull 2 parameter yang merupakan pengembangan dari dua distribusi yaitu distribusi Rayleigh dan distribusi Eksponensial. Distribusi Weibull 2 parameter ini banyak digunakan dalam merepresentasikan kecepatan dan distribusi angin, dimana angin sebagai sumber energi yang tidak dapat dikendalikan keberadaannya dan memiliki fluktuasi yang dapat didekati dengan pendekatan probabilistik. Selain itu juga karena cakupannya yang begitu luas dalam keserbagunaan, fleksibilitas dan kemanfaatannya dalam menggambarkan variasi kecepatan angin (Olaofe, 2012). Distribusi lain yang mempunyai aplikasi yang sama dalam merepresentasikan data kecepatan angin adalah distribusi Rayleigh, distribusi Eksponensial, distribusi Gamma, distribusi Lognormal dan distribusi Gaussian.

(15)

2

Dalam mengestimasi parameter model regresi nonlinear, salah satu metode yang biasa digunakan adalah kuadrat terkecil nonlinear. Metode kuadrat terkecil nonlinear merupakan metode kuadrat terkecil dalam kasus (intrinsik) nonlinear, yang digunakan untuk menduga parameter model dengan cara meminimumkan jumlah kuadrat sisaan. Secara konseptual metode kuadrat terkecil nonlinear sama dengan metode kuadrat terkecil pada model regresi linear, namun pada kenyataannya metode kuadrat terkecil nonlinear tidak mudah untuk dapat dikerjakan secara analitik, maka diperlukan metode untuk mengestimasi parameter model regresi nonlinear yaitu salah satunya adalah metode linearisasi (metode deret Taylor).

Berdasarkan uraian di atas, maka dalam penelitian ini dilakukan suatu kajian mengenai estimasi parameter distribusi Weibull 2 parameter dengan metode linearisasi (metode deret Taylor) dan memodelkan data kecepatan angin terbesar per bulan di Nusa Tenggara Barat.

1.2 Rumusan Masalah

Berdasarkan uraian latar belakang penelitian maka dapat dirumuskan masalah sebagai berikut:

1. Bagaimana mengestimasi parameter distribusi Weibull 2 parameter dengan menggunakan metode linearisasi (metode deret Taylor)?

2. Bagaimana penerapannya dalam memodelkan data kecepatan angin terbesar per bulan di Nusa Tenggara Barat yang berdistribusi Weibull 2 parameter?

1.3 Tujuan

Berdasarkan rumusan masalah di atas, penelitian ini memiliki tujuan sebagai berikut:

(16)

3

2. Menerapkannya dalam memodelkan data kecepatan angin terbesar per bulan di Nusa Tenggara Barat yang berdistribusi Weibull 2 parameter.

1.4 Manfaat

Hasil penelitian ini diharapkan dapat memberi manfaat untuk menambah wawasan tentang regresi nonlinear khususnya dalam mengestimasi parameter distribusi Weibull 2 parameter dengan menggunakan metode linearisasi (metode deret Taylor) dan menambah referensi apabila ingin mengembangkan ilmu regresi.

1.5 Batasan Masalah

(17)

BAB II

TINJAUAN PUSTAKA

2.1 Analisis Regresi

Analisis regresi adalah teknik analisis yang mencoba menjelaskan bentuk hubungan antara variabel-variabel yang mendukung sebab akibat. Prosedur analisisnya didasarkan atas distribusi probabilitas bersama variabel-variabelnya. Secara umum, dapat dikatakan bahwa analisis regresi berkenaan dengan mempelajari ketergantungan suatu variabel, yaitu variabel tak bebas (dependent variable) pada satu atau lebih variabel yang lain, yaitu variabel bebas

(independent variable) dengan maksud menduga dan atau meramalkan nilai rata-rata hitung (mean) atau rata-rata (populasi) dari variabel tak bebas (Firdaus, 2004).

Tujuan utama dari analisis regresi adalah mendapatkan dugaan

(estimation) dari suatu variabel dengan menggunakan variabel lain yang diketahui. Analisis regresi dapat dibedakan menjadi dua jenis yaitu regresi linear dan regresi nonlinear. Namun yang dibahas dalam penelitian ini adalah regresi nonlinear.

2.2 Regresi Nonlinear

Regresi nonlinear mengandung parameter yang bersifat nonlinear, dimana turunan persamaan terhadap salah satu parameter adalah fungsi dari parameter lain (masih mengandung parameter itu sendiri). Model regresi nonlinear merupakan bentuk hubungan antara variabel tak bebas (dependent variable)

dengan variabel bebas (independent variable) yang tidak linear dalam parameter. Secara umum model nonlinear ditulis sebagai berikut:

= ( ; ) + (2.1)

(18)

5

2.3 Metode Kuadrat Terkecil dalam Kasus Nonlinear

Model nonlinear yang dipostulat dengan bentuk:

= ( ; ) + (2.2)

dengan asumsi ( ) = 0, ( ) = dan ~ (0, ) maka jumlah kuadrat sisa untuk model nonlinear di atas didefinisikan sebagai berikut:

( ) = ∑ { − ( ; )} (2.3)

(Gallant, 1987).

Bila terdapat sebanyak n amatan data, maka persamaan (2.2) menjadi

= , , … , ; , , … , + (2.4)

untuk = 1,2, … , dapat dituliskan dalam bentuk alternatifnya

= ( ; ) + (2.5)

dengan adalah galat ke = 1,2, … , dengan asumsi kenormalan galat dapat dituliskan sebagai ∼ ( , ).

= _⋮ ∼ ( , )

(Karim, 2009).

Nilai dugaan kuadrat terkecil bagi akan dilambangkan dengan . Nilai dugaan ini adalah nilai yang meminimumkan ( ). Untuk mendapatkan nilai dugaan kuadrat terkecil yaitu dengan mendiferensialkan persaman (2.3) terhadap , sehingga mempunyai bentuk

(19)

6

∑ { − ( ; )} ( ; ) = 0 (2.7)

Persamaan (2.7) disebut persamaan normal untuk model nonlinear yang merupakan hasil estimasi parameter (Draper dan Smith, 1992).

Model nonlinear seringkali tidak dapat diselesaikan secara analitik, maka perlu dilakukan metode iterasi untuk menduga parameter di dalam suatu sistem nonlinear.

Pada sebagian masalah nonlinear, cara yang sering dilakukan dan ternyata berhasil adalah menuliskan persamaan normal secara terperinci dan mengembangkan suatu teknik iteratif untuk memecahkannya bergantung pada persamaan normalnya dan metode iterasi yang digunakan dalam memperoleh taksiran parameter, diantaranya adalah metode linearisasi (metode deret Taylor), metode turunan terjal (Stepest descent) dan metode jalan tengah Marquadrt (Marquadrt’s compromise).

2.4 Metode Linearisasi (Metode Deret Taylor)

Metode linearisasi menggunakan hasil dari kuadrat terkecil dalam beberapa tahap. Misalkan model yang ditentukan berbentuk:

= ( ; ) + (2.8)

(20)

7

Bentuk deret Taylor adalah sebagai berikut:

( ) = ( ) + ( )( − ) + ( )_! ( − ) + ⋯

+ ( )( )_! ( − ) (2.9)

Bila dilakukan penguraian deret Taylor bagi ( ; ) disekitar titik = ( , , … , ) dan penguraian sampai turunan pertama, maka dapat dikatakan bahwa bila dekat pada maka :

Maka persamaan (2.10) dapat dituliskan sebagai berikut

− = ∑ + (2.11)

(21)

8 demikian vektor akan meminimumkan jumlah kuadrat galat.

( ) = ∑ − ( , ) − ∑ (2.15)

(Karim, 2009).

Proses iteratif ini dilanjutkan terus sampai solusi yang diperoleh konvergen, dengan kata lain sampai langkah iterasi dan ( + 1) berlaku

( )− / < , = 1,2, … , (2.16) Dimana adalah suatu bilangan positif yang telah ditetapkan sebelumnya (misalnya 0.000001). Pada setiap tahap prosedur iterasi, sebaiknya ( ) dihitung untuk melihat apakah terjadi penurunan nilainya (Draper dan Smith, 1992).

2.5 Asumsi Regresi Nonlinear

(22)

9

1. Asumsi independen

Untuk menguji error independen yaitu dengan melihat plot ACF nya. Jika nilai autokorelasi berada dalam batas selang kepercayaan dari korelasi yang telah ditentukan yaitu −_√ ,_√ , maka korelasi bernilai 0 atau dapat dikatakan tidak ada korelasi, jadi error independen (Bates dan Watts, 1988).

2. Asumsi kenormalan

Uji normalitas bertujuan untuk menguji apakah variabel error berdistribusi normal atau tidak dalam model regresi tersebut. Pengujian normalitas data dilakukan dengan menggunakan metode chart (normal P-Plot). Jika pada grafik normal P-Plot data mengikuti garis lurus maka dapat dikatakan berdistribusi normal (Gujarati, 1999).

3. Asumsi identik

(23)

10

2.6 Distribusi Weibull

Distribusi Weibull telah secara luas digunakan untuk beberapa kejadian acak. Prinsip utilitas distribusi Weibull adalah menghasilkan sebuah pendekatan yang baik untuk hukum probabilitas dari beberapa variabel random (Hines dan Montgomery, 1989).

Probability density function (pdf) yang merupakan suatu fungsi yang menyatakan nilai kemungkinan terjadinya kejadian tertentu dari distribusi Weibull diberikan sebagai:

( | , ) = − ; ≥ 0, , > 0 (2.17)

Cumulative density function (cdf) yang menyatakan probabilitas terjadinya kejadian sampai kejadian tertentu dari distribusi Weibull diberikan sebagai berikut:

( | , ) = ∫ ( | , ) = 1 − − (2.18)

(Rinne, 2009).

Misalkan X variabel acak berdistribusi Weibull dengan parameter dan , maka

( ) = Γ 1 + (2.19)

( ) = Γ 1 + − Γ 1 + (2.20)

(Hines dan Montgomery, 1989).

2.6.1 Uji Mann untuk Distribusi Weibull

Untuk menguji data berdistribusi Weibull, hipotesa dalam uji Mann

(24)

11

: Data berdistribusi Weibull. : Data tidak berdistribusi Weibull.

Wilayah kritis untuk uji ini adalah terima apabila < ( , , ). Nilai F ini diperoleh dari tabel distribusi F.

Uji statistik untuk uji Mann adalah

= ∑

∑ (2.21)

Dimana = dan =

= −

= − 1 − _..

Dengan keterangan sebagai berikut:

= Nilai pendekatan Mann untuk data ke-

= Banyaknya data

= Data ke- (data kecepatan angin yang telah diurutkan dari yang terkecil sampai dengan yang terbesar)

2.7 Matriks

Berikut adalah beberapa definisi terkait dengan matriks.

Definisi 2.1 (Anton dan Rorres, 2004). Sebuah matriks adalah susunan

(25)

12

= _× =

⋯ ⋯ ⋮ ⋮ ⋮ ⋮

⋯

(2.22)

Entri disebut elemen matriks pada baris ke- dan kolom ke- . Jika = , maka matriks tersebut dinamakan matriks bujur sangkar.

Definisi 2.2 (Anton, 2000). Jika adalah sebarang matriks × , maka

transpos , dinyatakan dengan , didefinisikan sebagai matriks × yang didapatkan dengan mempertukarkan baris dan kolom dari yaitu, kolom pertama dari adalah baris pertama dari , kolom kedua dari adalah baris kedua dari , dan seterusnya.

Definisi 2.3 (Anton dan Rores, 2004). Diberikan adalah matriks bujur

sangkar. Jika terdapat matriks yang ukurannya sama sedemikian rupa sehingga

(26)

BAB III

METODE PENELITIAN

3.1 Alat

Alat yang digunakan dalam proses pengolahan data adalah software SAS 9 dan Minitab 16.

3.2 Sumber Data dan Variabel Penelitian

Data yang digunakan dalam penelitian ini merupakan data sekunder, yaitu data kecepatan angin terbesar per bulan di Nusa Tenggara Barat pada tahun 2009 sampai tahun 2014 yang didapatkan dari Badan Meteorologi Klimatologi dan Geofisika (BMKG) Stasiun Klas I Kediri Nusa Tenggara Barat.

Adapun variabel yang digunakan dalam penelitian ini sebagai berikut t adalah waktu (bulan) dan s adalah kecepatan angin terbesar per bulan (knot).

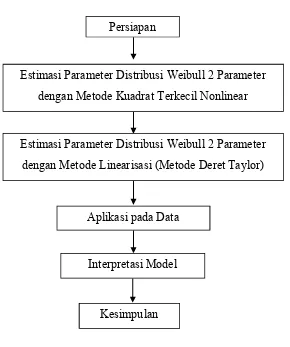
3.3 Langkah-Langkah Penelitian

(27)

14

Dari bagan yang tertera di atas, berikut diberikan penjelasan dari masing-masing tahapan.

1. Persiapan

Pada tahap persiapan ini, dilakukan studi literatur yang memberikan informasi-informasi yang dibutuhkan oleh peneliti sesuai dengan permasalahan yang diangkat.

2. Estimasi Parameter Distribusi Weibull 2 Parameter dengan Metode Kuadrat Terkecil Nonlinear

Pada tahap ini, dilakukan estimasi parameter distribusi Weibull 2 parameter dengan metode kuadrat terkecil nonlinear.

Estimasi Parameter Distribusi Weibull 2 Parameter dengan Metode Kuadrat Terkecil Nonlinear

Kesimpulan Persiapan

Gambar 3.1 Bagan Langkah-Langkah Penelitian

Interpretasi Model Aplikasi pada Data

(28)

15

3. Estimasi Parameter Distribusi Weibull 2 Parameter dengan Metode Linearisasi (metode Deret Taylor)

Pada tahap ini, dilakukan estimasi secara iterasi dengan penguraian deret Taylor, sehingga didapatkan suatu model regresi nonlinear.

4. Aplikasi Pada Data

Berikut diberikan bagan dari aplikasi data pada proses estimasi parameter dengan metode linearisasi (metode deret Taylor).

Gambar 3.2 Bagan Aplikasi Data pada Proses Estimasi dengan Metode Linearisasi (Metode Deret Taylor).

Selesai

Penentuan Nilai Dugaan Parameter Awal Mulai

Data

Iterasi dengan Metode Linearisasi (Metode Deret Taylor)

Perhitungan Mean dan Varian Uji Distribusi Data

Ya

(29)

16

Berikut ini diberikan penjelasan pada bagan di atas:

a. Data yang digunakan adalah data kecepatan angin terbesar per bulan yaitu pada Januari 2009 sampai September 2014 dengan jumlah = 69.

b. Uji Distribusi Data

Pada tahap ini, data kecepatan angin terbesar yang diperoleh akan diuji apakah mengikuti distribusi Weibull 2 parameter atau tidak. Uji yang digunakan adalah uji Mann.

c. Penentuan Nilai Dugaan Parameter Awal

Prosedur pendugaan nonlinear membutuhkan nilai dugaan parameter awal. d. Melakukan iterasi dengan metode linearisasi (metode deret Taylor) sampai

hasilnya konvergen. Apabila proses konvergensinya tercapai, estimasi parameter dapat dimasukkan ke dalam model regresi nonlinear.

e. Perhitungan Mean dan Varian

Pada tahap ini dilakukan proses perhitungan mean dan varian dari model yang didapat.

5. Interpretasi Model Regresi Nonlinear

(30)

BAB IV

HASIL DAN PEMBAHASAN

Persamaan regresi nonlinear dengan bentuk

= ( ; ) +

memiliki nilai parameter yaitu yang akan diestimasi. Pada bab ini dibahas mengenai estimasi parameter regresi nonlinear menggunakan metode linearisasi (metode deret Taylor) dengan menggunakan data kecepatan angin terbesar dan

diolah menggunakan software SAS 9.

4.1 Metode Kuadrat Terkecil Nonlinear

Estimasi parameter distribusi Weibull dapat diketahui dengan metode kuadrat terkecil nonlinear. Untuk mencari nilai estimasi parameter, perlu diketahui

cumulative density function (cdf) Weibull.

Cumulative density function (cdf) dapat diketahui dari probability density function (pdf) Weibull seperti pada persamaan (2.18)

( | , ) = − (4.1)

( ) = −

sehingga

( ) = ∫ ( )

( ) = ∫ −

Misalkan = maka = ( ) , jadi = sehingga

(31)

18

( ) = ∫ exp( )

( ) = ∫ −

( ) = ∫ exp(− )

( ) = 1 − (4.2)

Cumulative density function (cdf) Weibull yang merupakan fungsi

nonlinear dengan bentuk ( ) = 1 − − yang terdiri dari dua

parameter. Digunakan metode kuadrat terkecil untuk meminimumkan jumlah kuadrat sisa dengan terlebih dahulu menaksir parameter pada model tersebut dan selanjutnya menyelesaikan persamaan normalnya dengan metode linearisasi (metode deret Taylor).

Model cumulative density function (cdf) tersebut akan dibentuk kedalam

model probability density function (pdf) sehingga menghasilkan persamaan

regresi nonlinear yaitu sebagai berikut:

= − +

Prosedur estimasi parameter regresi nonlinear menggunakan metode kuadrat terkecil dalam kasus nonlinear adalah sebagai berikut:

1. Membentuk sebuah fungsi dan

= ; , = ∑

= ∑ −

= ∑ − ( ; , ) (4.3)

2. Menentukan turunan dari terhadap dan , kemudian hasil turunannya

disamakan dengan nol

(32)

19

∑ − ; , ; , = 0 (4.4)

= ∑ (−2) − ; , ; ,

∑ − ; , ; , = 0 (4.5)

3. Menentukan turunan terhadap parameter dan

; ,

= − (4.6)

; ,

= − (4.7)

Dari persamaan (4.4) dan (4.5) didapat persamaan normal dari turunan di atas yaitu sebagai berikut:

∑ − −

∑ 1 − − = 0 (4.8)

∑

⎝ ⎛−

⎠ ⎞ −

∑ 1 −

⎝ ⎛−

⎠

⎞ = 0 (4.9)

(33)

20

4.2 Metode Linearisasi (Metode Deret Taylor)

Estimasi parameter menggunakan metode linearisasi (metode deret Taylor) mengharuskan untuk menentukan nilai awal bagi parameter karena berpengaruh terhadap proses iterasi mencapai konvergen atau tidaknya, dan diharapkan akan diperbaiki dalam proses iterasi.

Dilakukan penguraian deret Taylor bagi ; , disekitar nilai awal

dan . Penguraian deret Taylor dilakukan sampai turunan pertama fungsi terhadap parameter-parameternya karena akan dihasilkan grafik berbentuk garis lurus yang merupakan hasil dari penguraian deret Taylor turunan pertama suatu persamaan regresi linear yang dihasilkan.

; , = ; , + ∑ ; , ( − ) ; , ( − ) (4.10)

Bila disederhanakan notasi menjadi

= ; ,

= 1 −

= ; , ; ,

= − −

= ( − )( − )

Dari persamaan (4.10) maka bentuknya menjadi

− = ∑ + (4.11)

(34)

21

Maka taksiran bagi diberikan oleh

= ( ) ( − ) (4.15)

dengan demikian vektor akan meminimumkan jumlah kuadrat galat.

( ) = ∑ − ( , ) − ∑ (4.16)

4.3 Aplikasi Pada Data

Data yang digunakan dalam penelitian ini merupakan data sekunder yang diperoleh dari Badan Meteorologi dan Geofisika (BMKG) Stasiun Klas I Kediri Nusa Tenggara Barat tahun 2009 sampai tahun 2014. Penggunaan data kecepatan angin terbesar per bulan yang digunakan yaitu pada Januari 2009 sampai

September 2014, dengan jumlah sampel = 69. Variabel yang digunakan dalam

(35)

22

4.3.1 Uji Distribusi Data

Data kecepatan angin terbesar per bulan diuji apakah mengikuti distribusi

Weibull atau tidak. Uji yang digunakan adalah uji Mann. Berikut adalah

perhitungan dalam melakukan uji Mann untuk kecepatan angin.

a. Hipotesis

: Data kecepatan angin berdistribusi Weibull. : Data kecepatan angin tidak berdistribusi Weibull.

b. Statistik uji

Statistik uji yang digunakan adalah uji Mann yang mengikuti persamaan

(2.21).

= ∑

∑

= . ( ._{( .} ₎ )

= 1.203010611

c. Kriteria keputusan dan kesimpulan

Jika nilai < = . , . maka diterima dan ditolak.

Berdasarkan perhitungan di atas diperoleh < = 1.203010611 <

1.7721 maka diterima dan dapat disimpulkan bahwa data berdistribusi

Weibull.

4.3.2 Penentuan Nilai Dugaan Parameter Awal

Prosedur pendugaan nonlinear membutuhkan nilai dugaan parameter awal. Nilai-nilai awal itu diharapkan akan diperbaiki dalam proses iterasi sampai menghasilkan solusi yang konvergen. Pada penelitian ini menggunakan garis resisten untuk penentuan nilai dugaan parameter awal. Dibandingkan dengan

menggunakan kuadrat terkecil, garis resisten tidak terpengaruh terhadap outlier

dan menghasilkan jumlah harga mutlak error lebih kecil daripada metode kuadrat

(36)

23

konvergensinya. Jadi dari persamaan (4.2) dapat ditentukan nilai dugaan parameter awalnya.

( ) = 1 −

( ) =

( )=

( ) = −

Misalkan

= _{( )} = ln (−ln(1 − ( )))

dengan ( ) =( . ) yang merupakan peluang kumulatif

=

= b

a = - b

Maka dengan menggunakan persamaan garis resisten didapatkan nilai median (pada Lampiran 3). Median digunakan karena resisten terhadap pencilan, sehingga diperoleh

b =

=

._.

= 4.76502755

a = ( ) ( )

=

. . ( . )

= −13.80869704

Karena = b dan a = - b maka

(37)

24

Dari nilai dan yang diperoleh dapat digunakan sebagai nilai dugaan parameter awal.

4.3.3 Estimasi Parameter Distribusi Weibull 2 Parameter dengan Metode Linearisasi (Metode Deret Taylor)

Dengan bentuk persamaan = − + dapat

mengestimasi parameter distribusi Weibull 2 parameter dengan metode linearisasi (metode deret Taylor), sehingga dari persamaan (4.11), (4.12), (4.13) dan (4.14) didapat iterasinya adalah sebagai berikut

Iterasi 0

Substitusi fungsi kumulatif Weibull dengan adalah kecepatan angin dan nilai

= 4.76502755, = 18.13643312 maka diperoleh yaitu

= ; , = 1 − =

Substitusi peluang distribusi Weibull sehingga diperoleh

(38)

25

Dihitung turunan masing-masing parameter dan sehingga diperoleh

=

Dilakukan perhitungan untuk memperoleh penduga bagi menggunakan

persamaan (4.15) yaitu sebagai berikut

= 0.109035 0.0874322_{0.0874322 0.302567}

( ) = 11.9375_−3.44955 −3.449555_4.301871

( − ) = −0.0736243_−0.139734

= −0.396869237

−0.347144613

Maka akan diperoleh nilai dugaan untuk dan sebagai berikut

= 4.36816_17.7893

Nilai SSE untuk iterasi 0 sebagai berikut

( ) _{= ∑} ₋ _{; ,}

(39)

26

Untuk melihat kekonvergenannya, maka dengan menggunakan persamaan (2.16) diperoleh yaitu

< = . _. . > 0.0001

= |0.08328783| > 0.0001

< = . _. . > 0.0001

= |0.01940732| > 0.0001

Karena nilai error parameter dan lebih dari 0.0001 solusi konvergen belum

diperoleh maka proses iterasi dilanjutkan.

Iterasi 1

= 4.36816 dan = 17.7893 maka diperoleh yaitu

(40)

27

=

= 0.12500331 0.086530683_{0.086530683 0.288648246}

( ) = 10.09456297_{−3.026138011} −3.026138011_4.371596936

( − ) = 0.00998621_0.000553515

= −0.099131414

−0.027799905

= 4.467294932_17.7614886

( ) _{= ∑} ₋ _{; ,}

(41)

28

< = . _. . > 0.0001

= |0.022694017| > 0.0001

< = . _. . > 0.0001

= |0.001562733| > 0.0001

Iterasi 2

= ; , = 1 − =

(42)

29

=

⎣ ⎢ ⎢ ⎢ ⎢

⎡−0.060404447 −0.048681482_0.03687295 _{−0.078131011} −0.049642128

−0.060404447 −0.060404447

⋮ 0.004898339

−0.073888068 −0.048681482 −0.048681482

⋮

−0.092360048⎦⎥

⎥ ⎥ ⎥ ⎤

= 0.119613526 0.085406444_{0.085406444 0.298585561}

( ) = 10.50595147_{−3.005088234} −3.005088234_4.208689447

( − ) = 0.000366045_{−0.001581328}

= 0.008597687

−0.007755319

= 4.47589262_17.75373328

( ) _{= ∑} ₋ _{; ,}

(43)

30

< = . _. . > 0.0001

= |0.0085976867| > 0.0001

< = . _. . > 0.0001

= |0.000436637| > 0.0001

Iterasi 3

(44)

31

=

= 0.119002391 0.085202055_{0.085202055 0.299936891}

( ) = 10.5416075_{−2.997567538} −2.997567538_4.188678382

( − ) = 0.000103089_{−0.000196341}

= 0.001675272

−0.001131426

= 4.477567891_17.75260186

( ) _{= ∑} ₋ _{; ,}

(45)

32

< = . _. . > 0.0001

= |0.000374288| > 0.0001

< = . _. . < 0.0001

= |0.0000637289| < 0.0001

Iterasi 4

= ; , = 1 − =

(46)

33

=

⎣ ⎢ ⎢ ⎢ ⎢

⎡−0.060263821 −0.048782432_{0.036938535 −0.078159704} −0.049508349

−0.060263821 −0.060263821

⋮ 0.005081359

0.074114877 −0.048782432

0.048782432 ⋮

−0.092604979⎦⎥

⎥ ⎥ ⎥ ⎤

= 0.119002391 0.085202055_{0.085202055 0.299936891}

( ) = [10.54859751]

( − ) = [−1.2140858005953805]

=[0.000146916]

= 4.477714808_17.75260186

Diperoleh nilai untuk = 4.477714808 dan = 17.75260186 dengan nilai

SSE untuk iterasi 4 sebagai berikut

( ) _{= ∑} ₋ _{; ,}

(47)

34

< = . _. . < 0.0001

= |0.0000328116| < 0.0001

< = . _. . < 0.0001

= |0.0000637289| < 0.0001

Karena nilai error parameter dan kurang dari 0.0001 solusi konvergen sudah

tercapai maka proses iterasi berhenti.

Tabel 4.1 Ringkasan Hasil Iterasi

Iterasi SSE

0 4.765032755 18.13643312 0.255267494

1 4.36816 17.7893 0.181342626

2 4.467294932 17.7614886 0.180297886

3 4.47589262 17.75373328 0.180280053

4 4.477567891 17.75260186 0.180279595

Dari hasil iterasi yang ke empat telah diperoleh iterasi yang konvergen,

sehingga iterasi dapat berhenti. Didapat untuk nilai parameter = 4.477714808

dan nilai parameter = 17.75260186, dengan nilai MSE sebagai berikut

=

= .

(48)

35

Tabel 4.2 Ringkasan Hasil Iterasi Menggunakan SAS 9

Iterasi SSE

0 4.7650 18.1364 0.2553

1 4.4856 17.7426 0.1803

2 4.4779 17.7523 0.1803

3 4.4779 17.7524 0.1803

Dapat dilihat pada Tabel 4.2 iterasi menunjukan hasil yang hampir sama

dengan tabel 4.1. Jadi diperoleh nilai taksiran parameternya adalah = 4.4779

dan nilai parameter = 17.7524 dengan nilai MSE = 0.00269. Didapatkan

model cumulative density function (cdf) sebagai berikut

( ) = 1 − − _. . (4.17)

Tabel 4.3 Tabel Analisis Varian (ANOVA)

Sumber

Derajat Bebas

(db)

Sum Square (SS)

Mean Square (MS)

F

hitung Pr > F

Model 2 22.8185 11.4093 4240.19 < 0.0001

Error 67 0.1803 0.00269

Total 69 22.9988

Dari tabel di atas, untuk uji ketepatan model dapat dihitung nilai dari koefisien determinasi ( ) dan uji serentak (uji F).

1. Koefisien determinasi ( )

(49)

36

Nilai dari koefisien determinasi ( ) = 0.99216 menunjukan besarnya

keragaman yang mampu dijelaskan oleh model dan dapat dikatakan model yang diperoleh tepat karena keragamannya cukup besar yaitu 99.216%.

2. Uji serentak (uji F)

: Model dikatakan tidak tepat : Model dikatakan tepat

Dari uji F dapat dilihat = 0.0001 < = 0.05 yang berarti ditolak,

maka model yang diperoleh tepat.

Dalam pemeriksaan asumsi model regresi nonlinier, sama halnya dengan melakukan pemeriksaan asumsi model regresi linier sederhana yaitu pemeriksaan

mengenai asumsi error. Asumsi tersebut antara lain asumsi independen, asumsi

kenormalan dan asumsi identik dari error.

1. Asumsi independen

Untuk menguji asumsi autokorelasi dengan nilai error tidak saling

mempengaruhi atau independen, maka digunakan hipotesis berikut

∶ = 0, = 1,2, … ,

(Korelasi antar error bernilai nol atau tidak terdapat korelasi antar error

yang satu dengan error yang lainnya)

∶ ≠ 0, = 1,2, … ,

(Korelasi antar error bernilai tidak sama dengan nol atau terdapat

(50)

37

Dari nilai autokorelasi yang diperoleh (pada Lampiran 4), terlihat bahwa semua nilai autokorelasi berada dalam batas yang telah ditentukan yaitu

−_√ ,_√ dimana batas menunjukan selang kepercayaan dari korelasi, maka

korelasi bernilai 0 jadi hipotesis awal akan diterima.

Selain itu, dapat dilihat pada plot autokorelasi dari error, apabila terdapat

nilai autokorelasi pada tiap lag yang berada di luar batas kepercayaan 95%, maka hipotesis awal akan ditolak. Dari Gambar 4.1 di atas, terlihat bahwa

tidak ada lag yang berada di luar batas garis kepercayaan, sehingga hipotesis

awal diterima. Hal ini menunjukkan bahwa tidak terdapat korelasi antara nilai

error yang satu dengan yang lainnya, sehingga dapat dikatakan bahwa asumsi

autokorelasi error terpenuhi dan error independen.

2. Asumsi normal

Untuk menguji asumsi kenormalan dapat digunakan statistik uji Kolmogorov

-Smirnov dengan hipotesis berikut.

∶ error menyebar mengikuti distribusi normal

(51)

38

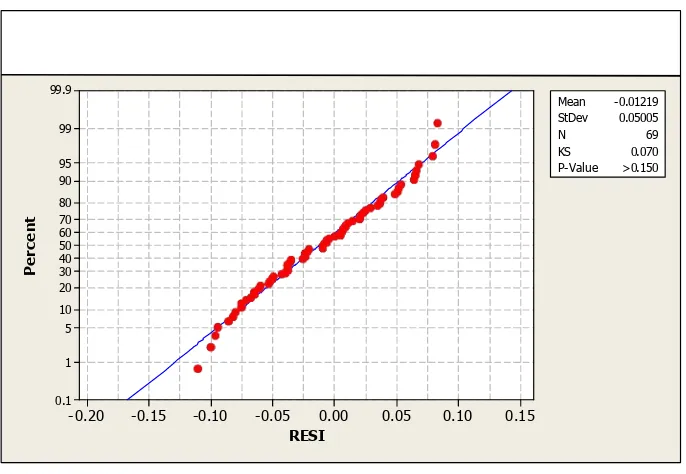
Gambar 4.2 Plot Kenormalan Error

Pengujian asumsi kenormalan dari error, dilakukan dengan membandingkan

nilai Kolmogorov-Smirnov yang diperoleh dengan nilai tabel

Kolmogorov-Smirnov. Karena diperoleh nilai = 0.07 yang lebih kecil dibandingkan

nilai = 0.164 yang artinya diterima, sehingga dapat dikatakan

bahwa error menyebar mengikuti distribusi normal. Dapat dilihat juga pada

hasil plot kenormalan pada Gambar 4.2, bahwa plot data cenderung dapat

didekati dengan garis lurus dengan nilai p-value 0.150 > 0.05 yang artinya

diterima.

3. Asumsi identik

Untuk menguji asumsi identik dari error, dapat digunakan statistik uji Glejser

dengan hipotesis sebagai berikut:

∶ tidak terjadi gejala heteroskedastisitas

(52)

39

Tabel 4.4 Tabel Uji t

Parameter Estimasi Nilai t Pr > |t|

a 0.018245 0.05 0.9590

b 4.808E36 0.00 0.9995

Pendeteksian pada uji Glejser ini dilakukan dengan meregresikan nilai mutlak

residual terhadap variabel independen. Dari hasil perhitungan tidak terjadi gejala heteroskedastisitas, dimana tidak ada nilai t hitung yang signifikan atau nilai signifikan lebih dari 0.05 (p > 0.05). Jadi secara keseluruhan dapat disimpulkan bahwa tidak ada masalah heterokedastisitas.

Pengujian asumsi identik juga dapat dilihat dari plot pencaran titik antara nilai

variabel independen dengan nilai error berikut.

0.146

tertentu, sehingga dapat dikatakan error konstan tidak dipengaruhi oleh

perubahan nilai prediksi yang dihasilkan dari model. Hal ini menunjukan

varian error konstan atau terjadi homokedastisitas, sehingga asumsi identik

(53)

40

Berdasarkan pengujian asumsi error yang telah dilakukan, dapat dilihat

bahwa semua asumsi terpenuhi sehingga dapat dikatakan bahwa model memenuhi

asumsi error regresi.

4.3.4 Perhitungan Mean dan Variansi

Mean dari distribusi Weibull yaitu

( ) = = ∫ ( )

= ∫ −

Misal = maka = dan =

= ∫ [− ]

= Γ 1 + (4.18)

Varian dari distribusiWeibull

= ∫ ( − ) ( )

= ∫ ( − 2 + ) ( )

= ∫ ( ) − 2 ( ) +

= ∫ ( ) −

= Γ 1 + − βΓ 1 +

(54)

41

Nilai mean dari kecepatan angin dapat diperoleh dengan menggunakan persamaan (4.18) yaitu

( ) = Γ 1 +

= 17.7524Γ 1 + _.

= 17.7524Γ(1.223318966)

= 16.19574

Variansi dari kecepatan angin dapat diperoleh dengan menggunakan persamaan (4.19) yaitu

( ) = Γ 1 + − Γ 1 +

= 17.7524 Γ 1 + _. − Γ 1 + _.

= 17.7524 [Γ(1.446637933) − [Γ(1.223318966)] ]

= 16.82444214

4.4 Interpretasi Model

Berdasarkan cumulative density function (cdf) yang diperoleh pada

persamaan (4.17) dapat ditentukan probability density function (pdf) distribusi

Weibull 2 parameter adalah

= _. . . . − _.

.

(4.20)

Sehingga akan menghasilkan kurva probability density function (pdf) distribusi

(55)

42

30 25

20 15

10 5

0 0.10

0.08

0.06

0.04

0.02

0.00

X

De

ns

ity

Gambar 4.4 Grafik Data Kecepatan Angin Terbesar terhadap Peluang Weibull

(56)

BAB V

PENUTUP

Berdasarkan hasil analisis dan pembahasan di atas, dapat ditarik beberapa kesimpulan sebagai berikut:

5.1 Kesimpulan

1. Hasil estimasi parameter dengan menggunakan metode linearisasi (metode deret Taylor) diperoleh

= + ( ) ( − ) = + ( ) ( − )

dimana

= ; , = 1 −

= 〈 − 〉 =

⎣ ⎢ ⎢ ⎢ ⎢ ⎢

⎡ − 1 −

− 1 − ⋮

− 1 − _⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎤

(57)

44 Tenggara Barat diperoleh sebuah model yaitu

= _. . . . − _.

.

Dari model tersebut diperoleh nilai keragaman yang cukup besar yaitu 99.216%, dapat dikatakan model yang diperoleh tepat.

5.2 Saran

(58)

45

DAFTAR PUSTAKA

Anton, H dan Rorres, C. 2004. Dasar-dasar Aljabar Linear Elementer Versi Aplikasi Edisi 8 Jilid 1, diterjemahkan oleh: Refina I dan Irzam H, Erlangga, Jakarta.

Anton, H. 2000. Dasar-dasar Aljabar Linear Edisi 7 Jilid 1. Erlangga, Jakarta. Bates, D.M dan Watts, D.G, 1988, Nonlinear Regression Analysis and Its

Applications, Jhon Wiley and Son, Canada.

Draper, N. dan Smith H., 1992, Analisis Regresi Terapan Ed. 2, diterjemahkan oleh: Bambang Sumantri, Gramedia Pustaka Utama, Jakarta.

Ebeling, C.E., 1997, Realibility and Maintainability Engineering, McGraw Hill, Singapore.

Firdaus, M., 2004, Ekonometrika Suatu Pendekatan Aplikatif, PT. Bumi Aksara, Jakarta.

Gallant, R.A, 1987, Nonlinear Statistical Models, Jhon Wiley and Son, NewYork. Gujarati, D., 1999, Basic Econommetrics Fourth Edition, McGraw Hill, New

York.

Hines, W.W dan Montgomery, D.C., 1989, Probabilitas dan Statistika dalam Ilmu Rekayasa dan Manajemen Ed.2, diterjemahkan oleh: Rudiansyah, UI Press, Jakarta.

Karim, M.E., 2009, Non-Linier Models, University of Dhaka, Bangladesh.

Olaofe, Z.O dan Folly, K.A., 2012, Statistical Analysis of the Wind Resources at Darling for Energy Production, International Journal of Renewable Energy Research, Vol.2 No.2, hal 1.

Rinne, H, 2009, The Weibull Distribution, CRC Press, United States of America.

Suliyanto, 2011, Ekonometrika Terapan: Teori dan aplikasi dengan SPSS, Andi

(59)

Lampiran 1. Data Kecepatan Angin Terbesar Per Bulan di Wilayah Nusa Tenggara Barat Tahun 2009- 2014

Tahun 2009 2010 2011 2012 2013 2014

(60)

Lampiran 2. Perhitungan Uji Mann untuk Kecepatan Angin

( ) ( ) ( )

− ( )

( ) − ( )

-0.35615 0.061536 2.833213 2.772589 0.060625 0.985183

-0.29461 0.040484 2.833213 2.772589 0.060625 1.497509

-0.25413 0.040119 2.833213 2.772589 0.060625 1.511112

-0.21401 0.039812 2.890372 2.833213 0.057158 1.435724

-0.1742 0.03956 2.890372 2.833213 0.057158 1.444859

-0.13464 0.039364 2.890372 2.833213 0.057158 1.452055

-0.09528 0.039224 2.944439 2.890372 0.054067 1.378435

-0.05605 0.03914 2.944439 2.890372 0.054067 1.381377

-0.01691 0.039115 2.944439 2.890372 0.054067 1.382277

0.022203 0.039149 2.944439 2.890372 0.054067 1.381056

0.061352 0.039247 2.944439 2.890372 0.054067 1.377626

0.100598 0.039411 2.944439 2.890372 0.054067 1.371894

0.140009 0.039646 2.944439 2.890372 0.054067 1.363756

0.179655 0.039958 2.944439 2.890372 0.054067 1.353102

0.219613 0.040354 2.944439 2.890372 0.054067 1.339808

0.259967 0.040844 2.944439 2.890372 0.054067 1.323737

0.300812 0.041439 2.995732 2.944439 0.051293 1.237801

0.342251 0.042153 3.044522 2.995732 0.04879 1.157461

0.384404 0.043003 3.044522 2.995732 0.04879 1.134564

0.427407 0.044014 3.044522 2.995732 0.04879 1.108514

0.471421 0.045214 3.044522 2.995732 0.04879 1.079091

0.516635 0.046643 3.044522 2.995732 0.04879 1.046044

0.563278 0.048351 3.091042 3.044522 0.04652 0.96213

0.611629 0.05041 3.135494 3.091042 0.044452 0.881798

0.662039 0.05292 3.135494 3.091042 0.044452 0.839988

(61)

Lampiran 2: Lanjutan

( ) ( ) ( )

− ( )

( ) − ( )

0.770981 0.059934 3.218876 3.178054 0.040822 0.681119

0.830914 0.064997 3.218876 3.178054 0.040822 0.628059

0.895911 0.07179 3.295837 3.258097 0.03774 0.525702

0.967702 0.081381 3.401197 3.367296 0.033902 0.416576

1.049083 0.096004 3.433987 3.401197 0.03279 0.341547

1.145087 0.121348 3.663562 3.637586 0.025975 0.214058

1.266435 -1.26643 3.713572 3.688879 0.024693 -0.0195

ln( ) − ln ( ) 34.94314348

ln( ) − ln ( ) 1205.53845

( ) ( ) ( )

− ( )

( ) − ( )

-4.92725 1.105921 2.302585 2.197225 0.105361 0.09527

-3.82133 0.518224 2.302585 2.197225 0.105361 0.203311

-3.3031 0.343964 2.397895 2.302585 0.09531 0.277094

-2.95914 0.258901 2.484907 2.397895 0.087011 0.336079

-2.70024 0.208356 2.564949 2.484907 0.080043 0.384164

-2.49188 0.17484 2.564949 2.484907 0.080043 0.457806

-2.31704 0.15099 2.564949 2.484907 0.080043 0.530118

-2.16605 0.13316 2.639057 2.564949 0.074108 0.556535

-2.03289 0.119332 2.639057 2.564949 0.074108 0.621023

-1.91356 0.108303 2.639057 2.564949 0.074108 0.684264

-1.80526 0.099308 2.639057 2.564949 0.074108 0.746242

-1.70595 0.091839 2.639057 2.564949 0.074108 0.806937

(62)

( ) ( ) ( )

− ( )

( ) − ( )

-1.52857 0.080169 2.639057 2.564949 0.074108 0.924402

-1.4484 0.075534 2.639057 2.564949 0.074108 0.981127

-1.37287 0.0715 2.639057 2.564949 0.074108 1.036482

-1.30137 0.067961 2.639057 2.564949 0.074108 1.090442

-1.23341 0.064837 2.70805 2.639057 0.068993 1.06409

-1.16857 0.062063 2.70805 2.639057 0.068993 1.111654

-1.10651 0.059587 2.70805 2.639057 0.068993 1.157844

-1.04692 0.057368 2.70805 2.639057 0.068993 1.202631

-0.98955 0.055372 2.70805 2.639057 0.068993 1.245986

-0.93418 0.053571 2.70805 2.639057 0.068993 1.287881

-0.88061 0.051941 2.70805 2.639057 0.068993 1.328282

-0.82867 0.050464 2.70805 2.639057 0.068993 1.367158

-0.7782 0.049124 2.772589 2.70805 0.064539 1.313797

-0.72908 0.047905 2.772589 2.70805 0.064539 1.34721

-0.68117 0.046798 2.772589 2.70805 0.064539 1.379095

-0.63437 0.045791 2.772589 2.70805 0.064539 1.409415

-0.58858 0.044877 2.772589 2.70805 0.064539 1.43813

-0.54371 0.044048 2.772589 2.70805 0.064539 1.4652

-0.49966 0.106998 2.772589 2.70805 0.064539 0.603176

-0.39266 0.392661 2.833213 2.772589 0.060625 0.154394

ln( ) − ln ( ) 29.47357

(63)

Lampiran 3. Perhitungan Pendugaan Nilai Awal Parameter

Urutan ( ) − ( − ( )) ( ) (− ( − ( )))

1 9 0.007273 2.197225 -4.92362

2 9 0.021979 2.197225 -3.81767

3 10 0.036905 2.302585 -3.29942

4 11 0.052056 2.397895 -2.95543

5 12 0.067441 2.484907 -2.6965

6 12 0.083067 2.484907 -2.48811

7 12 0.09894 2.484907 -2.31324

8 13 0.115069 2.564949 -2.16222

9 13 0.131463 2.564949 -2.02903

10 13 0.14813 2.564949 -1.90966

11 13 0.16508 2.564949 -1.80133

12 13 0.182322 2.564949 -1.70198

13 13 0.199866 2.564949 -1.61011

14 13 0.217723 2.564949 -1.52453

15 13 0.235906 2.564949 -1.44432

16 13 0.254425 2.564949 -1.36875

17 13 0.273293 2.564949 -1.29721

18 14 0.292525 2.639057 -1.22921

19 14 0.312133 2.639057 -1.16433

20 14 0.332134 2.639057 -1.10222

21 14 0.352543 2.639057 -1.04258

22 14 0.373377 2.639057 -0.98517

23 14 0.394654 2.639057 -0.92975

24 14 0.416394 2.639057 -0.87612

25 14 0.438617 2.639057 -0.82413

26 15 0.461346 2.70805 -0.77361

(64)

Urutan ( ) − ( − ( )) ( ) (− ( − ( )))

28 15 0.508413 2.70805 -0.67646

29 15 0.532805 2.70805 -0.6296

30 15 0.557806 2.70805 -0.58374

31 15 0.583448 2.70805 -0.5388

32 15 0.609766 2.70805 -0.49468

33 16 0.636794 2.772589 -0.45131

34 16 0.664574 2.772589 -0.40861

35 16 0.693147 2.772589 -0.36651

36 16 0.722561 2.772589 -0.32495

37 16 0.752866 2.772589 -0.28387

38 16 0.784119 2.772589 -0.24319

39 17 0.81638 2.833213 -0.20288

40 17 0.849716 2.833213 -0.16285

41 17 0.884202 2.833213 -0.12307

42 18 0.91992 2.890372 -0.08347

43 18 0.956962 2.890372 -0.04399

44 18 0.995428 2.890372 -0.00458

45 18 1.035433 2.890372 0.03482

46 18 1.077106 2.890372 0.074278

47 18 1.120591 2.890372 0.113856

48 18 1.166054 2.890372 0.153625

49 18 1.213682 2.890372 0.193658

50 18 1.263692 2.890372 0.234038

51 18 1.316336 2.890372 0.274852

52 19 1.371906 2.944439 0.316201

53 20 1.430746 2.995732 0.358196

(65)

Urutan ( ) − ( − ( )) ( ) (− ( − ( )))

55 20 1.559958 2.995732 0.444659

56 20 1.631417 2.995732 0.489449

57 20 1.708378 2.995732 0.535544

58 21 1.791759 3.044522 0.583198

59 22 1.882731 3.091042 0.632724

60 22 1.982815 3.091042 0.684517

61 24 2.09404 3.178054 0.739095

62 24 2.219203 3.178054 0.797148

63 24 2.362304 3.178054 0.859638

64 26 2.529358 3.258097 0.927966

65 29 2.730029 3.367296 1.004312

66 30 2.981344 3.401197 1.092374

67 38 3.317816 3.637586 1.199307

68 40 3.828641 3.688879 1.34251

69 45 4.927254 3.806662 1.594782

Scatter Plot antara ( ) dan (− ( − ( )))

4.0 3.5

3.0 2.5

2.0 2

1

0

-1

-2

-3

-4

-5

x

(66)

Pengelompokan _{( )} dan (− ( − ( )))

Kelompok Bawah Tengah Atas

2.197225 -4.92362 2.639057 -0.87612 2.890372 0.113856 2.197225 -3.81767 2.639057 -0.82413 2.890372 0.153625

2.302585 -3.29942 2.70805 -0.77361 2.890372 0.193658

2.397895 -2.95543 2.70805 -0.72443 2.890372 0.234038

2.484907 -2.6965 2.70805 -0.67646 2.890372 0.274852

2.484907 -2.48811 2.70805 -0.6296 2.944439 0.316201

2.484907 -2.31324 2.70805 -0.58374 2.995732 0.358196

2.564949 -2.16222 2.70805 -0.5388 2.995732 0.400966

2.564949 -2.02903 2.70805 -0.49468 2.995732 0.444659

2.564949 -1.90966 2.772589 -0.45131 2.995732 0.489449 2.564949 -1.80133 2.772589 -0.40861 2.995732 0.535544 2.564949 -1.70198 2.772589 -0.36651 3.044522 0.583198 2.564949 -1.61011 2.772589 -0.32495 3.091042 0.632724 2.564949 -1.52453 2.772589 -0.28387 3.091042 0.684517 2.564949 -1.44432 2.772589 -0.24319 3.178054 0.739095 2.564949 -1.36875 2.833213 -0.20288 3.178054 0.797148 2.564949 -1.29721 2.833213 -0.16285 3.178054 0.859638 2.639057 -1.22921 2.833213 -0.12307 3.258097 0.927966 2.639057 -1.16433 2.890372 -0.08347 3.367296 1.004312 2.639057 -1.10222 2.890372 -0.04399 3.401197 1.092374 2.639057 -1.04258 2.890372 -0.00458 3.637586 1.199307

2.639057 -0.98517 2.890372 0.03482 3.688879 1.34251

(67)

(68)

(69)

(70)

Asumsi normal error

Pengujian asumsi identik error dengan menggunakan SAS 9

(71)

(72)

Nonlinear OLS Summary of Residual Errors

DF DF

Adj Equation Model Error SSE MSE Root MSE R-Square R-Sq

y 2 67 1.7283 0.0258 0.1606 -30.302 -30.769

Nonlinear OLS Parameter Estimates (Not Converged)

Approx Approx Parameter Estimate Std Err t Value Pr > |t|

(73)

Lampiran 6. Perhitungan Peluang Kumulatif Data Kecepatan Angin

Bulan-Tahun Kecepatan _(knot) Peluang

Januari 2009 13 0.219474

Februari 2009 20 0.818306

Maret 2009 15 0.375182

April 2009 13 0.219474

Mei 2009 13 0.219474

Juni 2009 9 0.046626

Juli 2009 15 0.375182

Agustus 2009 10 0.073678

September 2009 13 0.219474

Oktober 2009 15 0.375182

November 2009 15 0.375182

Desember 2009 18 0.654923

Januari 2010 17 0.561203

Februari 2010 14 0.291993

Maret 2010 12 0.158987

April 2010 13 0.219474

Mei 2010 16 0.466281

Juni 2010 40 1

Juli 2010 16 0.466281

Agustus 2010 13 0.219474

September 2010 12 0.158987

(74)

November 2010 16 0.466281

Desember 2010 14 0.291993

Januari 2011 30 0.999972

Februari 2011 20 0.818306

Maret 2011 13 0.219474

April 2011 14 0.291993

Mei 2011 24 0.978897

Juni 2011 12 0.158987

Juli 2011 24 0.978897

Agustus 2011 17 0.561203

September 2011 18 0.654923

Oktober 2011 16 0.466281

November 2011 18 0.654923

Desember 2011 15 0.375182

Januari 2012 26 0.996

Februari 2012 18 0.654923

Maret 2012 29 0.999877

April 2012 22 0.926706

Mei 2012 18 0.654923

Juni 2012 20 0.818306

Juli 2012 18 0.654923

(75)

September 2012 18 0.654923

Oktober 2012 17 0.561203

November 2012 15 0.375182

Desember 2012 15 0.375182

Januari 2013 24 0.978897

Februari 2013 45 1

Maret 2013 20 0.818306

April 2013 13 0.219474

Mei 2013 14 0.291993

Juni 2013 9 0.046626

Juli 2013 16 0.466281

Agustus 2013 14 0.291993

September 2013 14 0.291993

Oktober 2013 13 0.219474

November 2013 22 0.926706

Desember 2013 18 0.654923

Januari 2014 18 0.654923

Februari 2014 38 1

Maret 2014 16 0.466281

April 2014 11 0.110659

Mei 2014 14 0.291993

(76)

Juli 2014 19 0.742168

Agustus 2014 21 0.880192

September 2014 18 0.654923

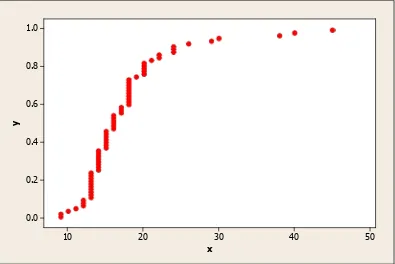
Grafik data kecepatan angin terbesar terhadap peluang kumulatif Weibull

50 40

30 20

10 1.0

0.8

0.6

0.4

0.2

0.0

x