ANALISIS DATA KUALITATIF CHI SQUARE

(1)

BAB I

PENDAHULUAN

A. Latar Belakang Penulisan

Pengolahan data merupakan bagian vital bagi setiap organisasi bisnis dan untuk setiap pengambilan keputusan managemen yang sangat signifikan. Hasil dari pengolahan data tersebut menjadi dasar bagi perencanaan jangka panjang perusahaan. Dalam area fungsional keuangan, informasi dari data yang diambil memberikan dasar dalam menentukan anggaran dan pengendalian biaya. Pada bagian pemasaran, informasi tersebut dibutuhkan untuk merencanakan produk baru, kompensasi tenaga penjual, dan beberapa keputusan penting lainnya

Seperti yang kita ketahui, bahwa kegiatan menganalisis akan selalu ada pada kegiatan sehari-hari hal tersebut yang melatarbelakangi penulis menyusun makalah ini untuk menambah dan melatih pemahaman tentang pengolahan data mentah menjadi informasi.

Maka dalam hal ini, penulis melakukan pengujian terhadap suatu objek yaitu Usia Kepala Keluarga yang ada di Kp. Papanggungan Rt. 08 dan 09 Rw. 13 Desa Mekarsari.

B. Perumusan Masalah

Dari uraian yang telah diberikan dalam latar belakang masalah, dapat dirumuskan sebagai berikut:

 Bagaimana mengolah data yang telah diperoleh disekitar kita menjadi sebuah informasi?

 Bagaimana mengaplikasikan teori pada data di kehidupan nyata?

C. Maksud dan Tujuan Penulisan

Adapun tujuan dari penyusunan makalah ini adalh sebagi berikut:

 Mengetahui cara mengolah data yang diperoleh.

 Mengetahui aplikasi teori yang telah disampaikan di perkuliahan dengan data pada kehidupan

(2)

BAB II

LANDASAN TEORI

A. Pengertian Uji Chi-Square

Uji chi-square adalah salah satu uji statistic non parametik yang cukup sering digunakan dalam penelitian. Uji chi-square ini bias diterapkan untuk pengujian kenormalan data, pengujian data yang berlevel nominal atau untuk menguji perbedaan dua atau lebih proporsi sampel. Uji chi-square diterapkan pada kasus dimana akan diuji apakah frekuensi yang akan di amati (data observasi) bebeda secara nyata ataukah tidak dengan frekuensi yang diharapkan (expected frekuensi harapan yang didasarkan atas hipotesis dilambangkan . Ekspresi matematis tentang distribusi chi kuadrat hanya tergantung pada suatu parameter, yaitu derajat kebebasan (d.f.).

Chi kuadrat mempunyai masing–masing nilai derajat kebebasan, yaitu distribusi (kuadrat standard normal) merupakan distribusi chi kuadrat dengan d.f. = 1, dan nilai variabel tidak bernilai negative. Kegunaan dari chi square untuk menguji seberapa baik kesesuaian diantara frekuensi yang teramati dengan frekuensi harapan yang didasarkan pada sebaran yang akan dihipotesiskan, atau juga menguji perbedaan antara dua kelompok pada data dua kategorik untuk dapat menguji signifikansi asosiasi dua kelompok pada data dua katagorik tersebut (Sri,1990).

(3)

Rumus:

X2 = Σ ( O – E )2 E

O : nilai Observasi (pengamatan) E : nilai Expected (harapan) Df = (b-1) (k-1)

b : jumlah baris k : jumlah kolom

B. Kegunaan Chi-Square

Adapun kegunaan dari uji Chi-Square, adalah :

1. Ada tidaknya asosiasi antara 2 variabel (Independent test) 2. Apakah suatu kelompok homogen atau tidak (Homogenity test)

3. Uji kenormalan data dengan melihat distribusi data (Goodness of fit test)

C. Uji Kenormalan Data Dengan Chi-Square.

Salah satu bentuk probabilitas yang penting peranannya dalam statistic inferensia adalah distribusi normal. Maka setelah suatu kelompok data diolah dengan statistic deskriptif atau telah diketahui nilai rata-rata, variaans dan sebagainya, sebelun data tersebut diolah dengan statistik inferensia data tersebut seharusnya diuji apaka data tersebut berdistribusi normal atau tidak.

Hal ini penting mengingat pengolahan statistik terbagi atas sstatistik parametik dan statistik non parametik. Pengolahan data menggunakan statistik parametik memiliki syarat diantaranya bahwa data harus berdistribusi normal, artinya data yang tidak berdistribusi normal tidak dapat diolah menggunakan statistik parametik tetapi hanya dapat diolah menggunakan distribuasi non parametik.

(4)

D. Langkah-Langkah Uji Kenormalan

Langkah-langkah dalam menguji kenormalan suatu data adalah sebagai berikut:

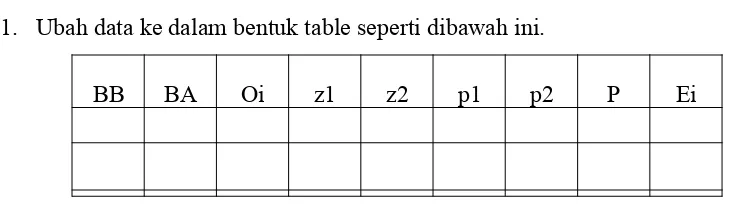
1. Ubah data ke dalam bentuk table seperti dibawah ini.

BB BA Oi z1 z2 p1 p2 P Ei

Kolom BB diisi dengan batas bawah kelas. Kolom BA diisi dengan batas atas kelas. Sedangkan kolom Oi diisi dengan frekuensi dari masing-masing kelas.

Kemudian kolom z1dan z2 diisi dengan menggunakan rumus :

z=x-xS

Dimana nilai x diperoleh dari kolom BB untuk z1 dan kolom BA untuk z2. nilaix merupakan rata-rata dan nilai S merupakan simpangan baku atau standar deviasi. Dalam excel ditulis

=(sel BB-sel rata-rata)/ sel simpangan baku

Untuk mengisi kolom p1 dan p2, gunakan fungsi NORMSDIST. Secara umum rumus untuk fungsi ini ditulis :

=NORMSDIST(z)

Selanjutnya kolom P merupakan nilai selisih dari p1 - p2. Sedangkan kolom Ei (expected value) diisi dengan mengalikan nilai pada P dengan jumlah data.

2. Setelah didapat nilai Oi dan Ei. Selanjutnya mengitung Chi-square dengan menggunakan

fungsi CHITEST dan CHIINV, maka diperoleh :

 Mencari nilai Chi-square probabilitas.=CHITEST(actual_range, expected_range)

 Mencari nilai Chi-square hitung.=CHIINV(probability, degrees_freedom)

3. Setelah nilai Chi-square hitung diperoleh maka selanjutnya mencari nilai Chi-square

(5)

E. Analisis Hasil

 Membuat hipotesis :

H0 :Data Berdistribusi Normal.

H1 : Data Tidak Berdistribusi Normal

Uji antara beberapa k proporsi

Pengujian chi kuadrat dapat digunakan untuk menguji kesamaan dari dua proporsi atau lebih. Pengujian kesamaan proporsi sama dengan pengujian independensi.

1. Uji Proporsi yang Dihipotesiskan : nilai proporsi yang dihipotesiskan d.f. = k – m – 1

2. Uji Beda Dua Proporsi d.f. = (r - 1)(k - 1)

3. Uji Beda k Proporsi : hipotesis nol tidak benar. d.f. = (r - 1)(k - 1)

Statistik chi kuadrat untuk menguji kebebasan dapat juga diterapkan untuk menguji apakah k populasi binom memiliki parameter yang sama p. Sesungguhnya uji ini merupakan perluasan uji yang dijelaskan anara dua proporsi menjadi selisih antara k populasi.

Alternatifnya bahwa populasi proporsi itu tidak semuanya sama yang (ekivalen) dengan pengujian bahwa terjadinya keberhasilan atau kegagalan tidak bergantung pada populasi yang diambil sampelnya. Menghitung di dalam uji proporsi ini frekuensi harapan dihitung seperti cara yang diterangkan sama dengan uji kebebasan dan bersama–sama dengan frekensi yang teramati perhitungan menggunakan rumus dari uji kebebasan, yaitu (Walpole,1995) Dan dengan:

V = (2 - 1)(k - 1) = k – 1

Mengambil wilayah kritik diderajat bebas yang berbentuk , maka dapat disimpulkan mengenai tidak semuanya sama

 Kaidah keputusan :

Jika Chi-square hitung < Chi-square tabel, maka H0 diterima. Artinya data berdistribusi normal.

Jika Chi-square hitung > Chi-square tabel. maka H0 ditolak. Artinya data tidak berdistribusi

(6)

 Pengambilan keputusan

(7)

BAB III

PENGUMPULAN DAN PENGOLAHAN DATA

A. Pengumpulan data

Studi kasus adalah masalah nyata yang ada dikehidupan sehari-hari. Studi kasus ini diambil dari simulasi percobaan yang pernah dilakukan.

Kegiatan pengambilan data dan wawancara dilaksanakan pada: Hari/tanggal : Rabu, 2 November 2011

Waktu : 13.00 s.d 14.00 WIB

Media : Wawancara Langsung

Narasumber : Ketua Rt. 08 dan 09

(8)

22 KK22 62

Data diatas diolah dalam Micr. Excel sebagai berikut : Diketahui :

Xmax merupakan nilai tertinggi dari data. Xmin merupakan nilai terkecil dari data, BK merupakan banyak kelas, R merupakan Range dan interval merupakan panjang kelas.

Maka, tabel distribusi frekuensi dan histogramnya adalah :

(9)

Dari hasil pengujian statistik deskriptif melalui Micr. Excel diperoleh data sebagai berikut :

Usia

Mean 44

Standard Error

2.33710 7

Median 42

Mode 43

Standard Deviation

12.8008 6

Sample Variance

163.862 1

Kurtosis 0.11529

Skewness

0.79747 2

Range 50

Minimum 25 Maximum 75

Sum 1320

(10)

Rata-rata : 44

Standar Deviasi : 12.80086

n (jumlah) : 30

Dengan melakukan langkah-langkah pengujian kenormalan seperri pada teori yaitu: 1. Mengubah data ke dalam bentuk tabel dibawah ini.

2. Setelah didapat

nilai Oi dan Ei.

Selanjutnya mengitung Chi-square dengan menggunakan fungsi CHITEST dan CHIINV, maka diperoleh :

Oi Ei 16 11.69 6 7.10 8 5.34

 Mencari nilai Chi-square probabilitas.

Oi Ei Chitest 16 11.69 _0.21367

5 6 7.10

8 5.34

Maka diketahui Chi-square probabilitas adalah 0.213675

(11)

 Mencari nilai Chi-square hitung.

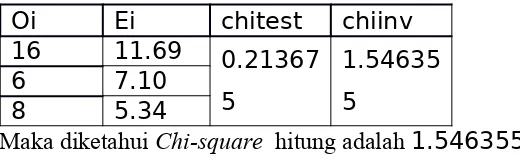
Oi Ei chitest chiinv 16 11.69 _0.21367

Maka diketahui Chi-square hitung adalah 1.546355

3. Setelah nilai Chi-square hitung diperoleh maka selanjutnya mencari nilai Chi-square tabel dimana nilai Chi-square tabel diperoleh dengan menggunakan fungsi CHIINV. Hanya untuk probabilitas disesuaikan dengan taraf signifikannya. CHIINV dengan taraf signifikannya adalah 5% atau 0.05. Maka didapat

Oi Ei chitest chiinv

chinv

nilai Chi-square tabel adalah 3.841459.

C. Analisis Hasil

 Membuat hipotesis :

H0 :Data Berdistribusi Normal.

H1 : Data Tidak Berdistribusi Normal

 Kaidah keputusan :

Jika Chi-square hitung < Chi-square tabel, maka H0 diterima. Artinya data berdistribusi normal.

Jika Chi-square hitung > Chi-square tabel. maka H0 ditolak. Artinya data tidak berdistribusi

normal.

 Pengambilan keputusan

Dari hasil perhitungan diperoleh nilai Chi-square hitung sebesar 1.546355 dan Chi-square tabel sebesar 3.841459.

Sehingga didapat hasil Chi-square hitung < Chi-square tabel, maka H0 diterima.

(12)

BB BA Nilai Tengah 24.5 33.5 29

(13)

BAB IV

PENUTUP

A. Kesimpulan

Dari data diatas saya menyimpulkan bahwa data yang saya peroleh dari narasumber, merupakan Data Berdistribusi Normal berdasarkan pengujian Chi-square yang telah dilakukan. B. Penutup

Saya menyadari bahwa makalah ini masih jauh dari sempurna, oleh karena itu kritik dan saran dari semua pihak yang bersifat membangun selalu kami harapkan demi kesempurnaan makalah ini.

(14)

DAFTAR PUSTAKA

 Fransisca, deka. 2010, UJI BEDA PROPORSI (CHI – SQUARE), (tersedia pada URL: http://

dekafransiscamarthadewi.blogspot.com/2010/06/uji-beda-proporsi-chi-square.html pada tanggal 6 november 2011 pukul 8.51 WIB)

 Satria, Eri. 2011, Labkom STIE YASA ANGGANA GARUT.

 Sofyan, oke. 2010, UJI BEDA PROPORSI (CHI – SQUARE), (tersedia pada URL:

(15)

STATISTIK EKONOMI 2

“