BAB II
LANDASAN TEORI
2.1Data dan Variabel
2.1.1 Data
Pengertian data menurut Webster New World Dictionary adalah things known or
assumed, yang berarti bahwa data itu sesuatu yang diketahui atau dianggap. Diketahui
artinya yang sudah terjadi merupakan fakta (bukti). Data juga dapat didefinisikan
sekumpulan informasi atau nilai yang diperoleh dari pengamatan (observasi) suatu
objek, data dapat berupa angka dan dapat pula merupakan lambang atau sifat. Pada
dasarnya kegunaan data (setelah diolah dan dianalisis) ialah sebagai dasar yang
objektif di dalam proses pembuatan keputusan/ kebijaksanaan dalam rangka untuk
memecahkan persoalan.
Menurut sifatnya , data dapat digolongkan menjadi dua, yaitu:
a. Data Kualitatif yaitu data yang tidak berbentuk angka.
b. Data Kuantitatif yaitu data yang berbentuk angka.
Bila ditinjau dari cara memperolehnya, data dapat dibagi menjadi dua, yaitu:
a. Data Primer yaitu data yang dikumpulkan sendiri oleh perorangan/ atau suatu
organisasi secara langsung dari objek yang diteliti dan untuk kepentingan study
yang bersangkutan yang dapat berupa interviu atau observasi.
b. Data Sekunder yaitu data yang diperoleh/ dikumpulkan dan disatukan oleh
Menurut waktu pengumpulannya, data digolongkan menjadi dua, yaitu :
a. Data Cross Section ialah data yang dikumpulkan pada suatu waktu tertentu
untuk menggambarkan keadaan dan kegiatan pada waktu tersebut. Misalnya,
data penelitian yang menggunakan kuesioner.
b. Data Berkala ialah data yang dikumpulkan dari waktu ke waktu untuk melihat
perkembangan suatu kejadian/ kegiatan selama periode tersebut. Misalnya,
perkembangan uang yang beredar.
2.1.2Variabel
S.H.Situmorang dkk, 2010. Variabel adalah suatu yang dapat membedakan atau
mengubah variasi pada nilai. Nilai dapat berbeda pada waktu yang berbeda untuk
objek atau orang yang sama, atau nilai dapat berbeda dalam waktu yang sama untuk
objek atau orang yang berbeda.
Menurut hubungan antara suatu variabel dengan variabel lainnya, variabel
terbagi atas beberapa yaitu :
1. Variabel bebas yaitu variabel yang menjadi sebab terjadinya atau
terpengaruhnya variabel tak bebas.
2. Variabel tak bebas yaitu variabel yang nilainya dipengaruhi oleh variabel
bebas.
3. Variabel moderator yaitu variabel yang memperkuat atau memperlemah
hubungan antara suatu variabel bebas dengan tak bebas.
4. Variabel intervening, seperti halnya variabel moderator, tetapi nilainya tidak
dapat diukur, seperti kecewa, marah, gembira, senang, sedih, dan lain
sebagainya.
2.2 Uji Validitas dan Reliabilitas Data
Pengujian validitas data digunakan untuk mengetahui apakah variabel-variabel dalam
penelitian dapat menggambar keinginan konsumen dan mampu mengungkapkan
sesuatu yang diukur oleh penelitian tersebut. Tinggi rendahnya validitas suatu variabel
menunjukkan sejauh mana data yang dikumpulkan tidak menyimpang dari gambaran
tentang variabel yang dimaksud.
Rumus:
𝑟= 𝑁( 𝑋𝑌)−( 𝑋. 𝑌)
𝑁 𝑋2 − ( 𝑋)2 𝑁 𝑌2 − ( 𝑌)2 1 2
Keterangan:
r = Koefisien korelasi product moment
N = Jumlah sampel
X = Skor setiap variabel
Y = Skor total setiap responden
Uji reliabilitas data dilakukan untuk mengetahui tingkat kepercayaan hasil
suatu pengukuran. Suatu kuesioner dikatakan reliabel jika jawaban seseorang terhadap
pertanyaan adalah konsisten dari waktu ke waktu. Nilai suatu kuesioner dianggap reliabel jika memberikan nilai α > 0,60, (Ghozali, 2005).
2.3Teori Permainan
Aminudin, 2005. Teori permainan merupakan suatu model matematika yang
digunakan dalam situasi konflik atau persaingan antara berbagai kepentingan yang
saling berhadapan sebagai pesaing. Dalam permaian peserta adalah pesaing.
Keuntungan bagi yang satu merupakan kerugian bagi yang lain. Model-model
kerugian, dan jumlah startegi yang digunakan dalam permainan. Bila jumlah pemain
ada dua, permainan disebut sebagai permainan dua pemain. Bila keuntungan atau
kerugian sama dengan nol, disebut permainan jumlah nol.
Teori permainan mula-mula dikemukakan oleh seorang ahli matematika
Prancis yang bernama Emile Borel pada tahun 1921. kemudian, John Von Neemann
dan Oskar Morgenstern mengembangkan lebih lanjut sebagai alat untuk merumuskan
perilaku ekonomi yang bersaing.
2.3.1 Unsur-unsur Dasar Teori Permainan
Pada bagian ini akan dijelaskan beberapa unsur dasar yang sangat penting dalam
pemecahan setiap kasus dengan teori permainan, dengan mengambil contoh
permainan dua pemain jumlah nol dimana matriks pay off-nya ditunjukan dalam tabel
berikut:
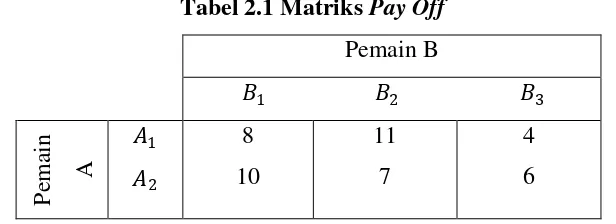
Tabel 2.1 Matriks Pay Off
Pemain B
𝐵1 𝐵2 𝐵3
P
emain A
𝐴1 𝐴2
8
10
11
7
4
6
Dari contoh tabel permainan di atas dapat dijelaskan dasar-dasar teori
permainan sebagai berikut:
1. Angka-angka dalam matriks pay off (matriks permainan) menunjukkan
hasil-hasil atau pay off dari strategi-strategi permainan yang berbeda-beda, dimana
hasil-hasil merupakan ukuran efektifitas. Bilangan positif menunjukkan
keuntungan bagi pemain baris dan kerugian bagi pemain kolom.
2. 𝐴𝑖 dan 𝐵𝑗 merupakan alternatif strategi-strategi yang dimiliki oleh
yang menyeluruh dari pemain sebagai reaksi atas aksi yang mungkin dilakukan
oleh pesaing.
3. Nilai permainan adalah hasil yang diperkirakan per permainan atau rata-rata
pay off sepanjang permainan. Suatu permainan dikatakan adil apabila nilainya
sama dengan nol.
4. Suatu permainan dikatakan dominan bila setiap pay off dalam strategi adalah
superior terhadap setiap pay off yang berhubungan dalam suatu strategi
alternatif. Pada matriks di atas hal ini terjadi untuk pemain B, kedua strategi 𝐵1
dan 𝐵2 didominasi oleh strategi 𝐵3. Sehingga strategi 𝐵1 dan 𝐵2 dapat
direduksi. Artinya pemain B menjalankan strategi optimalnya adalah 𝐵3.
Sedangkan pemain A memilih strategi 𝐴2 karena berusaha mencari
keuntungan maksimal. Jadi nilai permainan untuk kasus di atas adalah 6 .
5. Tujuan dari model permainan adalah mengidentifikasi strategi mana yang
optimal untuk setiap pemain.
2.3.2 Klasifikasi Permainan
a. Berdasarkan jumlah langkah dan pilihan
Permainan diklasifikasikan menjadi dua, yaitu:
i. Permainan berhingga, yaitu suatu permainan yang mempunyai
sejumlah langkah yang berhingga dengan setiap langkah yang memuat
sejumlah pilihan yang berhingga pula.
ii. Permainan tak berhingga, untuk setiap permainan selain permainan
berhingga.
b. Berdasarkan jumlah pemain
Suatu permainan dikatakan permainan n orang jika jumlah orang yang bermain adalah
c. Berdasarkan jumlah pembayaran
i. Permainan berjumlah nol adalah suatu permainan dengan jumlah
kemenangan kedua belah pihak sama dengan nol. Hal ini berarti bahwa
jummlah pembayaran yang diterima oleh salah satu pemain yang
menang sama dengan jumlah pembayaran yang dibayarkan oleh pihak
yang kalah. Bila ada dua orang yang bermain di dalam permainan maka
dinamakan permainan berjumlah nol dari dua orang.
ii. Permainan berjumlah tidak nol, yaitu permainan dengan total
pembayaran dari masing-masing pemain pada akhir suatu permainan
tidak sama dengan nol. Permainan ini dapat dimainkan oleh dua orang
ataupun n orang.
2.3.3 Permainan Berjumlah Nol Dari Dua Orang
Kartono, 1994. Konsep dasar yang memuat dalam teori permainan dapat dijelaskan
oleh permainan yang sederhana yang dimainkan oleh dua orang atau dua pemain.
Untuk selanjutnya akan dibahas hal-hal pokok yang sesungguhnya menjadi inti dari
teori permainan, yaitu menentukan solusi optimum bagi kedua pihak yang saling
bersaing tersebut yang bersesuaian dengan strategi optimumnya. Ada dua macam
strategi optimum, yaitu strategi murni dan strategi campuran.
a. Strategi Murni
Permainan dengan strategi murni adalah suatu permainan dengan posisi pilihan
terbaiknya bagi setiap pemain dicapai dengan memilih satu strategi tunggal. Dalam
permainan dengan strategi murni, pemain pertama (pemain baris) yaitu pemain yang
berusaha memaksimumkan kemenangan (keuntungan) yang minimum sehingga
kriteria strategi optimumnya adalah kriteria maximin. Sedangkan pemain kedua
(pemain kolom) yaitu pemain yang berusaha meminimumkan kekalahan (kerugian)
Apabila nilai maximin sama dengan nilai minimax maka permainan ini dapat
diselesaikan dengan strategi murni dimana titik keseimbangan telah tercapai. Titik
keseimbangan ini dikenal sebagai titik pelana.
b. Strategi Campuran
Di dalam permainan dimana permainan tersebut tidak mempunyai titik pelana maka
para pemain akan bersandar kepada apa yang disebut sebagai strategi campuran. Hal
ini berarti pemain pertama akan memainkan setiap strategi baris dengan proporsi
waktu (probabilitas) tertentu. Demikian juga untuk pemain kedua, ia akan memainkan
setiap strategi kolom dengan proporsi waktu (probabilitas) tertentu. Oleh karena itu
dalam suatu permainan yang diselesaikan dengan strategi campuran, strategi dari
setiap pemain akan mempunyai probabilitas yang menunjukan proporsi waktu atau
banyaknya bagian yang dipergunakan untuk melakukan strategi tersebut. Jadi tugas
dari setiap pemain adalah menentukan proporsi waktu (probabilitas) yang diperlukan
untuk memainkan strateginya.
c. Aturan Dominasi
Sebelum menyelesaikan suatu permainan, perlu dipertimbangkan apakah ada baris
atau kolom dalam matriks pembayarannya yang tidak efektif pengaruhnya di dalam
penentuan strategi optimum dan nilai permainan. Bila ada maka baris atau kolom yang
seperti itu bisa dihapus atau tidak dipakai. Hal itu berarti bahwa probabilitas untuk
memilih strategi sesuai baris atau kolom tersebut sama dengan nol.
Dengan demikian ukuran matriks pembayaran yang tersisa akan lebih kecil. Hal ini
akan mempermudah untuk menyelesaikannya. Aturan demikian ini dinamakan aturan
dominasi.
i. Aturan dominasi bagi pemain pertama 𝑃1 (pemain baris). Karena pemain
𝑃1 (pemain baris) merupakan pemain yang berusaha untuk
baris dengan semua elemen dari baris tersebut adalah sama atau lebih kecil
(sekolom) dari baris yang lain maka baris tersebut dikatakan didominasi
dan baris itu dapat dihapus. Jika dalam suatu permainan yang berukuran
m x n terdapat 𝐻(𝑖,𝑗) ≤ 𝐻(𝑘,𝑗) untuk semua 𝑗 = 1, 2,…,𝑛 maka baris k
mendominasi baris i. Sedangkan jika 𝐻(𝑖,𝑗) ≤ 𝐻(𝑖,𝑘) untuk semua 𝑖=
1, 2, …, 𝑚 maka kolom k mendominasi kolom j.
ii. Aturan dominasi bagi pemain kedua 𝑃2 (pemain kolom). Karena pemai 𝑃2
(pemain kolom) merupakan pemain yang berusaha untuk meminimumkan
kekalahan / kerugiannya maka bila terdapat suatu kolom dengan semua
elemen dari kolom tersebut adalah sama atau lebih besar dari elemen dalam
posisi yang sama (sebaris) dari kolom yang lain maka kolom tersebut
dikatakan didominasi dan kolom itu dapat dihapus. Jika dalam suatu
permainan yang berukuran m x n terdapat 𝐻(𝑖,𝑗) ≤ 𝐻(𝑖,𝑘) untuk semua
𝑖= 1, 2,…,𝑚 maka kolom k mendominasi kolom j.
Keterangan:
𝐻(𝑖,𝑗) = Elemen matriks pay off baris ke-i dan kolom ke-j 𝐻(𝑘,𝑗) = Elemen matriks pay off baris ke-k dan kolom ke-j 𝐻(𝑖,𝑘) = Elemen matriks pay off baris ke-i dan kolom ke-k
Aturan dominasi ini dapat diulang lagi jika masih ada baris atau kolomnya
yang didominasi oleh baris atau kolom yang lain. Dan ini memungkinkan matriks
pembayaran semula akan tersisa menjadi matriks pembayaran dengan satu elemen
saja. Bila hal ini dapat terjadi maka permainannya dapat diselesaikan dengan strategi
murni dengan nilai permainan sesuai dengan elemen yang tersisa tersebut. Tetapi tidak
semua permainan yang mempunyai titik pelana dapat diselesaikan dengan aturan
2.3.4 Metode Penyelesaian Masalah dalam Teori Permainan
Yang dimaksud dengan menyelesaikan permainan adalah usaha mencari strategi
optimum dan nilai permainan yang secara umum dapat dirumuskan sebagai berikut:
𝑋= 𝑥1,𝑥2,…,𝑥𝑚 dan 𝑌= 𝑦1,𝑦1,…,𝑦𝑛 yang mengoptimumkan nilai harapan
Metode yang akan digunakan dalam penelitian ini adalah metode program linier.
Dalam penyelesaian suatu permainan dengan metode program linier ini, kita
sering dihadapkan kepada masalah metode simplex dualitas. Untuk suatu permainan
dengan matriks pembayaran yang berukuran besar (m x n) dan tidak mempunyai titik
pelana serta metode dominasi tidak dapat digunakan untuk mereduksi ukuran matriks
pembayaran menjadi lebih kecil, maka program linier menawarkan suatu metode
penyelesaian yang efesien.
Tabel 2.2 Nilai Probabilitas Strategi Pemain
Keterangan:
𝑥𝑖 = probabilitas pemain 𝑃1 memilih strategi ke-i. 𝑦𝑗 = probabilitas pemain 𝑃2 memilih strategi ke-j.
𝑎𝑖𝑗 = nilai pembayaran yang bersesuaian dengan strategi ke-i pemain 𝑃1
dan ke-j pemain 𝑃2.
= 1 yang akan menghasilkan
𝑚𝑎𝑥 𝑚𝑖𝑛 𝑎𝑖1𝑥𝑖
Hal ini menunjukkan bahwa strategi campuran optimum pemain 𝑃1 memenuhi
𝑚𝑎𝑥 𝑚𝑖𝑛 𝑎𝑖1𝑥𝑖
Persoalan ini dapat disajikan ke bentuk program linier sebagai berikut:
maka persoalan itu menjadi:
Perumusan program linier di atas dapat disederhanakan dengan membagi
(n+1) pembatas dengan v. Pembagian ini berlaku untuk 𝑣> 0. Jika 𝑣= 0 maka
pembagian tidak berlaku. Sebaliknya, jika 𝑣 < 0 maka pembagian ini juga tidak
berlaku namun dapat diubah menjadi 𝑣 > 0 dengan menambahkan suatu konstanta
positif k pada semua elemen dalam matriks pembayaran yang akan menjamin nilai
permainan untuk matriks yang dimodifikasi ini lebih besar dari nol. Sebagai pedoman,
diambil 𝑘 ≥ harga mutlak dari elemen yang terkecil sehingga sebelum merumuskan
ke bentuk program linier perlu diperiksa nilai maximin barisnya karena bila nilai
maximin tersebut negatif maka ada kemungkinan nilai permainannya negatif atau nol.
Dengan demikian matriks pembayarannya perlu dimodifikasi dahulu dan
sebagai konsekuensinya adalah bila solusi optimum telah diperoleh maka nilai
permainan yang sebenarnya ditentukan dengan dengan mengurangi sebesar k tadi dari
nilai permainan yang dimodifikasi.
Pada umumnya jika nilai maximinnya positif maka nilai permainannya lebih
besar dari pada nol (terutama permainan yang mempunyai titik pelana). Oleh karena
itu di dalam pembentukan rumusan program linier diasumsikan bahwa 𝑣> 0.
Pembatas-pembatas dalam rumusan program linier di atas menjadi:
Bila dinotasikan 𝑋𝑖 =𝑥𝑖
𝑣 ;𝑖= 1, 2,…,𝑚 maka
𝑋𝑖 𝑚
𝑖=1
= 1
𝑣
Karena max𝑣= min1𝑣 maka
Persoalan di atas menjadi:
Meminimumkan 𝑧= 1𝑣
Berdasarkan pembatas
𝑎𝑖𝑗𝑋𝑖 ≥1 ; 𝑗 = 1, 2,…,𝑛 𝑚
𝑖=1
𝑋𝑖 ≥ 0 ; 𝑖= 1, 2,…,𝑚
Dari sini kemudian diselesaikan dengan metode simpleks. Penyelesaian bagi
pemain 𝑃2 merupakan dual dari penyelesaian pemain 𝑃1. Jadi penyelesaian optimum
bagi salah satu pemain dapat memberikan penyelesain optimum bagi pemain lainnya
walaupun penyelesaian bagi pemain 𝑃2 merupakan dual dari penyelesaian pemain 𝑃1.
Perhitungan penyelesaian optimum pemain 𝑃2 dapat dilakukan dengan menggunakan
metode simpleks dan penyelesain pemain 𝑃1 merupakan dualnya. Dan pada
kenyataannya bahwa lebih mudah untuk menghitung penyelesaian pemain 𝑃2 dengan
metode simpleks dahulu.
b. Untuk pemain 𝑷𝟐 (pemain kolom)
Dengan cara yang sama akan diperoleh:
memaksimumkan 𝑤= 𝑌1+ 𝑌2+⋯+𝑌𝑛
berdasarkan pembatas-pembatas:
𝑎𝑖𝑗𝑌𝑗 ≤1 ; 𝑖 = 1, 2,…,𝑚 𝑛
𝑖=1
2.4 Program Linier
Fien Zulfikarijah, 2004. Konsep program linier ditemukan dan diperkenalkan pertama
kali oleh George Dantzig yang berupa metode mencari solusi masalah program linier
dengan banyak variabel keputusan. Program linier dapat didefinisikan sebagai
pembuatan rencana kegiatan-kegiatan dengan menggunakan suatu model umum dalam
pemecahan masalah pengalokasian sumber daya yang terbatas secara optimal.
Dalam model program linier terdapat asumsi-asumsi yang harus dipenuhi,
yaitu:
1. Proportionality (kesebandingan), artinya perubahan nilai fungsi tujuan dan
penggunaan sumber daya adalah proporsional (sebanding) dengan perubahan
kegiatan, contoh: 𝑍=𝐶1𝑋1, dalam persamaan ini dapat diartikan setiap
peningkatan 𝑋1 sebesar 1 unit akan meningkatkan Z sebesar 𝐶1.
2. Additivity (penambahan), artinya nilai tujuan setiap kegiatan bersifat
independent (bebas/ tidak saling bergantung) dan dalam program linier
dianggap bahwa kenaikan nilai tujuan (Z) yang diakibatkan oleh suatu
kegiatan dapat langsung ditambahkan tanpa mempengaruhi bagian nilai
kegiatan lain.
3. Divisibility (pembagian), dalam program linier diperbolehkan menggunakan
angka pecahan.
4. Certainty (kepastian), artinya nilai parameter yang terdapat dalam model
program linier diketahui secara pasti.
Model umum program linier dapat dirumuskan ke dalam bentuk matematika
sebagai berikut:
𝑀𝑎𝑘𝑠𝑖𝑚𝑢𝑚𝑘𝑎𝑛𝑎𝑡𝑎𝑢𝑀𝑖𝑛𝑖𝑚𝑢𝑚𝑘𝑎𝑛𝑍= 𝑐𝑗𝑥𝑗
𝑛
𝑗=1
, 𝑢𝑛𝑡𝑢𝑘 𝑗= 1, 2,…,𝑛
Kendala:
𝑎𝑖𝑗 𝑛
𝑗=1
2.5 Metode Simpleks
Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang bergerak
selangkah demi selangkah, dimulai dari titik ekstrim pada daerah fisibel (ruang solusi)
menuju titik ekstrim yang optimum. Dalam metode simpleks terdapat beberapa
definisi penting, yaitu:
a. Solusi Basis, yaitu solusi dimana terdapat sebanyak-banyaknya m variabel
berharga bukan nol.
b. Solusi basis fisibel, yaitu solusi variabel pada suatu solusi basis berharga
nonnegatif.
c. Solusi fisibel titik ekstrim, yaitu solusi fisibel yang tidak terletak pada suatu
segmen garis yang menghubungkan dua solusi fisibel lainnya.
2.5.1 Algoritma Metode Simpleks untuk Persoalan Maksimasi
Untuk menyelesaikan persoalan maksimasi program linier dengan menggunakan
metode simpleks, terdapat beberapa langkah, yaitu:
1. Konversikan formulasi persoalan ke dalam bentuk standar.
2. Cari solusi basis fisibel (BFS).
3. Jika seluruh variabel nonbasis mempunyai koefisien nonnegatif pada baris
fungsi tujuan, maka solusi basis fisibel sudah optimal. Jika pada baris fungsi
tujuan masih ada variabel dengan koefisien negatif, pilih salah satu variabel
yang mempunyai paling negatif pada baris tersebut. Variabel ini akan
memasuki status variabel basis, karena itu variabel ini disebut sebagai variabel
yang masuk basis (entering variable, disingkat EV)
4. Hitung rasio dari ruas kanan dan koefisien EV pada setiap baris EV yang
mempunyai koefisien positif. Variabel basis pada baris pembatas dengan rasio
positif terkecil akan berubah status menjadi variabel nonbasis. Variabel ini
kemudian disebut sebagai variabell yang meninggalkan basis (leaving
variable/ disingkat LV). Lakukan operasi baris elementer untuk membuat
koefisien EV pada baris dengan rasio positif terkecil ini mmenjadi berharga 1
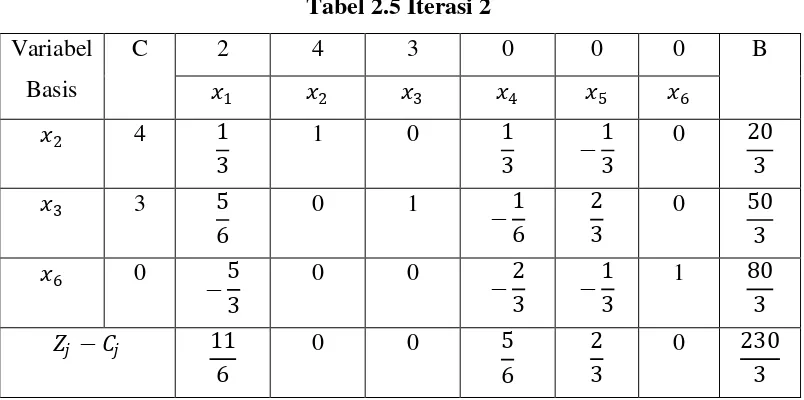
Tabel 2.5 Iterasi 2
fisibel sudah optimal, dengan maksimum Z = 230
3 untuk 𝑥2 =
2.5.2 Algoritma Metode Simpleks untuk Persoalan Minimasi
Sama halnya dengan penyelesaian persoalan maksimasi, untuk persoalan minimasi
juga menggunakan langkah-langkah penyelesaian, yaitu:
1. Konversikan formulasi persoalan ke dalam bentuk standar.
2. Cari solusi basis fisibel (BFS).
3. Jika seluruh variabel nonbasis mempunyai koefisien nol atau negatif pada baris
fungsi tujuan, maka solusi basis fisibel sudah optimal. Jika pada baris fungsi
tujuan masih ada variabel dengan koefisien positif, pilih salah satu variabel
yang mempunyai paling positif pada baris tersebut. Variabel ini akan
memasuki status variabel basis, karena itu variabel ini disebut sebagai variabel
yang masuk basis (entering variable, disingkat EV)
4. Hitung rasio dari ruas kanan dan koefisien EV pada setiap baris EV. Variabel
basis pada baris pembatas dengan rasio terkecil akan berubah status menjadi
variabel nonbasis. Variabel ini kemudian disebut sebagai variabel yang
meninggalkan basis (leaving variable/ disingkat LV). Lakukan operasi baris
menjadi berharga 1 dan berharga nol pada baris-baris lainnya. Kemudian
kembali ke langkah 3.
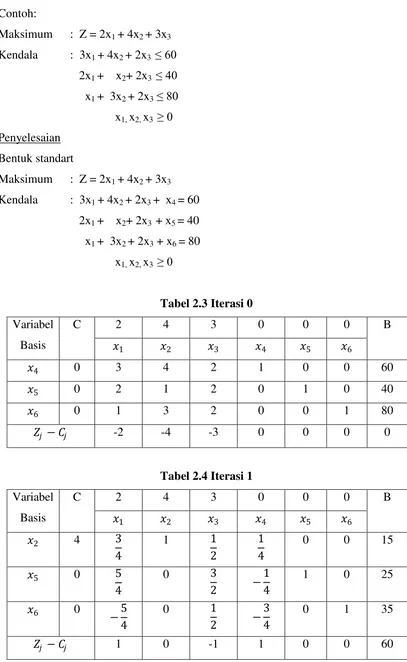
Contoh:
Minimum : Z = 8x1 + 10x2 + 7x3 + 6x4 + 11x5 + 9x6 Kendala : 12x1 + 9x2 + 25x3 + 20x4 + 17x5 + 13x6≥ 60
35x1 + 42x2 + 18x3 + 31x4 + 56x5 + 49x6 ≥ 150 37x1 + 53x2 + 28x3 + 24x4 + 29x5 + 20x6≥ 125 Xj≥ 0 ; j = 1, 2, 3, ..., 6
Penyelesaian
Bentuk standart
Minimum : Z = 8x1 + 10x2 + 7x3 + 6x4 + 11x5 + 9x6 + Mx10 + Mx11 + Mx12 Kendala : 12x1 + 9x2 + 25x3 + 20x4 + 17x5 + 13x6– x7 + x10 = 60
35x1 + 42x2 + 18x3 + 31x4 + 56x5 + 49x6– x8 + x11 = 150 37x1 + 53x2 + 28x3 + 24x4 + 29x5 + 20x6– x9 + x12 = 125
Tabel 2.6 Iterasi 0
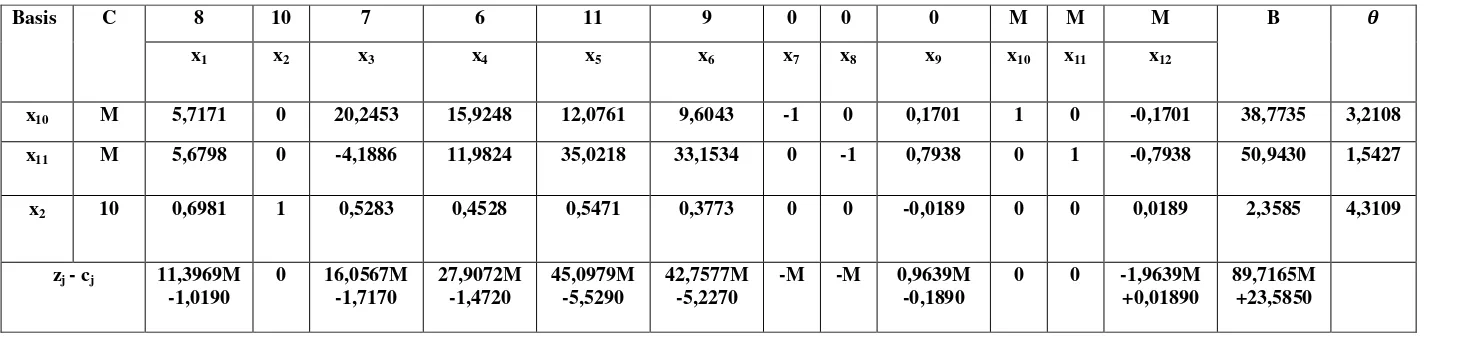
Tabel 2.7 Iterasi 1
Basis C 8 10 7 6 11 9 0 0 0 M M M B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
x10 M 12 9 25 20 17 13 -1 0 0 1 0 0 60 6,6667
x11 M 35 42 18 31 56 49 0 -1 0 0 1 0 150 3,5714
X12 M 37 53 28 24 29 20 0 0 -1 0 0 1 125 2,3585
zj - cj 84M-8 104M-10 71M-7 75M-6 102M-11 82M-9 -M -M -M 0 0 0 335M
Basis C 8 10 7 6 11 9 0 0 0 M M M B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12
x10 M 5,7171 0 20,2453 15,9248 12,0761 9,6043 -1 0 0,1701 1 0 -0,1701 38,7735 3,2108
x11 M 5,6798 0 -4,1886 11,9824 35,0218 33,1534 0 -1 0,7938 0 1 -0,7938 50,9430 1,5427
x2 10 0,6981 1 0,5283 0,4528 0,5471 0,3773 0 0 -0,0189 0 0 0,0189 2,3585 4,3109
zj - cj 11,3969M -1,0190
0 16,0567M -1,7170
27,9072M -1,4720
45,0979M -5,5290
42,7577M -5,2270
-M -M 0,9639M -0,1890
0 0 -1,9639M +0,01890
Tabel 2.8 Iterasi 2
Tabel 2.9 Iterasi 3
Basis C 8 10 7 6 11 9 0 0 0 M M B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11
x10 M 3,6401 0 21,7765 11,5424 0 -2,5201 -1 0,3659 -0,1197 1 -0,3659 20,1437 0,925
X5 11 0,1720 0 -0,1268 0,3629 1 1,004 0 -0,0303 0,024 0 0,0303 1,5427 -12,1664
X2 10 0,604 1 0,5977 0,2543 0 -0,172 0 0,0166 -0,032 0 -0,0166 1,5145 2,5339
zj - cj 3,6401M-0,068
0 21,7765M-2,4178
11,5424M+0, 5349
0 -2,5201M +2,044
-M 0,3659M-0,1673
-0,1197M -0,056
0 -0,3659M +0,1673
20,1437M +16,9697
Basis C 8 10 7 6 11 9 0 0 0 M B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
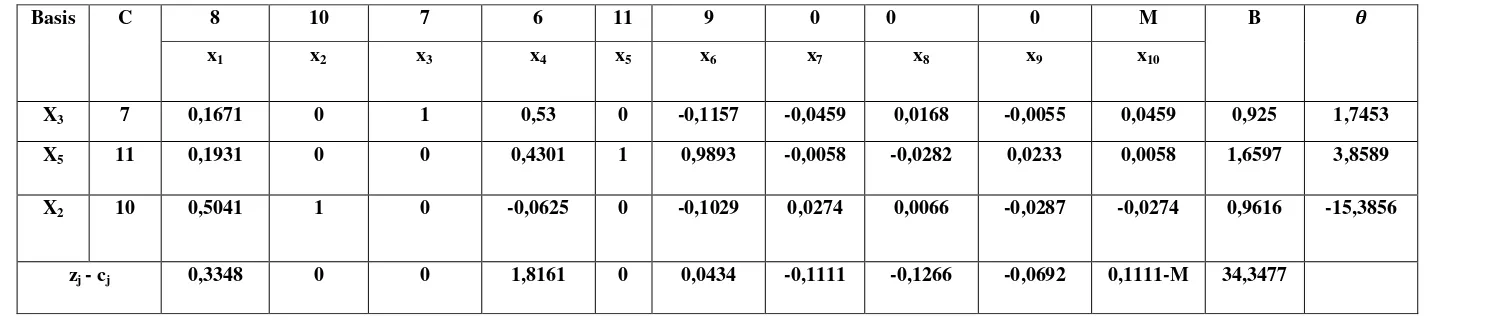
X3 7 0,1671 0 1 0,53 0 -0,1157 -0,0459 0,0168 -0,0055 0,0459 0,925 1,7453
X5 11 0,1931 0 0 0,4301 1 0,9893 -0,0058 -0,0282 0,0233 0,0058 1,6597 3,8589
X2 10 0,5041 1 0 -0,0625 0 -0,1029 0,0274 0,0066 -0,0287 -0,0274 0,9616 -15,3856
Tabel 2.10 Iterasi 4
Tabel 2.11 Iterasi 5
Basis C 8 10 7 6 11 9 0 0 0 B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9
X4 6 0,3153 0 1,8868 1 0 -0,2183 -0,0866 0,0317 -0,0104 1,7453 -7,995
X5 11 0,0575 0 -0,8115 0 1 1,0832 -0,0314 -0,0418 0,0278 0,909 0,8392
X2 10 0,5238 1 0,1179 0 0 -0,1165 0,022 0,0086 -0,0294 1,0707 -9,1906
zj - cj -0,2377 0 -3,4267 0 0 0,4404 0,0458 -0,1836 -0,0506 31,1778
Basis C 8 10 7 6 11 9 0 0 0 B 𝜽
x1 x2 x3 x4 x5 x6 x7 x8 x9
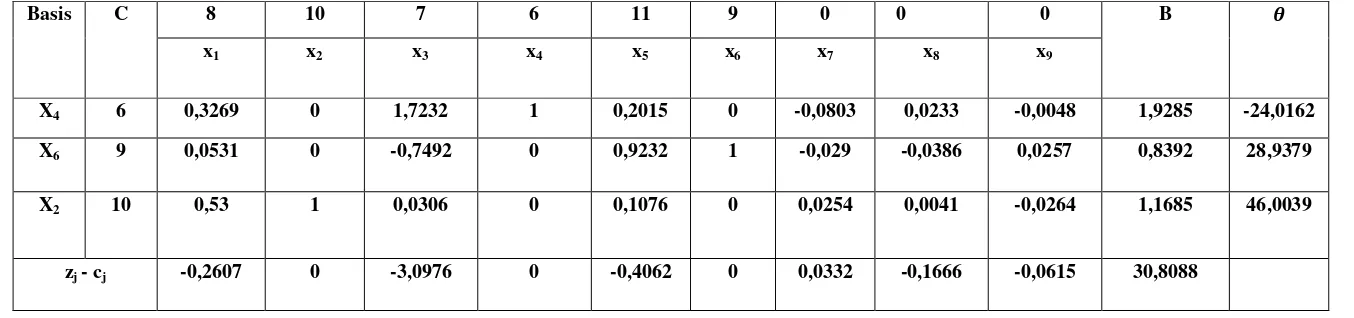
X4 6 0,3269 0 1,7232 1 0,2015 0 -0,0803 0,0233 -0,0048 1,9285 -24,0162
X6 9 0,0531 0 -0,7492 0 0,9232 1 -0,029 -0,0386 0,0257 0,8392 28,9379
X2 10 0,53 1 0,0306 0 0,1076 0 0,0254 0,0041 -0,0264 1,1685 46,0039
Tabel 2.12 Iterasi 6
Karena zj– cj ≤ 0, maka solusi optimal telah diperoleh.
Dengan nilai minimum Z = 29,8482 ; x2 = 0,4335 ; x4 = 4,2522 ; x7 = 28,9379 ; x1 = x3 = x5 = x6 = x8 = x9 = 0
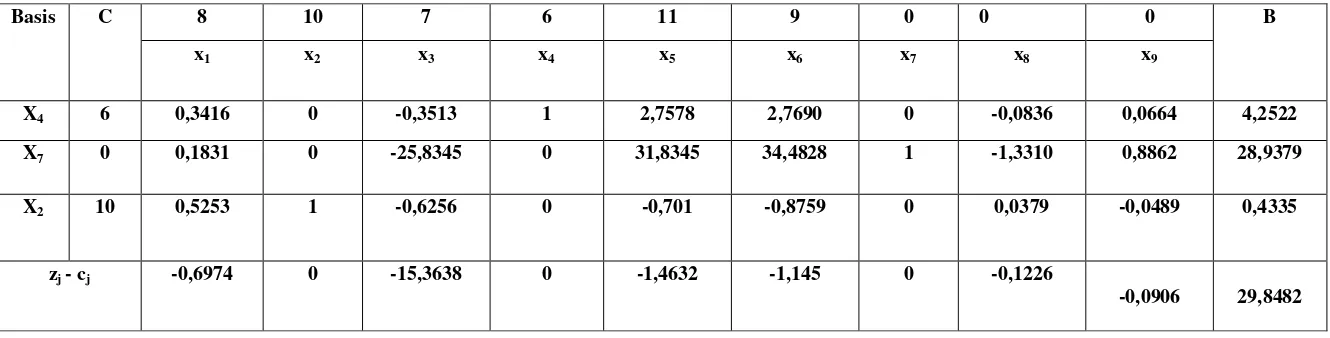
Basis C 8 10 7 6 11 9 0 0 0 B
x1 x2 x3 x4 x5 x6 x7 x8 x9
X4 6 0,3416 0 -0,3513 1 2,7578 2,7690 0 -0,0836 0,0664 4,2522
X7 0 0,1831 0 -25,8345 0 31,8345 34,4828 1 -1,3310 0,8862 28,9379
X2 10 0,5253 1 -0,6256 0 -0,701 -0,8759 0 0,0379 -0,0489 0,4335
zj - cj -0,6974 0 -15,3638 0 -1,4632 -1,145 0 -0,1226
2.6 Teori Dualitas
Ide dasar yang melatar belakangi teori dualitas adalah bahwa setiap persoalan program
linier mempunyai suatu program linier lain yang saling berkaitan yang disebut dual,
sedemikian sehingga solusi pada persoalan semula (yang disebut primal) juga
memberi solusi pada dualnya.
Adapun hubungan antara primal dan dual adalah sebagai berikut:
1. Koefisien fungsi tujuan primal menjadi konstanta ruas kanan bagi dual,
sedangkan konstanta ruas kanan primal menjadi koefisien fungsi tujuan dual.
2. Untuk setiap pembatas primal ada satu variabel dual dan untuk setiap variabel
primal ada satu pembatas dual.
3. Tanda ketidaksamaan pada pembatas akan bergantung pada fungsi tujuannya.
4. Fungsi tujuan berubah bentuk (maksimasi menjadi minimasi dan sebaliknya).
5. Setiap kolom pada primal berkorespondensi dengan baris (pembatas) pada
dual.
6. Setiap baris (pembatas) pada primal berkorespondensi dengan kolom pada
dual.
7. Dual dari dual adalah primal.
Untuk lebih jelas lagi dapat dilihat pada tabel berikut ini:
Tabel 2.13 Primal dan Dual