www.elsevier.com/locate/orms
On the structure and complexity of the 2-connected Steiner network
problem in the plane
Emily Larson Luebke, J. Scott Provan
∗Department of Operations Research, University of North Carolina, Chapel Hill, NC 27599-3180, USA
Received 1 August 1999; received in revised form 1 September 1999
Abstract
We consider the problem of nding a minimum Euclidean length graph 2-connecting a set of points in the plane. We show that the solution to this problem is an edge-disjoint union of full Steiner trees. This has three important corollaries. The rst is a proof that the problem is NP-hard, even in the sense of nding a fully polynomial approximation scheme. The second is a complete description of the solutions for 2SNPP for rectangular arrays of lattice points. The third is a linear-time algorithm for constructing an optimal solution to 2SNPP given its topological description. c2000 Published by Elsevier Science B.V. All rights reserved.
Keywords:Network graphs; Design; Survivability; Steiner tree; Polynomial approximation
1. Introduction
An important problem in the construction of sur-vivable networks (see [3]) is the 2-Connected Steiner Network Problem in the Plane(2SNPP). 2SNPP has an input a setZ ofkterminalpoints in the plane, and as output the minimum Euclidean length 2-connected network of straight line segments which contains all of the points ofZ. (The distinction between edge- and vertex-connectivity is not important in this context, since the optimal solution will be the same for both versions.) Previous work on the 2-connected prob-lem has concentrated primarily on the graphical ver-sion, where the 2-connected network is chosen from
∗Corresponding author.
E-mail address:[email protected] (J.S. Provan)
a weighted graph (see [3]). This problem has been shown to be NP-hard, the reduction coming directly from the Hamiltonian Circuit problem. Some struc-tural results are available for the Euclidean problem [5,16], but the complexity of 2SNPP is still open.
The 1-connected analogue to this problem is the well-known Steiner Tree Problem, which involves nding the minimum length network (which is in fact a tree) connecting all pairs of terminals. This problem has enjoyed considerable attention (see [8]) and is known to be NP-hard [2]. A complete set of solutions to the problem has been found by Brazil et al. [1] when the points ofZ form a rectangular lattice of integer points. Construction algorithms — most recently the algorithm of Warme et al. [17] — solve the Steiner tree problem by putting together sets offull Steiner trees(FSTs). These are minimum length trees on a
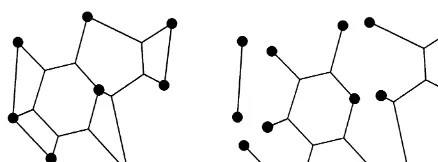
Fig. 1. A partition into full Steiner subnetworks.
subset of the terminals such that the terminals are all
end (degree 1) vertices of the tree. FSTs are easy to construct geometrically and typically span a small number of the terminals, and so are excellent building blocks for Steiner tree solutions.
In this paper we give an interesting result concern-ing the structure of an optimal solution to 2SNPP, namely, that the solution is made up of an edge-disjoint union of FSTs. We then give three important conse-quences of this result. The rst is a proof that 2SNPP is NP-hard, even in the sense of nding a “fully polynomial approximation scheme”. The second is a complete characterization of the 2SNPP solutions for rectangular lattices, thus extending the results of Brazil et al. The third shows that there exists a linear-time algorithm for constructing the geometric solution to the 2SNPP given the topological solution, and we outline a rudimentary enumerative solution algorithm for solving 2SNPP along the same lines as those suggested for the Steiner tree problem.
2. The structural result
Consider optimal solution F associated with a 2SNPP instance Z. It follows immediately from the results in [12] that every vertex ofFhas degree 2 or 3, and that the nonterminal vertices of F — which we will callSteiner vertices— are of degree exactly 3. Now the edgesFcan be partitioned uniquely into nonempty setsT1; : : : ;Trwith the property that each Tiis maximal with respect to the fact that every pair of edges inTi can be connected by a path in F— with possibly coincident endpoints — each of whose interior vertices are Steiner vertices (see Fig. 1). We call Ti afull Steiner subnetwork (FSS) of F. It follows that two distinct FSSs intersect only at a
Fig. 2. Cycles intersecting in a simple path composed of Steiner points.
set of terminal vertices. We can now state the main structural result.
Proposition 1. For any optimal solution F to
2SNPP;each FSS ofFis in fact a FST.
To prove this result, we rst give a lemma that is interesting in its own right.
Lemma 1. If two cycles of Fintersect in a simple
path;then this path must have an interior vertex that is a terminal.
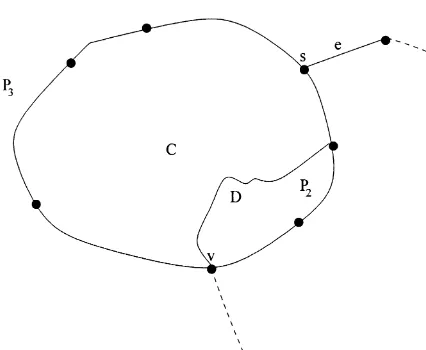
Proof. LetC1andC2be two cycles ofFthat intersect in a simple pathP all of whose interior vertices are Steiner points, and choose these cycles so that the number of edges in P is as small as possible (see Fig. 2). Suppose there is at least one interior vertexs
onP. Sincesis a Steiner point, we know thatsmust be of degree exactly 3, and so there must be a unique edgeeadjacent to vthat is not onP, and hence not on either cycle.
SinceFis a solution to the 2SNPP, thenemust be part of a cycleD, which must then contain an edgef
ofP. FollowDstarting witheaway fromfuntil the rst pointvat whichDagain intersects either C1 or
C2, sayC1. Then by continuing onC1 in the appro-priate direction back throughftoswe obtain a cycle
Fig. 3. Cycle in full Steiner component.
The pathPmust therefore contain exactly one edge (v1; v2). Remove (v1; v2) and consider all cuts (X; V\
X) inF\{(v1; v2)}. The only cuts that have changed are those with v1 ∈ X and v2 ∈ V \X, so examine those cuts. Clearly v1 and v2 both lie in the cycle
C1∪C2\{(v1; v2)}, and so (X; V\X) must have at least two of the edges from this cycle in it. We conclude that all cuts inF\{(v1; v2)}have at least two edges in them, and soF\{(v1; v2)}is a solution to the 2SNPP. This contradicts the fact thatFis an optimal solution to the 2SNPP, and the lemma follows.
Proof of Proposition 1. LetSbe a FSS forF, and suppose thatScontains a cycleC. We can chooseC to contain at most one terminal, for if it contains at least one terminalt, pick the two edgese1ande2onC adjacent tot. By the denition of FSS there must be a cycle inScontaininge1 ande2 and containing no terminal vertices other thant. This will be our choice forC.
Choose one of the Steiner pointssonC, and con-sider the unique edgeeadjacent tosthat is not part of
C (see Fig. 3). SinceF is a solution to the 2SNPP, thenemust be part of a cycle D, which must there-fore also contain one of the edges ofC adjacent to
e. Form the pathP1by followingDstarting atsand going throughe, to the rst pointvthat is again onC. Nowsandvpartition the edges ofCinto pathsP2 andP3. Further, sinceCcontains at most one terminal, then at least one of P2 or P3, say P2, has all of its
interior vertices Steiner points. It follows that the cycle formed by pathsP1andP2intersectsCinP2, violating the conditions of Lemma 1. Thus such a cycle cannot exist, and so all the FSSs are trees. By the denition of FSS these trees can have terminals only at the end vertices, and the result follows.
3. NP-hardness of 2SNPP
In this section we prove that 2SNPP is NP-hard. In particular, we reduce a special form of the Euclidean Traveling Salesman Problem to it. The ETSP involves nding the minimum Euclidean-length circuit through a given set of points on the Euclidean plane. The Trav-eling Salesman Problem has always been closely as-sociated with 2-connected network problems (see, for example [4]), as a TSP circuit through a set of points is also a feasible — though not necessarily optimal — solution to 2SNPP for that set of points. We rst show that under special conditions the TSP solution is in fact the optimal solution to 2SNPP.
Lemma 2. LetZ be a set ofkinteger lattice points. Then
• Every solution to2SNPPis of length at leastk.
• The only solutions to2SNPP of length exactlyk
are TSP circuits such that every two successive points are adjacent in the lattice.
• All other solutions are of length at leastk+√2−1.
Proof. LetFbe an optimal solution to 2SNPP onZ. From Proposition 1 we can partitionFinto a set of edgese1; : : : ; enconnecting vertices ofZ, together with a setT1;T2; : : : ;Tt of FSTs each of which spans at least 3 terminals. Fori=1; : : : ; t, letkibe the number of terminals on Steiner treeTi. Now the minimum length
spanning treeon this set of terminals is of length at leastki−1. The result of Du and Hwang [6] on the
Steiner ratioshows that the lengthTimust be at least
√
3
2 (ki−1)¿ ki=2: (∗) This means that the total length ofFis
l(F) =
n
X
i=1
l(ei) + t
X
j=1
¿n+
with the rst inequality being strict unless l(ei) = 1 for all i; and the last inequality being strict unless
t= 0. Now each terminal must be contained in at least two distinct sets ofe1; : : : ; en;T1;T2; : : : ;Tt, so that 2n+Pti=1ki= 2k. Thus
l(F)¿k
with equality holding only whent=0 and eachl(ei)= 1, that is, when the solution is a Hamiltonian circuit through the vertices ofZ with each successive pair of points being distance 1 apart.
Finally, ifFis notof the above sort then one of the following must hold:
Case 1: F contains an edge between two non-adjacent lattice points. Thenl(F)¿k+√2−1.
Case2:Fcontains a FST on four or more termi-nals. Using (∗) we have thatl(F)¿k+ (√3=2)(4−
1)−4=2¿ k+√2−1.
Case3:F contains two FST on at least 3 termi-nals each. Again using (∗), we have thatl(F)¿k+ 2((√3=2)(3−1)−3=2)¿ k+√2−1.
Case4:Fcontains exactly one FST on 3 terminals. Since each terminal in a 2SNPP must be at least degree 2, then the number of edges inF, excluding those in the FST, must be at least⌈(2k−3)=2⌉=k−1, with each edge of length at least 1. Using the Steiner ratio we havel(F)¿k−1 + (√3=2)(3−1)¿ k+√2−1.
The result follows.
Corollary 1. 2SNPPisNP-hard.
Proof. Itai et al. [9] (see also [10]) show that the following problem is NP-complete:
Input: SetZ integer lattice points in the plane.
Question: Does there exist a Hamiltonian circuit through the points of Z such that the dis-tance between each successive pair of points is 1?
It follows immediately from Lemma 2 that for any instance of HCGG the 2SNPP will be lengthk if and only if HCGG has the required Hamiltonian circuit.
We note that the decision version of 2SNPP — Does there exist a solution to 2SNPP for given setZ
that is of length at most a given rational numberN? — is not known to be in NP, due to the problem of comparing sums of irrational distances. An approach for solving this class of problems that has been suc-cessful in several related papers [13–16] is to nd a
fully polynomial approximation scheme(FPAS) for 2SNPP. Here we wish to have an algorithm which, given instance Z for 2SNPP and accuracy bound , will nd an-approximationto SNPP, that is, a fea-sible solutionFfor this instance whose length ˆl sat-ises ( ˆl−l∗)=l∗¡ , where l∗ is the length of the optimal solution for this instance. Further, this algo-rithm must have a running time that is polynomial in 1= and the length of the input describingZ. Hsu and Hu [5] give a polynomial algorithm to nd a (√3−1)-approximation for 2SNPP. There is a limit to how far these types of results can go, however, as the next results shows.
Corollary 2. A FPAS for 2SNPP will not exist un-lessP = NP.
Proof. For any instance of HCGG, we have from Lemma 2 that a solution to 2SNPP that isnota HCGG solution must have length at leastk+√2−1¿ k+ 0:414. Now for = 0:414=k, an -approximation to 2SNPP will have length less thank+0:414 if and only if HCGG has a feasible solution. It follows that there can be no algorithm that nds an-approximation in time polynomial in 1==k=0:414 unless P = NP.
4. The solution to 2SNPP for rectangular arrays of lattice points
In this section we consider solutions of 2SNPP in the case where Z forms an m×n rectangular ar-ray of integer lattice points on the Euclidean plane. An elegant solution to the Steiner tree problem for this class of instances was found by Brazil et al. [1]. Lemma 2 can be used to nd a simple set of corre-sponding solutions for the 2-connected case.
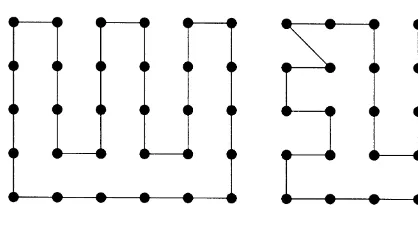
Fig. 4. Solutions to 2SNPP on a rectangular lattice.
single circuit through the points ofZ of length
• kif eithermornis even;
• k+√2−1if bothnandmare odd.
Proof. If either n or m is even, then it is easy to construct a circuit consisting entirely of adjacent lat-tice points (see Fig. 4 (a), for example) which by Lemma 2 is optimal. If both n andm are odd, then by a simple parity argument there can be no circuit consisting entirely of adjacent lattice points through the odd number of vertices ofZ. By Lemma 2 the op-timal 2SNPP solution must therefore have length at leastk+√2−1. It is also easy to construct a circuit consisting entirely of adjacent lattice points except for one diagonal lattice edge (see Fig. 4(b), for example), and this has length exactlyk+√2−1. The corollary follows.
5. Finding a 2SNPP from topological structure
Results by Melzak [11] and Hwang [7] establish a linear-time algorithm to construct a geometric re-alization for a solution to the Steiner tree problem based on the topological description of the solution. Proposition 1 allows these results to apply immedi-ately to 2SNPP. In particular, suppose we are given a topological description of a solution to 2SNPP, in the form of a 2-connected graphGwhose vertices are designated as either labeled terminal vertices or Steiner vertices. We wish to construct a geometric solution corresponding to G, by placing the Steiner points correctly in the plane and drawing straight lines between Steiner points and terminal points so
that the resulting plane network corresponds to the optimal solution for 2SNPP. Proposition 1 shows that by rst partitioning G into its FSSs we obtain a set of edge-disjoint FSTs that will individually have the same properties as they do for the Melzak construc-tion. By using the linear-time Hwang implementation of the Melzak construction to place each of the trees, we obtain the following obvious corollary:
Corollary 4. The optimal solution to 2SNPP for given instance Z can be constructed from its topo-logical description in linear time.
The real importance of Corollary 4 is that it gives a basis for constructing a solution to 2SNPP by e-cient enumeration of the appropriate graph topologies. Proposition 1 shows that there can be at most 3(k−2) Steiner points in any optimal solution, since each FST that spans a subset ofkiof the terminals, can obtain at mostki−2 Steiner points, and each terminal is con-tained in at most 3 FSTs. Thus one method of solving 2SNPP could be to enumerate all possible 2-connected graphs on thek terminals and at most 3(k−2) pro-posed Steiner points and then to construct the associ-ated geometric solutions, choosing the best as the op-timal 2SNPP solution. This enumeration, however, is not practical, and so it is necessary to extend ecient FST enumeration and pruning techniques, like those used in [17] for STP, to the 2SNPP problem. We leave this problem for future research.
References
[1] M. Brazil, J.H. Rubinstein, D.A. Thomas, J.F. Weng, N.C. Wormald, Minimal Steiner trees for rectangular arrays of lattice points, J. Combin. Theory Ser. A 79 (1997) 181–208.
[2] M.R. Garey, R.L. Graham, D.S. Johnson, The complexity of computing Steiner minimal trees, SIAM J. Appl. Math. 32 (1977) 835–859.
[3] M. Grotschel, C.L. Monma, M. Stoer, Design of survivable networks, in: M.O. Ball, T.L. Magnanti, C.L. Monma, G.L. Nemhauser (Eds.), Network Models, Handbooks in Operations Research and Managements Science Series, Vol. 7, North-Holland, New York, 1995, pp. 617–672. [4] G.N. Frederickson, J. Ja’Ja’, On the relationship between the
biconnectivity augmentation and traveling salesman problems, Theoret. Comput. Sci. 9 (1982) 189–201.
[6] D.-Z. Hu, F.K. Hwang, A proof of Gilbert and Pollack’s conjecture on the Steiner ratio, Algorithmica 7 (1992) 121–135.
[7] F.K. Hwang, A linear time algorithm for full Steiner trees, Oper. Res. Lett. 4 (1986) 235–237.
[8] F.K. Hwang, D.S. Richards, P. Winter, The Steiner Tree Problem, North-Holland, New York, 1992.
[9] A. Itai, C.H. Papadimitriou, J. Szwarcter, Hamiltonian paths in grid graphs, SIAM J. Comput. 11 (1982) 676–686. [10] D. Johnson, C.H. Papadimitriou, Computational complexity,
in: E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan, D.B. Shmoys (Eds.), The Traveling Salesman Problem, Wiley, New York, 1986, pp. 37–85 (Chapter 2).
[11] Z.A. Melzak, On the problem of Steiner, Canad. Math. Bull. 4 (1961) 143–148.
[12] C.L. Monma, B.S. Munson, W.R. Pulleyblank, Minimum weight two-connected spanning networks, Math. Programming 46 (1990) 153–171.
[13] J.S. Provan, Convexity and the Steiner tree problem, Networks 18 (1988) 55–72.
[14] J.S. Provan, An approximation scheme for nding Steiner trees with obstacles, SIAM J. Comput. 17 (1989) 920–934.
[15] J.S. Provan, A fully polynomial approximation scheme for the Euclidean Steiner augmentation problem, in: D.-Z. Du, J.M. Smith, J.H. Rubinstein (Eds.), Advances in Steiner Trees, Kluwer Academic Publishers, Dordrecht, 2000, pp. 235–253.
[16] K.T. Talluri, Issues in the design and analysis of survivable networks, Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, 1991.