Persamaan schwarzschild dan implikasinya pada lintasan partikel.

PERSAMAAN SCHWARZSCHILD

DAN IMPLIKASINYA PADA LINTASAN PARTIKEL

ABSTRAK

Telah dilakukan penelitian tentang implikasi persamaan Schwarzschild pada bentuk lintasan dan perubahan geometri ruang suatu partikel bergerak. Partikel yang bergerak di daerah r >α _{berada dalam bak-waktu, tetapi kalau partikel di daerah}

α <

SCHWARZSCHILD EQUATION

AND ITS IMPLICATION ON PARTICLE TRAJECTORY

ABSTRACT

PERSAMAAN SCHWARZSCHILD

DAN IMPLIKASINYA PADA LINTASAN PARTIKEL

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Fisika

Oleh:

Dewa Ayu Ratmi Yanti NIM : 013214014

PROGRAM STUDI FISIKA JURUSAN FISIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

SCHWARZSCIHLD EQUATION

AND ITS IMPLICATION ON PARTICLE TRAJECTORY

Scription

Presented as Partial Fulfillment of the Requirements To Obtain the Sarjana Sains Degree

In Physics

By :

Dewa Ayu Ratmi Yanti Student Number 013214014

PHYSICS STUDY PROGRAM PHYSICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

SKRIPSI

PERSAMAAN SCHWARZSCHILD

DAN IMPLIKASINYA PADA LINTASAN PARTIKEL

Oleh :

Dewa Ayu Ratmi Yanti Nim : 013214014

Telah disetujui oleh :

Pembimbing

SKRIPSI

PERSAMAAN SCHWARZSCHILD

DAN IMPLIKASINYA PADA LINTASAN PARTIKEL

Dipersiapkan dan ditulis oleh Dewa Ayu Ratmi Yanti

NIM : 013214014

Telah dipertahankan di depan Panitia Penguji Pada tanggal 12 Maret 2008

dan dinyatakan memenuhi syarat Susunan Panitia Penguji

Nama Lengkap Tanda tangan

Ketua Dr. Ign. Edi Santosa, MS. ... Sekretaris Drs. Drs. Vet. Asan Damanik, M.Si. ...

Anggota Drs. Drs. Vet. Asan Damanik, M.Si. ... Anggota Dr. Agung Bambang Setyo Utomo, SU ... Anggota Dr. Ign. Edi Santosa, MS ...

Yogyakarta, Maret 2008

Fakultas Sains dan Teknologi

Universitas Sanata Dharma Dekan,

MOTTO DAN PERSEMBAHAN

" Apapun yang engkau lakukan,

Apapun yang engkau makan,

Apapun yang engkau persembahkan

atau berikan sebagai sumbangan

serta pertapaan

dan apapun yang engkau lakukan,

lakukanlah kegiatan itu sebagai

persembahaan kepada-Ku

wahai putra Kunti”

Bhagawad-gita Sloka 9.27

PERSEMBAHAN :

"Skripsi ini aku persembahkan untuk Ayah, Ibu, adik –

adikku dan Sinar kekasihku yang selalu memberikan

dukungan, semangat, doa, dan kasih sayang sepanjang

PERSAMAAN SCHWARZSCHILD

DAN IMPLIKASINYA PADA LINTASAN PARTIKEL

ABSTRAK

Telah dilakukan penelitian tentang implikasi persamaan Schwarzschild pada bentuk lintasan dan perubahan geometri ruang suatu partikel bergerak. Partikel yang bergerak di daerah r >α berada dalam bak-waktu, tetapi kalau partikel di daerah

α

<

SCHWARZSCHILD EQUATION

AND ITS IMPLICATION ON PARTICLE TRAJECTORY

ABSTRACT

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Ida Sang Hyang Widhi Wasa atas segala asung kerta wara nugrahanya sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini berjudul : ”PERSAMAAN SCHWARZSCHILD DAN IMPLIKASINYA PADA LINTASAN PARTIKEL”, yang diajukan sebagai salah

satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Fisika Universitas Sanata Dharma Yogyakarta.

Penulis mengucapkan terima kasih kepada semua pihak yang telah membantu penulis baik berupa waktu, tenaga, bimbingan, dorongan, dan sumbang saran yang penulis butuhkan dalam penyelesaian skripsi ini. Pada kesempatan ini penulis ingin mengucapkan terima kasih kepada:

1. Bapak Drs. Drs. Vet. Asan Damanik, M.Si. selaku dosen pembimbing yang telah banyak meluangkan waktu untuk membimbing, mendampingi, memberikan dorongan dan semangat dalam pengerjaan tugas akhir ini.

2. Ayah dan Ibuku tercinta yang tanpa henti memberikan dukungan, dorongan, doa, dan kasih sayang sehingga penulis dapat menyelesaikan skripsi ini.

4. Sinar yang selama ini selalu menemaniku, memberikan dorongan, semangat dan doanya pada waktu pengerjaan tugas akhir ini.

5. Om mift dan Ninik Cuyak terimakasih atas semua dorongan dan dukungannya.

6. Temen-teman Bali, Ketut, Wawan, Sidi, Gde, Wandi, Andika, yang selalu memberikan semangat dan menjadi sahabat yang baik bagiku serta menemaniku mengerjakan skripsi.

7. Temen-teman fisika, Manggar, Frida, Ratna, Nari, Vemby, Toni, yang selama bertahun-tahun selalu berjuang bersamaku.

8. Ir.Sri Agustini Sulandari, M.Si selaku dosen pendamping akademik yang sudah banyak memberikan pendampingan selama menjadi mahasiswa.

9. Seluruh Staff Pengajar Jurusan Fisika yang telah memberikan pengajaran dan pendampingan.

10.Teman-teman yang rela menunggu giliran pada saat bimbingan, Minto, Kia, Danang terimakasi sudah mau bersabar.

11.Semua pihak yang tidak dapat disebutkan satu demi satu. Terimakasih atas segala bantuannya.

Akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi dunia pendidikan dan khususnya pembaca.

Yogyakarta, Februari 2008

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini adalah karya saya dan tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya suatu karya ilmiah.

Yogyakarta, Februari 2008

Penulis

Dewa Ayu Ratmi Yanti

DAFTAR ISI

HALAMAN JUDUL………... HALAMAN PERSETUJUAN PEMBIMBING………... HALAMAN PENGESAHAN .……….. HALAMAN MOTO PERSEMBAHAN …………...………. ABSTRAK ………. ABSTRACT ……….. KATA PENGANTAR ………... PERNYATAAN KEASLIAN KARYA………. DAFTAR ISI ………. BAB I. PENDAHULUAN………. 1.1. Latar Belakang ………. 1.2. Perumusan Masalah ………. 1.3. Batasan Masalah ……….. 1.4. Tujuan dan Manfaat Penelitian ……… 1.4.1. Tujuan Penelitian ………... 1.4.2. Manfaat Penelitian ………. 1.5. Sistematika Penulisan ………... BAB II. DASAR TEORI ………... BAB III. METODA PENELITIAN………...

3.1. Jenis Penelitian ………. 3.2. Sarana Penelitian ……….. 3.3. Langkah-Langkah Penelitian ……… BAB IV. HASIL PEMBAHASAN...………... 4.1. Orbit Planet ...………... 4.2. Perubahan Geometri dan Sifat Fisis Ruang ...………. 4.3. Lintasan Cahaya dan Panjang Fokus ... BAB V. PENUTUP...………... 5.1. Kesimpulan ...………... 5.2. Saran ... DAFTAR PUSTAKA ……… LAMPIRAN ...

BAB I

PENDAHULUAN

1.1.Latar Belakang

Pada tahun 1916, sebulan setelah Einstein mempublikasikan teori relativitas umum, seorang ahli astronomi dari Jerman yang bernama Schwarzschild menemukan penyelesaian persamaan medan gravitasi Einstein. (Lawrie, 1998)

μυ μυ

μυ R g kT

R ⎟ =

⎠ ⎞ ⎜

⎝

⎛ _−Λ −

2 1

(1.1)

Dengan R _υ tensor Ricci (yang digambarkan terikat dengan dua indeks dari tensor Riemann), R merupakan skalar kelengkungan Ricci (R = g υR _υ), tetapan kosmologi, g

Λ

υ tensor orde dua kovarian, k kopling antara geometri dan materi yang menunjukan kuat gaya gravitasi dan T _υ adalah tensor tekanan. Penyelesaian sederhana persamaan medan Einstein yang menggambarkan bagaimana ruang waktu (space-time) mengkerut akibat medan gravitasi suatu bintang yang sangat besar dan padat (massive) yang telah menjadi lubang hitam (Black Hole). Jadi secara singkat dapat dinyatakan bahwa lubang hitam memiliki percepatan gravitasi dan kerapatan (massa jenisnya) sangat besar.

jari-jari matahari, maka suatu partikel yang ingin melepaskan diri dari permukaan benda itu haruslah mempunyai kecepatan yang lebih besar dari kecepatan cahaya (c). (Will, 1989)

Lubang hitam memiliki beberapa sifat-sifat fisis yang sangat menarik, antara lain lintasan partikel (cahaya) dalam medan gravitasi lubang hitam tidak lurus, melainkan melengkung. Hal ini dikarenakan lubang hitam memiliki medan (percepatan) gravitasi yang sangat besar sehingga lintasan cahaya akan melengkung. Dalam hal ini bentuk lintasan suatu partikel ditentukan oleh kuat atau besar medan gravitasi didalam ruang dimana partikel tersebut melintas. Dengan menggunakan koordinat bola sferis

(

r,θ,φ

)

, elemen lintasan (ds) sebuah partikel dalam medan gravitasi yang sangat lemah (lintasannya berbentuk garis lurus, karena medan gravitasinya kecil) diberikan oleh (Lord,1979)

ds2 =c2dt2 −dr2 −r2(dθ2 +sin2θdφ2) (1.2) Jika ada medan gravitasi yang sangat besar maka, elemen lintasan (ds) sebuah partikel (lintasannya melengkung, karena medan gravitasinya sangat besar) diberikan oleh (Lawrie, 1998)

( sin )

2 1 2

1 2 2 2 2

2 2 2

2 2

2 _{r d}θ θ_dφ

r c GM dr dt

c r c

GM

ds − +

⎟ ⎠ ⎞ ⎜

⎝ ⎛ − − ⎟

⎠ ⎞ ⎜

⎝ ⎛ −

= (1.3)

ruang tanpa medan gravitasi. Sedangkan pada persamaan (1.3) lintasan berada dalam ruang yang memiliki medan gravitasi yang sangat besar.

Konstanta 2 ₂

c

GM _{pada persamaan (1.3)disebut jari-jari Schwarzschild}

( )

_{α ,}

atau

2

2

c GM

=

α (1.4)

sehingga persamaan (1.3) dapat dituliskan kembali menjadi

( sin )

1 1

1 2 2 2 2 2 2 2

2 θ θ φ

α α

d d

r dr

r dt

c r

ds − +

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟

⎠ ⎞ ⎜ ⎝ ⎛ −

= (1.5)

1.2.Perumusan Masalah

Sebagaimana diuraikan pada latar belakang masalah bahwa lubang hitam memiliki sifat-sifat fisis yang berbeda dengan alam yang memiliki medan gravitasi lemah, menyebabkan penelitian sifat-sifat fisis dan geometri lubang hitam merupakan penelitian yang sangat menarik. Dari persamaan (1.5) kalau r =α maka ds2 menjadi tak berhingga (singularitas). Jika r<α, maka suku-suku yang memuat koordinat ruang

(

r,θ,φ

)

mendominasi ds2 agar diperoleh lintasan yang berniali real. Jadi antara titik r =α dan r <α terjadi perubahan fisis dan geometri.

1. Perubahan fisis dan geometri apa yang terjadi, jika sebuah partikel melintas dari r >α ke r <α melewati titik singular r =α .

2. Menentukan ”titik fokus” lubang hitam sebagai fungsi α dan besar fisis terkait.

1.3.Batasan Masalah

Penelitian ini dibatasi pada masalah :

1. Perubahan fisis dan geometri apa yang terjadi jika sebuah partikel melewati titik α =r.

2. Penentuan ”titik fokus” lubang hitam, kalau lubang hitam tersebut berperilaku sebagai sebuah lensa positif.

1.4.Tujuan dan Manfaat Penelitian

1.4.1. Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk :

1. Mengetahui perubahan fisis dan geometri apa yang terjadi pada suatu lubang hitam, jika sebuah partikel melintas dari r>α melewati r=α menuju daerah r<α

1.4.2. Manfaat Penelitian

1.5.Sistematika Penulisan

Hasil penelitian ditulis dengan sistematika sebagai berikut : BAB I. PENDAHULUAN

Pada Bab I dijelaskan mengenai latar belakang masalah, rumusan masalah, batasan masalah, tujuan dan manfaat penelitian, dan sistematika penulisan. BAB II. DASAR TEORI

Dalam Bab II dijabarkan tentang persemaan Schwarzschild dan lintasan partikel dalam medan gravitasi yang sangat besar (lubang hitam).

BAB III. METODOLOGI PENELITIAN

Pada Bab III dijelaskan tentang jenis penelitian, sarana penelitian, dan langkah-langkah penelitian.

BAB IV. HASIL DAN PEMBAHASAN

Pada Bab IV ditampilkan hasil penelitian serta pembahasannya. BAB V. KESIMPULAN DAN SARAN

BAB II

DASAR TEORI

Jarak antara dua titik dalam ruang diberikan oleh (Lawrie, 1998) :

ds2 = g_μυdxμdxυ (2.1)

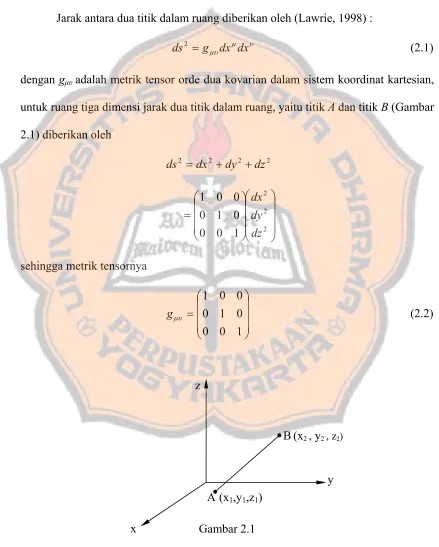
dengan g υadalah metrik tensor orde dua kovarian dalam sistem koordinat kartesian, untuk ruang tiga dimensi jarak dua titik dalam ruang, yaitu titik A dan titik B (Gambar 2.1) diberikan oleh

2 2 2 2 dz dy dx

ds = + +

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 2 2 2 1 0 0 0 1 0 0 0 1 dz dy dx

sehingga metrik tensornya

(2.2) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 1 0 0 0 1 μυ g Gambar 2.1 (x1,y1,z1)

y B (x2, y2 , z2)

A z

Jika digunakan koordinat bola sferis (r,θ,φ), maka panjang lintasan (elemen garis) antara dua titik diberikan oleh

2 2 2 2 2 2

2 _{dr r d}θ _{r sin} θ _dφ

ds = + +

(2.3) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 2 2 2 2 2 2 sin 0 0 0 0 0 0 1 φ θ θ d d dr r r sehingga diberikan ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = θ μυ 2 2 2 sin 0 0 0 0 0 0 1 r r g

Dalam ruang dimensi 4 (ruang Minkowski) tanpa gravitasi, elemen garis ds

didapat dari 2 2 2 2 2 2 dz dy dx dt c

ds = − − −

(2.4) ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = 2 2 2 2 2 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 dz dy dx dt c

sehingga menghasilkan metrik tensor

(2.5) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 μυ g

Kalau digunakan koordinat bola sferis, elemen garis atau lintasan menjadi : 2 2 2 2 2 2 2 2 2

sin θ φ

θ r d

d r dr dt c

(2.6) ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = 2 2 2 2 2 2 2 2 sin 0 0 0 0 0 0 0 0 1 0 0 0 0 1 φ θ θ d d dr dt c r r yang menghasilkan (2.7) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = θ μυ 2 2 2 sin 0 0 0 0 0 0 0 0 1 0 0 0 0 1 r r g

Jika ada medan gravitasi, maka elemen garis atau lintasan dalam ruang dapat dituliskan sebagai (2.8) ) sin ( ) ( ) ( )

( 2 2 2 2 2 2 2

2 θ θ φ

d d r r C dr r B dt c r A

ds = − − +

dengan A(r), B(r), dan C(r) sebagai fungsi kuat medan gravitasi. Dengan menggunakan transformasi r′=rC1/2 dapat diperoleh A(r) = eυ dan B(r) = e

sedemikian hingga A(r) dan B(r) bernilai mendekati 1 jika r→∞. Dengan demikian persamaan (2.8) dapat dituliskan kembali menjadi

(2.9) )

sin

( 2 2 2

2 2 2

2

2 υ λ θ θ φ

d d r dr e dt c e

ds = − − +

sehingga metrik tensornya ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = θ λ υ μυ 2 2 2 sin 0 0 0 0 0 0 0 0 0 0 0 0 r r e e g

Nilai υ dan dapat ditentukan dengan menggunakan persamaan geodesik (Lord, 1979) 0 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ρ σ μ ρσ μ U U ds dU (2.10) dengan ds dx U μ μ ₌

, dan adalah lambang Christoffel. Yang didefinisikan

sebagai (Joshi, 1980)

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ρσ μ

(

ρμ σ σμ ρ ρσ μ ρσ μ ∂ − ∂ + ∂ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ g g g 2 1

)

(2.11)

atau bisa juga ditulis

μυ ρσ υ ρσ μ g Γ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ dengan ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ + ∂ ∂ = Γ λ ρσ ρ σλ α λρ ρα ρσ υ x g x g x g g 2 1

Sehingga persamaan (2.10) sama dengan

(2.12)

[

]

∫

∫

= − − −

= ds e (U4)2 e (U1)2 r2(U2)2 r2sin2 (U3)2 1/2ds

0 δ δ ν λ θ

dengan c = 1, dan persamaan (2.12) adalah integran lintasan yang diminimalkan. Persamaan (2.12) menghasilkan

μ μ x F U F ds d ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂

, (2.13)

dengan F adalah integran pada persamaan (2.12), persamaan (2.13) identik dengan persamaan (2.10). sehingga dapat dihasilkan simbol Christoffel dari persamaan tersebut. Sebagai contoh, jika ditulisμ =4(ct =x4), maka

4

4 2e U

U

F ₌ υ

∂ ∂ 0 4 = ∂ ∂ x F

maka persamaan (2.12) menjadi

(

2e U4

)

=0

ds

d υ

(2.14)

Dengan menggunakan relasi

ds dr dr d ds d ₌

, persamaan (2.14) menghasilkan

(

2 4

)

=

(

2e ct

)

=0

ds d U e ds

d _{υ υ &}

0 ) ( = + υ υ e ds d t e t& &

& 0 = ′ + υ υ _υ e r t e

t& & &

0 = ′

+ r t

t& & &

& _{υ (2.15)}

Dengan demikian lambang Christoffel dapat dihasilkan dari persamaan diatas. Lambang Christoffel yang tidak bernilai nol adalah

υ′ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ 2 1 14 4 υ′ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ 2 1 14 1 λ υ υ_′ − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ e 2 1 44 1 λ′ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ 2 1 11 1 r e−λ

juga diperlukan relasi (Lord, 1976)

, log −g

∂ = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ρ λρ λ

dengan g =−eν+λr4sin2θ , sehingga

θ λ ν sin log log 2 2

log −g = − + r+ (2.16)

Tensor Ricci R _υ pada persamaan (1.1) dapat juga dituliskan sebagai

(

)

ρ ρ μ μ _μ ρ ρ λ λμ ρ μ ρ . . ) (log log g v v v g

R _{v v} −

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − −

= (2.17)

Agar penyelesaian persamaan medan gravitasi Einstein pada persamaan (1.1) linear, nilai R υ harus sama dengan nol. Dari persamaan (2.16) yang memberikan nilai nol adalah ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ + ′ ′ − ′ + ′ − = = r v v v v e

R v 2

2 2 2 1 0 2 . 44 λ λ (2.18) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ − ′ ′ − ′ + ′′ = = r v v v

R λ 2λ

2 2 2 1 0 2

11 (2.19)

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′+ ′ + ′ − − = = − − 2 ) ( 1

0 R₂₂ e λr e λr v λ (2.20)

dari R₁₁ = R₄₄ =0, diperoleh λ′+v′=0, sehingga λ+v=konstan. Nilai konstanta tersebut adalah nol, karena + υ mendekati nol ketika r→∞, sehingga

v − =

Persamaan (2.18) menjadi

0 2

2 + ′ =

′ + ′′

r v v v

yaitu,

( )

rev ″ =0

( )

v ′ =

re konstanta (2.22)

Substitusi persamaan (2.21) ke persamaan (2.20) menghasilkan

( )

rev ′ =1

sehingga

r e

ev = λ =1−α (2.23)

dengan α adalah tetapan integrasi. Pernyataan (2.23) adalah g44 yang di identifikasi sebagai 1+2φ/c2, adalah potensial Newton (untuk suatu pusat massa M, φ =MG/r. Dengan demikian tetapan α pada persamaan (2.23) menjadi (Lord, 1979)

(2.24)

2

/ 2GM c

=

α

yang dikenal sebagai jari-jari Schwarzschild. Substitusikan persamaan (2.24) dan (2.23) ke dalam persamaan (2.9) sehingga akan menghasilkan

) sin

( 2

1 2

1 2 2 2 2

2 2 2

2 2

2 θ θ ϕ

d d

r

r c GM dr dt

c r c

GM

ds − +

⎟ ⎠ ⎞ ⎜

⎝ ⎛ − − ⎟

⎠ ⎞ ⎜

⎝ ⎛ −

sehingga metrik tensor Schwarzschild

⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟

⎠ ⎞

⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜

⎝ ⎛

− − −

− −

=

θ

μυ

2 2 2 2

2

sin 0

0 0

0 0

0

0 0

2 1

1 0

0 0

0 2

1

r r r c

GM r

c GM

g (2.26)

BAB III

METODE PENELITIAN

3.1. Jenis Penelitian

Jenis penelitian yang dilakukan dalam penulisan skripsi ini adalah penelitian studi pustaka.

3.2. Sarana Penelitian

Sarana yang dibutuhkan dalam peyelesaian skripsi ini adalah buku-buku yang berhubungan dengan topik lubang hitam, tensor dan teori relativitas umum.

3.3. Langkah – langkah penelitian

Langkah – langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:

1. Menelusuri bahan-bahan mengenai lubang hitam, metrik, tensor dan relativitas umum dari buku-buku maupun dari internet.

2. Merumuskan atau mengolaborasi kerangka pemikiran teori dan konsep atau teori yang terkait dengan lubang hitam, metrik, tensor dan relativitas umum dari bahan-bahan yang dikumpulkan.

3. Merumuskan perubahan fisis dan geometri yang terjadi pada suatu lintasan partikel pada lubang hitam, dan menentukan titik fokus suatu lubang hitam sebagai fungsi α secara numerik atau matematik.

BAB IV

HASIL DAN PEMBAHASAN

4.1. Orbit Planet

Gerak suatu planet yang mengorbit pada matahari yang memiliki massa yang sangat berat dapat diperoleh dengan menyelesaikan persamaan Schwarzschild, pada

persamaan (2.25). Jika diambil

2

π

θ = , maka persamaan (2.9) menjadi

(4.1)

2 2 2 2

2

2 υ υ φ

d r dr e dt c e

ds = − − −

kalau persaman (4.1) dibagi ds2 dihasilkan

1=eυc2t&2 −e−υr&2 −r2φ&2 (4.2) Dari persamaan (2.15) dapat diperoleh

( )

e t =0

ds d _υ&

(4.3)

sehingga

eυt&=k (konstanta) (4.4) substitusi persamaan (4.4) ke dalam persamaan (4.2) menghasilkan

2 2

2 2 2

1 α φ

α

φ& &

& k r

r r

r + − = − + (4.5)

Persamaan gerak orbit Newton hanya pada suku terakhir persamaan (4.5). Jika persamaan (4.5) dikalikan dengan

2 4 2

h r d

ds ₌

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

diperoleh r h r k r r d

dr α _α

ϕ ⎟_⎠ + ⎞ ⎜ ⎝ ⎛ _{+ −} + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 4 2 2 2

1 (4.6)

Dengan mengganti variabel radial

u

r= 1 ⎟

⎠ ⎞ ⎜ ⎝ ⎛ ₌₋ 2 u du

dr persamaan (4.6) menjadi

(

2

)

2 3 2

2

/

1 h u

k u u d

du _{α α}

ϕ⎟⎟_⎠ =− + + − + ⎞ ⎜⎜ ⎝ ⎛ (4.7)

Jika persamaan (4.7) dideferensialkan terhadap φ, maka diperoleh

2 3 2 2 2 2 2 u h u d u

d α α

ϕ =− + + (4.8)

Kalau diambil

u =u₀ +ε (4.9) Dengan u0 adalah penyelesaian umum untuk persamaan orbit planet Newton dan adalah suatu gangguan kecil. Substitusi persamaan (4.9) ke (4.8) menghasilkan

(

)

(

)

2 3 2 2 0 2 0 2 2 2 0

2 α α ε

ε ϕ ε ϕ + + + + − = + u h u d d d u d

₀2 ₀ 2

2 0 2 3 3 2 3

2 α εα αε

α

ε+ + + +

− −

= u u

h

u (4.10)

Karena _{0 2} 2h

u = α , dan kalau sangat kecil suku 2 dapat diabaikan sehingga

persamaan diferensial untuk dapat dituliskan

(

₀

)

₀2

2 2

2 3 1

3 u u

d

d _{α ε α}

ϕ

ε _{= − +}

Penyelesaian persamaan (4.11) dapat dituliskan sebagai

( )

B

A +

= ζϕ

ε cos (4.12)

dengan A, B, dan ζ adalah konstanta (lihat Lampiran). Jika ζ = 1, maka dihasilkan orbit lingkaran. Dengan mendeferensialkan persamaan (4.12) terhadap φ kemudian menyamakannya dengan nol, maka diperoleh

ζ π

ϕ = 2n (4.13)

Substitusi persamaan (4.12) ke dalam (4.11) dapat menghasilkan nilai ζ, yaitu

ζ2 =1−3αu₀ (4.14) sehingga lintasan planet terjadi pada

, 2 3 1 2 ~ 3 1

2

0 0

⎟ ⎠ ⎞ ⎜

⎝ ⎛ + ±

− ±

= n u

u

n _{π α}

α π

φ

(

2 3

) (

,0, 2 3

) (

, 4 6

)

...

...

~ π παu₀ π παu₀ π παu₀

ϕ − − + +

4.2. Perubahan Geometri dan Sifat Fisis Ruang

Ditinjau perubahan geometri dan sifat fisis ruang yang dialami oleh sebuah partikel bergerak dari kedudukan atau posisi r >α ke posisi r<α . Dari persamaan (2.25), jika r>α, maka nilai koefisien (positif) sehingga suku yang mengandung waktu (t) haruslah bernilai lebih besar dari suku-suku yang lain agar . Dengan kata lain, partikel yang melintas dalam medan gravitasi yang ditimbulkan oleh massa M pada daerah

0 > = λ υ

e e

0

2 >

ds

α

>

time-like). Secara skematis lintasan partikel dalam ruang bak-waktu diperlihatkan pada Gambar 4.1

Sekarang Waktu

Masa lalu Masa depan

Lintasan partikel

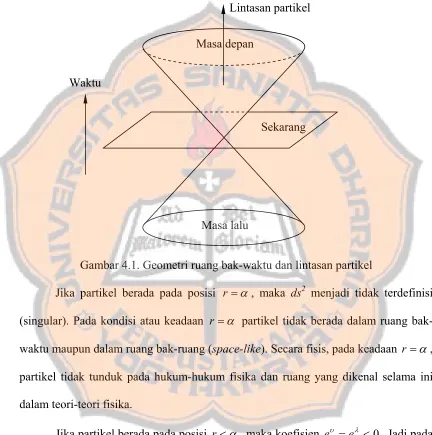
Gambar 4.1. Geometri ruang bak-waktu dan lintasan partikel

Jika partikel berada pada posisi r =α , maka ds2 menjadi tidak terdefinisi (singular). Pada kondisi atau keadaan r =α partikel tidak berada dalam ruang bak-waktu maupun dalam ruang bak-ruang (space-like). Secara fisis, pada keadaan r=α , partikel tidak tunduk pada hukum-hukum fisika dan ruang yang dikenal selama ini dalam teori-teori fisika.

Jika partikel berada pada posisi r<α , maka koefisien . Jadi pada keadaan seperti itu kalau , nilai dari suku-suku yang tidak mengandung waktu (t) pada persamaan (2.25) harus lebih besar dari nilai suku yang mengandung t. Secara fisis partikel yang berada pada daerah

0 < = λ

υ _e

e

0

2 >

ds

α

<

bak-ruang. Geometri bak-ruang dan lintasan partikel di dalamnya diperlihatkan pada Gambar 4.2.

Bak - cahaya

Lintasan partikel

Gambar 4.2. Geometri bak-ruang dan lintasan partikel

Waktu

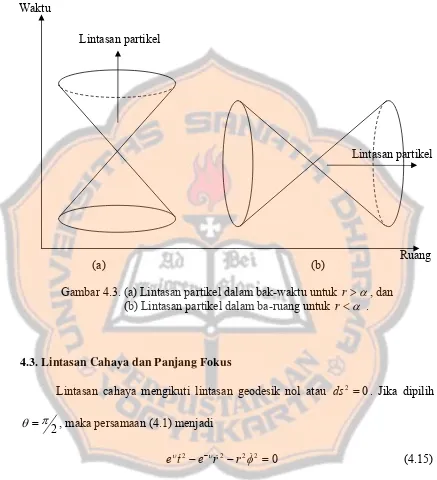
(a) (b)

Lintasan partikel

Ruang Lintasan partikel

Gambar 4.3. (a) Lintasan partikel dalam bak-waktu untuk r >α , dan (b) Lintasan partikel dalam ba-ruang untuk r<α .

4.3. Lintasan Cahaya dan Panjang Fokus

Lintasan cahaya mengikuti lintasan geodesik nol atau ds2 =0. Jika dipilih

2

π

θ = , maka persamaan (4.1) menjadi

(4.15) 0

2 2 2

2 − −υ − φ =

υ_{& & &}

r r e t e

Dengan menggunakan eυt&=k, persamaan (4.15) dapat ditulliskan menjadi

(4.16)

2 2

2 2

2 φ& α φ&

& r k r

jika persamaan (4.16) dikalikan 2 4 ₂ h r =

φ& _{, dan variabel radial (r) diatas menjadi}

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = u r

u 1 , maka persamaan (4.16) menjadi

₂ 2 3 2 2 h k u u d

du _{+ = +}

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ _α

ϕ (4.17)

Kalau persamaan (4.17) dideferensialkan terhadap φ, maka

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = + − = β β α ϕ 2 3 , 2 2 2 u u d u d (4.18)

Jika suku β u2 diabaikan, maka penyelesaian persamaan (4.18) diberikan oleh )

cos(φ +δ = A

u (4.19)

dengan A adalah tetapan,

Lintasan cahaya yang diperoleh dari persamaan (4.19) adalah

) cos( 1 1 δ φ+ = = A u

r (4.20)

yang merupakan garis lurus r = konstan untuk φ+δ konstan. Jika penyelesaian persamaan (4.18) dipilih berbentuk

ε φ + = Acos

u (4.21)

dengan fungsi φ, maka diperoleh

Dengan mengandaikan penyelesaian (4.22) berbentuk

φ

ε =a+bcos2 (4.23)

yang kalau dimasukkan ke (4.22) diperoleh

2

2

A a= β dan

6

2

A

b= β (4.24)

Jadi penyelesaian persamaan (4.23) dapat dituliskan

⎟

⎠ ⎞ ⎜

⎝ ⎛ + =

3 2 cos 1 2

2 φ

β

ε A (4.25)

Dengan demikian, persamaan (4.21) menjadi

3 2 cos 3 cos

2 2

2

A A

A

u = φ −β φ+ β (4.26)

jika diambil r→∞, maka u→0. Untuk r→∞ persamaan (4.26) menjadi

2 2

2

3 2 cos 3 cos

0= A φ−βA φ + βA (4.27)

Nilai cos dapat diperoleh dari (4.27), yaitu φ

_⎟⎟

⎠ ⎞ ⎜

⎜ ⎝ ⎛

+ ±

= ₂

0 2 0

9 8 1 1 2 3 cos

r

r β

β

φ (4.28)

1

ϕ

2

ϕ

0

r

α

0

r

Gambar 4.4. Pembelokan cahaya dalam medan gravitasi

Pada persamaan (4.28) nilai cos adalah antara -1 sampai +1, mengharuskan φ

nilai 0 >>1

β

r

. Dengan demikian diperoleh

0 0

3 2 ~ cos

r

r α

β

φ − =− (4.29)

Dari Gambar 4.4. terlihat bahwa sudut pembelokan cahaya pada medan gravitasi sebesar

0 2 0

4 2

r c

GM r

d = = α

θ (4.30)

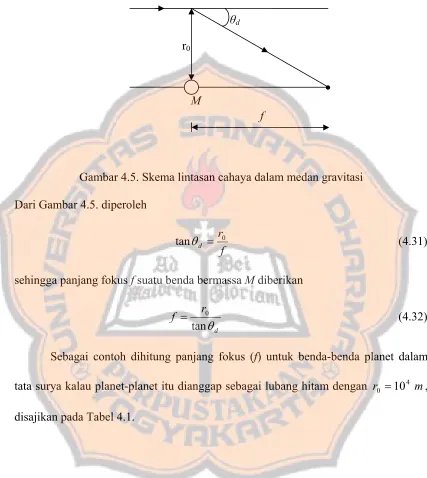
Gambar 4.5. Skema lintasan cahaya dalam medan gravitasi Dari Gambar 4.5. diperoleh

r0

•

f

θd

M

f r

d

0

tanθ = (4.31)

sehingga panjang fokus f suatu benda bermassa M diberikan

d

r f

θ

tan 0

= (4.32)

Sebagai contoh dihitung panjang fokus (f) untuk benda-benda planet dalam tata surya kalau planet-planet itu dianggap sebagai lubang hitam dengan ,

disajikan pada Tabel 4.1.

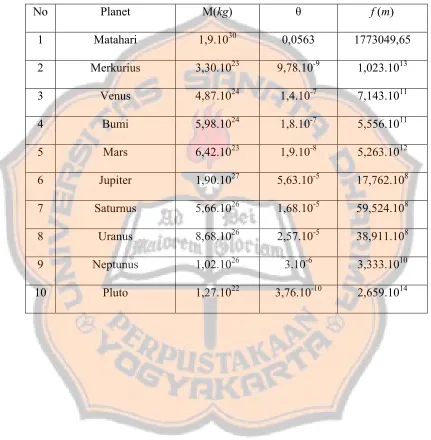
Tabel 4.1. Panjang fokus (f) untuk planet-planet di dalam tata surya kalau planet itu dianggap sebagai lubang hitam untuk r 4 m

0 =10

No Planet M(kg) θ f (m)

1 Matahari 1,9.1030 0,0563 1773049,65

2 Merkurius 3,30.1023 9,78.10-9 1,023.1013

3 Venus 4,87.1024 1,4.10-7 7,143.1011

4 Bumi 5,98.1024 1,8.10-7 5,556.1011

5 Mars 6,42.1023 1,9.10-8 5,263.1012

6 Jupiter 1,90.1027 5,63.10-5 17,762.108 7 Saturnus 5,66.1026 1,68.10-5 59,524.108 8 Uranus 8,68.1026 2,57.10-5 38,911.108 1,02.1026 3.10-6 3,333.1010 9 Neptunus

BAB V

PENUTUP

5.1. Kesimpulan

Berdasarkan keseluruhan proses yang telah dilakukan dalam penelitian ini dapat diperoleh kesimpulan sebagai berikut :

1. Lintasan atau orbit suatu planet dapat diperoleh dari penyelesaian

persamaan Schwarzschild. Dengan memilih

2

π θ = .

2. Perubahan geometri dan sifat fisis ruang yang dialami oleh suatu partikel yang bergerak dari daerah r>α ke daerah r <α dalam medan gravitasi yang ditimbulkan oleh massa M, yaitu pada daerah

α

>

r partikel berada dalam bak-waktu dan pada daerah r <α

partikel berada dalam bak-ruang.

3. Lintasan cahaya mengikuti persamaan godesik ds2 =0, dengan

2

π

θ = . Panjang suatu titik fokus (f) suatu benda bermassa M dalam

5.2. Saran

Karena yang diteliti dalam penelitian ini hanyalah masalah orbit planet, perubahan geometri dan sifat fisis partikel yang bergerak dari r >α menuju r<α , dan pembelokan lintasan cahaya dalam medan gravitasi yang ditimbulkan oleh massa

DAFTAR PUSTAKA

Joshi, A. W., 1980, “Matrics and Tensor in Physics”, New Delhi Banglore Bombay Calcuta : Wiley Eastern Limited.

Lord, E. A., 1976, Tensor Relativity and Cosmology, United Kingdom: University of Edinburgh Scotland.

Lawire, I. D., 1998, “A unified Grand Tour of Theoritical Physics”, Philadelphia: Institut of Physics Publishing.

Will, C., 1989, The New Physics, New York: Canbridge University.

LAMPIRAN

Persamaan diferensial pada persamaan (4.11) mempunyai penyelesaian

sebagai fungsi φ, dengan menggunakan metoda operator

ϕ d d D= 2 0 0 2 2 2 3 ) 1 3

( u u

d

d _{α ε α}

ϕ

ε _{= − +}

(4.11)

dengan , dan ζ2 =3αu₀ −1

α ζ 3 1 2 0 + =

u . Sehingga persamaan (4.11) menjadi

2 2 2 2 2 ) 1 ( 6 1 ₊ + = ζ α ε ζ ϕ ε d d

dimana ( 1) ( )

6

1 _{2 2}

tetapan K

= +

ζ

α , sehingga dapat dituliskan menjadi

K d d = −ζ ε ϕ ε 2 2 2 jika K i D i

D− ζ)( + ζ)ε = (

dengan (D+iζ)ε =u, maka

K u i

D− )− =

( ζ

Persamaan diatas dapat juga dituliskan menjadi

β α = + y dt y d 2 2 2 β α = + y D )

( 2 2

β α

α − =

+i D i y

D )( )

β

α =

+i u

D )

(

β

α =

+i u u D

α β

i D u

+ =

β α = +i u dt du

Jika persamaan di atas dideferensialkan terhadap dt maka,

( )

i t i t

e u e dt

du _{α β α}

=

integralkan persamaan di atas

∫

∫

d(eiαtu)= βeiαtdt

hasilnya adalah

k e i u

eiαt = iαt +

α β 1

k dt e e

u = −iαt

∫

β iαt +

t i

e k i

u α

α β ₊ − =

sehingga

k dt e e

y i

D− α) = −iαt

∫

β iαt + (

Apabila persamaan ini digunakan untuk menyelesaikan persamaan (4.11), maka akan menjadi

K u i

D− ) =

K u i d

du _{− ζ =}

ϕ ζϕ ζϕ ζϕ ζϕ ζ ϕ ϕ ζ ϕ i i i i e u i d du d du e u e i u e d d − − − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = + − = ) ( K u e d d

eiζϕ ( −iζϕ )=

ϕ K e u e d

d iζϕ iζϕ

ϕ − − ₌ ) ( ϕ ζϕ

ζϕ_{u e Kd}

e

d( −i )= −i

∫

∫

−ζϕ ₌ −ζϕ _ϕ d e K u e

d( i ) i

∫

∫

− − − = = ϕ ϕ ζϕ ζϕ ζϕ ζϕ d e K e u d e K u e i i i i

Dengan demikian dapat dituliskan menjadi

∫

− = = + ζ ε ζϕ ζϕ ϕ d e K e u i

D ) i i

(

∫

− − _{ε = ϕ} ϕ ζϕ ζϕ ζϕ ζϕ d e K e e d d

e i ( i ) i i

∫

−

= ϕ

ε

ϕ eζϕ e ζϕ Ke ζϕd

d

d _{i 2i i}

) (

ϕ ϕ

ε ζϕ ζϕ

ζϕ _{e Ke d d}

e

d₍ i ₎=₍ 2i

∫

−i ₎

(

ϕ

)

ϕ ε ζϕ ζϕ ζϕ d d e K e

(

ϕ

)

ϕ ε ζϕ ζϕ ζϕ d d Ke e

e−i

∫

i

∫

−i

= 2 C e i K d

Ke i i +

− = − −

∫

ζϕ ζϕ ζ ϕ

dengan , maka menghasilkan

∫

⎜⎜_⎝⎛− + ⎟⎟_⎠⎞ = − _ϕ ζ ε ζϕ ζϕ ζϕ d e C i Ke e i i i 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + − = − 2 2 2

2 _2i e C

C e

i K

e iζϕ iζϕ iζϕ

ζ ζ

[

ζϕ ζϕ

]

ζϕ ζϕ ζ ζ ζ i i i i e e C K e C i Ce K − − + + = + + = 2 2 2 2

Apabila , sehingga akan menghasilkan (eiζϕ +e−iζϕ)=2cos(ζϕ)

)) cos( 2 ( 2 ζϕ ζ ε = K +C

) cos( 2

2 ζϕ

ζ

ε = K + C

B K ₌

2

ζ 2C = A

dimisalkan dan , dengan demikian hasilnya adalah (pada persamaan

(4.12))

) cos(ζϕ