KOMBINATORIK DAN PELUANG

(1)

KOMBINATORIK DAN PELUANG

Penulis

Drs. Marsudi Rahardjo, M.Sc.Ed.

Edit & Layout:

Titik Sutanti, S.Pd.Si., M.Ed.

PUSAT PENGEMBANGAN DAN PENBERDAYAAN PENDIDIK

DAN TENAGA KEPENDIDIKAN MATEMATIKA

KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN

2015

(2)

ii

KATA PENGANTAR

Puji syukur ke hadirat Tuhan Yang Maha Esa, karena atas karunia-Nya, bahan ajar ini dapat diselesaikan dengan baik. Bahan ajar ini diharapkan dapat menjadi salah satu rujukan dalam usaha peningkatan mutu pengelolaan pembelajaran matematika di sekolah serta dapat dipelajari secara mandiri oleh peserta diklat di dalam maupun di luar kegiatan diklat.

Diharapkan dengan mempelajari bahan ajar ini, peserta diklat E-Training Terstruktur dapat menambah wawasan dan pengetahuan sehingga dapat mengadakan refleksi sejauh mana pemahaman terhadap mata diklat yang sedang/telah diikuti.

Kami mengucapkan terima kasih kepada semua pihak yang telah berpartisipasi dalam proses penyusunan bahan ajar ini. Kepada para pemerhati dan pelaku pendidikan, kami berharap bahan ajar ini dapat dimanfaatkan dengan baik guna peningkatan mutu pembelajaran matematika di negeri ini.

Demi perbaikan bahan ajar ini, kami mengharapkan adanya saran untuk penyempurnaan di masa yang akan datang. Saran dapat disampaikan kepada kami di PPPPTK Matematika dengan alamat: Jl. Kaliurang KM. 6, Sambisari, Condongcatur, Depok, Sleman, DIY, Kotak Pos 31 YK-BS Yogyakarta 55281. Telepon (0274) 881717, 885725, Fax. (0274) 885752. email: sekretariat@p4tkmatematika.org

Sleman, Mei 2015

Kepala PPPPTK matematika

Prof.Dr. rer.nat. Widodo, M.S NIP 196210311989031002

(3)

iii

Daftar Isi

KATA PENGANTAR ... ii

Daftar Isi ... iii

PENDAHULUAN ... 1

A. Pengantar Isi ... 1

B. Target Kompetensi ... 5

C. Strategi Pembelajaran ... 6

BAHAN BACAAN I KOMBINATORIK ... 7

A. Prinsip Perkalian ... 7

B. Contoh Terapan Prinsip Perkalian ... 10

BAHAN BACAAN II KOMBINATORIK DAN PELUANG PADA PENGUNDIAN ... 13

A. Konsep Peluang dan Frekuensi Harapan ... 13

B. Ruang Sampel, Titik Sampel, Peristiwa, dan Relasi Antarperistiwa ... 17

C. Relasi Antar Peristiwa ... 24

Latihan 1 ... 25

BAHAN BACAAN III KOMBINATORIK DAN PELUANG PADA PENGAMBILAN SAMPEL ... 28

A. Notasi Faktorial ... 28

B. Permutasi ... 29

C. Kombinasi ... 31

D. Terapan Dalam Pemecahan Masalah Pengambilan Sampel ... 35

E. Permutasi Dengan Beberapa Unsur Sama (Penggunaan Aturan Kombinasi) ... 39

F. Aturan/Prinsip Kombinasi ... 42

G. Identifikasi Masalah Pada Pada Pengambilan Sampel ... 46

Latihan 2 ... 52

UMPAN BALIK DAN TINDAK LANJUT ... 54

A. Rangkuman ... 54

B. Evaluasi ... 57

Latihan 3 ... 57

C. Tindak Lanjut ... 61

(4)

(5)

ETraining Terstruktur 2015 – PPPPTK Matematika 1

PENDAHULUAN

A. Pengantar Isi

Bahan bacaan ini diperuntukkan bagi guru matematika sekolah menengah peserta ETraining Terstruktur meliputi guru SMP, SMA, dan SMK. Materi Kombinatorik dan Peluang yang diberikan pada bahan bacaan ini terdiri dari 3(tiga) macam. Bahan Bacaan I dengan topik “Kombinatorik dan Peluang pada Penyusunan Bilangan”, Bahan Bacaan II dengan topik “Kombinatorik dan Peluang pada Pengundian” dan Bahan Bacaan III dengan topik “Kombinatorik dan Peluang pada Pengambilan Sampel”. Bahan Bacaan I dan II lebih cocok untuk bahan ajar guru SMP, sementara materi peluang untuk guru SMA/SMK lebih cocok pada Bahan Bacaan III, akan tetapi peserta ETraining diharapkan mempelajari seluruh Bahan Bacaan sebagai bahan referensi.

Pendekatan pembelajaran yang dipilih penulis pada modul ini lebih banyak terkait dengan teori pembelajran Bruner tahap 2 dan 3. Teori pembelajran Bruner terdiri atas 3 (tiga) tahapan yakni: (1) Enactive/kongkrit dimana pendekatan

pembelajarannya melalui peragaan menggunakan obyek sesungguhnya, (2)

Econic/semi kongkrit dimana pendekatan pembelajarannya melalui

gambar-gambar. Dan (3) Symbolic/abstrak dimana pendekatan pembelajarannya hanya menekankan pada penalaran logis yakni obyek-obyek pembelajaran dan

penalarannya sudah cukup dibayangkan di alam pikiran. Jika pembelajaran matematika sekolah dilakukan melalui ketiga tahapan seperti itu maka Bruner menjamin bahwa siswa/peserta didik akan mampu mengembangkan pengetahuannya jauh melampaui apa yang pernah mereka terima dari gurunya.

Landasan psikologi pembelajaran berikutnya adalah “Psikologi perkembangan

Piaget (baca “Piase”). Menurut Piaget (setelah melakukan pengamatan selama 60 tahun) perkembangan kognitif (intelektual) manusia sepanjang hayat hanya dibagi dalam 4(empat) tahapan saja. Keempat tahapan itu adalah: (1) Sensory Motor (umur 0 s.d 2 tahun) yakni tahapan ingin tahu tentang obyek-obyek di alam

(6)

2 ETraining Terstruktur 2015 – PPPPTK Matematika

anak pada belajar bahasa, yakni jika dalam lingkungan pergaulannya berbicara dalam 6 bahasa, maka anak akan mampu berbicara dalam 6 bahasa itu sekaligus. Tapi sayangnya pada tahapan ini anak belum mampu mengadakan pernalaran dengan baik, mereka hanya bisa menirukan tapi belum mmpu bernalar, (3) Konkrit

Operasioanal (umur 6 s.d 11 tahun) yakni tahapan pembelajarannya diperagakan

melalui peragaan menggunakan obyek-obyek sesungguhnya (obyek-obyek konkrit). Dan terakhir (4) Berpikir abstrak (lebih dari 11 tahun) adalah anak dapat

menagkap konsep-konsep matematika cukup melalui obyek-obyek yang dapat

dibayangkan di alam pikiran.

Peluang adalah ukuran ketidakpastian munculnya suatu peristiwa/kejadian

dalam suatu ruang sampel hasil dari sebuah eksperimen. Eksperimen yang dimaksud dalam ilmu peluang adalah “percobaan acak” di mana si pelaku eksperimen dijamin tidak dapat mengatur hasil eksperimennya. Sehingga jika tidak ada jaminan bahwa “si pelaku eksperimen tidak dapat mengatur hasil eksperimennya” maka dikatakan bahwa eksperimen yang dilakukannya “tidak fair” atau “tidak adil”.

Ukuran ketidakpastian yang dimaksud merupakan nilai frekuensi relatif

munculnya peristiwa itu jika eksperimen yang dilakukannya adalah berulang

sampai dengan tak hingga kali. Namun karena ketidakmungkinan seseorang

melakukan eksperimen sampai dengan tak hingga kali, maka biasanya orang (si pelaku eksperimen) hanya akan melakukannya sampai dengan ribuan kali tertentu saja. Sebagai contoh misalnya untuk mengetahui berapa peluang munculnya masing-masing sisi mata uang logam jika diadakan eksperimen melalui “tossing” dengan cara melambungkannya ke udara dan membiarkannya jatuh ke sebuah lantai bersemen.

Untuk mengetahui nilai peluangnya penulis mengambil hikmah dari buku rujukan “Applied Finite Mathematics” karangan Prof. Howard Anton untuk eksperimen

tehadap sekeping mata uang logam. Terinspirasi dengan eksperimen tersebut penulis di tahun 2001 mencoba untuk melakukannya secara pribadi atas sebuah paku payung standar (warna putih gilap) yang biasa digunakan untuk menata taplak-taplak

(7)

ETraining Terstruktur 2015 – PPPPTK Matematika 3 meja pada sebuah hajatan. Paku payung semacam ini selanjutnya kita sebut/definisikan sebagai “paku payung standar”.

Kini seperti yang akan kita ketahui pada bahan bacaan II, setelah dilakukan eksperimen berulang mulai dari 1.000 kali, 5.000 kali, 10.000 kali, 15.000 kali, hingga 20.000 kali akan tampak bahwa nilai frekuensi relatifnya memiliki nilai kecenderungan ke bilangan 0,5 untuk munculnya muka angka (A) pada mata uang logam dan memiliki nilai kecenderungan ke bilangan 0,31 untuk munculnya hasil miring pada paku payung standar. Selanjutnya dengan pembulatan yang sudah dianggap cukup baik hingga 1 tempat desimal akan diperolah nilai kecenderungan frekuensi relatif munculnya masing-masing hasil adalah 0,5 untuk munculnya muka angka pada mata uang logam dan 0,3 untuk munculnya hasil miring pada paku payung standar. Dalam bentuk pecahan biasa peluang masing-masing adalah

2 1

dan . 10

3

Kedua obyek eksperimen ini (mata uang logam dan paku payung) sengaja diangkat sebagai contoh obyek eksperimen agar kesalahan persepsi selama ini bahwa berbicara masalah peluang selalu dianggap bahwa peluang munculnya peristiwa A dalam ruang sampel S yakni AS adalah

P(A) = ) ( ) ( S n A n _{selalu benar}

padahal tidak selalu benar.

Rumus nilai peluang tersebut benar jika obyek eksperimennya berdistribusi (tersebar secara) seragam dan tidak benar jika obyek eksperimennya tidak

berdistribusiseragam.

Perhitungan nilai peluang untuk setiap peristiwa AS selalu benar jika kita gunakan prinsip penjumlahan, yakni peluang munculnya peristiwa AS sama dengan jumlah peluang munculnya masing-masing titik sampel yang terdapat pada peristiwa A.

(8)

Sebagai contoh selidiki bahwa pada contoh ini peluang munculnya ruang sampel S adalah

P(S) = P({s1}) + P({s2}) + P({s3}) +

P({s4})

= ₁₀₀9 + ₁₀₀21 + ₁₀₀21 + ₁₀₀49

= ₁₀₀100 = 1.

Dengan cara yang sama akan diperoleh

P(A) = 100

,

58 P(B) = 100

,

91 dan P(AB) =

.

100 49

Lebih lanjut amati bahwa ruang sampel S pada contoh di atas adalah ruang sampel yang tidak berdistribusi seragam. Mengapa? Sebab seperti yang dapat kita lihat ternyata tidak semua titik sampel dalam ruang sampel S berpeluang sama untuk muncul.

Kini sebagai pembanding coba amati contoh yang kedua berikut ini.

Selidiki bahwa pada contoh yang kedua ini peluang munculnya ruang sampel S adalah P(S) = P({s1}) + P({s2}) + P({s3}) + P({s4}) = 4 1 + 4 1 + 4 1 + 4 1 = 4 4 = 1.

Dengan cara yang sama maka untuk setiap peristiwa A, BS akan diperoleh

P(A) = 4

,

2 P(B) = 4

,

3 dan P(AB) = 4

.

1

Amati bahwa ruang sampel S pada contoh yang kedua di atas adalah ruang sampel S yang berdistribusi seragam. Mengapa? Sebab seperti yang dapat kita lihat ternyata

semuatitik sampel dalam ruang sampel S berpeluang sama untuk muncul. Peluang

S A 100 21 s2 s3 100 21 100 9 _s₁ 100 49 _s₄ B Gambar 1a Gambar 1b S A B s1 4 1 4 s2 1 s3 4 1 s4 4 1

(9)

ETraining Terstruktur 2015 – PPPPTK Matematika 5 munculnya masing-masing titik sampel dalam ruang sampel S adalah P({si }) = 1₄

untuk setiap si  S.

Selidiki pula bahwa untuk perhitungan nilai peluang munculnya peristiwa A dalam uang sampel S yakni AS pada contoh yang kedua ini juga akan berlaku rumus P(A) = ( )

.

) ( S n A n

Sementara rumus tersebut tidak berlaku untuk contoh yang pertama.

Kini amati bahwa untuk ruang sampel S pada contoh yang kedua ini jika kita gunakan

rumus peluang munculnya peristiwa AS berupa P(A) = ( ) ) ( S n A n

untuk setiap peristiwa

AS maka nilai peluang munculnya peristiwa A, B S masing-masing adalah: P(A) = _nn₍(_SA₎)= ₄2 = 1₂

,

P(B) = n_n(₍_SB₎) = ₄3

.

Selidiki bahwa hasil-hasil tersebut ternyata sama nilai peluangnya dengan jika kita gunakan perhitungan menggunakan prinsip penjumlahan. Pembahasan selengkapnya dapat dipelajari pada bagian III.

B. Target Kompetensi

Target kompetensi yang hendak dicapai dari bahan diklat ini adalah “Peserta diklat E-Training Terstruktur dapat menentukan banyaknya semua hasil yang mungkin (kombinatorik) dari suatu eksperimen (percobaan acak sedemikian sehingga si pelaku eksperimen dijamin tidak dapat mengatur hasil eksperimennya) terhadap

sejumlah obyek tertentu yang selanjutnya kita sebut “obyek eksperimen”.

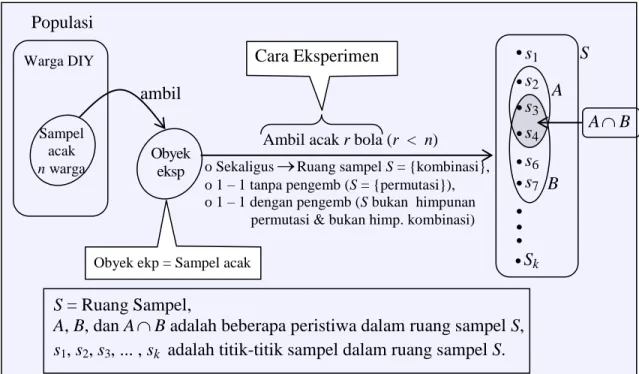
Himpunan semua hasil (eksperimen) yang mungkin yang diperoleh dari sejumlah obyek eksperimen yang diberikan (diketahui) didefinisikan sebagai “Ruang Sampel” dan umumnya dilambangkan menggunakan huruf kapital “S”. Selanjutnya peserta diklat dapat menentukan banyak angota (banyak titik sampel yang terdapat pada setiap peristiwa yang didefinisikan dalam ruang sampel S) yakni peristiwa A, BS dalam bentuk kata-kata/kalimat, menentukan nilai peluangnya, serta

(10)

mengidentifikasi relasi antarperistiwa dalam ruang sampel S tersebut untuk eksperimen yang berupa:

1. Pengundian (tidak melibatkan perhitungan permutasi dan kombinasi) 2. Pengambilan Sampel (melibatkan perhitungan permutasi dan kombinasi)

Pengundian yang dimaksud adalah eksperimen (percobaan acak) yang melibatkan

obyek-obyek seperti misalnya: mata uang logam, dadu, paku payung, kartu

gambar yakni kartu-kartu yang salah satu sisinya bergambar dan sisi lainnya kosong (tidak bergambar), dan lain-lain. Sementara pengambilan sampel yang dimaksud adalah pengambilan acak dari sebagian obyek (sampel) yang berasal dari

sejumlah obyek yang jumlahnya lebih banyak (populasi). Bedakan antara

“konsep sampel” dengan “konsep ruang sampel”. Sampel adalah sebagian dari keseluruhan (populasi), sedangkan ruang sampel adalah himpunan semua hasil yang mungkin terjadi dalam suatu eksperimen (percobaan acak/tindakan acak).

C. Strategi Pembelajaran

Pembelajaran dilakukan dengan sistem ETraining, di mana peserta harus masuk/login ke sistem Etraining PPPPTK Matematika pada alamat diklatonline.p4tkmatematika.org menggunakan user ID dan password yang telah disediakan admin. Peserta mempelajari materi melalui bahan bacaan-bahan bacaan yang disediakan secara mandiri. Selanjutnya, peserta mengikuti forum diskusi untuk mendiskusikan topik-topik sesuai materi yang sedang dijadwalkan maupun berkonsultasi dengan fasilitator. Untuk mengetahui pencapaian kompetensi, peserta diklat mengerjakan tugas dan tes akhir. Keseluruhan strategi pembelajaran dilaksanakan secara daring (online) penuh. Interaksi antara peserta dengan fasilitator dilakukan secara daring (online) dalam forum diskusi maupun fasilitas chatting dan email.

(11)

BAHAN BACAAN I

KOMBINATORIK

Kombinatorik adalah teknik menghitung banyak anggota ruang Sampel. Yakni

banyak cara munculnya hasil-hasil yang mungkin pada suatu eksperimen (percobaan acak). Untuk dapat memahaminya dengan baik perhatikan contoh masalah dan cara penyelesaiannya berikut ini.

A. Prinsip Perkalian

Masalah 1

Misalkan kita adakan eksperimen (percobaan acak) berupa pengundian sekaligus sebuah paku payung standar (warna putih gilap) dan sebuah dadu. Pertanyaannya adalah ada berapa macam (ada berapa cara) hasil yang mungkin terjadi pada eksperimen tersebut?

Penyelesaian

Amati bahwa dari masalah yang dikemukakan di atas, obyek eksperimen, cara eksperimen, dan hasil-hasil yang mungkin masing-masing adalah seperti yang digambarkan berikut. Gambar 2 diundi sekaligus Obyek Ekp. Cara Ekp. I II m t 1 2 3 4 5 6 1 2 3 4 5 6 ( t, 6) = s12 ( t, 5) = s11 ( t, 4) = s10 ( t, 3) = s9 ( t, 2) = s8 ( t, 1) = s7 ( m, 6)= s6 (m, 5) = s5 (m, 4) = s4 (m, 3) = s3 (m, 2) = s2 (m, 1) = s1 6 cara 2 cara I II S n(S) = 12 Hasil-hasil yang mungkin Keterangan Hasil miring m = Hasil terlentangt = Kemungkinan

(12)

Berdasarkan kerangka penyelesaian yang digambarkan di atas dapat kita lihat bahwa obyek eksperimen I adalah sebuah paku payung sementara obyek eksperimen II adalah sebuah dadu. Cara eksperimennya adalah diundi sekaligus. Sedangkan hasil-hasil yang mungkin berupa pasangan berurutan (m, 1), (m, 2), (m, 3), … dan seterusnya hingga (t, 6). Atau jika ditulis dalam bentuk lambang titik-titik sampel semuanya ada 12. Keduabelas titik sampel yang dimaksud adalah s1, s2, s3, ... , s12. Sehingga ruang sampel S dari eksperimen di atas adalah:

S = {(m, 1), (m, 2), (m, 3), … , (t, 6)} atau S = { s1, s2, s3, …. , s12}. Maka n(S) = 12.

Kini pertanyaan selanjutnya adalah apa kira-kira hubungan antara n(S) = 12 dengan banyaknya hasil yang mungkin untuk obyek eksperimen I yakni n(I) = 2 dan banyaknya hasil yang mungkin untuk obyek eksperimen II yakni n(II) = 6?

Amati bahwa setelah dicermati secara seksama ternyata

n(S) = 12 = 2  6 = n(I)  n(II).

Dengan demikian, n(S) merupakan hasil perkalian antara banyaknya cara munculnya hasil yang mungkin pada obyek eksperimen I dengan banyaknya cara munculnya hasil yang mungkin pada obyek eksperimen II, yakni

n(S) = 2  6 = n1  n2.

Kini bagaimana jika obyek eksperimennya sebanyak k., yakni obyek eksperimen I, II, III, … dan seterusnya hingga K. Misalkan masing-masing obyek dapat terjadi dalam n1 cara, n2 cara, n3 cara, dan seterusnya hingga nk cara. Berapakah banyak anggota ruang sampel S jika kesemua obyek eksperimen itu diundi sekaligus? Apakah kita sepakat jika kesemua obyek eksperimen itu diundi sekaligus maka ruang sampel S akan memuat titik sampel sebanyak

Jika kita sepakat dengan dugaan di atas dari mana kita dapat menyimpulkannya? Apakah kita menyimpulkannya berdasarkan pola atau dari kerangka berpikir lain yang mungkin dalam bentuk gambar atau bentuk apa yang mungkin.

n(S) = n1  n2  n3  …  nk

(13)

ETraining Terstruktur 2015 – PPPPTK Matematika 9 Perlu diingat bahwa jika kita dapat menyampaikannya dalam bentuk gambar, menurut Bruner (Jerome Bruner, 1915–...) peserta didik akan dapat

menangkapnya secara jelas dan akan mampu mengembangkan

pengetahuannya jauh melebihi dari apa yang pernah mereka terima dari gurunya.

Banyak anggota S seperti yang ditunjukkan pada petak di atas selanjutnya dikenal sebagai “prinsip perkalian”. Gambaran lebih lanjut seperti berikut.

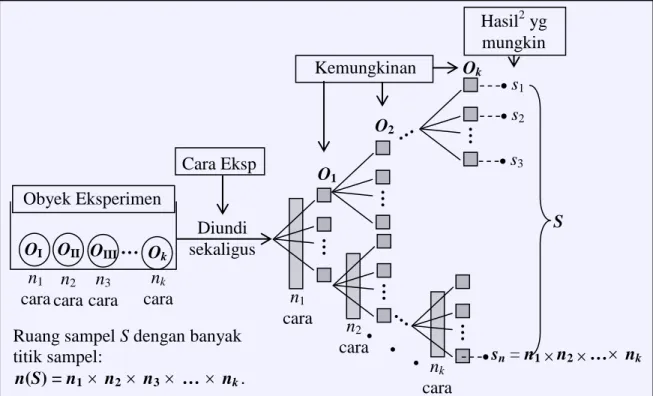
Dari kerangka berpikir yang digambarkan di atas kemungkinan terjadinya obyek eksp

O1, O2, O3, ... dan seterusnya hingga obyek eksperimen Ok masing-masing dapat terjadi dalam n1 cara, n2 cara, ... , dan seterusnya hingga nk cara. Maka secara nalar hasil-hasil eksperimen yang mungkin terjadi adalah sebanyak n1  n2  n3  …  nk cara. Yakni dari titik-titik sampel s1, s2, s3, ... , hingga sn

=

n1 n2 … nk .

Gambar 3 OI OII OIII … O_k Diundi sekaligus n1 cara n2 cara n3 cara nk cara Obyek Eksperimen Cara Eksp

Ruang sampel S dengan banyak titik sampel: n(S) = n1  n2  n3  …  nk . O2 nk cara … … … … … … _… s1 s2 s3 sn = n1 n2 … nk S n1 cara _n 2 cara Ok O1 Hasil2 yg mungkin Kemungkinan

(14)

B. Contoh Terapan Prinsip Perkalian

Masalah 2

Misalkan dari himpunan {0, 1, 2, 3} akan dibuat bilangan 3(tiga) angka antara 100 dan 320. Pertanyaannya adalah ”Ada berapa cara (ada berapa hasil yang mungkin) untuk membentuk bilangan 3(tiga) angka antara 100 dan 320 pada eksperimen ini?

Penyelesaian

1. Dengan penalaran Lengkap

Selidiki dari masalah yang diketahui bahwa Obyek eksperimennya adalah himpunan berupa {0, 1, 2, 3}. Cara ekperimennya adalah ”Ada berapa cara (ada berapa hasil yang mungkin) bilangan 3(tiga) angka yang dapat dibentuk antara 100 dan 320 pada eksperimen ini?

Jawab

Untuk memperjelas pemahaman gambaran penyelesaiannya adalah seperti berikut. Bilangan ratusan yang mungkin dari bilangan 3(tiga) yang dapat dibentuk antara 100 dan 320 yaitu (100 < x < 320) , yakni x berupa bilangan tiga angka antara 100 dan 320 adalah:

o Ratusannya yang mungkin dari himpunan {0, 1, 2, 3} untuk bilangan tiga angka antara 100 dan 320 adalah 1, 2, dan 3 sebab 0 tidak mungkin menempati tempat ratusan. .Mengapa?

o Bilangan puluhan yang mungkin untuk menaempati tempat puluhan jika

ratusannya 1 dari himpunan {0, 1, 2, 3} adalah semua elemen dari bilangan 0, 1, 2, 3. Sehingga untuk ratusan 1 puluhan yang mungkin adalah 1, 2, 3. Yakni semua elemen dari {0, 1, 2, 3} yaitu bilangan 0, 1, 2, 3. Khusus untuk ratusan 1 karena harus memenuhi syarat bilangan x dengan 100 < x < 320 adalah 1, 2, dan 3. Maka bilangan puluhan yang mungkin jika ratusan 1 untuk menempati tempat puluhan adalah 1, 2, dan 3, Sementara untuk ratusan 2, bilangan puluhan yang mungkin untuk memenuhi tempat puluhan adalah semua bilangan yang

(15)

ETraining Terstruktur 2015 – PPPPTK Matematika 11 disediakan. Yakni bilangan 0, 1, 2, dan 3. Sedangkan untuk ratusan 3, bilangan puluhan yang mungkin agar memenuhi syarat 100 < x < 320 adalah 0 dan 1. o Satuan yang mungkin jika ratusannya 3 dari bilangan 3 (tiga) angka x yang

memenuhi syarat 100 < x < 320 adalah puluhannya 0 dan 1. Semenrata bilangan satuannya agar memenuhi sayarat 100 < x < 320 adalah semua bilangan 0, 1, 2, dan 3. .

Sehingga gambaran penalaran selengkapnya adalah seperti berikut.

{0, 1, 2, 3}

Obyek Eksp

Dibuat bilangan 3 angka yang angka-angkanya antara100 dan 320. Cara Eksperimen n(S) = 39 1 3 0 1 0 2 1 3 (311) = s37 (312) = s38 (313) = s39 (310) = s36 S III Sat I Rat II Pul

Hasil-hasil yang mungkin

0 2 1 3 3 (101) = s1 (103) = s3 1 (102) = s2 2 0 2 1 3 (131) = s13 (132) = s14 (133) = s15 (130) = s12 1 0 2 (110) = s4 (111) = s5 (112) = s6 (113) = s7 3 2 2 3 0 2 1 3 0 0 2 1 3 (201) = s17 (202) = s18 (203) = s19 (200) = s16 (231) = s29 (132) = s30 (233) = s31 (230) = s28 1 1 cara 3 cara 4 cara 1 cara 1 cara 3 cara 4 cara 1 cara 2 cara 4 cara 4 cara Gambar 4

(16)

2. Dengan Cara Singkat

Karena dari himpunan {0, 1, 2, 3} akan dibuat bilangan 3 (tiga) angka antara 100 dan 320 yakni bilangan cacah x yang memenuhi syarat 100 < x < 320 adalah seperti berikut.

o Bilangan yang mungkin untuk menempati tempat ratusan adalah bilangan 1, 2, dan 3. Dalam hal ini tidak mungkin 0 menempati tempat ratusan. Mengapa? Sebab hasil seperti 023 bilangan sesungguhnya adalah 23. Sehingga bilangan yang mungkin untuk menempati tempat ratusan sebanyak 3 cara. Artinya n(ratusan) = 3.

o Bilangan yang mungkin untuk menempati tempat puluhan adalah 0, 1, 2 dan 3 untuk ratusan 1 dan 2, serta 0, 1 untuk ratusan 3. Sehingga n(puluhan) = 4.

o Bilangan yang mungkin untuk menempati tempat satuan jika ratusannya 1 dan puluhannya 0 adalah 1, 2, dan 3; jika ratusannya 1 dan puluhannya 1, 2, 3 adalah 0, 1, 2, 3. Sedangkan jika ratusannya 2, semua puluhan dan semua satuan mungkin, yaitu 0, 1, 2, dan 3. Sementara jika ratusannya 3, puluhannya 0, 1 bilangan satuan yang mungkin adalah 0, 1, 2, 3. Sehingga n(satuan) = 4.

o Banyak anggota ruang sampel S adalah

n(S) = Jumlah dari n(Ratusan)  n(Puluhan)  n(Satuan) = (113) + (134) + (144) + (124)

= 3 + 12 + 16 + 8 = 39.

(17)

BAHAN BACAAN II

KOMBINATORIK DAN PELUANG PADA PENGUNDIAN

A. Konsep Peluang dan Frekuensi Harapan

Masalah 1 (Konsep Peluang)

Apa yang akan terjadi bila kita undi sekeping mata uang logam sebanyak 20.000 kali dan apa yang akan terjadi jika kita undi sebuah paku payung standar (warna putih gilap) sebanyak 20.000 kali?

Penyelesaian

Untuk diketahui bahwa hasil eksperimen yang pernah dilakukan oleh seseorang (Anton, 1982:79) dan eksperimen pribadi oleh penulis di tahun 2001 diperoleh hasil-hasil seperti berikut.

(Sumber: Anton :1982,79. Applied Finite Mathematics).

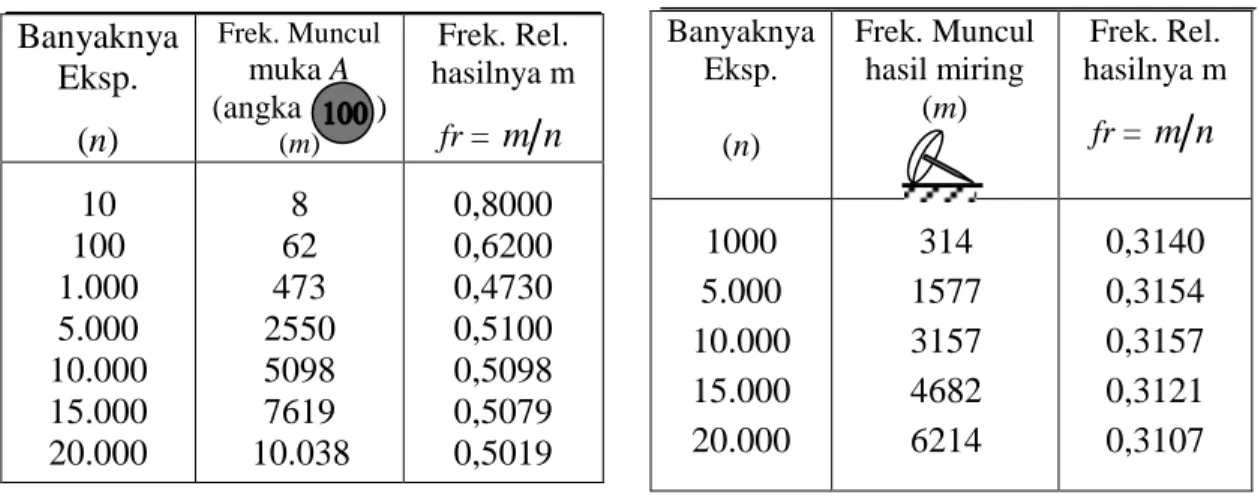
Banyaknya Eksp. (n) Frek. Muncul muka A (angka ) (m) Frek. Rel. hasilnya m fr = m n 10 100 1.000 5.000 10.000 15.000 20.000 8 62 473 2550 5098 7619 10.038 0,8000 0,6200 0,4730 0,5100 0,5098 0,5079 0,5019 Tabel 1 a

(Sumber: Eksperimen Pribadi, 2001).

Tabel 1 b Banyaknya Eksp. (n) Frek. Muncul hasil miring (m) Frek. Rel. hasilnya m fr = m n 1000 5.000 10.000 15.000 20.000 314 1577 3157 4682 6214 0,3140 0,3154 0,3157 0,3121 0,3107

(18)

Dari kedua obyek eksperimen (percobaan acak) seperti yang diperlihatkan pada tabel di atas tampak bahwa semakin banyak eksperimen dilakukan maka frekuensi realtif munculnya muka angka (A) pada mata uang logam nilai frekuensi relatifnya akan semakin mendekati nilai 0,5000 sementara untuk eksperimen yang sama terhadap paku payung (fines) diperoleh hasil bahwa nilai frekuensi relatifnya akan semakin mendekati nilai 0,3100.

Perhatikan bahwa dalam 1 (satu) tempat desimal maka nilai frekuensi relatif munculnya muka angka (A) pada sekeping mata uang logam dan munculnya hasil miring (m) pada paku payung jika eksperimen dilakukan sampai dengan tak hingga kali masing-masing adalah seperti berikut.

fr (A) = 2 1 = 0,5 dan fr ({m}) = 10 3 .

Peluang munculnya suatu hasil eksperimen didefinisikan sebagai nilai frekuensi relatif munculnya hasil itu jika eksperimen yang dilakukannya diulang-ulang sampai dengan tak hingga kali. Oleh sebab itu maka selanjutnya dikatakan bahwa:

Peluang munculnya muka angka A pada mata uang logam adalah:

dan

Peluang munculnya hasil miring paku payung adalah:

P(A) = 2 1 ) (

lim

__ f_r A  n P({m}) = . 10 3 }) ({

lim

__ f_r m  n P({m}) = 10 3 Peluang Miring P({t}) = 1 – 10 3 = 10 7 Peluang Terlentang P(A) = 2 1 Peluang Muncul Muka Angka (A)

P(G) = 1 – 2 1 = 2 1 Peluang Muncul Muka Gambar (G)

Untuk Sekeping Mata Uang Logam Untuk Sebuah Paku Payung

(19)

ETraining Terstruktur 2015 – PPPPTK Matematika 15 Selanjutnya karena hasil eksperimen yang mungkin untuk mata uang logam hanyalah muka angka A atau muka gambar G sementara untuk paku payumg hanyalah hasil miring m, atau terlentang t maka

Catatan

Obyek-obyek eksperimen yang menghasilkan nilai peluang yang sama jika diundi disebut obyek-obyek eksperimen yang seimbang (homogin) sementara obyek-obyek eksperimen yang menghasilkan nilai peluang yang tidak sama jika diundi disebut obyek-obyek eksperimen yang tak seimbang (non-homogin). Pada contoh di atas

mata uang logam termasuk obyek eksperimen yang seimbang sementara paku payung termasuk obyek eksperimen yang tak seimbang.

Kini misalkan ada pertanyaan berapakah peluang munculnya hasil berdiri {b} jika sebuah paku payung standar diundi dengan cara melambungkannya ke udara dan membiarkannya jatuh di laintai bersemen?

Jika pada suatu eksperimen (percobaan acak) suatu peristiwa A

pasti terjadi maka peristiwa itu disebut sebagai suatu

kepastian. Sementara itu jika pada suatu eksperimen suatu peristiwa A tak mungkin terjadi maka peristiwa itu disebut sebagai suatu kemustahilan.

Kini kita sudah dapat mengidentifikasi manakah diantara obyek-obyek eksperimen berikut ini yang merupakan obyek eksperimen setimbang dan manakah diantara obyek-obyek eksperimen berikut ini yang merupakan obyek eksperimen tak setimbang. Setimbang berarti jika obyek eksperimen itu diundi maka masing-masing hasil yang mungkin berpeluang sama untuk muncul.

Gambar 6

Hasil Berdiri

Mungkinkah? {b}

(20)

Masalah 2 (Konsep Frekuensi Harapan)

Dari nilai-nilai peluang munculnya hasil-hasil yang mungkin pada sekeping mata uang logam dan sebuah paku payung (fines) jika diadakan pengundian kepada masing-masing obyek eksperimen itu bagaimana frekuensi harapan munculnya hasil yang mungkin jika pengundian dilakukan hingga 100.000 kali?

Penyelesaian

Jika pengundian dilakukan hingga 100.000 kali maka frekuensi harapan (fh)

munculnya:

Muka Angka Muka Gambar

fh (A) = 100.000P(A) fh (A) = 100.000P(G) = 100.000 2 1 = 100.000 2 1 = 50.000 kali. = 50.000 kali.

Hasil Miring Hasil Terlentang

fr (A) = 100.000P({m}) fr (A) = 100.000P({t}) =100.000  10 3 = 100.000  10 7 = 30.000 kali. = 70.000 kali.

Jadi jika pengundian atas sekeping mata uang logam dilakukan sebanyak 100.000 kali maka frekuensi harapan munculnya muka angka adalah sebanyak 50.000 kali dan frekuensi harapan munculnya muka gambar juga sebanyak 50.000 kali. Sementara untuk sebuah paku payung jika pengundian dilakukan sebanyak 100.000 kali maka

Gambar 7

(a) (b) (c)

terlentang (t) miring (m) Obyek Tak Setimbang

muka A (angka)

muka G (gambar)

(21)

ETraining Terstruktur 2015 – PPPPTK Matematika 17 frekuensi harapan munculnya hasil miring sebanyak 30.000 kali dan hasil terlentang sebanyak 70.000 kali.

Catatan

Frekuensi harapan (fh) munculnya banyak kali hasil A yang diharapkan

jika eksperimen (percobaan acak) dilakukan sebanyak n kali

didefinisikan sebagai

fh (A) = n P(A).

B. Ruang Sampel, Titik Sampel, Peristiwa, dan Relasi Antarperistiwa

Masalah 1 (Konsep Ruang Sampel, Titik Sampel, dan Peristiwa)

Misalkan 2 (dua) keping mata uang logam diundi sekaligus. Masalah yang ditanyakan adalah: (a) Hasil-hasil apa saja yang mungkin terjadi pada eksperimen tersebut? (b) Tentukan ruang sampel, titik-titik sampel, dan peristiwa A yang didefinisikan sebagai peristiwa munculnya muka gambar G tepat sebanyak 1 kali, serta peristiwa B didefinisikan sebagai peristiwa munculnya muka gambar G tepat sebanyak 2 kali.

Gambarkan kesemuanya itu dalam bentuk diagram pohon dan kemudian dalam bentuk diagram Venn.

Penyelesaian

a. Dalam Bentuk Diagram Pohon

Dalam bentuk diagram pohon gambaran selengkapnya dari eksperimen (percobaan acak) tersebut adalah seperti berikut.

Gambar 8 diundi sekaligus ? Obyek Ekp. I II Cara Ekp.

(22)

18 ETraining Terstruktur 2015 – PPPPTK Matematika Berdasarkan peragaan gambar 9 di atas maka:

Ruang sampelnya adalah S = {(A, A), (A, G), (G, A), (G, G)} atau S ={s1, s2, s3, s4}.

Hasil-hasil yang mungkin seperti s1, s2, s3, s4 masing-masing disebut titik sampel, dan himpunan bagian dari ruang sampel disebut sebagai periistiwa/kejadian dalam rauang sampel S. Pada contoh ini

A = peristiwa munculnya muka gambar G tepat sebanyak 1 kali = {s2, s3}, dan

B = peristiwa munculnya muka gambar G tepat sebanyak 2 kali = {s4} masing-masing disebut peristiwa/kejadian dalam ruang sampel S. Peristiwa B dalam S yang tepat

memiliki 1 titik sampel disebut sebagai peristiwa elementer atau peristiwa

sederhana. Sementara peristiwa A yang memiliki lebih dari 1 titik sampel disebut sebagai peristiwa majemuk.

b. Dalam Bentuk Diagram Venn

Dalam bentuk diagram Venn kerangka pemikirannya adalah seperti berikut.

S = Ruang sampel hasil eksperimen.

s1, s2, s3, dan s4 adalah titik-titik sampel dalam ruang sampel S.

A, B  S masing-masing disebut peristiwa dalam ruang sampel S.

Gambar 9 diundi sekaligus Obyek Ekp. Cara Ekp. Hasil-hasil Yang Mungkin A G A G A G (A,A) = s1 B A S (A,G) = s2 (G,A) = s3 (G,G) = s4 Kemungkinan I II I II s1 s2 s3 s4 A B S Gambar 9.b

(23)

ETraining Terstruktur 2015 – PPPPTK Matematika 19 Peristiwa A yang memiliki lebih dari 1 titik sampel disebut peristiwa majemuk dan peristiwa B yang memiliki tepat 1 titik sampel disebut peristiwa sederhana (peristiwa elementer/ elementary event).

A. Peluang Pada Pengundian

Masalah 1

Dua buah paku payung standar (warna putih gilap) diundi sekaligus. Jika A adalah peristiwa munculnya hasil kembar dan B adalah peristiwa munculnya hasil terlentang minimal sebanyak 1 kali. Pertanyaannya adalah:

a. Gambarkan hasil-hasil eksperimen yang mungkin terjadi dalam bentuk diagram pohon (termasuk ruang sampel S dan peristiwa A dalam S yakni

AS)

b. Gambarkan hasil-hasil eksperimenya dalam bentuk diagram Venn. c. Tentukan P(A) yakni peluang munculnya peristiwa A.

d. Tentukan P(B) yakni peluang munculnya peristiwa B. e. Tentukan relasi antara peristiwa A dan B.

Penyelesaian

a. Dengan Penalaran Lengkap

Pertama kita gambar kerangka pemikiran berkenaan dengan hasil-hasil yang mungkin: ruang sampel S, peristiwa A dan B, serta teknik perhitungan nilai-nilai peluangnya. Gambaran selengkapnya seperti berikut.

diundi sekaligus Obyek Ekp. Cara Ekp. I II Gambar 10 Gambar 10.a Keterangan Hasil miring m = Hasil terlentangt = diundi sekaligus Obyek Ekp. Cara Ekp. I II 10 7 10 3 I A S 100 100 Total = P({(m,m)}) = 100 9 10 3 10 3





P({(m , t)}) = ₁₀3



₁₀7



₁₀₀21 P({(t , m)}) = ₁₀7



₁₀3



₁₀₀21 P({(t , t)}) = ₁₀7



₁₀7



₁₀₀49 = 1 + m t m t (m,m) (m, t) (t , m) (t , t) 10 3 10 7 10 3 10 7 II = s1 = s2 = s3 = s4 m t 10 7 P({t}) = P({m}) = ₁₀3 , B Hasil-hasil yang mungkin

(24)

Dari peragaan gambar di atas akan tampak dengan jelas ruang sampel S pada eksperimen itu, peristiwa A, peristiwa B, dan perhitungan nilai peluang masing-masing. Jika A adalah peristiwa munculnya hasil kembar maka

A = {(m, m), (t, t)} = {s1, s4} sehingga

P(A) = ({s1, s4}) = P({s1}) + P({s4})

= ₁₀₀9 + ₁₀₀49 = ₁₀₀58 = 0,58.

Jika ruang sampel dan peristiwa A, BS di atas kita gambarkan dalam bentuk diagram Venn maka gambaran kerangka pemikiran selengkapnya adalah seperti berikut. P(A) = P({s1}) + P({s4}) = ₁₀₀9 + ₁₀₀49 = ₁₀₀58 = 0,58. P(B) = P({s4}) + P({s2}) + P({s3}) = ₁₀₀49 + ₁₀₀21 + ₁₀₀21 = ₁₀₀91 = 0,91.

Jadi peluang munculnya peristiwa/kejadian

A dan B dalam ruang sampel S yakni A, BS

masing-masing adalah P(A) = 0,58 dan P(B) = 0,91.

b. Dengan Cara Singkat

Jika A adalah peristiwa/kejadian munculnya hasil kembar pada kedua paku payung, maka A = {(m, m), (t, t)}. Sehingga P(A) = P({(m, m)}) + P({(t, t)}) = P({(m)})P({(m)}) + P({(m)})P({(m)}) = ₁₀3



₁₀3 + ₁₀7



₁₀7 = ₁₀₀9 + ₁₀₀49 = ₁₀₀58 = 0,58. S A 100 21 s2 s3 100 21 100 9 _s₁ 100 49 _s₄ B Gambar 10.b

(25)

ETraining Terstruktur 2015 – PPPPTK Matematika 21 Jika B adalah peristiwa/kejadian munculnya hasil terlentang minimal 1 kali maka berarti peristiwa B = {muncul t satu kali atau muncul t dua kali} = {(m, t), (t, m), (t, t)} = {s2, s3, s4}. Maka

P(B) = P({(m, t)}) + P({(t, m)}) + P({(t, t)})

= P({m})P({t}) + P({t})P({m)) + P({t})P({t}) = ₁₀3



₁₀7 + ₁₀7



₁₀3 + ₁₀7



₁₀7

= ₁₀₀21 + ₁₀₀21 + ₁₀₀49 = ₁₀₀91 = 0,91.

Jadi peluang munculnya peristiwa BS adalah P(B) = ₁₀₀91 = 0,91.

Selidiki bahwa P(A) = 100 58 , P(B) =100 91 , dan P(AB)= 100

.

49 Karena P(AB)=100 49  100 58  ₁₀₀91

.

Maka berartiP(AB)  P(A)  P(B). Sehingga A

dan B adalah dua peristiwa tak bebas. Untuk lebih jelasnya lihat relasi antar peristiwa yang digambarkan dalam bentuk diagram Venn berikut ini.

Masalah 2

Dua keping mata uang logam diundi sekaligus. Jika A adalah peristiwa munculnya muka angka pada mata uang logam I dan B adalah peristiwa munculnya muka gambar pada mata uang logam II.

Pertanyaannya adalah:

a. Gambarkan hasil-hasil eksperimen yang mungkin terjadi dalam bentuk diagram pohon (termasuk ruang sampel S dan peristiwa A dan peristiwa B dalam S yakni A, B S)

b. Gambarkan hasil-hasil eksperimen tersebut dalam bentuk diagram Venn.

c. Tentukan P(A) dan P(B) yakni peluang munculnya masing-masing dari peristiwa

A dan peristiwa B

d. Tentukan relasi antara peristiwa A dan B.

Gambar 11 diundi sekaligus Obyek Ekp. Cara Ekp. I II

(26)

Penyelesaian

a. Dengan Penalaran Lengkap

Pertama kita gambar kerangka pemikiran berkenaan dengan hasil-hasil yang mungkin: ruang sampel S, peristiwa A dan B, serta teknik perhitungan nilai-nilai peluangnya. Gambaran selengkapnya seperti berikut.

Dari peragaan gambar di atas akan tampak dengan jelas ruang sampel S pada eksperimen itu, peristiwa A, peristiwa B, dan perhitungan nilai peluang masing-masing. Jika A adalah peristiwa munculnya muka angka pada mata uang logam I, maka

A = {(A, A), (A, G) }= {s1, s2} sehingga

P(A) = ({s1, s2}) = P({s1}) + P({s2}) = 2 1 2 1



+ 2 1 2 1



= 4 1 + 4 1 = 4 2 = 2

.

1

Jika ruang sampel S dan peristiwa A, BS di atas kita gambarkan dalam sebuah bentuk diagram Venn maka gambaran kerangka pemikiran selengkapnya adalah seperti berikut. Gambar 11.a Hasil-hasil Yang Mungkin A G A G A G I II diundi sekaligus Obyek Ekp. Cara Ekp. I II (A,A) = s1 B A S (A,G) = s2 (G,A) = s3 (G,G) = s4 2 1 2 1 2 1 2 1 2 1 2 1 4 1 4 1 4 1 4 1 Total = P(S) = = 1 4 4

Hasil2 yang Mungkin Untuk

Mata Uang Logam Ke

P(B) = = ₄2 2 1 P(A) = = ₄2 2 1

(27)

ETraining Terstruktur 2015 – PPPPTK Matematika 23 P(A) = P({s1}) + P({s2}) = ₄1 + ₄1 = ₄2 = 1₂

.

P(B) = P({s2}) + P({s4}) = ₄1 + ₄1 = 4 2 = 2

.

1

Jadi peluang munculnya peristiwa/kejadian A dan B dalam ruang sampel S yakni A,

BS masing-masing adalah P(A) =2 1

dan P(B) = 2

.

1

Sementara peluang munculnya peristiwa (AB) adalah P(AB) = P({s2})

= 4

.

1

b. Dengan Cara Singkat

Jika A adalah peristiwa/kejadian munculnya muka angka pada mata uang logam I, dan

B adalah peristiwa munculnya muka gambar G pada mata uang logam II, maka

masing-masing peristiwa yang dimaksud adalah:

A = {s1, s2} dan B = {s2, s4}. Sehingga AB = {s2}.

Selidiki dari diagram Venn (Gambar 11.b) maupun dari diagram pohon (Gambar 11.a) bahwa

P(AB) = P({s2}) = 4

.

1

Kini kita selidiki apakah P(AB) = P(A) P(B) .

4 1 = 2 1  2 1 4 1 = 4

.

1

Karena P (AB) = P(A)P(B) maka berarti A dan B adalah dua peristiwa bebas. Untuk lebih jelasnya lihat relasi antar peristiwa yang digambarkan dalam bentuk diagram Venn berikut ini.

A s1 4 1 s2 4 1 s3 4 1 s4 4 1 B S Gambar 11.b

(28)

C. Relasi Antar Peristiwa

Misalkan ruang sampel S berdistribusi seragam (S homogin) yakni masing-masing

titik sampel dalam S berpeluang sama untuk muncul. A, BS. Relasi antara peristiwa A dan B dalam ruang ruang sampel S digambarkan seperti berikut.

a. Dalam ruang sampel S (S homogin)

A dan B adalah dua peristiwa lepas.

AB =  dan AB  S

b. A dan B adalah dua peristiwa komplemen.

A = bukan B atau B = bukan A, ditulis B = Ac_P(Ac_{) = 1 – P(A) atau}

) ' (A P = 1 – P(A) untuk 'A = Ac_. c. P(A) = 10 7 , P(B) = 10 5 , P(A  B) = 10 2 .

Ternyata P(A  B)  P(A)  P(B) , maka

A dan B adalah dua peristiwa tak bebas.

d. P(A) = 10 7 , P(B) = 10 5 , P(A  B) = 10 2 .

Ternyata P(A  B) = P(A)  P(B) , maka

A dan B adalah dua peristiwa bebas.

A B S Gambar 12.a S A B Gambar 12.b S A B Gambar 12.d Gambar 12.c S A B

(29)

Latihan 1

1. Sekeping mata uang logam dan 2(dua) buah paku payung diundi sekaligus. Misalkan S adalah ruang sampel pada eksperimen itu.

(a) Gambarkan diagram pohon ruang sampel S, titik sampel s1, s2, s3, ... dan seterusnya dalam S, serta peristiwa-peristiwa A, B dan AB dalam S jika A adalah peristiwa munculnya muka gambar G pada mata uang logam dan munculnya hasil kembar pada paku payung. Sementara B adalah peristiwa munculnya hasil miring m pada paku payung sebanyak 2 kali. Tentukan peristiwa A, B, dan AB dalam bentuk himpunan.

(b) Gambarkan ruang sampel S, titik-titik sampel s1, s2, s3, ... dan seterusnya, serta peristiwa-pristiwa A dan B dalam sebuah diagram Venn.

(c) Apakah A dan B merupakan 2 peristiwa lepas, bebas, tak bebas, atau komplemen?

2. Ada berapa cara hasil yang mungkin terjadi jika 4 keping mata uang logam, 1 buah dadu, dan 2 buah paku payung diundi sekaligus. Kemukakan alasan dan penalarannya Gambar 13 S? diundi sekaligus II I III Obyek Eksp Cara Eksp

(30)

3. Tiga buah dadu diundi sekaligus. Misalkan S adalah ruang sampel pada eksperimen itu.

(a) Tentukan n(S) yakni banyak anggota ruang sampel S. Jelaskan. Apakah ruang sampel S berdistribusi seragam? Yakni masing-masing titik sampelnya berpeluang sama untuk muncul. Kemukakan alasannya.

(b) Jika A, B, C, dan D masing-masing adalah peristiwa munculnya muka 1 sebanyak 0 kali, 1 kali, 2 kali, dan 3 kali. Tentukan n(A), n(B), n(C), dan n(D) yakni banyak anggota titik sampel dari masing-masing peristiwa dalam ruang sampel S.

(c) Kemukakan relasi diantara peristiwa A, B, C, dan D apakah saling lepas atau saling partisi dalam ruang sampel S. Kemukakan alasannya.

4. Tiga keping mata uang logam (I, II, dan III) diundi sekaligus. Misalkan S adalah ruang sampel pada eksperimen itu. A, B, dan C adalah peristiwa-peristiwa dalam S dengan:

A = peristiwa munculnya muka gambar pada mata uang ke II atau ke III B = peristiwa munculnya muka angka pada mata uang ke I atau ke II

Tentukan relasi antara peristiwa A dan B.

5. Sekeping mata uang logam diundi sebanyak 100 kali. Tentukan frekuensi harapan munculnya:

a. Muka angka dalam pengundian itu. b. Muka gambar dalam pengundian itu.

6. Sebuah paku payung diundi sebanyak 1000 kali. Tentukan frekuensi harapan munculnya: Gambar 18 ? diundi sekaligus II I III Obyek Eksp Cara Eksp

(31)

ETraining Terstruktur 2015 – PPPPTK Matematika 27 a. Hasil miring dalam pengundian itu.

b. Hasil terlentang dalam pengundian itu.

7. Sebuah dadu dilambungkan sebanyak 1200 kali. Tentukam frekuensi harapan munculnya:

a. Mata dadu genap dalam pengundian itu. b. Mata dadu prima dalam pengundian itu.

c. Mata dadu genap dan mata dadu prima dalam pengundian itu.

8. Tiga lembar kartu bergambar diundi sekaligus dengan cara melemparkannya ke udara dan membiarkannya jatuh di tanah. Pertanyaannya adalah:

a. Jika S adalah ruang sampel dari eksperimen itu, tentukan n(S) = ... yakni banyak anggota S dalam eksperimen itu.

b. Jika AS adalah peristiwa munculnya muka gambar sebanyak 2 kali, tentukan peluang munculnya peristiwa A.

c. Jika BS adalah peristiwa munculnya muka gambar sebanyak 1 kali, tentukan peluang munculnya peristiwa B.

d. Jika CS adalah peristiwa tak satupun kartu gambar muncul dalam eksperimen itu, tentukan peluang munculnya peristiwa C.

(32)

BAHAN BACAAN III

KOMBINATORIK DAN PELUANG PADA PENGAMBILAN

SAMPEL

A. Notasi Faktorial

Masalah

Misalkan pada sebuah lomba tebak tepat yang diikuti oleh 3 regu yakni regu A, regu B, dan regu C. Misalkan pada lomba ini disediakan 3 hadiah (hadiah I, II, dan III). Pertanyaannya adalah ada berapa cara hadiah-hadiah itu dapat diberikan pada para pemenang?

Penyelesaian

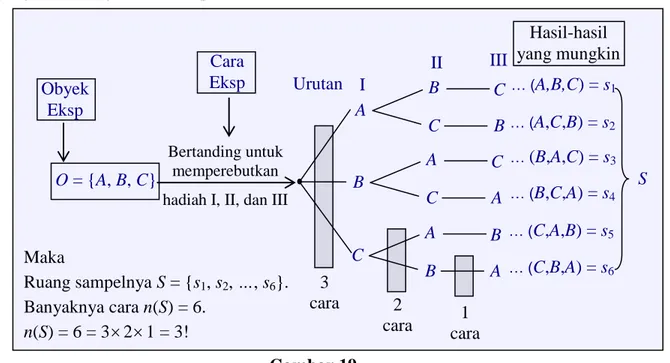
Misalkan obyek eksperimen O = {A, B, C} adalah himpunan 3 (tiga) regu peserta tebak tepat. Karena pada eksperimen ini pada umumnya diberikan hadiah I, II, dan III yang tidak sama nilai rupiahnya maka berarti urutan pemenang memiliki makna yakni hadiah I lebih besar dari hadiah II, hadiah II lebih besar dari hadiah III, dan seterusnya (bila regu dan hadiahnya lebih banyak). Sehingga gambaran penyelesaiannya adalah seperti berikut.

Gambar 19 Maka Ruang sampelnya S = {s1, s2, …, s6}. Banyaknya cara n(S) = 6. n(S) = 6 = 321 = 3! Urutan S I _C… (A,B,C) = s1 A B C B C B A C A B C A B A II III … (A,C,B) = s2 … (B,A,C) = s3 … (B,C,A) = s4 … (C,A,B) = s5 … (C,B,A) = s6 3 cara 2 cara _cara1 Hasil-hasil yang mungkin O = {A, B, C} Bertanding untuk memperebutkan hadiah I, II, dan III

Obyek Eksp

Cara Eksp

(33)

ETraining Terstruktur 2015 – PPPPTK Matematika 29 Perhatikan bahwa berdasarkan peragaan gambar di atas maka hasil-hasil yang mungkin adalah (A,B,C), (A,C,B), (B,A,C), … , (C,B, A) atau s1, s2, s3, s4, s5, dan s6. Maka ruang sampelnya adalah S dengan banyak anggotanya n(S) = 6. Perhatikan pula bahwa n(S) = 6 berasal dari hasil kali 321. Bentuk perkalian 321 itu selanjutnya didefinisikan sebagai 3! (baca”3 faktorial). Yakni:

Dengan melihat penalaran seperti yang dikemukakan di atas maka untuk setiap bilangan cacah n maka

Lebih lanjut didefinisikan (disepakati) bahwa

B. Permutasi

Masalah

Misalkan pada suatu lomba tebak tepat yang diikuti oleh 3 regu (regu A, regu B, dan regu C) hanya menyediakan 2 macam hadiah saja yakni hadiah I dan hadiah II. Pertanyaannya adalah ada berapa cara hadiah-hadiah itu dapat diberikan kepada para pemenang?

Penyelesaian

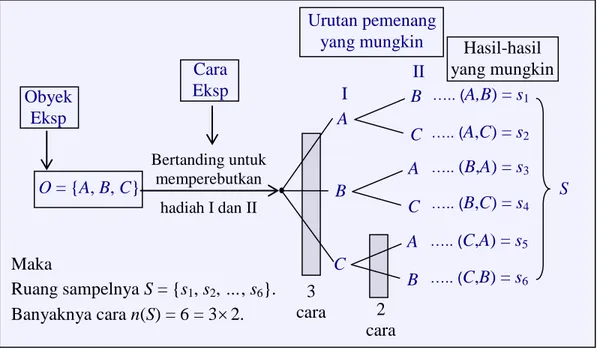
Misalkan obyek eksperimen O = {A, B, C} adalah himpunan regu peserta tebak tepat. Karena pada eksperimen ini hanya menyediakan 2 hadiah maka gambaran penyelesaiannya adalah seperti berikut.

n! = n(n – 1)(n – 1)(n – 1) … 21. 3! = 321.

(34)

Dari gambaran kerangka berpikir di atas maka ada 6 cara hadiah I dan II dapat diberikan kepada para pemenang. Sehingga banyak anggota ruang sampelnya adalah

n(S) = 6. Ruang sampel S yang dimaksud adalah

S = {(A, B), (A,C), (B, A), (B,C), (C, A), (C, B) } = { s1, s2, s3, …, s6}.

Perhatikan bahwa n(S) = 6 tidak lain berasal dari 3 cara dan 2 cara. Yakni:

n(S) = 6 = 32 = 1 1 2 3  = ! 1 ! 3 = )! 2 3 ( ! 3  .

Amati bahwa susunan elemen hasil (pemenang lomba) seperti (A, B)(B, A) sebab (A,

B) artinya juara I adalah regu A dan juara keduanya adalah regu B. Sementara

susunan elemen hasil seperti (B, A) artinya B juara I dan A juara II. Karena (A, B)(B,

A) maka berarti susunan urutan mempunyai makna.

Jika susunan urutan elemennya mempunyai makna maka susunan eleman-elemen itu selanjutnya disebut sebagai eleman-eleman-elemen permutasi. Sehingga n(S) = 6 artinya banyaknya permutasi 2 hadiah dari 3 peserta (regu) adalah S dengan

Gambar 20 Maka Ruang sampelnya S = {s1, s2, …, s6}. Banyaknya cara n(S) = 6 = 32. O = {A, B, C} Bertanding untuk memperebutkan hadiah I dan II Obyek Eksp Cara Eksp _I A B C B A C C A B II S ….. (A,B) = s1 ….. (A,C) = s2 ….. (B,A) = s3 ….. (B,C) = s4 ….. (C,A) = s5 ….. (C,B) = s6 2 cara 3 cara Hasil-hasil yang mungkin Urutan pemenang yang mungkin

(35)

ETraining Terstruktur 2015 – PPPPTK Matematika 31 n(S) = dari peaerta hadiah P 3 2 = 3 2 dari P = 3 2 P = )! 2 3 ( ! 3  . Yakni n(S) = 3 2 P = )! 2 3 ( ! 3  .

Selidiki jika banyaknya peserta n dan banyaknya hadiah yang disediakan r (tentu r 

n) maka akan selalu benar bahwa banyak anggota ruang sampel S adalah n(S) dengan n(S) = n r P . n r P = )! ( ! r n n  . Catatan n r

P artinya banyaknya permutasi (susunan urutan punya makna/diperhatikan) dari

pasangan berurutan r obyek yang berasal dari obyek eksperimen sebanyak n adalah

)! ( ! r n n  .

C. Kombinasi

Masalah

Misalkan dari 4 bersaudara Ali (A), Budi (B), Cahya (C), dan Doni (D) diundang 2 orang wakilnya untuk rapat keluarga. Pertanyaanya adalah ada berapa cara undangan itu dapat dipenuhi? Bagaimana pula jika yang diundang adalah 3 orang dari 4 bersaudara itu?

Penyelesaian

Dari masalah yang dikemukakan di atas maka obyek eksperimennya adalah O = {A, B,

C, D} sedangkan eksperimennya adalah mengundang hadir dalam rapat keluarga sebanyak 2 orang wakilnya. Bagaimana bila eksperimennya diganti dengan

mengundang hadir dalam rapat keluarga sebanyak 3 orang wakilnya. Ruang sampel dari masing-masing eksperimen itu adalah himpunan semua hasil yang mungkin

(36)

32 ETraining Terstruktur 2015 – PPPPTK Matematika Tabel 3

No. Obyek

Eksperimen

Cara Eksperimen Hasil-hasil yang Mungkin (Hadir) 1. 2. O = {A, B, C, D} O = {A, B, C, D} Mengundang 2 orang wakilnya untuk rapat keluarga Mengundang 3 orang wakilnya untuk rapat keluarga

(A,B) = s1 .... baca A dan B = s1. (A,C) = s2 (A,D) = s3 (B,C) = s4 (B,D) = s5 (C,D) = s6 (A,B,C) = s1 (A,B,D) = s2 (A,C,D) = s3 (B,C,D) = s4

Perhatikan bahwa rangkaian hasil-hasil eksperimen yang mungkin terjadi seperti di atas selanjutnya disebut elemen-elemen kombinasi sebab elemen hasil seperti (A,B) dan (B,A) hanya diwakili oleh (A,B) saja? Mengapa? Sebab (A,B) artinya yang hadir adalah A dan B. Sedangkan (B,A) artinya yang hadir adalah B dan A. Karena yang hadir adalah A dan B sama dengan yang hadir adalah B dan A. Maka susunan hasil eksperimen seperti (A,B) = (B,A).

Karena susunan hasil seperti (A,B) = (B,A) maka secara lebih tepat dapat diganti dengan {A,B} sebab jelas bahwa penulisan himpunan tidak memungkinkan adanya pengulangan elemen dan susunan elemen-elemennya tidak diperhatikan. Yakni {A,B} = {B,A}. Hal yang sama {A,B,C} = {B,C,A} = {C,A,B} dan lain-lain sebab sama-sama berarti bahwa yang hadir adalah si A, si B, dan si C. Oleh sebab itu penulisan elemen-elemen kombinasi akan lebih tepat jika ditulis dalam bentuk himpunan bukan dalam bentuk pasangan berurutan.

Dalam bentuk himpunan, banyaknya hasil yang mungkin jika 4 bersaudara {A, B, C, D} diundang 2 orang wakilnya untuk rapat keluarga maka Kini dalam bantuk himpunan

n(S) = 6

(37)

ETraining Terstruktur 2015 – PPPPTK Matematika 33 bagian banyaknya hasil yang mungkin adalah sama dengan banyaknya kombinasi 2 elemen dari 4 elemen yang tersedia dilambangkan dengan

4 2

C atau C(4,2) atau 4C2 atau .

2 4      

Maka C₂4 6dan C₃44. Penurunan rumus lebih lanjut: Untuk 4 2 C (Kombinasi 2 dari 4). Tabel 4 Macam Kombinasi

Jika Elemen-elemen Kombinasi

itu dipermutasikan Banyaknya _Permutasi

s1 = {A,B} s2 = {A,C} s3 = {A,D} s4 = {B,C} s5 = {B,D} s6 ={C,D} (A, B), (B, A) (A, C), (C, A) (A, D), (D, A) (B, C), (C, B) (B, D), (D, B) (C, D), (D, C) 2! 2! 2! 2! 2! 2! 6 4 2  C _ faktor P elemen Total 2 4 2 4 3 12     6  2! Untuk 4 3 C (Kombinasi 3 dari 4) Tabel 5 Macam Kombinasi

Jika Elemen-elemen Kombinasi itu Dipermutasikan _Banyaknya Permutasi

s1 = {A,B,C}

s2 = {A,B,D} s3 = {A,C,D} s4 = {B,C,D}

(A,B,C), (A,C,B), (B, A,C), (B, C,A), (C, A, B), (C, B, A) (A,B,D), (A,D,B), (B, A,D), (B, D,A), (D, A, B), (D, B, A)

(A,C,D), (A,D,C), (C, A,D), (C, D,A), (D, A, C), (D, C, A) (B,C,D), (B,D,C), (C, B,D), (C,D, B), (D, B, C), (D, C, B) 3! 3! 3! 3! 4 4 3  C Total = 4 3 2 24 3 4 3   faktor P 4  3! = 24

(38)

34 ETraining Terstruktur 2015 – PPPPTK Matematika Perhatikan bahwa pola yang dapat diamati adalah:

! 2 ! 2 6 12 3 4 4 2 4 2      C  P ! 3 ! 3 4 24 2 3 4 ₃4 4 3       C  P

Dengan penalaran yang sama maka secara umum akan berlaku bahwa:

! r C P n r n r   atau ! r P C n r n r  = ! )! ( ! r r n n  atau ! )! ( ! r r n n Cn r  _ Contoh Pehitungan Hitunglah: a.C320 ... b. C₁₇20 ... Jawab

a. Karena selisih antara 3 dan 20 relatif jauh, maka rumus yang lebih praktis digunakan adalah 20

3

P = 20 turun satu-satu sebanyak 3 faktor dibagi 3 faktorial.

Yakni: ! r P C n r n r  sehingga 1140. 1 2 3 18 19 20 1 2 3 ) 2 20 )( 1 20 ( 20 ! 3 20 3 20 3 _ _           P C

b. Karena 17 dan 20 berselisih relatif dekat, maka rumus yang lebih praktis digunakan adalah ! )! ( ! r r n n C_rn   , sehingga 1140. ! 17 6 ! 17 18 19 20 ! 17 ! 3 ! 20 ! 17 )! 17 20 ( ! 20 20 17 _         C

Suatu hal penting yang harus/perlu diketahui dan harus selau diingat adalah banyaknya kombinasi bersesuaian dengan bilangan-bilangan pada segitiga Pascal. Yakni:

3 faktor 3 faktor

(39)

ETraining Terstruktur 2015 – PPPPTK Matematika 35 Dengan hafal 5 hingga 6 baris segitiga Pascal di atas maka kita akan dapat menuliskan nilai-nilai banyaknya kombinasi secara lebih cepat.

D. Terapan Dalam Pemecahan Masalah Pengambilan Sampel

Masalah

Misalkan suatu eksperimen berupa pengambilan acak sebanyak 2 bola akan kita lakukan atas sebuah kotak yang berisi 3 buah bola seukuran bernomor 1, 2, 3. Pertanyaannya adalah ada berapa cara (macam hasil yang mungkin terjadi) jika

eksperimen yang kita lakukan (berupa pengambilan 2 bola secara acak) itu adalah pengambilannya:

(1) sekaligus,

(2) satu demi satu tanpa pengembalian, (3) satu demi satu dengan pengembalian.

Penyelesaian

Untuk memperjelas permasalahan, masing-masing ruang sampel yang dihasilkan pada ekspermen itu akan diberikan dalam bentuk gambar diagram pohon seperti berikut. 1 1 1 1 1 3 1 2 3 1 4 6 4 1 1 5 10 10 5 1 1 0 0 C 1 0 C C1₁ 2 0 C C₁2 C2₂ 3 0 C C₁3 C₁3 C3₃ 4 0 C C₁4 C4₂ C₃4 C4₄ 5 0 C C₁5 C5₂ C5₃ C54 C55

Segitiga Pascal Kombinasi

Gambar 21

(40)

36 ETraining Terstruktur 2015 – PPPPTK Matematika 1. Pengambilan Sampel Sekaligus (Eksp 1)

Dari gambar peragaan tersebut maka:

S = { s1, s2, s3 } disebut ruang sampel, yakni himpunan dari semua hasil yang mungkin terjadi dalam eksperimen itu.

Elemen-elemen dalam ruang sampel S yakni s1, s2, dan s3 masing-masing disebut titik-titik sampel, yakni hasil-hasil yang mungkin terjadi pada eksperimen itu.

Peristiwa A = {s1, s3 }yang merupakan himpunan bagian dari ruang sampel S, disebut

peristiwa/ kejadian dalam ruang sampel S tepatnya adalah peristiwa terambilnya

jumlah kedua nomor bola ganjil.

Pada ruang sampel S tersebut s1 = (1,2), s2 = (1,3), dan s3 = (2,3) masing-masing disebut elemen-elemen kombinasi sebab susunan (1,2) = (2,1) sehingga hanya dihitung sebagai 1 titik sampel saja. Mengapa?, sebab terambilnya bola bernomor 1 dengan bola bernomor 2 sama artinya dengan terambilnya bola bernomor 2 dengan bola bernomor 1.

Banyaknya kombinasi = dari obyek obyek C2 3 = 3 2 dari C = 3 2 C = 3. Maka n(S) = 3 =C . 23 1 2 3 Eksp1:ambil acak 2 bola sekaligus 1 2 1 3 2 3 … s1 … s2 … s3 S A Hasil-hasil yang mungkin

Ambil acak 2 bola sekaligus. Hasil-hasil yang

mungkin? A S s2 s1 s3 (a) _(b) Gambar 22

(41)

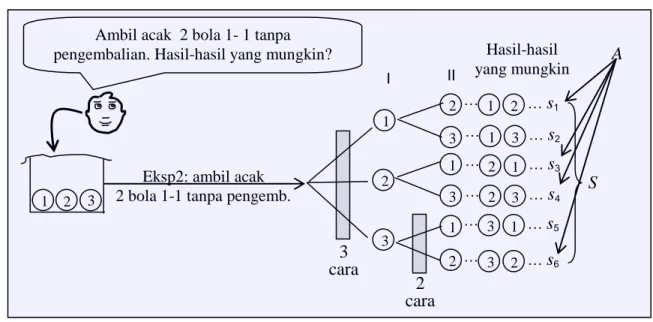
2. Pengambilan Sampel Satu Demi Satu (1 – 1) Tanpa Pengembalian (Eksp 2)

Diagram Venn yang bersesuaian dengan diagram pohon di atas adalah seperti berikut.

Dengan cara pemikiran yang sama dengan no.a, maka:

Ruang sampel S = {s1, s2, s3, . . . , s6}, maka n(S) = 6. Peristiwa A = {s1, s3, s4, s6}, maka n(A) = 4.

Perhatikan bahwa dari kedua diagram di atas:

S = {s1, s2, … , s6} disebut ruang sampel dari eksperimen itu. Selidiki bahwa s1, s2, …. , s6 masing-masing merupakan elemen-elemen permutasi. Mengapa?, sebab tidak ada pengulangan obyek eksperimen pada setiap susunan elemennya dan urutan susunan

elemen-elemennya diperhatikan (memiliki makna), yakni susunan elemen (1,2)

(2,1). Sebab (1,2) berarti yang terambil pertama adalah bola bernomor 1 dan yang terambil kedua adalah bola bernomor 2, sehingga susunan elemen (1,2) (2,1). Selidiki bahwa banyaknya anggota ruang sampel S adalah n(S) = 6 = 3

2

P . Gambar 23

1 2 3

Eksp2: ambil acak 2 bola 1-1 tanpa pengemb.

Hasil-hasil yang mungkin Ambil acak 2 bola 1- 1 tanpa

pengembalian. Hasil-hasil yang mungkin?

S I II 1 2 3 2 3 1 3 1 2 1 2 … s1 … 1 3 … s2 … 2 1 … s3 … 2 3 … s4 … 3 1 … s5 … 3 2 … s6 … A 3 cara 2 cara S A s5 s1 s4 s2 s3 s6 Gambar 23.a

(42)

3. Pengambilan Satu Demi Satu Dengan Pengembalian (Eksp 3)

Dengan cara pemikiran yang sama dengan no.a, maka secara diagram Venn

Ruang sampel S = {s1, s2, s3, . . . , s9}, maka n(S) = 9 Peristiwa A = {s2, s4, s6, s8}, maka n(A) = 4.

Catatan Penting

Eksp 1: S memuat 3 titik sampel. S merupakan himpunan kombinasi sebab masing-masing titik sampel anggotanya berupa elemen-elemen kombinasi yakni pengulangan nomor bola tidak dimungkinkan dan urutan nomor bolanya tidak diperhatikan

Eksp 2: S memuat 6 titik sampel. S merupakan himpunan permutasi sebab masing-masing titik sampel anggotanya berupa elemen-elemen permutasi, yakni pengulangan nomor bola tidak dimungkinkan dan urutan nomor bolanya diperhatikan (punya makna)

Eksp 3: S memuat 9 titik sampel. S bukan himpunan permutasi maupun kombinasi sebab ada titik sampel yang susunan elemen-elemen nomor bolanya diulang.

S A s7 s2 s6 s3 s4 s8 s1 s5 s9 Gambar 24.a Gambar 24 1 2 3

Eksp 3:ambil acak 2 bola 1-1 dengan pengembalian

Ambil acak 2 bola 1– 1 dengan pengemb. Hasil-hasil yang mungkin?

I 1 2 3 Hasil-hasil yang mungkin S II _A 1 … 1 1 … s1 2 … 1 2 … s2 3 … 1 3 … s3 1 … 3 1 … s7 2 … 3 2 … s8 3 … 3 3 … s9

A = Peristiwa terambilnya jumlah kedua nomor bola ganjil A = {s2, s4, s6, s8}. _cara3

3 cara

(43)

E. Permutasi Dengan Beberapa Unsur Sama (Penggunaan Aturan

Kombinasi)

Perlu diketahui bahwa konteks permutasi dengan beberapa unsur sama dalam hal ini berbeda dengan permutasi yang telah dikemukakan sebelumnya. Letak perbedaannya ialah pada susunan elemen-elemennya. Permutasi (tanpa istilah tambahan) bermakna sebagai susunan elemen-elemen dari suatu hasil eksperimen yang tidak membolehkan adanya pengulangan elemen, sementara permutasi dengan beberapa unsur sama membolehkan adanya pengulangan elemen.

Masalah

Ada berapa cara kita dapat menuliskan susunan huruf yang berasal dari kata "MAMA".

Penyelesaian

Perhatikan bahwa huruf-huruf penyusun kata "MAMA" diambilkan dari himpunan {M,

A} yaitu himpunan huruf-huruf abjad terdiri atas huruf M dan A. Unsur M dan A

masing-masing diulang 2 kali pada kata MAMA. Berikut susunan huruf-huruf yang mungkin. 1. MMAA 2. MAMA M1 A1 M2 A2 3. AMMA M2 A2 M1 A1 4. AMAM M1 A2 M2 A1 5. AAMM M2 A1 M1 A2 6. MAAM

Dengan demikian, maka ada 6 cara untuk menulis susunan huruf berbeda yang berasal dari kata "MAMA".

Sekarang dari diagram itu perhatikan bahwa Ada 6 cara