MODEL PREDATOR DAN PREY DENGAN MODEL SUSCEPTIBLE - INFECTED SUSCEPTIBLE. Jl. Prof. H. Soedarto, S.H. Tembalang Semarang

34

SUSCEPTIBLE - INFECTED – SUSCEPTIBLE Firsty Nur Hidayati1, Sunarsih2, Djuwandi3

1,2,3

Program Studi Matematika F.MIPA Universitas Diponegoro Jl. Prof. H. Soedarto, S.H. Tembalang Semarang

Abstract. A predator-prey model with infected prey is an interaction between a predator and a prey population with infected prey. This model is a result of the predator-prey model with logistic growth in the prey population which is combined with Susceptible-Infected-Susceptible (SIS) model in the prey. The equations in this model are non linear differential equation with three dependent variables. In this system, H(t) is size of prey population at time t, I(t) is the fraction of the prey that are infectious at time t and P(t) is size of predator population at time t. It is assumed that infected prey are vulnerable than by a factor q≥1. Stability analysis system is done to all five equilibria in this linearized. Each of stability in those equilibria points is based on the eigen values.

Keywords: stability, SIS model, eigen value, equilibrium point

1. PENDAHULUAN

Interaksi populasi yang paling kelihatan adalah yang melibatkan pemangsaan (predasi, predation), dimana seekor pemangsa (predator) memakan mangsa (prey) [3]. Pemangsaan atau predasi diartikan sebagai pemanfaatan individu untuk memenuhi kebutuhan makanan bagi individu lain. Penggunaan satu individu oleh individu lain untuk makanan mempunyai pengaruh negatif pada pertumbuhan potensial populasi prey, dimana makanan biasanya diartikan dalam pengaruh yang positif pada pertumbuhan populasi predator [2]. Pada interaksi dua populasi tersebut, keberadaan populasi

prey yang terinfeksi dapat berpengaruh pada pemangsaan oleh predator yaitu prey yang terinfeksi akan lebih lemah sehingga lebih mudah diserang untuk dimangsa oleh

predator.

Model yang mendeskripsikan interaksi dua populasi yaitu predator dan

prey dengan prey yang terinfeksi adalah

model predator dan prey dengan prey yang terinfeksi. Dari model tersebut akan dicari solusi kesetimbangan dan dianalisis perilaku dari sistem yang dapat ditentukan dengan menganalisis kestabilan dari solusi kesetimbangan tersebut.

2. MODEL PREDATOR DAN PREY DENGAN PREY YANG TERIFEKSI

Model predator dan prey dengan

prey yang terinfeksi diperoleh dari model predator dan prey dengan pertumbuhan

logistik pada populasi prey yang dikombinasikan dengan model

Susceptible-Infected-Susceptible (SIS)

pada prey. Diasumsikan bahwa prey yang terinfeksi lebih mudah diserang untuk dimangsa oleh predator yang dinyatakan dengan q _{yang bernilai lebih besar atau} sama dengan 1. Model predator dan prey dengan prey yang terinfeksi dinyatakan dengan sistem persamaan sebagai berikut [1].

(

X qY

)

P a H K H r dt dH + −             − = 1 aXP Y H XY X K H r d H K H r b dt dX _{− + −}     − + −       − = θ (1 θ) β γ aqYP Y K H r d Y H XY dt dY ₋     − + − − =β γ (1 θ)

(

X qY

)

P cP ka dt dP_{= + −} dengan Y X H = + _, H Y I = dan I H X S= =1− (2.1.a) (2.1.b) (2.1.c) (2.1.d)

35 diperoleh sistem persamaan sebagai

berikut

( )

(

q I

)

P H a K H r dt dH       − + −       − = 1 1 1

( )

a

( )( )

q I P I K H r b I dt dI       − − −       − + − − = β1 γ θ 11

(

)

(

)

[

kaH q I c

]

P dt dP_{= + − −} 1 1

Ada lima solusi kesetimbangan model

predator dan prey dengan prey yang

terinfeksi yaitu E₀ =(0,0,0),E₁=

(

K,0,0

)

, = 2 E _                   − kaK c a r ka c 1 , 0 , , = 3 E _             ₊ − ,0 1 , 0

β

γ

b dan = 4 E _             _{+ −} − ,0 1 ,

β

θ

γ

b r K .

3. ANALISIS KESTABILAN SISTEM

PERSAMAAN YANG

DILINIERKAN

Persamaan (2.2.a), (2.2.b), dan (2.2.c) adalah sistem persamaan differensial non linier, untuk menganalisis kestabilan dari titik kesetimbangannya, terlebih dahulu dilakukan pelinieran terhadap persamaan (2.2.a), (2.2.b), dan (2.2.c) dan kemudian persamaan dimisalkan dengan sistem persamaan sebagai berikut:

2

( , , )

dH H

rH r aPH aqIPH aIPH

dt K U H I P = − − − + = 2 2 2 ( , , ) dI I I I bI dt H

r I aqPI aqI P aPI aI P

K V H I P β β γ θ = − − − + − + + − = ( , , ) dP

kaHP kaHqIP kaHIP cP dt W H I P = + − − = Kemudian, didefinisikan O₁ =H−H*, * 2 I I O = − dan O₃ =P−P* dengan H*, *

I dan P* merupakan suatu konstanta, maka dt dH dt dO = 1 , dt dI dt dO = 2 dan dt dP dt dO = 3

. Dengan demikian linierisasi dari persamaan (2.2.a), (2.2.b) dan (2.2.c) dengan menggunakan deret Taylor di titik

) , ,

(H* I* P* _{adalah sebagai berikut :}

(

)

* * * 1 1 * * 2 2 1 1 ( 1) ( 1) dO H r aP q I O dt K aH P q O     =  − − + −        + −_ − _

[

]

3 * * ) ) 1 ( 1 ( q I O aH + − − +

(

)(

)

* 2 1 * * * 2 ( 1) 1 2 dO I r O dt K H aP q I b r O K θ β γ θ   =       + − − − − + −     

[

]

3 * * ) 1 )( 1 (q I O aI − − − + * * 3 1 * * 2 * * 3 (1 ( 1) ) ( 1) (1 ( 1) ) dO kaP q I O dt kaH P q O kaH q I c O   =_ + − _   + −    + + − − 

Dari linierisasi di atas, diperoleh matriks Jacobian pada titik kesetimbangan

(

* * *

)

, ,I P H yaitu:

(

)

            − − + − − + − − − − + − − − = c I q kaH q P kaH I q kaP I q aI a K I r I q aH q P aH a P I H J ) ) 1 ( 1 ( ) 1 ( ) ) 1 ( 1 ( ) 1 )( 1 ( ) ) 1 ( 1 ( ) 1 ( , , * * * * * * * * 22 * * * * * 11 * * * θ dengan:

(

*

)

* * 11 1 ( 1) 2 1 aP q I K H r a _− + −      − =

(

)(

)

      − + − − − − = K H r b I q aP a * * * 22 β ( 1) 1 2 γ θ

Dianalisis perilaku kestabilan dari persamaan (2.2.a), (2.2.b), dan (2.2.c) dengan cara mensubstitusi nilai dari (2.2.a) (2.2.b) (2.2.c) (2.3.a) (2.3.b) (2.3.c) (2.4.a) (2.4.b) (2.4.c)

36

masing-masing titik kesetimbangan ke dalam persamaan (2.4.a), (2.4.b) dan (2.4.c) sebagai berikut.

a) Titik 1: E0 =(0,0,0)

Dengan mensubstitusikan titik ) 0 , 0 , 0 ( 0 =

E ke dalam persamaan (2.4.a), (2.4.b) dan (2.4.c), diperoleh sistem yang dilinierkan sebagai berikut.

1 1 _rO dt dO =

(

)

2 2 _{b O} dt dO − − =

β

γ

3 3 cO dt dO − =

Nilai eigen dari persamaan (2.5.a), (2.5.b) dan (2.5.c) adalah

λ

₁ =r,

λ

₂ =

β

−

γ

−b, dan

λ

3 =−c. Dengan demikian, titik

) 0 , 0 , 0 ( 0 =

E tidak stabil karena

λ

₁ =r>0. Grafik O₁(t), O₂(t) dan O₃(t) _dengan

0

1 >

λ , λ2 <0 _dan

λ

3 <0 (λ2 > λ3)

digambarkan sebagai berikut.

Gambar 1. Grafik O₁(t), O₂(t) dan O₃(t) untukE0 = (0,0,0) dengan λ1 >0, λ2 <0 dan

0

3 <

λ

(λ₂ >λ₃).

Dari Gambar 1. dapat dilihat bahwa populasi prey meningkat sampai pada jumlah yang tidak terbatas. Sedangkan populasi predator dan populasi prey yang menular per total populasi prey semakin berkurang.

b) Titik 2: E₁ =(K,0,0)

Dengan mensubstitusikan titik ) 0 , 0 , ( 1 K

E = ke dalam persamaan (2.4.a), (2.4.b) dan (2.4.c), diperoleh sistem yang dilinierkan sebagai berikut.

3 1 1 _{rO aKO} dt dO − − = 2 2 _{( b r)O} dt dO

θ

γ

β

− − + = 3 3 _{(kaK c)O} dt dO − =

Nilai eigen dari persamaan (2.6.a), (2.6.b) dan _{(2.6.c) adalah}

λ

₁ =−r, r b

θ

γ

β

λ

2 = − − + ,dan

λ

3 =kaK−c.

Dengan demikian, titik E1 =(K,0,0) stabil jika

λ

₂ dan

λ

₃ yang bernilai riil non positif. Grafik O₁(t), O₂(t) dan O₃(t)

dengan λ1 <0, λ2 <0 _dan

λ

3 <0 ( 3 2 1 λ λ λ > > ) digambarkan sebagai berikut.

Gambar 2. Grafik O₁(t), O₂(t) dan O₃(t) untuk E₁ =(K,0,0) dengan λ₁ <0,

0

2 <

λ dan

λ

₃ <0 (λ₁ >λ₂ >λ₃)

Dari Gambar 2. dapat dilihat bahwa populasi prey, populasi prey yang menular per total populasi prey dan populasi

predator semakin berkurang.

c) Titik 3: _                   − = kaK c a r ka c E₂ ,0, 1

Dengan mensubstitusikan titik                     − = kaK c a r ka c E₂ ,0, 1 ke dalam persamaan (2.4.a), (2.4.b) dan (2.4.c), diperoleh sistem yang dilinierkan sebagai berikut. (2.5.a) (2.5.b) (2.5.c) (2.6.a) (2.6.b) (2.6.c)

37 1 1 2 3 1 ( 1) dO rc O dt kaK cr c c q O O ka kaK k   = −        + −  −  −  −     2 2 ( 1) 1 dO c c r q b r O dt β kaK γ θ kaK      = − −  − − + −          2 1 3 ) 1 ( 1 1 q O kaK c a cr O kaK c kr dt dO       −       − +             − =

Nilai eigen dari persamaan (2.7.a), (2.7.b) dan (2.7.c) adalah:

( )

      − + −             − − − = kaK c r b kaK c q r γ θ β λ1 1 1 dan 2 4 2 2 2 2 2 2 3 , 2       − − ± − = kaK rc rc K a k c r kaK rc λ       − − ± − = kaK c rc K a k c r kaK rc 1 4 2 1 2 1 2 2 2 2 2 .

Dengan demikian, titik

                    − = kaK c a r ka c E₂ ,0, 1 stabil jika >1 c kaK dan

( )

      − + −             − − − = kaK c r b kaK c q r γ θ β λ₁ 1 1

bernilai riil non positif.

d) Titik 4: E3 =               ₊ − ,0 1 , 0

β

γ

b

Dengan mensubstitusikan titik

= 3 E _             ₊ − ,0 1 , 0

β

γ

b ke dalam persamaan (2.4.a), (2.4.b) dan (2.4.c), diperoleh sistem yang dilinierkan sebagai berikut 1 1 _rO dt dO =

(

)

2 1 2 1 1 O b O b K r dt dO + + − +               ₊ − = β γ β γ θ 3 ) 1 ( 1 b q b O a             ₊ −       ₊ − − + β γ β γ 3 3 _cO dt dO − =

Nilai eigen dari persamaan (2.9.a), (2.9.b) dan (2.9.c) adalah

λ

₁ =r,

λ

₂ =−

β

+

γ

+b, dan

λ

₃ =−c. Dengan demikian, titik E₃ =

              ₊ − ,0 1 , 0

β

γ

b

tidak stabil karena

0

1 =r>

λ

. Grafik O₁(t), O₂(t) dan O₃(t)

dengan 0<θ ≤1, q>1,

λ

₁ >0,

λ

₂ <0

dan

λ

₃ <0 (

λ

₂ <

λ

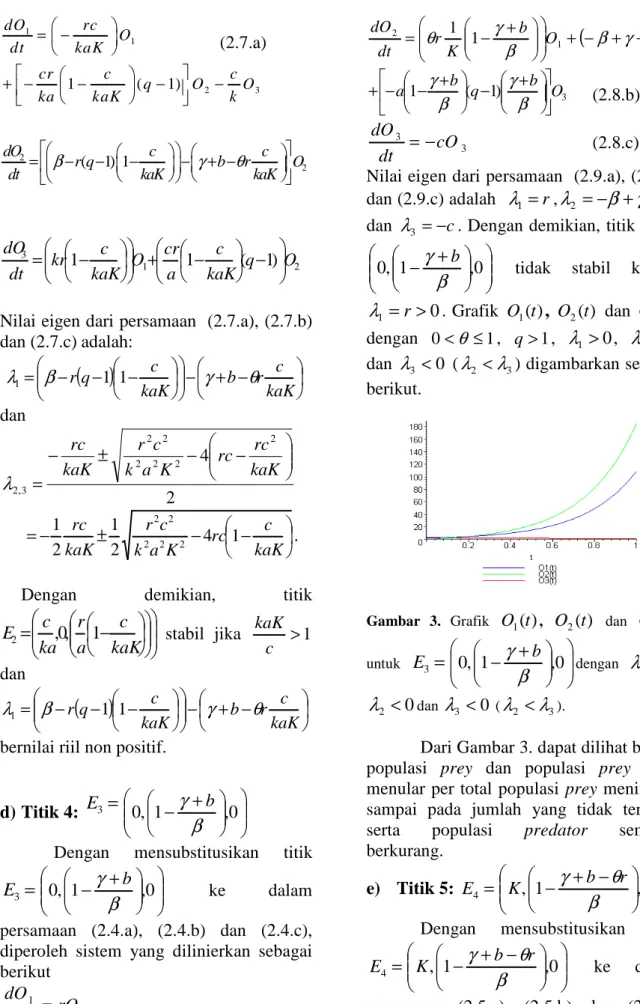
₃) digambarkan sebagai berikut.

Gambar 3. Grafik O₁(t), O₂(t) dan O₃(t)

untuk E₃ = _             ₊ − ,0 1 , 0

β

γ

b dengan

λ

₁ >0, 0 2 <

λ

dan

λ

₃ <0 (

λ

₂ <

λ

₃).

Dari Gambar 3. dapat dilihat bahwa populasi prey dan populasi prey yang menular per total populasi prey meningkat sampai pada jumlah yang tidak terbatas serta populasi predator semakin berkurang. e) Titik 5: E₄ = _             _{+ −} − ,0 1 ,

β

θ

γ

b r K

Dengan mensubstitusikan titik

= 4 E _             _{+ −} − ,0 1 ,

β

θ

γ

b r K ke dalam

persamaan (2.5.a), (2.5.b) dan (2.5.c), (2.7.a)

(2.8.a)

(2.8.b) (2.8.c)

38

diperoleh sistem yang dilinierkan sebagai berikut. 1 1 3 1 ( 1) 1 dO rO dt b r aK q

γ

θ

O

β

= −    _{+ −}  + −  + −  −       

(

)

2 1 2 1 1 dO b r r O dt K b r O

γ

θ

θ

β

β γ

θ

  _{+ −}  =  −      + − + + − 3 ) 1 ( 1 b r q b r O a             _{+ −} −       _{+ −} − − +

β

θ

γ

β

θ

γ

3 3 _{kaK 1 (q 1) 1} b r _{c O} dt dO         −               _{+ −} − − + =

β

θ

γ

Nilai eigen dari persamaan (2.9.a), (2.9.b) dan (2.9.c) adalah

λ

₁ =−r, r b

θ

γ

β

λ

2 =− + + − , dan c r b q kaK _−             _{+ −} − − + =

β

θ

γ

λ

₃ 1 ( 1) 1 .

Dengan demikian, titik E₄ =               _{+ −} − ,0 1 ,

β

θ

γ

b r K stabil jika 1 > − +b

θ

r

γ

β

dan c r b q kaK _−             _{+ −} − − + =

β

θ

γ

λ

₃ 1 ( 1) 1

bernilai riil non positif. Grafik O₁(t),

) ( 2 t O dan O₃(t) _dengan 0<θ ≤1, q>1, 0 1 <

λ

,

λ

₂ <0, dan

λ

3 <0 (λ1 >λ2 >λ3)

digambarkan sebagai berikut.

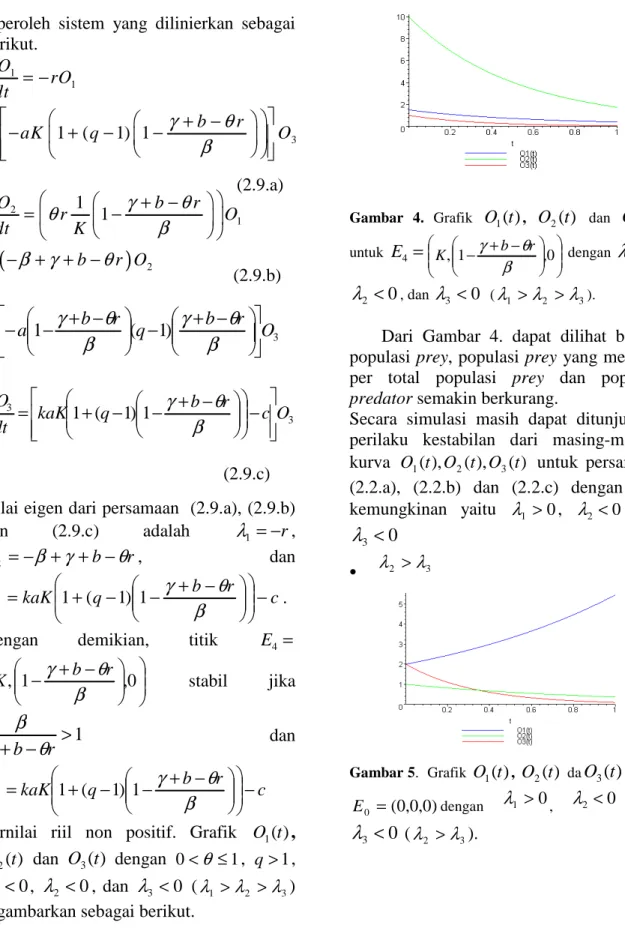
Gambar 4. Grafik O₁(t), O₂(t) dan O₃(t)

untuk E₄ = _             _{+ −} − ,0 1 , β θ γ b r K dengan

λ

₁ <0 0 2 <

λ

, dan

λ

₃ <0 (λ₁ >λ₂ >λ₃).

Dari Gambar 4. dapat dilihat bahwa populasi prey, populasi prey yang menular per total populasi prey dan populasi

predator semakin berkurang.

Secara simulasi masih dapat ditunjukkan perilaku kestabilan dari masing-masing kurva O₁(t),O₂(t),O₃(t) untuk persamaan (2.2.a), (2.2.b) dan (2.2.c) dengan tiga kemungkinan yaitu λ1 >0, λ2 <0 _dan

0

3 <

λ

• λ2 >λ3

Gambar 5. Grafik O₁(t), O₂(t) daO₃(t) untuk ) 0 , 0 , 0 ( 0 = E dengan λ1 >0_, λ2 <0 dan 0 3 <

λ

(λ₂ >λ₃). (2.9.a) (2.9.b) (2.9.c)

39 •λ2 <λ3

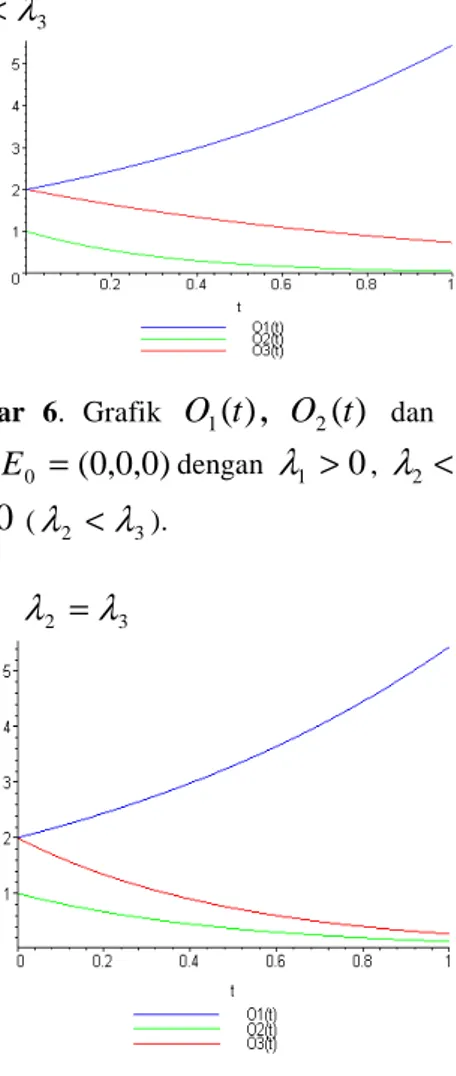
Gambar 6. Grafik O₁(t), O₂(t) dan O₃(t)

untuk E₀ =(0,0,0)dengan λ1 >0, λ2 <0 dan

0

3 <

λ

(λ₂ <λ₃).

• λ2 =λ3

Gambar 7. Grafik O₁(t), O₂(t) dan O₃(t)

untuk E₀ = (0,0,0)dengan λ1 >0, λ2 <0 dan

0

3 <

λ

(λ₂ =λ₃).

Dari Gambar 5, 6, dan 7. dapat dilihat bahwa populasi prey meningkat sampai pada jumlah yang tidak terbatas. Sedangkan populasi predator dan populasi

prey yang menular per total populasi prey

semakin berkurang.

4. PENUTUP

Model predator dan prey dengan

prey yang terinfeksi merupakan sistem

persamaan differensial non linier yang mempunyai tiga variabel tidak bebas yaitu

) (t

H _{yang menyatakan jumlah populasi}

prey pada waktu

t

, I(t) yang menyatakan jumlah populasi prey yang menular per total populasi prey pada waktu

t

_dan P(t)

yang menyatakan jumlah populasi

predator pada waktu

t

. Dari sistem

tersebut dicari solusi kesetimbangan sehingga diperoleh lima titik kesetimbangan dan pada tiap-tiap titik kesetimbangan tersebut dilakukan analisis kestabilan pada sistem yang dilinerkan yang berdasar pada nilai-nilai eigennya.

5. DAFTAR PUSTAKA

[1]. Hethcote, H. W, Wendy Wang, Litao Han, and Zhien Ma, (2004), A

Predator-Prey Model with Infected

Prey. Journal of Theoretical

Population Biology. 66 (September

13): 259-268.

http://www.elseiver.com/locate/ytpbi. (accessed November 12, 2009).

[2]. McNaughton, S. J and Larry L Wolf, (1990), Ekologi Umum. Yogyakarta: Gajah Mada University Press.

[3]. Neil, A. C, Jane B Reece, and Lawrence G Mitchel, (2004), Biologi

edisi kelima jilid 3. Jakarta: Penerbit