Informasi Dokumen
- Sekolah: Universitas
- Mata Pelajaran: Matematika Diskrit
- Topik: Matematika Diskrit (1)
- Tipe: kuliah
- Tahun: 2023
- Kota: Kota
Ringkasan Dokumen
I. Pendahuluan
Matematika Diskrit merupakan cabang matematika yang berfokus pada objek-objek diskrit, seperti bilangan bulat, graf, dan himpunan. Dalam konteks pendidikan, mata kuliah ini bertujuan untuk membekali mahasiswa dengan pemahaman dasar tentang konsep-konsep matematika yang digunakan dalam ilmu komputer dan teknik. Pembelajaran Matematika Diskrit sangat relevan dengan tujuan pendidikan, karena memberikan landasan yang kuat untuk memahami algoritma, struktur data, dan pemrograman.
II. Himpunan
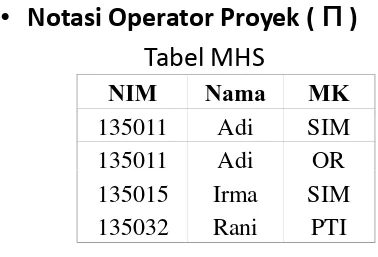
Himpunan adalah konsep dasar dalam Matematika Diskrit yang menjadi fondasi untuk memahami struktur yang lebih kompleks. Dalam mata kuliah ini, mahasiswa diperkenalkan dengan notasi himpunan, operasi dasar seperti union, intersection, dan difference. Pemahaman yang baik tentang himpunan sangat penting dalam analisis data dan pengembangan algoritma. Konsep ini juga digunakan dalam pengolahan data dan basis data, yang merupakan bagian integral dari ilmu komputer.
2.1 Notasi dan Operasi Himpunan
Notasi himpunan digunakan untuk mendefinisikan elemen-elemen dalam himpunan. Operasi seperti union (∪), intersection (∩), dan difference (-) digunakan untuk menggabungkan atau memisahkan himpunan. Pemahaman tentang operasi ini penting untuk analisis data dan pengembangan algoritma yang efisien.
III. Relasi dan Fungsi
Relasi dan fungsi adalah konsep penting dalam Matematika Diskrit yang memungkinkan mahasiswa untuk memahami hubungan antara elemen dalam himpunan. Relasi n-er dan fungsi biner merupakan bagian dari materi yang diajarkan. Mahasiswa juga belajar tentang sifat-sifat fungsi, seperti fungsi satu-satu (injective) dan onto (surjective), yang memiliki aplikasi luas dalam teori basis data dan pemrograman.
3.1 Relasi n-er
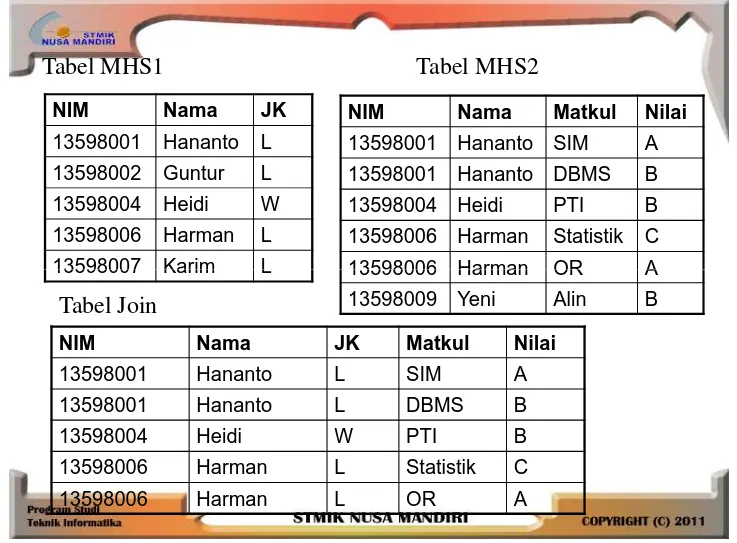
Relasi n-er menggambarkan hubungan antara n elemen dari himpunan. Contoh relasi ini dapat ditemukan dalam basis data, di mana relasi digunakan untuk menghubungkan data dari tabel yang berbeda. Pemahaman tentang relasi ini membantu mahasiswa dalam merancang dan mengelola basis data yang kompleks.
3.2 Fungsi
Fungsi adalah relasi khusus yang menghubungkan setiap elemen dari satu himpunan ke elemen lain. Mahasiswa belajar tentang berbagai jenis fungsi dan aplikasinya dalam pemrograman dan algoritma. Fungsi juga menjadi dasar untuk memahami konsep pemrograman fungsional.
IV. Logika dan Pembuktian
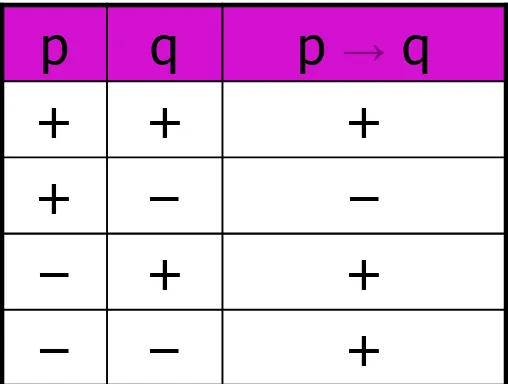
Logika proposisi dan teknik pembuktian adalah bagian penting dari Matematika Diskrit. Mahasiswa belajar tentang proposisi, negasi, konjungsi, disjungsi, dan implikasi. Teknik pembuktian, termasuk induksi matematika, juga diajarkan untuk membantu mahasiswa dalam membuktikan kebenaran pernyataan matematis. Pemahaman logika ini sangat penting dalam pengembangan algoritma dan pemrograman.
4.1 Logika Proposisi
Logika proposisi melibatkan analisis pernyataan yang dapat bernilai benar atau salah. Mahasiswa diajarkan untuk membangun tabel kebenaran dan menggunakan hukum logika untuk menyederhanakan pernyataan. Ini sangat berguna dalam merancang algoritma yang efisien.
4.2 Induksi Matematika
Induksi matematika adalah metode pembuktian yang digunakan untuk menunjukkan bahwa suatu pernyataan benar untuk semua bilangan bulat positif. Mahasiswa belajar untuk memahami langkah dasar induksi dan bagaimana menerapkannya dalam konteks yang lebih luas.
V. Kombinatorial
Kombinatorial adalah cabang Matematika Diskrit yang berfokus pada penghitungan, penyusunan, dan kombinasi objek. Mahasiswa belajar tentang prinsip dasar kombinatorial, seperti kaidah penjumlahan dan perkalian, serta teknik seperti permutasi dan kombinasi. Pengetahuan ini penting untuk analisis algoritma dan pengembangan solusi yang efisien.
5.1 Permutasi dan Kombinasi
Permutasi adalah cara untuk mengatur objek dalam urutan tertentu, sementara kombinasi adalah cara untuk memilih objek tanpa memperhatikan urutan. Mahasiswa belajar rumus dan aplikasi dari kedua konsep ini dalam berbagai konteks, termasuk algoritma dan analisis data.
VI. Graf
Graf adalah struktur data yang digunakan untuk merepresentasikan hubungan antara objek. Dalam Matematika Diskrit, mahasiswa belajar tentang konsep dasar graf, termasuk simpul, sisi, dan jenis graf seperti graf terarah dan tidak terarah. Pemahaman tentang graf sangat penting dalam pengembangan algoritma dan aplikasi dalam ilmu komputer.
6.1 Teori Graf
Teori graf mencakup studi tentang properti dan aplikasi graf. Mahasiswa belajar tentang algoritma graf, seperti pencarian DFS dan BFS, serta aplikasi praktisnya dalam jaringan dan basis data. Teori ini membantu mahasiswa dalam memahami struktur data yang kompleks.
VII. Kesimpulan
Matematika Diskrit adalah mata kuliah yang sangat penting dalam pendidikan tinggi, terutama bagi mahasiswa yang mempelajari ilmu komputer dan teknik. Dengan memahami konsep-konsep dasar seperti himpunan, relasi, logika, dan graf, mahasiswa dapat membangun fondasi yang kuat untuk belajar lebih lanjut tentang algoritma dan pemrograman. Pembelajaran ini tidak hanya bermanfaat dalam konteks akademis, tetapi juga dalam aplikasi dunia nyata di bidang teknologi dan informasi.
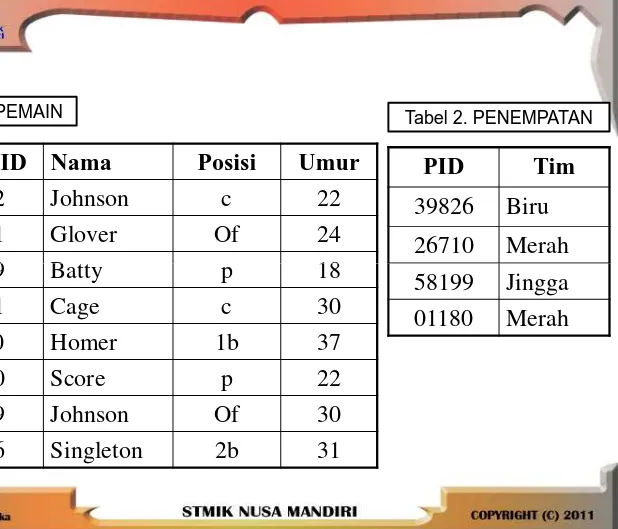
![Tabel 3. PeEMAIN [Nomor ID = PID ] PENEMPATAN](https://thumb-ap.123doks.com/thumbv2/123dok/3937114.1880534/42.842.118.692.249.439/tabel-peemain-nomor-id-pid-penempatan.webp)