commit to user
TEORI GANGGUAN UNTUK MENENTUKAN
KOREKSI ENERGI ELEKTRON PADA ATOM
BERUKURAN INTI TERTENTU
Disusun oleh :
LILA SYUKURILLA
M0208010
SKRIPSI
Diajukan untuk memenuhi sebagian
persyaratan mendapatkan gelar Sarjana Sains
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SEBELAS MARET
SURAKARTA
commit to user
v
TEORI GANGGUAN UNTUK MENENTUKAN KOREKSI ENERGI
ELEKTRON PADA ATOM BERUKURAN INTI TERTENTU
Lila Syukurilla
Jurusan Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sebelas Maret
ABSTRAK
Teori gangguan orde tiga telah berhasil dirumuskan berupa koreksi energi,
, dan koreksi fungsi gelombang, . Hasil koreksi energi orde satu, , dan
orde dua, , terhadap tingkat dasar untuk thallium adalah 4,3 dan
. Nilai (
; ) untuk tungsten, indium, molybdenum, tembaga,dan
kromium masing –masing adalah (2,7 ; ), (0,4 ; ),
( ; ), ( ; ) serta ( ;
). Koreksi energi orde tiga terhadap tingkat dasar untuk atom
thallium, tungsten, indium, molybdenum, tembaga,dan kromium masing-masing
adalah ; ;
; dan . Permodelan kurva energi potensial telah
berhasil dibuat menggunakan Wolfram Mathematica 7®. Hasil permodelan
menunjukkan adanya selisih kurva energi potensial antara inti berupa titik dan inti
berukuran tertentu. Selisih kurva tersebut diketahui sebagai hamiltonian
penggganggu.
commit to user
1.6. Sistematika Penulisan... 3
BAB II TINJAUAN PUSTAKA ... 4
2.1. Persamaan Schrödinger ... 4
2.2. Teori Gangguan Untuk Keadaan Non-degenerasi ... 7
2.2.1. Koreksi Energi Orde Satu ... 9
2.2.2. Koreksi Fungsi Gelombang Orde Satu ... 9
2.2.3. Koreksi Energi Orde Dua ... 10
2.2.4. Koreksi Energi Orde Satu ... 11
2.3. Atom dengan Inti Berukuran Tertentu ... 13
commit to user
ix
3.3. Metode Penelitian... 17
3.3.1. Studi Literatur ... 18
3.3.2. Koreksi Energi dan Fungsi Gelombang Orde Tiga ... 18
3.3.3. Koreksi Energi Orde Satu Terhadap Tingkat Dasar ... 19
3.3.4. Koreksi Energi Orde Dua Terhadap Tingkat Dasar ... 22
3.3.5. Koreksi Energi Orde Tiga Terhadap Tingkat Dasar ... 25
3.3.6. Permodelan Wolfram Mathematica 7 ... 25
BAB IV PEMBAHASAN ... 27
4.1. Koreksi Energi Orde Tiga ... 27
4.2. Koreksi Fungsi Gelombang Orde Tiga ... 28
4.3. Koreksi Energi Thallium ... 34
4.4. Koreksi Energi Tungsten ... 36
4.5. Koreksi Energi Indium ... 37
4.6. Koreksi Energi Molybdenum ... 38
4.7. Koreksi Energi Tembaga ... 39
4.8. Koreksi Energi Kromium ... 40
4.9. Permodelan Wolfram Mathematica 7 ... 41
BAB V PENUTUP ... 44
5.1. Simpulan ... 44
5.2. Saran ... 45
DAFTAR PUSTAKA ... xiii
commit to user
1
BAB I
PENDAHULUAN
1.1 Latar Belakang
Asumsi mengenai inti atom sebagai sebuah titik (point particle) bertujuan
untuk menyederhanakan bentuk potensialnya sehingga diperoleh penyelesaian
secara analitik. Namun, asumsi lebih real diperoleh dengan mendeskripsikan inti
atom sebagai partikel berukuran (finite size) serta memiliki distribusi massa dan
muatan yang seragam. Fakta ini menghasilkan bentuk potensial yang lebih
komplek, sehingga harus diselesaikan dengan metode pendekatan yang berbeda.
Atom bernomor massa besar memiliki jumlah elektron yang banyak, sehingga
gaya tarik-menarik antara inti dengan elektron tidak dapat diabaikan. Keadaan
yang demikian ini menyebabkan potensial elektron tersaji dalam bentuk integral
(Angelo, 2010). Secara analitik, potensial elektron pada atom dengan inti
berukuran merupakan sebuah gangguan. Nilai gangguan yang ditimbulkan relatif
kecil, mempertimbangkan ukuran dan muatan elektron. Oleh karenanya, metode
pendekatan yang digunakan adalah teori gangguan.
Teori gangguan merupakan salah satu metode pendekatan dalam kuantum
mekanik. Ruang lingkup teori gangguan tidak hanya sebatas tinjauan terhadap
tingkat energi dasar tetapi juga tingkat energi tereksitasi. Teori gangguan
berfungsi untuk menentukan solusi persamaan Schrödinger yang tidak dapat
diselesaikan secara eksak. Gangguan dalam suatu sistem menyebabkan persamaan
Schrödinger terbagi menjadi dua, yaitu bagian eksak dan bagian yang merupakan
gangguan. Analisis teori gangguan meliputi penentuan koreksi energi serta fungsi
gelombangnya (Winter, 1986).
Penggunaan teori gangguan dalam menentukan solusi suatu sistem komplek
telah banyak digunakan. Namun, teori gangguan yang digunakan baru sampai
koreksi energi orde 2 dan koreksi fungsi gelombang orde 1. Penurunan koreksi
energi dan fungsi gelombang hingga orde tiga bertujuan untuk memperoleh nilai
commit to user
membuat permodelan perbedaan bentuk kurva energi potensial dari atom dengan
inti berupa titik, dan atom dengan inti yang berukuran tertentu.
Thallium, tungsten, dan indium merupakan atom bernomer berat yang banyak
dimanfaatkan dalam bidang material. Secara lebih spesifik, Tungsten banyak
diaplikasikan dalam bidang instrumentasi listrik. Penelitian secara kuantum
terhadap ketiga atom tersebut telah banyak dilakukan. Namun, penelitian
mengenai keseluruhan koreksi energi elektron di dalam atom-atom tersebut belum
banyak dilakukan. Atom kromium, tembaga, dan molybdenum juga digunakan
dalam penelitian ini karena ketiganya memiliki karakteristik penghasil sinar-x.
Nilai jari-jari inti suatu atom sangat berpengaruh dalam perhitungan koreksi
energi. Hal ini ditunjukkan dengan adanya perbedaan kurva energi potensial untuk
inti berupa titik dan inti berukuran tertentu. Wolfram Mathematica 7® dapat
digunakan untuk memodelkan bentuk kurva energi potensial dari inti yang berupa
titik dan inti yang berukuran tertentu. Permodelan tersebut digunakan untuk
menganalisis besar hamiltonian pengganggu yang ada di dalam sistem.
1.2 Rumusan Masalah
Berdasarkan latar belakang tersebut maka dapat dibuat rumusan masalah
sebagai berikut:
1. Bagaimanakah bentuk koreksi energi dan fungsi gelombang orde tiga?
2. Berapakah nilai koreksi energi orde satu, dua, dan tiga untuk atom thallium,
tungsten, indium, molybdenum, tembaga, dan kromium?
3. Bagaimanakah analisis hamiltonian pengganggu dengan kurva untuk atom
thallium, tungsten, indium, molybdenum, tembaga, dan kromium?
1.3 Tujuan Penelitian
Sesuai dengan rumusan masalah, maka tujuan penelitian ini antara lain
adalah:
1. Menentukan persamaan koreksi energi dan fungsi gelombang orde tiga.
2. Menentukan nilai koreksi energi orde satu, dua, dan tiga untuk atom thallium,
commit to user
3. Membuat permodelan kurva energi potensial yang terganggu untuk atom
thallium, tungsten, indium, molybdenum, tembaga, dan kromium.
1.4 Batasan Masalah
Beberapa batasan yang perlu diberikan agar permasalahan menjadi terfokus
antara lain adalah sebagai berikut:
1. Koreksi energi dan fungsi gelombang orde tiga ditentukan berdasarkan teori
gangguan untuk keadaan non-degenarasi dan tak gayut waktu.
2. Koreksi energi orde satu, dua, dan tiga untuk atom thallium, tungsten, indium,
molybdenum, tembaga, dan kromium dilakukan terhadap energi tingkat dasar
.
3. Kurva energi potensial dibuat menggunakan Wolfram Mathematica 7®
1.5 Manfaat Penelitian
Manfaat penelitian ini adalah diketahuinya pengaruh ukuran jari-jari inti atom
terhadap nilai hamiltonian pengganggunya. Koreksi energi yang diperoleh dapat
digunakan sebagai informasi mengenai properti inti atom tersebut.
1.6 Sistematika Penelitian
Bab 1 penelitian ini berisi mengenai latar belakang dilakukannya penelitian,
tujuan, rumusan masalah, batasan masalah, manfaat serta sistematika penulisan.
Bab 2 berisi tentang teori yang dijadikan dasar penelitian ini. Pada bab 3
disampaikan mengenai metode yang digunakan, alokasi waktu dan tempat
penelitian, serta prosedur kerja. Bab 4 membahas mengenai penurunan koreksi
energi dan fungsi gelombang orde tiga, penentuan nilai koreksi untuk atom
Thallium, Tungsten, dan Indium, serta permodelan kurva energi potensial
menggunakan Wolfram Mathematica 7®. Bab 5 berisi tentang kesimpulan dan
commit to user
4
BAB II
TINJAUAN PUSTAKA
2.1 Persamaan Schrödinger
Besaran-besaran yang terkait dengan gerak partikel ditentukan dengan
pendekatan berbeda-beda di dalam mekanika kuantum. Fungsi gelombang
digunakan untuk merepresentasikan dinamika partikel yang bergerak, yang
diperoleh dari penyelesaian Persamaan Schrödinger dari partikel tersebut.
Persamaan Schrödinger memainkan peran yang secara logika analog dengan
pernyataan hukum II Newton.
Dasar penurunan persamaan Schrödinger berasal dari pembelajaran mengenai
gelombang elektromagnet. Gelombang elektromagnet dihasilkan dari adanya
perubahan medan elektromagnet di dalam ruang hampa. Kecepatan
perambatannya sama dengan kecepatan rambat cahaya yaitu 3.0 x 108 m/s. Secara
matematik, persamaan gelombang elektromagnet ditunjukkan oleh persamaan
(2.1).
(2.1)
Persamaan Schrödinger dapat dijabarkan berdasarkan prinsip-prinsip sebagai
berikut (Gasiorowicz, 1974):
1). Prinsip dualisme gelombang–partikel yang menyatakan bahwa perilaku
gelombang dari sebuah partikel disajikan dalam bentuk hubungan antara
momentum linear, ,dengan panjang gelombang .
(2.2)
adalah tetapan Planck, sedangkan adalah angka gelombang atau vektor
gelombang yang nilainya setara dengan .
2). Besarnya energi total dari sebuah partikel yang berperilaku sebagai
gelombang dapat dipandang sebagai energi gelombang gelektromagnetik atau
cahaya. Setiap satu foton, energinya terkuantisasi sebesar , sebagaimana
commit to user
(2.3)
adalah frekuensi gelombang, sedangkan adalah frekuensi sudut yang
nilainya setara dengan .
3). Besarnya energi total adalah jumlah total energi kinetik dan energi
potensial suatu partikel, sebagaimana ditunjukkan oleh persamaan (2.4)
hingga (2.7).
(2.4)
(2.5)
(2.6)
(2.7)
4). Persamaan Schrödinger dalam mekanika kuantum adalah persamaan energi
total seperti yang dinyatakan dalam mekanika klasik tetapi variable-variabel
dalam mekanika klasik diubah menjadi operator dalam mekanika kuantum.
Hubungan antara variabel dalam mekanika klasik dengan operator dalam
mekanika kuantum disebut prinsip korespondensi antara klasik dengan
kuantum, dan persamaan Schrödinger adalah Hamiltonian dalam mekanika
klasik.
Partikel berperilaku sebagai gelombang, sehingga persamaan gelombang
elektromagnetik (2.1) dapat didiferensialkan terhadap variabel-variabelnya yaitu
terhadap dan .
(2.8)
( ) (2.9)
(2.10)
commit to user
(2.12)
(2.13)
Berdasarkan persamaan (2.13) dapat diketahui bahwa variabel momentum
linear, ,dalam mekanika klasik dapat diubah menjadi operator momentum linier
dalam mekanika kuantum. Hal ini ditunjukkan oleh persamaan (2.16). Sedangkan
operator energi kinetiknya ditunjukkan oleh persamaan (2.17) (Flügge, 1971).
(2.14)
(2.15)
(2.16)
(2.17)
Huruf menunjukkan suatu bilangan imajiner, yaitu √ . Pendiferensialan
persamaan (2.1) terhadap variabel menghasilkan persamaan (2.18). Kemudian
persamaan (2.18) dikalikan dengan sehingga menghasilkan persamaan (2.19).
(2.18)
(2.19)
(2.20)
(2.21)
commit to user
Persamaan (2.22) menunjukkan operator energi total dalam mekanika kuantum.
Dengan demikian dapat dituliskan persamaan Schrödinger untuk sebuah partikel
bebas dalam sistem satu dimensi, yaitu arah sumbu , dalam mekanika kuantum
sesuai persamaan (2.23).
(2.23)
2.2 Teori Gangguan untuk Keadaan Non-degenerasi
Terdapat beberapa kasus mekanika kuantum yang tidak dapat diselesaikan
secara langsung karena bentuk sistem yang komplek. Metode pendekatan dapat
digunakan untuk menentukan solusi sistem tersebut. Teori gangguan
(perturbation theory) merupakan salah satu metode pendekatan secara matematis
yang berfungsi untuk mendeskripsikan sistem yang komplek menjadi lebih
sederhana.
Teori gangguan dapat dikelompokkan menjadi dua bagian yaitu teori
gangguan untuk keadaan non-degenerasi dan teori gangguan untuk keadaan
terdegenerasi. Keadaan non-degenerasi dideskrispikan sebagai sistem yang
memiliki energi berbeda untuk tiap tingkat energi berbeda. Sedangkan keadaan
terdegenerasi adalah sistem yang memiliki energi sama untuk tingkat energi
berbeda (Winter, 1986).
Persamaan Schrödinger (2.23) dapat dituliskan dalam bentuk persamaan
(2.24) dengan asumsi bahwa Persamaan Schrödinger tak gayut waktu.
Hamiltonian mengandung suku-suku , yaitu Hamiltonian yang tidak
terganggu. Persamaan (2.25) menyatakan persamaan Schrödinger untuk fungsi
gelombang yang eksak. Hamiltonian eksak diketahui sebagai ,
dengan adalah Hamiltonian penganggu. memiliki bentuk yang cukup
kompleks, sehingga digunakan metode pendekatan untuk menentukan
penyelesaiannya (Winter, 1986).
(2.24)
commit to user
Hamiltonian eksak dituliskan sesuai persamaan (2.26), dengan sebagai
faktor penentu adanya gangguan. Ketika bernilai 1, maka menggambarkan
adanya gangguan pada sistem. Sedangkan ketika bernilai 0 berarti sistem tidak
terganggu. Penggunaan asumsi bahwa berubah secara kontinu dari satu ke nol,
maka fungsi gelombang dan energi, dan , berubah secara halus menuju
fungsi gelombang dan energi yang tidak terganggu, dan .
(2.26)
dan diasumsikan sebagai deret pangkat tinggi dari yang dinyatakan
oleh persamaan (2.27). merupakan koreksi energi orde satu terhadap tingkat
energi ke- dan merupakan koreksi fungsi gelombang orde satu fungsi
gelombang ke- . dan adaah koreksi energi dan fungsi gelombang orde
dua, dan demikian seterusnya.
(2.27)
Persamaan (2.28) merupakan hasil substitusi persamaan (2.27) ke persamaan
(2.24). Koefisien dari pangkat yang sama dikelompokkan agar diperoleh
persamaan (2.29), (2.30), (2.31), dan (2.32). Persamaan (2.29) adalah persamaan
energi sistem untuk keadaan tidak terganggu, yaitu koefisien untuk . Sedangkan
(2.30), (2.31), dan (2.32) secara berturut-turut adalah persamaan untuk
menentukan koreksi orde satu, dua, dan tiga, yaitu koefisien untuk , , dan .
=
( )(
) (2.28)
(2.29)
(2.30)
(2.31)
commit to user 2.2.1 Koreksi Energi Orde Satu
Koreksi energi orde satu dapat diperoleh dengan mengalikan kedua ruas
persamaan (2.30) dengan . Hasil perkalian tersebut ditunjukkan oleh
persamaan (2.33). Persamaan (2.33) diintegralkan sehingga diperoleh persamaan
(2.34). 〈 〉 pada persamaan (2.34) dapat dituliskan seperti pada
persamaan (2.35) dengan asumsi bahwa merupakan hermitian (Skylaris, 2006).
(2.33)
〈 〉 〈 〉 〈 〉 〈 〉 (2.34)
〈 〉 = 〈 〉
〈 〉 = 〈 〉
〈 〉 = 〈 〉 (2.35)
Hasil substitusi persamaan (2.35) ke (2.34) menghasilkan persamaan (2.36).
Sebagaimana diketahui 〈 〉 bernilai nol, dan 〈 〉 bernilai satu.
Persamaan (2.36) disebut sebagai koreksi energi orde satu.
〈 〉 〈 〉 〈 〉 〈 〉
〈 〉 〈 〉
〈 〉 (2.36)
2.2.2 Koreksi Fungsi Gelombang Orde Satu
Koreksi orde satu terhadap fungsi gelombang dapat diperoleh dengan cara
menuliskan persamaan (2.30) menjadi persamaan (2.37). Kemudian
mensubtitusikan basis fungsi gelombang yang tidak terganggu, persamaan (2.38),
ke dalam persamaan (2.37). Persamaan (2.39) dikalikan dengan , kemudian
diintegralkan sehingga diperoleh persmaan (2.40) (Skylaris, 2006).
(2.37)
commit to user
∑ (2.39)
∑ 〈 〉 〈 〉 (2.40)
Bila nilai sama dengan , maka ruas kiri akan menjadi nol dan diperoleh
bentuk persamaan seperti (2.36). Bila tidak sama dengan , dan sama
dengan maka persamaan (2.40) berubah menjadi persamaan (2.41). Nilai
pada persamaan (2.42) disubtitusikan ke persamaan (2.38). Hasil akhir yang
ditampilkan pada persamaan (2.43) merupakan koreksi fungsi gelombang orde
satu.
〈 〉 (2.41)
〈 〉 〈 〉
〈 〉 〈 〉
〈 〉
〈 〉
〈 〉
〈 〉 (2.42)
∑ 〈 〉
(2.43)
2.2.3 Koreksi Energi Orde Dua
Koreksi energi orde dua diperoleh dengan menggunakan langkah-langkah
yang sama seperti penurunan koreksi energi orde satu. Persamaan (2.31) dikalikan
dengan , lalu diintegralkan sehingga diperoleh persamaan (2.44).
merupakan hermitian, sehingga persamaa (2.44) dapat disederhanakan menjadi
persamaan (2.45). 〈 〉 dan 〈 〉 bernilai nol, sedangkan 〈 〉
bernilai satu. Bentuk koreksi energi orde dua, persamaan (2.46), diperoleh dengan
commit to user
〈 〉 〈 〉
〈 〉 〈 〉 〈 〉
(2.44)
〈 〉 〈 〉
〈 〉 〈 〉 〈 〉
〈 〉 (2.45)
∑ 〈 〉
(2.46)
2.2.4 Koreksi Fungsi Gelombang Orde Dua
Koreksi fungsi gelombang orde dua diperoleh dengan langkah yang sama
seperti penurunan koreksi fungsi gelombang orde satu. Persamaan (2.38) sebagai
basis fungsi gelombang tidak terganggu dituliskan menjadi persamaan (2.47),
dengan nilai yang harus ditentukan terlebih dahulu. Persamaan (2.47)
disubtitusikan ke dalam persamaan (2.48) yang merupakan bentuk lain dari
persamaan (2.31) (Winter, 1986).
∑ (2.47)
(2.48)
Persamaan (2.47) dan hasil koreksi fungsi gelombang orde satu disubtitusikan
ke dalam persamaan (2.48). Hasil subtitusi tersebut dikalikan dengan ,
kemudian diintegralkan sehingga diperoleh persamaan (2.50). Bila nilai sama
dengan , maka ruas kiri akan menjadi nol dan diperoleh bentuk persamaan
seperti (2.46). Bila tidak sama dengan , dan sama dengan , maka persamaan
(2.50) berubah menjadi persamaan (2.51). Nilai pada persamaan (2.52)
disubtitusikan ke persamaan (2.48). Hasil akhir yang ditampilkan pada persamaan
commit to user
∑ ∑〈 〉〈 〉
∑ 〈 〉〈 〉
(2.53)
2.3 Atom dengan Inti Berukuran Tertentu
Asumsi inti berupa titik kurang real untuk diterapkan pada atom bernomor
besar, yaitu atom dengan jumlah proton yang besar. Hal ini dikarenakan gaya
elektrostatis yang terjadi di dalam inti berpengaruh terhadap energi elektron di
luar inti, sehingga tidak dapat diabaikan. Perhitungan kuantitatif untuk inti yang
berukuran tertentu memerlukan suatu bentuk distribusi muatan inti (Flügge,
1971). Asumsi yang digunakan adalah bahwa ini merupakan bola bermuatan yang
terdistribusi secara seragam dengan jari-jari dan muatan total . Rapat muatan
listrik dari inti dituliskan sesuai persamaan (2.54) dan (2.55).
⁄ (2.54)
(2.55)
Persamaan (2.56) dan (2.57) menunjukkan besarnya medan listrik yang
ditimbulkan oleh adanya suatu yang bermuatan. Berdasarakan Hukum Gauss,
energi potensial elektron yang berada di sekitar inti tersebut ditunjukkan oleh
persamaan (2.56) dan (2.57). Persamaan (2.56) menyatakan energi potensial
elektron untuk nilai yang kurang dari atau sama dengan . Sedangkan
persamaan (2.57) menyatakan energi potensial elektron untuk nilai yang lebih
besardari (Flügge, 1971). pada persamaan tersebut senilai dengan
.
( ) (2.56)
commit to user
Hamiltonian eksak, , didefinsikan pada persamaan (2.58), sedangkan
hamiltonian yang tidak terganggu, , didefinisikan pada persamaan (2.59).
Hamiltonian pengganggu, , merupakan selisih dari hamiltonian eksak dengan
hamiltonian yang tidak terganggu. dituliskan sesuai persamaan (2.60) yang
merupakan bentuk lain dari persamaan (2.26). Nilai
tereliminasi sehingga
diperoleh persamaan (2.61).
(2.58)
(2.59)
(2.60)
( ) (2.61)
Nilai hamiltonian pengganggu untuk nilai yang kurang dari atau sama
dengan berbeda dengan nilai hamiltonian penganggu untuk yang lebih besar
dari . Hal ini dikarenakan nilai potensial yang berbeda untuk kedua jenis
keadaan tersebut. Persamaan (2.63) menunjukkan bentuk hamiltonian penganggu
untuk nilai yang kurang dari atau sama dengan . Persamaan (2.65)
menunjukkan bentuk hamiltonian untuk nilai yang lebih dari .
( ) ( ) (2.62)
( ) (2.63)
( ) (2.64)
(2.65)
2.3.1 Thallium
Thallium (Tl) merupakan unsur kimia yang memiliki nomer atom 81.
Thallium termasuk golongan IIIA dalam sistem periodik unsur. Terdapat dua
commit to user
ditemukan dalam biji pyrites yang berfungsi untuk produksi asam sulfat. Selain
itu, Thallium juga ditemukan pada peleburan biji timbal (Pb) dan seng (Zn).
Beberapa penelitian thallium secara kuantum bertujuan untuk menentukan
pengaruh elektronnya dalam bentuk halida. Perhitungan nilai interaksinya
diturunkan berdasarkan teori gangguan yang mampu menganalisis adanya
simpangan ikatan di dalam thallium halida tersebut (Schwerdtfeger dan Ischtwan,
1993). Penelitian lainnya menganalisis mengenai adanya pemisahan spin elektron
pada thallium. Teori gangguan mampu digunakan untuk menginvestigasi jarak
pemisahan elektron tersebut (Wahlgren, et.al; 1997).
2.3.2 Tungsten
Tungsten (W) merupakan unsur kimia bernomer atom 74 yang memiliki lima
isotop yang stabil dengan berat massa antara lain 180, 182, 183, 184, dan 186.
Tungsten yang sering disebut dengan wolfram, termasuk golongan VIB dalam
sistem periodik unsur. Tungsten ditemukan pada mineral tungstenit, scheelit,
huebnertie, dan ferberit. Pemanfaatan tungsten sangat luas, antara lain sebagai
bahan pembuatan filamen pada lampu pijar, tabung elektron, dan televisi. Selain
itu tungsten juga digunakan dalam kegiatan pertambangan dan industri (Christian,
2006).
Penelitian mengenai tungsten banyak dilakukan, antara lain meliputi efek
ionisasi elektronnya, fotoionisasi, dan autoionisasinya. Analisis secara kuantum
dilakukan dengan teori gangguan untuk menentukan nilai koreksi energi
eksitasinya. Penelitian tungsten dan propertinya sangat menarik bagi para peneliti
karena nomer atomnya yang besar sehingga memiliki beberapa tingkatan energi
untuk dianalisis (Abdallah, et.al; 1992).
2.3.3 Indium
Indium (In) adalah unsur kimia golongan IIIA bernomer atom 49 yang
memiliki dua isotop dengan berat atom 113 dan 115. Indium banyak ditemukan
pada bijih besi, tembaga, dan timbal. Secara kimia, indium hampir sama dengan
galium dan thallium, dan menunjukkan properti di antara keduanya. Indium biasa
commit to user
indium klorida (InCl), dan beberapa senyawa indium lain dapat dimanfaatkan
dalam metode penumbuhan material (Cardelino, et.al; 2000).
Penelitian mengenai indium secara kuantum telah banyak banyak dilakukan
dalam usaha untuk mempelajari properti skala atom. Salah satunya adalah
mengenai efektivitas pita konduksi ketika dipengaruhi medan magnet. Medan
magnet yang kecil berpengaruh terhadapmobilitas elektron di dalam atom.
commit to user
17
BAB III
METODOLOGI PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian dilakukan di Jurusan Fisika Fakultas Matematika dan Ilmu
Pengetahuan Alam (MIPA) Universitas Sebelas Maret Surakarta. Penelitian
dilakukan mulai bulan Agustus-Desember 2011.
3.2 Peralatan Penelitian
Seperangkat laptop ASUS 1215P dengan softwareWolfram Mathematica 7®.
3.3 Metode Penelitian
Studi Literatur
Penentuan Koreksi Energi dan Fungsi Gelombang Orde Tiga
Penulisan Persamaan Koreksi Energi dan Fungsi Gelombang Orde Dua Penulisan Persamaan Koreksi Energi dan
Fungsi Gelombang Orde Satu
Penentuan Koreksi Energi dan Thalium, Wolfram, dan Indium
Permodelan Wolfram Mathematica 7®
Analisis
commit to user
Penelitian ini dilaksanakan dalam beberapa tahap sebagaimana ditunjukkan
oleh Gambar 3.1. Tahapan pertama adalah studi literatur terkait teori gangguan
yang tidak gayut waktu untuk keadaan non-degenerasi. Selanjutnya adalah
penulisan persamaan koreksi energi dan fungsi gelombang untuk orde satu dan
dua. Tahap keempat adalah penentuan koreksi energi dan fungsi gelombang orde
tiga. Koreksi energi dan fungsi gelombang orde satu, dua, dan tiga diaplikasikan
pada atom Thalium, Wolfram, dan Indium. Hasil perhitungan dibuat
permodelannya menggunakan Wolfram Mathematica 7®, kemudian dianalisis.
3.3.1 Studi Literatur
Studi literatur dilakukan untuk menurunkan persamaan koreksi energi dan
fungsi gelombang orde satu dan dua. Persamaan tersebut diekspansi dari
persamaan Schrödinger (2.24) dengan menggunakan asumsi adanya hamiltonian
pengganggu sesuai persamaan (2.26). Hasil penjabaran dikelompokkan dalam
koefisien-koefisien dengan pangkat yang sama. Persamaan untuk sistem yang
tidak terganggu dituliskan pada persamaan (2.29).
Koreksi energi dan fungsi gelombang orde satu dijabarkan menggunakan
dasar persamaan (2.30). Koreksi energi diperoleh dari hasil manipulasi matematis.
Koreksi fungsi gelombang dapat ditentukan setelah koreksi energi diperoleh.
Koreksi energi dan fungsi gelombang orde satu menjadi dasar penentuan koreksi
energi dan fungsi gelombang orde dua. Langkah-langkah yang digunakan sama
seperti pada penentuan koreksi energi dan fungsi gelombang orde satu.
3.3.2 Koreksi Energi dan Fungsi Gelombang Orde Tiga
Koreksi energi orde tiga diperoleh dengan menggunakan dasar persamaan
(2.32), yaitu koefisien dari pangkat tiga. Langkah penurunannya sama seperti
penurunan koreksi energi orde satu dan dua, yaitu sebagai berikut:
1. Mengalikan persamaan (2.32) dengan .
2. Mengintegralkan hasil perkalian tersebut dan menuliskan dalam persamaan
commit to user
3. Mengeliminasi persamaan dengan asumsi 〈 〉 〈 〉 dan
〈 〉 bernilai nol, sedangkan 〈 〉 bernilai satu, sehingga diperoleh
persamaan dengan bentuk sesuai persamaan (2.36) atau (2.45).
4. Mensubtitusikan nilai , yaitu koreksi fungsi gelombang orde dua yang telah
dituliskan pada persamaan (2.53)
Koreksi fungsi gelombang orde tiga diperoleh dengan langkah-langkah
sebagai berikut:
1. Menuliskan persamaan (2.32) menjadi seperti bentuk persamaan (2.37), yaitu
dikelompokkan sesuai fungsi gelombangnya.
2. Mensubtitusikan variabel-variabel yang telah diketahui ke dalam persamaan
pada langkah satu. Variabel tersebut antara lain koreksi energi orde 1, ;
koreksi fungsi gelombang orde 1, ; koreksi energi orde dua, ; dan
koreksi fungsi gelombang orde dua, .
3. Menentukan basis fungsi gelombang yang tidak terganggu, , sebagaimana
persamaan (2.38) atau (2.47).
4. Mensubtitusikan hasil pada langkah tiga ke dalam hasil pada langkah dua.
5. Mengalikan hasil pada langkah empat dengan suatu variabel , kemudian
mengintegralkan hasil perkalian tersebut.
6. Menentukan nilai , yaitu konstanta yang muncul pada langkah tiga.
7. Mensubtitusikan ke dalam persamaan dalam langkah 2.
3.3.3 Koreksi Energi Orde Satu Terhadap Tingkat Dasar
Koreksi energi orde satu untuk atom thallium, tungsten, indium, kromium,
tembaga, dan molybdenum dilakukan terhadap energi tingkat dasar. Langkah
perhitungannya adalah sebagai berikut:
a. Penentuan bentuk koreksi energi orde satu terhadap tingkat dasar
1). Menuliskan bentuk persamaan koreksi energi orde satu, persamaan (2.36),
commit to user
gelombang tingkat dasar, , ditunjukkan oleh persamaan (3.3). Nilai
, dengan adalah total massa elektron (Beiser, 1999).
〈 〉 (3.1)
∭ (3.2)
⁄
⁄ √ (3.3)
2). Menghitung nilai ∫ dan ∫ sebagaimana ditunjukkan oleh
persamaan (3.5) dan (3.7).
∫ [ ] (3.4)
∫ (3.5)
∫ [ ] (3.6)
∫ (3.7)
3). Mensubtitusikan persamaan (3.5) dan (3.7) ke dalam persamaan (3.2),
sehingga diperoleh persamaan (3.8).
∫ (3.8)
4). Mensubtitusikan nilai hamiltonian pengganggu, persamaan (2.63), dan
persamaan (3.3) ke dalam persamaan (3.8), sehingga diperoleh persamaan
(3.9).
∫
⁄
⁄ √ ( ) (3.9)
∫ ⁄ ( ) (3.10)
commit to user
5). Nilai ⁄ dianggap sebagai satu satuan karena fraksi kecil distribusi
terletak di dalam , dengan .
6). Menyelesaikan pengintegralan persamaan (3.11) sehingga diperoleh
persamaan (3.17).
∫ ( ) (3.12)
( ) (3.13)
( ) (3.14)
( ) (3.15)
(3.16)
(3.17)
7). Sebagaimana telah disebutkan pada sub bab 2.3 bahwa nilai adalah sama
dengan
. Subtitusi dan pada persamaan (3.17) menghasilkan
persamaan (3.18) dan (3.19).
(3.18)
(3.19)
(3.20)
8). Bentuk
merupakan persamaan untuk energi atom pada tingkat
dasar, . Energi atom hidrogen adalah , sehingga untuk
energi atom lain dapat dihitung dari hasil perkalian kuadarat nomer atom,
commit to user
9). Persamaan (3.20) adalah bentuk koreksi energi orde satu terhadap tingkat
dasar, dengan nilai dan tergantung pada jenis atom.
10).Nilai pada atom hidrogen adalah , sehingga nilai untuk atom lain
dapat diperoleh dari hasil pembagian dengan nomer atom tersebut.
11).Nilai diperoleh dari persamaan (3.21), dengan nilai adalah .
Variabel adalah jumlah dari proton dan elektron pada atom.
⁄ (3.21)
b. Perhitungan nilai koreksi energi atom
Langkah perhitungan koreksi energi orde satu untuk atom thallium, tungsten,
indium, kromium, tembaga, dan molybdenum adalah sebagai berikut:
1). Menentukan nilai
2). Menentukan nilai .
3). Menentukan energi tingkat dasar, untuk thallium, tungsten, indium,
kromium, tembaga, dan molybdenum.
4). Mensubtitusikan nilai , , dan ke dalam persamaan (3.20).
Perhitungan koreksi energi atom thallium diperoleh dua nilai karena terdapat
dua nilai , demikian juga pada atom indium. Sedangkan atom tungsten dan
kromium memiliki lima nilai R karena Tungsten memiliki lima isotop, yang
berarti memiliki lima jenis berat atom. Atom tembaga memiliki tiga isotop, dan
molybdenum memiliki tujuh isotop.
3.3.4 Koreksi Energi Orde Dua Terhadap Tingkat Dasar
Koreksi energi orde dua untuk atom thallium, tungsten, indium, kromium,
tembaga, dan molybdenum dilakukan terhadap energi tingkat dasar. Langkah
perhitungannya adalah sebagai berikut:
a. Penentuan bentuk koreksi energi orde dua terhadap tingkat dasar
commit to user
1). Menuliskan bentuk persamaan koreksi energi orde dua, persamaan (2.46),
menjadi bentuk koreksi energi orde dua terhadap tingkat dasar, persamaan
(3.24).
2). Menghitung terlebih dahulu nilai 〈 〉, dengan nilai
ditunjukkan oleh persamaan (3.25).
3). Persamaan (3.26) merupakan penurunan dari persamaan (3.25) yang telah
dihitung nilai ∫ dan ∫ .
5). Mensubtitusikan nilai hamiltonian pengganggu, persamaan (2.63) ke
dalam persamaan (3.29), sehingga diperoleh persamaan (3.30).
6). Menyelesaikan pengintegralan persamaan (3.30) sehingga diperoleh
commit to user
8). Persamaan (3.38) dimasukkan kembali ke persamaan (3.24) sehingga
commit to user
9). Persamaan (3.40) adalah bentuk koreksi energi orde dua terhadap tingkat
dasar, dengan nilai dan tergantung pada jenis atom.
10).Nilai dan ditentukan sebagaimana perhitungan pada koreksi energi
orde satu.
11).Nilai ditentukan oleh persamaan (3.40) dan (3.41).
Sebagaimana diketahui bahwa nilai
adalah , maka
persamaan (3.41) dapat dituliskan menjadi (3.42).
( )
(3.40)
(3.41)
(3.42)
b. Perhitungan nilai koreksi energi atom
Langkah perhitungan koreksi energi orde dua untuk atom thallium, tungsten,
indium, kromium, tembaga, dan molybdenum sama seperti langkah perhitungan
koreksi energi orde satu.
3.3.5 Koreksi Energi Orde Tiga Terhadap Tingkat Dasar
Koreksi energi orde tiga terhadap tingkat dasar untuk atom thallium,
tungsten, indium, kromium, tembaga, dan molybdenum diperoleh dengan langkah
yang sama sebagaimana koreksi energi terhadap tingkat dasar orde satu dan dua.
Penurunannya lebih komplek dikarenakan bentuk persamaan koreksi energi orde
tiga juga komplek. Persamaan koreksi energi orde tiga dijabarkan pada Lampiran
1 dan dijelaskan di pembahasan.
3.3.6 Permodelan Wolfram Mathematica 7®
Permodelan kurva energi potensial untuk atom thallium, tungsten, indium,
kromium, tembaga, dan molybdenum dilakukan menggunakan Wolfram
commit to user
energi potensial untuk inti berupa titik dan inti berukuran tertentu. Langkah
pembuatan kurva adalah sebagai berikut:
1. Menggunakan dasar persamaan (2.56) dan (2.57), menentukan nilai
untuk masing-masing isotop pada atom.
2. Mendefiniskan nilai , yaitu nomer atom.
3. Mendefiniskan yang senilai dengan
.
4. Membuat plot untuk persamaan (2.56) dengan range dari sampai , serta
membuat plot untuk persamaan (2.57) dengan range dari sampai 20 .
5. Membuat plot untuk persamaan (2.57) dengan range dari 0 sampai R.
6. Menggabungkan kedua plot dari langkah empat dan lima.
Permodelan kurva energi potensial ini menghasilkan beberapa plot untuk
commit to user
27
BAB IV
HASIL DAN PEMBAHASAN
4.1 Koreksi Energi Orde Tiga
Penurunan persamaan koreksi energi orde tiga dimulai dengan mengalikan
persamaan (2.32) dengan . Persamaan (4.1) diintegralkan, sehingga diperoleh
persamaan (4.2). Nilai 〈 〉 dapat dituliskan sebagai 〈 〉
sesuai penurunan pada persamaan (4.3) karena merupakan hermitian.
Konsekuensi dari persamaan (4.3) adalah nilai 〈 〉 di ruas kiri dan kanan
saling meniadakan.
(4.1)
〈 〉 〈 〉
〈 〉 〈 〉 〈 〉
〈 〉 (4.2)
〈 〉 = 〈 〉 〈 〉 = 〈 〉
〈 〉 = 〈 〉 (4.3)
〈 〉 〈 〉
〈 〉 〈 〉 〈 〉
〈 〉 (4.4)
〈 〉 〈 〉 〈 〉 〈 〉
〈 〉 (4.5)
Nilai 〈 〉, 〈 〉, dan 〈 〉 pada persamaan (4.4) adalah nol,
sedangkan nilai 〈 〉 adalah sama dengan satu. Persamaan (4.5) merupakan
commit to user
4.2 Koreksi Fungsi Gelombang Orde Tiga
Koreksi fungsi gelombang orde tiga dijabarkan dari persamaan (2.32) yang
dituliskan dalam bentuk persamaan (4.7). Koefisien dari fungsi gelombang yang
sama dikelompokkan menjadi satu. dapat dituliskan sebagai yaitu energi
sistem yang tidak terganggu. Selanjutnya mensubtitusi koreksi fungsi gelombang
commit to user
yang dilakukan dalam menurunkan koreksi fungsi gelombang orde dua.
Langkah selanjutnya adalah menuliskan basis fungsi gelombang tidak
terganggu seperti ditunjukkan pada persamaan (4.11). Bentuk persamaan (4.11)
diperoleh dari analogi persamaan (2.38) dan (2.47). Nilai pada persamaan
(4.11) berbeda dengan nilai pada persamaan (2.38) dan (2.47), oleh
karenanya harus ditentukan terlebih dahulu. Koreksi fungsi gelombang orde
tiga, , dapat diperoleh jika nilai diketahui. Terdapat beberapa langkah
commit to user
ke dalam persamaan (4.10). Hasil subtitusi, persamaan (4.12), dikalikan
dengan lalu diintegralkan, sehingga diperoleh persamaan (4.14)
commit to user
Bila nilai pada persamaan (4.17) sama dengan dan tidak sama dengan ,
maka ruas kiri akan menjadi nol dan diperoleh bentuk persamaan koreksi energi
commit to user
Nilai pada persamaan (4.23) disubtitusikan ke adalam persamaan (4.11)
sehingga diperoleh persamaan (4.25). Persamaan (4.25) disebut sebagai koreksi
fungsi gelombang orde tiga.
berpengaruh pada nilai jari-jari inti sebagaimana dirumuskan oleh persamaan
(3.21). Oleh karena itu terdapat dua perhitungan untuk setiap orde koreksi energi.
Dalam penelitian ini, koreksi energi orde satu, dua, dan tiga untuk atom thallium
dilakukan terhadap tingkat energi dasar .
4.3.1. Koreksi Energi Orde Satu Thallium
Koreksi energi orde satu secara umum ditunjukkan pada persamaan (2.36),
commit to user
persamaan (3.20). Penentuan nilai koreksi energi orde terhadap tingkat dasar
dilakukan dengan menentukan nilai , , dan energi tingkat dasar, . Nilai
ketiga variabel tersebut berbeda-beda untuk setiap atom.
Nilai untuk atom thallium dengan isotop 203 dan 205, masing-masing
adalah dan . Sedangkan nilai dan nya adalah
dan . Hasil subtitusi variabel-variabel tersebut ke
persamaan (3.20) menghasilkan nilai koreksi energi orde satu terhadap tingkat
dasar, , untuk atom thallium sebesar . Hal ini berarti bahwa besarnya
koreksi orde satu yang terdapat pada hasil eksak untuk energi tingkat dasar adalah
sebesar . Hasil koreksi untuk kedua isotop adalah sama, hal ini dikarenakan
nilai untuk kedua isotop hanya selisih nilai cukup kecil pada skala fermi.
4.3.2. Koreksi Energi Orde Dua Thallium
Koreksi energi orde dua terhadap tingkat dasar, , ditunjukkan pada
persamaan (3.39) yang merupakan bentuk penjabaran dari persamaan (2.46).
Variabel yang muncul pada persamaan (3.39) hampir sama dengan variabel pada
penentuan koreksi energi orde satu terhadap tingkat dasar, kecuali adanya nilai
. Nilai merupakan selisih energi tingkat dasar dengan
tingkat energi di atasnya. untuk atom thallium bernilai .
Perhitungan koreksi energi orde dua terhadap tingkat dasar atom thallium
menunjukkan hasil yang sama untuk kedua isotop, yaitu sebesar .
Nilai koreksi energi orde dua jauh lebih kecil dari hasil koreksi energi orde satu.
Halini sesuai dengan teori bahwa semakin tinggi orde koreksi maka
keakuratannya akan semakin tinggi.
4.3.3. Koreksi Energi Orde Tiga Thallium
Koreksi energi orde tiga terhadap tingkat dasar diperoleh beradasarkan
penurunan pada Lampiran 1. Koreksi energi orde tiga terhadaptingkat dasar untuk
atom thallium diperoleh dengan menghitung beberapa variabel terlebih dahulu.
〈 〉, 〈 〉, dan 〈 〉 untuk atom thallium
berturut-turut adalah , , dan . Niloai koreksi energi orde tiga terhadap
tingkat dasar untuk atom thallium adalah . Nilai tersebut jauh lebih
commit to user
Perhitungan untuk koreksi energi orde satu,dua, dan tiga terhadap tingkat
dasar untuk atom thallium disertakan dalam Lampiran 2.
4.4 Koreksi Energi Tungsten
Tungsten bernomor atom 74, merupakan atom golongan VIB, yang memiliki
lima buah isotop dengan berat atom 180,182, 183, 184, dan 186. Meskipun
memiliki lima buah isotop, akan tetapi dari hasil perhitungan hanya diperoleh dua
buah nilai . Hal ini dikarenakan nilai untuk isotop 182, 183, 184, dan 186
adalah sama. Oleh karenanya terdapat dua perhitungan untuk masing-masing
koreksi energinya. Perhitungan nilai koreksi energi orde satu, dua, dan tiga
terhadap tungkat dasar untuk atom tungsten disertakan pada Lampiran 3.
4.4.1. Koreksi Energi Orde Satu Tungsten
Sebagaimana thallium, perhitungan koreksi energi orde satu, , atom
tungsten dilakukan dengan terlebih dahulu menentukan nilai , , dan energi
tingkat dasar, . Nilai untuk atom thallium dengan isotop 180 dan 182,
masing-masing adalah dan . Sedangkan nilai dan
nya adalah dan . Hasil subtitusi variabel-variabel tersebut
ke persamaan (3.20) menghasilkan nilai koreksi energi orde satu terhadap tingkat
dasar untuk atom tungsten sebesar .
4.4.2. Koreksi Energi Orde Dua Tungsten
Nilai untuk atom tungsten bernilai . Perhitungan koreksi
energi orde dua terhadap tingkat dasar, , atom tungsten menghasilkan nilai
untuk isotop 180. Isotop 182, 183, 184, dan 186 menghasilkan
koreksi orde dua yang sama dengan isotop 180. Sebagaimana thallium, koreksi
energi orde dua terhadap tingkat dasar untuk atom tungsten lebih kecil dari
koreksi energi orde satu nya.
4.4.3. Koreksi Energi Orde Tiga Tungsten
Koreksi energi orde tiga terhadap tingkat dasar untuk atom tungsten diperoleh
dengan langkah yang sama seperti pada perolehan untuk atom thallium. Namun,
commit to user
yang berbeda pula. Hasil koreksi energi orde tiga terhadap tingkat dasar untuk
atom tungsten adalah .
4.5 Koreksi Energi Indium
Indium berada satu golongan dengan thallium, yaitu IIIA, dengan nomer atom
49. Indium memiliki dua buah isotop dengan berat atom 113 dan 115. Dua buah
isotop ini mengindikasikan adanya dua nilai yang berbeda, sehingga terdapat
dua perhitungan untuk masing-masing orde koreksi. Perhitungan koreksi energi
terhadap tingkat dasar untuk atom indium, secara lengkapi ditampilkan pada
Lampiran 4.
4.5.1. Koreksi Energi Orde Satu Indium
Penentuan nilai , , dan dilakukan dengan langkah yang sama dengan
kedua atom sebelumnya. untuk berat atom 133 adalah , sedangkan
untuk berat atom 114 adalah . Nilai dan untuk indium secara
berturut-turut yaitu dan . Hasil perhitungan
menunjukkan nilai koreksi energi orde satu terhadap tingkat dasar untuk atom
indium adalah . Kedua buah isotopnya memiliki nilai koreksi yang sama.
Dibandingkan dengan koreksi orde satu terhadap tingkat dasar untuk atom
thallium dan tungsten, koreksi energi orde satu atom indium lebih kecil. Fakta ini
mengindikasikan bahwa semakin kecil ukuran suatu atom, yang ditunjukkan
dengan semakin kecil nomer atomnya, maka semakin kecil koreksi yang
diperoleh. Atom dengan nomer yang lebih kecil, memiliki jumlah elektron yang
lebih sedikit, dengan demikian gangguan dari gaya tarik antar elektron lebih kecil.
4.5.2. Koreksi Energi Orde Dua Indium
Selisih nilai energi tingkat dasar dengan tingkat energi di atasnya, ,
untuk atom indium adalah . Perhitungan koreksi energi orde dua
terhadap tingkat dasar untuk kedua isotop indium juga menampilkan hasil yang
sama, yaitu . Nilai tersebut lebih kecil jika dibandingkan dengan
koreksi energi orde dua terhadap tingkat dasar untuk atom thallium dan tungsten.
Analisisnya sama seperti pada koreksi energi orde satu, yaitu pengaruh dari
commit to user 4.5.3. Koreksi Energi Orde Tiga Indium
Koreksi energi orde tiga terhadap tingkat dasar untuk atom indium
ditampilkan pada Lampiran 4. Hasil yang diperoleh adalah Hasil
ini jauh kebih kecil dibandingkan dengan koreksi energi orde satu dan dua
terhadap tingkat dasar untuk atom indium, dan juga lebih kecil koreksi energi orde
tiga terhadap tingkat dasar untuk atom thallium dan tungsten. Sebagaimana
analisis sebelumnya, hal ini dipengaruhi oleh ukuran atomnya.
4.6 Koreksi Energi Molybdenum
Koreksi energi molybdenum orde satu, dua, dan tiga terhadap tingkat dasar
ditampilkan pada Lamipran 5. Molybdenum memiliki tujuh buah isotop dengan
nomer atom 42. Ketujuh buah isotop yang dimiliki molybdenum menghasilkan
tiga jenis nilai .
4.6.1 Koreksi Energi Orde Satu Molybdenum
Nilai untuk berat atom 92 adalah . Sedangkan untuk berat
atom 94, 95, 96, 97, dan 98 memiliki nilai yang sama yaitu . Berat
atom 100 menghasilkan nilai jari-jari inti sebesar . Nilai dan
untuk atom molybdenum masing-masing adalah dan .
Koreksi energi orde satu terhadap tingkat dasar untuk berat atom 92 yaitu ,
sedangkan untuk berat atom yang lain memiliki nilai sama yaitu .
4.6.2 Koreksi Energi Orde Dua Molybdenum
Penentuan koreksi energi orde dua atom molybdenum dilakukan dengan
langkah yang sama seperti atom sebelumnya. Selisih energi tingkat satu dan dua
untuk atom molybdenum adalah . Koreksi energi orde dua untuk atom
molybdenum menghasilkan nilai . Nilai koreksi semakin mengecil
seiring bertambahnya orde koreksi serta berkurangnya ukuran atom.
4.6.3 Koreksi Energi Orde Tiga Molybdenum
Koreksi energi orde tiga diperoleh dengan menentukan 〈 〉,
〈 〉, dan 〈 〉 terlebih dahulu. Selain itu ditentukan pula nilai
selisih energi tingkat pertama dan ketiga, . Nilai untuk
commit to user
dalam persamaan koreksi energi orde tiga terhadap tingkat dasar. Koreksi energi
orde tiga terhadap tingkat dasar untuk atom molybdenum, , adalah
.
4.7 Koreksi Energi Tembaga
Tembaga (Cu) merupakan atom golongan IB yang bernomer atom 29 dan
memiliki isotop tiga buah dengan berat atom 63, 64, dan 65. Koreksi energi orde
satu, dua, dan tiga untuk atom tembaga dilakukan terhadap tingkat dasar.
Perhitungan selengkapnya ditampilkan pada Lampiran 6.
4.7.1 Koreksi Energi Orde Satu Tembaga
Penentuan nilai , , dan dilakukan dengan langkah yang sama dengan
atom-atom sebelumnya. Nilai untuk ketiga isotop yang dimiliki tembaga adalah
sama yaitu . Nilai dan nya adalah dan
. Koreksi energi orde satu terhadap tingkat dasar untuk atom tembaga
diperoleh dengan mensubtitusikan nilai , , dan ke dalam persamaan koreksi
energi orde satu terhadap tingkat dasar. Hasil perhitungan koreksi energi orde satu
terhadap tingkat dasar atom tembaga menunjukkan nilai .
4.7.2 Koreksi Energi Orde Dua Tembaga
Koreksi energi orde dua terhadap tingkat dasar untuk atom tembaga adalah
4.7.3 Koreksi Energi Orde Tiga Tembaga
Nilai 〈 〉, 〈 〉, dan 〈 〉 untuk atom tembaga
secara berurutan adalah , , dan . Ketiga nilai
tersebut dimasukkan ke dalam persamaan koreksi energi orde tiga terhaap tingka
dasar. Hasil yang diperoleh menunjukkan bahwa koreksi energi orde tiga terhadap
commit to user
dihitung nilai selisih energi tingkat pertama dan ketiga untuk atom tembaga yaitu
.
4.8 Koreksi Energi Kromium
Kromium merupakan atom golongan VIB, satu golongan dengan tungsten dan
molybdenum. Kromium memiliki lima buah isotop dengan berat atom 48, 50, 52,
53, dan 54. Nomer atom kromium yaitu 24, yang merupakan atom terkecil yang
digunakan dalam penelitian ini. Hasil perhitungan untuk koreksi energi orde satu,
dua, dan tiga terhadap tingkat dasar untuk atom kromium ditunjukkan pada
Lampiran 7.
4.8.1 Koreksi Energi Orde Satu Kromium
Kelima isotop yang dimiliki kromium menghasilkan dua jenis nilai , yaitu
4.8.2 Koreksi Energi Orde Dua Kromium
Hasil perhitungan koreksi energi orde dua terhadap tingkat dasar untuk atom
kromium menunjukkan hasil . Nilai ini diperoleh dengan terlebih
dahulu menentukan hasil perhitungan untuk . Nilai untuk
atom kromium adalah . Koreksi energi orde dua kromium nilainya lebih
kecil dibanding dengan koreksi energi orde satu atom kromium dan lebih kecil
dibanding dengan koreksi energi orde dua untuk atom-atom sebelumnya.
4.8.3 Koreksi Energi Orde Tiga Kromium
Nilai 〈 〉, 〈 〉, dan 〈 〉 untuk atom kromium
yaitu , , dan . Selisish energi tingkat pertama
dan ketiga untuk atom kromium adalah . Nilai-nilai tersbut disubtitusikan
ke dalam persamaan koreksi energi orde tiga terhadap tingkat dasar. Hasil yang
diperoleh untuk koreksi energi orde tiga terhadap tingkat dasar atom kromium
commit to user 4.9 Permodelan Wolfram Mathematica 7®
Wolfram Mathematica 7® merupakan sebuah software untuk alat bantu matematika yang dapat digunakan untuk memodelkan grafik dengan fasilitas yang
lebih lengkap. Grafik yang dihasilkan dapat diperoleh dari hasil tabulasi data
maupun dari hasil sketsa suatu fungsi. Permodelan yang dibuat dalam penelitian
ini adalah berupa kurva energi potensial untuk atom yang intinya dianggap
sebagai titik dan atom yang intinya berukuran tertentu. Hasil analisis kedua kurva
ini akan menampilkan permodelan hamiltonian pengganggu.
Script pembuatan kurva energi potensial dari Wolfram Mathematica 7®
ditampilkan pada Lampiran 8. Sedangkan grafik hasil permodelannya ditampilkan
pada Lampiran 9. Permodelan dibuat dengan menggunakan rumus energi
potensial pada persamaan (2.56) dan (2.57). Persamaan (2.56) digunakan untuk
nilai yang kurang dari atau sama dengan , berarti pada keadaan di dalam inti
yang diasumsikan berupa bola. Sedangkan persmaan (2.57) digunakan untuk nilai
yang lebih dari , yang berrati pada keadaan di luar inti. Dasar pembuatan kurva
energi potensial untuk inti atom yang berupa titik juga menggunakan persamaan
(2.57).
Kurva energi potensial dibuat untuk semua isotop yang dimiliki atom
thallium, tungsten, indium, kromium, tembaga, dan molybdenum. Namun,
beberapa isotop memiliki nilai yang sama, sehingga kurva yang terbentuk pun
identik. Pembuatan model kurva energi potensial ini tidak hanya dipengaruhi oleh
nilai dan berat atomnya, tetapi juga nomer dari atom. Semakin besar nomer
atomnya, maka nilai energi potensialnya semakin besar.
Pembuatan model kurva dengan Wolfram Mathematica 7® dilakukan dengan
membuat kurva energi potensial secara terpisah. Kurva energi potensial untuk inti
yang berukuran tertentu dibuat terlebih dahulu, kemudian membuat kurva untuk
inti yang berupa titik. Kurva untuk inti yang berukuran sendiri terbagi menjadi
dua yaitu untuk nilai yang kurang dari atau sama dengan dan nilai yang
lebih dari . Ketiga kurva tersebut digabungkan dan menjadi satu kesatuan.
Hasil penggabungan kurva energi potensial untuk inti yang berukuran tertentu
commit to user
tersebut terjadi untuk nilai yang kurang dari . Semakin mendekati nol, nilai
simpangan semakin besar, yang diindikasikan dengan jarak yang lebih lebar.
Simpangan ini lah yang diketahui sebagai hamiltonian pengganggu, yaitu selisih
antara energi potensial untuk inti yang berukuran tertentu dengan inti yang berupa
titik.
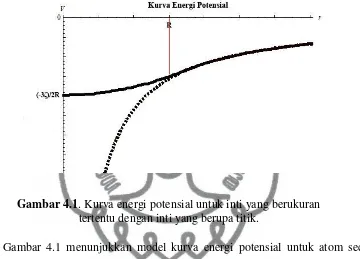
Gambar 4.1 menunjukkan model kurva energi potensial untuk atom secara
umum. Garis putus-putus merupakan kurva energi potensial untuk inti yang
berupa titik. Sedangkan garis penuh merepresentasikan kurva energi potensial
untuk inti yang berukuran tertentu. Sumbu-x menunjukkan variabel , sedangkan
sumbu-y menunjukkan nilai enrgi potensial yang merupakan fungsi dari . Kurva
tersebut merupakan hasil analogi dari keenam kurva yang telah dimodelkan untuk
atom thallium, tungsten, indium, kromium, tembaga, dan molybdenum.
Kurva energi potensial untuk atom thallium, tungsten, indium, kromium,
tembaga, dan molybdenum memiliki bentuk yang sama, namun nilai pada
sumbu-x dan sumbu-y yang berbeda. Nilai merupakan jari-jari inti yang dituliskan
sesuai persamaan (3.21). Nilai untuk masing-masing atom dan isotop berbeda.
Berdasarkan Gambar 4.1 diketahui bahwa kurva energi potensial untuk inti yang
berukuran tertentu dengan inti yang berupa titik memiliki nilai yang sama untuk
yang lebih dari .
commit to user
Kurva energi potensial untuk inti yang berukuran tertentu memiliki nilai pada
saat sama dengan nol, yaitu
. Nilai sama dengan nol adalah posisi ketika
elektron menempel pada kulit bola, yaitu permukaan luar dari ini. Kurva energi
potensial untuk inti yang berupa titik nilainya mengecil tak berhingga untuk
menuju nol. Hal ini sesuai teori, karena untuk inti yang berupa titik ketika nilai
commit to user
e. Koreksi energi orde satu, dua, dan tiga terhadap tingkat dasar untuk
atom tembaga adalah ; ; dan .
f. Koreksi energi orde satu, dua, dan tiga terhadap tingkat dasar untuk
atom kromium adalah ; ; dan .
3. Permodelan kurva energi potensial untuk atom thallium, tungsten, indium,
molybdenum, tembaga, dan kromium telah berhasil dibuat dan hasilnya
ditampilkan pada lampiran 6.
5.2 Saran
Penyempurnaan penelitian ini dapat dilakukan dengan menghitung nilai
koreksi energi orde satu untuk semua tingkat energi eksitasi pertama dan kedua
pada atom thallium, tungsten, indium, molybdenum, tembaga, dan kromium.
Kasus pada tingkat energi tereksitasi diselesaikan dengan teori gangguan untuk