ANALISIS KOMPLEKSITAS MASALAH OPTIMASI LINEAR
MENGGUNAKAN METODE INTERIOR PRIMAL-DUAL
DENGAN LANGKAH FULL-NEWTON
RINI MAEDIANENGSIH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2013
ABSTRAK
RINI MAEDIANENGSIH. Analisis Kompleksitas Masalah Optimasi Linear Menggunakan
Metode Interior Primal-Dual dengan Langkah Full-Newton. Dibimbing oleh BIB PARUHUM
SILALAHI dan MUHAMMAD ILYAS.
Metode interior primal-dual dengan langkah full-Newton adalah salah satu metode untuk menyelesaikan masalah optimasi linear. Metode ini dirancang sedemikian rupa sehingga solusi optimal diperoleh di dalam interior dari domain. Metode ini memiliki kompleksitas polinomial. Karya ilmiah ini membahas dan menganalisis kompleksitas algoritme masalah optimasi linear menggunakan metode interior primal-dual langkah full-Newton. Beberapa masalah optimasi linear diselesaikan dengan metode ini untuk melihat kesesuainnya dengan kompleksitas algoritme. Dari studi kasus yang telah dilakukan, dapat disimpulkan bahwa banyaknya iterasi sesuai dengan kompleksitas algoritme.
ABSTRACT
RINI MAEDIANENGSIH. Complexity Analysis of Linear Optimization Problems Using
Primal-Dual Interior Methods with Full-Newton Step. Supervised by BIB PARUHUM SILALAHI and
MUHAMMAD ILYAS.
Primal-dual interior method with full-Newton step is a method for solving linear optimization problems. This method is designed in such a way that an optimal solution is obtained an interior of the domain. It has polynomial complexity. This paper discusses and analyzes the complexity of linear optimization problems using primal-dual interior method with full-Newton steps. From the case studies that have been conducted, can be concluded that the number of iterations is in accordance with the complexity of the algorithm.
ANALISIS KOMPLEKSITAS MASALAH OPTIMASI
LINEAR MENGGUNAKAN METODE INTERIOR
PRIMAL-DUAL DENGAN LANGKAH FULL-NEWTON
RINI MAEDIANENGSIH
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2013
Judul Sripsi : Analisis Kompleksitas Masalah Optimasi Linear Menggunakan
Metode Interior Primal-Dual dengan Langkah Full-Newton.
Nama
: RINI MAEDIANENGSIH
NIM
: G54080044
Menyetujui,
Tanggal Lulus :
Pembimbing I
Dr. Ir. Bib Paruhum Silalahi, M.Kom.
NIP. 19670101 199203 1 004
Pembimbing II
Muhammad Ilyas, S.Si, M.Sc.
Mengetahui:
Ketua Departemen Matematika
Dr. Berlian Setiawaty, M.S.
NIP. 19650505 198903 2 004
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas segala rahmat dan karunia-Nya serta shalawat dan salam kepada Nabi Muhammad SAW sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Dr. Ir. Bib Paruhum Silalahi, M.Kom, selaku dosen pembimbing I (terima kasih atas semua ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini).
2. Muhammad Ilyas, S.Si, M.Sc, selaku dosen pembimbing II (terima kasih atas semua ilmu, saran dan motivasinya).
3. Dr. Ir. I Gusti Putu Purnaba, DEA, selaku dosen penguji (terima kasih atas semua ilmu dan sarannya).
4. Semua dosen Departemen Matematika (terima kasih atas semua ilmu yang telah diberikan). 5. Staf Departemen Matematika: Pak Yono, Bu Ade, Mas Heri, Bu Susi dan Mas Deni (terima
kasih atas bantuan dan motivasinya).
6. Keluargaku tercinta: Bapak, Mamah, adikku Rena dan Adelia (terima kasih atas doa, dukungan, kesabaran, kepercayaan dan kasih sayangnya).
7. Teman-teman kosan: Yuli, Sri, Davi, Chacha, Kak Nurul, Kak Tanti, Kak Runi (terima kasih atas bantuan, doa dan dukungannya).
8. Teman-teman satu bimbingan: Haya, Bram, Irwan (terima kasih atas bantuan dan dukungannya).
9. Sahabat terdekat: Roni, Nova, Dina, Aisyah (terima kasih atas semangat, doa dan dukungannya).
10. Teman-teman Math 45: Herlan, Prama, Arbi, Dini, Rahma, Mya, Pipin, Tiwi, Mega, Fuka, Annisa, Ana, Dimas, Fina dan yang lainnya (terima kasih atas dukungan, bantuan dan doanya). 11. Adik-adik Math 46: Sefira, Fitria, Anne, Mirna, Andri dan yang lainnya (terima kasih atas
dukungan, bantuan, dan doanya).
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
Bogor, April 2013
RIWAYAT HIDUP
Penulis dilahirkan di Ciamis pada tanggal 5 Februari 1990 sebagai anak pertama dari tiga bersaudara. Anak dari pasangan Muhaemin dan Eros Saripah.
Pada tahun 1996 penulis menyelesaikan pendidikan di TK LKMD Kuningan. Tahun 2002 penulis lulus dari SDN Tangkolo 1, Kuningan. Tahun 2005 penulis lulus dari SLTPN 3 Rancah, Ciamis. Tahun 2008 penulis lulus dari SMAN 2 Ciamis dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Ujian Saringan Masuk IPB (USMI). Penulis memilih Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi anggota Biro Kewirausahaan GUMATIKA IPB pada tahun 2009-2010. Kegiatan lain yang pernah diikuti oleh penulis yaitu sebagai pengajar Matematika untuk tingkat SMP di sebuah bimbingan belajar pada tahun 2012.
viii
DAFTAR ISI
Halaman DAFTAR TABEL ... ix DAFTAR LAMPIRAN ... ix I. PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Tujuan ... 1 1.3 Sistematika Penulisan ... 1II. LANDASAN TEORI ... 2
2.1 Sistem Persamaan Linear... 2
2.2 Matriks dan Vektor ... 2
2.3 Optimasi Linear dan Dualitas ... 3
2.4 Metode Newton ... 3
2.5 Kompleksitas ... 4
III. HASIL DAN PEMBAHASAN ... 5
3.1 Kondisi Optimal ... 5
3.2 Central Path... 5
3.3 Langkah Full-Newton ... 5
3.4 Ukuran Kedekatan ... 6
3.5 Kompleksitas Algoritme ... 7
IV. STUDI KASUS ... 11
V. SIMPULAN DAN SARAN ... 16
5.1 Simpulan ... 16
5.2 Saran... 16
DAFTAR PUSTAKA ... 16
ix
DAFTAR TABEL
Halaman
1 Hasil Iterasi pada Saat 𝑛 = 4, 𝑚 = 2, 𝜇 = 10, dan 𝜀 = 10−5 ... 11
2 Hasil Iterasi pada Saat 𝑛 = 4, 𝑚 = 2, 𝜇 = 100, dan 𝜀 = 10−5 ... 12
3 Hasil Iterasi pada Saat 𝑛 = 4, 𝑚 = 2, 𝜇 = 10, dan 𝜀 = 10−3 ... 12
4 Hasil Iterasi pada Saat 𝑛 = 6, 𝑚 = 3 𝜇 = 10, dan 𝜀 = 10−5 ... 13
5 Hasil Iterasi pada Saat 𝑛 = 6, 𝑚 = 3 𝜇 = 100, dan 𝜀 = 10−5 ... 14
6 Hasil Iterasi pada Saat 𝑛 = 6, 𝑚 = 3 𝜇 = 10, dan 𝜀 = 10−3 ... 15
DAFTAR LAMPIRAN
Halaman 1 Program MATLAB untuk Fungsi Langkah Newton ... 182 Program MATLAB untuk Kasus Dua Dimensi (𝑛 = 4) ... 19
I PENDAHULUAN
1.1 Latar Belakang
Pengoptimuman merupakan salah satu cabang matematika terapan yang mempelajari masalah meminimumkan atau memaksimum-kan. Dalam kehidupan sehari-hari banyak permasalahan yang memerlukan optimasi. Optimasi digunakan secara luas hampir di setiap aspek kehidupan, seperti di bidang teknik, ekonomi, manajemen dan industri. Banyak penelitian yang telah menghasilkan teknologi baru, dan metode baru dalam optimasi.
Pada tahun 1947, Dantzig mengajukan penggunaan metode simpleks untuk me-mecahkan masalah optimasi linear (OL). Daerah fisibel dari masalah optimasi linear adalah suatu polihedron. Metode simpleks bergerak dari verteks ke verteks dari polihedron untuk memperoleh solusi optimal. Metode ini dirancang sehingga nilai dari fungsi tujuan berubah secara monoton ke arah nilai optimal. Penemuan Dantzig telah menginspirasi begitu banyak penelitian dalam matematika. Terdapat banyak varian dari metode simpleks, yang dibedakan oleh aturan untuk memilih verteks yang akan dikunjungi (dikenal dengan aturan pivot) (Silalahi 2011). Pada tahun 1972, Klee dan Minty mem-berikan suatu masalah dengan metode simpleks memerlukan 2𝑛− 1 iterasi untuk menyelesaikan suatu masalah optimasi linear dengan 2n pertidaksamaan. Klee-Minty juga menunjukkan bahwa metode simpleks merlukan waktu eksponensial untuk me-nyelesaikan masalah optimasi linear. Contoh yang diberikan oleh Klee dan Minty kemudian dikenal dengan problem Klee-Minty (KM), yaitu
min 𝑦𝑚
kendala 𝜌𝑦𝑘−1 ≤ 𝑦𝑘≤ 1 − 𝜌𝑦𝑘−1 ,
k = 1,...,m dengan 𝑦0 = 0, (0,12) (Silalahi 2011).
Pada tahun 1979, Khachiyan meng-usulkan metode elipsoid untuk memecahkan permasalahan optimasi linear secara polinomial. Walaupun metode elipsoid ini memiliki kompleksitas polinomial, namun dalam penerapan secara komputasional metode ini tidak efisien (Silalahi 2011).
Pada tahun 1984, Karmarkar me-ngembangkan metode interior dan mem-presentasikan suatu algoritme (algoritme Karmarkar) yang memiliki kompleksitas polinomial yang lebih baik dari metode
elipsoid. Sesuai dengan namanya, metode ini akan melalui daerah dalam (interior) dari daerah solusi yang mungkin (feasible) dalam mencari solusi optimal. Hal ini berlawanan dengan metode simpleks yang bergerak dari verteks ke verteks (Silalahi 2011).
Dalam perkembangannya, metode ini telah dikembangkan dengan beberapa pendekatan. Secara umum metode ini dapat dikelompokkan menjadi tiga kategori, yaitu metode affine scaling, metode potential
reduction (barrier) dan metode central trajectory (path-following). Selain itu, persoalan yang bisa diselesaikan dengan metode ini juga mengalami perkembangan. Awalnya metode ini dikembangkan untuk pemrograman linear dan sekarang sudah dikembangkan untuk masalah-masalah yang lain, seperti pemrograman integer, pemrograman jaringan, pemrograman semidefinit (Mitchell 1998).
Dalam karya ilmiah ini akan digunakan metode interior primal-dual dengan langkah
full-Newton dalam memecahkan masalah
Klee-Minty tersebut. Selanjutnya akan dilakukan analisis kompleksitas algoritme dari masalah Klee-Minty dan menyelesaikan beberapa masalah optimasi linear untuk melihat kesesuaiannya dengan kompleksitas algoritme dengan bantuan software MATLAB R2008b.
1.2 Tujuan
Berdasarkan latar belakang di atas, maka tujuan karya ilmiah ini adalah
(i) Membahas metode interior primal-dual dengan langkah full-Newton.
(ii) Menganalisis kompleksitas algoritme interior primal-dual dengan langkah
full-Newton.
(iii) Menyelesaikan beberapa masalah Klee-Minty dan melihat kesesuaiannya dengan kompleksitas algoritme.
1.3 Sistematika Penulisan
Karya ilmiah ini terdiri dari lima bab. Bab pertama merupakan pendahuluan yang berisi latar belakang dan tujuan penulisan. Bab kedua berupa landasan teori yang berisi konsep. Bab ketiga berisi penjelasan metode interior primal-dual dengan langkah
full-Newton. Bab keempat merupakan studi kasus
2
II LANDASAN TEORI
2.1 Sistem Persamaan Linear
Definisi 1 (Sistem Persamaan Linear)
Suatu persamaan linear dalam n peubah (variable) adalah persamaan dengan bentuk
a1x1 + a2x2 + . . . + anxn = b
di mana a1, a2, . . . , an dan b adalah bilangan-bilangan real dan x1, x2, . . . ,xn adalah peubah. Dengan demikian maka suatu sistem linear dari m persamaan dalam n peubah adalah satu sistem berbentuk:
a11x1 + a12x2 + . . . + a1nxn = b1 a21x1 + a22x2 + . . . + a2nxn = b2
. . .
am1x1 + am2x2 + . . . + amnxn = bm
dengan aij dan bi semuanya adalah
bilangan-bilangan real. Kita akan menyebut sistem-sistem di atas sebagai sistem-sistem linear 𝑚 × 𝑛.
(Leon 2001)
2.2 Matriks dan Vektor Definisi 2 (Ortogonal)
Vektor – vektor x dan y di dalam ℝ2 (atau ℝ3
) dikatakan ortogonal jika xTy = 0.
(Leon 2001)
Definisi 3 (Hasil Kali Skalar di ℝ𝒏)
Misalkan x,y ∈ ℝ𝒏 dengan
x= 𝑥1 𝑥2 . . . 𝑥𝑛 , y= 𝑦1 𝑦2 . . . 𝑦𝑛
maka hasil kali skalar dari x dan y adalah 𝐱T𝐲 = 𝑥
1𝑦1 + 𝑥2𝑦2 + . . . + 𝑥𝑛𝑦𝑛
(Leon 2001)
Definisi 4 (Hadamard product)
Misalkan vektor x, y ∈ ℝ𝑛, X, Y ∈ ℝ𝑛×𝑛 dengan n menyatakan banyak baris dan banyak kolom pada matriks. Vektor x dan y didefinisikan sebagai berikut
x= 𝑥1 𝑥2 ⋮ 𝑥𝑛 , y= 𝑦1 𝑦2 ⋮ 𝑦𝑛
dan notasi diag(x) adalah matriks diagonal dengan unsur diagonal utama ialah vektor x
𝑿 = 𝑑𝑖𝑎𝑔 𝐱 = 𝑥1 0 ⋯ 0 0 𝑥2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 𝑥𝑛 𝒀 = 𝑑𝑖𝑎𝑔 𝐲 = 𝑦1 0 ⋯ 0 0 𝑦2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 𝑦𝑛
maka Hadamard product dari x dan y adalah
xy = Xy = Yx = yx
Dengan kata lain, Hadamard product adalah perkalian antara unsur dengan unsur yang seletak (componentwise) dari dua buah vektor yang berukuran sama. Componentwise juga berlaku pada operasi pembagian dan operasi akar untuk vektor x dan s sebagai berikut
𝐱 𝐬= 𝑥i 𝑠𝑖 = 𝑥1 𝑥2 ⋮ 𝑥𝑛 𝑠1 𝑠2 ⋮ 𝑠𝑛 𝐱 = 𝑥i= 𝑥1 𝑥2 ⋮ 𝑥𝑛 (Roos et al. 2006)
Definisi 5 (Norm dari Suatu Vektor di ℝ𝒏)
Misalkan x ∈ ℝ𝑛 dengan x= 𝑥1 𝑥2 ⋮ 𝑥𝑛 ,
maka norm dari vektor x di ℝ𝑛 adalah
𝐱 = 𝐱𝑇𝐱 = 𝑥
12+ 𝑥22+ ⋯ + 𝑥𝑛2
3
Definisi 6 (Ruang Baris dan Ruang Kolom)
Jika A adalah matriks 𝑚 × 𝑛, maka ruang bagian dari ℝ1×𝑛 yang direntang oleh
vektor-vektor baris dari A disebut ruang baris dari A. Ruang bagian dari ℝ𝑚 yang direntang oleh vektor-vektor kolom dari A disebut ruang kolom dari A.
(Leon 2001)
Definisi 7 (Ruang Nol)
Misalkan A adalah matriks 𝑚 × 𝑛. Misalkan
N(A) menyatakan himpunan semua penyelesaian dari sistem homogen 𝐀𝐱 = 𝟎. Jadi
𝑁 𝐀 = {𝐱 ∈ ℝ𝑛|𝐀𝐱 = 𝟎}
Himpunan semua penyelesaian dari sistem homogen 𝐀𝐱 = 𝟎 membentuk ruang bagian dari ℝ𝑛. Ruang bagian N(A) disebut kernel (ruang nol atau nullspace) dari A.
(Leon 2001)
2.3 Optimasi Linear dan Dualitas
Masalah optimasi linear dalam bentuk standar diberikan sebagai berikut
min{𝐜Tx : Ax = b, x ≥ 0} (P)
dengan, c, x ℝ 𝑛, b ℝ 𝑚 dan A ℝ 𝑚𝑥𝑛. Masalah (P) disebut masalah primal.
Masalah dual dari masalah primal (P) diberikan sebagai berikut
max {𝐛Ty : 𝐀Ty + s = c, s ≥ 0 } (D)
dengan, s ℝ𝑛 dan y ℝ𝑚. Masalah (D) disebut masalah dual.
Daerah fisibel dari (P) dan (D) masing-masing adalah :
:= {x : Ax = b, x ≥ 0} := {(y,s) : 𝐀Ty + s = c, s ≥ 0}
Daerah interior masalah (P) dan (D) didefinisikan sebagai berikut
0
:= {x : Ax = b, x > 0}, 0 := {(y,s) : 𝐀Ty + s = c, s > 𝟎}
(Silalahi 2011)
Definisi 8 (Daerah Fisibel)
Himpunan titik-titik yang memenuhi semua kendala dan pembatasan tanda pada optimasi linear.
(Winston 2004)
Definisi 9 (Solusi Optimal)
Solusi optimal pada masalah maksimisasi adalah suatu titik pada daerah fisibel dengan
nilai fungsi objektif paling besar. Sedangkan solusi optimal untuk masalah minimisasi adalah suatu titik pada daerah fisibel dengan nilai fungsi objektif paling kecil.
(Winston 2004)
Proposisi 1 ( Dualitas Lemah)
Misalkan x dan s masing-masing fisibel untuk (P) dan (D). Kemudian 𝐜Tx - 𝐛Ty = 𝐱Ts ≥ 0.
Akibatnya, 𝐜Tx terbatas di atas untuk nilai
optimal dari (D), dan 𝐛Ty terbatas di bawah
untuk nilai optimal dari (P). Selain itu, jika kesenjangan dualitas (duality gap) 𝐱Ts
bernilai nol maka x adalah solusi optimal untuk (P) dan (y,s) adalah solusi optimal untuk (D).
(Roos et al. 2006)
Bukti :lihat Roos Teorema 1 (Dualitas)
Jika (P) dan (D) fisibel maka kedua masalah tersebut mempunyai solusi optimal. Kemudian, x dan (y,s) adalah solusi optimal jika dan hanya jika 𝐱Ts = 0.
(Roos et al. 2006)
Bukti : lihat Roos
Definisi 10 (Kendala Redundant)
Kendala redundant adalah kendala yang tidak mengubah daerah fisibel dari masalah optimasi linear.
(Silalahi 2011)
Definisi 11 (Central Path)
Suatu kurva yang bergerak dari bagian dalam pada daerah fisibel menuju solusi optimal.
(Silalahi 2011)
2.4 Metode Newton
Metode Newton disebut juga metode Newton-Raphson. Metode Newton adalah suatu metode yang digunakan untuk menyelesaikan persamaan taklinear, yang dituliskan dalam bentuk :
𝑓𝑖 𝐱 = 𝟎, 𝑖 = 1,2, … , 𝑚
𝐱 = (𝑥1, 𝑥2, … , 𝑥𝑛)T.
Metode Newton Raphson dapat diturunkan dengan menggunakan orde pertama dari deret
4
Taylor. Sebagai contoh untuk fungsi satu peubah atau 𝑖 = 1, dan 𝐱 = 𝑥1∈ ℝ, orde
pertama deret Taylor 𝑓1(𝑥1) sebagai berikut
𝑓1 𝑥1 ≈ 𝑓 𝑥1.0 + 𝑓′ 𝑥1.0 𝑥1− 𝑥1.0
= 𝔣(𝑥1)
dengan 𝑥1.0 adalah hampiran awal (Munir
2003).
Dengan menggunakan metode Newton, fungsi taklinear dapat diubah menjadi fungsi
linear. Untuk mencari solusi persamaan 𝑓1 𝑥1 = 0, metode Newton melakukan
pendekatan dengan cara mencari solusi 𝔣 𝑥1 = 0, dengan 𝔣 adalah fungsi linear.
Selain itu, untuk fungsi dua peubah atau 𝑖 = 2, dan 𝐱 = (𝑥1, 𝑥𝟐)T ∈ ℝ. Deret Taylor
orde pertama dapat dituliskan untuk masing-masing persamaan sebagai berikut
𝑓1 𝑥1, 𝑥2 ≈ 𝑓1 𝑥1.0, 𝑥2.0 + 𝑥1− 𝑥1.0 𝜕𝑓1 𝑥1.0, 𝑥2.0 𝜕𝑥1 + 𝑥2− 𝑥2.0 𝜕𝑓1 𝑥1.0, 𝑥2.0 𝜕𝑥2 𝑓2 𝑥1, 𝑥2 ≈ 𝑓2 𝑥1.0, 𝑥2.0 + 𝑥1− 𝑥1.0 𝜕𝑓2 𝑥1.0, 𝑥2.0 𝜕𝑥1 + 𝑥2− 𝑥2.0 𝜕𝑓2 𝑥1.0, 𝑥2.0 𝜕𝑥2
dengan 𝑥1.0 dan 𝑥2.0 adalah hampiran awal
(Munir 2003).
Contoh 1
Diketahui fungsi taklinear f 𝑥1 = 𝑒𝑥1− 5𝑥1
dengan hampiran awal 𝑥1.0= 0.
𝑓1 𝑥1 ≈ 𝑓 𝑥1.0 + 𝑓′ 𝑥1.0 𝑥1− 𝑥1.0 𝑓1 𝑥1 ≈ 𝔣 𝑥1 = 0 𝔣 𝑥1 = 𝑓 0 + 𝑓′ 0 𝑥1− 0 = 𝑒0− 5 0 + 𝑒0− 5 𝑥 1− 0 = 1 + −4 𝑥1
Pada saat 𝔣 𝑥1 = 0 maka
1 + −4 𝑥1 = 0
𝑥1 = 1
4
Contoh 2
Diketahui fungsi taklinear dengan dua variabel sebagai berikut
𝑓1 𝑥1, 𝑥2 = 𝑥12− 𝑥1𝑥2+ 1 (1)
𝑓2(𝑥1, 𝑥2) = 𝑥22− 𝑥1𝑥2− 2 (2)
dengan hampiran awal 𝑥1.0= 0, 𝑥2.0= 1
Pelinearan untuk persamaan (1) 𝑓1 𝑥1, 𝑥2 ≈ 𝔣 𝑥1, 𝑥2 = 0 𝑥12− 𝑥1𝑥2+ 1 = 0 𝑓1 0,1 + −1 0 𝑥𝑥1− 0 2− 1 = 0 1 + −1 𝑥1 = 0 𝑥1 = 1
Jadi, persamaan baru setelah pelinearan adalah
−𝑥1+ 1 = 0
Pelinearan untuk persamaan (2) 𝑓2 𝑥1, 𝑥2 ≈ 𝔣 𝑥1, 𝑥2 = 0 𝑥22− 𝑥1𝑥2− 2 = 0 𝑓2 0,1 + −1 2 𝑥𝑥1− 0 2− 1 = 0 −1 + −1 𝑥1+ 2 𝑥2− 1 = 0 −𝑥1+ 2𝑥2− 3 = 0
Jadi, persamaan baru setelah pelinearan adalah
−𝑥1+ 2𝑥2= 3
Solusi dari 𝑥1 dan 𝑥2 dapat diperoleh dengan
mensubstitusikan persamaan (1) ke persamaan (2) sebagai berikut
− 1 + 2𝑥2 = 3
2𝑥2 = 4
𝑥2 = 2
Jadi, solusi dari 𝑥1 dan 𝑥2 setelah dilakukan
pelinearan adalah 𝑥1= 1dan 𝑥2= 2. 2.5 Kompleksitas
Definisi 12 (Kompleksitas)
Fungsi kompleksitas waktu 𝑓(𝑛) adalah fungsi yang mengukur banyak operasi dalam suatu algoritme yang mempunyai variabel input n.
III HASIL DAN PEMBAHASAN
3.1 Kondisi Optimal
Berdasarkan teorema dualitas, mencari solusi optimal dari masalah primal (P) dan masalah dual (D) sama halnya dengan menyelesaikan sistem
𝐀𝐱 = 𝐛, 𝐱 ≥ 𝟎 𝐀𝐓𝐲 + 𝐬 = 𝐜, 𝐬 ≥ 𝟎
𝐱𝐬 = 𝟎. dengan xs adalah Hadamard product.
Sistem (1) merupakan kondisi optimal untuk masalah optimasi linear. Baris pertama merupakan kendala fisibel masalah primal (P) dan baris kedua merupakan kendala fisibel masalah dual (D). Sedangkan baris ketiga disebut dengan kondisi pelengkap.
3.2 Central Path
Central path merupakan aspek penting
dari metode interior, yang akan membantu dalam membangun suatu algoritme umum untuk metode primal-dual. Secara geometrik,
central path merupakan kurva analitik yang
konvergen menuju solusi optimal. Untuk menyelesaikan sistem (1) kondisi pelengkap diubah menjadi xs = µe. Dengan,
µ adalah bilangan positif dan e adalah vektor
semua satu. Kendala baru ini disebut kondisi pemusatan. Sistem yang dihasilkan adalah
𝐀𝐱 = 𝐛, 𝐱 ≥ 𝟎 𝐀T𝐲 + 𝐬 = 𝐜, 𝐬 ≥ 𝟎
𝐱𝐬 = 𝜇𝐞. Solusi dari sistem (2) dinotasikan dengan
x(µ), y(µ), dan s(µ). x(µ) disebut µ-center
dari (P) dan (y(µ), s(µ)) disebut µ-center dari (D).
Himpunan semua x(µ) disebut central
path dari (P), demikian pula himpunan semua
(y(µ), s(µ)) disebut central path dari (D). Ketika µ berjalan menuju nol, maka x(µ),
y(µ), dan s(µ) konvergen ke solusi optimal
dari (P) dan (D).
3.3 Langkah Full-Newton
Langkah full-Newton merupakan metode yang dapat digunakan untuk mencari solusi pendekatan sistem (2). Diberikan pasangan fisibel primal-dual (x,(y,s)), kita ingin mencari ∆𝐱, ∆𝐲, dan ∆𝐬 sehingga
𝐱+ = 𝐱 + ∆𝐱,
𝐲+ = 𝐲 + ∆𝐲,
𝐬+ = 𝐬 + ∆𝐬.
memenuhi sistem (2), dengan kata lain 𝐀 𝐱 + ∆𝐱 = 𝐛, 𝐀T 𝐲 + ∆𝐲 + 𝐬 + ∆𝐬 = 𝐜,
𝐱 + ∆𝐱 𝐬 + ∆𝐬 = 𝜇𝐞. Dari sistem (3) diperoleh sistem baru sebagai berikut
𝐀∆𝐱 = 𝐛 – 𝐀𝐱, 𝐀T∆𝐲 + ∆𝐬 = 𝐜 – 𝐀T𝐲 – 𝐬,
𝐬∆𝐱 + 𝐱∆𝐬 + ∆𝐱∆𝐬 = 𝜇𝐞 − 𝐱𝐬. karena 𝐀𝐱 = 𝐛 dan 𝐀T𝐲 + 𝐬 = 𝐜, maka sistem berikut setara dengan sistem (4)
𝐀∆𝐱 = 𝟎, 𝐀T∆𝐲 + ∆𝐬 = 𝟎,
𝐬∆𝐱 + 𝐱∆𝐬 + ∆𝐱∆𝐬 = 𝜇𝐞 – 𝐱𝐬. Untuk mencari solusi sistem (5) digunakan metode Newton. Persamaan pertama dan persamaan kedua pada sistem (5) merupakan persamaan linear. Sedangkan, persamaan ketiga merupakan persamaan taklinear karena mengandung faktor kuadratik ∆𝐱∆𝐬. Untuk menyelesaikan sistem (5), persamaan ketiga dilinearkan dengan menggunakan metode Newton, sebagai berikut
s∆x + x∆s + ∆𝐱∆𝐬 = µe – xs 𝑠1 𝑠2 ⋮ 𝑠𝑛 ∆𝑥1 ∆𝑥2 ⋮ ∆𝑥𝑛 + 𝑥1 𝑥2 ⋮ 𝑥𝑛 ∆𝑠1 ∆𝑠2 ⋮ ∆𝑠𝑛 + ∆𝑥1 ∆𝑥2 ⋮ ∆𝑥𝑛 ∆𝑠1 ∆𝑠2 ⋮ ∆𝑠𝑛 - 𝜇 1 1 ⋮ 1 + 𝑥1 𝑥2 ⋮ 𝑥𝑛 𝑠1 𝑠2 ⋮ 𝑠𝑛 = 0 0 ⋮ 0 (2) (3) (4) (1) (5)
6
𝑠1∆𝑥1+ 𝑥1∆𝑠1+ ∆𝑥1∆𝑠1− 𝜇 + 𝑥1𝑠1= 0
𝑠2∆𝑥2+ 𝑥2∆𝑠2+ ∆𝑥2∆𝑠2− 𝜇 + 𝑥2𝑠2= 0
⋮
𝑠𝑛∆𝑥𝑛+ 𝑥𝑛∆𝑠𝑛+ ∆𝑥𝑛∆𝑠𝑛− 𝜇 + 𝑥𝑛𝑠𝑛 = 0
Misalnya, dilakukan pelinearan pada persamaan pertama sebagai berikut
𝑓1 ∆𝑥1, ∆𝑠1 ≈ 𝑓1 ∆𝑥1.0, ∆𝑠1.0 + 𝜕𝑓1 ∆𝑥𝜕∆𝑥1.0,∆𝑠1.0
1 ∆𝑥1− ∆𝑥1.0 +
𝜕𝑓1 ∆𝑥1.0,∆𝑠1.0
𝜕∆𝑠1 ∆𝑠1− ∆𝑠1.0 = 0,
dengan hampiran awal ∆𝑥1.0= ∆𝑠1.0= 0, sehingga diperoleh
𝑓1 0,0 + 𝜕𝑓1 0, 0 𝜕∆𝑥1 ∆𝑥1− 0 + 𝜕𝑓1 0,0 𝜕∆𝑠1 ∆𝑠1− 0 = 0 −𝜇 + 𝑥1𝑠1+ 𝑠1∆𝑥1+ 𝑥1∆𝑠1= 0 𝑠1∆𝑥1+ 𝑥1∆𝑠1= 𝜇 − 𝑥1𝑠1
Untuk persamaan kedua sampai dengan ke-n dilakukan pelinearan dengan cara yang sama, sehingga diperoleh
𝑠1∆𝑥1+ 𝑥1∆𝑠1− 𝜇 + 𝑥1𝑠1= 0
𝑠2∆𝑥2+ 𝑥2∆𝑠2− 𝜇 + 𝑥2𝑠2= 0
⋮
𝑠𝑛∆𝑥𝑛+ 𝑥𝑛∆𝑠𝑛− 𝜇 + 𝑥𝑛𝑠𝑛 = 0
Dapat juga ditulis 𝑠1 𝑠2 ⋮ 𝑠𝑛 ∆𝑥1 ∆𝑥2 ⋮ ∆𝑥𝑛 + 𝑥1 𝑥2 ⋮ 𝑥𝑛 ∆𝑠1 ∆𝑠2 ⋮ ∆𝑠𝑛 - 𝜇 1 1 ⋮ 1 + 𝑥1 𝑥2 ⋮ 𝑥𝑛 𝑠1 𝑠2 ⋮ 𝑠𝑛 = 0 0 ⋮ 0 s∆𝐱 + 𝐱∆𝐬 − 𝜇𝐞 + 𝐱𝐬 = 𝟎
Sehingga diperoleh persamaan baru yang merupakan persamaan linear, sebagai berikut
𝐀∆𝐱 = 𝟎 𝐀T∆𝐲 + ∆𝐬 = 𝟎
𝐬∆𝐱 + 𝐱∆𝐬 = 𝜇𝐞 – 𝐱𝐬
Sistem (6) dapat dinyatakan dalam bentuk matriks SPL sebagai berikut
𝐀 0 0 0 𝐀𝐓 1 𝐒 0 𝐗 ∆𝐱∆𝐲 ∆𝐬 = 00 𝜇𝐞 − 𝐱𝐬 Dengan X = diag (x) dan S = diag (s). Solusi ∆𝐱, ∆𝐲, dan ∆𝐬 dinamakan primal-dual langkah Newton. Dengan langkah
full-Newton diperoleh
𝐱+ = 𝐱 + ∆𝐱,
𝐲+ = 𝐲 + ∆𝐲,
𝐬+ = 𝐬 + ∆𝐬.
3.4 Ukuran Kedekatan
Pada proses mengikuti central path menuju solusi optimal dengan menggunakan langkah full-Newton, dihasilkan barisan titik-titik yang berada di sekitar central path. Diperlukan suatu ukuran untuk mengukur kedekatan (𝐱, (𝐲, 𝐬)) ke 𝜇-center dan central
path. Sebelum mendefinisikan ukuran kedekatan, terlebih dahulu merumuskan sistem linear (6) yang mendefinisikan arah Newton dalam kasus primal-dual. Untuk tujuan ini, kita definisikan vektor sebagai berikut
𝐝
x = 𝐮 ∆𝐱 𝐱,
𝐝
s = 𝐮 ∆𝐬 𝐬,
𝐝
y = ∆𝐲 𝜇 dengan 𝐮:=
𝐱𝐬 𝜇 (6)7
jika didefinisikan
𝑫 = diag
𝐱𝐬 maka sistem (6) setara dengan𝑨𝑫𝐝x = 𝟎
𝑨𝑫 T𝐝
y+ 𝐝s = 𝟎
𝐝x+ 𝐝s= 𝐮−1− 𝐮 Bukti :
(i)
Persamaan pertamaAD𝐝x = 0 AD 𝐮 ∆𝐱 𝐱 = 0 AD 𝐱𝐬 𝜇 ∆𝐱 𝐱 = 0 AD 𝐬 𝐱 ∆𝐱 𝜇 = 0 A 𝑥1s1 0 … 0 0 𝑥2𝑠2 0 ⋮ ⋮ … ⋱ ⋮ 0 … … 𝑥𝑛𝑠𝑛 𝑥1𝑠1 ∆𝑥1 𝑠2 𝑥2 ∆𝑥2 ⋮ 𝑠𝑛 𝑥𝑛 ∆𝑥𝑛 𝜇 = 0 𝐀 ∆𝑥1 ∆𝑥2 ⋮ ∆𝑥𝑛 𝜇 = 𝟎 𝐀 ∆𝐱 = 𝟎
Jadi, persamaan pertama terbukti.∎ (ii) Persamaan kedua
𝐀T∆𝐲 + ∆𝐬 = 𝟎 𝐀T𝐝 y 𝜇 + 𝐝s 𝐬 𝐮= 𝟎 𝐀T𝐝 y 𝜇 + 𝐝s 𝐬 𝐱𝐬 𝜇 = 𝟎 𝐀T𝐝 y 𝜇 + 𝐝s 𝐬𝜇 𝐱 = 𝟎 𝜇 𝐀T𝐝 y+ 𝐝s 𝐬 𝐱 = 𝟎 𝑫T 𝐀T𝐝 y+ 𝐝s 𝐬 𝐱 = 𝑫T𝟎 𝑫T𝐀T𝐝 y+ 𝐝s= 𝟎 𝐀𝑫 T𝐝 y+ 𝐝s = 𝟎
Jadi, persamaan kedua terbukti.∎ (iii) Persamaan ketiga
Ruas kiri 𝐬∆𝐱 + 𝐱∆𝐬 = s 𝜇 𝐝x d + x 𝜇 𝐝s 𝐝−1 = 𝜇 (𝐬𝐝𝐝x + x𝐝−1𝐝s) = 𝜇 (𝐮 𝜇𝐝−1𝐝𝐝x+ 𝐮 𝜇𝐝𝐝−1𝐝s) = 𝜇𝐮 (𝐝x+ 𝐝s) Ruas kanan 𝜇𝐞 − 𝐱𝐬 = 𝜇𝐞 − 𝐮 𝜇 𝐝 (𝐮 𝜇𝐝−1) = 𝜇𝐞 − 𝐮2𝜇𝐝𝐝−1 = 𝜇𝐞 − 𝐮2𝜇 = 𝜇𝐮𝐮−1− 𝜇𝐮2 = 𝜇𝐮 𝐮−1− 𝐮 𝐬∆𝐱 + 𝐱∆𝐬 = 𝜇𝐞 − 𝐱𝐬 𝜇𝐮(𝐝x+ 𝐝s) = 𝜇𝐮 𝐮−1− 𝐮 𝐝x+ 𝐝s = 𝐮−1− 𝐮
Jadi, persamaan ketiga terbukti.∎
Persamaan dari sistem (6) menunjukkan bahwa vektor 𝐝x dan 𝐝s adalah ruang nol dan
ruang baris dari matriks AD, ini berarti 𝐝x
dan 𝐝s ortogonal. Ortogonalitas dari 𝐝x dan
𝐝s mengimplikasikan bahwa
𝐝x 2+ 𝐝s 2= 𝐝x+ 𝐝s 2
= 𝐮−1− 𝐮 2
Perhatikan bahwa 𝐝x, 𝐝s dan 𝐝y adalah nol
jika dan hanya jika 𝐮−1− 𝐮 = 𝟎. Untuk mengukur jarak (x, (y, s)) ke 𝜇-center, di-gunakan ukuran 𝛿 𝐱, 𝐬; 𝜇 yang didefinisi-kan sebagai berikut
𝛿 𝐱, 𝐬; 𝜇 := 12 𝐮−1− 𝐮 := 1 2
𝜇 𝐱 𝐬
−
𝐱 𝐬 𝜇(Roos et al. 2006) 3.5 Kompleksitas Algoritme
Selanjutnya akan dibahas mengenai kompleksitas algoritme dari metode interior primal-dual dengan langkah full-Newton. Berikut ini adalah algoritmenya
Langkah 1. Pilih nilai awal
parameter akurasi 𝜀 > 0; parameter pendekatan 𝜏, 0 ≤ 𝜏 < 1;
8
strictly fisibel (𝐱0, 𝐲0, 𝐬0) dengan (𝐱0)T𝐬0= 𝑛𝜇0dan
𝛿(𝐱0, 𝐬0; 𝜇0) ≤ 𝜏;
parameter barrier 𝜃, 0 < 𝜃 < 1. Didefinisikan 𝐱 ≔ 𝐱0; 𝐬 ≔ 𝐬0;
𝐲 ≔ 𝐲0; 𝜇 ≔ 𝜇0;
Dengan penghitung iterasi awal 𝑘 = 0.
Langkah 2. Selama 𝑛𝜇 ≥ 𝜀 lanjut ke langkah 4
Langkah 3. Selainnya, STOP.
Langkah 4. Lakukan pencarian solusi baru 𝜇𝑘+1 = (1 − 𝜃)𝑘+1𝜇0
𝐱𝑘+1 = 𝐱𝑘 + ∆𝐱
𝐲𝑘+1 = 𝐲𝑘 + ∆𝐲
𝐬𝑘+1 = 𝐬𝑘 + ∆𝐬
Langkah 5. 𝑘 = 𝑘 + 1, kembali ke langkah 2
Lema 1
Jika langkah Newton primal-dual adalah fisibel maka (𝐱+)T𝐬+= 𝑛𝜇.
(Roos et al. 2006)
Bukti : lihat Roos
Vektor 𝐱+ dan 𝐬+ merupakan langkah
full-Newton primal-dual dan n adalah banyaknya
pertidaksamaan dari masalah primal-dual.
Lema 2
Metode interior primal-dual dengan langkah
full-Newton memiliki jumlah iterasi tidak
lebih dari
1 𝜃ln
𝑛𝜇0
𝜀
dan iterasi akan berhenti pada saat 𝑛𝜇 ≤ 𝜀. (Silalahi 2011)
Bukti :
Awalnya duality gap adalah n𝜇0, sehingga
dengan menggunakan Lema 1 diperoleh (𝐱0)T𝐬0= n𝜇0
Pada saat iterasi bertambah maka nilai 𝜇 dikalikan dengan faktor 1 − 𝜃 sebagai berikut
𝜇+= (1 − 𝜃)𝜇
Untuk iterasi pertama diperoleh (𝐱1)T𝐬1= (1 − 𝜃) n𝜇0
Untuk iterasi ke-k diperoleh (𝐱𝑘)T𝐬𝑘= (1 − 𝜃)𝑘 n𝜇0
Oleh karena itu, setelah iterasi ke-k duality
gap lebih kecil dari 𝜀 jika :
(1 − 𝜃)𝑘 n𝜇0 ≤ 𝜀
Dengan menggunakan logaritma maka di-peroleh
𝑘 ln 1 − 𝜃 + ln 𝑛𝜇0 ≤ ln 𝜀
−𝑘 ln 1 − 𝜃 − ln 𝑛𝜇0 ≥ − ln 𝜀
𝑘 (−ln 1 − 𝜃 ) − ln 𝑛𝜇0 ≥ − ln 𝜀
Karena – ln 1 − 𝜃 ≥ 𝜃, maka pertidaksamaan diatas tetap terpenuhi jika 𝑘𝜃 − ln 𝑛𝜇0 ≥ − ln 𝜀 𝑘𝜃 ≥ ln 𝑛𝜇0 − ln 𝜀 𝑘 ≥ 1 𝜃 (ln 𝑛𝜇0 − ln 𝜀 ) = 1 𝜃ln 𝑛𝜇0 𝜀 Jadi, Lema 2 terbukti.∎
Lema berikut ini memperlihatkan efek dari langkah Newton primal-dual.
Lema 3
Misal (𝐱, 𝐬) adalah pasangan primal-dual positif dan 𝜇 > 0 sedemikian rupa sehingga 𝐱T𝐬 = 𝑛𝜇.
Selanjutnya, jika 𝛿 ∶= 𝛿(𝐱, 𝐬; 𝜇) dan 𝜇+= (1 − 𝜃)𝜇 maka 𝛿(𝐱, 𝐬; 𝜇+)2 = 1 − 𝜃 𝛿2 + 𝜃2𝑛 4(1−𝜃) (Silalahi 2011) Bukti : Didefinisikan 𝛿+≔ 𝛿(𝐱, 𝐬; 𝜇+) dan 𝐮 = 𝐱 𝐬
𝜇 , maka dapat dituliskan
(𝛿+)2 = 1 2 (𝐮+)−1− 𝐮+ 2 = 14 (𝐮+)−1− 𝐮+ 2 Karena 𝐮+= 𝐱 𝐬 𝜇+ , diperoleh
9
𝐮
+=
𝐱 𝐬 𝜇+=
𝐱 𝐬 (1−𝜃)𝜇=
𝐱 𝐬 𝜇 1 1−𝜃=
𝐮 1−𝜃 (𝐮+)−1= 1 − 𝜃 𝐮 Sehingga diperoleh 𝛿+ 2= 1 4 1 − 𝜃 𝐮 − 𝐮 1 − 𝜃 2 =1 4 1 − 𝜃 𝐮−1− 𝐮 1 − 𝜃 2 =1 4 1 − 𝜃 𝐮−1− 𝐮 1 − 𝜃− 𝜃𝐮 1 − 𝜃+ 𝜃𝐮 1 − 𝜃 2 = 1 4 1 − 𝜃 𝐮−1− 𝐮 − 𝜃𝐮 1 − 𝜃+ 𝜃𝐮 1 − 𝜃 2 = 1 4 1 − 𝜃 𝐮−1− (1 − 𝜃)𝐮 1 − 𝜃 + 𝜃𝐮 1 − 𝜃 2 = 1 4 1 − 𝜃 𝐮−1− (1 − 𝜃)𝐮 1 − 𝜃 + 𝜃𝐮 1 − 𝜃 2 = 1 4 1 − 𝜃 (𝐮−1− 𝐮) 1 − 𝜃 + 𝜃𝐮 1 − 𝜃 2 = 1 4 1 − 𝜃 (𝐮−1− 𝐮) + 𝜃𝐮 1 − 𝜃 2Dari 𝐱T𝐬 = 𝑛𝜇 diperoleh 𝐮 2= 𝑛, seperti berikut
𝐮 2= 𝐮T𝐮 2= 𝐮T𝐮 = 𝑥1 𝑠1 𝜇 𝑥2𝑠2 𝜇 … 𝑥𝑛𝑠𝑛 𝜇 𝑥1𝑠1 𝜇 𝑥2𝑠2 𝜇 ⋮ 𝑥𝑛𝑠𝑛 𝜇 = 𝑥1𝑠1 𝜇 + 𝑥2𝑠2 𝜇 + ⋯ + 𝑥𝑛𝑠𝑛 𝜇 = 𝐱T𝐬 𝜇 = 𝑛 kemudian, 𝐮T𝐮−1= 𝑥1𝑠1 𝜇 𝑥2𝑠2 𝜇 ⋯ 𝑥𝑛𝑠𝑛 𝜇 𝜇 𝑥1𝑠1 𝜇 𝑥2𝑠2 ⋮ 𝜇 𝑥𝑛𝑠𝑛 = 1 + 1 + ⋯ + 1 = 𝑛. 1 = 𝑛 selanjutnya, 𝐮T 𝐮−1− 𝐮 = 𝐮T𝐮−1− 𝐮T𝐮 = 𝑛 − 𝐮 2= 𝑛 − 𝑛 = 0
Jadi u ortogonal terhadap 𝐮−1− 𝐮. Akibatnya,
(𝛿+)2= 1 − 𝜃
4 𝐮−1− 𝐮 2+
𝜃2 𝐮 2
10
Karena 𝐮−1− 𝐮 = 2𝛿 dan 𝐮 2= 𝑛, diperoleh
(𝛿+)2= 1 − 𝜃 𝛿2+ 𝜃2𝑛
4(1 − 𝜃) Jadi, Lema 3 terbukti.∎
Untuk menjamin nilai 𝛿 pada Lema 3 maka diperlukan Lema 4 dan akibat 1 sebagai berikut
Lema 4
Jika 𝛿 ≔ 𝛿(𝐱, 𝐬; 𝜇) ≤ 1, maka langkah Newton primal-dual fisibel yaitu 𝐱+ dan 𝐬+ taknegatif. Selain itu, jika 𝛿 < 1 maka 𝐱+ dan
𝐬+ positif dan
𝛿(𝐱+, 𝐬+; 𝜇) ≤ 𝛿2
2(1 − 𝛿2)
(Roos et al. 2006)
Bukti : lihat Roos Akibat 1
Jika 𝛿 ∶= 𝛿 𝐱, 𝐬; 𝜇 ≤ 21 , maka 𝛿 𝐱+, 𝐬+; 𝜇 ≤ 𝛿2.
(Silalahi 2011)
Teorema berikut ini adalah batas atas iterasi untuk metode interior primal-dual dengan langkah full-Newton. Teorema 2 Jika 𝜏 = 1 2 dan 𝜃 = 1 𝑛+1, maka jumlah
iterasi tidak lebih dari 𝑛 + 1 ln𝑛𝜇0
𝜀
Output dari primal-dual pasangan (x, s) yaitu 𝐱T𝐬 ≤ 𝜀.
(Silalahi 2011)
Bukti :
Misalkan dipilih 𝜏 = 1
2. Dengan
meng-gunakan akibat 1 yaitu 𝛿 𝐱, 𝐬; 𝜇 ≤ 21, maka setelah langkah Newton primal-dual diperoleh 𝛿 𝐱+, 𝐬+; 𝜇 ≤1
2. Setelah iterasinya ber-
tambah, nilai 𝜇 menjadi 𝜇+= (1 − 𝜃)𝜇. Dengan mengambil nilai 𝜃 = 1
𝑛+1, diperoleh 𝛿 𝐱+, 𝐬+; 𝜇+ 2 sebagai berikut 𝛿 𝐱+, 𝐬+; 𝜇+ 2 ≤ 1 − 𝜃 4 + 𝜃2𝑛 4 1 − 𝜃 = 1 − 𝜃 2+ 𝜃2𝑛 4 1 − 𝜃 = 𝜃2− 2𝜃 + 1 + 𝜃2𝑛 4 1 − 𝜃 = 1 𝑛 + 1 − 𝑛 + 12 + 1 +𝑛 + 1𝑛 4 1 − 1 𝑛 + 1 = 𝑛 + 1 𝑛 + 1 − 𝑛 + 12 + 1 4 1 − 1 𝑛 + 1 = 1 − 2 𝑛 + 1+ 1 4 1 − 1 𝑛 + 1 = 2 − 2 𝑛 + 1 4 1 − 1 𝑛 + 1 = 2 1 − 1 𝑛 + 1 4 1 − 1 𝑛 + 1 = 2 4= 1 2
Dari penyelesaian di atas diperoleh 𝛿 𝐱+, 𝐬+; 𝜇+ 2≤ 1
2= 𝜏. Ini berarti bahwa
𝛿(𝐱, 𝐬; 𝜇) ≤ 𝜏 tetap dipertahankan pada setiap iterasi. Dengan menggabungkan penjelasan di
atas dengan Lema 2 maka diperoleh Teorema 2.
IV STUDI KASUS
Untuk studi kasus pada metode interior digunakan masalah Klee-Minty dengan
𝜌 =
13 dan 𝑦0 = 0 yang diberikan oleh :
Minimumkan 𝑦𝑚,
Kendala 13𝑦𝑘−1 ≤ 𝑦𝑘≤ 1 −13𝑦𝑘−1
𝑘 = 1, … , 𝑚
Dengan 𝑛 menyatakan banyaknya pertidaksamaan dan 𝑚 menyatakan banyaknya variabel.
1) Pada saat 𝑛 = 4 dan 𝑚 = 2 Maksimumkan −𝑦2 Dengan kendala 𝑦1≤ 1 −𝑦1≤ 0 1 3 𝑦1− 𝑦2≤ 0 13 𝑦1+ 𝑦2≤ 1
Dengan menggunakan software
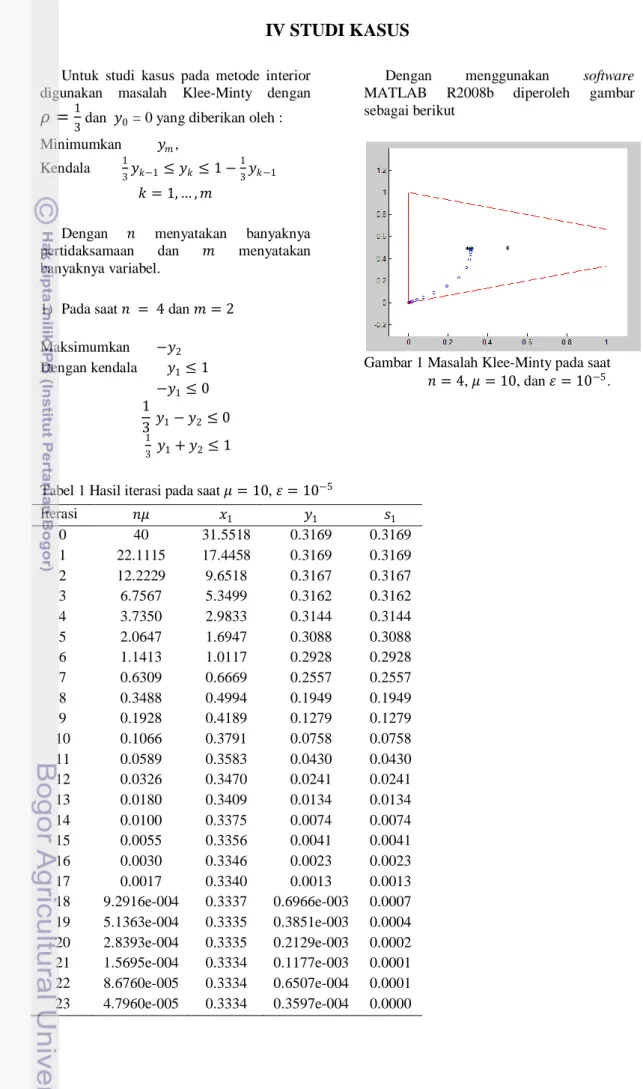
MATLAB R2008b diperoleh gambar sebagai berikut
Gambar 1 Masalah Klee-Minty pada saat 𝑛 = 4, 𝜇 = 10, dan 𝜀 = 10−5.
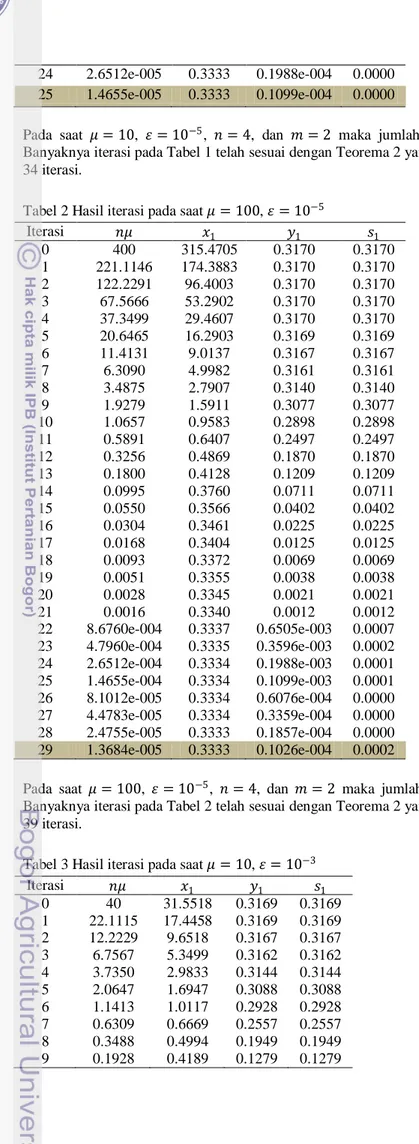
Tabel 1 Hasil iterasi pada saat 𝜇 = 10, 𝜀 = 10−5
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 40 31.5518 0.3169 0.3169 1 22.1115 17.4458 0.3169 0.3169 2 12.2229 9.6518 0.3167 0.3167 3 6.7567 5.3499 0.3162 0.3162 4 3.7350 2.9833 0.3144 0.3144 5 2.0647 1.6947 0.3088 0.3088 6 1.1413 1.0117 0.2928 0.2928 7 0.6309 0.6669 0.2557 0.2557 8 0.3488 0.4994 0.1949 0.1949 9 0.1928 0.4189 0.1279 0.1279 10 0.1066 0.3791 0.0758 0.0758 11 0.0589 0.3583 0.0430 0.0430 12 0.0326 0.3470 0.0241 0.0241 13 0.0180 0.3409 0.0134 0.0134 14 0.0100 0.3375 0.0074 0.0074 15 0.0055 0.3356 0.0041 0.0041 16 0.0030 0.3346 0.0023 0.0023 17 0.0017 0.3340 0.0013 0.0013 18 9.2916e-004 0.3337 0.6966e-003 0.0007 19 5.1363e-004 0.3335 0.3851e-003 0.0004 20 2.8393e-004 0.3335 0.2129e-003 0.0002 21 1.5695e-004 0.3334 0.1177e-003 0.0001 22 8.6760e-005 0.3334 0.6507e-004 0.0001 23 4.7960e-005 0.3334 0.3597e-004 0.0000
12
Pada saat 𝜇 = 10, 𝜀 = 10−5, 𝑛 = 4, dan 𝑚 = 2 maka jumlah iterasinya sebanyak 25 iterasi. Banyaknya iterasi pada Tabel 1 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 34 iterasi.
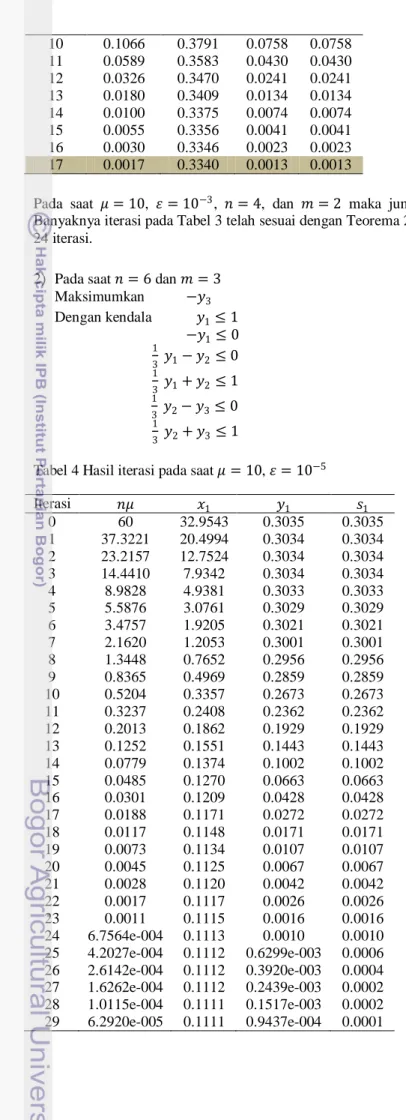
Tabel 2 Hasil iterasi pada saat 𝜇 = 100, 𝜀 = 10−5
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 400 315.4705 0.3170 0.3170 1 221.1146 174.3883 0.3170 0.3170 2 122.2291 96.4003 0.3170 0.3170 3 67.5666 53.2902 0.3170 0.3170 4 37.3499 29.4607 0.3170 0.3170 5 20.6465 16.2903 0.3169 0.3169 6 11.4131 9.0137 0.3167 0.3167 7 6.3090 4.9982 0.3161 0.3161 8 3.4875 2.7907 0.3140 0.3140 9 1.9279 1.5911 0.3077 0.3077 10 1.0657 0.9583 0.2898 0.2898 11 0.5891 0.6407 0.2497 0.2497 12 0.3256 0.4869 0.1870 0.1870 13 0.1800 0.4128 0.1209 0.1209 14 0.0995 0.3760 0.0711 0.0711 15 0.0550 0.3566 0.0402 0.0402 16 0.0304 0.3461 0.0225 0.0225 17 0.0168 0.3404 0.0125 0.0125 18 0.0093 0.3372 0.0069 0.0069 19 0.0051 0.3355 0.0038 0.0038 20 0.0028 0.3345 0.0021 0.0021 21 0.0016 0.3340 0.0012 0.0012 22 8.6760e-004 0.3337 0.6505e-003 0.0007 23 4.7960e-004 0.3335 0.3596e-003 0.0002 24 2.6512e-004 0.3334 0.1988e-003 0.0001 25 1.4655e-004 0.3334 0.1099e-003 0.0001 26 8.1012e-005 0.3334 0.6076e-004 0.0000 27 4.4783e-005 0.3334 0.3359e-004 0.0000 28 2.4755e-005 0.3333 0.1857e-004 0.0000 29 1.3684e-005 0.3333 0.1026e-004 0.0002
Pada saat 𝜇 = 100, 𝜀 = 10−5, 𝑛 = 4, dan 𝑚 = 2 maka jumlah iterasinya sebanyak 29 iterasi. Banyaknya iterasi pada Tabel 2 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 39 iterasi.
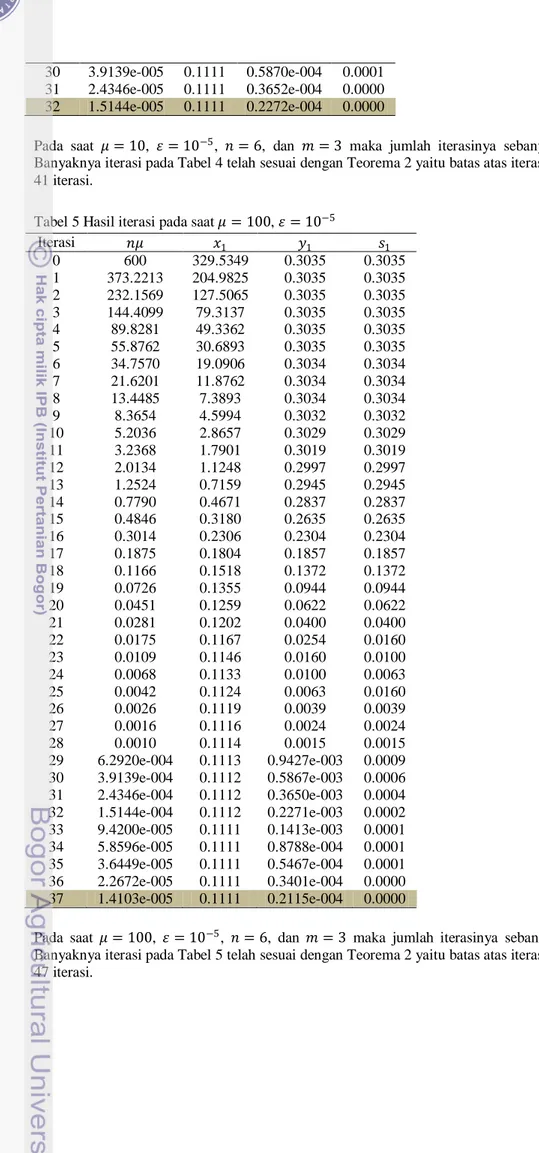
Tabel 3 Hasil iterasi pada saat 𝜇 = 10, 𝜀 = 10−3
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 40 31.5518 0.3169 0.3169 1 22.1115 17.4458 0.3169 0.3169 2 12.2229 9.6518 0.3167 0.3167 3 6.7567 5.3499 0.3162 0.3162 4 3.7350 2.9833 0.3144 0.3144 5 2.0647 1.6947 0.3088 0.3088 6 1.1413 1.0117 0.2928 0.2928 7 0.6309 0.6669 0.2557 0.2557 8 0.3488 0.4994 0.1949 0.1949 9 0.1928 0.4189 0.1279 0.1279 24 2.6512e-005 0.3333 0.1988e-004 0.0000 25 1.4655e-005 0.3333 0.1099e-004 0.0000
13 10 0.1066 0.3791 0.0758 0.0758 11 0.0589 0.3583 0.0430 0.0430 12 0.0326 0.3470 0.0241 0.0241 13 0.0180 0.3409 0.0134 0.0134 14 0.0100 0.3375 0.0074 0.0074 15 0.0055 0.3356 0.0041 0.0041 16 0.0030 0.3346 0.0023 0.0023 17 0.0017 0.3340 0.0013 0.0013
Pada saat 𝜇 = 10, 𝜀 = 10−3, 𝑛 = 4, dan 𝑚 = 2 maka jumlah iterasinya sebanyak 17 iterasi. Banyaknya iterasi pada Tabel 3 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 24 iterasi.
2) Pada saat 𝑛 = 6 dan 𝑚 = 3 Maksimumkan −𝑦3 Dengan kendala 𝑦1≤ 1 −𝑦1≤ 0 13 𝑦1− 𝑦2≤ 0 13 𝑦1+ 𝑦2≤ 1 13 𝑦2− 𝑦3≤ 0 13 𝑦2+ 𝑦3≤ 1
Tabel 4 Hasil iterasi pada saat 𝜇 = 10, 𝜀 = 10−5
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 60 32.9543 0.3035 0.3035 1 37.3221 20.4994 0.3034 0.3034 2 23.2157 12.7524 0.3034 0.3034 3 14.4410 7.9342 0.3034 0.3034 4 8.9828 4.9381 0.3033 0.3033 5 5.5876 3.0761 0.3029 0.3029 6 3.4757 1.9205 0.3021 0.3021 7 2.1620 1.2053 0.3001 0.3001 8 1.3448 0.7652 0.2956 0.2956 9 0.8365 0.4969 0.2859 0.2859 10 0.5204 0.3357 0.2673 0.2673 11 0.3237 0.2408 0.2362 0.2362 12 0.2013 0.1862 0.1929 0.1929 13 0.1252 0.1551 0.1443 0.1443 14 0.0779 0.1374 0.1002 0.1002 15 0.0485 0.1270 0.0663 0.0663 16 0.0301 0.1209 0.0428 0.0428 17 0.0188 0.1171 0.0272 0.0272 18 0.0117 0.1148 0.0171 0.0171 19 0.0073 0.1134 0.0107 0.0107 20 0.0045 0.1125 0.0067 0.0067 21 0.0028 0.1120 0.0042 0.0042 22 0.0017 0.1117 0.0026 0.0026 23 0.0011 0.1115 0.0016 0.0016 24 6.7564e-004 0.1113 0.0010 0.0010 25 4.2027e-004 0.1112 0.6299e-003 0.0006 26 2.6142e-004 0.1112 0.3920e-003 0.0004 27 1.6262e-004 0.1112 0.2439e-003 0.0002 28 1.0115e-004 0.1111 0.1517e-003 0.0002 29 6.2920e-005 0.1111 0.9437e-004 0.0001
14
30 3.9139e-005 0.1111 0.5870e-004 0.0001 31 2.4346e-005 0.1111 0.3652e-004 0.0000 32 1.5144e-005 0.1111 0.2272e-004 0.0000
Pada saat 𝜇 = 10, 𝜀 = 10−5, 𝑛 = 6, dan 𝑚 = 3 maka jumlah iterasinya sebanyak 32 iterasi. Banyaknya iterasi pada Tabel 4 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 41 iterasi.
Tabel 5 Hasil iterasi pada saat 𝜇 = 100, 𝜀 = 10−5
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 600 329.5349 0.3035 0.3035 1 373.2213 204.9825 0.3035 0.3035 2 232.1569 127.5065 0.3035 0.3035 3 144.4099 79.3137 0.3035 0.3035 4 89.8281 49.3362 0.3035 0.3035 5 55.8762 30.6893 0.3035 0.3035 6 34.7570 19.0906 0.3034 0.3034 7 21.6201 11.8762 0.3034 0.3034 8 13.4485 7.3893 0.3034 0.3034 9 8.3654 4.5994 0.3032 0.3032 10 5.2036 2.8657 0.3029 0.3029 11 3.2368 1.7901 0.3019 0.3019 12 2.0134 1.1248 0.2997 0.2997 13 1.2524 0.7159 0.2945 0.2945 14 0.7790 0.4671 0.2837 0.2837 15 0.4846 0.3180 0.2635 0.2635 16 0.3014 0.2306 0.2304 0.2304 17 0.1875 0.1804 0.1857 0.1857 18 0.1166 0.1518 0.1372 0.1372 19 0.0726 0.1355 0.0944 0.0944 20 0.0451 0.1259 0.0622 0.0622 21 0.0281 0.1202 0.0400 0.0400 22 0.0175 0.1167 0.0254 0.0160 23 0.0109 0.1146 0.0160 0.0100 24 0.0068 0.1133 0.0100 0.0063 25 0.0042 0.1124 0.0063 0.0160 26 0.0026 0.1119 0.0039 0.0039 27 0.0016 0.1116 0.0024 0.0024 28 0.0010 0.1114 0.0015 0.0015 29 6.2920e-004 0.1113 0.9427e-003 0.0009 30 3.9139e-004 0.1112 0.5867e-003 0.0006 31 2.4346e-004 0.1112 0.3650e-003 0.0004 32 1.5144e-004 0.1112 0.2271e-003 0.0002 33 9.4200e-005 0.1111 0.1413e-003 0.0001 34 5.8596e-005 0.1111 0.8788e-004 0.0001 35 3.6449e-005 0.1111 0.5467e-004 0.0001 36 2.2672e-005 0.1111 0.3401e-004 0.0000 37 1.4103e-005 0.1111 0.2115e-004 0.0000
Pada saat 𝜇 = 100, 𝜀 = 10−5, 𝑛 = 6, dan 𝑚 = 3 maka jumlah iterasinya sebanyak 37 iterasi. Banyaknya iterasi pada Tabel 5 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 47 iterasi.
15
Tabel 6 Hasil iterasi pada saat 𝜇 = 10, 𝜀 = 10−3
Iterasi 𝑛𝜇 𝑥1 𝑦1 𝑠1 0 60 32.9543 0.3035 0.3035 1 37.3221 20.4994 0.3034 0.3034 2 23.2157 12.7524 0.3034 0.3034 3 14.4410 7.9342 0.3034 0.3034 4 8.9828 4.9381 0.3033 0.3033 5 5.5876 3.0761 0.3029 0.3029 6 3.4757 1.9205 0.3021 0.3021 7 2.1620 1.2053 0.3001 0.3001 8 1.3448 0.7652 0.2956 0.2956 9 0.8365 0.4969 0.2859 0.2859 10 0.5204 0.3357 0.2673 0.2673 11 0.3237 0.2408 0.2362 0.2362 12 0.2013 0.1862 0.1929 0.1929 13 0.1252 0.1551 0.1443 0.1443 14 0.0779 0.1374 0.1002 0.1002 15 0.0485 0.1270 0.0663 0.0663 16 0.0301 0.1209 0.0428 0.0428 17 0.0188 0.1171 0.0272 0.0272 18 0.0117 0.1148 0.0171 0.0171 19 0.0073 0.1134 0.0107 0.0107 20 0.0045 0.1125 0.0067 0.0067 21 0.0028 0.1120 0.0042 0.0042 22 0.0017 0.1117 0.0026 0.0026 23 0.0011 0.1115 0.0016 0.0016
Pada saat 𝜇 = 10, 𝜀 = 10−3, 𝑛 = 6, dan 𝑚 = 3 maka jumlah iterasinya sebanyak 23 iterasi. Banyaknya iterasi pada Tabel 6 telah sesuai dengan Teorema 2 yaitu batas atas iterasinya sebanyak 29 iterasi.
2
V SIMPULAN DAN SARAN
5.1 Simpulan
(i) Metode interior primal-dual dengan langkah full-Newton dapat digunakan untuk menyelesaikan masalah optimasi linear.
(ii) Dari hasil analisis kompleksitas algoritme interior primal-dual dengan langkah full-Newton diketahui bahwa banyaknya iterasi yang diperoleh tidak lebih dari 𝑛 + 1 log𝑛𝜇𝜀0 .
(iii) Dari hasil pengkajian dapat disimpulkan bahwa semakin besar nilai n dan 𝜇0 yang
diberikan, maka jumlah iterasinya semakin meningkat. Sedangkan, semakin
besar nilai 𝜀 maka jumlah iterasinya semakin sedikit. Banyaknya iterasi yang diperoleh pada masing-masing nilai n, 𝜇0, dan 𝜀 tidak lebih dari
𝑛 + 1 log𝑛𝜇𝜀0 .
5.2 Saran
Pada karya ilmiah ini telah dilakukakn analisis banyaknya iterasi untuk masalah optimasi linear dengan metode titik interior. Untuk penelitian lanjutan dapat dilakukan perbandingan banyaknya iterasi untuk kasus taklinear dengan metode titik interior.
DAFTAR PUSTAKA
Grimaldi RP. 2004. Discrete and Combinatorial Mathematics: An Applied Introduction. Ed ke-5. New York: Pearson.
Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Ed ke-5. Bondan A, Penerjemah; Hardani HW, Editor. Jakarta: Erlangga. Terjemahan dari Linear Algebra
with Aplications.
Mitchell JE, P.M. Pardalos and M.G.C. Resende. 1998. Interior Point Methods for
Combinatorial Optimization. Kluwer Academic Publishers.
Munir Rinaldi. 2003. Metode Numerik. Bandung: Informatika.
Ross C, Terlaky T, and Vial J-Ph. 2006.
Interior Point Methods for Linear Optimization. New York: Springer.
Silalahi BP. 2011. On the Central Path of
Redundant Klee-Minty Problems. PhD
thesis. Roos C (promotor). Delft University of Technology. The Netherlands: TU Delft.
Winston WL. 2004. Operation Research:
Applications and Algorithms. Ed ke-4.
2
18
Lampiran 1 Program untuk Fungsi Langkah Newton
function [x,y,s]= Newton_step(A,b,c,x,y,s,mu);
rb = b - A*x; rc = c - A'*y - s; v = sqrt(x.*s/mu); r = v.^(-1)-v; D = diag(sqrt(x./s)); AA=A*D; M=AA*AA'; rhs = rb/sqrt(mu)+AA*(diag(v./s)*rc - r); dy=M\rhs; Dy = sqrt(mu)*dy; ds = diag(v./s)*rc - AA'*dy; dx = r - ds; Dx = x.*dx./v; Ds = s.*ds./v; alpha = 1; x = x + alpha*Dx; y = y + alpha*Dy; s = s + alpha*Ds; return
19
Lampiran 2 Program untuk Kasus Dua Dimensi
function [A,b,c,x,y,s,mu,opt] = zigzag_Nematollahi(n) n=4 A=[-1 1 1/3 1/3; 0 0 -1 1] c=[0;1;0;1]; b=[0;-1]; figure(3) clf y = [0.5 0.5]'; s = c - A'*y mu = 10 % mu = 100
% hilangkan tanda persen jika digunakan
x = mu./s
figure(3)
axis([0 1 0 1])
line('color',[0 0 0],'linestyle','*','erase','none','xdata', y(1),'ydata',y(2),'markersize',5);
for i = 1:250,
[x,y,s] = Newton_step(A,b,c,x,y,s,mu);
line('color',[0 0 0], 'linestyle','*','erase','none','xdata', y(1),'ydata',y(2),'markersize',5);
end rb = A*x-b; rc = c - A'*y - s; [x s] x y x.*s mu=(x'*s)/(n); theta = 1/sqrt(5); % theta = 1/sqrt(n+1)
% nilai theta bergantung pada n
eps = 10^(-3);
% eps = 10^(-5)
% hilangkan tanda persen jika digunakan
figure(3)
line('color',[0 1 0],'linestyle','o','erase','none','xdata', y(1),'ydata',y(2),'markersize',2);
20 Lanjutan Lampiran 2 it=0 while n*mu>eps, nmu=n*mu mu = (1-theta)*mu x y s [x,y,s] = Newton_step(A,b,c,x,y,s,mu);
line('color',[0 0 1],'linestyle','o','erase','none','xdata', y(1),'ydata',y(2),'markersize',2);
it=it+1 end
line('color',[1 0 0],'linestyle','*','erase','none','xdata',y(1),
'ydata',y(2),'markersize',4);
axis([-0.3 0.3 0 1])
axis([-0.1 1.1 -0.3 1.4]) xx=[0 1 1 0 0]
yy=[0 1/3 2/3 1 0]
line('color',[1 0 0],'linestyle','-','erase','none','xdata',xx,
'ydata',yy,'markersize',4);
y
21
Lampiran 3 Program untuk Kasus Tiga Dimensi
function [A,b,c,x,y,s,mu,opt] = zigzag_Nematollahi(n) n=6 A=[-1 1 1/3 1/3 0 0; 0 0 -1 1 1/3 1/3; 0 0 0 0 -1 1] c=[0;1;0;1;0;1]; b=[0;0;-1]; figure(3) clf y = [0.5 0.5 0.5]'; s = c - A'*y mu =10 % mu = 100
% hilangkan tanda persen jika digunakan
x = mu./s
figure(3)
axis([0 1 0 1])
line('color',[0 0 0],'linestyle','*','erase','none','xdata', y(1),'ydata',y(2),'markersize',5);
for i = 1:250,
[x,y,s] = Newton_step(A,b,c,x,y,s,mu);
line('color',[0 0 0], 'linestyle','*','erase','none','xdata', y(1),'ydata',y(2),'markersize',5);
end rb = A*x-b; rc = c - A'*y - s; [x s] x y x.*s mu=(x'*s)/(n); theta = 1/sqrt(7); % theta = 1/sqrt(n+1)
% nilai theta bergantung pada n
eps = 10^(-3);
% eps = 10^(-5)
% hilangkan tanda persen jika digunakan
figure(3)
line('color',[0 1 0],'linestyle','o','erase','none','xdata',y(1),
22 Lanjutan Lampiran 3 it=0 while n*mu>eps, nmu=n*mu mu = (1-theta)*mu x y s [x,y,s] = Newton_step(A,b,c,x,y,s,mu);
line('color',[0 0 1],'linestyle','o','erase','none','xdata', y(1),'ydata',y(2),'markersize',2);
it=it+1
%pause(0.2) %end
end
line('color',[1 0 0],'linestyle','*','erase','none','xdata',y(1),
'ydata',y(2),'markersize',4);
axis([-0.3 0.3 0 1])
axis([-0.1 1.1 -0.3 1.4]) xx=[0 1 1 0 0]
yy=[0 1/3 2/3 1 0]
line('color',[1 0 0],'linestyle','-','erase','none','xdata',xx,
'ydata',yy,'markersize',4);
y