BAB III TURUNAN FUNGSI

BAB III TURUNAN FUNGSI

Standar Kompetensi

Mahasiswa memahami konsep turunan fungsi dan teknik-teknik yang dapat digunakan untuk menentukan turunan, baik fungsi eksplisit y  f(x) maupun fungsi implisit f(x,y)0.

Kompetensi Dasar

Setelah mempelajari pokok bahasan turunan fungsi, diharapkan mahasiswa:

1. Dapat menentukan turunan fungsi dengan menggunakan definisi turunan fungsi. 2. Dapat menentukan turunan fungsi dengan menggunakan teorema turunan. 3. Dapat menentukan turunan fungsi dengan menggunakan dalil rantai

4. Dapat menentukan turunan fungsi f(x,y)0dengan menggunakan kaidah diferensial.

5. Dapat menentukan turunan fungsi parametrik. 6. Dapat menentukan turunan fungsi trigonometri. 7. Dapat menentukan turunan fungsi siklometri. 8. Menentukan turunan ke-n fungsi y  f(x). 9. Menentukan turunan ke-n fungsi f(x,y)0.

Bab III buku ini memuat hal-hal pokok yang berkaitan dengan turunan fungsi, antara lain (1) pengertian dan sifat turunan, (2) aturan rantai, (3) turunan fungsi implisit dan parametrik, (4) turunan fungsi trigonometri dan siklometri, (5) turunan tingkat tinggi.

3.1 Pengertian dan Sifat Turunan

Pembahasan tentang turunan dalam tulisan ini dibedakan menjadi dua kelompok besar yaitu, turunan fungsi berbentuk y  f(x) dan fungsi berbentuk f(x,y)0. Pada pengembangan selanjutnya terdapat beberapa turunan fungsi, diantaranya adalah fungsi

Untuk lebih memudahkan pemahaman bagi pembaca, masalah pertama yang dibahas adalah turunan fungsi berbentuk y  f(x).

Perhatikan gambar berikut.

Gambar 3.1

Pada gambar 3.1 di atas, garis L menyinggung kurva y  f(x) di titik )),`

( , (x f x

P sedangkan garis L melalui titik ₁ (x,f(x))dan titik (xx,f(xx)). Jika x

 mendekati nol, maka garis L1 akan mendekati garis L, sehingga gradien garis L1 akan mendekati gradien garis L. Hal ini dapat dinyatakan dalam bentuk limit sebagai berikut: ) 1 ( ... ... ) ( ) ( lim lim 0 0 1 x x f x x f m m x L x L           . Misal

(

x





x

)



t





x



t



x

Jika

x



0

maka

t 

x

Sehingga bentuk x x f x x f x _      ) ( ) ( lim

0 dapat ditulis dengan cara lain berbentuk

) 2 ...( ... ) ( ) ( lim x t x f t f x t _   X Y x _xx )) ( , (x f x P )) ( ), ( (x f x f x x Q   ) (x f y  1 L L

Bentuk (1) dan (2) tersebut di atas didefinisikan sebagai turunan pertama fungsi dari fungsi eksplisit y  f(x)dan dinotasikan dengan

dx dy , y , ' dx x df( ) , atau f' x( ).

Khusus pada notasi

 

y

Dy

dx

d

dx

dy





, D disebut operator diferensial.

Secara geometris, turunan fungsi y  f(x) merupakan kemiringan (gradien) yang dinotasikan dengan m dari garis singgung kurva fungsi tersebut di sebarang titik, misal

o

x

x  . Dengan demikian gradien kurvay  f(x)di titik x x_odapat dinyatakan dengan:

x

x

f

x

x

f

m

o o x

_









 

)

(

)

(

lim

0

Karena turunan didefinisikan dengan menggunakan limit sedangkan limit fungsi bisa tidak ada, maka fungsi mungkin tidak mempunyai turunan di beberapa titik tertentu.

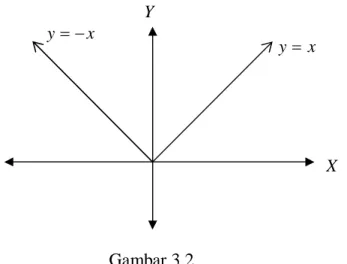
Sebagai contoh, perhatikan fungsi nilai mutlak f(x) x, yang grafiknya diberikan dalam gambar di bawah ini.

Jika kita memperhatikan gambar 3.2 di atas dengan cermat, maka kita akan dapatkan bahwa grafik fungsi nilai mutlak di atas berupa garis lurus, yang sebelah kanan sumbu y adalah berupa garis y = x sedangkan yang sebelah kiri sumbu y berupa garis y = -x. Garis di kanan dan kiri sumbu y mempunyai gradien yang berbeda,

Gambar 3.2 X Y x y x y 

sehingga patut dicurigai bahwa fungsi f(x) x tidak mempunyai turunan di perpotongan kurva dengan sumbu y, yaitu titik (0,0). Pembuktian bahwa fungsi

x x

f( ) tidak mempunyai turunan di titik (0,0) diberikan di bawah ini. Karena 1 1 lim lim | 0 | | | lim ) 0 ( ) 0 ( lim 0 0 0 0                          x x x x x x x x f x f dan 1 ) 1 ( lim lim | 0 | | | lim ) 0 ( ) 0 ( lim 0 0 0 0 _                   _{ }    x _x x _x x x x x x f f , maka x f x f x f x f x x            _{ }   ) 0 ( ) 0 ( lim ) 0 ( ) 0 ( lim 0 0 , sehingga x f x f f x _       ) 0 ( ) 0 ( lim ) 0 ( ' 0 tidak ada. Contoh:

1) Tentukan garis singgung kurva y  x2 di titik (2,4) Jawab

Gradien garis singgung kurva y  x2 di titik (2,4)adalah

m = '(2) lim (2 ) (2) lim (2 ) 2 lim(4 ) 4 0 2 2 0 0 _                   _x x x x f x f f x x x .

Oleh karena itu persamaan garis singgungnya adalah

4 4 ) 2 ( 4 4 ) ( ₀ 0          y m x x y x y x y

2) Tentukan apakah di x0fungsi y  x2 mempunyai turunan ? Jawab

Karena '(0) lim (0 ) (0) lim ( ) 0 lim 0 0 2 2 0 0 _                  _x x x x f x f f x x x , maka 2 x y  mempunyai turunan di x = 0.

Jika dalam menentukan turunan secara langsung dengan menggunakan definisi turunan, maka akan terdapat kesulitan-kesulitan dan memerlukan waktu yang relatif lebih lama. Untuk itu, diperlukan cara lain di samping dengan menggunakan definisi secara langsung, yaitu dengan menggunakan sifat dan rumus turunan.

Berikut diberikan beberapa sifat penting dalam pencarian turunan suatu fungsi. Misal f(x)dan g(x) fungsi-fungsi yang dapat diturunkan dan k sebarang bilangan real maka:

1. Aturan turunan fungsi konstanta

Jika y k maka 0

dx dy

Bukti

Menurut definisi turunan x k k x _    lim0 x x _    0 lim 0 = 0

2. Aturan turunan fungsi identintas

Jika y  x maka 1

dx dy

Bukti

Menurut definisi turunan x x f x x f dx dy x _       ) ( ) ( lim 0 x x x x x _       ) ( lim 0 x x x _    lim0

3. Aturan pangkat Jika n x y  maka _ n1 nx dx dy Bukti

Menurut definisi turunan x x f x x f dx dy x _       ) ( ) ( lim 0

x

x

x

x

n n x

_









 

)

(

lim

0 1 1 2 1 0 1 2 3 2 1 0 2 2 2 ) 1 ( 1 0 ) ( ... 2 ) 1 ( lim ) ( ... 6 ) 2 )( 1 ( 2 ) 1 ( lim ) ( ... ) ( lim                                                             n n n n x n n n n n n n n n n n x nx x x x n n nx x x x x n n n x x n n nx x x x x x x x nx x

4. Aturan turunan perkalian fungsi dengan konstanta

Jika y kf(x) maka kf' x( )

dx dy



Bukti

Menurut definisi turunan

x

x

f

x

x

f

dx

dy

x

_









 

)

(

)

(

lim

0

x

x

kf

x

x

kf

x

_









 

)

(

)

(

lim

0





x

x

f

x

x

f

k

x

_









 

)

(

)

(

lim

0





x

x

f

x

x

f

k

x x

_









   

)

(

)

(

lim

lim

0 0



kf

' x

(

)

5. Aturan jumlah Jika

y



f

(

x

)



g

(

x

)

maka f'(x) g'(x) dx dy   Bukti

Menurut definisi turunan

x

x

f

x

x

f

dx

dy

x

_









 

)

(

)

(

lim

0



 



x

x

g

x

f

x

x

g

x

x

f

x

_

















 

)

(

)

(

(

)

(

lim

0



 



x

x

g

x

x

g

x

f

x

x

f

x

_

















 

)

(

)

(

)

(

)

(

lim

0









x

x

g

x

x

g

x

x

f

x

x

f

x x

_



















   

)

(

)

(

lim

)

(

)

(

lim

0 0



f

'

(

x

)



g

'

(

x

)`

6. Aturan selisih Jika

y



f

(

x

)



g

(

x

)

maka f'(x) g'(x) dx dy   Bukti

Menurut definisi turunan

x

x

f

x

x

f

dx

dy

x

_









 

)

(

)

(

lim

0



 



x

x

g

x

f

x

x

g

x

x

f

x

_

















 

)

(

)

(

(

)

(

lim

0



 



x

x

g

x

x

g

x

f

x

x

f

x

_

















 

)

(

)

(

)

(

)

(

lim

0









x

x

g

x

x

g

x

x

f

x

x

f

x x

_



















   

)

(

)

(

lim

)

(

)

(

lim

0 0



f

'

(

x

)



g

'

(

x

)`

7. Aturan hasil kali. Jika y  f(x)g(x) maka f'(x)g(x) g'(x)f(x) f(x)g'(x) f'(x)g'(x) dx dy     Bukti

Menurut definisi turunan

x

x

f

x

x

f

dx

dy

x

_









 

)

(

)

(

lim

0



 



x

x

g

x

f

x

x

g

x

x

f

x

_













 

)

(

)

(

)

(

)

(

lim

0



 

 

 



x x g x x f x g x x f x g x f x x g x x f x _               ) ( ) ( ) ( ) ( ) ( ) ( ( ) ( lim 0









x

x

f

x

x

f

x

g

x

g

x

x

g

x

x

f

x

_





















 

)

(

)

(

)

(

)

(

)

(

)

(

lim

0









x

x

f

x

x

f

x

g

x

x

g

x

x

g

x

x

f

x x

_























   

)

(

)

(

)

(

lim

)

(

)

(

)

(

lim

0 0









x x f x x f x g x x g x x g x x f x x x x _                    ) ( ) ( lim ). ( lim ) ( ) ( lim ). ( lim 0 0 0 0  f(x)g'(x)g(x)f'(x)

8. Aturan hasil bagi.

Jika , ( ) 0 ) ( ) (   g x x g x f y maka ) ( ) ( ) ( ) ( ) ( ' 2 x g x g x f x g x f dx dy   Bukti

Menurut definisi turunan

x

x

f

x

x

f

dx

dy

x

_









 

)

(

)

(

lim

0

x

x

g

x

f

x

x

g

x

x

f

x

_













 

)

(

)

(

)

(

)

(

lim

0



(

)

(

)



)

(

)

(

)

(

)

(

lim

0

x

g

x

x

g

x

x

x

g

x

f

x

g

x

x

f

x



















 



( ) ( )



) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( lim 0 _{x g x x g x} x f x g x f x g x x g x f x g x x f x _{ }          











( ) ( )



) ( ) ( ) ( ) ( ) ( ) ( lim 0 _{x g x x g x} x g x x g x f x f x x f x g x _{ }          









) ( ) ( 1 lim . ) ( ) ( lim ). ( lim ) ( ) ( lim ). ( lim 0 0 0 0 0 _{x g x x g x} x g x x g x f x x g x x f x g x x x x x _{ }                    0 ) ( , ) ( ) ( ' ) ( ) ( ' ) ( 2    g x x g x g x f x f x g 9. Fungsi Majemuk Jika y



f(x)



n maka n



f(x)

 

1 f'(x)



dx dy n  Contoh

1. Tentukan turunan fungsi di bawah ini. a) yx812x5 4x410x36x5 Jawab

 

8 12

 

5 4

 

4 10

 

3 6

 

 

5 dx d x dx d x dx d x dx d x dx d x dx d dx dy       8x7 60x4 16x3 30x2 6 b) 6 2 3 2     x x x y Jawab 2 3 2 2 3 2 3 2 pembagian aturan 3 2 ) 6 ( 3 ). 2 ( ) 6 )( 1 2 ( ' ' ' 6 , 2 , ' 6 2                           x x x x x x v uv v u y x v x x u v u y x x x y



₃



2 2 3 4 6 6 12 6 2 '        x x x x x y c) y lnx Jawab

Berdasarkan definisi turunan x x x x x x f x x f dx dy x x _              ln ) ln( lim ) ( ) ( lim 0 0

x

e

x

x

x

x

x

x

x

x

x

x h x k x x x x x x x

1

ln

1

lim

ln

)

1

ln(

lim

1

ln

lim

ln

lim

1 1 1 0 0 0 0











































































         d) y  1 2x Jawab

Menurut definisi turunan y  f(x)

x

x

f

x

x

f

dx

dy

x











 

)

(

)

(

lim

0 x x x x x _         2 1 ) ( 2 1 lim 0 x x x x x x x x x x x _{1 2( ) 1 2} 2 1 ) ( 2 1 . 2 1 ) ( 2 1 lim 0 _{   }               .



x x x



x x x x o x _{1 2( ) 1 2} ) 2 1 ( ) ( 2 1 lim               X

x x x x _{1 2( ) 1 2} 2 lim 0 _{   }     x 2 1 2 2    x 2 1 1   





2 1 2 1    x e) x x x y    5 3 2 Jawab Misal ux3x2 maka u'16x v 5x maka v'1 Menurut sifat 7 jika

v u y  maka ' ' ₂ ' v uv v u y   Diperoleh ₂ 2 ) 5 ( ) 1 )( 3 ( ) 5 )( 6 1 ( ' x x x x x y        ₂ 2 2 10 25 3 6 31 5 x x x x x x       

25

10

5

30

3

2 2











x

x

x

x

f) Jika h(x) = xg(x) dan g(3) = 5 dan g’(3) = 2, carilah h’(3). Jawab

h

(

x

)



xg

(

x

)



aturan





perkalian







h

'

(

x

)



1

.

g

(

x

)



xg

'

(

x

)

11 ) 3 ( ' 3 ) 3 ( ) 3 ( '  g  g  h

3.2 Aturan Rantai (Chain Rule)

Aturan rantai umumnya digunakan untuk menentukan turunan fungsi yang bentuk umumnya y 



f(x)



n atau y  f



g(x)



.

Di bawah ini diberikan aturan rantai yang digunakan untuk menentukan turunan fungsi.

Jika f(x) dan g(x)keduanya mempunyai turunan, dan h = f o g adalah fungsi komposisi yang didefinisikan oleh h(x) = f(g(x)), maka h mempunyai turunan, yaitu h’ yang dinyatakan oleh

h ’(x) = f ’(g(x)). g ’(x)

Dalam notasi Leibniz, jika y = f(u) dan u = g(x) keduanya fungsi yang mempunyai turunan, maka dx du du dy dx dy  . Bukti: ) ( ' )) ( ( ' ) ( ) ( lim . )) ( ( ) ) ( ( lim ) ( ) ( lim . ) ( ) ( )) ( ( )) ( ( lim ) ( ) ( . ) ( ) ( )) ( ( )) ( ( lim )) ( ( )) ( ( lim ) ( ) ( lim ) ( ' 0 0 0 0 0 0 0 x g x g f t x g t x g p x g f p x g f t x g t x g x g t x g x g f t x g f t x g t x g x g t x g x g f t x g f t x g f t x g f t t h t x h x h t p t t t t t                                        Contoh 1. Jika y ex` maka ex dx dy  Bukti x x

e

y

y

y

y

y

x

e

y







ln





aturan



rantai







1



1

.

'



'





2. Jika y ax`, a11 maka a a dx dy x ln  Bukti y ax` xa logy

= a y ln ln Sehingga a y dy dx dy y a dx ln 1 1 . ln 1   

Dengan aturan rantai y a a a dy dx dx dy x ln ln 1    3. Jika a x dx dy maka a x a y a ln 1 , 1 , 0 , log    

Bukti nomor 3 ditinggalkan penulis sebagai latihan bagi pembaca.

3.3. Turunan Fungsi Implisit dan Fungsi Parametrik Turunan Fungsi Implisit

Fungsi implisit adalah fungsi yang secara umum ditulis dalam bentuk 0 ) , (x y  f Contoh: 1. x2  y2 250 2. x2y xy2 20 3. x2 y2 2xy10 4. cos xy y 0

Rumus-rumus turunan yang telah dijabarkan pada pasal sebelumnya berlaku jika fungsi dinyatakan dalam bentuk eksplisit atau y  f(x), sedangkan untuk fungsi yang dinyatakan dalam bentuk implisit yaitu fungsi yang bentuk umum penulisannya

0 ) , (x y 

f , turunannya dapat ditentukan dengan menggunakan kaidah diferensial, yaitu dengan cara mendiferensialkan masing-masing variabel fungsi tersebut.

1. Tentukan dx dy

dari x2  y2 40 Jawab

Dengan aturan diferensial masing-masing variabel diperoleh d(x2)d(y2)d(4)d(0) 2xdx2ydy00 xdx ydy0 y x dx dy    2. Tentukan dx dy dari x2y xy2 20 d(x2y)d(xy2)d(2)d(0) 



d(x2)yx2d(y)

 

 d(x)y2 xd(y2)



00 



2xdx.yx2dy

 

 dx.y2 x2ydy



0 



2xy y2



dx



x2 2xy



dy0



(

2

xy



y

2

)

dx





(

x

2



2

xy

)

dy

xy x y xy dx dy 2 2 2 2      3. Tentukan dx dy dari y  x x x Jawab Untuk menentukan dx dy

dari fungsi di atas, maka bentuk fungsinya diubah terlebih dahulu menjadi bentuk implisit, dan diperoleh:

x x x y  0 7 8    y x

Dengan mendiferensialkan masing-masing variabel diperoleh ) 0 ( ) ( ) (y8 d x7 d d  

0 7 8 7  6   y dy x dx dx x dy y7 7 6 8   Sehingga ₇ 6 8 7 y x dx dy  Latihan soal Tentukan dx dy

fungsi-fungsi berikut ini.

1. 2 1 4 x x y   2. 2xy3y2 2 xy30 3. x y sin 2 1   4. ycos2(2x1)0 5. 2 1 2 1 x y    6. _{y sec(1x)}32 7. cos(xy)2x3y2 0 8. yxx2 3y10 9. cos( ) 2 3 2 0    x y xy y 10. _{y sin}4_1x 11. cos xy y 0

Turunan Fungsi Parametrik

Fungsi parametrik adalah fungsi yang secara umum ditulis dalam bentuk

) (x

f











)

(

)

(

t

y

y

t

x

x

Contoh 1.        t t y t x 2 1 2 2.        t y t t x 1 cos sin

Turunannya dapat ditentukan dengan menurunkan masing-masing bagian, selanjutnya gunakan aturan rantai.

Contoh: Tentukan

dx dy

dari fungsi parametrik dibawah ini.

1.        t t y t x 2 1 2 Jawab

Jika variabel x dan y diturunkan terhadap parameter t, maka diperoleh

2  dt dx dan  t2 1 dt dy .

Karena yang dicari adalah dx dy

maka dengan menggunakan aturan rantai diperoleh:

2 1 2 .     t dt dx dt dy dx dt dt dy dx dy 2.        t y t x 3 1 ) 1 2 ( sin Jawab

) 1 2 cos( 2   t dt dx dan t dt dy 3 1 2 3    .

Karena yang dicari adalah dx dy

maka dengan menggunakan aturan rantai diperoleh:

) 1 2 cos( 3 1 2 3 ) 1 2 cos( 2 3 1 2 3 .           t t t t dt dx dt dy dx dt dt dy dx dy . 3.        t y t x 2 1 ) 4 3 ln( Jawab

Jika variabel x dan y diturunkan terhadap parameter t, maka diperoleh

4 3 3   t dt dx dan t dt dy 2 1 1    .

Karena yang dicari adalah dx dy

maka dengan menggunakan aturan rantai diperoleh:

t t t t dt dx dt dy dx dt dt dy dx dy 2 1 3 ) 4 3 ( 4 3 3 2 1 1 .           . Soal-soal Tentukan dx dy

fungsi parametrik berikut ini.

1)           2 3 4 2 1 2 t t y t x 2)        t y t t x 1 2 3 cos 2 2 sin 3 3) _    3 2 2 3 t t x

4)        t y t t x 1 cos sin 5)





       t y t t x 1 3 cos sin ln 6)          3 2 2 2 3 2 sin 2 t t y t x

3.4 Turunan Fungsi Trigonometri dan Siklometri

Rumus dasar dari turunan trigonometri adalah turunan fungsi sinus dan cosinus, sedangkan turunan fungsi trigonometri yang lainnya dan turunan fungsi siklometri dapat ditentukan dengan rumus turunan sinus dan cosinus, sifat turunan, dan aturan rantai. Tentukan dx dy untuk 1. y sinx Jawab

Menurut definisi turunan

y



sin

x

x x x x x x f x x f y x y x x _                sin ) sin( lim ) ( ) ( lim ' sin 0 0 x x x x x x x x x x h x x cos 2 1 . 1 . cos 2 2 1 . 2 2 sin lim 2 2 cos lim 2 2 sin 2 2 cos 2 lim 0 0 0                  2. y cosx Jawab . x x x x x x f x x f y x y h x _               cos ) cos( lim ) ( ) ( lim ' cos 0 0

x x x x x x x x x x h x x sin 2 1 . 1 . sin 2 2 1 . 2 2 sin lim 2 2 sin lim 2 2 sin 2 2 sin 2 lim 0 0 0                     

3. Turunan fungsi trigonometri yang lain. a) y tanx b) y cotx c) y secx d) y cscx e) y arcsinx f) y arctanx g) y arcsecx h) y sin4(ex lnx) i) y exsin2(x21) Jawab a. x x x x x x y x x x y 2 2 pembagian aturan sec cos ) sin .( sin cos cos ' cos sin tan        b. x x x x x x y x x x y aturan pembagian ₂ csc2 sin ) .(cos cos ) (sin sin ' sin cos cot        c. x x x x x y x x y sec tan cos ) sin .( 1 ) .(cos 0 ' cos 1 sec 2 pembagian aturan               d. x x x x x y x x y csc cot sin ) .(cos 1 ) .(sin 0 ' sin 1 csc 2 pembagian aturan               e. 2 rantai aturan 1 1 cos 1 ' cos ' 1 sin arcsin x y y y y y x x y                1

Gambar 3.3 f. 2 2 2 rantai aturan 1 1 cos ' sec ' 1 tan arctan x y y y y y x x y                Gambar 3.4

g. yarcsecxxsecyaturan rantai1 y'secytany

1 1 cot cos ' 2    x x y y y Gambar 3.5

h. ysin4(ex lnx)aturan rantaiyu4,usin(exlnx),usinv,vex lnx

) ln ( sin ) ln cos( ) 1 ( 4 ) ln cos( ) 1 ( 4 . ' ) ln cos( ) 1 ( cos ' ) (sin , 1 3 3 4 x e x e x e x e x e u dx du du du y x e x e v v dx dv v dv d dx du x e dx dv x x x x x x x x                i. Bukti ) 1 ( 2 sin 2 ) 1 ( sin ) 1 cos( ) 1 sin( 2 . 2 ) 1 ( sin 2 ). 1 cos( ). 1 sin( 2 . ) 1 ( sin ) 1 ( sin ) 1 ( sin ' ) 1 ( sin 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 perkalian dan rantai aturan 2 2                             x xe x e x x xe x e x x x e x e dx x d e x dx de y x e y x x x x x x x x x y x 1 2  x 1 y 1 2  x x 1

3.5 Turunan Tingkat Tinggi

Jika y  f(x) fungsi yang dapat diturunkan, maka y ' f'(x) juga berupa

fungsi. Jika y ' f'(x) mempunyai turunan, maka y '' f''(x)adalah turunan kedua dari y  f(x)dan seterusnya.

Turunan ke-n suatu fungsi dinyatakan dengan _n

n

dx y d

Untuk n = 2 dinotasikan dengan ₂ 2 '' ''( ) 2 x f y y D dx dy dx d dx y d          

Untuk n = 3 dinotasikan dengan ₂ 3 ''' ' ''( )

2 3 3 x f y y D dx y d dx d dx y d          

Untuk n = 4 dinotasikan dengan ₃ 4 (4) (4)( )

3 4 4 x f y y D dx y d dx d dx y d          

Dan seterusnya. Bentuk-bentuk di atas dinamakan turunan tingkat tinggi atau turunan ke-n. Contoh: 1. Carilah 2 2 dx y d dari : a. 2 2 25   y x b. y lnt,xet c. y et2t,xlnet 1

2. Carilah turunan ke n dari fungsi di bawah ini: a. y ekx

b. y lnx

1. Dari contoh-contoh sebelumnya telah diperoleh dx dy dari x2 + y2 = 25, adalah y x dx dy   . Karena _               y x dx d dx dy dx d dx y d 2 2

Dan mengingat y adalah fungsi dari x, dengan aturan pembagian dan aturan rantai, diperoleh 3 2 2 2 2 . . 1 . . . y x y y y x x y y dx dy x dx dx y y x dx d                  Jadi 3 2 2 2 2 _. y x y dx y d    2. Tentukan ₂ 2 dx y d a.      t y e x t ln _{t t t} te e t e t dt dx dt dy dx dt dt dy dx dy 1 1 1 .      dt dx dt dx dy d dx dt dt dx dy d dx dy dx d dx y d                      . 2 2 = Oleh karena _{t t} t t t e t t e t te e te dt d dx dy dt d 2 2 2 1 1                    dan et dt dx  maka t t t e t t e e t t dx y d 2 2 2 2 2 ₁ 1       . b. y = et2t, x = ln (et +1)

dt dx dt dy dx dy  = ) 1 ( ) 1 2 ( 2    t t t t e e e t = (2t1)(et 1)et2 dt dx dt dx dy d dx dx dy d dx y d               2 2 = ) 1 ( ) 1 )( 1 2 ( 2 ) 1 2 ( ) 1 ( 2 2 2 2         t t t t t t t t e e e e t t e t e e = 2(et 1)2et2t (2t1)(et1)et2 2t(2t1)(et 1)2et2t 3. a. yekx  y'kekx y''k2ekx y' ''k3ekx ... y(n) knekx b. _n n n x n y x x y x y x y x y )! 1 ( ) 1 ( ... ! 2 ) 1 ( 2 . 1 ) 1 ( '' ' 1 ) 1 ( '' 1 ' ln 1 ) ( 3 2 3 2 2 _                 Soal-soal

1) Tentukan kemiringan pada kurva fungsi berikut di titik yang diberikan.

a. (0, 1) 1 1    dititik x y b. 1 1 1    dititik dengan x x y c. y12x3x2 di titik x = 1, -2 1 dan 4 1 d. 2 1 x y  , di titik (1,1)

2) Tentukan apakah fungsi di bawah ini mempunyai turunan pada titik yang diberikan. a. y  x1 di x = 1

c.             1 , 3 1 , 1 ) ( 2 2 x x x x x f di x = 1 d.              2 , 9 8 2 , 1 ) ( 2 2 x x x x x x f di x = 2

3) Masing-masing bentuk limit di bawah ini menyatakan turunan suatu fungsi )

(x f

y  . Tentukan bentuk fungsi dan turunan fungsi. a) x x x _      1 1 lim 0 b) x x x x x _      9 0 ) ( lim c) x x x x x _      2 cos ) ( 2 cos lim 0 d) x x x x x _       sin ) sin( lim 0

4) Dengan menggunakan definisi turunan, tentukan turunan fungsi-fungsi berikut: a. G(s)



s2 s1



s2 2



b. f(y)



y2 1





2y7



c. d cx b ax x h    ) ( d. 2 x c x b a y  

5) Carilah persamaan garis singgung pada kurva di titik yang diberikan. a. 1 2   x x y , di titik (1, 1) b. y x x, di titik (1, 2)

c. 1   x x y , di titik (4 ; 0,4) d. y  x x, di titik (1, 1)

6) Carilah titik pada kurva y x3 x2 x1yang garis singgungnya mendatar.

a) Gunakan aturah hasil kali sebanyak dua kali untuk membuktikan bahwa jika g

f , dan gfungsi-fungsi yang mempunyai turunan, maka berlaku '

' '

)

(fgh  f gh fg h fgh

b) Gunakan bagian (a) untuk menentukan turunan fungsi



4 1





2 3



    x x x x y 7) Tentukan nilai 1 1 lim 1000 1    x x x

8) Tulislah fungsi komposisi dalam bentuk f(g(x)). Tentukan fungsi sebelah dalam u = g(x) dan fungsi sebelah luar y = f(u). Kemudian carilah

dx dy

a. y(x2 4x6)2 b. y31x3 c. y x2 7x

9) Carilah turunan fungsi-fungsi berikut a.

y





3

x



2



10

(

5

x

2



x



1

)

12 b.

y



(

s

2



1

)

4

s

3



1

10) Carilah turunan pertama dari fungsi di bawah ini : a. xylny 1

b. ln   y 3 e xy x

d. lnxyln(xy)ex e. eyx xln ysin2x

11) Carilah nilai turunan pertama dari fungsi di bawah ini pada titik yang diberikan a. xylny xdi(0,1) b. xxy2y10di(1,0) c. 3 3 30 (1,3) di x y y x   d. x2y2 4xy12ydi(2,1) e. xxy2y40di(1,1)

13)Carilah turunan pertama fungsi yang diberikan a. y lnt2 1, xet b. 2 1, ln( 1)    t  t e x e y c.  t 2,  t 5 e x e y d. y et lnt, xet 4 e. y te t t x et t     2 , f. y t3 2t, x3t2 5

14)Carilah turunan kedua untuk fungsi-fungsi di bawah ini a. 3x3 3x2y8xy2 2y3 0 b. xy y3 2 c. x3  y4 2 3 d. y x33x e. y x3ln(x2 1) 15) Carilah nilai ₂ 2 dx y d

dari fungsi di bawah ini pada titik yang diberikan a. x3 y3 3xy di(0,0)

b. x2y4y3 4 di(2,1) c. x2 y2 25di(3,4) d. x2 y2 25di(3,4)x

16) Carilah turunan ke n, untuk n=3 dan 4 dari fungsi di bawah ini: a. y sinx

b. y cosx c. y sin(axb) d. y cos(pxq)

17) Carilah turunan dari fungsi di bawah ini: a. arctan( 5) 2 



e

x

y

b. yarccos(ex 5x) c. yexarcsin(ax2 b)