i
SISTEM PERSAMAAN LINEAR ALJABAR MAX-PLUS DAN APLIKASINYA DALAM MASALAH RAMP HANDLING PESAWAT
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Oleh:
REGINA WAHYUDYAH SONATA AYU NIM :111414060
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
iii
iv
HALAMAN PERSEMBAHAN
All Things are Difficult Before They are Easy (Thomas Fuller)
Mistakes are Often The Best Teachers (James A. Froude)
The Noblest Pleasure is The Joy of Understanding (Leonardo da Vinci)
Karya ini kupersembahkan kepada:
Tuhan Yesus dan Bunda Maria yang senantiasa menyertaiku
Bapa Ambros dan Mama Rosalia
Kakak Tian, Kakak Tini, Kakak Andy, Kakak Yovan dan Adik Etu
Keponakanku Chiko
v
vi
vii ABSTRAK
Regina Wahyudyah Sonata Ayu, 2015. Sistem Persamaan Linear Aljabar
Max-Plus dan Aplikasinya dalam Masalah Ramp Handling Pesawat. Skripsi.
Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.
Penelitian ini bertujuan untuk mengkaji penyelesaian sistem atas aljabar max-plus dengan , , , dan serta aplikasinya dalam masalah ramp handling pesawat. Penelitian ini diawali dengan mengkaji sub-penyelesaian terbesar dari sistem persamaan yang kemudian menjadi calon penyelesaian sistem. Selanjutnya, diselidiki mengenai eksistensi dan ketunggalan penyelesaian sistem persamaan . Langkah berikutnya adalah membahas aplikasi sistem atas aljabar max-plus dalam masalah ramp handling pesawat di bandara.
Hasil penelitian menunjukkan bahwa sistem atas aljabar max-plus dapat tidak mempunyai penyelesaian, mempunyai penyelesaian tunggal, atau mempunyai takhingga banyak penyelesaian. Diberikan matriks dengan
elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan . Sistem persamaan tidak mempunyai penyelesaian bila terdapat baris nol dalam matriks , mempunyai satu penyelesaian bila terdapat lone one pada setiap baris matriks dan mempunyai takhingga banyak penyelesaian bila
terdapat elemen slack dalam matriks . Aplikasi sistem persamaan dalam masalah ramp handling adalah untuk menentukan waktu mulai paling lambat bagi setiap aktivitas ramp handling sehingga semua aktivitas tersebut telah selesai pada waktu keberangkatan pesawat.
Kata kunci: Aljabar Max-Plus, Sistem Persamaan Linear Aljabar Max-Plus,
viii ABSTRACT
Regina Wahyudyah Sonata Ayu, 2015. System of Linear Equations in
Max-Plus Algebra and Its Application in Aircraft Ramp Handling Problem. Thesis.
Mathematic Education Study Program, Mathematic and Science Education Departement, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
This research aims to study the solution to system of over max-plus algebra where ,
, , and its application
in aircraft ramp handling problem. This research is started by studying the principal sub-solution that is the candidate for solution of . Furthermore, the existence and the uniqueness of the solution to are investigated. The next step is discussing the application of system of over max-plus algebra in aircraft ramp handling problem at airport.
The result shows that the system of has either no solution, one solution or an infinite number of solutions. Let with elements in each
column are not all equal to and . System of has no solution if there is a zero-row in , has one solution if each row of has a lone one and
has an infinite number of solutions if there are slack entries in . The application of system of in aircraft ramp handling problem is to determine the latest starting times for each ramp handling activity so that all of the activities are completed at the departure time of the plane.
Key word: Max-Plus Algebra, System of Linear Equations in Max-Plus Algebra, Ramp Handling.
ix
KATA PENGANTAR
Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa karena atas berkat dan rahmat-Nya penulis dapat menyelesaikan skripsi dengan judul “Sistem Persamaan Linear Aljabar Max-Plus dan Aplikasinya dalam Masalah
Ramp Handling Pesawat”. Skripsi ini disusun dalam rangka memenuhi salah satu
syarat untuk memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.
Banyak hambatan dan rintangan yang dialami oleh penulis selama penyusunan skripsi ini. Namun atas bantuan dan dukungan dari berbagai pihak, maka penulis dapat mengatasi segala hambatan dan rintangan yang dialami. Oleh karena itu, pada kesempatan kali ini penulis ingin mengucapkan terima kasih kepada:
1. Dr. M. Andy Rudhito, S.Pd. selaku Kaprodi Pendidikan Matematika Universitas Sanata Dharma sekaligus dosen pembimbing skripsi yang telah membimbing, memberikan kritikan dan masukan yang membangun dalam penyusunan skripsi ini.
2. Bapak Rohandi, Ph.D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan.
3. Kedua orang tuaku, Bapak Ambrosius Madut dan Ibu Rosalia Nuet serta saudara-saudaraku, Kristianus Panjo Candra, Kristiana Deti Sajutin, Didimus Andi Gunawan, Yuventus Yonavan Cahyono, dan Hersintus Suwenda Syah Suyoso yang senantiasa menyayangi dan mendukung penulis baik lewat doa, perhatian maupun dukungan materi.
4. Ibu Veronika Fitri Rianasari, S.Pd. M.Sc. selaku dosen pembimbing akademik yang telah membantu dan membimbing penulis terutama berkaitan dengan hal akademis selama penulis menempuh kuliah di Program Studi Pendidikan Matematika Universitas Sanata Dharma.
5. Bapak dan Ibu dosen di Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah membimbing dan mendidik penulis
x
selama menuntut ilmu di Program Studi Pendidikan Matematika Universitas Sanata Dharma..
6. Sahabat-sahabatku, Margaretha Nobilio Pasia Janu, Ana Karisma Adi Purwito, Theresia Veni Dwi Lestari, Yuliana Pebri Heriawati, Pilipus Neri Agustima dan Singgih Satriyo Wicaksono yang telah menemaniku serta berbagi suka duka selama menempuh kuliah di Universitas Sanata Dharma.
7. Adik-adikku tersayang, Imak, Itak dan Elisa serta teman-temanku, Yos, Eki dan Charles yang senantiasa mendukung dan menyemangati penulis dalam menyelesaikan tulisan ini.
8. Teman-teman seperjuangan di Program Studi Pendidikan Matematika Universitas Sanata Dharma angkatan 2011 yang telah berbagi pengalaman selama penulis menempuh kuliah di Universitas Sanata Dharma.
9. Semua pihak yang telah membantu penulis menyelesaikan tugas akhir ini, baik secara langsung maupun tidak langsung yang tidak dapat disebutkan satu persatu.
Penulis menyadari bahwa masih banyak kekurangan dalam penulisan skripsi ini. Oleh karena itu, dengan rendah hati, penulis mengharapkan kritik dan saran yang membangun demi kesempurnaan tulisan ini. Semoga tulisan ini dapat memberikan manfaat dan wawasan yang lebih kepada setiap pembaca.
Yogyakarta, 17 Juni 2015
xi DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH .. vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR SIMBOL ... xiii
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 4 C. Batasan Masalah ... 4 D. Tujuan Penelitian ... 4 E. Manfaat Penelitian ... 5 F. Metode Penelitian ... 5 G. Sistematika Penulisan ... 5
BAB II LANDASAN TEORI ... 7
A. Definisi dan Sifat-sifat Dasar Aljabar Max-Plus ... 7
B. Matriks dan Vektor atas Aljabar Max-Plus ... 12
BAB III SISTEM PERSAMAAN LINEAR ALJABAR MAX-PLUS ... 21
A. Sub-Penyelesaian Terbesar ... 22
B. Eksistensi dan Ketunggalan Penyelesaian Sistem Persamaan ...25
xii
C. Penyelesaian Sistem Persamaan dengan Program MATLAB
...44
BAB IV APLIKASI SISTEM PERSAMAAN LINEAR ALJABAR MAX-PLUS DALAM MASALAH RAMP HANDLING PESAWAT ... 50
A. Ramp Handling ... 50
B. Aplikasi Sistem Persamaan dalam Masalah Ramp Handling 52 BAB V PENUTUP ... 60
A. Kesimpulan ... 60
B. Saran ... 61
xiii
DAFTAR SIMBOL
( ) : himpunan tak kosong yang dilengkapi dengan dua operasi biner dan
: himpunan semua bilangan real
: : * + : operasi max : operasi plus ( ) : ( ) : { [ ] } : { , - }
: himpunan semua bilangan asli
: relasi “lebih kecil atau sama dengan” dalam aljabar max-plus : matriks „discrepancy‟
: matriks hasil reduksi
1 BAB I PENDAHULUAN
A. Latar Belakang
Aljabar merupakan cabang matematika yang menggeneralisasi bentuk aritmatika dengan menggunakan variabel-variabel untuk menggantikan bilangan-bilangan. Aljabar memiliki ruang lingkupnya sendiri antara lain aljabar dasar, aljabar linear, aljabar abstrak, dan sebagainya. Salah satu ruang lingkup aljabar yang masih tergolong baru adalah aljabar max-plus. Menurut Andersen (2002), aljabar max-plus muncul pada akhir tahun 1950‟an segera setelah topik mengenai Riset Operasi mulai dikembangkan. Sementara itu, menurut Butkovič (2000), aljabar max-plus telah dipelajari dan ditulis dalam bentuk makalah-makalah penelitian dan buku-buku pada awal 1960‟an dan dikembangkan secara intensif sejak tahun 1985.
Aljabar max-plus merupakan suatu contoh semiring yang terdiri dari himpunan * + dengan merupakan himpunan semua bilangan real, yang dilengkapi dengan operasi maksimum, dinotasikan dengan dan operasi penjumlahan, dinotasikan dengan . Dalam aljabar max-plus, operasi penjumlahan didefinisikan sebagai operasi maksimum sedangkan operasi perkalian didefinisikan sebagai operasi penjumlahan. Selanjutnya, ( * +, , ) dinotasikan dengan dan * + dinotasikan dengan . Elemen
merupakan elemen netral terhadap operasi dan 0 merupakan elemen identitas terhadap operasi .
Sebagai suatu semiring, aljabar max-plus merupakan semiring komutatif sekaligus idempoten (Subiono, 2013). Lebih jauh, aljabar max-plus merupakan semifield sebab untuk setiap di * + memiliki invers terhadap operasi , yakni ( * +)( * +) .
Sama halnya dalam aljabar linear, pasangan operasi ( ) dalam aljabar max-plus juga dapat diperluas untuk operasi matriks atas aljabar max-plus. Demikian juga, penjumlahan matriks atas aljabar max-plus hanya terdefinisi untuk matriks dengan ukuran yang sama. Matriks atas aljabar max-plus kemudian digunakan dalam merepresentasikan sistem persamaan linear aljabar max-plus untuk kemudian dicari penyelesaiannya. Representasi sistem persamaan linear yang dimaksud serupa dalam aljabar linear yakni berupa persamaan matriks . Namun demikian, berbeda dengan aljabar linear, aljabar max-plus tidak memiliki invers terhadap penjumlahan. Hal ini menyebabkan cara menyelesaikan sistem persamaan linear aljabar max-plus berbeda dengan sistem persamaan linear dalam aljabar biasa. Penyelesaian sistem persamaan linear aljabar max-plus, sebagaimana dalam aljabar biasa, tidak selalu ada dan bila ada tidak selalu tunggal.
Kehadiran sistem linear aljabar max-plus sangat membantu dalam memodelkan serta menganalisa Discrete Event System (DES) seperti sistem transportasi, sistem komunikasi, sistem produksi, sistem komputasi paralel, dan sebagainya. Namun demikian, menurut Subiono (2013), pendekatan aljabar max-plus diterapkan pada sistem yang hanya mempertimbangkan sinkronisasi tanpa konkurensi. Sinkronisasi berkaitan dengan ketersediaan beberapa sumber dalam
waktu bersamaan sedangkan konkurensi tampak ketika pada suatu saat seorang pengguna harus memilih beberapa sumber.
Penanganan pesawat di bandara atau lebih dikenal dengan istilah ramp
handling merupakan salah satu masalah sinkronisasi. Ramp handling merupakan
penanganan pesawat yang dilakukan di ramp area, yakni suatu pelataran yang ada di bandara. Ramp handling meliputi beberapa kegiatan antara lain
deplane/boarding, loading/unloading, refueling, dan lain-lain. Masing-masing
kegiatan memiliki durasi waktu yang berbeda untuk tiap pesawat. Kegiatan-kegiatan ini dilakukan secara simultan dan harus selesai pada waktu yang sudah ditentukan. Karena itu, perlu ditentukan waktu mulai paling lambat untuk setiap kegiatan sehingga semua kegiatan dipastikan telah selesai pada waktu keberangkatan (departure time) pesawat-pesawat dari bandara. Masalah ramp
handling ini terkait dengan masalah penyelesaian sistem persamaan linear
dimana matriks menyatakan durasi tiap kegiatan ramp handling untuk tiap pesawat, vektor menyatakan ground time pesawat dan akan ditentukan vektor yang menyatakan waktu mulai paling lambat untuk tiap kegiatan ramp handling.
Berdasarkan penjabaran di atas, penulis tertarik untuk mengkaji lebih jauh mengenai sistem persamaan linear aljabar max-plus serta aplikasinya dalam masalah ramp handling pesawat.
B. Rumusan Masalah
Pokok permasalahan yang akan dibahas dalam skripsi ini adalah
1. Bagaimana menentukan penyelesaian dari suatu sistem persamaan linear aljabar max-plus?
2. Bagaimana eksistensi dan ketunggalan penyelesaian dari suatu sistem persamaan linear aljabar max-plus?
3. Bagaimana aplikasi sistem persamaan linear aljabar max-plus dalam masalah
ramp handling pesawat?
C. Batasan Masalah
Pembahasan masalah dalam skripsi ini hanya dibatasi pada sistem persamaan linear aljabar max-plus berbentuk A x = b, sedangkan aplikasinya hanya dibatasi pada masalah ramp handling pesawat di bandara.
D. Tujuan Penelitian
Penulisan skripsi ini bertujuan untuk:
1. Mengetahui bagaimana cara menentukan penyelesaian sistem persamaan linear aljabar max-plus berbentuk A x = b.
2. Mengetahui bagaimana eksistensi dan ketunggalan penyelesaian sistem persamaan linear aljabar max-plus A x = b.
3. Mengetahui bagaimana aplikasi sistem persamaan linear aljabar max-plus tersebut dalam masalah ramp handling pesawat.
E. Manfaat Penelitian
Manfaat yang diperoleh melalui penulisan skripsi ini adalah: 1. Bagi penulis
Bila dalam perkuliahan penulis mempelajari struktur aljabar atas field, melalui penelitian ini penulis mendapat pengetahuan baru tentang contoh struktur aljabar lain yakni aljabar max-plus lebih khusus lagi mengenai sistem persamaan linear aljabar max-plus. Selain itu, penelitian ini juga menambah wawasan penulis mengenai aplikasi sistem persamaan linear aljabar max-plus dalam masalah ramp handling pesawat di bandara.
2. Bagi pembaca
Pembaca dapat memahami sistem persamaan linear A x = b dalam aljabar max-plus serta aplikasinya dalam masalah ramp handling pesawat di bandara.
F. Metode Penelitian
Metode yang digunakan dalam penelitian ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari buku-buku, jurnal-jurnal serta tesis-tesis yang berkaitan dengan topik skripsi.
G. Sistematika Penulisan
Tulisan ini akan mengkaji tentang sistem persamaan linear aljabar max-plus dan aplikasinya dalam masalah ramp handling pesawat. Untuk itu, tulisan ini akan dibagi dalam lima bab. Pada Bab I, terlebih dahulu akan dibahas mengenai latar belakang, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, metode penelitian dan sistematika penulisan skripsi ini. Selanjutnya,
pada Bab II akan dibahas mengenai definisi dan sifat-sifat dasar aljabar max-plus, dan vektor dan matriks atas aljabar max-plus yang akan melandasi pembahasan mengenai sistem persamaan linear aljabar max-plus dan aplikasinya dalam masalah ramp handling pesawat.
Inti dari tulisan ini terdapat dalam Bab III dan Bab IV. Pada Bab III akan dibahas mengenai sistem persamaan linear aljabar max-plus yang meliputi sub-penyelesaian terbesar, eksistensi dan ketunggalan sub-penyelesaian sistem persamaan
A x = b. Pada bab ini juga diberikan penyelesaian sistem persamaan A x = b
dengan program MATLAB guna mempermudah perhitungan, sedangkan pada Bab IV akan dibahas mengenai ramp handling dan aplikasi sistem persamaan A x =
b dalam masalah ramp handling.
Bagian terakhir dalam tulisan ini adalah Bab V yang berisi kesimpulan dari pembahasan pada Bab III dan Bab IV serta beberapa saran yang dapat digunakan dalam penelitian selanjutnya.
7 BAB II LANDASAN TEORI
Pada bab ini akan dibahas konsep-konsep yang diperlukan sebagai landasan teori dalam pembahasan mengenai sistem persamaan linear aljabar max-plus dan aplikasinya dalam masalah ramp handling pesawat. Pembahasan akan dibagi menjadi dua bagian, yakni: definisi dan sifat-sifat dasar aljabar max-plus serta matriks dan vektor atas aljabar max-plus.
A. Definisi dan Sifat-sifat Dasar Aljabar Max-Plus
Berikut ini akan diberikan definisi dan sifat-sifat dasar aljabar max-plus. Pembahasan akan diawali dengan definisi semiring.
Definisi 2.A.1
Suatu semiring (S, ) adalah suatu himpunan tak kosong S disertai dengan dua operasi biner dan yang memenuhi:
1. (S, ) komutatif dan asosiatif serta memiliki elemen netral, yakni: a.
b. ( ) ( ) c. ( )( )
2. (S, ) asosiatif serta memiliki elemen identitas, yakni: a. ( ) ( )
b. ( )( )
3. Sifat penyerapan elemen netral terhadap operasi , yakni:
4. Operasi distributif terhadap (distributif kiri dan distributif kanan), yakni berlaku
a. ( ) ( ) ( ) (distributif kiri) b. ( ) ( ) ( ) (distributif kanan)
Contoh 2.A.1
Diberikan * + dengan himpunan semua bilangan real, := dan := 0. Kemudian, dalam didefinisikan operasi dan yakni
berlaku:
( ) dan
Selanjutnya akan ditunjukkan ( , ) merupakan semiring. Bukti:
( , ) semiring sebab:
1. ( ) komutatif dan asosiatif serta memiliki elemen netral, yakni: a. ( ) ( )
b. ( ) * ( ) + ( ) * ( )+ ( ) c. ( )( ) ( )
( )
2. ( , ) asosiatif serta memiliki elemen identitas, yakni: a. ( ) ( ) ( )
b. ( )( ) 3. Sifat penyerapan elemen netral terhadap operasi , yakni:
( ) 4. Operasi distributif terhadap , yakni berlaku
a. ( ) ( )
( ) ( ) ( ) b. ( ) ( )
( ) ( ) ( )
( , ) kemudian cukup ditulis . Selanjutnya akan
diberikan definisi mengenai dua semiring khusus, yakni semiring komutatif dan semiring idempoten.
Definisi 2.A.3
Suatu semiring (S, ) merupakan semiring komutatif bila dan hanya bila berlaku sifat komutatif terhadap operasi , yakni .
Definisi 2.A.4
Suatu semiring (S, ) merupakan semiring idempoten bila dan hanya bila berlaku sifat idempoten terhadap operasi , yakni
Contoh 2.A.2
Bukti:
a. Semiring merupakan semiring komutatif sebab : .
b. Semiring merupakan semiring idempoten sebab :
( )
Lebih lanjut, dalam Subiono (2013) didefinisikan mengenai semifield yang merupakan ragam khusus dari semiring komutatif.
Definisi 2.A.5
Suatu semiring komutatif ( ) disebut semifield bila dan hanya bila setiap elemen a di * + mempunyai invers terhadap operasi , yaitu (
)( ) .
Contoh 2.A.3
Semiring komutatif merupakan semifield.
Bukti:
semifield sebab ( * +)( * +)
( ) ( ) ( ) .
Struktur aljabar ( , ) inilah yang kemudian disebut sebagai aljabar
max-plus. Elemen-elemen akan disebut juga sebagai skalar (Rudhito, 2003).
Sama halnya dalam aljabar biasa, operasi perkalian dikerjakan terlebih dahulu sebelum operasi penjumlahan, demikian juga halnya dalam aljabar
max-plus, operasi mempunyai prioritas daripada operasi . Berikut ini diberikan beberapa contoh yang mengilustrasikan operasi-operasi dalam .
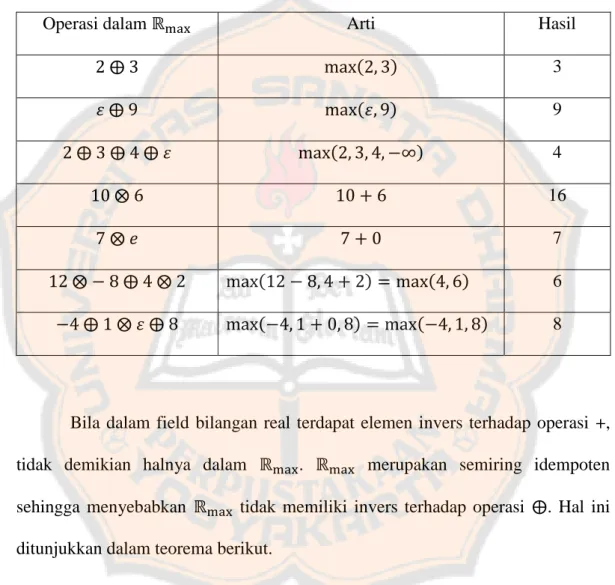
Tabel 1: Pengoperasian dalam .
Operasi dalam Arti Hasil
( ) 3 ( ) 9 ( ) 4 16 7 ( ) ( ) 6 ( ) ( ) 8
Bila dalam field bilangan real terdapat elemen invers terhadap operasi +, tidak demikian halnya dalam . merupakan semiring idempoten sehingga menyebabkan tidak memiliki invers terhadap operasi . Hal ini
ditunjukkan dalam teorema berikut.
Teorema 2.A.1 (Farlow, 2009)
Diberikan semiring ( ). Sifat idempoten dari berakibat bahwa
Bukti:
memiliki invers terhadap operasi yakni dirinya sendiri di mana ( )
Selanjutnya akan dibuktikan bahwa untuk setiap elemen dalam * + tidak memiliki invers yakni dengan mengambil sebarang * +. Misalkan bahwa mempunyai invers terhadap yaitu , didapat .
Tambahkan pada kedua ruas persamaan, didapat
Dengan sifat idempoten, persamaan menjadi . Hal ini bertentangan dengan .
Hal inilah yang kemudian membedakan aljabar max-plus dengan aljabar konvensional.
B. Matriks dan Vektor atas Aljabar Max-Plus
Pada bagian ini akan dibahas mengenai matriks dan vektor atas aljabar max plus serta relasi urutan di dalamnya. Himpunan matriks berukuran dalam aljabar max-plus dinotasikan dengan untuk . Elemen pada baris ke dan kolom ke dinotasikan dengan
atau , - untuk
dan Dalam hal ini matriks direpresentasikan sebagai berikut [ ]
Serupa dalam matriks real, pada matriks atas aljabar max-plus juga dapat didefinisikan operasi penjumlahan matriks, perkalian skalar, dan perkalian matriks. Selain itu, pada matriks atas aljabar max-plus juga dapat didefinisikan transpos matriks.
Definisi 2.B.1
Diberikan matriks , dan . Elemen ke-ij dari penjumlahan
matriks , perkalian skalar , serta transpos matriks didefinisikan sebagai 1. , - ( ), untuk dan 2. , - , untuk dan 3. , - , untuk dan Contoh 2.B.1
Diberikan matriks [ ] dan [
], maka a. [ ] [ ] b. [ ] [ ] c. [ ] Definisi 2.B.2
Misalkan dan maka elemen ke-ij dari perkalian matriks
, -
, ,
Contoh 2.B.2
Diberikan matriks [ ] dan [ ], maka
[ ] [ ] [ ] [ ] [ ] Teorema 2.B.1 (Rudhito, 2003)
Pernyataan-pernyataan berikut berlaku untuk sebarang skalar dan serta sebarang matriks , , dan asalkan operasi yang dimaksud terdefinisi.
1. ( ) ( ) 2. 3. 4. ( ) ( ) 5. ( ) ( ) 6. ( ) ( ) ( ) 7. ( ) ( ) ( )
Sifat-sifat lain dapat dibuktikan dengan menggunakan definisi operasi dan sifat-sifat operasi dalam Di bawah ini akan diberikan bukti untuk sifat 4.
Bukti:
Misalkan , - , , - dan [ ] . Elemen ke- kolom ke- matriks ( ) adalah
[( ) ] ( ) ( ) [ ( )] ( ) Definisi 2.B.3 (Rudhito, 2003)
Didefinisikan matriks dengan , - untuk semua dan .
Selanjutnya akan dibahas mengenai semimodul atas serta relasi urutan di dalamnya. Definisi semimodul berikut ini mengikuti definisi dalam Rudhito (2003).
Definisi 2.B.4
Misalkan (S, ) adalah semiring komutatif dengan elemen netral 0 dan elemen identitas 1. Semimodul M atas S adalah semigrup komutatif (M, ) bersama operasi perkalian skalar ●: , dituliskan sebagai ( ) ● yang memenuhi aksioma berikut:
i) ●( ) ● ● ii) ( )● ● ● iii) ●( ● ) ( )● iv) ●
v) ●
Elemen dalam semimodul dinamakan vektor.
Contoh 2.B.3
adalah semimodul atas
, dalam hal ini cukup ditulis
dimana
{ [ ] }
Untuk setiap dan untuk setiap didefinisikan operasi
dengan
, -
dan operasi perkalian skalar ● dengan
● ,
-Berdasarkan Teorema 2.B.1 1 dan 2 maka dapat disimpulkan bahwa ( ) merupakan semigrup komutatif dengan elemen netral , - . Selanjutnya, berdasarkan Teorema 2.B.1 5, 6 dan 7 maka dapat disimpulkan bahwa merupakan semimodul atas .
Definisi 2.B.5
Suatu relasi pada suatu himpunan P dinamakan urutan parsial pada P bila untuk semua memenuhi:
1. Sifat reflektif, yaitu:
2. Sifat antisimetris, yaitu: jika dan , maka 3. Sifat transitif, yaitu: jika dan , maka
Elemen dan dikatakan komparabel (comparable) jika atau . Sementara itu, dapat juga ditulis . Jika dan maka ditulis .
Definisi 2.B.6
Bila setiap dua elemen P komparabel, maka urutan parsial disebut urutan total.
Definisi 2.B.5 dan Definisi 2.B.6 di atas didasarkan pada definisi Wohlgemuth (dalam Rudhito, 2003). Berikut ini diberikan suatu teorema yang berkaitan dengan urutan parsial pada suatu semigrup komutatif idempoten.
Teorema 2.B.2 (Rudhito, 2003)
Jika ( ) semigrup komutatif idempoten maka relasi yang didefinisikan pada dengan merupakan urutan parsial pada .
Bukti:
Ambil sebarang
2. Jika dan maka dan . Karena komutatif maka .
3. Jika dan maka dan . Karena semigrup maka berlaku sifat asosiatif. Akibatnya,
( ) ( )
Sehingga .
Akibat 2.B.1 (Rudhito, 2003)
Relasi yang didefinisikan pada dengan
merupakan urutan parsial pada . Lebih lanjut, relasi pada merupakan urutan total.
Bukti:
Karena ( ) merupakan semigrup komutatif idempoten, maka menurut Teorema 2.B.2 relasi pada merupakan urutan parsial. Selanjutnya, untuk setiap berlaku:
( ) atau
( )
Jadi, relasi merupakan urutan total.
Relasi pada ekuivalen dengan relasi pada , sebab
Akibat 2.B.2 (Rudhito, 2003)
Relasi yang didefinisikan pada dengan
untuk setiap dan merupakan urutan parsial pada .
Bukti:
Berdasarkan Teorema 2.B.1 1, 2, dan 3 nampak bahwa ( ) merupakan
semigrup komutatif idempoten sehingga menurut Teorema 2.B.2 relasi pada merupakan urutan parsial.
Akibat 2.B.3 (Rudhito, 2003)
Relasi yang didefinisikan pada dengan
untuk setiap merupakan urutan parsial pada .
Bukti:
Berdasarkan Teorema 2.B.1 1, 2, dan 3 nampak bahwa ( ) merupakan semigrup komutatif idempoten sehingga menurut Teorema 2.B.2 relasi pada merupakan urutan parsial.
Relasi yang didefinisikan pada di atas bukan merupakan urutan total sebab terdapat matriks [ ] dan [ ] sedemikian sehingga
Demikian juga, relasi yang didefinisikan pada di atas bukan
merupakan urutan total sebab terdapat vektor , - r dan , -sedemikian sehingga
, - , - , - tetapi dan
Teorema 2.B.3 (Subiono, 2013)
Diberikan . Jika dengan , maka
( ) ( ).
Bukti:
Ambil sebarang dengan , maka ( )
( ) ( )
21 BAB III
SISTEM PERSAMAAN LINEAR ALJABAR MAX-PLUS
Sistem persamaan linear yang akan dibahas adalah sistem persamaan berbentuk dengan , , , dan . Penyelesaian sistem ini adalah himpunan semua vektor sedemikian sehingga . Sistem persamaan dapat ditulis ulang dalam bentuk persamaan matriks yang lebih rinci dan kemudian dalam bentuk sistem ekuivalen persamaan max-plus sebagai berikut
[ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Bila ditulis dalam bentuk baku, maka sistem persamaan di atas menjadi *( ) ( ) ( )+
*( ) ( ) ( )+
*( ) ( ) ( )+
}
Penyelesaian sistem persamaan diperoleh dengan menyelesaikan sistem terakhir di atas secara simultan. Sama halnya dalam aljabar biasa, penyelesaian sistem persamaan tidak selalu ada. Sistem yang tidak memiliki penyelesaian ditunjukkan dalam contoh berikut.
Contoh 3.1
Diberikan matriks [
] dan [ ]. Persamaan tidak
mempunyai penyelesaian, sebab bila mempunyai penyelesaian berarti ada [ ] sehingga
[
] [ ] [ ]
Didapat , * + , dan * + . Nampak bahwa tidak akan ada sehingga * + dan * + . Jadi, tidak mempunyai penyelesaian.
Di lain pihak, sistem selalu mempunyai penyelesaian
karena untuk diperoleh . Karena itu, masalah
penyelesaian sistem persamaan dapat diperlemah dengan mendefinisikan konsep sub-penyelesaian terbesar dengan sebelumnya mendefinisikan konsep sub-penyelesaian.
A. Sub-Penyelesaian Terbesar
Berikut diberikan definisi mengenai penyelesaian dan sub-penyelesaian terbesar sistem persamaan .
Definisi 3.A
Diberikan dan . Sub-penyelesaian sistem persamaan
Definisi 3.B
Sub-penyelesaian terbesar adalah vektor terbesar yang memenuhi
, dinotasikan dengan .
Dengan kata lain, untuk setiap sub-penyelesaian dari sistem persamaan . Sub-penyelesaian terbesar tidak harus merupakan suatu penyelesaian dari . Sub-penyelesaian terbesar diberikan oleh teorema berikut.
Teorema 3.A.1 (Rudhito, 2003)
Diberikan dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan , maka
( )
untuk setiap * + dan * +.
Bukti: { ( ) dan ( )
( )
Jadi, sub-penyelesaian dari sistem persamaan adalah setiap vektor di mana komponen-komponennya memenuhi
( )
Jika vektor , - didefinisikan dengan ( ) maka diperoleh: ( ) ( ) dan ( )
Hal ini berarti bahwa merupakan sub-penyelesaian dari sistem persamaan . Karena ( ) , maka . Akibatnya, . Jadi, vektor merupakan sub-penyelesaian terbesar dari
sistem persamaan .
Teorema 3.A.1 menjelaskan penyelesaian dari sedangkan
Teorema 3.A.2 (Butkovič, 2000)
Diberikan dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan . memiliki penyelesaian bila dan hanya bila adalah penyelesaiannya.
Bukti:
Misalkan merupakan penyelesaian dari sistem . Karena merupakan sub-penyelesaian terbesar maka . Berdasarkan Teorema 2.B.3 diperoleh
.
Jadi,
B. Eksistensi dan Ketunggalan Penyelesaian Sistem Persamaan Pada pembahasan sebelumnya telah dibahas mengenai sub-penyelesaian terbesar dari sistem persamaan . Pada bagian ini akan dibahas mengenai eksistensi dan ketunggalan penyelesaian sistem persamaan . Berdasarkan Teorema 3.A.2 dapat disimpulkan bahwa eksistensi penyelesaian sistem persamaan ini ditentukan oleh sub-penyelesaian terbesarnya.
Diberikan matriks dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan . Sub-penyelesaian terbesar merupakan calon penyelesaian sistem persamaan yakni vektor dengan
[ ] [ ( ) ( ) ( )] [ ( ) ( ) ( )] [ * + * + * + ]
Selanjutnya didefinisikan matriks „discrepancy‟ dinotasikan dengan dimana
[ ]
Catatan bahwa setiap dapat ditentukan dengan mengambil nilai maksimum dari setiap kolom .
Untuk memprediksi banyaknya penyelesaian persamaan , maka selanjutnya didefinisikan matriks yang merupakan reduksi matriks sebagai berikut
[ ] di mana {
Di bawah ini akan diberikan contoh-contoh penyelesaian sistem persamaan .
Contoh 3.2
[ ], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ] [ ] [ ]
Perhatikan bahwa terdapat elemen bernilai 1 pada tiap baris matriks . Karena pada tiap kolom matriks pasti terdapat elemen bernilai 1, maka sistem persamaan pada contoh ini hanya memiliki satu penyelesaian. Elemen-elemen dari vektor penyelesaian dapat ditentukan dengan mengambil nilai maksimum dari tiap kolom , yakni:
* + * + * +
Dengan demikian, , - merupakan calon penyelesaian sekaligus menjadi satu-satunya penyelesaian dari sistem persamaan . Hal ini ditunjukkan sebagai berikut
[ ] [ ] [ * + * + * + * + ] [ ] Contoh 3.3
Tentukan penyelesaian jika
[
], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ] [ ] [ ]
Perhatikan bahwa terdapat elemen bernilai 1 pada tiap baris matriks . Hal ini
berarti bahwa sistem persamaan pada contoh ini juga hanya memiliki satu penyelesaian yakni , - . Hal ini ditunjukkan sebagai berikut
[ ] [ ] [ * + * + * + ] [ ]
Contoh 3.2 dan 3.3 di atas merupakan contoh sistem persamaan yang memiliki penyelesaian tunggal baik untuk kasus maupun . Berikut ini akan diberikan contoh-contoh sistem persamaan yang tidak memiliki penyelesaian baik untuk kasus , maupun kasus .
Contoh 3.4
Tentukan penyelesaian jika
[ ], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ] [ ]
Berdasarkan matriks diperoleh , - . Namun demikian, dari
matriks di atas terlihat bahwa terdapat baris yang tidak memiliki nilai maksimum yakni baris pertama atau dengan kata lain semua elemen dalam baris pertama bernilai 0. Hal ini mengisyaratkan bahwa sistem persamaan tidak memiliki penyelesaian. Hal ini diperkuat melalui perhitungan berikut:
[ ] [ ] [ * + * + * + * + ] [ ] [ ]
Dengan demikian, hanya merupakan sub-penyelesaian terbesar dan bukan merupakan penyelesaian sistem persamaan .
Contoh 3.5
Tentukan penyelesaian jika
[
], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ] [ ]
Berdasarkan matriks diperoleh , - . Namun demikian, dari matriks di atas terlihat bahwa semua elemen dalam baris pertama bernilai 0. Hal ini mengisyaratkan bahwa sistem persamaan dalam contoh ini tidak memiliki penyelesaian. Hal ini juga diperkuat melalui perhitungan berikut:
[ ] [ ] [ * + * + * + ] [ ] [ ]
Dengan demikian, hanya merupakan sub-penyelesaian terbesar dan bukan merupakan penyelesaian sistem persamaan .
Contoh 3.6
Tentukan penyelesaian jika
Berdasarkan matriks dan vektor diperoleh matriks
[ ]
[ ]
Berdasarkan matriks diperoleh , - . Serupa dengan dua contoh
sebelumnya, sistem persamaan dalam contoh ini juga tidak memiliki penyelesaian karena semua elemen pada baris kedua matriks -nya bernilai 0.
Hal ini ditunjukkan juga melalui perhitungan berikut:
[ ] [
] [ * +
* +] [ ] [ ]
Jadi, sistem persamaan linear tersebut hanya memiliki sub-penyelesaian terbesar namun tidak mempunyai penyelesaian.
Selanjutnya akan diberikan contoh-contoh sistem persamaan yang memiliki takhingga banyak penyelesaian baik untuk kasus , maupun kasus .
Contoh 3.7
Tentukan penyelesaian jika
[ ], [ ], dan [ ]
[ ] [ ]
Berdasarkan matriks diperoleh , - . Selanjutnya akan dicek apakah memang merupakan penyelesaian dari .
[ ] [ ] [ * + * + * + * + ] [ ]
Ternyata memang merupakan penyelesaian dari . Akan tetapi, pada baris kedua dan ketiga matriks terdapat lebih dari satu nilai maksimum atau dengan kata lain terdapat lebih dari satu elemen bernilai 1 pada kedua baris tersebut. Hal ini mengisyaratkan bahwa sistem persamaan memiliki takhingga banyak penyelesaian. Selain itu, berdasarkan Teorema 3.A.1 diperoleh bahwa elemen-elemen dari merupakan batas atas. Karena itu, elemen-elemen vektor penyelesaian dalam contoh ini harus mememenuhi , dan . Pada baris pertama dan keempat matriks nampak bahwa nilai maksimum terdapat pada kolom ke-3 karena itu . Pada baris kedua nilai maksimum terdapat pada kolom ke-2 dan ke-3 maka terdapat dua kemungkinan yakni atau . Bila nilai diubah maka akan mempengaruhi persamaan baris pertama dan keempat. Karena itu, selama maka persamaan pertama dan keempat akan selalu terpenuhi. Demikian halnya dengan
memilih maka persamaan baris akan selalu terpenuhi. Jadi, semua vektor yang berbentuk , - dengan dan juga memenuhi sistem persamaan.
Jadi, sistem persamaan dalam contoh ini memiliki takhingga banyak penyelesaian.
Contoh 3.8
Tentukan penyelesaian jika
[ ], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ] [ ]
Berdasarkan matriks diperoleh , - . Selanjutnya akan dicek apakah memang merupakan penyelesaian dari .
[ ] [ ] [ * + * + * + ] [ ]
Nampak bahwa memang merupakan penyelesaian dari sistem persamaan . Akan tetapi, dapat diperiksa bahwa semua yang memenuhi bentuk , - dengan juga memenuhi sistem persamaan di atas.
Jadi, sistem persamaan dalam contoh ini memiliki takhingga banyak penyelesaian.
Contoh 3.9
Tentukan penyelesaian jika
[
], [ ], dan [ ]
Berdasarkan matriks dan vektor diperoleh matriks
[ ]
[ ]
Berdasarkan matriks diperoleh , - . Selanjutnya ditunjukkan bahwa juga merupakan penyelesaian dari sistem persamaan yakni:
[ ] [
] [ * +
* + ] [ ]
Namun demikian, dapat diperiksa bahwa semua yang berbentuk , -dengan dan juga memenuhi sistem persamaan di atas.
Jadi, sistem persamaan pada contoh ini juga memiliki takhingga banyak penyelesaian.
Matriks dan berperan dalam menentukan perilaku sistem persamaan . Berikut ini diberikan teorema mengenai ada atau tidak adanya (eksistensi) penyelesaian .
Teorema 3.B.1
Diberikan sistem persamaan di mana dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan .
1. Jika terdapat baris nol pada matriks maka sistem tidak mempunyai penyelesaian.
2. Jika terdapat paling tidak satu elemen 1 pada tiap baris , maka
adalah penyelesaian dari sistem persamaan .
Bukti:
1. Misalkan baris nol pada matriks adalah baris ke dan andaikan merupakan penyelesaian dari sistem persamaan , maka
( ) Akibatnya,
.
Dengan demikian, tidak memenuhi persamaan ke- . Hal ini bertentangan dengan adalah penyelesaian dari sistem persamaan . Jadi, bukan merupakan penyelesaian dari sistem persamaan atau sistem persamaan tidak mempunyai penyelesaian.
2. Akan dibuktikan kontrapositifnya. Andaikan bukan merupakan penyelesaian dari sistem persamaan . BerdasarkanTeorema 3.A.1 diperoleh
Akibatnya,
( )
Jika bukan merupakan penyelesaian dari , maka terdapat sedemikian sehingga
( )
Hal ini ekuivalen dengan
Karena ( ) untuk beberapa , maka tidak ada elemen dalam baris dari yang bernilai 1.
Teorema 3.B.1 di atas digunakan untuk menentukan eksistensi penyelesaian sistem persamaan . Namun demikian, eksistensi ini belum menjelaskan kapan penyelesaiannya tunggal dan kapan penyelesaiannya taktunggal. Karena itu, untuk menentukan ketunggalan sistem persamaan diberikan definisi berikut.
Definisi 3.B
Elemen bernilai 1 pada suatu baris dinamakan elemen peubah tetap jika 1. Elemen tersebut merupakan satu-satunya elemen bernilai 1 pada baris
tersebut ( lone-one), atau
2. Elemen tersebut berada pada kolom yang sama dengan lone-one. Elemen-elemen bernilai 1 lainnya dinamakan elemen-elemen slack.
Tabel berikut ini akan menunjukkan elemen peubah tetap dari setiap contoh yang telah diberikan sebelumnya. Elemen yang dilingkari merupakan elemen peubah tetap
Tabel 2: Elemen Peubah Tetap Tidak Mempunyai Penyelesaian Satu Penyelesaian Takhingga Banyak Penyelesaian Contoh 3.4 [ ] Contoh 3.2 [ ] Contoh 3.7 [ ] Contoh 3.5 [ ] Contoh 3.3 [ ] Contoh 3.8 [ ] Contoh 3.6 [ ] Contoh 3.9 [ ]
Pada contoh 3.2, semua elemen bernilai 1 merupakan peubah tetap. Persamaan baris pertama menetapkan elemen , persamaan baris kedua menetapkan elemen , dan persamaan baris ketiga menetapkan elemen . Ketika sampai pada persamaan keempat, semua elemen sudah ditentukan. Setiap elemen yang sudah dipilih tidak dapat diubah karena bila diubah akan menimbulkan pertidaksamaan pada salah satu dari ketiga baris sebelumnya.
Pada contoh 3.3, semua elemen bernilai 1 juga merupakan peubah tetap. Persamaan baris pertama menetapkan elemen , persamaan baris kedua menetapkan elemen , dan persamaan baris ketiga menetapkan elemen
.
Pada contoh 3.7, terdapat elemen slack pada . Persamaan baris pertama menetapkan elemen . Pada persamaan baris kedua, terdapat dua kemungkinan untuk memenuhi persamaan yakni atau . Akan tetapi, nilai sudah ditetapkan sebelumnya yakni sama dengan 3. Jadi, asalkan maka persamaan baris diatasnya tidak akan berubah. Dengan cara yang sama, pada persamaan baris ketiga, asalkan maka persamaan baris diatasnya tidak akan berubah. Sedangkan, pada persamaan baris keempat, elemen penyelesaiannya sudah ditetapkan oleh persamaan baris pertama. Dengan demikian, dengan menetapkan dan asalkan serta , maka persamaan baris akan selalu benar.
Berikut ini diberikan teorema untuk menunjukkan bila mana persamaan memiliki penyelesaian tunggal dan bilamana penyelesaiannya taktunggal.
Teorema 3.B.2
Diberikan persamaan matriks dimana dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan serta penyelesaian persamaan ada.
1. Jika tiap baris memiliki lone one, maka penyelesaian sistem persamaan tunggal.
2. Jika terdapat elemen-elemen slack pada , maka sistem memiliki takhingga banyak penyelesaian.
Bukti:
1. Jika terdapat lone one pada tiap baris , maka terdapat satu elemen peubah tetap pada tiap baris . Hal ini berarti bahwa tidak akan ada elemen-elemen slack. Dengan demikian, semua elemen tetap dan penyelesaian sistem persamaan tunggal.
2. Misalkan adalah salah satu elemen slack pada dan merupakan penyelesaian dari . Karena tidak tetap, maka tidak terdapat elemen peubah tetap pada kolom ke dari . Jadi, persamaan dapat dipenuhi tanpa menggunakan elemen . Dengan demikian, meskipun nilai menunjukkan nilai maksimum yang mungkin untuk elemen ini, setiap nilai yang lebih kecil atau sama dengan tidak akan mempengaruhi eksistensi persamaan baris yang telah ditetapkan.
Sistem persamaan dalam Contoh 3.2 dan 3.3 memiliki penyelesaian tunggal karena pada tiap baris matriks -nya memiliki lone one. Sedangkan sistem persamaan dalam Contoh 3.7, 3.8 dan 3.9 memiliki
takhingga banyak penyelesaian karena terdapat elemen slack pada matriks -nya.
Akibat 3.B
Diberikan persamaan matriks di mana dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan serta
. Jika penyelesaian persamaan ada maka sistem memiliki
takhingga banyak penyelesaian.
Bukti:
Penyelesaian sistem persamaan ada maka tidak terdapat baris nol pada matriks Andaikan penyelesaian sistem tunggal maka terdapat lone one pada tiap baris . Sementara itu, berarti banyaknya persamaan lebih sedikit
daripada banyaknya variabel. Karena itu, pastilah terdapat slack pada matriks
. Hal ini bertentangan dengan penyelesaian sistem tunggal. Jadi, haruslah
sistem memliki takhingga banyaknya penyelesaian.
Pembahasan pada bagian A dan B dalam bab ini ditekankan pada sistem persamaan dengan dengan elemen-elemen pada setiap kolomnya tidak semuanya sama dengan dan . Berikut ini diberikan penyelesaian sistem persamaan untuk kasus-kasus lain.
Andaikan terdapat * + sedemikian sehingga untuk setiap * + dan maka berlaku hal-hal berikut
1. Jika elemen-elemen pada setiap baris matriks tidak semuanya sama dengan maka untuk sebarang . Hal ini berangkat dari fakta bahwa elemen netral merupakan elemen penyerap terhadap operasi .
2. Jika terdapat baris pada matriks dengan semua elemennya sama dengan maka sistem tidak memiliki penyelesaian. Hal ini ditunjukkan sebagai berikut. Andaikan baris tersebut adalah baris ke- . Persamaan ke- berbentuk
( ) * +
Mengingat untuk setiap berlaku
maka ( ) . Dengan kata lain, persamaan baris ke- tidak terpenuhi. Jadi, sistem tidak memiliki penyelesaian.
Berikut diberikan contoh-contoh untuk mengilustrasikan dua hal di atas.
Contoh 3.10
Diberikan sistem persamaan linear [
] [ ] [ ]
Sistem persamaan ini ekuivalen dengan
{ atau { atau { ( ) ( ) atau
Jadi, semua vektor yang berbentuk , - merupakan penyelesaian sistem di atas.
Contoh 3.11
Diberikan sistem persamaan linear [ ] [ ] [ ]
Sistem persamaan ini ekuivalen dengan
{ atau { atau {
Karena maka persamaan baris kedua tidak terpenuhi. Jadi, sistem persamaan di atas tidak memiliki penyelesaian.
Selanjutnya, andaikan terdapat * + sedemikian sehingga
untuk setiap * + dan terdapat * + sedemikian
sehingga maka berlaku hal-hal berikut
1. Jika elemen-elemen pada baris ke- matriks tidak semuanya sama dengan maka sistem tidak memiliki penyelesaian. Hal ini ditunjukkan sebagai berikut. Karena elemen-elemen pada baris ke- tidak semuanya sama dengan maka terdapat * + sedemikian sehingga . Agar persamaan ke- terpenuhi maka haruslah . Namun demikian, karena terdapat * + sedemikian sehingga maka persamaan ke- tidak terpenuhi. Jadi, sistem tidak memiliki penyelesaian.
2. Jika elemen-elemen pada baris ke- matriks semuanya sama dengan maka untuk sebarang . Hal ini berangkat dari fakta bahwa elemen netral merupakan elemen penyerap terhadap operasi .
Berikut diberikan contoh-contoh untuk mengilustrasikan dua hal di atas.
Contoh 3.12
Diberikan sistem persamaan linear [
] [ ] [ ]
Sistem persamaan ini ekuivalen dengan
{ atau { atau { ( ( ) )
Agar persamaan baris kedua terpenuhi maka haruslah . Namun demikian, jika maka persamaan baris pertama tidak terpenuhi sebab . Jadi, sistem di atas tidak memiliki penyelesaian.
Contoh 3.13
Diberikan sistem persamaan linear [
] [ ] [ ]
Sistem persamaan ini ekuivalen dengan
{ atau { atau atau
Jadi, semua vektor yang berbentuk , - merupakan penyelesaian sistem di atas.
Kasus selanjutnya adalah andaikan elemen-elemen pada setiap kolom matriks tidak semuanya sama dengan dan terdapat * + sedemikian sehingga . Jika maka . Hal ini ditunjukkan sebagai berikut. Persamaan ke- berbentuk . Karena maka
haruslah .
Contoh 3.13
Diberikan sistem persamaan linear [ ] [ ] [ ]
Sistem persamaan ini ekuivalen dengan
{ atau {
Agar persamaan baris kedua terpenuhi maka haruslah . Akibatnya, .
Jadi, , - merupakan penyelesaian sistem di atas.
C. Penyelesaian Sistem Persamaan dengan Program MATLAB Bila sistem memuat banyak persamaan, dalam hal ini ukuran matriks sangat besar maka perhitungan manual dirasa kurang efektif untuk menentukan penyelesaian sistem persamaan linear . Untuk itu, perlu dibuat program komputer untuk memudahkan perhitungan. Bahasa program yang akan digunakan adalah bahasa pemograman komputer MATLAB. Program ini akan menampilkan penyelesaian sistem persamaan linear . Program secara lengkap diberikan sebagai berikut dengan nama file solsislinmax.
% Program Matlab Penyelesaian Sistem Persamaan Linear Ax = b % Input: A = matriks max-plus Amxn
% b = vektor mx1
% Output: Menampilkan penyelesaian sistem
function x = solsislinmax
% Memasukkan matriks A dan b
A = input('Masukkan matriks A(mxn) = ');
disp(' ')
b = input('Masukkan matriks b(mx1) = '); disp(' ') [m,n]= size (A); [p,q]= size (b); if m == p & q == 1 A1=zeros(1,n); for j = 1:n if A(:,j)== -inf A1(j)=0; else A1(j)=1; end; end; Sum1 = sum(A1); b1=zeros(m,1); for i = 1:m if b(i)== -inf b1(i)=0; else b1(i)=1; end; end; Sum2 = sum(b1);
if Sum1 == n & Sum2 == m for i = 1:m for j = 1:n
D(i,j)= -b(i)+ A(i,j); end; end; xj = max(D); xc = -xj'; R = zeros(m,n); for j = 1:n for i = 1:m if D(i,j)== xj(j) R(i,j) = 1; else R(i,j) = 0; end; end; end;
Berikut ini diberikan hasil eksekusi untuk beberapa contoh soal yang telah diberikan pada bagian sebelumnya
c = zeros(m,1); for i = 1:m if R(i,:)== 0 c(i)= 0; else c(i)= 1; end end; Sum3 = sum(c); if Sum3 < m x = '{}'; else x = xc; end
%Menampilkan Penyelesaian Sistem
disp('Matriks A = '),disp(A)
disp('Matriks b = '),disp(b) disp('Matriks D = '),disp(D)
disp('Matriks R = '),disp(R)
disp('Penyelesaian sistem adalah '), disp('x = ')
disp(x) else
disp('Elemen-elemen tiap kolom matriks A tidak semuanya -inf dan elemen-elemen matriks b semuanya berhingga')
end;
% Peringatan sistem persamaan tidak dapat diselesaikan
else
disp('Ordo matriks A dan b tidak sesuai') end;
Contoh 3.2
Masukkan matriks A(mxn) = [1 6 11; 4 1 2; 8 -1 0; 10 5 12] Masukkan matriks b(mx1) = [12; 5; 8; 13] Matriks A = 1 6 11 4 1 2 8 -1 0 10 5 12 Matriks b = 12 5 8 13 Matriks D = -11 -6 -1 -1 -4 -3 0 -9 -8 -3 -8 -1 Matriks R = 0 0 1 0 1 0 1 0 0 0 0 1
Penyelesaian sistem adalah x =
0 4 1
Contoh 3.4
Masukkan matriks A(mxn) = [1 6 11; 4 1 2; 8 -1 0; 10 5 12] Masukkan matriks b(mx1) = [14; 6; 8; 13] Matriks A = 1 6 11 4 1 2 8 -1 0 10 5 12 Matriks b = 14 6 8 13 Matriks D = -13 -8 -3 -2 -5 -4 0 -9 -8 -3 -8 -1 Matriks R = 0 0 0 0 1 0 1 0 0 0 0 1
Penyelesaian sistem adalah x =
Contoh 3.9
Masukkan matriks A(mxn) = [1 6 11;4 1 2;8 -1 0;10 5 12] Masukkan matriks b(mx1) = [14;5;3;15] Matriks A = 1 6 11 4 1 2 8 -1 0 10 5 12 Matriks b = 14 5 3 15 Matriks D = -13 -8 -3 -1 -4 -3 5 -4 -3 -5 -10 -3 Matriks R = 0 0 1 0 1 1 1 1 1 0 0 1
Penyelesaian sistem adalah x =
-5 4 3
50 BAB IV
APLIKASI SISTEM PERSAMAAN LINEAR ALJABAR MAX-PLUS DALAM MASALAH RAMP HANDLING PESAWAT
A. Ramp Handling
Ramp handling merupakan kegiatan penanganan pesawat yang dilakukan di ramp area atau apron yakni suatu pelataran yang ada di bandara, saat jeda waktu
antara pesawat block-on (yakni saat ganjalan pesawat dipasang dan pesawat dalam posisi berhenti) hingga pesawat block-off (yakni saat ganjalan dilepas dan pesawat bersiap menuju landasan pacu). Waktu antara pesawat block-on dan pesawat
block-off ini dikenal dengan istilah ground time. Keberlangsungan kegiatan ramp handling berada dalam pengawasan dari satuan unit khusus yang dikenal dengan
istilah ramp dispatcher. Setiap petugas ramp dispatcher bertanggung jawab untuk mengawasi dan mengkoordinasi segala aktivitas ramp berkaitan dengan keberangkatan ataupun kedatangan pesawat. Secara umum, aktivitas-aktivitas yang dilakukan dalam ramp handling adalah sebagai berikut
1. Maintenance merupakan kegiatan pemeriksaan/pemeliharaan kondisi pesawat, termasuk kebersihan tempat duduk dan pantry.
2. Fueling/Refueling merupakan kegiatan pengisian bahan bakar pesawat. 3. Loading/Unloading berkaitan pelaksanaan bongkar muat barang/bagasi. 4. Aircraft Cleaning berkaitan dengan kegiatan membersihkan kabin pesawat
5. Catering berkaitan dengan penyediaan konsumsi bagi para penumpang selama penerbangan.
Menurut Widadi (2001), penanganan pesawat di bandara dibedakan atas dua cara yakni turnaround arrangement dan transit arrangement. Turnaround
arrangement adalah penanganan bagi pesawat yang mendarat di kota tujuan akhir
(destination) sedangkan transit arrangement adalah penanganan bagi pesawat yang mendarat di kota persinggahan atau transit. Penanganan pesawat ini dilakukan pada tempo waktu yang sudah ditentukan yakni sesuai dengan ground
time agar sesuai dengan jadwal penerbangan (departure time).
Lebih lanjut, Widadi menambahkan penanganan pesawat di bandara udara, baik turnaround arrangement maupun transit arrangement menganut sistem yang sama. Perbedaannya terletak pada lama waktu penanganannya. Penanganan
transit arrangement biasanya lebih pendek dibanding turnaround arrangement.
Hal ini disebabkan karena pada transit arrangement terdapat perbedaan dalam hal-hal tertentu, yaitu:
1. Kabin tidak dibersihkan seluruhnya.
2. Awak pesawat (crew) biasanya tidak diganti. 3. Penumpang transit tidak turun ke ruang transit.
4. Kadangkala konsumsi untuk penumpang sudah tersedia di dalam pesawat, kecuali jika ada penambahan penumpang pada saat-saat terakhir.
Prosedur penanganan pesawat di bandara udara antara satu jenis pesawat dengan jenis pesawat yang lain tidak sama. Hal ini tergantung tipe pesawat,
kondisi pesawat, jarak yang akan ditempuh pesawat, serta banyaknya penumpang. Namun, secara umum lama ground time untuk keperluan turnaround arrangement adalah 40 menit sampai 1 jam sedangkan untuk transit arrangement memerlukan minimal 25 menit untuk penerbangan domestik dan sekitar 1 jam untuk penerbangan internasional (Bazargan, 2004).
B. Aplikasi Sistem Persamaan dalam Masalah Ramp Handling Berdasarkan penjelasan di atas nampak bahwa kegiatan ramp handling merupakan salah satu masalah sinkronisasi yang merupakan salah satu karakteristik DES. Dalam masalah sinkronisasi, kejadian-kejadian (events) terjadi secara simultan dan harus selesai pada batas waktu yang ditentukan (deadline). Rangkaian kegiatan ramp handling dilakukan secara simultan dan harus selesai pada waktu yang ditentukan sehingga ketepatan jadwal tercapai.
Misalkan di suatu bandara terdapat tiga pesawat yakni pesawat A, B dan C telah tiba di gate-nya masing-masing. Pesawat-pesawat tersebut membutuhkan penanganan sebelum penerbangan berikutnya. Penanganan yang dibutuhkan berupa refueling, maintenance, food service dan luggage service. Masing-masing pesawat membutuhkan waktu yang berbeda untuk refueling dan food service (terkait dengan jarak tempuh penerbangan selanjutnya), maintenance (tergantung apakah ada masalah dalam penerbangan selanjutnya atau tergantung pada usia pesawat terbang tersebut), dan luggage service (berkaitan dengan jarak tempuh dan banyaknya penumpang). Ketiga pesawat tersebut akan ditangani sekaligus dengan asumsi bahwa tim yang bertugas memadai dan peralatan yang dibutuhkan pun memadai. Berikut ini diberikan matriks yang berisi waktu yang diperlukan
Gate 1 Gate 2 Gate 3
untuk penanganan pesawat per kegiatan penanganan (waktu kegiatan dalam menit). [ ] Contoh 4.1
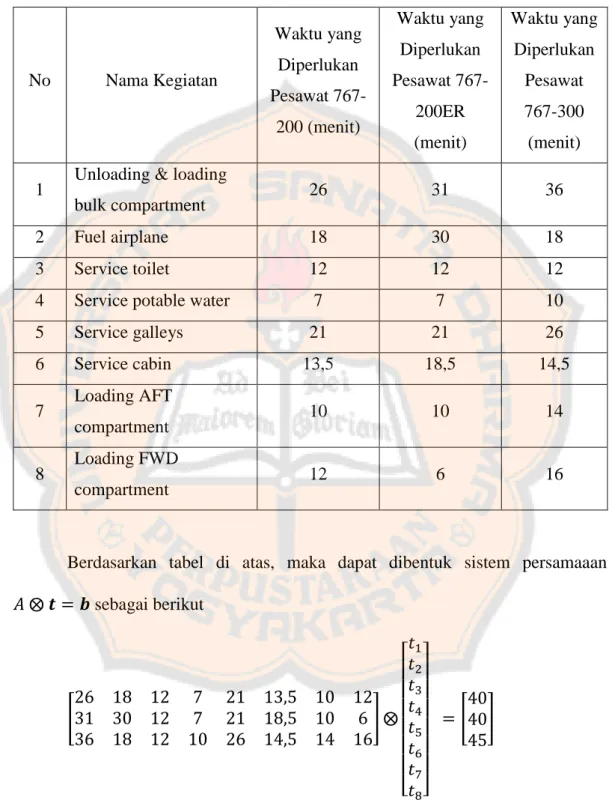
Ketiga pesawat memiliki ground time berturut-turut , , menit. Akan dicari waktu mulai paling lambat untuk kegiatan , , , dan sedemikian sehingga kegiatan terakhir sudah selesai pada waktu keberangkatan pesawat. Masalah ini dapat diformulasikan dalam bentuk sistem persamaan aljabar max-plus sebagai berikut.
[ ] [ ] [ ]
Dalam hal ini kita akan mencari vektor . Hasil eksekusi program MATLAB untuk sistem ini diberikan sebagai berikut
Masukkan matriks A(mxn) = [25 10 35 15;15 45 15 20;25 15 20 15] Masukkan matriks b(mx1) = [45;50;55] Matriks A = 25 10 35 15 15 45 15 20 25 15 20 15 Matriks b = 45 50 55