this PDF file Analisa Karakteristik Distribusi Tekanan dan Kecepatan Pada Bodi Aerodinamika Airfoil Dengan Metoda Panel Dalam Fenomena | Sasongko | Jurnal Teknik Mesin MES03050105
Teks penuh
Gambar
![Gambar 2. Ilustrasi Kerugian Kondisi Kutta[2]](https://thumb-ap.123doks.com/thumbv2/123dok/3661748.1467648/3.596.47.266.66.179/gambar-ilustrasi-kerugian-kondisi-kutta.webp)
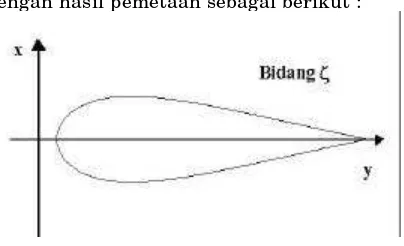
![Gambar 3. Ilustrasi Lingkaran[3]](https://thumb-ap.123doks.com/thumbv2/123dok/3661748.1467648/4.596.84.312.82.449/gambar-ilustrasi-lingkaran.webp)
![Gambar 6. Ilustrasi Metode Panel pada Bodi Airfoil[1]](https://thumb-ap.123doks.com/thumbv2/123dok/3661748.1467648/5.596.286.508.193.290/gambar-ilustrasi-metode-panel-pada-bodi-airfoil.webp)
![Gambar 7. Ilustrasi Lembaran Source dengan UniformFlow.[1]](https://thumb-ap.123doks.com/thumbv2/123dok/3661748.1467648/6.596.88.298.61.172/gambar-ilustrasi-lembaran-source-dengan-uniformflow.webp)
Dokumen terkait
Setelah adanya penyewaan sepeda online yang sudah menggunakan internet untuk mempromosikan nya, kini orang-orang pun bisa dengan mudah mengakses apapun dan mencari
Setiap sekolah harus melakukan penatausahaan keuangan secara baik dan tertib atas dana yang diterima mulai dari penyusunan Rencana Kerja dan Anggaran Sekolah (RKAS)
Berdasarkan hasil analisis yang dilakukan dengan menggunakan metode regresi pohon diperoleh kesimpulan bahwa cara belajar dan motivasi belajar adalah faktor
9 Ibid, Aqwa Naser Daulay dan Latief Ilhamy,hlm.. dapat memuaskan keinginan atau kebutuhan 10. Dari pengertian diatas dapat disimpulkan bahwa produk adalah sesuatu yang
Dan dari 56 ibu balita yang memiliki status pekerjaan tidak bekerja sebanyak 43 ibu balita (76,8%) memiliki frekuensi penimbangan balita dengan kategori cukup dan
Faktor yang menyumbang kepada kemajuan pertanian dalam kerajaan Angkor ialah terletak di lembah sungai Mekong. Di Kawasan ini tanahnya subur sesuai untuk kegiatan pertanian
Penggunaan antibiotik berspektrum luas akan berpeluang meningkatkan prevalensi resistensi antibiotik terhadap bakteri, seperti MRSA.Tujuan penelitian untuk mengetahui
Ana