Bab V. Untuk menentukan besarnya kecepatan suatu titik yang bergerak. terhadap sebuah badan yang juga bergerak, perhatikan titik B yang

(1)

Diktat Kinematika

Oleh : Ir Ir. Erwin Sulityo - Ir. Endi Sutikno.

Program Semi Que IV Tahun 2003 Fakultas Teknik Jurusan Mesin

Universitas Brawijaya 56 Bab V

K

E

C

E

P

A

T

A

N

D

A

N

P

E

R

C

E

P

A

T

A

N

P

A

D

A

D

U

A

T

I

T

I

K

Y

A

N

G

B

E

R

I

M

P

I

T

K

O

M

P

O

N

E

N

C

O

R

I

O

L

I

S

D

A

R

I

P

E

R

C

E

P

A

T

A

N

O

R

M

A

L

5.1 Kecepatan relatif dua titik berimpit

Untuk menentukan besarnya kecepatan suatu titik yang bergerak terhadap sebuah badan yang juga bergerak, perhatikan titik B yang bergerak terhadap badan M, yang pada saat bersamaan badan M tersebut bergerak dalam satu bidang, seperti terlihat pada gambar.

Ditetapkan sebuah system sumbu koordinat, X dan Y, dan akan digunakan untuk menentukan posisi absolute suatu titik dalam bidang X dan Y. Sebuah system sumbu yang kedua, c dan d ditetapkan pada badan M dan bergerak dalam cara yang sama seperti badan M

(2)

Diktat Kinematika

Universitas Brawijaya 57

bergerak. Sudut ? memberikan posisi sudut dari sumbu c dengan sumbu X

Pada gambar diatas menunjukkan bahwa perpindahan X dan Y dari titik B dapat dinyatakan sebagai berikut, dimana A merupakan satu titik tetap pada M :

XB = XA + c cos

θ

- d sin

θ

YB = YA + c sin

θ

+ d cos

θ

Dideferensialkan persamaan-persamaan di atas dan mengganti

dt dθ ω =

yaitu kecepatan sudut badan M, dengan menganggap bahwa c dan d adalah variable-variabel

θ

ω

θ

ω

sin

cos

sin

dt

dd

d

dt

dc

c

dt

dX

V

dt

dX

_x _A B B

=

−

+

−

c A B ? c d d ? O _XB YB XA YA Y M (c cos ? - d sin ?) (a) (c sin ? + d cos ?) X

(3)

Diktat Kinematika

Universitas Brawijaya 58 θ θ ω θ θ

ωcos sin sin cos

dt dd d dt dc c dt dY V dt dY _Y _A B B = = + + − + Dengan u_c dt dc = , u_d dt dd = , X A A

V

dt

dX

=

dan y A A

V

dt

dY

=

Maka x

ω

(

sin

θ

cos

θ

)

_c

cos

θ

_d

sin

θ

A x B

V

c

d

u

V

=

−

+

−

θ θ θ θ

ω( cos sin ) c sin dcos

y A Y

B V c d u u

V = + − + +

Dengan menjumlahkan persaman diatas secara vektor dan menyederhanakan seperti dibawah :

(a). VB = (VX

B V y

B)

(b). VA = (VX_A Vy_A)

(c). ω(csinθ +dcosθ) ω(ccosθ −dsinθ) = ω

(

c2 +d2

)

1/2

? (c cos ? - d sin ?) A B ? c d O Y (b) (c sin ? + d cos ?) X ? H R J R ? ? (c cos ? - d sin ?) ? (c sin ? + d cos ?) G 90-? ?

(4)

Diktat Kinematika

(d). (uc cos ? uc sin ?) =

[

₂ ₂

]

1/2

) sin ( ) cos (uc θ + uc θ = uc

(e). (ud cos ? ud sin ?) =

[

2 2

]

1/2

)

sin

(

)

cos

(

u

_d

θ

+

u

_d

θ

= ud Maka VB = V_B R ? uc ud

Tetapi V_B R? = VBm yaitu kecepatan suatu titik pada badan M yang

berimpit dengan titik B, karena A dan satu titik pada badan M yang berimpit dengan B adalah dua buah titik pada satu penghubung kaku. Juga, uc ud = u, yaitu kecepatan relatif B terhadap badan M. sehingga

persamaan diatas dapat dituliskan dalam bentuk :

VB = VM_B u

Sebagai kesimpulan , interpretasi persamaan diatas yaitu bahwa kecepatan sebuah titik yang bergerak terhadap satu badan yang juga bergerak, diperoleh dengan menjumlahkan secara vector kecepatan titik yang berimpit pada badan gerak dan kecepatan relatif terhadap badan, dengan menganggap badan diam.

Persamaan dapat dituliskan dalam bentuk siap pakai dengan menyebut titik gerak sebagai B3 titik berimpit pada badan M sebagai B4, sehingga bentuknya menjadi :

VB3 = VB 4 VB3B4

Interprestasi sebenarnya adalah bahwa kecepatan relatif, VB3B4, diamati

dengan menganalisa lintasan gerak titik B3 relatif ke penhubung 4 (penghubung dimana titik B3 bergerak ), dengan menganggap penghubung 4 diam.

(5)

Diktat Kinematika

5.2 Percepatan dua titik berimpit

Untuk menentukan percepatan relatif dua buah titik yang berimpit dimana satu titik bergerak terhadap satu body yang bergerak, seperti pada pasangan sliding (sliding pair). Maka analisa percepatan untuk keadaan tersebut diatas akan lebih rumit karena pusat kecepatan relatif untuk pasangan seperti ini berada di tak terhingga.

Penyelesaian untuk analisa kinematika dari problem diatas ialah dengan berdasarkan ketentuan bahwa hubungan yang mentransfergerakan dari pasangan seperti keadaan diatas berimpit pada satu titik.

Kedua titik yang berimpit dari pasangan link tersebut mempunyai kecepatan dan percepatan relatif satu dengan yang lainnya.

Dalam analisa ini kita akan mencari persamaan yang menentukan besarnya percepatan normal relatif antara kedua titik tersebut.

M Q S ? s ? s VQ S M Q S ? s z s VQ S ?zs Q pada link z S pada link s

M pada link z dan link s

(6)

Diktat Kinematika

Pada gambar (a) diatas link S bergerak dengan kecepatan sudut ? S , sedangkan titik Q bergerak diatas link S dengan jari-jari lintasan ? dan pusat lintasan M.

Dengan memisalkan MQ = link z dengan panjang ? yang berputar diatas link S dengan M sebagai pusatnya serta kecepa tan sudutnya ? ZS.

Pada gambar (b) Arah VQS keatas apabila ?ZS. Arahnya berlawanan arah putaran jarum jam dan arahnya akan kebawah bila ?ZS berputar searah putaran jarum jam.

Kecepatan Q relatif terhadap S : VQS = ? ? ZS. Atau

ρ ω QS ZS V ± =

Tanda positip ?ZS berlawanan dengan putaran jarum jam dan apabila negative arah ? ZS sama dengan putaran jarum jam.

Kecepatan sudut absolute dari link Z adalah : ?Z = ?S + ?ZS

Dengan menggunakan persamaan gerak relatif maka : ( AQM )n = ( AQS )n + ( ASM )n

( AQS )n = ( AQM )n + ( ASM )n

Kemudian ditinjau titik Q dan titik M pada link z.

M

Q

? ?zs

(7)

Diktat Kinematika

Universitas Brawijaya 62 ( AQM )n = ? 2 Z

ω

= ? (?S + ?ZS )2 = ? 2 S

ω

+ ? 2 ZS

ω

± 2 ?

ω

_S ?

ω

_ZS

Dengan memasukkan persamaan diatas dalam persamaan ini dihasilkan : ( AQM )n = ? 2 S

ω

+ ₂ 2 ρ ρVQS ± 2 ?

ω

_S ρ QS V ( AQM )n = ? 2 S

ω

+ ρ 2 QS V _± 2

ω

_S VQS Kemudian ditinjau titik S dan M pada link S.

( ASM )n = ? 2 S

ω

Mensubstitusikan persamaan () dan () kedalam persamaan () maka akan didapatkan : ( AQM )n = ? 2 S ω + ρ 2 QS V ± 2 ωS VQS - ? 2 S ω M S S ω ρ

(8)

Diktat Kinematika

Universitas Brawijaya 63 ( AQM )n = ρ 2 QS V ± 2

ω

_S VQS

Persamaan () menunjukkan besarnya percepatan normal titik Q yang bergerak diatas link S yang juga bergerak.

Komponen percepatan

ρ

2 QS V

adalah percepatan normal titik Q,

apabila link S diam.

Dalam hal ini berarti VQS = Vq , dan arah

ρ

2 QS V

adalah dari Q ke M.

Sedangkan komponen percepatan ± 2 ωS VQS disebut komponen

Coriolis dari percepatan normal titik Q relatif terhadap titik S.

Tanda positip menunjuj\kkan bahwa arah ωZS sama dengan arah ωS ,

dan komponen

+ 2 ωS VQS arahnya dari M menuju Q.

Sekarang apabila lintasan titik Q diatas link S adalah berpa garis lurus, maka dalam hal ini harga _ρ tak terhingga, sehingga komponen percepatan ρ 2 QS V harganya nol.

Jadi untuk kasus ini percepatan normal antara titik Q relatif terhadap S adalah :

( AQS )n = _± 2 ωS VQS

Selanjutnya percepatan normal titik S relatif terhadap titik Q.

(9)

Diktat Kinematika

Cara untuk menentukan arah komponen percepatan coriolis

Arah dari komponen percepatan coriolis dapat juga kita tentukan tanpa memperhatikan tanda positip atau negative dari komponen percepatan tersebut.

Arah dari 2 ωS VQS adalah sama dengan arah VQS yang diputar

900_{menurut arah putaran}

S

ω

.Sedangkan arah 2

ω

_S VSQ sama dengan arah VSQ yang diputar 900_{menurut arah putaran}

S

ω . Selain dengan pedoman diatas arah komponen percepatancoriolis dapat juga ditentukan sebagai berikut :

Arah percepatan coriolis 2

ω

_S VQS adalah sama dengan arah perkalian cros dari kecepatan sudut link pembawa ω_S dan kecepatan relatif antara titik Q dan S.

Jadi secara vektor hal tersebut diatas dapat dituliskan :

( AQS )coriolis = 2

ω

_S VQS ( ASQ )coriolis = 2 ωS VSQ

Komponen percepatan coriolis seperti yang telah kita bahas diatas terjadi pada dua titik yang berimpit dari dua buah link yang merupakan

(10)

Diktat Kinematika

Pada ketiga gambar diatas titik Q pada link q dan titik S pada link s. Pada gambar ini link q mempunyai gerakan sl iding, slip-rolling atau rolling pada link s.

Dalam hal ini link s dikatakan sebagai link pembawa

CONTOH SOAL :

(11)

Diktat Kinematika

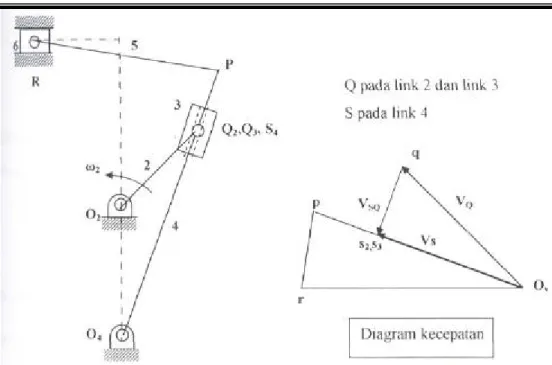
Pada mekanisme diatas diketahui data-data sebagai berikut :

Diagram Kecepatan

Kecepatan titik Q : VQ = (O2Q)ω₂

VQ diketahui tegak lurus O2Q arahnya sesuai

_ω

₂

Table diagram kecepatan

No Besaran Harga Arah 1 VQ = Ov - q _(O2Q) 2 ω - O2Q 2 VSQ = q - s ? ¦ O4S 3 VS = Ov - s ? - O4S 4 VP = Ov - p Diperoleh dengan ( S O V P O VP S 4 4 = ) 5 VR = Ov -r ? ¦ Lintasan titik R Dari diagram kecepatan didapat :

VSQ = q – s ( arah ke bawah) VS = o – s

(12)

Diktat Kinematika

Universitas Brawijaya 67 ?S = S O VS 4

( arahnya berlawanan putaran jarum jam )

Diagram Percepatan

Percepatan titik A yang berputar terhadap satu pusat tetap sama dengan

AQ = 2 2

)

(

O

Q

ω

2

(

O

2

Q

)

α

2

Harga O2A dan

_ω

₂ diketahui sehingga percepatan normal

2

2 )

(O Q ω 2dapat dihitung. Arah (O₂Q)ω22adalah sepanjang garis A – O2

dari A menuju O2 dan harga percepatan normalnya =

(

O

2

Q

)

α

2 =0.

AQ digambarkan dengan skala percepatan yang sesuai.

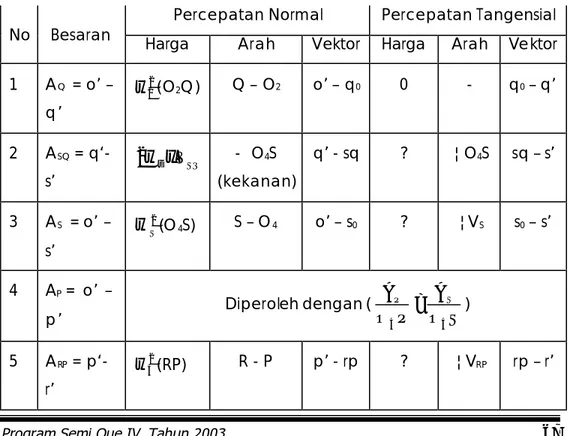
Pembuatan diagram percepatan dapat ditabelkan sebagai berikut :

Table diagram percepatan

Percepatan Normal Percepatan Tangensial No Besaran _Harga _Arah _{Vektor Harga Arah Vektor}

1 AQ = o’ – q’ 2 2

ω

(O2Q) Q – O2 o’ – q0 0 - q0 – q’ 2 ASQ = q‘- s’ SQ s

xV

ω

2

- O4S (kekanan) q’ - sq ? ¦O4S sq – s’ 3 AS = o’ – s’ 2 S

ω

(O4S) S – O4 o’ – s0 ? ¦VS s0 – s’ 4 AP = o’ – p’ Diperoleh dengan ( O S A P O A_P _S 4 4 = ) 5 ARP = p‘- r’ 2 5 ω (RP) R - P p’ - rp ? ¦VRP rp – r’

(13)

Diktat Kinematika

Universitas Brawijaya 68 6 AR = o’ – r’ 0 - o’ – r 0 ? ¦VR r0 – r’ Diagram percepatan SOAL-SOAL : s’ 2? S VSQ O’ so p’ sq q’ r’ VSQ ?S 2? S VSQ

(14)

Diktat Kinematika

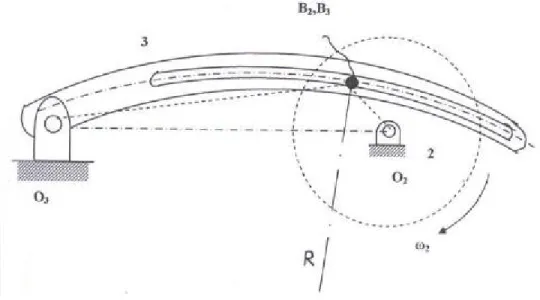
1. Suatu mekanisme seperti pada gambar dibawah diketahui : O2 O3 = 36 cm

O2 B2 = 8 cm O3 B3 = 32 cm R = 48 cm

Penghubung 2 sebagai penggerak berputar dengan kecepatan konstan ? 2 = 40 rad/det2_.

Tentukan ?3 dan a3 dengan membuat diagram kecepatan dan diagram percepatan lebih dahulu.

2. Kecepatan titik A adalah 12 m/det dengan penghubung 2 berputar pada suatu kecepatan sudut konstan dalam arah melawan putaran jam.

Dengan membuat polygon kecepatan dan polygon percepatan tentukan kecepatan sudut penghubung 4, 5, 6 dan kecepatan titik B serta percepatan titik C pada penghubung 5 (atau 6) dan percepatan sudut penghubung 3, 4, 5 dan 6.

(15)