BAB 2
LANDASAN TEORI
2.1. Kriptografi
Kriptografi berasal dari bahasa Yunani, kryptos dan graphikos. Kryptos berarti hidden (terpendam) dan graphikos berarti writing (tulisan). Menurut terminologinya, kriptografi adalah metodologi untuk menyamarkan isi dari pesan (Hoffstein, et al. 2008).
Menurut Kromodimoeljo (2010), “kriptografi adalah ilmu mengenai teknik enkripsi di mana data diacak menggunakan suatu kunci enkripsi menjadi sesuatu yang sulit dibaca oleh seseorang yang tidak memiliki kunci dekripsi.”
2.1.1. Terminologi
Seorang pengirim (sender) ingin mengirim pesan (plaintext; kadang-kadang disebut
cleartext) kepada orang yang dituju (receiver). Selain itu, pengirim ingin pesan yang
dikirim tidak dapat dibaca oleh orang lain yang menyadap (eavesdropper) percakapan atau pesan tersebut. Proses menyamarkan pesan sedemikian rupa untuk menyembunyikan substansinya disebut enkripsi. Sebuah pesan yang dienkripsi disebut
ciphertext. Proses untuk mengubah ciphertext kembali ke plaintext adalah dekripsi.
Pada standar ISO 7498-2 menggunakan istilah encipher untuk proses enkripsi dan
decipher untuk proses dekripsi. Skema rangkaian proses enkripsi dan dekripsi
ditunjukkan secara umum pada Gambar 2.1. (Schneier, 1996).
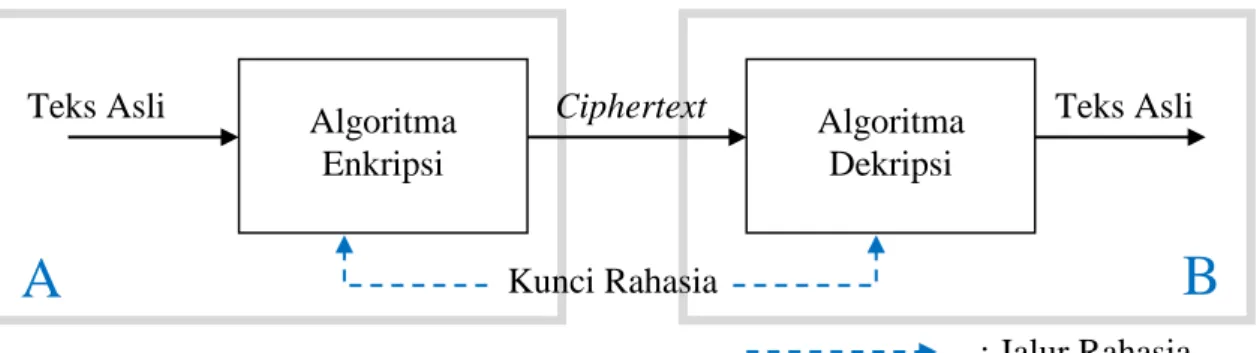
Seni dan ilmu untuk menjaga keamanan pesan disebut kriptografi dan pelakunya adalah kriptografer. Kriptanalis adalah yang melakukan kriptanalisis, yaitu seni dan ilmu untuk memecahkan pesan tersembunyi (ciphertext). Cabang matematika yang meliputi kriptografi dan kriptanalisis adalah kriptologi dan praktisinya disebut kriptologis (Schneier, 1996).
Gambar 2.1. Skema Proses Enkripsi dan Dekripsi (Schneier, 1996)
2.1.2. Tujuan kriptografi
Kriptografi bertujuan untuk memberikan layanan keamanan (Paar & Pelzl, 2010) sebagai berikut:
1. Kerahasiaan (Confidentiality)
Informasi dirahasiakan dari semua pihak yang tidak berwenang. 2. Keutuhan Data (Integrity)
Pesan tidak berubah dalam proses pengiriman hingga pesan diterima oleh penerima.
3. Autentikasi (Message Authentication)
Kepastian terhadap identitas setiap entitas yang terlibat dan keaslian sumber data.
4. Nirpenyangkalan (Nonrepudiation)
Setiap entitas yang berkomunikasi tidak dapat menolak atau menyangkal atas data yang telah dikirim atau diterima.
2.2. Kriptografi Klasik dan Kriptografi Modern
2.2.1. Kriptografi klasik
Menurut Ariyus (2008), kriptografi klasik merupakan suatu algoritma yang menggunakan satu kunci untuk mengamankan data dan sudah digunakan sejak empat abad yang lalu. Terdapat beberapa ciri dari kriptografi klasik, antara lain:
1. berbasis karakter,
2. menggunakan pena dan kertas saja (belum menggunakan komputer), 3. termasuk ke dalam kriptografi kunci simetri.
Contoh dari kriptografi klasik adalah Caesar Cipher, Vigènere Cipher, Affine
Cipher, Scytale Cipher dan Reverse Cipher.
Enkripsi Dekripsi
2.2.2. Kriptografi modern
Kriptografi modern berbeda dengan kriptografi klasik atau konvensional. Kriptografi
modern mempunyai kerumitan yang kompleks dan dibutuhkan komputer untuk
pengoperasiannya (Ariyus, 2008).
Kriptografi modern merupakan suatu perbaikan yang mengacu pada kriptografi klasik. Terdapat berbagai macam algoritma pada kriptografi modern yang menggunakan sistem kriptografi simetri (DES, AES, IDEA, A5, RC4 dan lainnya) dan sistem kriptografi asimetri (RSA, Rabin, ElGamal dan lainnya) jika dilihat dari penggunaan kuncinya. Selain menggunakan sistem kriptografi simetri dan asimetri, dalam kriptografi modern terdapat algoritma hibrida, yaitu algortima yang memanfaatkan dua tingkatan kunci. Dua tingkatan kunci tersebut adalah kunci rahasia (simetri) yang disebut juga session key (kunci sesi) untuk enkripsi data dan pasangan kunci rahasia (kunci publik) untuk pemberian tanda tangan digital serta melindungi kunci simetri (Ariyus, 2008). Dengan kata lain, algoritma hibrida merupakan penggabungan dari sistem kriptografi simetri dan sistem kriptografi asimetri.
2.3. Sistem Kriptografi
Sistem kriptografi adalah algoritma, seluruh kemungkinan plaintext, ciphertext dan kunci. P adalah notasi yang digunakan untuk plaintext, C adalah ciphertext, E adalah fungsi enkripsi dan D adalah fungsi dekripsi (Schneier, 1996). Sedangkan untuk kunci dapat dinotasikan sebagai K.
Berdasarkan kunci yang dipakai, algoritma kriptografi dibagi menjadi tiga, yaitu algoritma simetri (menggunakan satu kunci untuk enkripsi dan dekripsi), algoritma asimetri (menggunakan kunci yang berbeda untuk enkripsi dan dekripsi) dan fungsi
hash (Ariyus, 2008).
Selain berdasarkan kunci yang dipakai, karakteristik kriptografi juga dibagi berdasarkan tipe operasi yang dipakai untuk enkripsi dan dekripsi serta berdasarkan tipe pengolahan pesan (Sadikin, 2012).
2.4. Kriptografi Berdasarkan Kunci yang Dipakai
2.4.1. Sistem kriptografi simetri
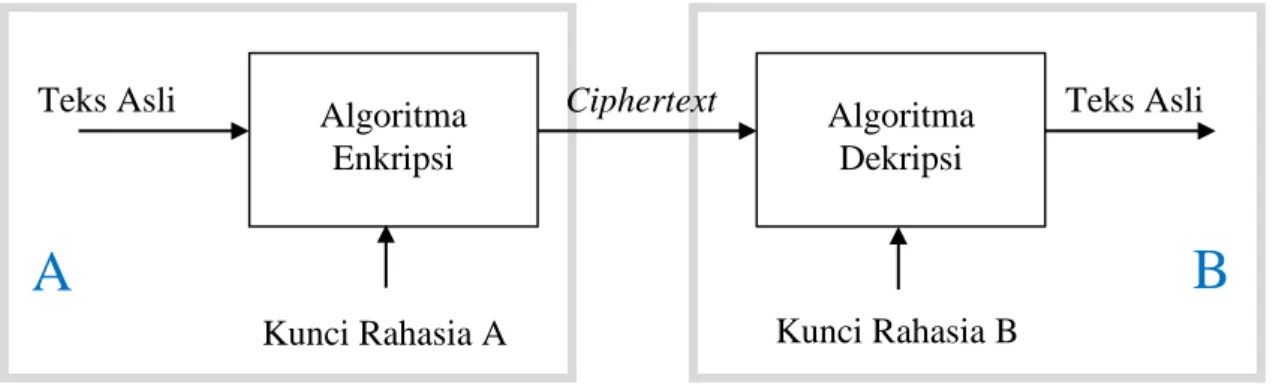
Algoritma kriptografi simetri (symmetric cryptosystems atau secret key cryptosystems) adalah suatu algoritma kriptografi yang memiliki kunci enkripsi yang sama dengan kunci dekripsi dan kunci tersebut bersifat rahasia (Smart, 2004). Algoritma ini disebut juga dengan algoritma klasik atau konvensional karena sudah ada sejak lebih dari 4000 tahun yang lalu (Ariyus, 2008).
Pada algoritma ini, pengirim dan penerima pesan harus menyetujui suatu kunci tertentu sebelum saling berkomunikasi. Keamanan pada algoritma ini tergantung pada kunci yang digunakan. Jika kunci diketahui oleh orang lain, maka orang lain dapat melakukan enkripsi dan dekripsi pesan. Oleh karena itu, keamanan atau kerahasiaan kunci dalam algoritma ini sangat penting dan algoritma ini disebut juga dengan algoritma secret key encipherment (Sadikin, 2012). Selain melalui persetujuan oleh kedua pihak tentang kunci, kunci dapat ditetapkan oleh salah satu pihak yang kemudian kunci tersebut dikirimkan kepada pihak lain menggunakan jalur distribusi yang aman. Skema algoritma kriptografi simetri dapat dilihat pada Gambar 2.2.
Gambar 2.2. Skema Sistem Kriptografi Simetri (Fauzana, 2013)
Kriptografi yang termasuk algoritma kunci simetri adalah One Time Pad (OTP),
Data Encryption Standard (DES), RC2, RC4, RC5, RC6, Message Digest (MD), International Data Encryption Algorithm (IDEA), Twofish, Magenta, FEAL, SAFER,
LOKI, CAST, Rijndael (Advanced Encryption Standard), Blowfish, GOST, A5 (Stream
Cipher), Kasumi dan lain-lain.
Algoritma Enkripsi
Algoritma Dekripsi
Kunci Rahasia
Teks Asli Ciphertext Teks Asli
: Jalur Rahasia
2.4.2. Sistem kriptografi asimetri
Kunci yang digunakan dalam algoritma asimetri (asymmetric cryptosystems atau public
key cryptosystems) untuk melakukan enkripsi dan dekripsi berbeda (Smart, 2004).
Algoritma ini dikenal juga sebagai kriptografi kunci publik dan merupakan bagian sistem kriptografi modern, yaitu kunci enkripsi (public key) dimiliki oleh pengirim dan kunci dekripsi (private key) dimiliki oleh penerima pesan. Skema algoritma kriptografi asimetri dengan kunci publik dapat dilihat pada Gambar 2.3.
Gambar 2.3. Skema Kriptografi Asimetri Kunci Publik (Sadikin, 2012)
Sistem kriptografi asimetri kunci publik pertama kali diusulkan oleh Diffie dan Hellman pada tahun 1976. Ide kriptografi kunci publik sebenarnya mirip dengan cara kerja kunci gembok, misalnya terdapat sebuah peti yang berisi pesan rahasia, lalu peti itu dikunci dengan gembok di mana gembok ini dimiliki oleh semua orang (gembok bekerja seperti public key). Peti terkunci tersebut kemudian dikirim ke tujuan atau penerima yang memiliki kunci untuk membuka gembok. Penerima dapat membuka gembok apabila kunci yang dipegang olehnya merupakan pasangan dari gembok tersebut. Kunci yang dipegang oleh penerima bekerja seperti private key (Sadikin, 2012).
Sistem kriptografi kunci publik memiliki kunci untuk enkripsi Ke dan kunci
untuk dekripsi Kd yang berbeda. Kunci untuk enkripsi Ke disebut juga sebagai kunci
publik (KPublik) bersifat tidak rahasia sehingga dapat didistribusikan melalui saluran
tidak aman. Sedangkan kunci dekripsi Kd disebut juga kunci privat (KPrivat) bersifat
rahasia dan harus dijaga kerahasiaannya oleh pemegang kunci. Berikut ini adalah algoritma sistem kriptografi kunci publik (Sadikin, 2012).
Algoritma Enkripsi
Algoritma Dekripsi
KPublikB
Teks Asli Ciphertext Teks Asli
A
B
Pembangkit Kunci
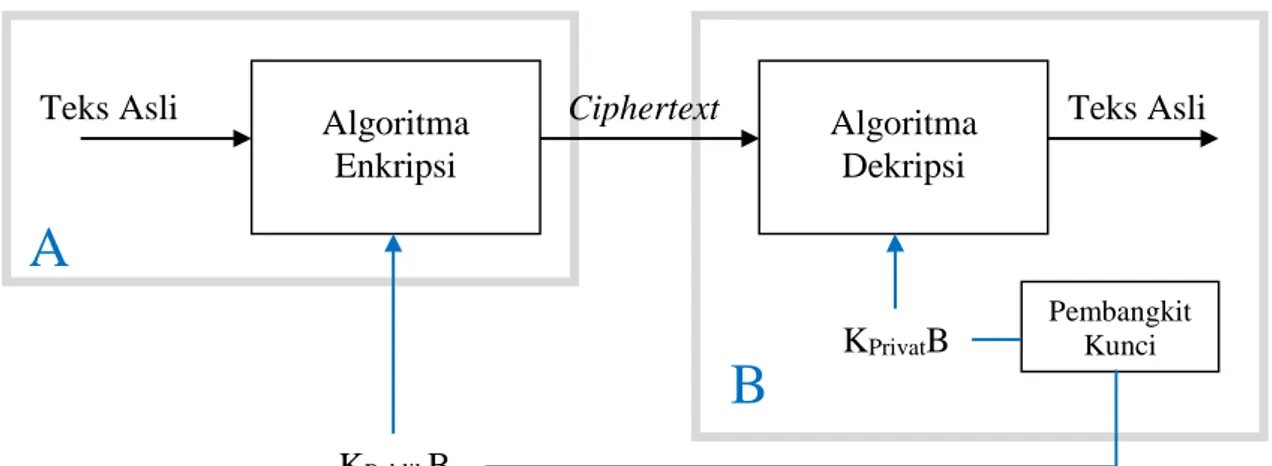
1. Sebelum A melakukan enkripsi, B membangkitkan sepasang kunci yaitu kunci privat dan kunci publik milik B dengan memanggil fungsi PembangkitKunci().
(KPublikB, KPrivatB) PembangkitKunci()
B memublikasikan kunci publik (KPublikB) dan menjaga kerahasiaan kunci privat
(KPrivatB).
2. A melakukan enkripsi sebuah teks asli (P) dengan kunci publik B (KPublikB)
menghasilkan sebuah teks sandi (C) dengan memanggil fungsi enkripsi (E).
C E(KPublikB, P)
A mengirim teks sandi (C) ke B melalui saluran tidak aman.
3. B mendekripsi teks sandi (C) dengan kunci privat B (KPrivatB) untuk
mendapatkan teks asli (P) dengan fungsi dekripsi (D).
P D(KPrivatB, C)
B mendapatkan P jika teks sandi (C) dienkripsi dengan kunci publik B yang sesuai.
Jadi dalam kriptografi kunci publik, kunci publik dapat disebar-luaskan kepada umum dan sebaiknya disebar luaskan. Sebaliknya, kunci privat harus dirahasiakan oleh pemiliknya. Perlu untuk diingat, biasanya algoritma tidak dirahasiakan, bahkan enkripsi yang mengandalkan kerahasiaan algoritma dianggap sesuatu yang tidak baik (Kromodimoeljo, 2010). Hal ini sesuai dengan prinsip Kerckhoff yaitu semua algoritma kriptografi harus publik, hanya kunci yang rahasia (Munir, 2006).
Dalam kriptografi kunci asimetri, hampir semua algoritma kriptografinya menggunakan konsep kunci publik, seperti Rivest-Shamir-Adleman (RSA), El-Gamal, Rabin dan sebagainya. Kecuali algoritma Pohlig˗Hellman karena kunci enkripsi maupun kunci dekripsinya bersifat rahasia. (Fauzana, 2013). Skema algoritma kriptografi asimetri nirkunci publik (dengan asumsi kunci sudah diketahui oleh kedua belah pihak sebelumnya) dapat dilihat pada Gambar 2.4.
Gambar 2.4. Skema Kriptografi Asimetri Nirkunci Publik
2.4.3. Fungsi hash
Fungsi hash adalah sebuah fungsi yang masukannya adalah sebuah pesan dan keluarannya adalah sebuah sidik pesan (message fingerprint) (Ariyus, 2008).
“Fungsi hash sering disebut dengan fungsi hash satu arah (one-way function),
message digest, fingerprint, fungsi kompresi dan message authentication code (MAC)
yang merupakan suatu fungsi matematika yang mengambil masukan panjang variabel dan mengubahnya ke dalam urutan biner dengan panjang yang tetap. Fungsi hash biasanya diperlukan bila ingin membuat sidik jari dari suatu pesan. Sidik jari pada pesan merupakan suatu tanda bahwa pesan tersebut benar-benar berasal dari orang yang diinginkan” (Ariyus, 2008). Beberapa fungsi hash yang banyak dipakai adalah MD5 dan SHA.
2.5. Kriptografi Berdasarkan Tipe Operasi
Menurut Ariyus (2008) dan Sadikin (2012), dua teknik dasar yang biasa digunakan pada algoritma kriptografi untuk melakukan enkripsi dan dekripsi adalah sebagai berikut,
1. Teknik substritusi: Penggantian karakter teks asli dengan karakter lain.
2. Teknik transposisi (permutasi): Dilakukan dengan menggunakan permutasi karakter atau dengan kata lain elemen pada pesan berpindah posisi.
2.6. Kriptografi Berdasarkan Tipe Pengolahan Pesan
“Ketika melakukan penyandian pesan yang akan dienkripsi ataupun didekripsi, pesan diolah per satuan blok elemen yang disebut dengan block cipher. Cara lain adalah dengan menganggap masukan untuk enkripsi dan dekripsi sebagai aliran elemen secara terus menerus yang disebut dengan stream cipher” (Sadikin, 2012).
Algoritma Enkripsi
Algoritma Dekripsi
Kunci Rahasia B
Teks Asli Ciphertext Teks Asli
A
B
2.7. Teori Bilangan Integer
Teori bilangan integer atau bilangan bulat (ℤ) memiliki peran yang sangat besar dalam kriptografi pada umumnya serta merupakan pondasi bagi sistem kriptografi kunci publik (Munir, 2006). Berikut ini merupakan beberapa teori yang mendukung dalam penelitian ini.
2.7.1. Kemampuan dibagi habis (divisibility)
Misalkan a dan b adalah dua bilangan bulat dengan syarat a ≠ 0. Dinyatakan bahwa a habis membagi b (b mod a = 0) jika terdapat bilangan bulat c sedemikian sehingga
b = ac, maka hal tersebut dapat ditulis sebagai berikut (Munir, 2006).
a | b jika b = ac, c ∈ ℤ dan a ≠ 0 ... (2.1)
Beberapa properti keterbagihabisan dapat didasarkan sebagai berikut (Sadikin, 2012).
1. Jika 1 | a, maka a = ±1 ... (2.2) 2. Jika b | a dan a | b, maka a = ±b ... (2.3) 3. Jika d | b dan b | a, maka d | a ... (2.4) 4. Jika b mod a = r, maka berlaku a | (b – r) ... (2.5)
2.7.2. Divisor
Himpunan bilangan integer yang membagi habis sebuah bilangan integer disebut dengan divisor. Misalnya, 15 memiliki divisor: {1, 3, 5, 15}. Perlu untuk diperhatikan bahwa bilangan 1 yang hanya memiliki satu divisor yaitu 1 atau bilangan itu sendiri. Sedangkan bilangan integer lainnya paling sedikit memiliki dua divisor yaitu bilangan itu sendiri dan 1.
Bilangan integer i yang memiliki divisor {1, i} disebut bilangan prima, selain itu disebut sebagai bilangan komposit (Sadikin, 2012).
2.7.3. Faktor persekutuan terbesar (greatest common divisor)
Faktor persekutuan terbesar adalah elemen terbesar pada himpunan divisor dua bilangan integer. Dua bilangan dapat saja memiliki beberapa elemen divisor yang sama namun hanya satu yang terbesar (Sadikin, 2012). Misalnya, divisor 15 = { 1, 3, 5, 15 } dan
{ 1, 3, 5, 15 } dan yang terbesar ialah 15. Dengan kata lain, faktor persekutuan terbesar 15 dan 45 dapat dinotasikan sebagai GCD(15, 45) = 15 (Fauzana, 2013).
Dalam notasi matematika, faktor persekutuan terbesar d dari dua bilangan integer a dan b, di mana keduanya tidak sama dengan nol, didefinisikan sebagai berikut (Welschenbach, 2005):
d = GCD(a,b) jika d > 0, maka d | a, d | b ... (2.6)
(d | a dibaca d habis membagi a) dan jika terdapat bilangan d’,
di mana d’ | a dan d’ | b, maka d’ | d ... (2.7) Sebagai contoh, telah diketahui GCD(15, 45) = 15. Pembuktian dari persamaan (2.6) dapat dilihat dari 15/15 = 1 dan 45/15 = 3. Hal ini dikarenakan 15 merupakan salah satu divisor dari 15 dan 45.
Berikut ini beberapa aturan yang berlaku dalam faktor persekutuan terbesar (Welschenbach, 2005). 1. GCD(a,b) = GCD(b,a) ... (2.8) 2. GCD(a,0) = |a| ... (2.9) 3. GCD(a,b,c) = GCD(a, GCD(b,c))... (2.10) 4. GCD(a,b) = GCD(-a,b) ... (2.11) 2.7.4. Aritmatika modulo
Aritmatika modulo merupakan sisa hasil pembagian dua bilangan. Operator yang digunakan dalam aritmatika modulo adalah mod. Misalkan, jika bilangan integer a dibagi dengan bilangan integer yang lebih besar dari nol (b > 0), maka akan menghasilkan sisa bagi r (remainder) dengan hasil bagi s (quotient). Sehingga dapat dinotasikan sebagai berikut (Lipschutz & Lipson, 2007).
a mod b = r sedemikian sehingga a = bs + r, dengan 0 ≤ b < n ... (2.12)
Sebagai contoh, jika 23 mod 4 = 3, maka 23 = (4 × 5) + 3.
Jika a negatif, maka bagi |a| dengan b mendapatkan sisa bagi r’ (Munir, 2006). Sehingga didapatkan:
a mod b = b – r’, di mana r’ ≠ 0 dan a < 0 ... (2.13)
Sebagai contoh, jika |-23| mod 4 = 3, maka -23 mod 4 = 4 – 3 = 1.
Cormen, et al. (2009) menuliskan di dalam bukunya, untuk setiap bilangan bulat
a dan setiap bilangan bulat positif b, nilai a mod b adalah sisa (residu) dari hasil bagi a/b:
a mod b = a – b (a/b), di mana 0 ≤ a mod b < b ... (2.14)
Contohnya adalah 23 mod 4 = 23 – 4(23/4) = 23 – 4(5) = 23 – 20 = 3.
2.7.5. Algoritma Euclid
Euclid (±300 SM), seorang matematikawan klasik yang bekerja pada perpustakaan Alexandria pada zaman Ptolomeus I, membuat algoritma yang dapat menemukan GCD dua bilangan integer a dan b dengan cara rekursif (Sadikin, 2012). Algoritmanya tersebut dituliskan dalam buku Euclid yang terkenal, Element (Munir, 2006). Terdapat dua kasus (Sadikin, 2012), pertama kasus dasar, yaitu ketika b = 0.
GCD(a, 0) = a ... (2.15) Kasus kedua merupakan kasus umum, ketika b ≠ 0.
GCD(a, b) = GCD(b, a mod b) ... (2.16) Kasus dasar (2.15) menyatakan bila b = 0, maka didefinisikan nilai GCD adalah
a (merupakan stop condition). Sebab semua bilangan integer habis membagi 0 dan a
habis membagi dirinya sendiri (0 mod a = 0 dan a mod a = 0, perlu untuk diingat bahwa
a mod 0 = undefined).
Pada kasus umum (2.16) menyatakan untuk mencari GCD(a,b) dapat direduksi menjadi GCD(b, a mod b). Jadi kasus umum (2.16) dapat dikenakan berkali-kali sampai akhirnya akan bertemu dengan kasus dasar (2.15) untuk menemukan GCD(a,b) (Sadikin, 2012).
Contoh: Untuk menemukan GCD(31, 23), dengan menggunakan persamaan (2.15) dan (2.16): (2.16): GCD(31, 23) = GCD(23, (31 mod 23)) = GCD(23, 8) (2.16): GCD(23, 8) = GCD(8, (23 mod 8)) = GCD(8, 7) (2.16): GCD(8, 7) = GCD(7, (8 mod 7)) = GCD(7, 1) (2.16): GCD(7, 1) = GCD(1, (7 mod 1)) = GCD(1, 0) (2.15): GCD(1, 0) = 1
Sehingga dapat disimpulkan bahwa GCD(31, 23) = 1.
2.7.6. Relatif prima
Bilangan bulat positif i (i > 1) disebut bilangan prima jika pembaginya 1 dan i (Cormen,
menguji apakah i merupakan bilangan prima atau komposit adalah dengan membagi i dengan sejumlah bilangan prima, mulai dari 2 hingga bilangan prima yang lebih kecil atau sama dengan akar kuadrat dari i (2 ≤ x ≤ √𝑖). Jika i habis dibagi dengan salah satu dari bilangan prima tersebut, maka i adalah bilangan komposit dan jika tidak, maka i adalah prima (Munir, 2006). Hal ini berdasarkan teori dari Ibn al-Banna (ca. 1258-1339) dalam menemukan bilangan prima kurang dari i dengan menggunakan metode saringan Eratosthenes (Mollin, 2007). Sebagai contoh, misalkan bilangan yang ingin diuji keprimaannya adalah 23. Hasil dari √23 = 4,795831523, maka bilangan prima dari 2 hingga lebih kecil atau sama dengan 4,795831523 adalah 2 dan 3. Karena 23 tidak habis dibagi dengan 2 dan 3, maka 23 adalah bilangan prima. Berikut ini adalah langkah untuk menguji keprimaan dari 23 dengan menggunakan metode saringan Eratosthenes (Mollin, 2007).
Langkah 1: Tuliskan seluruh bilangan natural (asli) yang lebih kecil atau sama dengan 23 dan yang lebih besar dari 1. Lalu eliminasi bilangan yang lebih besar dari 2 dan merupakan kelipatan dari 2.
{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23} {2,3,5,7,9,11,13,15,17,19,21,23}
Langkah 2: Selanjutnya, eliminasi bilangan yang lebih besar dari 3 dan kelipatan dari 3.
{2,3,5,7,9,11,13,15,17,19,21,23} {2,3,5,7,11,13,15,17,19,21,23}
Langkah 3: Selanjutnya, eliminasi bilangan yang lebih besar dari 5 dan kelipatan dari 5.
{2,3,5,7,11,13,15,17,19,21,23}
Pada langkah ini, tidak ada yang dapat dieliminasi. Jika diteruskan dengan 7, 11, 13 dan bilangan selanjutnya, maka tidak ada lagi yang dapat dieliminasi dari himpunan bilangan ini. Hal tersebut menyatakan himpunan tersebut adalah himpunan bilangan prima dan membuktikan bahwa 23 adalah bilangan prima.
Dapat dilihat, pengujian keprimaan dari 23 dapat berhenti pada langkah 2, yaitu menguji 23 dengan membagi 23 dengan sejumlah bilangan prima, mulai dari 2 hingga bilangan prima yang lebih kecil atau sama dengan akar kuadrat dari 23 (2 ≤ x ≤ √23). Di mana x adalah 2 dan 3.
Terdapat metode lain yang dapat digunakan untuk menguji keprimaan suatu bilangan bulat, beberapa diantaranya adalah Teori Fermat (dibaca “Fair-ma”) (Munir, 2006) dan Miller-Rabin.
Dua bilangan bulat a dan b dikatakan relatif prima jika GCD(a,b) = 1. Jika a dan
b relatif prima, maka terdapat bilangan bulat m dan n sedemikian sehingga
ma + nb = 1 ... (2.17)
Bilangan-bilangan a1, a2, a3, …, an adalah relatif prima berpasangan (pairwise relatively prime) jika GCD(a1, a2, a3, …, an) = 1 (Cormen, et al. 2012). Contoh bilangan
yang relatif prima adalah 31 dan 23.
2.7.7. Persamaan Diophantine linier
Jika terdapat bilangan bulat a, b, c, x, y dalam bentuk persamaan:
ax + by = c,
dengan nilai a, b dan c yang diketahui, maka persamaan ini disebut sebagai persamaan Diophantine linier (Mollin, 2008).
2.7.8. Persamaan Diophantine linier dengan identitas Bézout
Jika nilai c pada persamaan Diophantine linier berikut ini,
ax + by = c,
adalah merupakan nilai faktor persekutuan terbesar dari a dan b atau dengan kata lain c = GCD(a,b), maka persamaan tersebut disebut sebagai persamaan Diophantine linier dengan identitas Bézout (Rosen, 2012).
2.7.9. Extended Euclidean
Algoritma Euclid dapat dikembangkan (disebut dengan algoritma Extended Euclid) agar dapat menemukan dua integer x dan y yang unik selain nilai GCD(a,b) sehingga memenuhi relasi yang ditunjukkan oleh persamaan (2.18) (Lipschutz & Lipson, 2007).
2.7.10. Inversi modulo
Jika a dan m relatif prima dan m > 1, maka inversi dari a mod m dapat ditemukan. Inversi dari a (mod m), disebut juga inversi perkalian, di mana bilangan bulat a-1 sedemikian sehingga
aa-1 ≡ 1 (mod m) ... (2.19) Pembuktian dari persamaan (2.19) dapat dilihat dari definisi relatif prima diketahui bahwa GCD(a, m) = 1 dan menurut persamaan (2.17) terdapat bilangan bulat
j dan k sedemikian sehingga
aj + mk = 1
yang mengimplikasikan bahwa aj + mk ≡ 1 (mod m). Karena mk ≡ 0 (mod m), maka aj ≡ 1 (mod m). Kekongruenan tersebut berarti bahwa j adalah inversi dari a (mod
m) atau dapat dinotasikan sebagai j = a-1 (Munir, 2006; Mollin, 2008).
Contoh: untuk inversi dari 31 (mod 23), penyelesaiannya dapat dilihat pada Tabel 2.1.
Tabel 2.1. Penyelesaian Contoh Soal Inversi Modulo
a-1 a-1 × 31 (mod 23)
1 8
2 16
3 1
Pada Tabel 2.1., iterasi berhenti ketika a-1a ≡ 1 (mod m) dan diperoleh a-1 = 3.
2.7.11. Modulo eksponensial
Permasalahan pada operasi modulo adalah bagaimana menghitung xy (mod z) dengan y yang sangat besar. Terdapat beberapa algoritma untuk menghitung modulo eksponensial, antara lain adalah dengan metode iteratif dan square and multiply.
Metode square and multiply mengasumsikan eksponen y dalam bentuk biner (mengekspresikan y sebagai sum of power dari 2), sehingga
𝑦 = ∑ 𝑦𝑖2𝑖 𝑡−1
𝑖=0
, 𝑦𝑖 ∈ {0,1}
Untuk menyelesaikan modulo eksponensial, berikut ini adalah algoritma dan contoh dari metode square and multiply: left-to-right variant (Smart, 2004).
Langkah 1: Untuk menghitung xy mod z, misalkan x = 65, y = 2 dan z = 713 maka representasi biner dari y adalah b = ‘10’, dengan index bit paling kanan bernilai 0, index paling kiri bernilai jumlah bit - 1 = 2 - 1 = 1.
Langkah 2: Tetapkan bilangan a = 1 lalu i = jumlah bit - 1 = 1.
Langkah 3: Jika i ≥ 0, maka hitung a = a2 mod z dan lanjutkan ke Langkah 4. Jika i < 0, maka hentikan algoritma dan hasil perhitungan adalah nilai a.
Langkah 4: Jika bi = ‘1’, maka hitung a = ax mod z dan i = i - 1. Kembali ke
Langkah 3.
Untuk penyelesaian xy mod z dengan x = 65, y = 2 dan z = 713 dapat dilihat pada
Tabel 2.2. berikut.
Tabel 2.2. Penyelesaian Contoh Soal Square and Multiply Left-to-Right Variant
i b[i] a2 a2 mod z b[i] == ‘1’ a
- - - 1
1 ‘1’ 1 1 Ya 65
0 ‘0’ 4225 660 Tidak 660 Dari Tabel 2.2. dapat disimpulkan bahwa 652 mod 713 = 660.
2.7.12. Algoritma Miller-Rabin
Algoritma pengujian bilangan prima ini disebut juga algoritma Selfridge-Miller-Rabin atau strong prime test. Ini merupakan penyempurnaan dari algoritma Fermat, dan bekerja dengan sangat baik dalam praktiknya (Galbraith, 2012). Algoritma ini dikembangkan oleh Michael Rabin yang didasarkan pada sebagian ide Gary Miller (Schneier, 1996).
Sampai saat ini algoritma pengujian bilangan prima yang banyak dipakai dalam sistem kriptografi adalah algoritma probabilistik Miller-Rabin yang memiliki komputasi yang ringan dan memberikan probabilitas yang tinggi (Sadikin, 2012). Berikut ini adalah algoritma Miller-Rabin (Cormen, et al. 2009).
Langkah 1: Pilih bilangan yang ingin diuji keprimaannya n, di mana n ≥ 3 dan
n merupakan bilangan ganjil (n mod 2 ≠ 0).
Langkah 2: Hitung n-1 = u2t, di mana u adalah bilangan ganjil dan t ≥ 1. Representasi bilangan biner dari n-1 adalah representasi biner dari bilangan ganjil u yang diikuti oleh bit 0 sebanyak t.
Langkah 3: Uji n yang akan diperiksa keprimaannya dengan bilangan integer sembarang a, di mana 2 ≤ a ≤ n-1 sebanyak s. Jika pengujian sudah sampai s kali, maka lanjutkan ke Langkah 6.
Langkah 4: Hitung 𝑥0 ≡ au (mod n).
Langkah 5: Hitung 𝑥𝑖 ≡ 𝑥𝑖−12(mod 𝑛) sebanyak t kali di mana 1 ≤ i ≤ t. Jika
𝑥𝑖 ≡ 1(mod 𝑛), 𝑥𝑖−1≢ 1 (mod n) dan 𝑥𝑖−1 ≢ n-1 maka hentikan
algoritma dengan menyatakan n adalah bilangan komposit. Selain dari itu, maka lanjut ke Langkah 3.
Langkah 6: Jika 𝑥𝑡 ≢ 1(mod 𝑛), maka hentikan algoritma dengan
menyatakan n adalah bilangan komposit. Jika tidak, maka hentikan algoritma dan nyatakan n adalah kemungkinan bilangan prima. Contoh: nilai yang akan diuji keprimaannya (n) adalah 23 (23 ≥ 3 dan 23 mod 2 ≠ 0), maka perhitungan menggunakan algoritma Miller-Rabin untuk menguji keprimaan dari n adalah sebagai berikut.
Hitung n-1 = u2t, di mana n-1 = 23-1 = 22.
n-1 = 2210 = 101102 u = 10112 = 1110
t = 1, karena jumlah digit 0 setelah u (10112) dalam biner n-1 sebanyak satu.
Sehingga n-1 = 22 = 2tu = 21 × 11.
Pilih nilai a secara acak sebanyak s. Dalam hal ini, nilai s adalah banyak digit dari n yaitu 2. Sehingga nilai a0 = 15 dan a1 = 4.
Pengujian dengan a0 (iterasi 1):
Hitung 𝑥0 ≡ au (mod n) ≡ 1511 (mod 23) ≡ 22 (mod 23)
Hitung 𝑥𝑖 ≡ 𝑥𝑖−12(mod 𝑛) sebanyak t kali di mana nilai t adalah 1.
Maka 𝑥1 ≡ 𝑥02(mod 𝑛) ≡ 222(mod 23) ≡ 1(mod 23).
Karena 𝑥1 ≡ 1(mod 23), 𝑥0 ≢ 1 (mod 23) dan 𝑥0 ≡ 22, maka dilanjutkan ke langkah berikutnya yaitu pengujian dengan nilai a1.
Hitung 𝑥0 ≡ au (mod n) ≡ 411 (mod 23) ≡ 1 (mod 23)
Hitung 𝑥𝑖 ≡ 𝑥𝑖−12(mod 𝑛) sebanyak t kali di mana nilai t adalah 1.
Maka 𝑥1 ≡ 𝑥02(mod 𝑛) ≡ 12(mod 23) ≡ 1(mod 23).
Karena 𝑥1 ≡ 1(mod 23), 𝑥0 ≡ 1 (mod 23), 𝑥0 ≢ 22 dan pengujian sudah dilakukan sebanyak s kali, maka dilanjutkan ke langkah terakhir.
Karena 𝑥𝑡≡ 𝑥1 ≡ 1(mod 23), maka algoritma dihentikan dan n dinyatakan kemungkinan bilangan prima.
2.7.13. Chinese remainder theorem
Chinese Remainder Theorem (CRT) ditemukan oleh seorang matematikawan Cina
bernama Sun-Tsu (disebut juga Sun Tse) sekitar 100 A.D (anno domini) atau 100 M (Stallings, 2011). Chinese Remainder Theorem (teorema sisa Cina), dinamai setelah masalah peninggalan Cina yang melibatkan sistem persamaan atau kekongruenan linier, menyatakan bahwa ketika modulus dari sistem kekongruenan linier yang berpasangan relatif prima, ada solusi unik dari sistem modulo produk dari modulus. Berikut ini adalah pertanyaan atau teka-teki Sun-Tsu (Rosen, 2012).
“Ada beberapa hal yang bilangannnya tidak diketahui. Bila
dibagi dengan 3, sisanya adalah 2, ketika dibagi oleh 5, sisanya adalah 3, dan ketika dibagi 7, sisanya adalah 4. Berapakah bilangan itu?”
Teka-teki tersebut dapat dituliskan sebagai berikut. Apa solusi dari sistem kekongruenan berikut ini?
x ≡ 2 (mod 3) x ≡ 3 (mod 5) x ≡ 4 (mod 7)
Sebelum menyelesaikan teka-teki tersebut, berikut ini adalah teorema sisa Cina (Chinese Remainder Theorem) (Rosen, 2012).
Misalkan m1, m2, …, mn adalah bilangan bulat positif yang relatif prima
berpasangan (pairwise relatively prime) yang lebih besar dari 1 dan a1, a2, …, an
merupakan bilangan bulat sembarang. Maka sistem kekongruenan linier
x ≡ a1 (mod m1), x ≡ a2 (mod m2), ⋯, x ≡ an (mod mn)
memiliki sebuah solusi unik modulo m = m1m2…mn. (Terdapat solusi x dengan
Solusi dari penyelesaian teka-teki Sun-Tsu tersebut adalah sebagai berikut (Wandani, 2012).
Langkah 1: Hitung hasil perkalian dari keseluruhan modulus.
M = m1m2…mn M = 3 × 5 × 7 = 105
Langkah 2: Buat himpunan penyelesaian untuk masing-masing persamaan dari bilangan terkecil hingga hasil perkalian modulus (M).
x1 = {2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47, 50, 53, 56, 59, 62, 65, 68, 71, 74, 77, 80, 83, 86, 89, 92, 95, 98, 101, 104} x2 = {3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, 98, 103} x3 = {4, 11, 18, 25, 32, 39, 46, 53, 60, 67, 74, 81, 88, 95, 102}
Langkah 3: X merupakan irisan dari keseluruhan himpunan penyelesaian tersebut.
X = x1 ∩ x2 ∩ … ∩ xn X = x1 ∩ x2 ∩ x3 = 53
Langkah 4: Agar tercapai seluruh bilangan yang memenuhi x, maka dihitung kelipatan persekutuan terkecil (Least Common Multiple) dari ketiga modulus (interval yang memenuhi x).
Berikut ini merupakan rumus untuk mencari LCM dari dua bilangan bulat positif (Rosen, 2012).
ab = GCD(a,b) . LCM(a, b) ... (2.20)
Dari persamaan (2.20) dapat disimpulkan:
LCM(𝑎, 𝑏) =GCD(𝑎,𝑏)𝑎𝑏 ... (2.21) GCD(GCD(3,5),7) = 1 dan LCM(LCM(3,5),7) = 105
Sehingga x memenuhi akan bilangan dalam interval 105 dimulai dari 53, yaitu x = 53 ± (k × 105). Atau interval ini dapat dituliskan: x ∈ X ± (k × LCM(m1,m2, …,mn)) ... (2.22)
Cara yang dapat digunakan untuk menyelesaikan teka-teki Sun-Tsu menurut Rosen (2012) adalah sebagai berikut.
Langkah 1: Hitung hasil perkalian dari keseluruhan modulus.
M = 3 × 5 × 7 = 105
Langkah 2: Hitung hasil bagi dari M dengan tiap-tiap modulus.
Mn = M/mn M1 = 105/3 = 35 M2 = 105/5 = 21 M3 = 105/7 = 15
Langkah 3: Hitung invers modulo (yn) dari (Mn mod mn). Maka diperoleh: y1 = 2, y2 = 1 dan y3 = 1
Langkah 4: Diperoleh solusi x dari teka-teki dengan menghitung rumus berikut ini.
x ≡ a1M1y1 + a2M2y2 + … + anMnyn ... (2.23) x ≡ a1M1y1 + a2M2y2 + a3M3y3 ≡ (2×35×2) + (3×21×1) + (4×15×1) x ≡ 263 ≡ 53 (mod 105).
2.8. Sistem Kriptografi Rabin
Sistem kriptografi Rabin atau Rabin Public Key pertama kali diperkenalkan pada tahun 1979 oleh Michael O. Rabin dalam upaya untuk peningkatan sistem kriptografi yang terdahulu yaitu RSA dengan memberikan solusi kriptografi yang keamanan matematisnya terbukti didasarkan pada masalah faktorisasi bilangan bulat atau integral
data type (Rădulescu, 2008). Schneier (1996) menuliskan tentang keamanan pada
sistem kriptografi Rabin, yaitu berada pada sulitnya mencari akar kuadrat modulo dari bilangan komposit. Di mana masalah ini setara dengan masalah faktorisasi.
Algoritma Rabin Public Key adalah salah satu algoritma kriptografi asimetris yang menggunakan kunci publik dan kunci privat. Algoritma Rabin Public Key merupakan varian algoritma Rivest Shamir Adleman (RSA). Fungsi dasar algoritmanya mirip dengan fungsi dasar dari algoritma RSA. Hanya saja komputasinya lebih sederhana dibandingkan algoritma RSA (Wandani, 2012).
2.8.1. Pembangkit kunci
Proses pembangkitan kunci adalah langkah pertama yang harus dilakukan dalam algoritma Rabin Public Key. Berikut ini algoritma untuk proses pembangkitan kunci pada algoritma Rabin Public Key (Schneier, 1996).
1. Pilih dua bilangan prima, p dan q, di mana keduanya kongruen terhadap 3 mod 4. Atau dengan kata lain, jika p dan q dimodulokan 4 akan menghasilkan 3.
p ≡ q ≡ 3 (mod 4) ... (2.24)
Misalkan p = 31 dan q = 23. Kedua bilangan ini (p dan q) merupakan private
key.
2. Hitung nilai n yang merupakan public key dengan rumus perkalian antara p dan
q (Rădulescu, 2008).
n = pq, n ∈ ℕ ... (2.25) n = 31 × 23 = 713.
Simpan dan rahasiakan nilai p dan q, sedangkan nilai n dapat disebarkan seluas-luasnya.
2.8.2. Proses enkripsi
Proses enkripsi pada algoritma Rabin Public Key menggunakan kunci publik n. Untuk melakukan enkripsi pesan (P), P harus lebih kecil dari n. Berikut adalah rumus untuk melakukan enkripsi pada algoritma Rabin Public Key (Schneier, 1996).
C = P2 mod n ... (2.26)
Berikut ini adalah contoh dan algoritma dalam melakukan enkripsi pesan (Rădulescu, 2008).
1. Terima kunci publik, n = 713.
2. Ekspresikan pesan P sebagai bilangan. Sehingga P = “A” = 65 (kode ASCII), P ∈ ℕ dan P < n.
3. Hitung C = 652 mod 713 = 660 dengan menggunakan rumus (2.26).
4. Kirim C = 660 = “ʔ” ke pemilik kunci publik.
2.8.3. Proses dekripsi
Proses dekripsi pada algoritma Rabin Public Key menggunakan kunci privat p dan q. Selama penerima pesan mengetahui p dan q, penerima pesan dapat menyelesaikan dua kekongruenan menggunakan Chinese Remainder Theorem (Schneier, 1996). Pada dekripsi, masalah yang dihadapi adalah menghitung √𝐶(mod 𝑛) (Galbraith, 2012).
Berikut ini adalah contoh dan algoritma dekrispi pada algoritma Rabin Public
1. Terima ciphertext C = “ʔ” = 660.
2. Hitung mp dan mq yangmerupakan akar kuadrat dari ciphertext C terhadap p
dan q.
𝑚𝑝 = 𝐶(𝑝+1) 4⁄ (mod 𝑝) ... (2.27)
𝑚𝑝 = 6608(mod 31) = 28
𝑚𝑞 = 𝐶(𝑞+1) 4⁄ (mod 𝑞) ... (2.28)
𝑚𝑞 = 6606(mod 23) = 4
3. Berdasarkan persamaan (2.17) dan (2.18), karena GCD(p,q) = 1 maka dapat diperoleh persamaan p × Yp + q × Yq = 1. Gunakan algotitma extended Euclidean untuk menghitung Yp dan Yq sehingga diperoleh nilai Yp = 3 dan
nilai Yq = -4.
4. Gunakan teorema sisa Cina (Chinese Remainder Theorem) untuk memperoleh empat kemungkinan nilai P (mod n) sedemikian sehingga 𝑃 ≡ ±𝑚𝑝(mod 𝑝) dan 𝑃 ≡ ±𝑚𝑞(mod 𝑞) (Galbraith, 2012). Berikut ini adalah rumus untuk menghitung empat kemungkinan hasil tersebut (Wandani, 2012).
𝑃𝑎 = 𝑚𝑝(mod 𝑝) 𝑃𝑐 = 𝑚𝑞(mod 𝑞) 𝑃𝑏 = −𝑚𝑝(mod 𝑝) 𝑃𝑑 = −𝑚𝑞(mod 𝑞)
Dengan menggunakan Chinese Remainder Theorem (CRT) maka diperoleh persamaan sebagai berikut.
𝑃1 = CRT(𝑃𝑎, 𝑃𝑐, 𝑝, 𝑞) = (𝑚𝑝𝑞𝑌𝑞+ 𝑚𝑞𝑝𝑌𝑝)(mod 𝑛) Misalkan, x = 𝑚𝑝𝑞𝑌𝑞 dan y = 𝑚𝑞𝑝𝑌𝑝. 𝑃1 = (𝑥 + 𝑦)(mod 𝑛) ... (2.29) 𝑃1 = (28 × 23 × −4 + 4 × 31 × 3)(mod 713) = 648 = “ʈ” 𝑃2 = CRT(𝑃𝑎, 𝑃𝑑, 𝑝, 𝑞) = (𝑚𝑝𝑞𝑌𝑞− 𝑚𝑞𝑝𝑌𝑝)(mod 𝑛) 𝑃2 = (𝑥 − 𝑦)(mod 𝑛) ... (2.30) 𝑃2 = (28 × 23 × −4 − 4 × 31 × 3)(mod 713) = 617 = “ɩ” 𝑃3 = CRT(𝑃𝑏, 𝑃𝑐, 𝑝, 𝑞) = (−𝑚𝑝𝑞𝑌𝑞+ 𝑚𝑞𝑝𝑌𝑝)(mod 𝑛) 𝑃3 = (−𝑥 + 𝑦)(mod 𝑛) ... (2.31) 𝑃3 = (−28 × 23 × −4 + 4 × 31 × 3)(mod 713) = 96 = “`”
𝑃4 = CRT(𝑃𝑏, 𝑃𝑑, 𝑝, 𝑞) = (−𝑚𝑝𝑞𝑌𝑞− 𝑚𝑞𝑝𝑌𝑝)(mod 𝑛)
𝑃4 = (−𝑥 − 𝑦)(mod 𝑛) ... (2.32) 𝑃4 = (−28 × 23 × −4 − 4 × 31 × 3)(mod 713) = 65 = “A”
5. Tentukan nilai yang benar dari keempat hasil (pada hal ini adalah nilai P4).
2.9. Citra Digital
“Citra adalah suatu representasi (gambaran), kemiripan atau imitasi dari suatu objek. Citra sebagai keluaran suatu sistem perekaman data dapat bersifat optik berupa foto, bersifat analog berupa sinyal-sinyal video seperti gambar pada monitor televisi atau bersifat digital yang dapat langsung disimpan pada suatu media penyimpan. Citra
digital adalah citra yang dapat diolah oleh komputer” (Sutoyo, et al. 2009).
Citra atau gambar dapat didefinisikan sebagai sebuah fungsi dua dimensi f(x,y) di mana x dan y adalah koordinat bidang datar, sedangkan harga fungsi f di setiap pasangan koordinat (x,y) disebut intensitas atau level keabuan (gray level) dari gambar di titik tersebut. Jika x, y dan f semuanya berhingga (finite) dan nilainya diskrit, maka gambarnya disebut citra digital atau gambar digital. Sebuah citra digital terdiri dari sejumlah elemen yang berhingga, di mana masing-masing mempunyai lokasi dan nilai tertentu. Elemen-elemen ini disebut sebagai picture element, image element, pels atau
pixels (Hermawati, 2013).
2.10. Jenis-jenis Citra Digital
“Ada banyak cara untuk menyimpan citra digital di dalam memori. Cara penyimpanan menentukan jenis citra digital yang terbentuk. Beberapa jenis citra digital yang sering digunakan adalah citra biner (monokrom), citra grayscale dan citra warna” (Sutoyo, et
al. 2009).
2.10.1. Citra biner (monokrom)
Dalam citra biner, hanya terdapat warna hitam dan putih. Dibutuhkan 1 bit di memori untuk menyimpan kedua warna ini. Gradasi warna pada citra biner dapat dilihat pada Gambar 2.5. dan contoh citra biner pada Gambar 2.6. (Sutoyo, et al. 2009).
Gambar 2.5. Gradasi Warna pada Citra Biner (Sutoyo, et al. 2009)
Gambar 2.6. Contoh Citra Biner
2.10.2. Citra grayscale (skala keabuan)
Banyaknya warna tergantung pada jumlah bit yang disediakan di memori untuk menampung kebutuhan warna. Citra 1 bit memiliki 2 warna, citra 2 bit mewakili 4 warna, citra 3 bit mewakili 8 warna, citra 5 bit mewakili 32 warna, citra 6 bit mewakili 64 warna, citra 7 bit mewakili 128 warna dan citra 8 bit mewakili 256 warna. Semakin besar jumlah bit warna yang disediakan di memori, semakin halus gradasi warna terbentuk (Sutoyo, et al. 2009). Contoh dari citra grayscale dapat dilihat pada Gambar 2.7.
Gambar 2.7. Contoh Citra Grayscale
2.10.3. Citra warna (true colour)
Setiap pixel pada citra warna mewakili warna yang merupakan kombinasi dari tiga warna dasar yaitu red, green dan blue (RGB). Setiap warna dasar menggunakan penyimpanan 8 bit atau 1 byte, yang berarti setiap warna mempunyai gradasi sebanyak
256 warna. Berarti setiap pixel mempunyai kombinasi warna sebanyak 2563 = 16.777.216 warna. Itulah sebabnya format ini dinamakan true colour karena mempunyai jumlah warna yang cukup besar sehingga bisa dikatakan hampir mencakup semua warna di alam (Sutoyo, et al. 2009).
Penyimpanan citra true colour di dalam memori berbeda dengan citra grayscale. Setiap pixel dari citra grayscale 256 gradasi warna diwakili oleh 1 byte, sedangkan 1
pixel citra true colour diwakili oleh 3 byte di mana masing-masing byte
merepresentasikan warna merah (red), hijau (green) dan biru (blue) (Sutoyo, et al. 2009). Contoh citra warna dapat dilihat pada Gambar 2.8.
Gambar 2.8. Contoh Citra Warna
2.11. Format File Citra Bitmap
“Citra bitmap sering disebut juga dengan citra raster” (Sutoyo, et al. 2009). Format file citra bitmap merupakan format file citra yang tidak mengalami proses kompresi sehingga kualitas citra yang dihasilkan lebih baik daripada file citra dengan format lain (Wandani, 2012).
“Citra bitmap menyimpan data kode citra secara digital dan lengkap (cara penyimpanannya adalah per pixel). Citra bitmap dipresentasikan dalam bentuk matriks atau dipetakan dengan menggunakan bilangan biner atau sistem bilangan lain. Citra ini memiliki kelebihan untuk memanipulasi warna, tetapi untuk mengubah objek lebih sulit.Tampilan bitmap mampu menunjukkan kehalusan gradasi bayangan dan warna dari sebuah gambar. Oleh karena itu, bitmap merupakan media elektronik yang paling tepat untuk gambar-gambar dengan perpaduan gradasi warna yang rumit, seperti foto dan lukisan digital. Citra bitmap biasanya diperoleh dengan cara scanner, camera
2.12. Steganografi
2.12.1. Definisi steganografi
Steganografi adalah jenis komunikasi tersembunyi yang secara harfiah berarti “tulisan tersembunyi” (Kipper, 2004). “Steganografi berasal dari Bahasa Yunani, yaitu steganos yang artinya tulisan tersembunyi (covered writing)” (Munir, 2006). Pesan tersebut bersifat terbuka, sering dilihat semua orang, tetapi tidak terdeteksi karena keberadaan makna pesan tersebut rahasia. Deskripsi lain yang populer untuk steganografi adalah “tersembunyi di depan mata (hidden in plain sight)” (Kipper, 2004).
Salah satu perbedaan steganografi dengan kriptografi adalah di mana pesan pada kriptografi bersifat acak, tidak dapat dibaca dan keberadaan akan pesan rahasia sering diketahui. Sedangkan steganografi menyembunyikan pesan dalam pesan lain (media) dan pesan atau media tersebut terlihat seperti normal (Kipper, 2004).
“Steganografi membutuhkan dua properti, yaitu media penampung dan pesan rahasia. Media penampung yang umum digunakan adalah gambar, suara, video atau teks. Pesan yang disembunyikan dapat berupa sebuah artikel, gambar, daftar barang, kode program atau pesan lain” (Munir, 2006).
2.12.2. Perbedaan steganografi dan kriptografi
Menurut Kipper (2004), perbedaan antara steganografi dan kriptografi adalah sebagai berikut.
1. Steganografi: Menyembunyikan pesan dalam pesan lain dan terlihat seperti grafis normal, video, atau file suara. Kriptografi: Pesan dienkripsi (terlihat seperti kumpulan karakter yang tidak memiliki arti).
2. Steganografi: Sebuah koleksi gambar grafis, file video atau file suara pada media penyimpanan (disk) yang mungkin tidak terlihat mencurigakan. Kriptografi: Sebuah kumpulan karakter acak pada media penyimpanan (disk) yang mungkin terlihat mencurigakan.
3. Steganografi: Penguping (eavesdropper) yang cerdas dapat mendeteksi sesuatu yang mencurigakan dari perubahan mendadak dari format pesan (yaitu, teks ke gambar grafis). Kriptografi: Penguping (eavesdropper) yang cerdas dapat mendeteksi komunikasi rahasia dari pesan yang telah dikodekan secara kriptografis.
4. Steganografi: Membutuhkan kehati-hatian ketika menggunakan kembali gambar atau file suara. Kriptografi: Membutuhkan kehati-hatian ketika menggunakan kembali kunci.
5. Steganografi: Tidak ada hukum yang terkait dengan steganografi. Kriptografi: Ada beberapa undang-undang yang melarang kriptografi.
2.12.3. Perbedaan steganografi dan watermarking
Menurut Kipper (2004), perbedaan antara steganografi dan watermarking adalah informasi pada steganografi harus tersembunyi oleh pihak lain yang tidak menyadari adanya informasi tersebut dan hal ini bersifat opsional pada watermarking. Steganografi
modern harus terdeteksi hanya jika informasi rahasia (kunci) diketahui.
Watermarking memiliki hubungan dengan steganografi dan merupakan aplikasi
dari steganografi, hanya saja digunakan dalam konteks yang berbeda. Pada steganografi ketahanan (robustness) tidak menjadi aspek yang penting (tidak memiliki ketahanan atau memiliki ketahanan yang terbatas) dan tujuannya untuk menyembunyikan fakta bahwa ada informasi yang tersembunyi. Sedangkan pada watermarking dirancang untuk menjadi kuat (robust) dan dirancang untuk membawa informasi tersembunyi meskipun tidak selalu terlihat (Kipper, 2004).
Menurut Munir (2006), pesan rahasia pada steganografi disembunyikan ke dalam media penampung di mana media penampung tersebut tidak berarti apa-apa (hanya sebagai pembawa). Sedangkan pada watermarking, media penampung dan informasi yang disembunyikan memiliki keterkaitan yaitu media penampung dilindungi atau ditandai kepemilikannya dengan pemberian informasi berupa label hak cipta (watermark) seperti gambar atau suara yang disembunyikan ke dalam media penampung tersebut.
2.12.4. Konsep dan Terminologi Steganografi
Terdapat beberapa istilah yang berhubungan dengan steganografi (Munir, 2006; Maurer & Basin, 2010), antara lain:
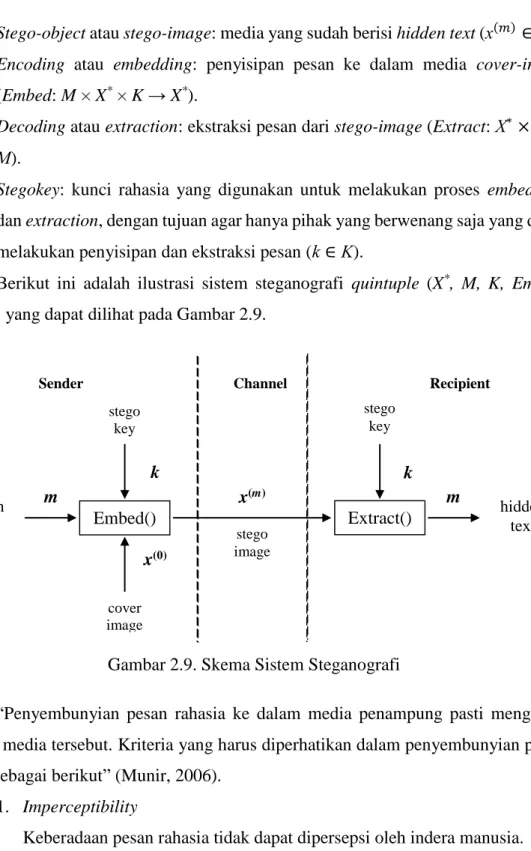
1. Hidden text atau embedded message: pesan yang disembunyikan (m∈ M). 2. Cover-object atau cover-image: media yang digunakan untuk menyembunyikan
3. Stego-object atau stego-image: media yang sudah berisi hidden text (x(𝑚)∈ X*). 4. Encoding atau embedding: penyisipan pesan ke dalam media cover-image
(Embed: M × X* × K → X*).
5. Decoding atau extraction: ekstraksi pesan dari stego-image (Extract: X∗× K →
M).
6. Stegokey: kunci rahasia yang digunakan untuk melakukan proses embedding dan extraction, dengan tujuan agar hanya pihak yang berwenang saja yang dapat melakukan penyisipan dan ekstraksi pesan (k∈ K).
Berikut ini adalah ilustrasi sistem steganografi quintuple (X*, M, K, Embed, Extract) yang dapat dilihat pada Gambar 2.9.
Gambar 2.9. Skema Sistem Steganografi
“Penyembunyian pesan rahasia ke dalam media penampung pasti mengubah kualitas media tersebut. Kriteria yang harus diperhatikan dalam penyembunyian pesan adalah sebagai berikut” (Munir, 2006).
1. Imperceptibility
Keberadaan pesan rahasia tidak dapat dipersepsi oleh indera manusia.
2. Fidelity
Kualitas dari media penampung tidak berubah banyak akibat penyisipan sehingga tidak dapat dipersepsi oleh indera manusia (sulit untuk mengetahui bahwa terdapat pesan di dalam media).
m x(m) m k k x(0) hidden text hidden text stego key stego key stego image cover image Recipient Channel Sender Embed() Extract()
3. Recovery
Pesan yang disembunyikan harus dapat diungkapkan kembali (reveal). Karena tujuan dari steganografi adalah untuk menyembunyikan data (data
hiding), maka sewaktu-waktu pesan rahasia di dalam stego-object harus
dapat diambil kembali.
2.12.5. Teknik penyembunyian data
Teknik penyisipan data ke dalam cover-object dapat dilakukan dalam dua macam ranah, yaitu ranah spasial dan ranah transformasi (Munir, 2006).
1. Ranah Spasial atau Ranah Waktu (Spatial/Time Domain)
Teknik ini memodifikasi langsung nilai byte dari cover-object (nilai byte dapat merepresentasikan intensitas/warna pixel dan amplitudo). Contoh metode yang tergolong ke dalam teknik ranah spasial adalah metode LSB.
2. Ranah Transformasi (Transform Domain)
Teknik ini memodifikasi langsung hasil transformasi frekuensi sinyal. Contoh metode yang tergolong teknik ranah transformasi adalah spread spectrum.
2.13. Metode Pemetaan Titik Hitam dengan Pencarian Sekuensial
Metode ini merupakan modifikasi dari metode FOF dan EOF dengan mengadopsi ciri atau karakteristik dari masing-masing metode FOF, EOF dan LSB untuk keperluan penyembunyian pesan. Ide dasarnya adalah penyembunyian garis hitam (dari metode FOF dan EOF) dan ukuran dimensi citra yang tidak bertambah (mengadopsi kelebihan metode LSB) dengan cara menyisipkan garis (titik-titik) hitam ke dalam pixel berwarna hitam pada citra dua dimensi.
Kemungkinan kekurangan yang akan diperoleh dari metode tersebut adalah pesan rahasia yang akan disisipkan terbatas sesuai dengan jumlah pixel berwarna hitam pada citra. Sebelum menyisipkan pesan diperlukan pemetaan pixel (titik) hitam dengan pencarian sekuensial untuk memperoleh jumlah dan posisi titik hitam (ruang) yang dapat digunakan untuk menyisipkan data.
2.13.1. Pencarian sekuensial
Pencarian sekuensial atau pencarian linier atau pencarian lengkap (exhaustive) adalah pencarian yang dilakukan secara berulang hingga melalui keseluruhan bilangan di dalam larik (array). Gambar 2.10. menunjukkan pencarian linier untuk nilai 77 dalam sebuah larik yang sudah terurut secara menaik (Stephens, 2013).
Gambar 2.10. Pencarian Linier di Dalam Larik yang Terurut (Stephens, 2013) Pencarian linier juga bekerja dalam barisan bilangan yang belum terurut. Algoritma ini mungkin perlu perulangan (loop) melalui seluruh elemen di dalam larik untuk menyimpulkan bahwa elemen (item) tidak ada, sehingga kasus terburuk
(worst-case) algoritma ini adalah O(N) (Stephens, 2013).
Bahkan dalam kasus rata-rata (average-case), run time algoritma ini adalah O(N). Jika ditambahkan sejumlah langkah yang diperlukan untuk mencari setiap item dalam array, maka didapatkan 1 + 2 + 3 + ... + N = N * (N + 1) / 2. Jika jumlah tersebut dibagi dengan N untuk mendapatkan waktu pencarian rata-rata untuk semua item N, maka didapatkan (N + 1) / 2, yang masih O(N) (Stephens, 2013).
Algoritma ini jauh lebih lambat dari pencarian biner atau pencarian interpolasi, tetapi memiliki keuntungan di mana algoritma ini bekerja pada linked list dan unsorted
list (Stephens, 2013).
2.13.2. Ilustrasi pemetaan titik hitam
Jika terdapat citra seperti pada Gambar 2.11, maka sebelum melakukan penyembunyian data, citra harus diperiksa terlebih dahulu untuk memperoleh jumlah titik hitam (ruang) yang dapat digunakan untuk menyisip data yang akan disembunyikan dan index (posisi) dari titik hitam tersebut.
Gambar 2.11. Citra Berdimensi 10 × 10 pixels (RGB, format BMP)
Tabel 2.3. adalah matriks dari Gambar 2.11, di mana tiap pixel direpresentasikan dalam tiga nilai yaitu red, green dan blue.
Tabel 2.3. Matriks dari Gambar 2.11. i j 0 1 2 3 4 5 6 7 8 9 0 22, 22, 22 141, 198, 63 46, 49, 146 166, 124, 82 236, 0, 140 109, 207, 246 109, 207, 246 109, 207, 246 109, 207, 246 109, 207, 246 1 237, 28, 36 37, 177, 67 141, 198, 63 141, 198, 63 166, 124, 82 109, 207, 246 46, 49, 146 109, 207, 246 46, 49, 146 109, 207, 246 2 166, 124, 82 237, 28, 36 141, 198, 63 166, 124, 82 46, 49, 146 0, 0, 0 109, 207, 246 109, 207, 246 109, 207, 246 109, 207, 246 3 237, 28, 36 237, 28, 36 237, 28, 36 255, 255, 255 46, 49, 146 255, 255, 255 26, 26, 26 255, 255, 255 255, 255, 255 255, 255, 255 4 255, 255, 255 255, 255, 255 37, 28, 28 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 15, 3, 3 255, 255, 255 5 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 6 255, 255, 255 24, 15, 15 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 42, 33, 33 255, 255, 255 255, 255, 255 255, 255, 255 7 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 23, 2, 2 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 8 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 9 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255 255, 255, 255
Untuk melakukan pemetaan, dihitung jumlah pixel (panjang data yang akan dipetakan) yang terdapat di dalam citra dengan melakukan perkalian baris dengan kolom, hasilnya adalah 100.
Pada kasus ini, yang dianggap sebagai titik hitam adalah pixel yang memiliki nilai R, G dan B antara 0 hingga 42 (0 ≤ x ≤ 42). Dilakukan pencarian secara sekuensial dari index pertama hingga index terakhir, jika nilai R, G dan B memenuhi persyaratan, maka nilai index akan disimpan ke dalam sebuah list.
Hasil percobaan kasus ini akan diperoleh nilai hitam = [ (0,0), (1,6), (2,4), (4,7), (5,2), (6,3), (6,6), (8,4) ]. Index tersebut didapatkan karena dalam pencarian dilakukan perkolom (dari baris 1 kolom 1, baris 2 kolom 1, baris 3 kolom 1 dan seterusnya). Untuk lebih jelasnya, posisi (index) dari hasil pencarian titik hitam dapat dilihat pada Tabel 2.5. yang ditandai dengan teks yang dicetak tebal.
Setelah pencarian dan pemetaan selesai, dihitung panjang dari list untuk memperoleh jumlah pixel yang dapat digunakan untuk menyembunyikan data. Jika jumlah pixel hitam sama atau lebih dari jumlah data yang akan disembunyikan, maka steganografi dapat dilakukan. Jika jumlah pixel hitam lebih kecil dari jumlah data yang akan disembunyikan, maka harus dilakukan penggantian citra.
2.14. Penelitian yang Relevan
1. Pada penelitian terdahulu yang dilakukan oleh Nasution (2013) tentang “Implementasi Sistem Keamanan Data Menggunakan Steganografi Teknik First Of
File dan Hill Cipher Kunci Ganda”, menyebutkan metode FOF tidak jauh berbeda
dengan metode EOF. Pada metode FOF, pesan disisipkan pada awal file, sedangkan pada metode EOF, pesan disisipkan pada akhir file. Hasil penelitiannya menunjukkan data hasil enkripsi disimpan diawal file citra bitmap sehingga membuat ukuran file citra bitmap lebih besar dari semula dan citra stego hasil penyisipan pesan memiliki garis atau gradasi berwarna hitam pada bagian atas (header) citra stego. Banyaknya garis hitam pada file citra bitmap berbanding lurus dengan panjang karakter hasil enkripsi plaintext (ciphertext). Dengan kata lain semakin panjang karakter ciphertext maka garis hitamnya semakin tebal.
2. Aditya, et al. (2010) dalam penelitiannya yang berjudul “Studi Pustaka untuk Steganografi dengan Beberapa Metode”, menunjukkan bahwa pada metode LSB, pesan yang disisip, ukurannya harus lebih kecil dari citra penampung, tetapi lain
halnya pada metode EOF ukuran pesan yang akan disisipi bisa lebih besar dari ukuran citranya. Pada metode LSB citra yang telah disisipi pesan tidak terlalu mempengaruhi ukuran citranya, tetapi akan mempengaruhi kualitas citranya. Sedangkan pada metode EOF, kualitas citra setelah disisipi pesan tidak berubah, tetapi akan mengubah ukuran citranya. Penelitian ini membahas perbandingan metode LSB dengan EOF.
3. Muko, et al. (2012) membuat penelitian dengan judul “Aplikasi Enkripsi SMS dengan Metode Rabin pada Android” menunjukkan kelebihan dan kekurangan dari algoritma Rabin. Kelebihannya adalah proses enkripsi teknik kriptografi Rabin terbilang sederhana sehingga proses enkripsi membutuhkan waktu yang relatif cepat dan teknik kriptografi Rabin efektif untuk digunakan pada resource yang sederhana dengan processor yang tidak dapat melakukan komputasi yang kompleks dan rumit, seperti perangkat mobile. Kekurangannya adalah hasil dekripsi kurang efektif dikarenakan menghasilkan empat kemungkinan plaintext berbeda yang semuanya diberikan kepada pengguna dan selanjutnya pengguna harus mementukan mana diantara keempat plaintext tersebut yang benar. Pada penelitian ini digunakan dua cara dalam menentukan hasil dekripsi yang benar, yaitu dengan dekripsi manual dan dengan autodekripsi.

![Tabel 2.2. Penyelesaian Contoh Soal Square and Multiply Left-to-Right Variant i b[i] a 2 a 2 mod z b[i] == ‘1’ a](https://thumb-ap.123doks.com/thumbv2/123dok/4563159.3319128/14.892.305.646.599.731/tabel-penyelesaian-contoh-soal-square-multiply-right-variant.webp)