An efficient probabilistic finite element method
for stochastic groundwater flow
Harald Osnes & Hans Petter Langtangen*
aSINTEF Applied Mathematics, P.O. Box 124, Blindern, N-0314 Oslo, Norway
Mechanics Division, Department of Mathematics, University of Oslo, P.O. Box 1053, Blindern, N-0316 Oslo, Norway
(Received 27 February 1997; revised 15 October 1997; accepted 1 December 1997)
We present an efficient numerical method for solving stochastic porous media flow problems. Single-phase flow with a random conductivity field is considered in a standard first-order perturbation expansion framework. The numerical scheme, based on finite element techniques, is computationally more efficient than traditional approaches because one can work with a much coarser finite element mesh. This is achieved by avoiding the common finite element representation of the conductivity field. Computations with the random conductivity field only arise in integrals of the log conductivity covariance function. The method is demonstrated in several two- and three-dimensional flow situations and compared to analytical solutions and Monte Carlo simulations. Provided that the integrals involving the covariance of the log conductivity are computed by higher-order Gaussian quadrature rules, excellent results can be obtained with characteristic element sizes equal to about five correlation lengths of the log conductivity field. Investigations of the validity of the proposed first-order method are performed by comparing nonlinear Monte Carlo results with linear solutions. In box-shaped domains the log conductivity standard deviation jY may be as large as 1.5, while the head variance is considerably influenced by nonlinear effects as jY approaches unity in more general domains.q1998 Elsevier Science
Limited. All rights reserved
Keywords: stochastic hydrology, perturbation methods, groundwater flow moments.
1 INTRODUCTION
The prediction of groundwater flow and transport from mathematical models involves considerable uncertainty due to the presence of heterogeneities in natural formations. During the last two decades stochastic models have been developed to consistently quantify the uncertainty in sub-surface hydrology. Such models usually involve stochastic partial differential equations, and these have mostly been studied from an analytical point of view, see Dagan,7–9 Gelhar,16 Neuman et al.,21 Christakos et al.,5 Oliver et
al.22 Rubin.24Since analytical solution methods are often restricted to simple aquifer geometries, more general numerical approaches are desired for stochastic flow models to be of practical interest in engineering case stu-dies. Numerical solution of stochastic partial differential
equations is unfortunately often several orders of magnitude more CPU time-consuming than the solution of the equa-tions in a corresponding deterministic model. Nevertheless, numerical solution strategies have received increased inter-est along with the rapid development of computer power.
Numerical methods for stochastic groundwater flow fall basically into two categories; Monte Carlo simulation (MCS)2,3,25 and perturbation-based techniques. The latter methods are usually considered as more efficient than MCS, but are also less general and assume small stochastic variability. Another important difference is that the MCS method requires assumptions about the probability distribu-tions of input quantities, while specifying second-order moments is sufficient in the context of perturbation meth-ods. The combination of finite element discretization and lower-order perturbation expansion of stochastic quantities is usually known as stochastic finite element methods (SFEM) or probabilistic finite element methods (PFEM). SFEM/PFEM have been used for some time in the field of
Printed in Great Britain. All rights reserved 0309-1708/98/$ - see front matter PII: S 0 3 0 9 - 1 7 0 8 ( 9 7 ) 0 0 0 4 4 - 4
185
structural engineering.12,19,20 Applications to groundwater flow and transport have been reported by Dettinger et al.13 and Townley et al.29
Following well-established experimental and theoretical studies on groundwater flow, e.g. Freyberg,15 Sudicky,26 Leblanc et al.,18Dagan,8Gelhar,16 Christakos4and Bellin
et al.,2the hydraulic conductivity can be characterized as a spatial random field. We limit the uncertain physical con-ditions to a homogeneous random conductivity field in the present paper. In a traditional SFEM/PFEM approach, the number of stochastic variables is dictated by the required spatial resolution of the conductivity field. The total work is usually proportional to the square of the number of tic variables. Hence, any reduction in the number of stochas-tic variables has an important effect on the efficiency and feasibility of SFEM/PFEM.
In this paper we present and investigate the performance of an improved probabilistic finite element method where the number of stochastic variables is of the same order as the number of degrees of freedom needed to describe the expectation and variance fields of the head. Notice that the correlation scale of the conductivity is much smaller than for the head response, which means that the head behaves considerably smoother than the conductivity. Thus, the number of stochastic variables is dramatically reduced. The method is based on an approach called the weighted integral method, which has previously been pre-sented for stress analysis with emphasis on one-dimensional beam structures.10,11,27,28 In Section 2 we formulate the stochastic partial differential equation governing stationary, single-phase, incompressible porous media flow. Section 3 concerns the derivations of approximate expectation and covariance for hydraulic head using the weighted integral method. Thereafter, in Section 4, the method is carefully examined in 2D flow cases where analytical solutions of our stochastic boundary value problem are available. More general 2D and 3D flow problems are analysed by comparing the results of the weighted integral approach to MCS. The perturbation expansions used in the present numerical method require that the variations of the conduc-tivity and head fields are not too large. To investigate the limitation of the proposed methodology due to the assump-tions in the first-order perturbation framework, we present in Section 5 some parameter studies, where the variance of the log conductivity field is varied in the context of nonlinear MCS. These nonlinear results are compared with first-order solutions. The final section includes a summary of the main findings and a discussion of the approach.
2 THE GOVERNING EQUATIONS
We consider steady saturated flow described by the pressure equation
=·(T=H)¼0 (1)
in a domain D, Rd. Here, H(x) is the hydraulic head, T
(x) is the isotropic conductivity, x is a spatial point, and d is the number of space dimensions. Eqn (1) is obtained by combining Darcy’s law and the mass balance equation. Associated boundary conditions are given by
H¼f(x)for x[]D1and
]H
]n¼g(x)for x[D2, (2)
where]D¼]D1∪]D2is the boundary of D, while f and g are prescribed (deterministic) functions, and ]H/]n means differentiation in the outward normal direction.
The conductivity T is regarded as a random field. Without serious restrictions, we write T¼exp(Y). This is a reason-able way of writing the nonnegative conductivity. Notice that no assumption is made on the probability distribution of T (or Y). We assume that Y¼mYþY9, where mYis the
expectation of Y, and Y9is the stochastic deviation from the mean. Because T is random, the response H in eqn (1) also becomes a stochastic field. We therefore become concerned with the computation of statistical properties of the head field. In particular, we focus on the expectation and the covariance structure of H.
The numerical method to be presented in this paper relies on a standard first-order Taylor series expansion of the sto-chastic boundary value problem [eqns (1) and (2)]. We start by expanding the conductivity in a series with powers of the perturbation Y9. Only the first two terms are retained. This procedure results in the following stochastic boundary value problem:
=·{exp(mY)(1þY9)=H}¼0 for x[D: (3)
H¼f(x)for x[]D1, (4)
]H
]n¼g(x)for x[]D2, (5)
which forms the basis for the numerical method to be developed in the next section.
3 DERIVATION OF HEAD MOMENTS
The solution of the stochastic boundary value problem [eqns (3)–(5)] is accomplished by a finite element discretization and a first-order perturbation expansion of H. The domain D is divided into E finite elements D(e), D¼cEe¼1D(
e)
. It will be advantageous to work with finite element basis functions that have constant derivatives. Hence, we apply elements of triangular or tetrahedral type. Letting Ni(x) denote the
pie-cewise linear finite element basis functions, the random
H(x) field is approximated by
H<
XN
i¼1
hiNi(x) (6)
where hi is the approximate head value at node i, and N
denotes the total number of nodes. Employing a Galerkin method to eqn (3) equaiton (4) eqn (5) we arrive at the system
where K is the coefficient (stiffness) matrix, h ¼ {h1,h2,…,hN}T is the vector of approximate nodal values
({}Tmeans the transpose), and the right-hand-side vector p contains contributions from the boundary conditions.
Provided that the expectation mY ¼E[Y] is constant on
each element, the contribution to K from element e, denoted
K(e), can be expressed as follows:
K(e)¼
is a stochastic variable. B(e)is a matrix containing first deriva-tives of the test functions belonging to element e. It looks like
B(e)¼
spatial coordinates. Because the basic functions are piece-wise linear, B(e)is constant. The global coefficient matrix K may now be written
3 3 or 4 3 4 matrices in 2D and 3D, respectively) are regarded as N 3 N matrices where all but the entries
belonging to the finite element e are zero. Furthermore,
K0 is the standard finite element discretization of the (possibly variable coefficient) Laplace operator when the
multiplicative stochastic part of the input field T is neglected. We also observe that K is a function of the random variables Y(1), Y(2),…, Y(E). Thus, from eqn (7) it follows that the head vector depends on these random variables. We expand h in a first-order series around
E[Y(e)]¼0,
where ˆh is the first-order approximation of the stochastic
vector h. Both h0¼{h01, …, h0N} T
and ]h/]YðeÞ¼{]h1/ ]YðeÞ, …, ]hN/]Y(e)}T are vectors of N components. Eqns
(11) and (12) are inserted into eqn (7). Following, e.g. Deodatis and Shinozuka11 and Der Kiureghian and Ke,12 terms of equal order in Y(e)are grouped and solved sepa-rately. This leads to the zero-order problem
K0h0¼p: (13)
Furthermore, there are E first-order problems
K0
]h
]Y(e)¼ ¹DK
(e)
0 h0; e¼1, …,E: (14)
All the boundary conditions are supposed to be fulfilled by the zero-order solution. Thus, the right-hand-side of eqn (14) is set to zero for all nodes with prescribed head values. It is recognized that the E þ 1 equation systems (13) and (14) contain the same coefficient matrix K0. More-over, the matrix is efficiently computed by integrating the elemental contributions K0
(e)
analytically.
First, the relation (13) is solved for h0. Thereafter, h0 serves as a part of the known right-hand-sides of the equa-tion systems for]h/]Y(e), e¼1,…, E. From these solutions we can easily construct the first two moments of the approx-imate stochastic head field. To first order, the expectation is given by
E[hˆ]¼h0: (15)
From eqns (11), () and (13) it follows that this approximate expectation of H is obtained by solving the flow eqn (1) with exp(mY) as a conductivity field. The covariance
becomes
The integration of the log conductivity covariance must normally be carried out by numerical techniques.
To summarize, the present technique yields first-order approximations to the head expectation and covariance without the common discretization of the random input field Y in terms of finite elements. The method relies solely on specification of the mean and covariance structure of Y. Normally, the finite element mesh used for Y has to be very much finer than the one needed for the response H. With the approach of the present paper one can use a fairly coarse mesh designed to resolve the moments of H. However, the integration of the covariance of Y9then needs higher-order quadrature. In the next section we investigate the accuracy of the proposed approach for various mesh sizes and order of the numerical integration rules.
The method described in this section has been implemen-ted in a compact Cþþprogram using object-oriented pro-gramming techniques and the Diff-pack14library. To obtain reference results in general cases, a solver for eqns (1) and (2) based on MCS and standard finite element discretization of the conductivity field is also included in the program. Moreover, the MCS module may be used to solve the sto-chastic order problem defined as follows. The first-order expansions exp(mY)(1 þ Y9) and H0 þ H1 for the conductivity and head, respectively, are inserted into eqn (1). Here, H0is the deterministic zero-order term, and H1 is the stochastic first-order perturbation. After neglecting products of first-order quantities we obtain the equations
=2H0¼0, (18)
=2H1¼ ¹=·{Y9=H0}, (19)
where it is assumed that mY is constant. The boundary
conditions for the deterministic problem (18) are given by eqn (2), while the stochastic eqn (19) is subjected to homo-geneous boundary conditions.
4 NUMERICAL EXAMPLES
Here, we examine 2D and 3D test problems. In the 3D situation we have chosen a simple box geometry, while we use a square domain and a more generally shaped geo-metry in the 2D cases. For the square domain we compare the results of the proposed method with analytical solutions of eqns (18) and (19) derived by Osnes.23In the 3D example and the more general 2D case, the reference results are obtained by solving the problems (18) and (19) using MCS. The reference solutions are derived under the assump-tion of lognormally distributed conductivity, whereas the weighted integral method requires knowledge of the first two moments of the input field. In the square 2D geometry, we use the separate exponential covariance function,j2Yexp (¹lx¹x9l/I¹ly¹y9l/I), for the log conductivity. Here,jY2 is the log conductivity variance, x¼ ðx;yÞand x9¼(x9,y9) are the points of consideration, and I is the correlation scale. In the 3D and general 2D problems the more usual isotropic
covariance function is applied;jY2exp(¹r/I), where r is the distance between x and x9. In all cases the expectation is constant, and the covariance is stationary.
For the square 2D domain we set D¼[0,L]3[0,L], while
the 3D geometry is given by D¼[0,L]3[0,B]3[0,B]. At x
¼0,L the head is given prescribed constant values. The rest of the boundary is impermeable. This implies that the (first-order) head expectation is linear in x. The results to be reported are obtained for log conductivity standard devia-tion equal to 0.5. However, due to the linearity of the pro-blem this choice is of no importance. Furthermore, except from the general 2D case, we have chosen JI¼0.5, where J is the length of the mean head gradient vector. Four different grids are examined in the case of the square 2D geometry. With D as the characteristic element size, the finest grid has D ¼ I/2, a medium resolution has D ¼ I, a coarse mesh hasD¼2I, and a very coarse grid hasD¼5I. The domain [0,L]3[0,L] is typically divided into squares of size D3D, and each square is divided into two triangles. In the 3D case two grids are applied; a mesh with D¼2I and a very coarse grid ofD¼5I.
4.1 Square aquifer
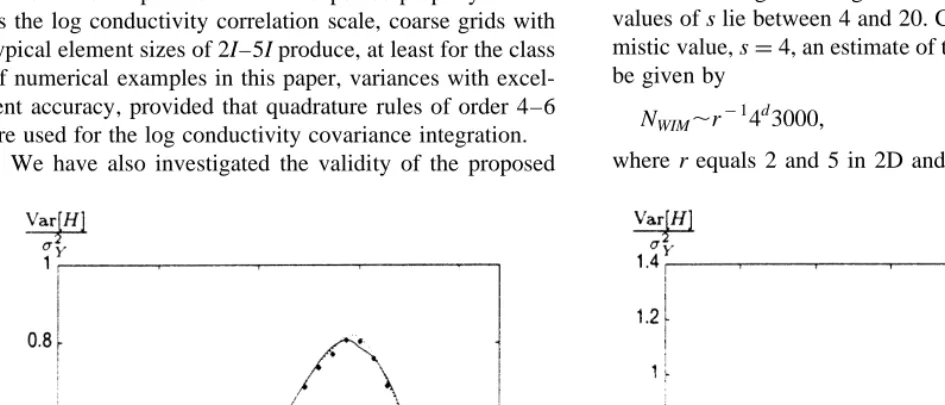
Let L/I ¼20. In Fig. 1(a) head variances are shown in the streamline direction. The analytical solution is compared with the results from the very coarse grid using the weighted inte-gral approach with various Gaussian quadrature rules (on tri-angles)6,30for the covariance integral. Results in the transverse direction are depicted in Fig. 1(b). It is seen that the sixth-order integration offers fairly accurate solutions, while the results from the second- and fourth-order rules overestimate the var-iance considerably. Fig. 2 shows corresponding solutions obtained by the coarse grid. While the second- and third-order rules give poor results, the solutions from the fourth-and fifth-order integrations are of high quality. A somewhat unexpected feature is the fact that the second-order result is more accurate than the third-order solution. Numerical experi-ments performed by the authors show that polynomial func-tions of second order are exactly integrated by both schemes, while the second-order rule may be more accurate than the third-order method for exponential functions. In Fig. 3 analy-tical results are compared with weighted integral solutions using a grid with medium resolution. The results using the fourth- and fifth-order numerical integration rules are very accurate, while the second- and third-order solutions overesti-mate the variance slightly. Using the fine grid (Fig. 4), the head variance is excellently resolved, regardless of the integration order. One should particularly notice that even the behaviour near the boundaries is accurately captured.
The accuracy of the method has also been investigated for rectangular geometries, showing very similar behaviour as in the square domain case.
4.2 Two-dimensional aquifer with nontrivial geometry
for a more general 2D aquifer. The geometry is depicted in Fig. 5. Also shown are the boundary conditions (H¼10 at
b1, H¼0 at b2and]H/]n¼0 at b3) and the lines, l1and l
2, for plotting of results. Along these lines we define length coordinates s1and s2, starting from the lower and left ends of l1and l2, respectively. The log conductivity covariance function is isotropic, and the correlation length I is equal to unity. For the present domain there is no analytical solution available. Reference results must therefore be computed by MCS. In order to obtain high accuracy the realizations of the random conductivity field are generated by a matrix method where all internodal covariances are taken into account, see Osnes.23 The MCS results are based on 300 realizations, using a grid with 3840 bilinear elements.
The weighted integral method is run on two different triangular meshes. Variances obtained on a very coarse grid with 30 elements are illustrated in Fig. 6. It is seen that while the second-order integration solution over-estimates the variance considerably, the results of the fourth- and fifth-order methods are relatively good. The coarse mesh used is depicted in Fig. 7. Fig. 8 shows that the variance is well resolved for all integration rules, when a finer grid, containing 224 elements, is used. However, near
the corner point at the right end of the line l2, the results are slightly inaccurate. The expectation obtained by MCS is well approximated by h0for the mesh with 224 elements, while the expectation, using the very coarse grid, shows somewhat inferior accuracy near the corner point.
4.3 Three-dimensional problem
We consider a stochastic first-order problem in a simple box-shaped 3D domain defined in Section 4, with L/I ¼ 20 and B/I¼10. The isotropic log conductivity covariance function is employed. There is no analytical solution avail-able for the present problem. Therefore, a reference solution is obtained by MCS, using a mesh with 3456 trilinear ele-ments. This solution is compared with weighted integral results on two different tetrahedral grids. In the weighted integral method the computations of the covariance inte-grals are carried out using Gaussian quadrature rules from Jinyun.17Results from a very coarse grid, withD¼5I and 80 tetrahedral elements, are depicted in Fig. 9. It is seen that while the second- and third-order integration rules over-estimate the variance, the fifth-order solution is relatively accurate. Corresponding results from a grid with 1250 Fig. 1. Head variance for square domain and very coarse grid (D¼5I). The analytical solution (solid line) is compared with numerical solutions obtained by integrating the covariance function by rules of second-order (dashed line), fourth-order (S) and sixth-order (þ). (a)
Variation along the line y¼L=2 as a function of x/I. (b) Variance along the line x¼L/2 as a function of y/I.
Fig. 2. Head variance for square domain and coarse grid (D¼2I). The analytical solution (solid line) is compared with numerical solutions obtained by integrating the covariance function by rules of second-order (dashed line), third-order (line points), fourth order (þ) and fifth
elements andD¼2I are shown in Fig. 10. The third-order rule still gives values that are too large, while the solutions obtained by the second- and fifth-order integrations are of high quality.
5 NONLINEAR RESULTS
The weighted integral method is shown to yield excellent results for several 2D and 3D problems. However, the method is based on a first-order series expansion. Thus the following important question arises naturally: What kind of accuracy limitations exist for typical first-order methods? Based on a single realization of the conductivity field Aba-bou et al.1claimed that head variances are well resolved by first-order theories forjYas large as approximately 2. On the
other hand, careful investigations performed by Chin et al.3 indicate upper limits to be given by jY ¼ 1 for velocity covariances and transverse dispersion andjY¼1.5 for long-itudinal dispersivity. Due to the lack of generally valid con-clusions regarding limitations of perturbation methods, we have compared stochastic first-order results from Osnes23 and the present paper with MCS solutions of the stochastic nonlinear eqn (1) for different values ofjY. the MCS results are based on 3000 realizations of the conductivity field, which are generated by the accurate matrix method used in the Section 4.2 and Section 4.3. Fig. 11 shows variances for the square domain, which is divided into 4096 bilinear elements in the context of MCS. It is seen that the agreement is relatively high for jY # 1.5, while the solution is
considerably affected by nonlinear terms for jY ¼ 2. It should be noted that the flow is in the negative x-direction. Fig. 3. Head variance for square domain and medium grid (D¼I). The analytical solution (solid line) is compared with the numerical solutions obtained by integrating the covariance function by rules of second-order (dashed line), third-order (line points), fourth-order (þ) and fifth-order (A). (a) Variance along the line y¼L=2 as a function of x/I. (b) Variance along the line x¼L/2 as a function of y/I.
Fig. 4. Head variance for square domain and fine grid (D¼1/2I). The analytical solution (solid line) is compared with numerical solutions obtained by integrating the covariance function by rules of second-order (dashed line), third-order (line points), fourth-order (þ) and
Corresponding results for the more general 2D geometry, with 3840 elements, are depicted in Fig. 12. It appears that the solutions begin to diverge asjYapproaches unity. This simple investigation indicates that the effects of nonlinea-rities upon statistical moments of head are more pronounced near singularities in the flow field than in smooth regions.
When it comes to simulation times of the MCS approach compared to the weighted integral method, we typically experience that the latter technique is about an order of
magnitude faster than MCS. However, this is dependent on the problem and especially on the grid size, as we explain in the final section.
6 SUMMARY AND DISCUSSION
In this paper we have examined an efficient numerical approach for single-phase groundwater flow models con-taining a random conductivity field. Here, the boundary conditions have been of Dirichlet and Neuman type. Effects of wells, recharge and anisotropic media are easily included. However, further research is required in order to extend the method to deal with more complicated problems, including single-phase transport and unsaturated flow. The method is based on finite element discretization of the head response and a first-order stochastic perturbation expansion of the conductivity and head fields. A general distribution function can be allowed for the conductivity, in principle, but the method approximationes the true distribution by a normal distribution. By using triangular or tetrahedral elements, the coefficient matrices may be obtained efficiently by exact, analytical integration. Furthermore, one is able to avoid discretizing the usually fine-scale conductivity field by finite elements and instead work solely with the expectation and the covariance function of the conductivity. The expectation is treated as constant on each element, which of course implies an implicit discretization. However, in real porous formations the mean conductivity is usually very slowly varying or exhibits large discontinuous jumps, so the error introduced by the constant elemental representation is gen-erally negligible. To completely avoid the influence of such discretization effects, we have used a globally constant expectation in the numerical examples. The covariance of the conductivity must be integrated over the elements using, e.g. Gaussian quadrature rules. If this integration is Fig. 5. General 2D domain with boundary conditions (H¼10 at
b1, H¼0 at b2and]H/]n¼0 at b3). The dashed lines (l1and l2)
are defined for plotting purposes.
Fig. 6. Head variance for a general domain. Comparison of MCS solutions (solid lines) and weighted integral results from a very coarse grid
sufficiently accurate, the element sizes can be tailored to the slowly varying head moments rather than the fine-scale con-ductivity field. From Osnes23it is seen that, depending on the direction of the separation vector, the correlation scale for the head is approximately 4–10 times as large as the log conductivity scale. Compared with standard techniques, like the probabilistic finite element method, the present approach can therefore employ much coarser meshes. Our numerical examples confirm this expected property. With I as the log conductivity correlation scale, coarse grids with typical element sizes of 2I–5I produce, at least for the class of numerical examples in this paper, variances with excel-lent accuracy, provided that quadrature rules of order 4–6 are used for the log conductivity covariance integration.
We have also investigated the validity of the proposed
first-order method. Stochastic nonlinear MCS results for different values of jY are compared with first-order solu-tions obtained here and in Osnes.23In regular domains jY may be as large as 1.5, while the head variance is consider-ably influenced by nonlinear effects asjYapproaches unity in more general domains.
One should notice that the present method, as well as ordinary stochastic finite element methods for the same class of problems, requires work of order N2, where N is the number of nodes in the grid. Although N can be signifi-cantly smaller in the present approach than in conventional stochastic finite element methods, the asymptotic work esti-mate is of course a serious disadvantage when simulating large-scale 3D phenomena. Monte Carlo methods lead to work of order MN, where M is the number of simulations demanded by the estimator to obtain sufficient accuracy. We believe that M is independent of N. The typical size of M depends strongly on the problem of consideration. For example, M ¼2000 ensures that the limits of a 95% con-fidence interval for the head variance deviates less than 7% from the estimated value. In our computations we have chosen M ¼ 3000. On the other hand, N is governed by the fine-scale variations in the (log) conductivity field. The ratio of the number of nodes required by the MCS method, NMCS, and the present weighted integral method, NWIM, and can be written as sd, where d is the number of
space dimensions, and s is the ratio of the number of nodes in one direction. if we assume that the MCS method needs 2–4 elements per correlation length I, and that the element size in the weighted integral method can be 2I–5I, typical values of s lie between 4 and 20. Choosing the most pesse-mistic value, s¼4, an estimate of the break even point may be given by
NWIM,r¹ 1
4d3000, (20)
where r equals 2 and 5 in 2D and 3D, respectively. The r Fig. 7. The coarse mesh containing 30 triangular elements.
Fig. 8. Head variance for a general domain. Comparison of MCS solutions (solid lines) and weighted integral results from an intermediate
factor is related to our use of triangular and tetrahedral elements [n nodes in (3) results in approx. 2pn(5pn) ele-ments]. In the work estimate we have not taken the com-putation of the covariances in the weighted integral method into account. Utilizing the decay of the correlation func-tion, the covariance computation will be of the same order as the solution of the finite element problems. Note that the cost of higher-order quadrature rules is quite small; an n-order rule typically has about nþ2 points, and the total cost increases linearly with the number of elements. Asymptotically, this increased cost has little effect.
This rough indication shows that MCS will be superior in large 3D simulations when NWIM. 40 000. The proposed
method, however, is much faster on small and medium-sized 2D flow problems and makes production runs of sto-chastic groundwater flow problems feasible on today’s
workstations and PCs. Both classes of methods are well suited for concurrent computing and can potentially run with optimal speed-up. Parallel super-computers will there-fore be an important means for simulating large-scale pro-blems regarding stochastic groundwater flow.
ACKNOWLEDGEMENTS
The authors thank Dr Gerhard Zumbusch for his assistance with higher-order numerical integration rules for triangles and tetrahedra. Financial support has been received from the Research Council of Norway through the technology program Numerical Computations in
Applied Mathematics (110673/420) and through a grant of
computing time (Programme for Supercomputing).
Fig. 10. Head variance for a 3D domain. MCS solutions (solid lines) are compared with weighted integral results using a grid withD¼2I. The numerical integration rules of the covariance integrals are of second-order (dashed lines), third-order (S) and fifth-order (þ). (a) Variance in the streamline direction, y¼z¼B=2. (b) Variance in the transverse horizontal direction, x¼L/2, z¼B/2. (c) Variance in the
vertical direction, x¼L/2, y¼B/2.
Fig. 9. Head variance for a 3D domain. MCS solutions (solid lines) are compared with weighted integral results using a very coarse grid.
D¼5I. The numerical integration rules of the covariance integrals are of second-order (dashed lines), third-order (S) and fifth-order (þ). (a) Variance in the streamline direction, y¼z¼B=2. (b) in the transverse horizontal direction, x¼L/2, z¼B/2. (c) Variance in the vertical
REFERENCES
1. Ababou, R., McLaughlin, D., Gelhar, L. W. and Tompson, A. F. B. Numerical simulation of three-dimensional saturated flow in randomly heterogeneous porous media. Transp. Porous Media, 1989, 4, 549–565.
2. Bellin, A., Salandin, S. and Rinaldo, A. Simulation of dis-persion in heterogeneous porous formations: Statistics, first-order theories, convergence of computations. Water Resour. Res., 1992, 28, 2211–2227.
3. Chin, D. A. and Wang, T. An investigation of the validity of first-order stochastic dispersion theories in isotropic porous media. Water Resour. Res., 1992, 28, 1531–1542.
4. Christakos, G., Random Field Models in Earth Sciences. Academic Press, San Diego, 1992.
5. Christakos, G., Miller, C. T. and Oliver, D. L. Stochastic perturbation analysis of groundwater flow. Spatially variable
soils, semi-infinite domains and large fluctuations. Stochastic Hydrol. Hydraul., 1993, 7, 213–239.
6. Cowper, G. R. Gaussian quadrature formulas for triangles. Int. J. Num. Mech. Eng., 1973, 7, 405–408.
7. Dagan, G. Solute transport in heterogeneous porous forma-tions. J. Fluid Mech., 1984, 145, 151–177.
8. Dagan, G. Statistical theory of groundwater flow and trans-port: Pore to laboratory, laboratory to formation and forma-tion to regional scale. Water Resour. Res., 1986, 22, 120S– 135S.
9. Dagan, G., Flow and Transport in Porous Formations. Springer-Verlag, Berlin, 1989.
10. Deodatis, G. The weighted integral method. I: Stochastic stiffness method. ASCE J. Engng. Mech., 1991, 117, 1851– 1864.
11. Deodatis, G. and Shinozuka, M. The weighted integral method. II: Response variability and reliability. ASCE J. Engng. Mech., 1991, 117, 1865–1877.
Fig. 11. Head variance for square domain, L/I¼ B/I¼20. Comparison of analytical first-order results from Osnes23 (solid lines) and numerical solutions of eqn (1) obtained by MCS for different values ofj
Y;jY¼0:5 (dashed lines),jY¼1:2 (S),jY¼1.5 (þ),jY¼2.0 (A). (a) Variance in the streamline direction. (b) Variance in the transverse direction.
Fig. 12. Head variance for the general domain obtained by MCS. Comparison of stochastic first-order results obtained by the weighted
integral method (solid lines) and MCS solutions of eqn (1) for different values ofj
12. Der Kiureghian, A. and Ke, J.-D. The Stochastic element method in structural reliability. Probab. Engng. Mech., 1988, 3, 83–91.
13. Dettinger, M. D. and Wilson, J. L. First order analysis of uncertainty in numerical models of groundwater flow, Part 1 Mathematical development. Water Resour. Res., 1981, 17, 149–161.
14. Diffpack World Wide Web home page: http://www.oslo.sin-tef.no/diffpack.
15. Freyberg, D. L. A natural gradient experiment on solute transport in a sand aquifer, 3, Spatial moments and the advec-tion and dispersion of nonreactive tracers. Water Resour. Res., 1986, 22, 2031–2046.
16. Gelhar, L. J. Stochastic subsurface hydrology from theory to applications. Water Resour. Res., 1986, 22, 135S–145S. 17. Jinyun, Y. Symmetric Gaussian quadrature formulae for
tet-rahedronal regions. Comp. Meth. Appl. Mech. Engng., 1984,
43, 349–353.
18. Leblanc, D. R., Garabedian, S. P., Hess, K. M., Gelhar, L. W., Quadri, R. D., Stollenwerk, K. G. and Wood, W. W. Large-scale natural gradient tracer test in sand and gravel, Cape Cod, Massachusetts. 1. Experimental design and observed tracer movement. Water Resour. Res., 1991, 27, 895–910.
19. Liu, W. K., Mani, A. and Belytschko, T. Finite element methods in probabilistic mechanics. Probab. Engng. Mech., 1987, 2, 201–213.
20. Liu, W. K., Belytschko, T. and Mani, A. Applications of probabilistic finite element methods in elastic/plastic dynamics. J. Engng. Industry, ASME, 1987, 109, 2–8. 21. Neuman, S. P. and Zhang, Y.-K. A quasi-linear theory of
non-Fickian and Fickian subsurface dispersion, 1.
Theoretical analysis with application to isotropic media. Water Resour. Res., 1990, 26, 887–902.
22. Oliver, L. D. and Christakos, G. Diagrammatic solutions for hydraulic head movements in 1-D and 2-D bounded domains. Stochastic Hydrol. Hydraul., 1995, 9, 269–296.
23. Osnes, H. Stochastic analysis of head spatial variability in bounded rectangular heterogeneous aquifers. Water Resour. Res., 1995, 31, 2981–2990.
24. Rubin, Y. Stochastic modeling of macrodispersion in hetero-geneous proous media. Water Resour. Res., 1990, 26, 133– 141.
25. Smith, L. and Freeze, R. A. Stochastic analysis of steady state groundwater flow in a bounded domain, 2, Two-dimen-sional simulations. Water Resour. Res., 1979, 15, 1543– 1559.
26. Sudicky, E. A. A natural gradient experiment on solute trans-port in a sand aquifer: Spatial variability of hydraulic con-ductivity and its role in the dispersion process. Water Resour. Res., 1986, 22, 2069–2082.
27. Takada, T. Weighted integral method in stochastic finite ele-ment analysis. Probab. Engng. Mech., 1990, 5, 146–156. 28. Takada, T. Weighted integral method in multi-dimensional
stochastic finite element analysis. Probab. Engng. Mech., 1990, 5, 158–166.
29. Townley, L. R. and Wilson, J. L. Computationally efficient algorithms for parameter estimation and uncertainty propaga-tion in numerical models of groundwater flow. Water Resour. Res., 1985, 21, 1851–1860.