PENDAHULUAN. Pembagian Statistik

PENDAHULUAN

PERANAN STATISTIKA

Disadari atau tidak peranan statistika telah banyak digunakan dalam kehidupan sehari-hari. Dunia penelitian atau riset, dimanapun dilakukan, bukan saja telah mendapatkan manfaat yang baik dari statistika tetapi sering harus menggunakannya. Untuk mengetahui apakah cara yang baru ditemukan lebih baik daripada cara lama, melalui riset yang dilakukan di laboratorium, atau penelitian yang dilakukan dilapangan perlu dilakukan penilaian statistika. Statistika juga mampu menentukan apakah faktor yang satu dipengaruhi atau mempengaruhi yang lainnya.

STATISTIK DAN STATISTIKA

Kata statistik dipakai untuk menyatakan kumpulan data, bilangan maupun non bilangan yang disusun dalam table atau diagram yang menggambarkan suatu persoalan. Statistik dapat diartikan sebagai kumpulan

fakta tentang suatu persoalan baik merupakan hasil penelitian yang umumnya berbentuk angka yang disusun dalam tabel atau diagram sehingga dapat menggambarkan keadaan dari persoalan tersebut.

Statistik yang menjelaskan sesuatu hal, biasanya diberi nama statistik mengenai hal yang bersangkutan, misalnya statistik penduduk, statistik

pendidikan, statistik pertanian dan lain-lain.

Sedangkan kata statistika adalah pengetahuan yang berhubungan dengan cara-cara pengumpulan data, pengolahan atau penganalisaaannya dan dilakukan penarikan kesimpulan berdasarkan kumpulan data dan penganalisaan yang telah dilakukan. Ada dua cara untuk mempelajari statistika, jika akan membahas statistika secara mendasar dan teoritis maka yang dipelajari digolongkan kedalam statistika matematis atau statistiak tetoritis. Disini diperlukan dasar matematika yang kuat dan mendalam  Pembagian Statistik Statistik Inferens (induktif) Deskriptif Teknik pengumpulan, pengolahan dan penyajian data hanya untuk

dipelajari karakteristiknya dan tidak untuk dilakukan penarikan kesimpulan secara umum

Teknik pengumpulan, pengolahan dan penyajian data sebagai alat untuk penarikan kesimpulan yang berlaku umum dari persoalan yang diamati

 Pengumpulan Data

Pengambilan data dengan sampling secara Random ialah cara pengambilan sampel secara acak artinya bahwa setiap elemen mempunyai kesempatan yang sama untuk terpilih menjadi anggota sampel. Sedangkan pengambilan data secara Non-Random ialah cara pengambilan sampel dimana setiap elemen tidak mempunyai kesempatan yang sama untuk menjadi anggota sampel.

MEMBACA DAN MENGINTERPRETASIKAN DATA  Pengertian

Data menurut Webter’s New World Dictionary ialah sesuatu yang

diketahui dan dianggap. Pengertian lain mengenai data ialah keterangan yang dapat memberikan gambaran tentang suatu keadaan atau persoalan.

 Proses yang dilalui agar data dapat dibaca dan diinterpretasikan Agar dapat dibaca dan diinterpretasikan maka data tersebut diolah dengan menggunakan metoda-metoda statistika. Secara umum tahapan proses yang dilalui untuk memudahkan dalam pembacaan data serta intrepretasi data adalah sebagai berikut :

START

Pengumpulan

Data

Pengolahan

Data

Penyajian

Data

END Observasi Langsung Questionnaire Melalui Organisasi, Sumber lainnya Metoda Statistika Tabel Grafik/ Diagram Pengumpulan Data Melalui pengambilan sample dari populasi Elemen Populasi diselidiki satu persatu Sampling Sensus Non Random Random Non Probability sampling Probabilitling

PENGUMPULAN DAN PENYAJIAN DATA

 Tujuan

- Untuk memperoleh gambaran tentang suatu persoalan atau keadaan - Sebagai dasar untuk pengambilan keputusan atau pemecahan

persoalan  Kegunaan

- Sebagai dasar dari suatu perencanaan

- Sebagai pengontrol terhadap pelaksanaan dari perencanaan - Evaluasi hasil akhir kerja

 Pembagian data 1. Menurut sifat :

-data kualitatif : data yang tidak berbentuk angka -data kuantitatif : data yang berupa angka-angka 2. Menurut Sumber :

-data internal : data yang menggambarkan keadaan didalam suatu organisasi atau perusahaan

-data eksternal : data yang menggambarkan keadaan diluar suatu organisasi atau perusahaan

3. Menurut cara Memperoleh :

-data primer : data yang dikumpulkan, dan diolah langsung dari objeknya

-data sekunder :data yang sudah jadi karena sudah dikumpulkan oleh organisasi atau orang lain

4. Menurut waktu pengumpulan :

-Cross section data :data yang dikumpulkan pada waktu tertentu -Time series data :data yang dikumpulkan dari waktu ke waktu  Cara pengumpulan data

1. Mengadakan penelitian langsung ke lapangan terhadap objek yang akan diteliti atau diselidiki menggunakan daftar "Questionnaire" yang dikirimkan melalui pos maupun diserahkan langsung kepada responden

2. Menggunakan seluruh atau sebagian data yang sudah di kumpulkan oleh orang atau organisasi lain.

 Syarat-syarat data yang baik 1.Data harus objektif

2.Data harus mewakili 3.Data harus relevan

4.Data harus tepat waktu "Up to date"

 Penyajian data

1) Penyajian dalam bentuk tabel

Penyajian tabel statistik harus mempunyai bentuk sederhana dan jelas, adapun macam -macam tabel sbb : one way table, two ways table, three ways table

a. One way table

Keterangan yang memuat satu karakteristik, Contoh : Tahun Jumlah Wisatawan

1980 1981 1982 561.178 600.151 592.046

b. Two ways table

Keterangan yang memuat dua karakteristik, Contoh :

Tahun 1980 1981

Kategori Kamar TPK(%) Kamar TPK(%)

Bintang 5&4 Bintang 3 Bintang 2 Bintang 1 4225 1467 1469 433 71,9 52,3 36,4 54,3 4225 1483 1444 424 76,5 70,3 55,7 55,0

c. Three ways table

Keterangan yang memuat tiga karakteristik, contoh :

Uraian

HOTEL BINTANG

SATU DUA TIGA EMPAT LIMA

1. Jumlah kamar tersedia 2. Rata-rata tingkat

penghunian kamar (%) 3. Rata-rata lama tinggal

(hari) 42 42,86 1,0 1.009 49,50 2,09 256 53,51 0,84 1.331 61,36 4,09 178 41,63 3,72

 Penyajian data dalam bentuk diagram atau grafik

Penyajian data dalam bentuk diagram atau grafik sering digunakan untuk memperoleh gambaran secara visual mengenai persoalan atau keadaan yang diselidiki atau dipecahkan.

Bentuk grafik yang sering digunakan adalah :

a. Diagram batang (Diagram batang tunggal dan Diagram batang majemuk)

b. Diagram garis : untuk menggambarkan perkembangan suatu keadaan (Diagram garis tunggal dan Diagram garis majemuk)

c. Diagram pastel : untuk memudahkan dalam melihat perbandingan antar sektor kegiatan

d. Diagram lambang: menggunakan lambang dan simbol

e. Diagram peta : untuk menyajikan data statistik yang lebih menekankan pada lokasi dimana data tentang suatu persoalan terjadi.

Dari hal tersebut diatas maka dapat diambil kesimpulan bahwa : a) Penyajian data dalam bentuk tabel dapat memberikan angka-angka

yang lebih teliti.

b) Penyajian data dalam bentuk grafik dapat memudahkan dalam membaca dan mengiterpretasikan data dalam persoalan yang sedang diamati.

2) Penyajian data dengan diagram

 Diagram batang tunggal dan diagram garis tunggal Dari data one way table:

Diagram garis tunggal Diagram batang tunggal

100.000 - 200.000 - 300.000 - 400.000 - 500.000 - 600.000 - 700.000 - 1980 1981 1982 Jml wisatawan Tahun 100.000 - 200.000 - 300.000 - 400.000 - 500.000 - 600.000 - 700.000 - 1980 1981 1982 Jml wisatawan Tahun

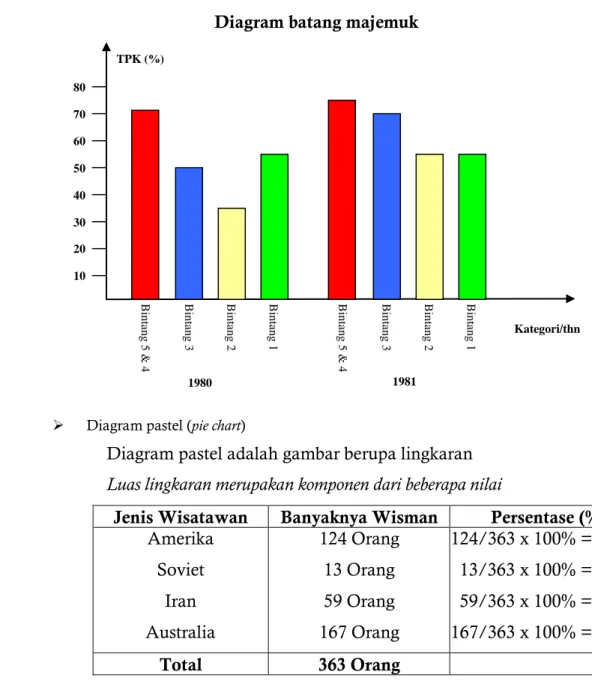
 Diagram batang majemuk dan diagram garis majemuk Dari data two ways table:

Diagram garis majemuk

Diagram batang majemuk

 Diagram pastel (pie chart)

Diagram pastel adalah gambar berupa lingkaran

Luas lingkaran merupakan komponen dari beberapa nilai

Jenis Wisatawan Banyaknya Wisman Persentase (%) Amerika Soviet Iran Australia 124 Orang 13 Orang 59 Orang 167 Orang 124/363 x 100% = 34,2 13/363 x 100% = 3,6 59/363 x 100% = 16,2 167/363 x 100% = 46 Total 363 Orang 100 % B in ta n g 1 B in ta n g 2 B in ta n g 3 B in ta n g 5 & 4 B in ta n g 1 B in ta n g 2 B in ta n g 3 B in ta n g 5 & 4 10 20 30 40 50 60 70 80 1980 1981 TPK (%) Kategori/thn B in ta n g 1 B in ta n g 2 B in ta n g 3 B in ta n g 5 & 4 B in ta n g 1 B in ta n g 2 B in ta n g 3 B in ta n g 5 & 4 1000 2000 3000 4000 1980 1981 Jml kamar

Amerika (A) = 34,2/100 x 3600 _{= 123,12}0 Soviet (B) = 3,6/100 x 3600 _{= 12,96}0 Iran (C) = 16,2/100 x 3600 _{= 58,32}0 Australia (D) = 46/100 x 3600 _{= 165,6}0 3600 DISTRIBUSI FREKUENSI

Data yang diperoleh langsung dari hasil observasi pada umumnya masih merupakan data kasar atau data mentah (raw data). Data mentah ini, secara langsung belum dapat memberikan gambaran tentang persoalan atau keadaan yang bersifat kuantitatif.

Penyusunan data yang paling sederhana adalah dalam bentuk erei (array), yaitu suatu bentuk penyusunan data dimana data disusun secara teratur dari data dengan nilai terkecil hingga nilai terbesar atau sebaliknya.

Sebagai ilustrasi, misalnya dari hasil observasi tentang lamanya tinggal dari 60 wisatawan asing yang datang ke Indonesia pada bulan Januari 1985, dimana data diambil secara random, diperoleh data sebagai berikut :

24 32 9 14 25 18 13 10 21 8 14 12 6 15 16 12 4 11 20 5 15 15 23 14 8 17 13 27 22 28 12 16 19 13 8 10 2 20 6 11 15 9 18 3 23 26 13 27 15 30 14 10 9 2 11 16 12 7 6 31 sumber : data fiksius (karangan belaka)

A

C

D

Dari kumpulan data tersebut diatas sepintas lalu kita sukar untuk menentukan nilai ekstrim (nilai data terkecil dan nilai data terbesar) dan jarak (range). Jarak (range) adalah merupakan beda antara nilai data terbesar dan nilai

data terkecil dalam suatu kumpulan data. Oleh karena itu, kumpulan data

tersebut diatas perlu kita susun kedalam bentuk erei (array). Dalam bentuk array, data tersebut dapat disusun sbb:

2 8 11 14 16 23 2 8 11 14 17 24 3 8 12 14 18 25 4 9 12 15 18 26 5 9 12 15 19 27 6 9 12 15 20 27 6 10 13 15 20 28 6 10 13 15 21 30 7 10 13 16 22 31 7 11 14 16 23 32

Dari kumpulan data diatas, kita dengan mudah mengetahui dua nilai ekstrim, yaitu nilai data terkecil adalah 2, dan nilai data terbesar adalah 32. Dengan demikian jarak atau rentang (range) untuk kumpulan data tersebut ialah 32 - 2 = 30. Meskipun demikian array itu sendiri bukan merupakan cara penyusunan yang memuaskan guna menggambarkan distribusi data

statistik. Oleh karena itu, data tersebut perlu disusun kedalam daftar atau tabel DISTRIBUSI FREKUENSI.

 PENYUSUNAN TABEL DISTRIBUSI FREKUENSI

Pada dasarnya penyusunan data kedalam tabel distribusi frekuensi dapat dibagi atas 3 langkah, yaitu :

1. Menentukan jumlah atau banyaknya kelas interval, biasanya jumlah kelas interval ini diambil paling sedikit 5 kelas atau paling banyak 15 kelas.

Untuk menentukan jumlah atau banyaknya kelas interval, pada thn 1926 STURGES, mengemukakan sebuah rumus yang kemudian dikenal sebagai "Kriterium Sturges". melalui persamaan sbb.:

k = 1 + 3,322 log n

Dimana: k = jumlah atau banyaknya kelas interval

n = jumlah atau banyaknya data hasil observasi Apabila persamaan tersebut kita gunakan untuk menentukan jumlah kelas interval dari data hasil observasi tentang lamanya tinggal dari 60 wistawan asing yang datang ke Indonesia pada bulan Januari 1985, akan diperoleh jumlah kelas interval sebesar :

K = 1 + 3,322 log n = 1 + 3,322 log 60 = 1 + 3,322 .(1,778) = 1 + 5,906516 = 6,906516 ≈ 7

jadi dari kumpulan data tersebut diatas, akan dibagi dalam 7 kelas interval 2. Menentukan Jarak atau Rentang (Range) dan panjang kelas interval :

Jarak atau rentang adalah beda antara nilai data terbesar dan nilai data terkecil. Jarak atau rentang ini berguna dalam menentukan panjang kelas interval ( i = p )

Rentang = Data Terbesar - Data Terkecil

Untuk soal tersebut diatas maka dapat dihitung jarak dari kumpulan data tersebut adalah :

32 -2 = 30

Kemudian selanjutnya menentukan panjang kelas interval (i = p), yaitu sebagai berikut :

Rentang

Kelas Interval

Dengan menggunakan persamaan tersebut maka diperoleh : I = p = 30 / 7

= 4,2857 4,3

3. Mentabulasikan angka-angka ke dalam kelas-kelas yang sesuai dan menghitung frekuensinya. Telah diketahui bahwa data terkecil adalah 2 dan data terbesar adalah 32 data tersebut akan dikelompokan ke dalam 7 kelas dengan panjang interval tiap kelas adalah 4,3

Sehingga diperoleh : Kelas interval ke-1 Kelas interval ke-2 Kelas interval ke-3 Kelas interval ke-4 Kelas interval ke-5 Kelas interval ke-6 Kelas interval ke-7

Kelas Interval TALLY Frekuensi

2.0---6.2 6.3---10.5 10.6---14.8 14.9---19.1 19.2---23.4 23.5---27.7 27.8---32.0 IIII III IIII IIII I IIII IIII IIII IIII IIII II IIII I IIII IIII 8 11 14 12 6 5 4 TOTAL 60 I = P = 4,3 4,3 4,3 4,3 4,3 4,3

Dengan demikian data observasi lamanya tinggal 60 wisatawan asing yang datang ke indonesia pada bulan januari adalah tertera pada tabel berikut :

TABEL PEYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi 2.0---6.2 6.3---10.5 10.6---14.8 14.9---19.1 19.2---23.4 23.5---27.7 27.8---32.0 8 11 14 12 6 5 4 TOTAL 60

Tetapi didalam praktek rumus struges ini mempunyai beberapa kelemahan apabila digunakan sebagai pedoman mutlak untuk menentukan jumlah atau banyak kelas interval karena rumus sturges tidak selamanya menghasilkan jumlah atau banyaknya kelas interval yang dapat digunakan secara praktis didalam penyusunan distrbusi frekuensi dari sekumpulan data hasil observasi.

Sebagai contoh apabila data tersdebut diatas akan disajikan dalam bentuk tabel distribusi frekuensi dengan panjang kelas interval = 7 maka diperoleh kelas interval :

Rentang

Kelas Interval

7 = 30 / kelas interval, maka : kelas interval = 30/ 7

= 4,285 = 5

Kelas Interval TALLY Frekuensi 2--- 8

9---15

16---22

23---29

30---36

IIII IIII III

IIII IIII IIII IIII IIII IIII IIII I IIII III III 13 25 11 8 3 TOTAL 60 I = P =

TABEL PEYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi

2--- 8 9---15 16---22 23---29 30---36 13 25 11 8 3 Total 60

Beberapa istilah yang sering dijumpai dalam penyusunan distribusi frekuensi, antara lain :

1. Ujung-bawah: untuk soal diatas adalah 2, 9, 16, 23, 30 2. Ujung-atas: untuk soal diatas adalah 8, 15, 22, 29, 36

3. Batas - bawah (Lower Limit) : adalah ujung-bawah dikurangi dengan bilangan…

0,5 Untuk data yang tercatat dalam satuan 0,05 Untuk data yang tercatat dalam satu desimal 0,005 Untuk data yang tercatat dalam dua desimal,dst

4. Batas - atas (Upper Limit) : ujung-atas ditambah dengan bilangan…

0,5 Untuk data yang tercatat dalam satuan 0,05 Untuk data yang tercatat dalam satu desimal

0,005 Untuk data yang tercatat dalam dua desimal,dst Dalam persoalan yang sedang dibahas maka diketahui bahwa : Batas-bawah : Kelas Interval ke - 1 : 2 - 0.5 = 1.5

2 : 9 - 0.5 = 8.5 3 : 16 - 0.5 = 15.5

4 : 23 - 0.5 = 22.5 5 : 30 - 0.5 = 29.5

Batas-atas : Kelas Interval ke - 1 : 8 + 0.5 = 8.5 2 : 15 + 0.5 = 15.5

3 : 22 + 0.5 = 22.5 4 : 29 + 0.5 = 29.5 5 : 36 + 0.5 = 36 .5 5. Tanda Kelas ("Class Mark")

Tanda kelas disebut juga titik tengah atau mid-point adalah bilangan yang harganya ada di tengah-tengah kelas interval. Tanda kelas atau titik tengan juga merupakan harga rata-rata dari tiap-tiap kelas interval atau sebuah nilai yang mewakili nilai-nilai yang terdsapat pada tiap kelas interval.

) ( 2 / 1 UjungBawah UjungAtas Tengah Tanda kelas Tanda

Melalui proses perhitungan maka diketahui utk persoalan diatas adalah : Kelas Interval ke - 1 : 1/2 (2 + 8 ) = 5 2 : 1/2(9 + 15 ) = 12 3 : 1/2(16 + 22) = 19 4 : 1/2(23 + 29 ) = 26 5 : 1/2(30 + 36 ) = 33 Demikian pula untuk data dengan panjang kelas intervalnya = 7, dan tanda kelas atau titik tengah kelas interval ke-1 = 1/2 (2+8) = 5 maka untuk menentukan tanda kelas atau titik tengah berikutnya adalah : Kelas Interval ke- 2 : 5 + 7 = 12 3 : 12 + 7 = 19 4 : 19 + 7 = 26 5 : 26 + 7 = 33  Macam Distribusi Frekuensi Distribusi frekuensi dibagi atas 3 kategori, yaitu : 1. Distribusi frekuensi biasa : adalah distribusi frekuensi yang banyaknya dapat dinyatakan dalam frekuensi yang sebenarnya 2. Distribusi Frekuensi relatif : adalah distribusi frekuensi yang banyaknya data dinyatakan dalam proporsi atau persen 3. Distribusi Frekuensi Kumulatif : adalah distribusi frekuensi yang frekuensi-frekuensinya dijumlahkan selangkah demi selangkah. Distribusi Frekuensi Kumilatif ini dibagi lagi dua macam yaitu : 1) Distribusi frekuensi kumulatif "kurang dari" 2) Distribusi frekuensi kumulatif "atau lebih" Untuk lebih jelas dapat dilihat dalam contoh: 1. Distribusi frekuensi biasa : TABEL PEYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995 Kelas Interval Frekuensi 2.0--- 8 9---15 16---22 23---29 30---36 13 25 11 8 3 Total 60

2. Distribusi Frekuensi relatif

Apabila suatu data akan disajikan kedalam bentuk distribusi frekuensi relatif maka frekuensinya harus diubah dulu kedalam proporsi atau persentasenya, yaitu :

a. Untuk Proporsi : dengan membagi frekuensi tiap kelas terhadap total dikalikan dengan bilangan 1,00

Misal frekuensi relatif utk interval ke-1: 13/60 x 1,00 = 0,22

ke-2 : 25/60 x 1,00 = 0,42

Dengan cara yang sama digunakan untuk menghitung frekuensi relatif dari data pada tabel.

b. Untuk Persentase : dengan membagi frekuensi tiap kelas terhadap total dikalikan 100,0 %

Misal frekuensi relatif utk interval ke-1 : 13/60 x 100% = 22%

ke-2 : 25/60 x 100% = 42%

Dengan cara yang sama maka dapat diperoleh hasil sebagai berikut : TABEL PEYEBARAN LAMANYA TINGGAL DARI

60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995 Kelas Interval Frekuensi relatif

2.0---8 9---15 16---22 23---29 30---36 0,22 0,42 0,18 0,13 0,05 Total 1.00 TABEL PEYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995 Kelas Interval Frekuensi Relatif (%) 2.0---8 9---15 16---22 23---29 30---36 21,7 41,7 18,3 13,3 5,0 Total 100.00

3. Distribusi frekuensi kumulatif

Berikut ini adalah contoh tabel distribusi frekuensi kumulatif "kurang dari"dan "atau lebih" dari data yang terdapat pada tabel berikut :

TABEL FREKUENSI KUMULATIF "KURANG DARI" UNTUK PENYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING YANG DATANG

KE INDONESIA, JANUARI 1995 Kelas Interval Frekuensi Kumulatif Kurang dari 2 Kurang dari 9 Kurang dari 16 Kurang dari 23 Kurang dari 30 Kurang dari 37 0 13 38 49 57 60

TABEL DISTRIBUSI FREKUENSI KUMULATIF "ATAU LEBIH" UNTUK PENYEBARAN LAMANYA TINGGAL DARI

60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995 Kelas Interval Frekuensi Kumulatif

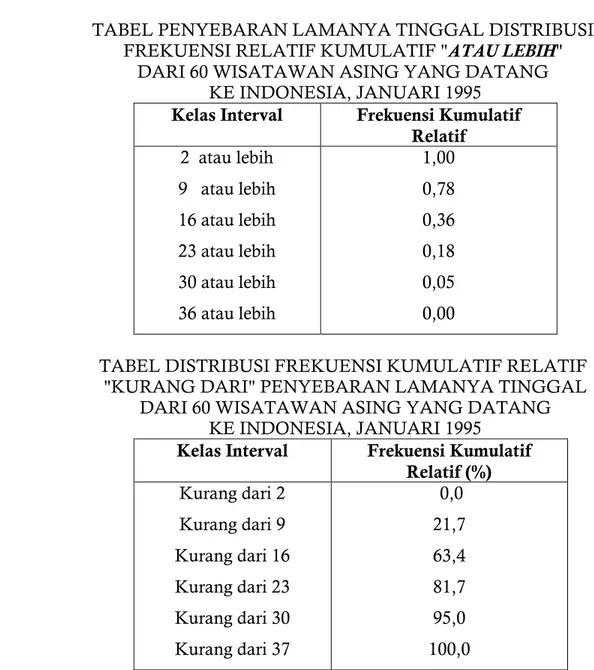
2 atau lebih 9 atau lebih 16 atau lebih 23 atau lebih 30 atau lebih 36 atau lebih 60 47 22 11 3 0 Total 100,00

TABEL PENYEBARAN LAMANYA TINGGAL DISTRIBUSI FREKUENSI KUMULATIF RELATIF "KURANG DARI"

DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi Kumulatif Relatif Kurang dari 2 Kurang dari 9 Kurang dari 16 Kurang dari 23 Kurang dari 30 Kurang dari 37 0,00 0,22 0,64 0,82 0,95 1,00

TABEL PENYEBARAN LAMANYA TINGGAL DISTRIBUSI FREKUENSI RELATIF KUMULATIF "ATAU LEBIH"

DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi Kumulatif Relatif 2 atau lebih 9 atau lebih 16 atau lebih 23 atau lebih 30 atau lebih 36 atau lebih 1,00 0,78 0,36 0,18 0,05 0,00

TABEL DISTRIBUSI FREKUENSI KUMULATIF RELATIF "KURANG DARI" PENYEBARAN LAMANYA TINGGAL

DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi Kumulatif Relatif (%) Kurang dari 2 Kurang dari 9 Kurang dari 16 Kurang dari 23 Kurang dari 30 Kurang dari 37 0,0 21,7 63,4 81,7 95,0 100,0

TABEL DISTRIBUSI FREKUENSI RELATIF KUMULATIF "ATAU LEBIH" PENYEBARAN LAMANYA TINGGAL

DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1995

Kelas Interval Frekuensi Kumulatif Relatif (%) 2 atau lebih 9 atau lebih 16 atau lebih 23 atau lebih 30 atau lebih 36 atau lebih 100,0 78,3 36,6 18,3 5,0 0,0

PENYAJIAN DATA DISTRIBUSI FREKUENSI

Penyajian data distribusi frekuensi kedalam bentuk diagram atau grafik terdapat tiga macam yaitu :

1. Histogram Frekuensi 2. Poligon Frekuensi 3. Ogive

1. Histogram Frekuensi

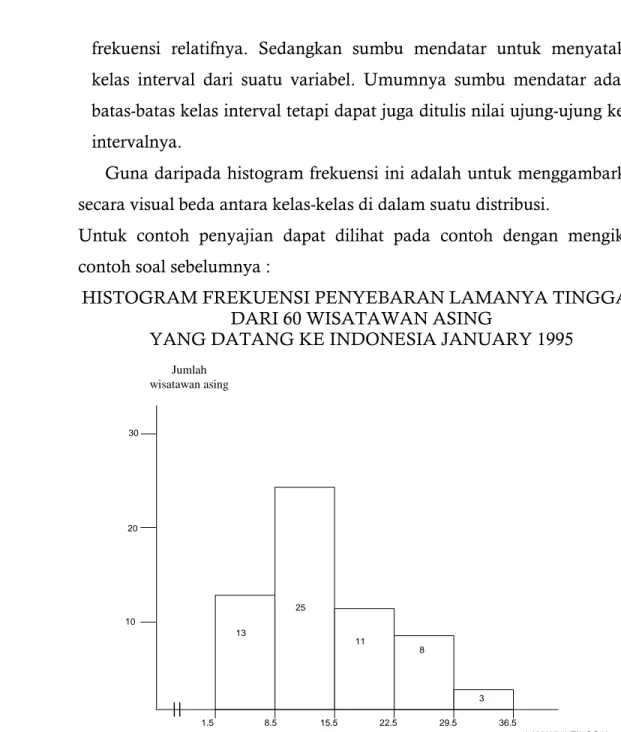
Pada bentuk histogram frekuensi sumbu tegak (vertikal) digunakan untuk menyatakan frekuensi, baik frekuensi sebenarnya maupun

frekuensi relatifnya. Sedangkan sumbu mendatar untuk menyatakan kelas interval dari suatu variabel. Umumnya sumbu mendatar adalah batas-batas kelas interval tetapi dapat juga ditulis nilai ujung-ujung kelas intervalnya.

Guna daripada histogram frekuensi ini adalah untuk menggambarkan secara visual beda antara kelas-kelas di dalam suatu distribusi.

Untuk contoh penyajian dapat dilihat pada contoh dengan mengikuti contoh soal sebelumnya :

HISTOGRAM FREKUENSI PENYEBARAN LAMANYA TINGGAL DARI 60 WISATAWAN ASING

YANG DATANG KE INDONESIA JANUARY 1995

Jumlah wisatawan asing 13 25 11 8 3 10 20 30

2. Poligon Frekuensi

Distribusi frekuensi dapat juga disajikan dalam bentuk poligon frekuensi, dimana sumbu tegak untuk menyatakan frekuensi baik frekuensi relatif maupun frekuensi sebenarnya sedangkan sumbu mendatar untuk titik tengah atau tanda kelas.

Guna dari poligon frekuensi ini adalah apabila kita ingin melakukan perbandingan dua buah distribusi frekuensi.

Untuk lebih jelas dapat dilihat dalam contoh grafik dibawah ini dengan melihat pada persoalan sebelumnya. Contoh :

POLIGON FREKUENSI PENYEBARAN LAMANYA TINGGAL DARI 60 WISATWAN ASING YANG DATANG

KE INDONESIA,JANUARY 1995

POLIGON FREKUENSI RELATIF (%) PENYEBARAN LAMANYA TINGGAL DARI 60 WISATWAN ASING

YANG DATANG KE INDONESIA,JANUARY 1995

3. OGIVE

Pada dasarnya ogive merupakan distribusi frekuensi kumulatif. Sumbu tegak untuk menyatakan banyak data atatu frekuensi sedangkan sumbu mendatar digunakan untuk menentukan ujung - ujung bawah dari kelas interval (apabila dalam penyusunan distribusi frekuensi kumulatifnya menggunakan ujung bawah dari kelas interval.) atau batas-batas bawah kelas interval (apabila dalam penyusunan distribusi

2 5 12 19 26 33 37 LAMANYA TINGGAL 10 13.3 5.0 18.3 2 41.7 21.7 Jumlah wisatawan asing 20 30 2 5 12 19 26 33 37 LAMANYA TINGGAL 10 ₃ 8 11 2 25 2 13 2 Jumlah wisatawan asing 20 30

frekuensi kumulatifnya menggunakan batas-batas bawah dari kelas interval).

Ogive dibagi 2, yaitu :

1. Ogive untuk distribusi frekuen "Kurang dari" 2. Ogive untuk distribusi frekuensi "atau lebih"

Berikut adalah contoh yang diambil dari permasalahan sebelumnya : OGIVE TENTANG PENYEBARAN LAMANYA TINGGAL

DARI 60 WISATAWAN ASING YANG DATANG KE INDONESIA, JANUARI 1985

(Data diambil dari tabel distribusi frekuensi kumulatif relatif "kurang dari")

Kuesioner dan Wawancara

 Petunjuk pembuatan kuesioner.

Pertanyaan dalam kuesioner harus disusun dengan secermat mungkin :

A. perjelas lagi hubungan antara metode dengan masalah dan hipotesis. Buatlah matriks yang menghubungkan antara masalah, hipotesis, variable, indikator, dan pertanyaan

B. Rumuskan pertanyaan dengan memperhatikan hal-hal berikut : 1. Sesuaikan bahasa dengan tingkat pengetahuan responden.

Untuk daerah pedesaan, misalnya, lebih baik kita menggunakan bahasa daerah. Untuk kebanyakan orang, kata persepsi sebaiknya diganti dengan kata tanggapan.

2. Gunakan kata-kata yang mempunyai arti yang sama bagi setiap orang

3. Hindari pertanyaan yang panjang karena pertanyaan yang panjang seringkali mengaburkan dan membingungkan

4. Janganlah beranggapan bahwa responden memiliki informasi faktual. Misal, Seorang ibu mungkin melaporkan acara televisi yang disenangi anak, tetapi pendapat ibu tidak selalu sesuai dengan pendapat anak.

Jml wisatawan "kurang dari" "atau lebih" 2 9 16 23 30 37 Lamanya tinggal 60 40 20 0

5. Bentuklah kerangka pemikiran yang ada dalam benak anda. Janganlah bertanya : berapa majalah yang anda baca? Bertanyalah : apa saja majalah yang and baca?

6. Sarankanlah semua alternatif atau tidak samasekali

7. Lindungi harga diri responden. Janganlah bertanya : sebutkan kalimat-kalimat yang benar diantara kalimat yang tercantum dibawah ini. Katakanlah : saya ingin tahu pendapat Bapak, manakah diantara kalimat-kalimat dibawah ini yang menurut Bapak benar

8. Jika anda terpaksa menanyakan hal yang kurang mengenakkan responden, mulailah bertanya tentang hal-hal yang positif

9. Tentukan apakah anda memerlukan pertanyaan langsung, tak langsung atau pertanyaan tak langsung disusul dengan pertanyaan langsung

10. Hindari kata-kata yang bermakna banyak, kata-kata seperti partisipasi, pengaruh, solidaritas, rasa bangga, harus diganti dengan kata-kata yang lebih spesifik seperti ikut KB, menyumbangkan uang, dan menyimpan piagam penghargaan 11. Hindari pertanyaan yang bersifat mengarahkan responden pada

jawaban tertentu. Janganlah bertanya : apakah anda selalu berperan serta dalam program pembangunan? Bertanyalah :

apakah anda menganjurkan orang lain untuk menjadi akseptor KB?

12. Pertanyaan harus dibatasi pada satu gagasan saja. Janganlah bertanya: apakah anda membaca surat kabar/ majalah/ buku? Jadikanlah pertanyaan ini menjadi tiga kalimat pertanyaan C. Organisasikan kuesioner secara sistematis

1. Mulailah dengan pertanyaan yang mudah dan disenangi oleh responden. Ajukan pertanyaan yang membangkitkan minat 2. Jangan mengondisikan jawaban pada pertanyaan berikutnya

dengan pertanyaan sebelumnya

3. Gunakan urutan pertanyaan untuk melindungi harga diri responden

4. Pertanyaan terbuka sebaiknya dikurangi

5. topik pertanyaan harus disusun sedemikian rupa sehingga dapat dipahami oleh responden. Urutan pertanyaan harus wajar dan mudah ditangkap maksudnya.

D. Lakukan prauji kuesioner. Pilihlah sejumlah responden yang representatif. Ajukan pertanyaan-pertanyaan itu dan lihat kemungkinan salah paham atau makna yang membingungkan.

PENGUKURAN "CENTRAL TENDENCY" DAN PENYEBARAN "DISPERSION"

A.Simbol dan Notasi

Didalam melakukan pengukuran-pengukuran nilai suatu variabel yang diselidiki dapat digunakan persamaan-persamaan model matematika yang sederhana, dimana menggunakan notasi dan simbol yang umum digunakan hal ini dapat memepermudah pemakaian dan perhitungan.

B. Sifat Penjumlahan

1. jika x1,x2,…. Adalah variabel yang dikalikan dengan nilai konstanta(bilangan tetapa maka persamaannya : n

i i n i i k x kx 1 1

2. Penjumlahan dari perkalian dua variabel sama dengan jumlah perkalian antara dua variabel pertama sampai dua varibel ke-n

xnyn y x y x y x n i i i 1 1 2 2 ... 1

3. Hasil penjumlahan dari jumlah atau selisih dari beberapa variabel atau perkalian bilangan tetap dengan variabel adalah sama dengan jumlah atau selisih dari penjumlahan variabel-variabel atau perkalian-perkalian bilangan tetap dengan variabel tersebut.

n i i n i i n i i n i i i i qy rz p x q y r z px 1 1 1 1 ) (

C. Pengukuran Central Tendency

Selain data sistematis yang menyertakan tabel serta grafik dalam memperjelas gambaran mengenai suatu persoalan atau keadaan dari suatu populasi /sampel masih diperlukan ukuran lain yang dapat mewakili data tersebut. Dalam menggunakan ukuran Central Tendensi umumnya yang sering digunakan adalah sbb : rata-rata (avarages), rata-rata-rata-rata hitung (Arithmatic Mean), Median, Modus. Ukuran yang dihitung dari data sampel adalah statistik

Ukuran yang dihitung dari data populasi adalah parameter Central Tendensy debagi ke dalam 2 bagian yaitu :

1. Pengukuran Central Tendensy Untuk "Ungrouped data" (data yang tidak dikelompokan)

2. Pengukuran Central Tendensy untuk "Grouped data"(data yang dikelompokan)

 PENGUKURAN UNGROUPED DATA

1. Rata-rata hitung (Arithmatic mean)

adalah nilai yang didapat dari penjumlahan semua nilai data dibagai dengan banyaknya data.

Populasi : N x u n i i 1 _{Sampel :} N x x n i i 1 _

2. Rata-rata hitung ditimbang (Weighted arithmatic mean)

Pada persamaan ini setiap nilai variabel mempunyai faktor penimbang yang sama yaitu w1,w2,….,wn. Pada kenyataan faktor penimbang ini adalah frekuensi dari setiap nilai variabel yang telah kita tentukan.

3. Median (Me)

Median adalah harga atau nilai yang bersifat bahwa 50% dari data telah disusun menurut urutan besarnya, lebih kecil atau sama dengan bilangan tersebut dan untuk 50 % lagi akan lebih besar dari bilangan tersebut.

Dalam menghitung median ada 2 cara yang dapat digunakan yaitu : 1. Data Ganjil Me =Xk ; dimana k = 2 1 n 2. Data Genap Me =

2

1 k k

x

x

4. Modus (Mo)

Modus ialah nilai darisuatu kumpulan data yang paling sering muncul atau data dengan frekuensi terbanyak. Modus tidak selalu bersifat

kuantitatif (berupa angka atau bilangan) tetapi juga bersifat kualitatif (berupa atribut).

 PENGUKURAN UNTUK GROUPED DATA

Hal yang perlu diperhatikan dalam menghitung central tendency untuk grouped data ialah harus tersedianya lembar kerja "Worksheet" karena tanpa lembar kerja tidak akan dapat menggunakan rumus-rumus tersebut.

1. Rata-rata hitung (arithmatic Mean) a. Long Method k i i k i i i f x f x 1 1

dimana : k = jumlah kelas interval

fi = Frekuensi kelas-kelas interval Xi = Titik tengah kelas interval

b. Short Method (cara koding)

k i i k i i i f u f p x x 1 1 0

dimana : Xo = nilai titik tengah yang ditransformasikan ke Ui = 0 p = Panjang kelas Interval

Ui = Transformasi nilai titik tengah yang berturut-turut lebih kecil dan atau lebih besar dari X0 (…,-3,-2,-1,0,+1,…). Tetapi cara ini dapat digunakan apabila panjang kelas interval (I = P) dalam suatu distribusi frekuensi sama besar. 2. Median f F n p b Me 2

Dimana : b = batas bawah kelas interval yang berisi median P = Panjang kelas interval

n = Banyaknya data atau jumlah frekuensi

F = Jumlah frekuensi ukuran kelas dengan tanda-tanda kelas yang lebih kecil dari tanda-tanda kelas median f = Frekuensi kelas median

3. Modus 2 1 1 b b b p b Mo

dimana : b = batas bawah kelas modal p = Panjang kelas interval

b1= beda frekuensi antara kelas modal dengan frekuensi kelas interval yang mendahuluinya

b2 = beda frekuensi antara kelas modal dengan frekuensi kelas interval berikutnya.

 Karakteristik Mean, Median dan Modus

Pada umumnya mean, median dan modus dapat mempunyai nilai yang cukup sesuai bagi penggambaran data dalam suatu kumpulan data akan tetapi tingkat penyesuaian terhadap penggambaran data tersebut sangat bergantung pada keadaan data tersebut. Data dapat dikatakan mewakili suatu kumpulan data untuk proses perhitungan Mean apabila nilai data tersebut serba sama atau HOMOGEN tetapi apabila data yang dimiliki tidak sama atau HETEROGEN maka hasil yang diperoleh untuk perhitungan tersebut kurang mewakili keadaan data sesungguhnya.

Begitu pula dengan proses perhitungan median, perhitungan ini dianggap dapat mewakili apabila data yang dimiliki homogen. Selain itu kelemahan perhitungan ini tidak dapat menggambarkan sejauh mana penyebaran nilai minimum dan maksimum atau "nilai ekstrim" dalam suatu kumpulan data terhadap mediannya.

Sedangkan modus merupakan nilai yang mempunyai pengertian "nilai yang paling sering muncul.

 Penyebaran "DISPERSION"

Pengukuran penyebaran adalah pengukuran tingkat penyebaran nilai dalam suatu kumpulan data terhadap rata-ratanya. Ukuran penyebaran bermacam-macam diantaranya : Simpangan baku "standard deviation", Simpangan rata-rata ("mean deviation"), Variansi (Variation), Koefisien variasnsi(Cooficient of variation), serta untuk data-data yang bersifat dikelompokan "grouped data" dan yang tidak dikelompokan "ungrouped data".

 Pengukuran penyebaran"dispersion" untuk Ungrouped data 1. Simpangan baku dan variansi

Persamaan model matematis untuk variansi adalah sbb : - Untuk Populasi N x N i i 1 2 2 ) (

dimana : N = banyaknya data dalam populasi = rata-rata populasi atau 2 1 1 2 2 N x N x N i i N i i -Untuk sampel a. Ukuran sampel n 30 1 ) ( 1 2 2 n x x s n i i

dimana : n = banyaknya data dalam sampel

x = rata-rata sampel atau ) 1 ( ) ( 1 2 1 2 2 n n x x n s n i n i i b. Ukuran sampel n > 30 n x x s n i i 1 2 2 ) ( atau 2 1 2 1 2 2 ) ( n x x n s n i n i i

Simpangan baku merupakan akar dari variansi, maka untuk rumus standar deviasi dapat diperoleh sebagai berikut :

2. Untuk populasi N u x N i i 1 2 ) ( atau 2 1 1 2 N x N x N i i N i i 3. Untuk Sampel a. Ukuran sampel n 30 1 ) ( 1 2 n x x s n i i atau ) 1 ( ) ( 1 2 1 2 n n x x n s n i n i i i b. Ukuran sampel n > 30 n x x s n i i 1 2 2 ) ( atau 1 ₂ 2 1 2 ) ( n x x n s n i n i i

 Pengukuran penyebaran "Dispersion" untuk grouped data 1. Simpangan rata-rata n x x f SR k i i i 1 ) (

dimana : FI = frekuensi kelas interval k = banyaknya kelas interval x = nilai rata-rata

2. Variansi dan Simpangan baku a. untuk populasi N u x f s N i i i 1 2 2 ) (

cara koding "short method" 2 1 2 1 2 2 1 N u f N u f p n s k i i i k i i i b. untuk sampel n 30 1 1 2 n x x f s k i i i

cara koding"short method" ) 1 ( 1 2 1 2 2 2 n n u f u f n p s k i i k i i i i - n > 30 n x x f s k i i i 1 2 2

cara koding "Short Method"

2 1 2 1 2 2 2 n u f u f n p s k i i k i i i i 3. Simpangan baku N x s k i i 1 2 ) (

cara koding "short method"

2 1 2 1 2 n u f u f n p s k i i k i i i i -sampel n 30 1 1 2 n x x f s k i i i cara koding "short method"

) 1 ( 1 2 1 2 n n u f u f n p s k i i k i i i i - Untuk sampel n > 30 1 1 2 n x x f s k i i i cara koding "short method"

2 1 2 1 2 n u f u f n p s k i i k i i i i  Koefisien Variansi

Ukuran -ukuran yang telah diperlihatkan sebelumnya adalah ukuran penyebaran mutlak dan hanya digunakan pada suatu distribusi definitif. Apabila akan membandingkan tingkat penyebaran antara dua

kumpulan data atau lebih dimana data-data tersebut mempunyai satuan berbeda maka ukuran penyebarab mutlak tidak dapat digunakan karena makin besar data yang digunakan makin besar pula nilai penyebarannya.

Untuk dapat membandingkan lebih dari satu kumpulan data maka digunakan dispersi relatif salah satunya dinamakan koefisien variansi.  Koefisien variansi populasi

% 100

x

v

dimana : = simpangan baku populasi rata-rata populasi

 Koefisian variansi sampel % 100 x x s v

dimana : s = simpangan baku sampel x = rata-rata Sampel

berdasarkan rumus diatas maka dapat diambil kesimpulan bahwa untuk kumpulan data yang mempunyai nilai koefisien variansi lebih besar dari kumpulan lainnya maka data tersebut mempunyai sifat heterogen dibandingkan dengan kumpulan data lainnya.

Contoh-contoh Perhitungan :

 Rata-rata hitung (Arithmetic Mean)

Jika dalamsuatu observasi diperoleh data sebagai berikut :

Wisatawan Asing Pengeluaran Perhari

(Orang) (US $)

30 79,5

20 84.4

9 104.0

41 62.0

Maka rata-rata hitungnya untuk pengeluaran perhari :

n

X

X

n i i 1 = = 82.38

 Rata-rata hitung ditimbang (Weighted Arithmetic Mean)

n i i n i i i

W

X

W

X

1 1 = = 53.965 30(79.5) + 20(84.0) + 9(104.0) + 41(62.0) 30 + 20 + 9 + 41 79.5 + 84.0 + 104.0 + 62.0 4

Catatan :

n

i

i

X

1 dibaca Sigma Xi dimana i dari 1 s/d n

 Median (Me)

Kalau ada sekelompok nilai sebanyak n kemudian diurutkan mulai dari yang terkecil Xi sampai dengan yang terbesar Xn, maka nilai yang ada ditengah-tengah disebut median

- Untuk data ganjil (n ganjil) Me = Xk dimana

2

1

n

K

Contoh : variable X dengan nilai-nilai ;

X1 = 9.0; X2 = 6.5; X3 = 5.0; X4 = 11.5; X5 = 4.0; X6 = 8.0; X7 = 7.5 Kita harus susun dulu menurut urutan besarnya

4.0 5.0 6.5 7.5 8.0 9.0 11.5

X

1

;

X

2

;

X

3

;

X

4

;

X

5

;

X

6

; X

7

Me = Xk dimana

2

1

n

K

=

2

1

7

= 4 Me = X4 = 7.5

- Untuk data genap (n genap)

Me =

2

1 k k

X

X

; dimana K =

2

n

=

2

8

= 4 Me =

2

1 4 4

X

X

=

2

5 4

X

X

=

2

0

.

8

0

.

7

=

2

15

= 7.5  Modus (Mo)

Adalah suatu bilangan atau nilai dari sekumpulan data yang terdapat paling sering atau data dengan frekuensi yang terbanyak

X f 2 2 5 1 7 1 Modus--- 9 3 10 2 11 1 12 1

 Simpangan rata-rata (Mean Deviation) SR =

n

X

X

_i

X

X

_i dibaca harga mutlak dari selisih Xi dengan

X

Contoh : dari hasil observasi diperoleh data dengan nilai-nilai sbb. : 3.4; 8.6; 6.5; 5.7; 10.8 i X

_X

X

_i

X

X

_i

X

3.4 8.6 6.5 5.7 10.8 7.0 -3.6 1.6 -0.5 -1.3 3.8 3.6 1.6 0.5 1.3 3.8 35.0 10.8 n X X i =

5

0

.

35

= 7.0 SR =

n

X

X

_i =

5

8

.

10

= 2.16

 Simpangan Baku (Standard Deviation) & Variansi (Variation) Untuk menghindari harga mutlak bagi pengukuran dispersi, maka deviasi nilai-nilai observasi terhadap rata-ratanya

X

_i

X

harus dipangkatkan dua (dikuadratkan). Deviasi kuadrat ini disebut juga variansi (variation), dan akar dari variansi disebut simpangan baku.

i X

_X

_X

_i

_X

_X

_X

2 i 2 i

X

3.4 8.6 6.5 5.7 10.8 7.0 -3.6 1.6 -0.5 -1.3 3.8 12.96 2.56 0.25 1.69 14.44 11.56 73.96 42.25 32.49 116.64 35.0 31.90 276.90 Rumus I Variansi :

n

X

X

S

n i i 1 2 2 =

1

5

90

.

31

= 7.975 Standard Deviasi : 2

S

S

= 7.975 = 2.824 Rumus II Variansi :

1

1 2 1 2 2

n

n

X

X

n

S

n i n i i i =

1

5

5

35

90

.

276

5

2 = 7.975 Standard Deviasi : 2

S

S

= 7.975 = 2.824

 Penghitungan Median (Me) untuk data berkelompok

f

30

-

39

4

40

-

49

6

50

-

59

8

60

-

69

12

70

-

79

9

80

-

89

7

90

-

99

4

Jumlah

50

Kelas

Rumus Median = Med =

m i

f

f

n

C

Lo

0

2

Dimana ; Lo = Nilai batas bawah dari kelas yang

mengandung atau memuat nilai median

n = Jumlah semua frekuensi

0

i

f = Jumlah frekuensi dari semua kelas dibawah

kelas yang mengandung Median (kelas yang mengandung Median tidak termasuk)

Not diatas bukan pangkat nol

m

f = Frekuensi dari kelas yang mengandung

Median

C = Besarnya kelas interval, jarak antara kelas

yang satu dengan yang lainnya atau besarnya kelas interval yang mengandung Median

50% observasi =

2 50

= 25 --- f₁ f₂ f₃ = 4 + 6 + 8 = 18

Untuk mencapai nilai 25 masih kurang 7, perlu ditambah dengan frekuensi kelas keempat.

Maka; Lo = 59,5 ; C = 10 ; 2 n = 2 50 = 25 ; 0 i f = 18 ; fm= 12 Med = 59,5 + 12 18 25 10 = 59,5 + 5,83 = 65,33

 Penghitungan Modus (Mo) untuk data berkelompok

f

30

-

39

4

40

-

49

6

50

-

59

8

60

-

69

12

70

-

79

9

80

-

89

7

90

-

99

4

Jumlah

50

Kelas

Rumus Modus = Mo = ₀ 2 0 1 0 1 f f f C Lo

Dimana ; Lo = Nilai batas bawah dari kelas yang memuat

Modus

fmo = Frekuensi kelas yang mengandung Modus

0 1

f = f_mo- f_mo1 = selisih frekuensi kelas yang

memuat modus dengan frekuensi kelas sebelumnya

0 2

f = f_mo- f_{mo 1} = selisih frekuensi kelas yang

memuat modus dengan frekuensi kelas sesudahnya

Not diatas bukan pangkat nol

C = Besarnya kelas interval, jarak antara kelas yang satu

dengan yang lainnya atau besarnya kelas interval yang mengandung Median

mo

f = 12 ; Frekuensi kelas yang mengandung Modus,

nilai tertinggi Lo = 59,5; C = 10; fmo 1= 8; fmo1= 9; 0 1 f = 12 – 8 = 4; f20 = 12 – 9 = 3 Mo = ₀ 2 0 1 0 1 f f f C Lo = 59,5 + 3 4 4 10 = 59,5 + 5,714 = 65,214

 Penghitungan X rata-rata (X), Variansi (S), dan Standard Deviasi (Sd) untuk data berkelompok

Kelas f Tanda Kelas fiXi X Xi - X (Xi - X )2 fi(Xi - X )2

(Xi)

31 - 40

1

35.5

35.50

-41.12 1,690.85

1,690.85

41 - 50

2

45.5

91.00

-31.12

968.45

1,936.91

51 - 60

5

55.5

277.50

-21.12

446.05

2,230.27

61 - 70

15

65.5

982.50

76.62

-11.12

123.65

1,854.82

71 - 80

25

75.5

1,887.50

-1.12

1.25

31.36

81 - 90

20

85.5

1,710.00

8.88

78.85

1,577.09

91 - 100 12

95.5

1,146.00

18.88

356.45

4,277.45

80

6,130.00

13,598.75

Rumus i i i f X f X = 80 00 . 130 , 6 = 76,62 RUMUS I Rumus Variansi (S2_{) =} 1 2 n X Xi f_i = 1 80 75 . 598 , 13 = 172.14

Rumus Standard Deviasi =

S

2

=

172

.

14

= 13.12 RUMUS II Rumus Variansi (S2_{) =} 1 2 2 n n X f X f n _{i i i i}

Kelas f Tanda Kelas X X2 fiXi fiXi 2

(Xi)

31 - 40

1

35.5

1,260.25

35.50

1,260.25

41 - 50

2

45.5

2,070.25

91.00

4,140.50

51 - 60

5

55.5

3,080.25

277.50

15,401.25

61 - 70

15

65.5

76.62

4,290.25

982.50

64,353.75

71 - 80

25

75.5

5,700.25

1,887.50

142,506.25

81 - 90

20

85.5

7,310.25

1,710.00

146,205.00

91 - 100

12

95.5

9,120.25

1,146.00

109,443.00

80

6,130.00

483,310.00

Rumus Variansi (S2_{) =} 79 80 ) 00 . 130 , 6 ( 00 . 310 , 483 80 2 x x = 320 , 6 00 . 900 , 576 , 37 00 . 800 , 664 , 38 = 320 , 6 00 . 900 , 087 , 1 = 172.14

Rumus Standard Deviasi =

S

2