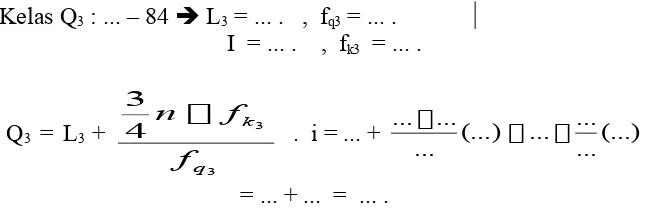SATUAN ACARA PERKULIAHAN (SAP)
Prodi/jurusan : S-1/PAI(Reguler/Ekstention)
Mata Kuliah : Statistik Pendidikan
SKS
Waktu pertemuan Pertemuan ke
: : :
3 (tiga) 90 menit 1
Dosen Pengampuh : Drs. Ach. Nur Syamsudin,M.Pd.
Standar Kompetensi : Bersikap teliti dan cermat serta trampil dalam menggunakan statistik sebagai alat analisis penelitian pendidikan.
Kompetensi Dasar : 1. Memiliki konsep dasar tentang istilah-istilah dalam statistik pendidikan.
2. Memiliki konsep menyajikan data dalam laporan penelitian yang bersifat diskreptif.
3. Mampu memahami konsep ukuran sentral. 4. Memahami konsep ukuran simpangan.
Indikator : 1. Menjelaskan konsep data kuantitatif, kualitatif, populasi dan sampel
2. Membaca sajian data dalam bentuk diagram garis dan diagram batang
3. Mengidentifikasi nilai suatu data yang ditampilkan pada tabel dan diagram
4. Menyajikan data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogive serta penafsirannya
5. Menafsirkan data data dalam bentuk diagram batang, garis, lingkaran dan ogiv
6. Menjelaskan konsep mean 7. Menjelaskan konsep median 8. Menjelaskan konsep mode 9. Menjelaskan konsep range 10. Menjelaskan konsep varians
11. Menjelaskan konsep simpangan baku Tahapan Aktivitas:
Persiapan (15 menit)
1. Menjelaskan kepada mahasiswa tentang pelaksanaan mata kuliah statistik pendidikan sesuai dengan pertemuan dan membagi materi sesuai dengan banyaknya kelompok
2. Menjelaskan bahwa disetiap akhir pertemuan ada tugas yang harus dikerjakan oleh mahasiswa dalam rangka mempertajam konsep-konsep dasar.
Pelaksanaan/Penyajian (75 menit)
1. Menngkondisikan mahasiswa untuk bekerja dalam kelompok terdiri dari 3-5 orang 2. Menjelaskan tugas yang harus dilakukan oleh tiap kelompok
3. Memberikan materi dalam bentuk modul untuk didiskusikan mahasiswa dalam kelompoknya masing-masing
5. Memberi penegasan hasil diskusi/validasi jawaban
6. Kelompok yang bekerja dengan baik mendapat penghargaan dari dosen
Penutup (30 menit)
1. Bersama mahasiswa membuat kesimpulan/rangkuman 2. Memberikan tes individu
3. Memberikan tugas berupa latihan soal. Evaluasi proses dan produk belajar
1. Keaktifan dalam kelas 20 %
2. Ujian pertengahan semester 20 %
3. Ujian akhir semester 20 %
4. Tugas individu 10 %
5. Proposal (analisa hasil penelt) 30 %
Jumlah 100 %
Deskripsi tugas-tugas
1. Keaktifitasan kelas: anda diharapkan terlibat aktif memberikan konstribusi pemikiran, baik berupa pertanyaan maupun komentar, dalam suasana bebas resiko (free riks environment). 2. Ujian pertengahan semester adalah ujian pertengahan pertama untuk materi yang hanya
digunakan dari perkuliahan awal sampai pertengahan semester.
3. Ujian akhir semester adalah ujian akhir untuk pertengahan kedua perkuliaan.
4. Tugas individu dan kelompok: Anda membedah dua soal tentang statistik pendidikan yang telah dimuat dalam sebuah materi teaching plan.
5. Proposal (analisis hasil penelitian): Anda membuat satu proposal analisis hasil penelitian sesuai petunjuk dosen. Tugas ini kemungkinan dapat Anda kembangkan menjadi bagian dari skripsi
Saran-saran
1. Jangan segan-segan melakukan kontak di dalam kelas atau di kampus mengenai hal-hal yang tidak atau kurang jelas.
2. Biasakanlah bekerja dengan rencana terjadwal; sangat tidak arif menunda-nunda sebuah pekerjaan, apalagi pekerjaan yang memerlukan perenungan dan refleksi.
3. Buatlah rencana belajar atau studi anda untuk satu semester ini diatas selembar kertas manila.
4. Butir 1, 2, dan 3 sangat membantu anda untuk tidak mengalami kesulitan di belakang dan tidak membuat anda stres.
MATERI:
.
A. PENGUMPULAN DAN PENYAJIAN DATA.
Pengantar materi:
Untuk menghindari kejenuhan membaca data berupa angka-angka (tabel), suatu kumpulan angka/data banyak kita jumpai disajikan dalam bentuk diagram. Hal ini diperlukan guna menarik perhatian pembaca. Data merupakan keterangan-keterangan dari objek-objek yang diamati. Makin lengkap data-data yang dikumpulkan biasanya makin baik dan makin memperkuat kesimpulan dan ramalan yang di hasilkan.
Dari segi bentuknya, data dapat dibedakan sebagai berikut : 1) Data kuantitatif, yaitu data yang berbentuk bilangan.
Misalnya, data tentang ukuran tinggi badan, data tentang upah buruh, dll. Data Kuantitatif dibedakan menjadi dua :
a. Data Diskrit, yaitu data yang diperoleh dari hasil mencacah atau membilang. Misalnya, data tentang benyak mahasiswa semester VII STAI Daruttaqwa. b. Data Kontinu, yaitu data yang diperoleh dari hasil mengukur.
Misalnya, data tentang tinggi badan dan berat badan mahasiswa. 2) Data kualitatif, yaitu data yang tidak berbentuk bilangan.
Misalnya data tentang pekerjaan orang tua murid, data tentang mutu barang, (apakah kualitasnya tinggi, sedang atau rendah).
Populasi dan sampel.
Populasi adalah keseluruhan data yang menjadi obyek penelitian, sedang sampel adalah sebagian dari populasi. Misalnya, Sekarung beras merupakan populasi dan apabila seseorang ingin melihat kualitas beras tersebut maka orang tersebut cukup mengambil segenggam beras yang merupakan sampel
1. PENGUMPULAN DATA.
Macam-macam cara pengumpulan data, antara lain:
1) Penelitian lapangan (pengamatan langsung) atau observasi.
Pengumpulan data dilakukan langsung mengadakan penelitian ke lapangan atau laboratorium terhadap suatu objek penelitian.
Standar Kompetensi : Bersikap teliti dan cermat serta trampil dalam menggunakan statistik sebagai alat analisis penelitian pendidikan.
Kompetensi Dasar :
Memiliki konsep dasar tentang istilah-istilah dalam statistik pendidikan.
Memiliki konsep menyajikan data dalam laporan penelitian yang bersifat diskreptif. Mampu memahami konsep ukuran sentral.
2) Wawancara (interview).
Pengumpulan data dilakukan dengan wawancara langsung kepada objek atau kepada orang yang mengetahui persoalan objek.
3) Angket (kuesioner).
Pengumpulan data dilakukan dengan menggunakan daftar isian atau suatu daftar pertanyaan yag telah disiapkan dan disusun oleh peneliti sedemikian rupa sehingga nantinya di dapatkan jawaban atau isian yang dikehendaki.
4) Media cetak atau elektronika, dll.
2. PENYAJIAN DATA.
Data dapat disajikan dalam bentuk daftar (tabel) atau gambar. Gambar meliputi kartogram (peta) dan diagram. Maksud dari penyajian data adalah untuk mempermudah membaca data. Kegunaan diagram antara lain untuk memperjelas dan mempertegas penyajian data.
1. Diagram Lambang (piktogram) 2010
Piktogram lebih cocok untuk menyajikan data 2009 jika data tersebut menunjukkan jumlah (angka)
yang besar. Ukuran harus diperhatikan pada
piktogram. 126000 kg 1008000 kg
Penjualan Susu Perah
2. Diagram Lingkaran.
Diagram ini lebih cocok untuk menunjukkan perbandingan Suntik jika data tersebut terdiri atas beberapa kategori.
Dalam diagram lingkaran, lingkaran dibagi atas juring-ju- Pil juring sesuai dengan data yang disajikan. Luas masing-masing juring sebanding dengan sudut pu- IUD sat lingkaran (panjang busurnya).
Prosentase KB Mandiri 2010
3. Diagram Batang
Diagram batang dilengkapi dengan skala dan kata-kata yang jelas sehingga ukuran ukuran data yang bersangkutan dapat dibaca dari diagram.
Jumlah produksi Susu Perbandingan Jumlah Banyaknya Mobil Jumlah Kasus Remidi 2007 - 2010 Guru 2008-2010
50
50 A 50 40
40 B 40 25 30
20 20 C
07 08 09 10 SD SMP 10 20 30 40 07 08 09 10 2008 2010 Pribadi belum tuntas
2009 Angkot tuntas
diagram batang tunggal diagram batang berganda diagram batang horizontal diagram batang bersusun
4. Diagram Garis.
Diagram garis dipergunakan untuk menggambarkan perkembangan (pertumbuhan) suatu hal (kegiatan) dari waktu ke waktu secara terus-menerus.
Melalui diagram garis ini kita sering melakukan interpolasi dan ekstrapolasi. Interpolasi adalah memperkirakan nilai diantara
akan datang.
Produksi Telur 2001-2005 (kg)
: Ayam Buras : Ayan Petelur
2001 2002 2003 2004 2005
` 5. Tabel Distribusi Frekuensi.
Apabila terdapat data yang jumlahnya cukup ba- Interval Frekuensi nyak maka akan lebih efektif dan simple jika pe- 41 – 50 6 nyajiannya dalam tabel distribusi frekuensi. 31 – 40 3 Data dikelompokkan dalam beberapa kelas/inter- 21 – 30 7 val di mana dalam satu interval memuat/mengan 11 – 20 4
dung beberapa data tunggal. 1 – 10 10
30
Agar mudah memperoleh keterangan dari data ada beberapa cara menyatakan sekumpulan data dalam Distribusi frekuensi, sbb:
a. Distribusi frekuensi tunggal
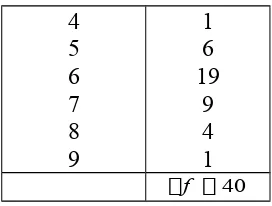
Berikut adalah nilai PAI pada raport semester 2 dari 40 siswa kelas X: 40 50 60 70 80 60 70 60 80 80 90 70 50 60 60 70 60 70 60 50
70 50 60 60 70 50 50 60 70 70 50 70 70 80 80 70 80 40 90 60
Jika data itu akan di susun dalam daftar distri Nilai (X) Turus/ Tally
f
busi frekuensi tunggal, caranya: 40 II 2
1. Nilai diurutkan dari terendah s/d tertinggi. 50 IIII II ... 2. Data diitulis dalam kolom nilai yang biasa 60 ... ...
nya dinyatakan dengan variabel x 70 ... 12
3. Dengan pertolongan turus (tally) dapat di - 80 ... ... tentukan frekuensi masing-masing nilai. 90 .... ...
40
b. Distribusi frekuensi berkelompok.
Berikut ini adalah hasil evaluasi (tes) mata pelajaran PAI kelas X dari 40 siswa tersebar sebagai berikut.
75 84 60 68 53 70 67 57 67 70 76 63 68 66 67 64 44 34 62 60 56 56 63 61 69 38 48 68 62 81 64 65 55 64 49 54 72 39 66 25
Dari data itu diperoleh ukuran paling rendah (minimal) ... dan ukuran paling tinggi (maksimal) ... .
Selisih ukuran tertinggi dengan ukuran terendah disebut Jangkauan (range, rentang), J = 84 – ... = ... .
Jika data akan di susun dalam tabel distribusi frekuensi, anda ikuti langkah sbb: 50
1). Semua ukuran harus termuat dalam kelas-kelas interval. Ukuran minimum termuat dalam kelas-kelas interval terendah (tidak perlu menjadi batas bawah), ukuran maksimum termuat dalam kelas interval tertinggi (tidak perlu menjadi batas atas).
2). Tentukan range/jangkauan (J) = nilai maksimum – nilai minimum.
3). Tentukan banyaknya kelas interval dengan rumus k = 1 +3,3 log n; n = banyak ukuran (data), k = banyak kelas interval.
4). Tentukan lebar kelas dengan rumus i =
k jangkauan
Data itu disusun dalam tabel sebagai berikut:
Jangkauan = ... .
Banyanya kelas interval : k = 1 + 3,3 log ( ... ) = 1 + 3,3 ( ... )
= 1 + ... = 6,287
....Lebar kelas ( i ) = ....
6 ...
k
jangkauan
Nilai (X) Turus (Tally) Frekuensi ( f ) Nilai Tengah
24 – 32 I 1 28
33 – 41 ... ... ...
... – 50 ... ... ...
51 – ... ... 6 55
... – ... ... ... ...
... – ... ... ... ...
... – 86 II ... 82
Jumlah ...
Dari kelas interval 1: 24 – 32 dapat diidentifikasi beberapa hal, sbb: 24 disebut batas bawah kelas , 32 disebut batas atas kelas. 24 – 0,5 = ... . disebut tepi bawah kelas.
32 + ... = ... . disebut tepi atas kelas. c. Menyusun Daftar Distribusi Frekuensi Kumulatif.
Jumlah frekuensi yang memiliki nilai kurang dari batas nyata (tepi atas) suatu inteval tertentu disebut frekuensi kumulatif kurang dari (fk kurang dari).
Jumlah frekuensi yang memiliki nilai lebih dari batas bawah nyata (tepi bawah) interval tertentu disebut frekuensi kumulatif lebih dari (fklebih dari).
Tabel Distribusi frekuensi kumulatif :
Lihat tabel ”Hasil evaluasi PAI kelas X” pada sub bagian b:
Nilai (x) Frekuensi (f) Tepi atas (U)
24 – 32 1 32,5 ...
33 – 41 ... ... 32,5 4 ...
... – 50 ... ... ... ... ...
51 – ... 6 ... ... ... 33
... – ... ... 68,5 ... 32 ...
... – ... ... ... ... ... ...
... – 86 ... ... 77,5 ... 2
40 40
30 30
20 20
10 10
0 0
23,5 32,5 41,5 50,5 59,5 68,5 77,5 86,5 23,5 32,5 41,5 50,5 59,5 68,5 77,5 86,5
Frekuensi komulatif kurang dari Frekuensi kumulatif lebih dari Kurva/grafik garis yang terjadi disebut dengan OGIVE
Jika dalam penelitian memerlukan frekuensi kumulatif dalam prosentase, maka fk dibagi denganf kemudian dikalikan 100%. Frekuensi kumulatif seperti itu dinamakan frekuensi kumulatif relatif.
Nilai (x)
Frekuensi kumulatif Frekuensi kumulatif relatif (%)
fk
fk
fk
fk
24 – 32 1 40 2,5 100
33 – 41 4 ... ... ...
... – 50 ... ... ... 90
51 – ... ... 33 ... ...
... – ... 32 ... 80 67,5
... – ... ... ... ... ...
... – 86 ... 2 100 ...
d. Histogram dan Poligon frekuensi.
Suatu diagram yang menyajikan data yang disusun dalam kelas-kelas interval (distribusi frekuensi) dalam bentuk batangan persegi panjang disebut Histogram. Jika titik-titik tengah sisi atas persegi panjang pada histogram di hubungkan, maka diperoleh sebuah poligon frekuensi. Agar poligonnya tertutup, maka sebelah kiri dan kanan histogram ditambahkan dengan satu kelas interval lagi dengan frekuensi nol.
20
15 Poligon frekuensi 10
5 0
Permasalahan untuk didiskusikan mahasiswa:
Dalam sebuah tes statistika pendidikan mahasiswa semester VII jurusan PAI STAI Daruttaqwa Gresik didapat:
60 49 90 73 51 72 61 73 58 59 70 70 61 81 62 85 63 63 74 46 60 75 40 73 91 63 88 64 85 41 99 50 55 72 95 71 42 72 96 42 1. Buatlah tabel distribusi frekuensi dengan batas bawah kelas adalah 38.
2. Susun dan lukis tabel frekuensi komulatif lebih dari dan kurang dari beserta ogive-nya!
....
B. PENGOLAHAN DATA.
1. UKURAN TENDENSI SENTRAL (UKURAN PEMUSATAN).
Ada tiga buah ukuran yang sangat penting yang dianggap mewakili kelompoknya. Ketiga ukuran itu adalah mean, median, dan modus.
a. Rata-rata (mean):
Mean atau rata-rata hitung (_
x), yaitu Jumlah semua ukuran dibagi banyaknya ukuran. 1). Mean data tunggal:
Keterangan :
x = rata-rata hitung (mean)
n = banyak nilai (ukuran) , xi = data ke- i
Masalah 1:
Tentukan mean dari : 11, 10, 12, 9, 8, 12, 9, 9, 7, 13 Penyelesaian:
2). Mean data kelompok:
Pada tabel distribusi frekuensi berkelompok, kita hanya dapat mengetahui fre-kuensi untuk masing-masing kelas interval. Kita menganggap bahwa frefre-kuensi di dalam setiap kelas interval tersebar merata. Dengan demikian , perhitungan pada data berkelompok tidak seteliti sebagaimana dengan data tunggal.
Masing-masing kelas interval diwakili oleh titik tengahnya.
Mean dari data berkelompok sama dengan mean dari titik-titik tengah interval kelas yang dapat dihitung seperti pada data tunggal, dengan aturan:
(1). Mean (x) =
Tentukan mean dari data kelompok yang Berat (Kg) f
datanya terlihat pada tabel ! 50 – 52 5 Berat (kg) Titik tengah Interval
Hasil yang diperoleh dengan cara ini, mungkin masih mengandung kesalahan karena bilangannya besar.
Untuk memperkecil kesalahan ditempuh cara dengan menggunakan rata-rata sementara. Dari tabel ditentukan rata-ata sementara yaitu titik tengah interval, misalnya Ms= 57.
Untuk mempermudah hitungan, simpangan (d) dapat diganti : d'
i
Modus adalah nilai atau ukuran yang paling sering terdapat (muncul).
b.1. Modus data tunggal:
Masalah 3:
Tentukan modus dari : 6, 8, 5, 6, 7, 11, 10, 12, 9, 8, 12, 9, 9, 7, 13 Penyelesaian:
b.2. Modus data kelompok:
Untuk menentukan modus data berkelompok ada beberapa cara pendekatan, antara lain:
1). Modus besar, yaitu nilai titik tengah kelas interval yang memiliki frekuensi terbanyak. Kelas interval yang memilki frekuensi terbanyak disebut kelas modus.
Pendekatan ini jarang digunakan sebab penyimpangannya terlalu besar. 2). Dengan menggunakan rumus yang diperoleh dari histogram.
Masalah 4 :
Perhatikan tabel distribusi frekuensi berikut.
Tabel berat badan 50 mahasiswa semester VII STAI-DA Gresik Berat(x)
(kg) Titik tengah interval(x1)
Frekuensi (f) 50 – 52
53 – 55 56 – 58 59 – 61 62 – 64
51 54 57 60 63
5 17 14 10 4
50
a. Modus besar = ... . ( adalah titik tengah kelas modus [53 – 55] ) b. Menggunakan rumus.
Distribusinya dianggap merata, maka kita dapat menetapkan bahwa jarak modus dari tepi bawah dan tepi atas kelas tersebut sebanding dengan selisih frekuensi kelas modus dengan kelas yang mendahuluinya.
Rumus modus: Modus (Mo) = L +
2 1
1
d d
d
. i
L = Tepi bawah kelas modus i = Interval kelas = lebar kelas
d1 = Selisih fekuensi kelas modus dengan frekuensi kelas sebelumnya. d2 = Selisih fekuensi kelas modus dengan frekuensi kelas sesudahnya. Modus terletak pada kelas modus: 53 – ....
d1 = 17 – .... , d2 = 17 – .... , i = .... , dan L = 52,5
Modus = Lo +
2 1
1
d d
d
. i = ... +12 ....(...) ...
= ... + ... = ....
c. Median (Md) :
1). Median data tunggal:
Median adalah ukuran yang ditengah-tengah jika banyaknya data ganjil, atau rata– rata kedua nilai tengah jika banyaknya data genap.
Jika n ganjil, median : ( 1)
Jika n genap, median:
2
Modus (Mo) = .... (sebab frekuensinya paling banyak, yaitu muncul 3 kali).
Masalah 6 :
Tentukan mean, median, dan modus dari data yang ada pada tabel berikut.
Nilai(x) f.x
Suatu distribusi frekuensi mungkin tidak ada modusnya (bilamana distribusi tidak mempunyai modus?)
Jika hanya ada satu modus dinamakan unimodal. Jika ada dua modusnya dinamakan bimodal.
Ada beberapa cara menentukan median dari data berkelompok antara lain: 1). Menggunakan ogive 2). Mengunakan histogram 3). Mungunakan rumus. Masalah 7:
Berat (x)
(kg) f
50 – 52 53 – 55 56 – 58 59 – 61 62 – 64
5 17 14 10 4
50
Tentukan mediannya! Penyelesaian:
1). Menggunakan ogive.
Untuk mengambar ogive kita buat tabel : Berat (x)
(Kg) f fk
50 – 52 5 5
53 – 55 17 ...
56 – 58 14 ...
59 – 61 10 ...
62 – 64 4 46
50
Median adalah ukuran tengah. Kita tentukan
2 1
n pada sumbu frekuensi kumulatif, yaitu ... .
fk Dari titik 25 ditarik garis mendatar 50 memotong ogive di titik A, kemudi- 45 an dari titik A ditarik tegak lurus memotong sumbu ukuran berat
di M. 36
Dengan anggapan bahwa penye-
baran ukuran di 55,5-58,5 merata, 25 A
maka: 22
Median = 55,5 + (... ...) ...
36 ... 25
= 55,5 + (...)
... 3
5 M
= ... . 52,5 55,5 58,5 61,5 64,5
2). Menggunakan histogram. f
17
14
Median adalah suatu ukuran (nilai)
yang membagi data menjadi dua
bagian yang sama frekuensinya. D N C Luas persegi panjang pada histo-
gram sebanding dengan frekuensi. Jadi median dapat digambarkan Suatu titik M pada sumbu menda-tar (sumbu berat).
Garis MN membagi luas bidang DCUL berbanding (58,5-55,5) :14, sehingga luas bidang persegi panjang seluruhnya menjadi dua bagian
yang sama luasnya. 0 L M U 52,5 55,5 58,5 61,5 64,5
Keterangan :
L = Tepi bawah kelas, U = Tepi atas kelas dan Md = median Median mempunyai nilai: Md = 55,5 + .(...)
...
3 = ... .
3). Menggunakan rumus.
Dengan mengikuti langkah-langkah cara menentukan (mencari) median menggunakan histogram, kita dapat menemukan rumus untuk mencari median sebagai berikut.
Banyaknya ukuran (frekuensi) = n. Tentukan nilai
2 1
n untuk menentukan kelas median, yaitu kelas terletaknya median.
fk = Frekuensi kumulatif sebelum kelas median. fm = Frekuensi kelas median.
L = Tepi bawah kelas median U= Tepi atas kelas median Perhatikan histogram pada gambar di atas :
LM : LU = Luas LMND : Luas LUCD
LM : i =
m k
m k
f f n LM f
f
n
2
1 :
2
1 . i
Jadi: Median (Md) = L + m
k
f f n
2 1
. i
Lihat tabel : ½ n = ... . , Kelas Md : 55,5 -58.5 = 3 , L = ... . , i = ... . , fk = ... . , dan f m = ... .
Jadi, Median (Md) = ... +
... ...
25
. ... = 55,5 +...
Jawablah pertanyaan di bawah ini dengan benar ! 1. Sebutkan pengertian rata-rata (mean) menurut Anda?
2. Berapa nilai rata-rata (mean) tunggal untuk mata kuliah pengantar komunikasi? 75 77 80 85 88 90 79 55 58 57 85 80
3. Apa yang anda ketahui tentang mode atau modus? 4. Berapa nilai modus tunggal untuk motivasi dosen?
85 88 65 55 60 70 57 59 60 70 70 80 5. Sebutkan pengertian median menurut Anda?
6. Berapa nilai median tunggal untuk pengetahuan mengajar dosen? 90 95 90 80 85 88 99 96 70 75 70 60
7. Diketahui data hasil pilkada di kabupaten Gresik sbb: 60 65 70 60 65 68 79 76 50 55 55 44 49 50 68 70 74 77 75 75 77 79 55 58 57 60 62 61 66 65 Tabulasikan data tersebut menjadi data kelompok (distribusi). Hitunglah :
a. Rata-rata (Mean) b. Modus
c. Median
d. Kuartil (Q):
Suatu data dapat diurutkan dari yang terkecil s.d terbesar, sehingga Jika banyaknya ukuran lebih dari atau sama dengan 4
n4
, maka dapat ditentukan tiga ukuranyang membagi kelompok data yang telah diurutkan menjadi empat kelompok data yang sama banyaknya.
Ketiga ukuran (nilai) yang membagi kelompok data menjadi 4 bagian sama banyak tersebut disebut kuartil, diberi lambang Q1, Q2 dan Q3.
Q1 = Kuartil bawah , Q1 membagi kelompok ukuran menjadi 4 1
bagian dengan nilai kurang dari Q1 dan
4 3
bagian dengan nilai lebih dari Q1.
Q2 = Kuartil tengah [median (Md)] , Q2 membagi kelompok ukuran menjadi 4 2
dengan nilai kurang dari Q2 dan 4 2
bagian dengan nilai lebih dari Q2. Q3 = Kuarti atas , Q3 membagi kelompok ukuran mejadi
4 3
bagian dengan nilai kurang dari Q3 dan
4 1
bagian dengan nilai lebih dari Q3.
Kuartil bukan ukuran yang ada hubungannya dengan niai rata-rata, melainkan hanya sebagai ukuran lokal.
1. Kuartil data tunggal:
Ukuran-ukuran diurutkan menurut besarnya mulai dari yang terkecil.
Mula-mula ditentukan Q2 (median), kemudian tentukan Q1, yaitu nilai tengah
dari bagian I (kiri), kemudian tentukan Q3, yaitu nilai tengah dari bagian II
(kanan).
¼ ¼ ¼ ¼
Xmin Q1 Q2 = Md Q3 Xmax Masalah 8:
Nilai raport seorang siswa kelas XI untuk 9 bidang mata pelajaran adalah sebagai berikut : 8, 7, 7, 6, 5, 6, 8, 6, 7. Tentukanlah: Q1, Q2 (Md), Q3!
Penyelesaian :
Ukuran (data) diurutkan dahulu dengan n = 9. 5, ... , ... , ... , 7, ... , ... , 8, ...
Q1 Md = x5 = 7 Q3
Bagian I ( kiri dari Q2) ada 4 ukuran, maka Q1 = ....
... 6 ... 2
3 2
x
x
Bagian II (kanan dari Q2) ada 4 ukuran, maka Q3 = ....
2 ... ... 2
8 7
x
x
Masalah 9 :
4
d.1. Kuartil data Kelompok:
Seperti menetukan median (Q2) pada data berkelompok, menentukan kuartil bawah (Q1) dan kuartil atas (Q3) -pun dapat dilakukan dengan tiga cara, yaitu : 1). Dengan ogive. 2). Dengan histogram. 3). Dengan rumus
Khusus untuk langkah menggunakan Ogive dan histogram tidak jauh berbeda dengan langkah-langkah menentukan Median data kelompok.
Dapat pula kita gunakan rumus untuk menentukan Kuartil bawah (Q1) dan kuiartil atas (Q3) sebagai berikut:
Q1 = L1 +
Tabel berikut adalah distribusi frekuensi upah Upah (Rp) f fk
Kelas Q3 : ... – 84 L3 = ... . , fq3 = ... . I = ... . , fk3 = ... .
Q3 = L3 +
3 3
4 3
q k
f f
n
. i = ... + (...)
... ... ... (...) ...
... ...
= ... + ... = ... . 2. UKURAN PENYEBARAN (DISPERSI)
Pengertian ukuran penyebaran (dispersi)
Ukuran pemusatan (tendensi sentral) seperti mean, median, dan modus merupakan ukuran yang dapat dipakai sebagai wakil dari sekumpulan data (ukuran).
Tetapi gambaran yang diberikan kadang-kadang tidak jelas dan kurang banyak memberikan arti.
Oleh karena itu, perlu diberikan keterangan mengenai penyebaran ukuran itu sendiri yang disebut ukuran penyebaran (dispersi).
Ukuran dispersi ada beberapa macam, diantaranya adalah : a. Jangkauan atau range (J) :
Jangkauan atau range merupakan ukuran penyebaran yang paling sederhana.
Range sekumpulan data dirumuskan sebagai selisih nilai tertinggi (nilai maksimum) dan nilai terendah (nilai minimum) data tersebut.
1). Range dari data tunggal:
J = Xmaks – Xmin Masalah 11 :
Tentukanlah range dari nilai : 6, 8, 3, 3, 4, 4, 6, 6, 8, 8, 8, 7, 7, 9, 10 Penyelesaian:
J = ... – ... = ... .
2). Range dari data kelomppok:
Range dari data berkelompok dapat ditentukan dengan 3 cara:
1). Range = selisih titik tengah kelas tertinggi dengan titik tengah kelas terendah.
2). Range = selisih tepi atas kelas tertinggi dengan tepi bawah kelas terendah. 3). Range = selisih batas atas kelas tertinggi dengan batas bawah kelas terendah Masalah 12 :
Tabel berikut adalah distribusi frekuensi upah Upah (Rp) f
buruh pada suatu perusahaan. 40 – 48 7
Tentukan Nilai jangkauan atau range ! 49 – 57 10 58 – 66 15
Penyelesaian : 67 – 75 12
1. J = Xin – Xio = ... – ... = ... . 76 – 84 9
85 – 93 5
2. J = Ln – Lo = ... – ... = ... . 94 – 102 2
60
3. J = Bn – Bo = ... – 40 = ... .
b. Jangkauan semi-interkuartil (simpangan kuartil) (Qd) :
Selain pengertian range diatas ada bentuk range yang laihn yang bisa dipakai sebagai ukuran penyebaran, yaitu jangkauan semi-interkuartil.
Jangkauan interkuartil adalah selisih antara kuartil atas dengan kuartil bawah (Q3– Q1)
Hal ini menunjukkan bahwa 50% dari data terletak antara Q3 dan Q1.
Pada umumnya orang lebih suka menggunakan Jangkauan semi-interkuartil yang dirumuskan dengan Qd =
2 1
(Q3 – Q1) Masalah 13 :
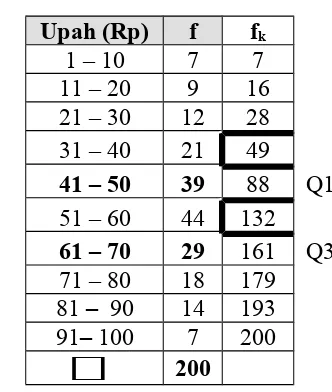
Tabel berikut adalah distribusi frekuensi upah Upah (Rp) f fk
Buruh pada suatu perusahaan. 1 – 10 7 7
Tentukan simpangan kuartil! 11 – 20 9 16
21 – 30 12 28
Penyelesaian : 31 – 40 21 49
Q1 = .... + (... – 49) . ( ... ) / 39 = ... + ... 41 – 50 39 88 Q1
= ... . 51 – 60 44 132
Q3 = ... + (... – 132) . ( ... ) / 29 = ... + ... 61 – 70 29 161 Q3
= ... . 71 – 80 18 179
81 – 90 14 193
Jadi : Qd = ½ (... – ... ) = ... . 91– 100 7 200
200
c. Simpangan rata-rata atau deviasi rata-rata (SR) :
Simpangan rata-rata adalah ukuran dispersi yang menyatakan penyebaran nilai-nilai terhadap mean.
Dispersi suatu data akan kecil jika nilai-nilai tersebut terkonsentrasi pada ratanya. Sebaliknya, dispersi akan besar jika nilai-nilai (data) tersebar dari rata-ratanya.
1). Simpangan rata-rata untuk data tunggal:
Pada data: x1, x2 , x3 ,x4 , ... , xn memiliki rata-rata hitung (mean) =x, maka simpangannya dapat dinyatakan dengan:
(x1 - x), (x2 - x), (x3 -x), (x4 - x), ... , (xn -x) Jumlah harga mutlak untuk simpangan-simpangan itu adalah:
x
x1 + x2 x + x3x + x4 x + ... + xn x
sehingga simpangan rata-rata seluruh data dapat dirumuskan sebagai:
SR =
n
i n 1 1
x
x1 atau SR =
n x x n
i
1 1
Jika suatu data : x1, x2, x3 , x4, ... , xk dengan masing-masing frekuensi
SR =
Tentukan simpangan rata-rata dari : 3, 4, 6, 8, 9 Penyelesaian:
2). Simpangan rata-rata untuk data kelompok:
Pada data berkelompok setiap kelas diwakili oleh titik-titik tengahnya.
Simpangan rata-rata pada data berkelompok adalah simpangan rata-rata titik-titik tengah interval kelas terhadap mean dari data itu.
Masalah 15 :
Tentukan simpangan rata-rata dari data yang terdapat pada tabel berikut jika diketahui rata-rata hitung tinggi siswa adalahx= 149,5.
Hasil pengukuran tinggi badan siswa kelas II. No Nilai Titik tegah (xi)
d. Simpangan baku/Deviasi standar (S):
Jika datanya terdiri atas sekelompok ukuran : x1, x2, x3, x4, ... , xk, dan masing-Tabel ukuran jari tengah
Panjang (x) Frekuensi(f)
xi x
Penyederhanaan rumus simpangan baku :
S = (bila data tunggal berbobot), maka:
S =
Untuk menghindari bilangan-bilangan besar, digunakan deviasi sementara (simpangan sementara ) sehingga rumus simpangan menjadi
Permasalahan untuk didiskusikan mahasiswa:
1. Hasil pengamatan suatu jenis barang sebanyak 40 kotak tercatat dalam kg yang terdekat adalah sebagai berikut:
127, 146, 143, 119, 152, 146, 159, 147, 164, 137, 149, 139, 142, 159, 151, 139, 130, 135, 177, 145, `32, 156, 135, 144, 14\52, 167, 157, 162, 140, 134, 140, 145, 149, 166, 171, 156, 125, 176, 154, 146.
Tentukan:
a. Range c. Buat kurva ogive-nya
b. Tabel distribusi frekuensinya d. Nilai dari kuartil & simpangan kuartil 2. Diketahui data tunggal: 10, 9, 8, 10, 12, 15, 6, 10
Tentukan nilai dari:
a. Range (jangkauan) c. Simpangan rata-rata b. Simpangan kuartil d. Simpangan baku.
3. Dari tabel distribusi berkelompok berikut, tentukanlah: Interval f
a. Jangkauan (range). 80 – 84 2
b. Simpangan kuartil. 75 – 79 3
c. Simpangan rata-rata. 70 – 74 6
d. Simpangan baku. 65 – 69 11
60 – 64 12
55 – 59 4
50 – 54 3
45 – 49 2
40 – 44 1
35 – 39 2
30 – 34 1
25 – 29 1
Jawablah pertanyaan di bawah ini dengan benar! 1. Sebutkan pengertian range menurut Anda?
2. Berapa nilai range untuk mata kuliah pengantar statistika sosial? 75 77 80 85 88 90 79 55 58 57 85 80
3. Apa yang anda ketahui tentang standar deviasi? 4. Sebutkan pengertian variasi (varians) menurut anda? 5. Diketahui data hasil kompetensi mengajar dosen.
90 99 100 110 100 90 105 90 100 80 85 80 90 75 85 99 89 65 55 60 70 57 59 60 70 70 80 95 99 90
Tabulasikan data tersebut menjadi data kelompok, kemudian hitunglah nilai simpangan baku (standard deviasi) dan variasi (varians) serta buatlah grafik batang dan lingkaran dengan langkah-langkahnya.
MENGUKUR MINAT MAHASISWA TERHADAP MATERI BELAJAR
Menurut anda materi belajar tentang statistika (lingkarilah angka 1, 2, 3, 4 atau 5 diantara pernyataan berikut):
Menyenangkan 1 2 3 4 5 Membosankan
Bermanfaat 1 2 3 4 5 Tidak Bermanfaat
Menarik 1 2 3 4 5 Tidak Menarik
Sangat perlu dipelajari 1 2 3 4 5 Tidak perlu dipelajari
Menantang 1 2 3 4 5 Tidak Menantang
Perlu disebar luaskan 1 2 3 4 5 Tidak Perlu disebar
luaskan Mempunyai korelasi
dengan masalah
sehari-hari 1 2 3 4 5
Tidak Mempunyai korelasi dengan masalah
sehari-hari
Petunjuk Penilaian:
1. Jika rata-rata jawaban berkisar angka 1 dan 2 maka materi pembelajaran menarik minat mahasiswa.
2. Jika rata-rata jawaban berkisar angka 4 dan 5 maka materi pembelajaran tidak menarik minat mahasiswa, sehingga perlu adanya perubahan metode, media, strategi pembelajaran, dll.
Gresik, 03 Maret 2011 Dosen Pengampuh,