SISTEM PENGOLAHAN ISYARAT. Kuliah 5 Transformasi Fourier

TKE 2403

SISTEM PENGOLAHAN ISYARAT

Kuliah 5 – Transformasi Fourier

(Bagian II)

Indah Susilawati, S.T., M.Eng.

Program Studi Teknik Elektro

Fakultas Teknik dan Ilmu Komputer

Universitas Mercu Buana Yogyakarta

KULIAH 5

SISTEM PENGOLAHAN ISYARAT

TRANSFORMASI FOURIER

(Bagian II)

Teori Konvolusi

Misalkan ada suatu hasil kali dari 2 sinyal, kira-kira seperti apakah transformasi Fourier-nya?

∫

∞ ∞ − −

=

y

t

y

t

e

dt

t

y

t

y

F

[

₁

(

)

₂

(

)]

₁

(

)

₂

(

)

jωt ₍₈₆₎

Pertama, yi(t) dituliskan sebagai inverse transformasi Fourier dari Yi(ω) sebagai

berikut.

∫

∞ ∞ −

=

ω

ω

π

ω

d

e

Y

t

y

_{i i}

(

)

j t

2

1

)

(

₍₈₇₎

Maka substitusi persamaan (87) ke persamaan (86) menjadi,

dt

e

d

e

Y

d

e

Y

t

y

t

y

F

jαt j t jωt

π

α

α

π

− ∞ ∞ − Ω ∞ ∞ − ∞ ∞ −

⎭

⎬

⎫

⎩

⎨

⎧

Ω

Ω

⎭

⎬

⎫

⎩

⎨

⎧

=

∫

∫

∫

(

)

2

1

)

(

2

1

)]

(

)

(

[

_{1 2 1 2}

Dengan cara mengubah urutan pengintegralan, maka pernyataan di atas dapat dinyatakan kembali sebagai,

Ω

Ω

⎭

⎬

⎫

⎩

⎨

⎧

∫ ∫

∫

∞ ∞ − ∞ ∞ − ∞ ∞ − − + Ω

d

d

Y

Y

dt

e

j t

α

α

π

π

ω α

)

(

)

(

2

1

2

1

2 1 ) (

Dan suku yang berada di dalam kurung adalah merupakan fungsi delta, sehingga,

Ω

Ω

−

+

Ω

=

∫ ∫

∞ ∞ − ∞ ∞ −

d

d

Y

Y

t

y

t

y

F

δ

α

ω

α

α

π

(

)

(

)

(

)

2

1

)]

(

)

(

[

_{1 2 1 2 (88)} atau

Ω

Ω

⎭

⎬

⎫

⎩

⎨

⎧

−

+

Ω

=

∫ ∫

∞ ∞ − ∞ ∞ −

d

Y

d

Y

t

y

t

y

F

(

)

(

)

(

)

2

1

)]

(

)

(

[

_{1 2}

δ

α

ω

₁

α

α

₂

π

Dan dengan menggunakan sifat proyeksi fungsi delta, persamaan tersebut dapat ditulis kembali menjadi,

Ω

Ω

Ω

−

=

∞

∫

∞ −

d

Y

Y

t

y

t

y

F

(

)

(

)

2

1

)]

(

)

(

[

_{1 2 1}

ω

₂

π

(89)

Pernyataan di sebelah kanan tanda sama dengan disebut konvolusi

(convolution) dari dua fungsi Y1(ω) dan Y2(ω) dan sering dituliskan dengan

notasi sebagai berikut.

Ω

Ω

Ω

−

=

∗

∞

∫

∞ −

d

Y

Y

Y

Y

(

)

(

)

2

1

)

(

)

(

_{2 1 2} 1

ω

ω

π

ω

(90)

Hasil yang sama juga diperoleh jika digunakan

α

α

ω

α

π

ω

ω

Y

Y

Y

d

Y

(

)

(

)

2

1

)

(

)

(

_{2 1 2} 1

∗

=

∫

−

∞ ∞ − (91)

Persamaan (89) seringkali disebut dengan teori konvolusi.

Dengan cara analisis yang sejenis, dapat diperlihatkan bahwa

τ

τ

τ

τ

τ

τ

ω

ω

d

t

y

y

d

y

t

y

Y

Y

F

)

(

)

(

)

(

)

(

)]

(

)

(

[

2 1 2 1 2 1 1

−

=

−

=

∫

∫

∞ ∞ − ∞ ∞ − − (92)

Teori Parseval

Misalkan konvolusi dari fungsi Y(ω) dengan dirinya sendiri sebagai berikut.

∫

∫

∞ ∞ − − ∞ ∞ −

=

=

Ω

Ω

Ω

−

=

∗

dt

e

t

y

t

y

t

y

F

d

Y

Y

Y

Y

t jω

ω

π

ω

ω

2

)]

(

[

)]

(

)

(

[

)

(

)

(

2

1

)

(

)

(

Jika ω = 0 maka

∫

∫

∞ ∞ − ∞ ∞ −

=

Ω

Ω

Ω

−

Y

d

y

t

dt

Y

(

)

(

)

[

(

)]

2

2

1

π

(93) Dan jika *

)

(

)]

(

[

)]

(

[

)

(

_⎟⎟

=

Ω

⎠

⎞

⎜⎜

⎝

⎛

=

=

Ω

−

∗ ∞ ∞ − Ω − ∞ ∞ − Ω −

∫

∫

y

t

e

dt

y

t

e

dt

Y

Y

j t j t Maka

∫

∫

∞ ∞ − ∞ ∞ − ∗

_Ω

_Ω

₌

Ω

Y

d

y

t

dt

Y

(

)

(

)

[

(

)]

2

2

1

π

Atau dinyatakan

∫

∫

∞ ∞ − ∞ ∞ −

=

Ω

Ω

d

y

t

dt

Y

(

)

2

[

(

)]

2

2

1

π

(94)

Persamaan ini disebut teori Parseval yang menyatakan bahwa jika didefinisikan daya dari sebuah fungsi z(.) sebagai

∫

∞ ∞ −

=

(.)

.

(.)]

[

z

z

2

d

P

Pengaruh Ukuran Sampel Berhingga

Dalan kenyataan yang sebenarnya, sinyal tidak pernah diukur dari t = −∞ sampai t = ∞. Apa pengaruhnya pada transformasi Fourier jika hanya mengambil suatu bagian waktu tertentu saja dari sebuah sinyal?

Dengan menggeser titik asal pada koordinat waktu, dapat diasumsikan bahwa sinyal diukur dari t = −τ / 2 hingga t = τ / 2. Dengan demikian integral Fourier-nya menjadi,

∫

− −

=

2 2

)

(

)

(

τ τ ω

ω

x

t

e

dt

X

j t ₍₉₅₎

Atau dapat dinyatakan dengan cara berikut.

∫

∞ ∞ − −

=

w

t

x

t

e

dt

X

(

ω

)

(

)

(

)

jωt ₍₉₆₎

Dengan w(t) adalah fungsi jendela (window function), yang dalam hal ini berbentuk kotak (rectangular). Perhatikan Gambar 34.

Persamaan (96) merupakan transformasi sebuah hasil kali, sehingga menurut teori konvolusi maka

Ω

Ω

−

Ω

=

∞

∫

∞ −

d

X

W

t

x

t

w

F

(

)

(

)

2

1

)]

(

)

(

[

ω

π

(97)

Pada pembahasan terdahulu telah ditemukan transformasi Fourier untuk fungsi yang berbentuk seperti pada Gambar 34 yaitu,

2 2 sin ) ( Ω ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Ω = Ω τ W (98) Sehingga

( )

Ω

Ω

−

=

∫

∞ ∞ − Ω Ω

d

X

t

x

t

w

F

sin

(

)

2

1

)]

(

)

(

[

2 2

ω

π

τ (99)

Ini merupakan rumus umum, untuk melihat bagaimana pengaruhnya maka misalkan x(t) adalah gelombang sinus

x(t) = sin (αt) dengan spektrum

[

( ) ( )

]

) (ω =π δ ω −α −δ ω+α j X

atau secara grafis digambarkan pada Gambar 35. Persamaan (99) memberikan

( )

_[

_]

Ω

+

Ω

−

−

−

Ω

−

=

∫

∞ ∞ − Ω Ω

d

j

t

x

t

w

F

sin

(

)

(

)

2

1

)]

(

)

(

[

2 2

π

δ

ω

α

δ

ω

α

π

τ (100)

( )

_[

_]

( )

2 ) ( 2 ) ( 2 2

sin

2

1

)

(

sin

2

1

α ω τ α ω τ

α

ω

δ

π

− − ∞ ∞ − Ω Ω

=

Ω

−

Ω

−

∫

d

_j

j

j

Integral suku yang kedua menghasilkan

( )

_[

_]

( )

2 ) ( 2 ) ( 2 2

sin

2

1

)

(

sin

2

1

α ω τ α ω τ

α

ω

δ

π

+ + ∞ ∞ − Ω Ω

=

Ω

+

Ω

−

∫

d

_j

j

j

Sehingga hasil akhirnya dapat dinyatakan

( )

( )

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

−

=

₊ + − − 2 ) ( 2 ) ( 2 ) ( 2 ) (

sin

sin

2

1

)]

sin(

)

(

[

_{ω α} τ α ω α ω τ α ω

α

j

t

t

w

F

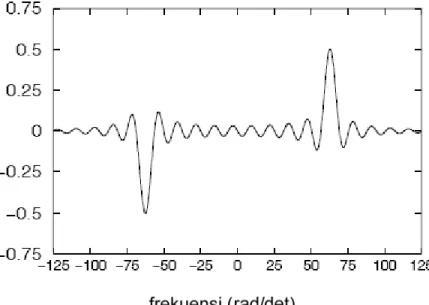
₍₁₀₁₎

Secara grafis persamaan (101) diperlihatkan pada Gambar 36.

ma

gni

tu

d

e

Gambar 36. Spektrum gelombang sinus dikonvolusikan dengan jendela kotak

Puncak-puncak pada spektrum mempunyai lebar 4π / τ , dan akan semakin lebar saat τ semakin kecil. Sehingga pengaruh jendela kotak terletak pada lebar puncak-puncak pada spektrum yang dihasilkan. Saat τ Æ ∞ maka akan diperoleh karakterisasi frekuensi yang tajam.

Diferensiasi dan Integrasi

Misalkan transformasi Fourier sebuah turunan

dt dx sebagai berikut,

∫

∞ ∞ − − •

=

e

dt

dt

dx

t

x

F

[

(

)]

jωt ₍₁₀₂₎

Untuk menyelesaikan persamaan (102) dibutuhkan rumus integrasi bagian per bagian yaitu:

{

_∫

} {

_{∫ ∫}

}

∫

=

−

dt

dt

dv

dt

t

u

dt

t

u

t

v

dt

t

v

t

u

(

)

(

)

(

)

(

)

(

)

Dengan menggunakan integral bagian per bagian ini pada persamaan (102) dan memisalkan

dt dx t

[

]

[

(

)

]

(

)

(

)

)

)(

(

)

(

)]

(

[

ω

ω

ω

ω ω ω ω

X

j

t

x

e

dt

e

j

t

x

t

x

e

dt

e

dt

dx

t

x

F

t j t j t j t j

+

=

−

−

=

=

∞ ∞ − − ∞ ∞ − − ∞ ∞ − − ∞ ∞ − − •

∫

∫

(103)

Catatan : Sebuah sinyal x(t) akan mempunyai transformasi Fourier jika sinyal tersebut mempunyai daya yang besarnya berhingga, yaitu

∫

∞ ∞ − ∞ < = C dt t x( )2 (104)

Jika x(t) adalah fungsi sinus maka sinyal sinus merupakan sinyal yang dayanya tak berhingga, namun di pembahasan yang lalu diketahui bahwa transformasi Fourier-nya adalah fungsi delta (yang merupakan fungsi yang sebenarnya bukan fungsi). Dengan demikian maka suku pertama pada persamaan (103) akan menjadi nol sehingga,

)

(

)

(

)]

(

[

e

ω

dt

j

ω

X

ω

dt

dx

t

x

F

=

∫

j t

=

∞ ∞ − − • (105)

Dari persamaan (105) diketahui bahwa diferensiasi atau penurunan pada domain waktu ekivalen atau sama dengan perkalian dengan faktor jω dalam domain frekuensi. Dalam hal ini juga berlaku bahwa,

) ( ) ( ] ( [ ( ) jω X ω dt x d F t x F _n n n n = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (106) Misalkan,

∫

∞ − = t x d t z( ) (τ) τ

sedemikian sehingga z(t)=x(t), maka ini berarti bahwa dari persamaan (105),

⎥

⎦

⎤

⎢

⎣

⎡

=

=

=

∫

∞ − • t

d

x

F

j

t

z

F

j

X

z

F

(

)

(

ω

)

(

ω

)

[

(

)]

(

ω

)

(

τ

)

τ

Atau

ω

ω

τ

τ

j

X

d

x

F

t

)

(

)

(

_⎥

=

⎦

⎤

⎢

⎣

⎡

∫

∞ − (107)

Dengan demikian dapat disimpulkan bahwa integrasi dalam domain waktu ekivalen dengan pembagian oleh jω dalam domain frekuensi.

Tanggapan Frekuensi dan Tanggapan Impuls

Tinjau sistem berikut,

) (t x y k y c y m + + = • • • (108)

Persamaan di atas dicirikan dalam domain waktu oleh fungsi diferensial orde dua yang bergantung pada x(t) – menjadikannya cukup sulit untuk diselesaikan. Bagaimana jika diselesaikan dalam domain frekuensi?

Dengan mengambil transformasi Fourier pada kedua sisi pada persamaan (108) maka diperoleh,

[

x(t) F y k y c y m F = ⎥⎦ ⎤ ⎢⎣ ⎡ ••₊ • ₊

]

(109)

Transformasi Fourier merupakan operator linier yaitu memiliki sifat yang dinyatakan pada persamaan berikut.

) ( ) ( )] ( [ )] ( [ )] ( ) ( [ 2 1 2 1 2 1 ω ω bX aX t x bF t x aF t bx t ax F + = + = + (110)

Aplikasi persamaan (110) pada persamaan (109) menghasilkan

[ ] [ ]

y F x(t) F k y F c y mF + = ⎥⎦ ⎤ ⎢⎣ ⎡ + ⎥⎦ ⎤ ⎢⎣ ⎡•• • (111)

Dan dengan menggunakan persamaan (106) diperoleh m (jω)2 Y(ω) + c (jω) Y(ω) + k Y(ω) = X(ω) atau (−m ω2 + j c ω + k) Y(ω) = X(ω) (112) Jika didefinisikan k jc m H + + − = ω ω ω) ₂ 1 ( (113) maka diperoleh Y(ω) = H(ω) X(ω) (114)

Fungsi H(ω) sering disebut dengan istilah tanggapan frekuensi atau frequency

response.

Misalkan dicari inverse transformasi Fourier dari persamaan (114), maka diperoleh (115)

∫

∞ ∞ − − = h x t dt t y( ) (τ) ( τ)

dalam hal ini

[

( )

]

)

(t F 1 H ω

h = − (116)

Apakah h(t) mempunyai arti yang penting?

Misalkan x(t) = δ(t) maka dari persamaan (115), ) ( ) ( ) ( ) (t h t dt h t y =

∫

− = ∞ ∞ − τ δ τ

Maka dengan demikian h(t) adalah penyelesaian dari

) (t h k h c h m + + =δ • • • (117)

Fungsi h(t) sering disebut dengan istilah tanggapan impuls atau impulse

Misalkan bahwa x(t) = ejωt, maka substitusi pada persamaan (115) menghasilkan (118) t j j t j t j

e

H

dt

e

h

e

dt

e

h

dt

t

x

h

t

y

ω ωτ ω τ ω

ω

τ

τ

τ

τ

)

(

)

(

)

(

)

(

)

(

)

(

) (

=

=

=

−

=

∫

∫

∫

∞ ∞ − ∞ ∞ − − ∞ ∞ −

Dengan demikian jika x(t) merupakan suatu fungsi harmonik ejωt, maka keluarannya adalah ejωt dikalikan dengan tanggapan frekuensinya.