BAB 2
LANDASAN TEORI
2.1. Kriftografi
2.1.1. Definisi Kriptografi
Kriptografi (Crypthography) berasal dari bahasa Yunani yaitu dari dua suku kata Crypto dan
Graphia. Crypto artinya menyembunyikan, sedangkan graphia artinya ilmu. Kriptografi, secara umum adalah ilmu dan seni untuk menjaga kerahasiaan berita yang mempelajari teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan data, keabsahan data, integritas data, serta autentikasi data, yang dilakukan oleh seorang Kriptographer [Ariyus, Dony. 2008].
Dalam kriptografi, setiap orang dimungkinkan untuk bebas memilih metode untuk merahasiakan pesan. Metode tersebut berbeda-beda untuk setiap pelaku kriptografi sehingga penulisan pesan rahasia mempunyai estetika tersendiri. Estetika penulisan pesan rahasia ini menjadikan kriptografi sebagai sebuah seni. Pada perkembangan selanjutnya, kriptografi dikenal sebagai disiplin ilmu yang menggunakan teknik matematika untuk keamanan informasi, seperti privasi dan autentikasi.
Ada empat tujuan mendasar dari ilmu kriptografi ini yang juga merupakan aspek keamanan informasi, yaitu [Schneier, Bruce. 1996]:
1. Kerahasiaan (Confidentiality)
Kerahasiaan adalah layanan yang digunakan untuk menjaga isi dari informasi dari siapapun kecuali yang memiliki otoritas atau kunci rahasia untuk membuka/mengupas informasi yang telah disandi.
2. Integritas Data (Data Integrity)
3. Otentikasi (Autentication)
Otentikasi adalah berhubungan dengan identifikasi/pengenalan, baik secara kesatuan sistem maupun informasi itu sendiri, dua pihak yang saling berkomunikasi harus saling memperkenalkan diri. Informasi yang dikirimkan melalui kanal harus diautentikasi keaslian, isi datanya, waktu pengiriman, dan lain-lain.
4. Ketiadaan Penyangkalan (Non-repudiation).
Ketiadaan penyangkalan adalah usaha untuk mencegah terjadinya penyangkalan terhadap pengiriman terciptanya suatu informasi oleh yang mengirimkan/membuat.
2.2. Algoritma El Gamal
El Gamal merupakan suatu sistem kriptografi asimetris, yang pertama kali ditemukan oleh Taher El Gamal pada tahun 1984. Algoritma ini pada mulanya digunakan untuk digital signature, namun kemudian dimodifikasi sehingga bisa digunakan untuk enkripsi dan dekripsi [Mollin, R. A. 2007].
2.2.1. Algoritma Membangkitan Pasangan Kunci
1. Pilih bilangan prima p ( p harus dites melalui primality test untuk membukitkan merupakan bilangan prima atau tidak, p dapat di-share di antara anggota kelompok).
2. Pilih dua buah bilangan acak, g dan x, dengan syarat g<p dan 1 x p– 2.
3. Hitung y = gx mod p [Schneier, Bruce. 1996]. Hasil dari algoritma ini:
a. Kunci public: tripel (y, g, p) b. Kunci privat: pasangan (x, p)
2.2.1.1. Algoritma Miller - Rabin
Algoritma pengujian bilangan prima ini juga disebut algoritma Selfridge-Miller-Rabin atau
probabilistik Miller-Rabin yang memiliki komputasi yang ringan dan memberikan probabilitas yang tinggi. Berikut ini adalah algoritma Miller-Rabin (Cormen, et al. 2009).
Langkah 1: Pilih bilangan yang ingin diuji keprimaannya n, dimana n≥3 dan n
merupakan bilangan ganjil (nmod 2 ≠ 0).
Langkah 2: Hitung n-1 = u2t, dimana u adalah bilangan ganjil dan t≥1. Representasi bilangan biner dari n-1 adalah representasi biner dari bilangan ganjil u yang diikuti oleh bit 0 sebanyak t.
Langkah 3: Uji n yang akan diperiksa keprimaannya dengan bilangan integer
sembarang a, dimana 2≤a≤n-1 sebanyak s kali. Jika pengujian sudah
sampai s kali, maka lanjutkan ke Langkah 6.
Langkah 4: Hitung ≡au (mod n).
Langkah 5: Hitung sebanyak t kali dimana 1≤i≤t. Jika , 1 (mod n) dan ≢n-1 maka hentikan
algoritma dengan menyatakan n adalah bilangan komposit. Selain dari itu, maka lanjut ke Langkah 3.
Langkah 6: Jika , maka hentikan algoritma dengan menyatakan n
adalah bilangan komposit. Jika tidak, maka hentikan algoritma dan nyatakan n adalah kemungkinan bilangan prima.
Contoh :
Langkah 1: misalnya bilangan prima n = 11 Langkah 2: n-1 = u2t
11 – 1 = u2¹
10 = u2 2u = 10
u = 5
Langkah 3: misalkan a = 4 Langkah 4: ≡au (mod n)
mod n = au
mod n = 45
mod n = 1024
= 1024 mod 11
= 1
2.2.2. Enkripsi El Gamal
Berikut adalah langkah mengenkripsi sebuah pesan pada algoritma El Gamal [Munir, Rinaldi. 2006],
1. Susun plainteks menjadi blok-blok m1, m2, …, (nilai setiap blok di dalam selang [0, p– 1].
2. Pilih bilangan acak k, yang dalam hal ini 1 k p– 2.
3. Setiap blok m dienkripsi dengan rumus [Munir, Rinaldi. 2006]:
a = gk mod p
b = ykm mod p
Pasangan a dan b adalah cipherteks untuk blok pesan m. Jadi, ukuran cipherteks dua kali ukuran plainteksnya [Munir, Rinaldi. 2006].
2.2.3. Dekripsi El Gamal
Berikut ini adalah langkah-langkah dalam mendekripsi sebuah pesan plaintext dengan menggunakan algoritma El Gamal [Munir, Rinaldi. 2006],
1. Gunakan kunci privat x untuk menghitung (ax)– 1 = ap – 1 – x mod p
2. Hitung plainteks m dengan persamaan [Munir, Rinaldi. 2006]:
m = b/ax mod p = b (ax)– 1 mod p
2.2.4. Contoh Cara Kerja El Gamal
Berikut ini ada contoh cara kerja El Gamal dalam mengenkripsi dan mendekripsi sebuah pesan, sebagai berikut:
p = bilangan prima k = bilangan acak m = plaintext a dan b = chiperteks
x = bilangan acak Misal p = 2357, g = 2 dan x = 1751.
Hitung: y = gx mod p = 21751 mod 2357 = 1185 Hasil: Kunci public: (y = 1185, g = 2, p = 2357)
Kunci privat: (x = 1751, p = 2357).
Bob menghitung
a = gk mod p = 21520 mod 2357 = 1430
b = ykm mod p= 11851520 (2035) mod 2357 = 697
Jadi, cipherteks yang dihasilkan adalah (1430, 697). Bob mengirim cipherteks ini ke Alice, oleh alice 1/ax = (ax)– 1 = a p – 1 – x mod p = 1430605 mod 2357 = 872
m = b/ax % p = 697 (872) mod 2357 = 2035
2.3. Algoritma Huffman
Algoritma Huffman adalah salah satu algoritma kompresi. Algoritma huffman merupakan
algoritma yang paling terkenal untuk mengompres teks. Terdapat tiga fase dalam menggunakan algoritma Huffman untuk mengompres sebuah teks, pertama adalah fase pembentukan pohon Huffman, kedua fase encoding dan ketiga fase decoding. Pengkodean Huffman adalah teknik untuk mengompresi data. Algoritma greedy Huffman melihat terjadinya masing-masing karakter dan sebagai string biner secara optimal Huffman coding
adalah bentuk coding statistik yang mencoba untuk mengurangi jumlah bit yang diperlukan untuk merepresentasikan string dari simbol [Mathur, M. K., Loonker, S. & Saxena, D. 2012].
Prinsip yang digunakan oleh algoritma Huffman adalah karakter yang sering muncul di-encoding dengan rangkaian bit yang pendek dan karakter yang jarang muncul di-encoding
dengan rangkaian bit yang lebih panjang. Teknik kompresi algoritma Huffman mampu memberikan penghematan pemakaian memori sampai 30%. Algoritma Huffman mempunyai kompleksitas O (n log n) untuk himpunan dengan n karakter. Algoritma Huffman, yang dibuat oleh seorang mahasiswa MIT bernama David Huffman pada tahun 1952, merupakan salah satu metode paling lama dan paling terkenal dalam kompresi teks. Algoritma Huffman menggunakan prinsip pengkodean yang mirip dengan kode Morse, yaitu tiap karakter (simbol) dikodekan hanya dengan rangkaian beberapa bit, dimana karakter yang sering muncul dikodekan dengan rangkaian bit yang pendek dan karakter yang jarang muncul dikodekan dengan rangkaian bit yang lebih panjang [Mathur, M. K., Loonker, S. & Saxena,
D. 2012].
kodenya, dan fase kedua untuk mengubah pesan menjadi kumpulan kode yang akan ditransmisikan. Sedangkan berdasarkan teknik pengkodean simbol yang digunakan, algoritma Huffman menggunakan metode symbolwise. Metode symbolwise adalah metode yang menghitung peluang kemunculan dari setiap simbol dalam satu waktu, dimana simbol yang lebih sering muncul diberi kode lebih pendek dibandingkan simbol yang jarang muncul.
Metode Huffman Dinamis merupakan kelanjutan dari metode Huffman statis dengan menambah atau mengurangi suatu proses tertentu pada metode Huffman statis. Ide dasar dari metode ini adalah meringkas tahapan metode Huffman tanpa perlu menghitung jumlah karakter keseluruhan dalam membangun pohon biner.
Metode Huffman dinamis adalah suatu metode dengan kemungkinan kemunculan dari setiap simbol tidak dapat ditentukan dengan pasti selama pengkodean. Hal ini disebabkan oleh perubahan pengkodean secara dinamis berdasarkan frekuensi dari simbol yang telah diolah sebelumnya. Metode ini dikembangkan oleh trio Faller, Gallager dan Knuth, kemudian dikembangkan lebih lanjut oleh Vitter [Merdiyan, Meckah dan Wawan Indarto, 2007].
2.3.1. Kompresi Data
Kompresi data dalam bidang ilmu komputer, ilmu pengetahuan dan seni adalah sebuah penyajian informasi kedalam bentuk yang lebih sederhana [Arizka, R. U. 2011]. Kompresi data dapat diartikan juga sebagai proses yang dapat mengubah sebuah aliran data masukan (sumber atau data asli) kedalam aliran data yang lain (keluaran atau data yang dikompresi) yang memiliki ukuran yang lebih kecil.
Metode kompresi data dapat dikelompokkan dalam dua kelompok besar yaitu metode lossless
dan metode lossy yaitu: 1. Metode lossless
Pada teknik ini tidak ada kehilangan informasi. Jika data dikompresi secara lossless, data asli dapat direkonstruksi kembali sama persis dari data yang telah dikompresikan, dengan kata lain data asli tetap sama sebelum dan sesudah kompresi. Secara umum teknik
lossless digunakan untuk penerapan yang tidak bisa mentoleransi setiap perbedaan antara data asli dan data yang telah direkonstruksi. Data berbentuk tulisan misalnya file teks, harus dikompres menggunakan teknik lossless, karena kehilangan sebuah karakter saja dapat mengakibatkan kesalahpahaman. Lossless compression disebut juga dengan
-metode ini adalah Shannon-Fano Coding, Huffman Coding, Arithmetic Coding, Run Length Encoding dan lain sebagainya [Arizka, R. U. 2011].
2. Metode lossy
Pada teknik ini akan terjadi kehilangan sebagian informasi. Data yang telah dimanfaatkan dengan teknik ini secara umum tidak bisa direkonstruksi sama persis dari data aslinya. Di dalam banyak penerapan, rekonstruksi yang tepat bukan suatu masalah.
Sebagai contoh, ketika sebuah sample suara ditransmisikan, nilai eksak dari setiap
sample suara belum tentu diperlukan, tergantung pada yang memerlukan kualitas suara yang direkonstruksi, sehingga banyaknya jumlah informasi yang hilang di sekitar nilai dari setiap
sample dapat ditoleransi. Biasanya teknik ini membuang bagian-bagian data yang sebenarnya tidak begitu berguna, tidak begitu dirasakan, tidak begitu dilihat sehingga manusia masih beranggapan bahwa data tersebut masih bisa digunakan walaupun sudah dikompresi, misalnya pada gambar dan MP3, contoh metode ini adalah Transform Coding, Wavelet, dan lain-lain. Lossy compression disebut juga irreversible compression karena data asli mustahil untuk dikembalikan seperti semula. Kelebihan teknik ini adalah rasio kompresi yang tinggi dibanding metode lossless.
Keuntungan dari metode lossy atas lossless adalah dalam beberapa kasus metode lossy
menghasilkan file kompresi yang lebih kecil dibandingkan dengan metode lossless. Metode
lossy sering digunakan untuk mengkompresi suara, gambar dan video karena data tersebut dimaksudkan kepada human interpretation dimana pikiran dapat dengan mudah “mengisi
bagian-bagian yang kosong” atau melihat kesalahan yang sangat kecil atau inkonsistensi. Sedangkan lossless digunakan untuk mengkompresi data untuk diterima ditujuan dalam kondisi asli seperti dokumen teks. Lossy akan mengalami generation loss pada data sedangkan pada lossless tidak terjadi karena data yang hasil dekompresi sama dengan data asli.
2.3.2. Dekompresi
tersebut, jadi isi dari file sudah tertulis oleh catatan header sehingga hanya tinggal menuliskan kembali pada saat proses dekompresi.
Secara umum proses kompresi dan dekompresi lossless dapat dilihat pada gambar 2.1.
Kompresi Dekompresi
Gambar 2.1 Alur Teknik lossless Kompresi-Dekompresi Data
2.3.3. Pembentukan Pohon Huffman
Kode Huffman pada dasarnya merupakan kode prefiks (prefix code). Kode prefiks adalah himpunan yang berisi sekumpulan kode biner, dimana pada kode prefik ini tidak ada kode biner yang menjadi awal bagi kode biner yang lain. Kode prefiks biasanya direpresentasikan sebagai pohon biner yang diberikan nilai atau label. Untuk cabang kiri pada pohon biner diberi label 0, sedangkan pada cabang kanan pada pohon biner diberi label 1. Rangkaian bit yang terbentuk pada setiap lintasan dari akar ke daun merupakan kode prefiks untuk karakter yang berpadanan. Pohon biner ini biasa disebut pohon Huffman.
Langkah-langkah pembentukan pohon Huffman adalah sebagai berikut:
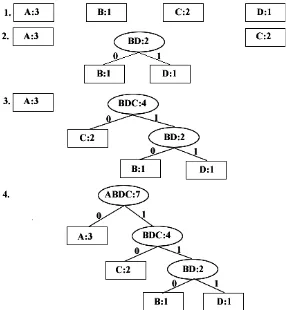
1. Baca semua karakter di dalam teks untuk menghitung frekuensi kemunculan setiap karakter. Setiap karakter penyusun teks dinyatakan sebagai pohon bersimpul tunggal. Setiap simpul di-assign dengan frekuensi kemunculan karakter tersebut.
2. Terapkan strategi algoritma greedy sebagai berikut: gabungkan dua buah pohon yang mempunyai frekuensi terkecil pada sebuah akar. Setelah digabungkan akar tersebut akan mempunyai frekuensi yang merupakan jumlah dari frekuensi dua buah pohon-pohon
penyusunnya.
3. Ulangi langkah 2 sampai hanya tersisa satu buah pohon Huffman, agar pemilihan dua pohon yang akan digabungkan berlangsung cepat, maka semua yang ada selalu terurut menaik berdasarkan frekuensi.
Sebagai contoh, dalam kode ASCII string 7 huruf “ABACCDA” membutuhkan representasi
7 × 8 bit = 56 bit (7 byte), dengan rincian sebagai berikut: Data Asli
(.txt, .doc)
A = 01000001 B = 01000010 A = 01000001 C = 01000011 C = 01000011 D = 01000100 A = 01000001
Pada string di atas, frekuensi kemunculan A = 3, B = 1, C = 2, dan D = 1,
Gambar 2.2 Pohon Huffman untuk Karakter “ABACCDA”
2.3.4. Proses Encoding
Encoding adalah cara menyusun string biner dari teks yang ada. Proses encoding untuk satu karakter dimulai dengan membuat pohon Huffman terlebih dahulu. Setelah itu, kode untuk satu karakter dibuat dengan menyusun nama string biner yang dibaca dari akar sampai ke daun pohon Huffman.
2. Mulai dari akar, baca setiap bit yang ada pada cabang yang bersesuaian sampai ketemu daun dimana karakter itu berada
3. Ulangi langkah 2 sampai seluruh karakter di encoding
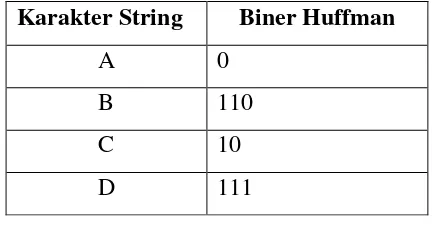
Sebagai contoh kita dapat melihat tabel dibawah ini, yang merupakan hasil encoding
untuk pohon Huffman pada tabel 2.1.
Tabel 2.1 Kode Huffman untuk Karakter “ABCD”
Karakter String Biner Huffman
A 0
B 110
C 10
D 111
2.3.5. Proses Decoding
Decoding merupakan kebalikan dari encoding. Decoding berarti menyusun kembali data dari
string biner menjadi sebuah karakter kembali. Decoding dapat dilakukan dengan dua cara, yang pertama dengan menggunakan pohon Huffman dan yang kedua dengan menggunakan tabel kode Huffman.
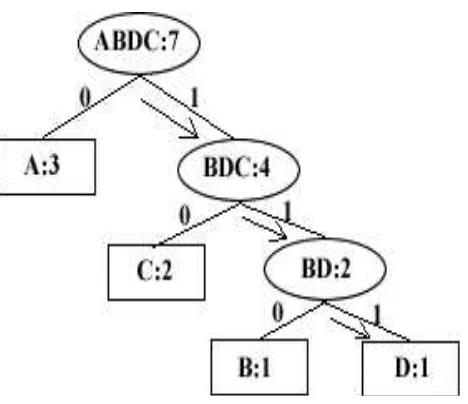
Langkah-langkah men -decoding suatu string biner dengan menggunakan pohon Huffman adalah sebagai berikut:
1. Baca sebuah bit dari string biner. 2. Mulai dari akar.
3. Untuk setiap bit pada langkah 1, lakukan traversal pada cabang yang bersesuaian. 4. Ulangi langkah 1, 2 dan 3 sampai bertemu daun. Kodekan rangkaian bit yang telah
dibaca dengan karakter di daun.
Gambar 2.3 Proses Decoding dengan Menggunakan Pohon Huffman
Setelah kita telusuri dari akar, maka kita akan menemukan bahwa string yang mempunyai kode Huffman “111” adalah karakter D.
Cara yang kedua adalah dengan menggunakan tabel kode Huffman. Sebagai contoh kita akan menggunakan kode Huffman pada Tabel 1 untuk merepresentasikan string
“ABACCDA”. Dengan menggunakan Tabel 1 string tersebut akan direpresentasikan menjadi
rangkaian bit: 0 110 0 10 10 1110. Jadi, jumlah bit yang dibutuhkan hanya 13 bit. Dari Tabel 1 tampak bahwa kode untuk sebuah simbol/karakter tidak boleh menjadi awalan dari kode simbol yang lain guna menghindari keraguan (ambiguitas) dalam proses dekompresi atau
decoding, karena tiap kode Huffman yang dihasilkan unik, maka proses decoding dapat dilakukan dengan mudah. Contoh: saat membaca kode bit pertama dalam rangkaian bit
“011001010110”, yaitu bit “0”, dapat langsung disimpulkan bahwa kode bit “0” merupakan pemetaan dari simbol “A”. Kemudian baca kode bit selanjutnya, yaitu bit “1”. Tidak ada
kode Huffman “1”, lalu baca kode bit selanjutnya, sehingga menjadi “11”. Tidak ada juga
kode Huffman “11”, lalu baca lagi kode bit berikutnya, sehingga menjadi “110”. Rangkaian
kode bit “110” adalah pemetaan dari simbol “B”.
2.3.6. Kompleksitas Algoritma Huffman