ANALISIS DAN KONTROL OPTIMAL
PADA MODEL PENYEBARAN VIRUS HIV DALAM TUBUH MANUSIA
SKRIPSI
WHENI SUKOKARLINDA
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
ANALISIS DAN KONTROL OPTIMAL
PADA MODEL PENYEBARAN VIRUS HIV DALAM TUBUH MANUSIA
SKRIPSI
WHENI SUKOKARLINDA
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
LEMBAR PENGESAHAN NASKAH SKRIPSI
Judul : Analisis dan Kontrol Optimal pada Model Penyebaran Virus HIV dalam Tubuh Manusia
Penyusun : Wheni Sukokarlinda NIM : 080810556
Pembimbing I : Dr. Fatmawati, M.Si Pembimbing II : Yayuk Wahyuni, Dra., M.Si Tanggal Seminar : 13 Agustus 2012
Disetujui Oleh :
Pembimbing I
Dr. Fatmawati, M.Si NIP. 19730704 199802 2 001
Pembimbing II
Yayuk Wahyuni, Dra., M.Si NIP. 19641224 199102 2 001
Mengetahui :
Ketua Program Studi S-1 Matematika, Fakultas Sains dan Teknologi,
Universitas Airlangga
PEDOMAN PENGGUNAAN SKRIPSI
KATA PENGANTAR
Alhamdulillahirobbil’alamiin, segala puji bagi Allah Subhanahu wa Ta’ala. Berkat rahmat, taufiq dan hidayah-Nya, penulis dapat menyelesaikan skripsi dengan judul ”Analisis dan Kontrol Optimal Pada Model Penyebaran
Virus HIV Dalam Tubuh Manusia”.
Dalam menyusun skripsi ini, penulis mengucapkan terima kasih yang
sebesar-besarnya kepada:
1. Dr. Fatmawati, M.Si selaku dosen pembimbing I yang dengan sabar telah
memberikan banyak pengarahan, masukan, perhatian, pengetahuan.
2. Yayuk Wahyuni, Dra, M.Si selaku dosen pembimbing II yang telah
memberikan banyak arahan, masukan, waktu, tenaga dan pikiran.
3. Auly Damayanti S.Si., M.Si selaku dosen wali selama menjadi mahasiswa
matematika di Universitas Airlangga yang telah banyak memberikan
pengarahan demi kesuksesan menjadi mahasiswa matematika.
4. Dr. Miswanto, M.Si selaku ketua departemen matematika yang telah
membantu melancarkan proses belajar mengajar selama di perkuliahan.
5. Kedua orang tua, Bapak Sukotjo dan Ibu Susilowati yang telah memberikan
do’a, semangat, kasih sayang, materi yang begitu besar serta pengorbanan
6. Kakak dan adik, Wempy Gatot Sukowaloyo dan Whendy Suko Trirega yang
telah memberikan masukan, semangat, do’a, dan juga sebagai sumber inspirasi
karena prestasi-prestasi yang telah diraihnya selama menempuh pendidikan.
7. Marisa, Ekaswari Pusparini dan Okta Permatasari sabagai teman terbaik
selama menjadi mahasiswa yang telah memberikan arahan, masukan,
motivasi, serta tempat keluh kesah panulis.
8. Yanuar Dwi Sasongko sebagai teman spesial yang telah memberikan
masukan, arahan, semangat, materi, serta pengorbanannya selama
penyelesaian skripsi.
9. Muhammad Jainal Abidin sabagai teman berharga yang telah memberikan
segala kebaikannya demi mensukseskan penulis.
10.Miming, Adise, Rizki Eka, Desty dan I Putu, serta seluruh teman
seperjuangan matematika angkatan 2008 atas kekeluargaan, dan dukungannya.
Serta pihak-pihak lain yang tidak dapat disebutkan satu persatu, terima kasih atas
segala bantuan dalam penyelesaian skripsi ini.
Penulis menyadari bahwa skripsi ini masih ada kekurangan-kekurangan.
Oleh karena itu, kritik dan saran yang membangun terus penulis harapkan agar
skripsi ini dapat lebih baik lagi. Selain itu, semoga skripsi ini dapat bermanfaat
dan menambah pengetahuan pembaca dan menjadi salah satu hal yang bisa
mendongkrak IPTEK di Indonesia.
Surabaya, Agustus 2012 Penulis
Wheni Sukokarlinda, 2012, Analisis dan Kontrol Optimal Pada Model Penyebaran Virus HIV Dalam Tubuh Manusia. Skripsi ini di bawah bimbingan
Dr. Fatmawati, M.Si dan Yayuk Wahyuni, Dra., M.Si, Departemen Matematika, Fakultas Sains dan Teknologi, Universitas Airlangga, Surabaya.
ABSTRAK
Virus HIV merupakan salah satu virus yang dapat menyebabkan penyakit
Acquired Immune Deficiency Syndrome (AIDS) dengan cara menyerang sistem
kekebalan tubuh. Orang yang terkena virus ini akan menjadi rentan terhadap infeksi oportunistik. Penyakit akibat HIV sangat berbahaya dan harus dicegah penyebarannya. Dari permasalahan tersebut, pada skripsi ini akan dibentuk model Penyebaran virus HIV dalam tubuh manusia serta menganalisis kestabilan model dan menentukan bentuk kontrol optimal. Dalam menentukan kestabilan sistem digunakan kriteria kestabilan Routh-Hurwitz sedangkan untuk menentukan bentuk kontrol
optimal digunakan Prinsip Maksimum Pontryagin. Berdasarkan hasil analisis model
tanpa kontrol diperoleh dua titik setimbang yaitu titik setimbang bebas penyakit = ( dan titik setimbang endemik = ( ) Titik setimbang akan stabil asimtotis jika nilai ambang batas < dan akan stabil asimtotis jika > sedangkan bentuk kontrol optimalnya adalah ( ( ( ) ) Hasil simulasi menunjukkan keefektifan
pengendalian dengan pengontrol (obat ARV) yang dapat mengurangi populasi sel CD4 yang terinfeksi virus HIV sehingga penyebaran virus HIV dapat ditekan dan dapat memaksimumkan sel CD4 yang sehat dengan biaya pemberian obat ARV yang minimum.
Kata Kunci: HIV, Kriteria Kestabilan Routh-Hurwitz, Kontrol Optimal, Nilai
Wheni Sukokarlinda, 2012, Analysis and Optimal Control of Model Spread of HIV Virus in Human Body. This final project is under advised by Dr. Fatmawati,
M.Si and Yayuk Wahyuni, Dra., M.Si, Matematics Departement, Science and Technology Faculty, Airlangga University, Surabaya.
ABSTRACT
HIV is one of the viruses which can cause a disease called Acquired Immune Deficiency Syndrome (AIDS) by attacking the immune system. People who are exposed to this virus will become susceptible to opportunistic infections. Diseases caused by HIV is very dangerous and should be prevented from spreading. Of These problems, in this thesis will be established models HV virus spread in the human body and also analyze the stability of the model and determine the optimal control shape.In determining the stability of the system we used Routh-Hurwitz stability criteria, and to determine the optimal control form we used Pontryagin Maximum Principle. Based on the analytical model without control, the results obtained two equilibrium points, they are the disease-free equilibrium point = ( and the endemic equilibrium point = ( ) The equilibrium point will be asymptotically stable if the threshold value < and will be asymptotically stable if > , while the optimal control form is ( ( ( ) ) The simulation result showed the effectiveness of
control by a controller (ARV drugs) which can reduce the population of CD4 cells infected by HIV virus so that the spreading of HIV virus can be suppressed and be able to maximize the healthy CD4 cells with the minimum cost of ARV drugs.
Keywords: HIV, Routh-Hurwitz Stability Criterion, Optimal Control, Threshold
Halaman
HALAMAN JUDUL ... i
LEMBAR PERNYATAAN ... ii
LEMBAR PENGESAHAN ... iii
LEMBAR PEDOMAN PENGGUNAAN SKRIPSI ... iv
KATA PENGANTAR ... v
ABSTRAK ... vii
ABSTRACT ... viii
DAFTAR ISI ... ix
DAFTAR TABEL ... xi
DAFTAR GAMBAR ... xii
DAFTAR LAMPIRAN ... xiii
BAB I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 3
1.3 Tujuan ... 3
1.4 Manfaat ... 3
1.5 Batasan Masalah ... 4
BAB II TINJAUAN PUSTAKA 2.1 Sel CD4 ... 5
2.2 HIV ... 6
2.5 Kestabilan dari Sistem Linier ... 14
2.6 Masalah Kontrol Optimal ... 17
2.7 Prinsip Maksimum Pontryagin ... 18
BAB III METODE PENELITIAN ... 20
BAB IV PEMBAHASAN 4.1 Model HIV ... 22
4.2 Titik Setimbang Model ... 27
4.3 Analisis Kestabilan Lokal ... 30
4.3.1 Kestabilan Lokal Titik Setimbang Bebas Penyakit ... 30
4.3.2 Kestabilan Lokal di Titik Setimbang Endemi ... 34
4.4 Penyelesaian Kontrol Optimal ... 37
4.5 Simulasi ... 40
BAB V KESIMPULAN DAN SARAN 5.1 Kesimpulan ... 52
5.2 Saran ... 53
DAFTAR PUSTAKA ... 54
DAFTAR TABEL
No Judul Halaman
4.1 Interaksi Model HIV 24
4.2 Parameter model HIV dan Nilainya 42
DAFTAR GAMBAR
No Judul Halaman
2.1 HIV mengikat pada reseptor sel CD4 5
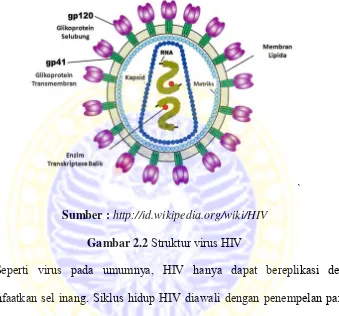
2.2 Struktur virus HIV 7
4.1 Diagram blok model HIV sebelum diberi pengontrol 25
4.2 Populasi sel CD4 yang sehat sebelum diberi pengntrol
(obat ARV)
45
4.3 Populasi sel CD4 yang sehat setelah diberi pengontrol
(obat ARV)
45
4.4 Populasi sel CD4 yang terinfeksi virus HIV sebelum
diberi pengontrol (obat ARV)
46
4.5 Populasi sel CD4 yang terinfeksi virus HIV setelah
diberi pengontrol (obat ARV)
47
4.6 Populasi virus HIV sebelum diberi pengontrol (obat
ARV)
48
4.7 Populasi virus HIV setelah dieri pengontrol (obat
ARV)
49
DAFTAR LAMPIRAN
No. Judul Lampiran
1. Skrip M-File pada MATLAB untuk Model Penyebaran Virus HIV Tanpa
Pengontrol.
2. Skrip M-File pada MATLAB untuk Model Penyebaran Virus HIV degan
Pengontrol.
3. Output pada Command Window MATLAB untuk Model Penyebaran
Virus HIV Tanpa Pengontrol.
4. Output pada Command Window MATLAB untuk Model Penyebaran
BAB I PENDAHULUAN
1.1 Latar Belakang
Acquired Immune Deficiency Syndrome (AIDS) adalah sekumpulan gejala
dan infeksi yang timbul karena rusaknya sistem kekabalan tubuh manusia akibat
infeksi virus Human Immunodeficiency Virus (HIV). Virus HIV sendiri
merupakan virus yang memperlemah kekebalan tubuh manusia dengan cara
menyerang sel CD4. Sel CD4 adalah salah satu jenis dari sel darah putih (limfosit)
yang merupakan bagian penting dari sistem kekebalan tubuh. Orang yang terkena
virus ini akan menjadi rentan terhadap infeksi oportunistik (penyakit yang muncul
karena sistem kekebalan tubuh sudah rusak atau melemah).
Pada Januari 2006, Joint United Nations Programme on HIV and AIDS
(UNAIDS) dan World Health Organization (WHO) memperkirakan bahwa AIDS
telah menyebabkan kematian lebih dari 25 juta orang sejak pertama kali
ditemukan pada tahun 1981. Di Jakarta hingga Juni tahun 2011 penderita HIV
mencapai 1.184 orang (Wardah, 2012). Data tersebut diperoleh dari Sistem
Informasi AIDS Jakarta. Nominal tersebut diperoleh hanya dalam satu daerah,
belum di daerah-daerah lain di Indonesia. Besarnya jumlah kematian disebabkan
karena virus HIV menunjukkan bahwa penyakit tersebut sangat berbahaya dan
harus dicegah penyebarannya.
Dalam perkembangan ilmu pengetahuan bidang matematika, ilmuwan
HIV, salah satunya dengan mengkonstruksikan dinamika penyebaran virus HIV
dalam bentuk model matematika. Model penyebaran virus HIV tersebut dapat
ditinjau dari sisi internal (di dalam tubuh manusia) dan eksternal (di luar tubuh
manusia atau lingkungan sekitar). Pada penelitian ini akan dibahas mengenai
model penyebaran virus HIV dalam tubuh manusia [14], karena penyebaran virus
HIV dari dalam tubuh masih sulit untuk ditangani, karena obat untuk
menyembuhkan penyakit HIV masih belum ditemukan. Di dalam model
penyebaran virus HIV dalam tubuh manusia dibagi menjadi tiga kelompok yaitu
populasi/jumlah sel CD4 yang belum terkena virus HIV, populasi Sel CD4 yang
telah terinfeksi virus HIV, dan populasi virus HIV. Secara garis besar, model
penyebaran virus HIV dalam tubuh menggambarkan alur penyebaran dari sel CD4
yang sehat menjadi terinfeksi dengan faktor–faktor penting yang mempengaruhi.
Untuk menekan penyebaran virus HIV dalam tubuh dapat digunakan suatu
pengontrol berupa obat.
Berdasarkan World Health Organization (WHO), penyebaran virus HIV
dapat ditekan dengan pemberian obat Antiretroviral (ARV). Pemberian obat ARV
masih dipercaya sebagai cara yang efektif dalam menekan penyebaran virus HIV
dalam tubuh, karena obat tersebut dapat menghambat replikasi virus HIV dalam
tubuh manusia. Meskipun penanganan yang telah ada dapat memperlambat laju
perkembangan virus HIV, namun penyakit ini belum benar – benar dapat
disembuhkan.
Berdasarkan permasalahan tersebut, dalam penelitian ini penulis akan
sel CD4 serta virus HIV dengan pemberian obat ARV. Untuk mengoptimalkan
pemberian obat ARV digunakan prinsip Maksimum Pontryagin, sehingga
diharapkan perkembangan virus HIV dapat ditekan dan jumlah sel CD4 yang
sehat dapat meningkat.
1.2 Rumusan Masalah
Rumusan masalah yang akan diteliti dalam skripsi ini adalah:
1. Bagaimana kestabilan dari titik setimbang pada model penyebaran virus HIV
dalam tubuh?
2. Bagaimana bentuk kontrol yang optimal dari model penyebaran virus HIV
dalam tubuh dengan pemberian obat ARV?
1.3 Tujuan
Dalam penulisan skripsi ini, penulis mempunyai tujuan sebagai berikut :
1. Mendapatkan kestabilan dari titik setimbang pada model penyebaran virus
HIV dalam tubuh.
2. Mendapatkan bentuk kontrol yang optimal dari model penyebaran virus HIV
dalam tubuh dengan pemberian obat ARV.
1.4 Manfaat
Manfaat yang akan dicapai dari skripsi ini adalah memberikan pengetahuan
pengendalian optimalnya dengan menggunakan obat, sehingga hasil dari skripsi
ini dapat berguna untuk mengontrol penyebaran virus HIV dalam tubuh.
1.5 Batasan Masalah
Mengacu pada rumusan masalah di atas, maka ruang lingkup penyelesaian
penulisan skripsi ini dibatasi dengan:
1. Model HIV diamati dalam 1 ml darah yang jumlah sel CD4 antara 800-1200
sel.
2. Model HIV dan parameter yang digunakan dalam penelitian ini diambil dari
Shirazian dan Farahi (2010).
BAB II
TINJAUAN PUSTAKA
Dalam skripsi ini, tinjauan pustaka yang digunakan adalah sebagai
berikut:
2.1 Sel CD4
Menurut Upaya Kesehatan dan Lintas Wilayah (UKLW) Balikpapan [5], sel
T dibagi menjadi dua jenis yaitu Sel T-4 (CD4 atau CD4+) dan sel T-8 (CD8). Sel
CD4 adalah salah satu jenis dari sel darah putih (limfosit) yang merupakan bagian
penting dari sistem kekebalan tubuh, sedangkan sel CD8 adalah sel penekan yang
mengakhiri tanggapan kekebalan. Sel CD8 juga disebut sebagai sel pembunuh,
karena sel tersebut membunuh sel kanker atau sel yang terinfeksi virus. Sel CD4
memiliki protein pada permukaannya, protein tersebut bekerja sebagai reseptor
untuk HIV. Virus HIV menempel pada reseptor CD4 itu seperti kunci dan
gembok.
Sumber : http://www.thebody.com
Sel CD4 merupakan sel penting sehubungan dengan Human Immunodeficiency
Virus (HIV), karena saat HIV menulari manusia, sel yang terinfeksi adalah sel
CD4. Kode genetik HIV menjadi bagian dari sel CD4. Setelah lama orang
terinfeksi HIV, jumlah sel CD4 orang tersebut semakin menurun. Ini tanda bahwa
sistem kekebalan tubuh semakin rusak. Semakin rendah jumlah CD4, semakin
mudah untuk sakit. Ada jutaan kelompok sel CD4 dalam tubuh manusia. Setiap
kelompok sel CD4 dirancang khusus untuk melawan kuman tertentu. Saat HIV
mengurangi jumlah sel CD4, beberapa kelompok sel CD4 dapat diberantas total.
Jika hal itu terjadi, maka orang tersebut akan kehilangan kemampuan untuk
melawan kuman yang seharusnya dihadapi oleh kelompok sel CD4.
2.2 HIV
Menurut Jenny (2006), Human Immunodeficiency Virus (HIV) adalah suatu
virus yang dapat menyebabkan penyakit Acquired Immune Deficiency Syndrome
(AIDS). Virus ini menyerang manusia lebih khususnya menyerang sistem
kekebalan (imunitas) tubuh, sehingga tubuh menjadi lemah dalam melawan
infeksi. Dengan kata lain, kehadiran virus HIV dalam tubuh akan menyebabkan
defisiensi (kekurangan) sistem imun.
Menurut Schoub (1999), berdasarkan strukturnya HIV memiliki diameter
100-150 nm dan berbentuk sferis (spherical) hingga oval. Selubung virus HIV
berasal dari membran sel inang yang sebagian besar tersusun dari lipida. Di dalam
selubung tersebut terdapat bagian yang disebut sebagai protein matriks. Selain itu
yaitu genom dan kapsid. Genom adalah materi genetik pada bagian inti virus yang
berupa dua kopi utas tunggal RNA. Sedangkan, kapsid adalah protein yang
membungkus dan melindungi genom.
`
Sumber : http://id.wikipedia.org/wiki/HIV Gambar 2.2 Struktur virus HIV
Seperti virus pada umumnya, HIV hanya dapat bereplikasi dengan
memanfaatkan sel inang. Siklus hidup HIV diawali dengan penempelan partikel
virus dengan reseptor pada permukaan sel inang, di antaranya adalah CD4 dan
CXCR5 yang ada pada sel darah putih. Sel-sel yang menjadi target HIV adalah sel
dendrit, sel CD4, dan makrofaga. Sel-sel tersebut terdapat pada permukaan
lapisan kulit dalam (mukosa) penis, vagina dan oral yang biasa menjadi tempat
awal infeksi HIV. Selain itu, HIV juga dapat langsung masuk ke aliran darah serta
bereplikasi di noda limpa. Setelah menempel, selubung virus akan melebur (fusi)
dengan membran sel sehingga isi partikel virus akan terlepas di dalam sel.
Selanjutnya, enzim transkriptase yang dimiliki HIV akan mengubah genom virus
manusia sehingga dapat menyisip atau terintegrasi dengan DNA manusia. DNA
virus yang menyisip di DNA manusia disebut sebagai provirus dan dapat bertahan
cukup lama di dalam sel. Saat sel teraktivasi, enzim-enzim tertentu yang memiliki
sel inang akan memproses provirus sama dengan DNA manusia, yaitu diubah
menjadi mRNA. Kemudian, mRNA akan dibawa keluar dari inti sel dan menjadi
cetakan untuk membuat protein dan enzim HIV. Sebagian RNA dari provirus
merupakan genom RNA virus. Bagian genom RNA tersebut akan dirakit dengan
protein dan enzim hingga menjadi virus utuh. Pada tahap perakitan inti virus,
enzim protease virus berperan penting untuk memotong protein panjang menjadi
bagian pendek yang menyusun inti virus. Apabila HIV utuh telah matang, maka
virus tersebut dapat keluar dari sel inang dan mendapatkan selubung dari
membran permukaan sel inang, sehingga menjadi virus baru hasil replikasi
terhadap sel inang (sel CD4). Virus yang baru tersebut akan terus bereplikasi
dengan sel CD4 lain yang ada pada tubuh manusia. Karena sel CD4 berada pada
sel darah putih yang mengalir keseluruh tubuh manusia, maka sel CD4 yang
terinfeksi HIV juga akan menyebar keseluruh tubuh manusia sehingga
menimbulkan penyakit salah satunya yaitu AIDS.
HIV dapat ditularkan melalui injeksi langsung ke aliran darah, serta kontak
membran mukosa atau jaringan yang terluka dengan cairan tubuh tertentu yang
berasal dari penderita HIV. Cairan tertentu itu meliputi darah, semen, sekresi,
cairan vagina, dan ASI. Beberapa jalur penularan HIV yang telah diketahui adalah
melalui hubungan seksual, pemberian ASI dari ibu ke anak, penggunaan
Sampai saat ini tidak ada vaksin atau obat yang benar-benar dapat
menyembuhkan penyakit HIV atau AIDS. Satu-satunya cara yang diketahui untuk
penekanan virus HIV adalah pemberian obat antiretroviral (ARV) yang pada
dasarnya hanya untuk menghambat replikasi virus HIV dalam tubuh.
2.3 Matriks
Definisi 2.1 Jika merupakan matriks berukuran , maka vektor tak nol
di dalam dinamakan vektor eigen dari jika adalah kelipatan skalar
dari , yakni:
Skalar dinamakan nilai eigen dari dan dikatakan vektor eigen yang
bersesuaian dengan .
Teorema 2.2 Jika merupakan matriks berukuran maka
pernyataan-pernyataan berikut ekuivalen satu sama lain:
(a) adalah nilai eigen dari .
(b) Sistem persamaan ( ) mempunyai solusi tak trivial.
(c) Ada vektor tak nol didalam sehingga .
(d) adalah solusi dari persamaan karakteristik det( )
(Anton, 1987)
Definisi 2.3 Jika merupakan matriks berukuran , dan adalah skalar
maka eksponensial matriks didefinisikan sebagai:
Lemma 2.4 Jika adalah matriks yang mempunyai invers maka ( )
Definisi 2.5 Matriks yang berukuran dapat didiagonalkan, jika terdapat
sebuah matriks invertible , sehingga berlaku:
dengan
[
]
adalah nilai eigen dari matriks , dengan .
(Weisstein, 1999)
Berdasarkan Lemma 2.4 dan Definisi 2.5 diperoleh:
( )
Dari persamaan di atas, dapat digunakan untuk mencari nilai dari .
Contoh: Misalkan matriks *
+. Nilai eigen dari adalah
dan . Berdasarkan nilai eigen tersebut diperoleh vektor eigen yang
bersesuaian dengan dan berturut-turut adalah ( ) dan
( ), oleh karena itu
( ), (
Dari hasil tersebut didapatkan
[
],
dan turunan terhadap (dapat berupa waktu) adalah
dengan setiap elemen dari matriks diturunkan atau diintegralkan terhadap .
(Graham, 1980)
Definisi 2.9 Sistem persamaan diferensial orde satu dalam tiga persamaan
disebut sebagai sistem autonomous jika dapat ditulis ke dalam bentuk :
( )
( )
dengan fungsi dan tidak tergantung pada waktu atau dengan kata
lain variabel tidak muncul secara eksplisit.
(Jones, 2003)
Contoh: Sistem
( ) ( )
( ) ( ) ( )
merupakan sistem autonomous, sedangkan sistem
( ) ( )
( ) ( )
bukan merupakan sistem autonomouus.
Definisi 2.10 Diberikan persamaan diferensial automous
( ). Titik ̅
dikatakan titik setimbang jika memenuhi ( ̅) .
(Olsder, 1992 )
Definisi 2.11 Sebuah persamaan diferensial linear dalam variabel ( ) ( ) ( ) dapat dinyatakan sebagai:
( )
dengan adalah konstanta.
Sedangkan sistem persamaan diferensial linear dengan persamaan dan
variabel, dinyatakan sebagai:
̇ ( ) ( ) ( ) ( )
̇ ( ) ( ) ( ) ( )
̇ ( ) ( ) ( ) ( )
dengan adalah skalar dengan sehingga dapat dinyatakan
dalam bentuk:
̇( ) ( ) ( )
Dengan dan ( ) dinamakan vektor keadaan (state). Solusi dari
sistem (2.1) adalah
( )
dimana ( ) dinamakan nilai awal dari system
(Bronson, 2007)
2.5 Kestabilan dari Sistem Linier
Definisi 2.12 Sistem linier ̇( ) ( ) dikatakan stabil asimtotis jika
( )
dengan ( ) adalah solusi dari sistem tersebut.
Teorema 2.13 Sistem ̇( ) ( ) adalah stabil asimtotis jika dan hanya jika
semua nilai eigen dari , yakni ( ) mempunyai bagian real negatif dan
dinotasikan sebagai ( ( )) .
(Zhou, 1996)
Pada permasalahan tertentu kestabilan dari titik setimbang tidak dapat
diamati karena tanda bagian real dari nilai eigen tidak mudah ditentukan, oleh
karena itu perlu digunakan metode lain untuk menentukan tanda bagian real dari
nilai eigen . Kriteria Routh-Hurwitz adalah suatu metode untuk menunjukkan
kestabilan sistem dengan memperhatikan koefisien dari persamaan karakteristik
tanpa menghitung akar-akar karakteristik secara langsung.
Teorema 2.14 (Kriteria Routh-Hurwitz) Diberikan persamaan karakteristik:
(2.2)
dengan , , adalah bilangan real. Diberikan matriks Hurwitz
dinotasikan , yang berisi koefisien dari persamaan karakteristik (2.2)
Akar-akar persamaan karakteristik (2.2) akan negatif atau mempunyai
bagian real negatif jika dan hanya jika ( ) .
Menurut Kriteria Routh-Hurwitz, akar-akar persamaan karakteristik (2.3) bernilai
det |
| sehingga akibatnya
( ) maka didapatkan dua kondisi, yaitu
i. dan
ii. dan
Untuk kondisi (ii) tidak mungkin terjadi, karena jika maka tidak akan
terpenuhi . Sehingga dapat disimpulkan bahwa akar-akar
persamaan karakteristik (2.3) bernilai negatif atau mempunyai bagian real negatif
jika dan hanya jika
dan
2.6 Masalah Kontrol Optimal
Pada umumnya masalah kontrol optimal adalah suatu masalah dengan
tujuan mencari kontrol ( ) yang dapat mengoptimalkan (memaksimumkan atau
meminimumkan) indeks performansi. Indeks performansi diformulasikan sebagai
berikut:
( ( ) ) ∫ ( ( ) ( ) ) (2.4)
dengan kendala
̇ ( ( ) ( ) ) ( ) (2.5)
dengan dan masing-masing adalah waktu awal dan akhir, dan adalah
Kontrol ( ) merupakan kontrol optimal, jika disubstitusikan ke dalam
sistem (2.5) akan memperoleh keadaan yang optimal ( ) dan pada saat yang
sama juga dapat mengoptimalkan indeks performansi (2.4).
(Lewis, 1995)
2.7 Prinsip Maksimum Pontryagin
Dalam menyelesaikan permasalahan kontrol optimal, salah satu metode
yang dapat digunakan adalah prinsip maksimum Pontryagin. Prinsip maksimum
pontryagin merupakan suatu kondisi sehingga dapat diperoleh penyelesaian
kontrol optimal yang sesuai dengann tujuan (memaksimalkan indeks
performansi).
Prosedur menyelesaikan masalah kontrol optimal dengan menggunakan
prinsip maksimum Pontryagin adalah sebagai berikut:
Diberikan persamaan state:
̇ ( ( ) ( ) ) (2.6)
dengan ( ) dan ( ) , dan indeks performansi:
( ( ) ) ∫ ( ( ) ( ) ) (2.7)
dimana nilai kondisi batas ( ) dan diberikan, dan ( ) bebas.
Syarat cukup untuk memaksimalkan indeks performansi adalah
mengkonversi persamaan (2.6) dan (2.7) ke dalam masalah memaksimalkan
fungsi Hamiltonian. Untuk mendapatkan syarat tersebut dilakukan
1. Bentuk fungsi Hamiltonian yaitu kombinasi fungsi dari suatu masalah
( ( ( ) ( ) )) dan perkalian fungsi subyek berbentuk persamaan
diferensial ( ( ( ) ( ) )) dengan suatu faktor pengali yang dinamakan
pengali Lagrange ( ). Berikut bentuk fungsi Hamiltonian:
( ( ) ( ) ( ) ) ( ( ) ( ) ) ( ) ( ( ) ( ) )
2. Maksimumkan terhadap semua vektor kontrol ( ) yaitu
( ) sehingga diperoleh ( ) ( ( ) ( ) )
3. Gunakan hasil dari Langkah 2 ke dalam Langkah 1 dan tentukan yang
optimal, yaitu
( ( ) ( ) ( ) ) ( ( ) ( ) )
4. Selesaikan sekumpulan persamaan:
1. Persamaan state yaitu persamaan kendala pada model
̇ ( ) ( *
dengan diberikan nilai ( ) .
2. Persamaan co-state atau persamaan adjoint ( ) yang terkait dengan
kendala akumulasi dari variabel keadaan.
̇ ( ) ( *
dengan diberikan nilai ( ) ( )
5. Untuk memperoleh kontrol yang optimal, substitusikan solusi ( ) dan
( ) dari Langkah 4 ke dalam kendali optimal ( ) pada Langkah 2.
BAB III
METODE PENELITIAN
Langkah-langkah yang digunakan dalam menyelesaikan skripsi ini adalah
sebagai berikut :
1. Mengkaji model dasar penyebaran virus HIVdalam tubuh.
2. Menentukan titik setimbang pada Langkah 1.
3. Melinierisasi sistem pada Langkah 1 dengan menggunakan matriks Jacobian.
4. Menguji kestabilan dari titik setimbang yang diperoleh pada Langkah 2
dengan menggunakan kriteria kestabilan Routh-Hurwitz.
5. Mengkonstruksi input kontrol pada model HIV.
6. Mendefinisikan indeks performansi berdasarkan Prinsip Maksimum
Pontryagin.
7. Menentukan input kontrol yang optimal pada Langkah 5, dengan tahap-tahap
sebagai berikut:
1. Membentuk fungsi hamiltonian.
2. Memaksimumkan fungsi hamiltonian sehingga diperoleh fungsi kontrol
optimal.
3. Menentukan bentuk fungsi hamiltonian yang optimal.
4. Menyelesaikan persamaan state dan co-state.
5. Mensubstitusi solusi dari tahap 4 ke dalam fungsi kontrol optimal pada
8. Mensubstitusikan input kontrol yang telah didapat pada Langkah 7 ke dalam
sistem sehingga diperoleh bentuk sistem umpan balik keadaan (State
Feedback) yang optimal.
9. Mensimulasikan hasil model HIV tanpa input dan dengan input kontrol dalam
bentuk numerik menggunakan software MATLAB.
BAB IV PEMBAHASAN
Pada bab ini akan dibahas mengenai kestabilan model HIV dan kontrol
optimal. Dari model HIV akan dicari titik setimbang yang kemudian dianalisis
kestabilan dari setiap titik tersebut. Berikutnya akan dicari bentuk kontrol optimal
dari model HIV menggunakan Prinsip Maksimum Pontryagin dan disimulasikan
menggunakan toolbox DOTcvp pada software MATLAB.
4.1 Model HIV
Pada umumnya, ada banyak faktor yang menyebabkan terjadinya infeksi
HIV pada manusia, baik secara internal (dalam tubuh manusia) maupun eksternal
(keadaan atau lingkungan sekitar). Namun pada penulisan ini, dibentuk
asumsi-asumsi yang membatasi kasus infeksi HIV dan struktur populasi sebagai berikut:
1. Infeksi HIV terjadi secara internal yaitu didalam tubuh manusia.
2. Tidak ada virus lain yang menyerang tubuh selain virus HIV.
3. Populasi terdiri atas tiga subpopulasi, yaitu:
( ) adalah populasi sel CD4 yang sehat (belum terkena virus HIV) pada
saat .
( ) adalah populasi sel CD4 yang telah terinfeksi virus HIV pada saat .
( ) adalah populasi virus HIV saat .
4. Laju pertumbuhan sel CD4 dalam tubuh konstan.
Berikut adalah notasi dan definisi dari masing-masing variabel yang
digunakan dalam pembahasan ini:
̇( ) adalah laju perubahan populasi sel CD4 yang sehat pada saat
̇( ) adalah laju perubahan populasi sel CD4 yang terinfeksi virus HIV
saat
̇( ) adalah laju perubahan populasi virus HIV saat
( ) adalah populasi sel CD4 yang sehat pada saat
( ) adalah populasi sel CD4 yang terinfeksi virus HIV saat
( ) adalah populasi virus HIV saat
adalah laju pertumbuhan sel CD4 yang sehat
adalah laju kematian sel CD4 yang sehat secara alami
adalah laju sel CD4 yang terinfeksi virus HIV
adalah laju kematian sel CD4 yang terifeksi virus HIV
adalah laju replikasi virus HIV di dalam sel CD4
adalah laju kematian virus HIV secara alami
adalah bobot dari pengontrol (obat ARV)
( ) adalah presentase input kontrol berupa dosis obat ARV saat
adalah batas atas pengontrol
adalah batas bawah pengontrol
adalah waktu awal pengamatan saat sel CD4 yang terinfeksi virus HIV
adalah waktu akhir pengamatan saat sel CD4 yang terinfeksi virus HIV
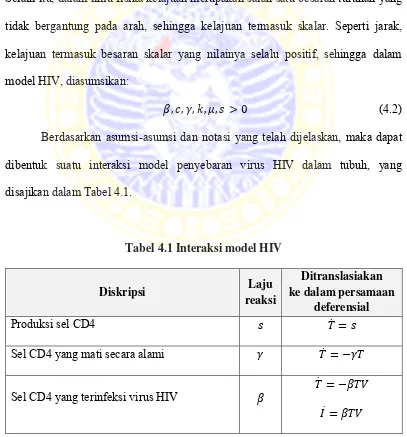
Selain itu, dalam ilmu fisika kelajuan merupakan salah satu besaran turunan yang
tidak bergantung pada arah, sehingga kelajuan termasuk skalar. Seperti jarak,
kelajuan termasuk besaran skalar yang nilainya selalu positif, sehingga dalam
model HIV, diasumsikan:
(4.2)
Berdasarkan asumsi-asumsi dan notasi yang telah dijelaskan, maka dapat
Sel CD4 yang terinfeksi virus HIV
mengalami kematian ̇
Replikasi virus HIV di dalam sel CD4 ̇
Virus HIV yang mati secara alami ̇
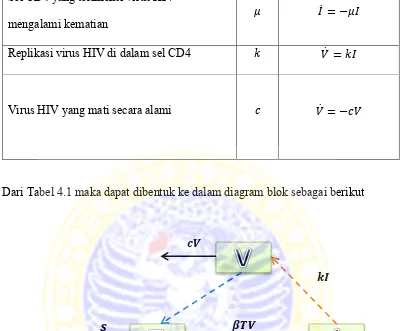
Dari Tabel 4.1 maka dapat dibentuk ke dalam diagram blok sebagai berikut
Keterangan:
: akan mengalami penambahan populasi, namun tidak mengurangi
populasi .
: menyerang namun tidak mempengaruhi jumlah dan .
Gambar 4.1 Diagram blok model HIV sebelum diberi pengontrol
𝒔
𝜸𝑻
𝜷𝑻𝑽
Dari gambar 4.1, panah masuk mengartikan bahwa pada , , dan akan
meningkatkan/ menambah jumlah populasi di setiap populasi , , dan . Untuk
panah keluar dari , , dan mengartikan bahwa pada , , dan akan
menurunkan/ mengurangi jumlah populasi di setiap populasi , , dan .
Sedangkan untuk garis putus.putus dari ke menunjukkan bahwa pada akan
mengalami penambahan populasi, namun tidak mengurangi populasi , karena
dalam kasus ini replikasi virus HIV terjadi pada sel CD4 yang terinfeksi, namun
pada saat menghasilkan virus HIV, jumlah sel CD4 tidak berkurang.
Berdasarkan Tabel 4.1 dan Gambar 4.1 di atas, maka dapat dibentuk suatu
model penyebaran virus HIV dalam tubuh manusia sebagai berikut:
̇ ( )
̇ ( )
̇ ( )
Pada Persamaan (4.3) laju perubahan sel CD4 yang sehat akan meningkat
karena dipengaruhi oleh laju pertumbuhan sel CD4 dan akan menurun karena
adanya sel CD4 yang mati secara alami serta interaksi antara sel CD4 yang sehat
dengan virus HIV. Pada Persamaan (4.4) laju perubahan sel CD4 yang terinfeksi
virus HIV akan meningkat karena penambahan jumlah sel CD4 yang terinfeksi
virus yang diakibatkan adanya kontak atau interaksi antara sel CD4 yang sehat
dengan virus HIV dan menurun karena adanya sel CD4 yang terinfeksi virus HIV
HIV akan terus bertambah karena virus mengalami replikasi didalam sel CD4 dan
akan menurun ketika virus HIV mengalami mati secara alami.
Untuk menganalisis kestabilan sistem dari model HIV di atas, maka
langkah pertama yang dilakukan adalah menentukan titik setimbang dari model
tersebut. Sebelum itu, karena model berbentuk nonliner maka perlu dilakukan
pelinieran terlebih dahulu dengan menggunakan matriks Jacobian. Selanjutnya
Titik setimbang tersebut disubstitusikan pada persamaan model HIV yang telah
dilinierkan sehingga dapat dibentuk persamaan karakteristik untuk mendapatkan
nilai karakteristik, dimana nilai karakteristik tersebut akan digunakan untuk
menentukan kestabilan dari sistem tersebut. Untuk lebih jelasnya akan dijelaskan
pada subab berikut.
4.2 Titik Setimbang Model
Berdasarkan Definisi 2.10, model penyebaran virus HIV dalam tubuh
akan memiliki titik setimbang jika memenuhi . Pada model ini
terdapat dua titik setimbang yaitu titik setimbang bebas penyakit dan titik
setimbang endemi.
Titik setimbang bebas penyakit adalah suatu kondisi dimana tidak terjadi
penyebaran virus HIV dalam tubuh manusia. Titik tersebut didapatkan pada saat
yakni suatu keadaan dimana tidak terjadi infeksi virus HIV pada sel CD4
dan yakni keadaan dimana tidak ada virus HIV dalam tubuh manusia. Titik
setimbang bebas penyakit ini dapat dinyatakan dalam ( ) ( )
̇
(4.6)
̇
(4.7)
̇
(4.8)
Berdasarkan Persamaan (4.6), (4.7), dan (4.8) maka didapatkan titik
setimbang bebas penyakit = ( ).
Titik setimbang endemik yaitu suatu kondisi dimana terjadi penyebaran
virus HIV dalam tubuh manusia yang menyerang sel CD4. Titik setimbang
endemik dinyatakan dalam ( ), dengan mengasumsikan
dan diperoleh:
̇
(4.9)
̇
(4.10)
Substitusi Persamaan (4.9) dan (4.10) ke dalam persamaan ̇
( ) ( )
(4.11)
Substitusi Persamaan (4.11) ke dalam Persamaan (4.10), diperoleh:
( )
(4.12)
Kemudian substitusi Persamaan (4.11) ke dalam Persamaan (4.9), diperoleh
( ( ))
(4.13)
Berdasarkan persamaan (4.11), (4.12), dan (4.13) didapatkan titik
setimbang endemik = ( ). Setelah didapatkan titik
setimbang bebas penyakit dan endemik selanjutnya akan dianalisis
4.3 Analisis Kestabilan Lokal
Pada sistem Persamaan (4.3), (4.4), dan (4.5) dalam model HIV terlihat
bahwa sistem tersebut merupakan sistem autonomous yang tak linier, maka untuk
mendapatkan kestabilan dari sistem model HIV di titik-titik kesetimbangan
dan perlu dilakukan pelinieran terlebih dahulu menggunakan matriks Jacobian.
Misalkan persamaan-persamaan dari model HIV didefinisakan sebagai:
̇ = ( ) (4.14)
̇ ( ) (4.15)
̇ ( ) (4.16)
Dengan menggunakan Definisi 2.6, maka matriks Jacobian dari sistem Persamaan
(4.14), (4.15) dan (4.16) adalah
Berdasarkan Teorema 2.4 mengenai kestabilan, maka dengan menggunakan nilai
eigen dari matriks dapat ditentukan kestabilan dari sistem. Karena pada kasus ini
diperoleh dua titik setimbang yaitu titik setimbang bebas penyakit dan endemik
, maka perlu dilakukan analisis kestabilan disetiap titik tersebut.
4.3.1 Kestabilan Lokal di Titik Setimbang Bebas Penyakit
Matriks Jacobian dari titik setimbang bebas penyakit ( )
(
)
(4.18)
Selanjutnya berdasarkan matriks Jacobian (4.18) dapat dibentuk persamaan
karakteristik dari matriks (4.18) dengan menggunakan ( ) , yaitu
Berdasarkan Teorema 2.14, maka dari persamaan karakteristik (4.19) diperoleh:
Berdasarkan Persamaan (4.19), syarat agar titik setimbang bebas penyakit stabil
asimtotis, adalah
dan
Pertama akan ditunjukkan bahwa . Karena laju kematian virus HIV
( ) laju kematian sel CD4 yang terinfeksi virus HIV ( ), dan laju kematian sel
CD4 secara alami ( ) bernilai positif, maka jelas bahwa:
(4.20)
Agar maka
(4.21)
(4.22)
Dari uraian di atas, jika maka . Selanjutnya didefinisikan
sebagai bilangan reproduksi dasar yang menyatakan banyaknya kasus baru dari
sel terinfeksi yang muncul akibat masuknya sel terinfeksi dalam suatu populasi
virgin. Dalam kasus ini, bilangan reproduksi dasar didefinisikan sebagai rasio
pertumbuhan dan kematian dari populasi sel CD4 yang sehat, sel CD4 yang
terinfeksi dan virus HIV. Dari sini bilangan reproduksi dasar dapat digunakan
sebagai tolok ukur terjadi atau tidaknya suatu penyakit. Sehingga
Dengan syarat di atas akan ditunjukkan bahwa .
Perhatikan kembali bahwa , sehingga berlaku atau
, akibatnya
(4.23)
Terakhir akan dibuktikan bahwa , atau ,
( ) ( ) ( )
)
Perhatikan kembali bahwa , sehingga . Karena diperoleh
yang berarti Selain itu karena diperoleh
yang berarti sehingga
( )
( ) ( )
(4.24)
Teorema 4.1 Titik setimbang bebas penyakit pada model HIV akan stabil
asimtotis pada ( ), jika memenuhi nilai ambang batas bebas
penyakit
=
4.3.2 Kestabilan Lokal di Titik Setimbang Endemik
Matriks Jacobian dari titik setimbang endemik ( )
Selanjutnya dapat dibentuk persamaan karakteristik dari matriks (4.25) dengan
(( )( )( )) (( ) ( )( ))
(( ) ( ) ( ))
( )( ) ( )
( ) ( ) ( ) (4.26)
Berdasarkan Teorema 2.14, maka dari persamaan karakteristik (4.26) diperoleh:
Berdasarkan Persamaan (4.26), syarat agar titik setimbang endemik stabil
asimtotis adalah
dan .
Pembuktian pertama yaitu , berdasarkan asumsi (4.2) maka jelas
terpenuhi bahwa:
(4.27)
serta untuk pembuktian terlihat jelas bahwa:
Berdasarkan (4.26), dengan proses yang sama pada saat mencari syarat kestabilan
pada titik setimbang bebas penyakit, untuk titik setimbang endemik jika dipenuhi
maka . Sehingga didapatkan bilangan reproduksi
dasar endemik = atau disebut sebagai nilai ambang batas endemik.
Selanjutnya akan dibuktikan atau
( ) ( )
Berdasarkan asumsi (4.2) maka
(4.30)
Berdasarkan uraian di atas diperoleh teorema berikut:
Teorema 4.2 Titik setimbang endemik pada model HIV akan stabil asimtotis
pada ( ) jika memenuhi nilai ambang batas bebas
penyakit
= .
Selanjutnya untuk mendapatkan jumlah sel CD4 sehat yang maksimum
dengan biaya pengobatan yang minimal, maka perlu dicari bentuk kontrol optimal
4.4 Penyelesaian Kontrol Optimal
Pada masalah kontrol optimal ini, tujuan yang akan dicapai adalah
memaksimalkan sel CD4 yang sehat dengam meminimalkan biaya pengontrol
(obat ARV). Pada tahap ini akan didapatkan bentuk pengontrol (obat ARV) yang
optimal menggunakan Prinsip Maksimum Pontryagin. Dari tujuan tersebut dapat
dibentuk fungsi tujuan sebagai berikut:
( ) ∫ ( ) (4.31)
dengan variabel kontrol adalah dan variabel keadaannya [ ].
Pada model HIV, pemberian pengontrol (obat ARV) diberikan saat sel CD4
diserang oleh virus HIV, oleh karena itu bentuk Constrain dari fungsi tujuan
(4.31) adalah
̇ ( )
̇( ) ( )
̇
dengan kondisi batas
dan
yang berarti bahwa waktu yang digunakan yaitu waktu dari awal pengamatan saat
diberi pengontrol ( ) sampai waktu terakhir pengamatan setelah diberi
( ) dibatasi dari 0 sampai 1 ( dari 0% sampai 100%). Untuk nilai awal dari
seluruh populasi diasumsikan bernilai positif yang dinotasikan dengan
( ) ( ) ( )
Berdasarkan Prinsip Maksimum Pontryagin (2.7), hal pertama yang harus
dilakukan adalah menentukan fungsi Hamiltonian. Berikut bentuk fungsi
Hamiltonian:
( ) ( ) ( )
( ) ( ) (
( ) ( ( ))
)
( ( )) ( ( ) )
( )
Untuk mendapatkan kondisi optimal maka harus memenuhi kondisi stasioner dari
( ) dengan menyelesaikan persamaan state ̇ dan co-state ̇. Berikut
kondisi stasioner yang harus dipenuhi:
( )
Karena batasan nilai , , maka diperoleh beberapa kemungkinan hasil
{
( ) ( )
( )
( )
Dari beberapa kemungkinan di atas, maka pengontrol yang optimal adalah
( ( ( )) ).
Karena pada bentuk pengontrol mengandung variabel state ( dan ),
maka selanjutnya akan diselesaikan persamaan state untuk mendapatkan variabel
tersebut.
̇
sehingga diperoleh
̇
̇ ( )
̇
Selain variabel state juga terdapat varibel co-state ( dan ) atau variabel
adjoin pada bentuk pengontrol , maka perlu diselesaikan persamaan co-state
untuk mendapatkan variabel tersebut
̇
sehingga diperoleh
̇ ( )
̇
Setelah mendapatkan nilai dari variabel state dan co-state selanjutnya
disubstitusikan pada pengontrol . Substitusikan persamaan yang telah
diperoleh kedalam persamaan state untuk memperoleh bentuk solusi yang
optimal. Berikut hasil optimal yang didapatkan:
̇ ( ( ( ( )) ))
̇ ( ( ( ( )) ))
̇
Berdasarkan uaraian di atas, untuk mendapatkan , dan dari bentuk
yang optimal maka perlu menyelesaikan persamaan state dan co-state yang
berbentuk nonlinier dan berjumlah enam persamaan. Karena sistem persamaan
nonlinier sulit untuk diselesaikan secara analitik, oleh karena itu perlu
diselesaikan secara numerik.
4.5 Simulasi
Berdasarkan penjelasan pada Subab 4.4 penyelesaian kontrol optimal sulit
diselesaikan secara analitik maka penyelesaian kontrol optimal diselesaikan secara
numerik. Hal ini dilakukan dengan mensimulasikan permasalahan kontrol
MATLAB dengan mendefinisikan masalah optimal kontrol pada M-File dengan
parameter yang diketahui. Dalam simulasi model penyebaran virus HIV dalam
tubuh manusia dengan MATLAB maka state didefinisikan dengan ( )
( ) ( ) indeks performansi didefinisikan menjadi state baru yaitu
( ) dan pengontrol ( ).
Langkah – langkah yang harus dilakukan dalam penggunaan DOTcvp
adalah:
Langkah 1
Settings untuk IVP (initial value problem)
data.odes.res(1) = (masukkan fungsi dinamik sistem)
data.odes.t0 = (masukkan waktu awal)
data.odes.tf = (masukkan waktu akhir)
Langkah 2
NLP (Non Linier Problem) definition:
Data.nlp.RHO = (masukkan jumlah interval waktu)
Data.nlp.problem = (pilih fungsi min/max)
Data.nlp.J0 = (masukkan indeks performansi)
Data.nlp.u0 = (masukkan nilai awal pengontrol)
Data.nlp.ub = (masukkan batas atas pengontrol)
Data.nlp.1b = (masukkan batas bawah pengontrol)
Memanggil main function
[data]=dotcvp_main(data)
Simulasi dilakukan dengan cara dua kali runing, yang pertama sebelum
diberi pengontrol dan yang kedua setelah diberi pengontrol. Selanjutnya akan
dibandingkan secara langsung sistem sebelum diberi pengontrol dan sesudah
diberi pengontrol. Pada simulasi ini, pemberian pengontrol (obat ARV) dilakukan
selama 1000 hari. Berikut adalah parameter yang akan digunakan:
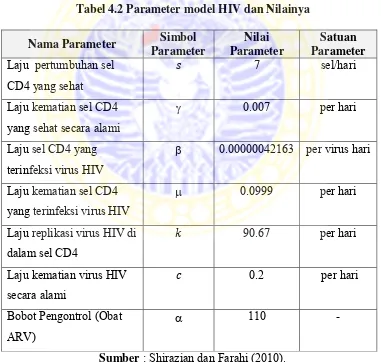
Tabel 4.2 Parameter model HIV dan Nilainya Nama Parameter Simbol
0.00000042163 per virus hari
Laju kematian sel CD4
Sumber : Shirazian dan Farahi (2010).
Tabel 4.2 menunjukkan nilai-nilai dari seluruh laju yang digunakan pada simulasi,
disimbolkan sebagai , memiliki nilai 7 sel/ hari, artinya bahwa dalam penelitian
ini sel CD4 yang sehat akan tumbuh sebnyak 7 sel dalam sehari, dan selanjutnya
parameter-parameter yang lain mempunyai makna yang sama.
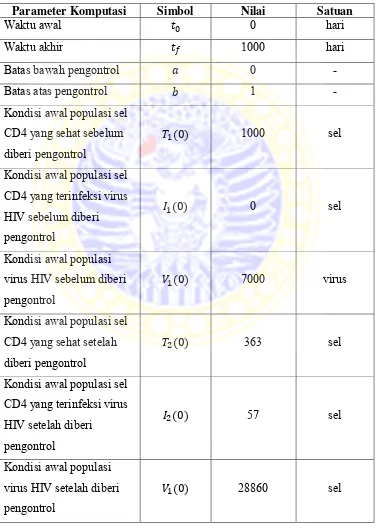
Tabel 4.3 Parameter Komputasi
Parameter Komputasi Simbol Nilai Satuan
Sumber: Shirazian dan Farahi (2010).
Proses simulasi dilakukan dengan mengamati jumlah populasi sel CD4
yang sehat, sel CD4 yang terinfeksi dan virus HIV, baik sebelum diberi obat ARV
maupun setelahnya. Sebelum diberi pengontrol virus HIV dapat menyebar ke
seluruh tubuh dan menyebabkan penyakit HIV. Oleh karena virus HIV tidak dapat
dihilangkan seluruhnya dalam tubuh manusia, maka perlu dilakukan
penghambatan replikasi virus HIV dalam tubuh dengan pemberian obat ARV.
Dalam hal ini pemberian obat ARV berupa bobot dari dosis obat yang seharusnya
diberikan pada manusia. Populasi sel CD4 yang sehat akan terus meningkat
sejalan dengan menurunnya populasi sel CD4 yang terinfeksi dan populasi virus
HIV. Semakin meningkatnya jumlah sel CD4 yang sehat, maka pemberian dosis
obat ARV juga akan berkurang selaras dengan perilaku sel CD4 tersebut.
Simulasi pertama dilakukan untuk kondisi dimana tidak ada pemberian
kontrol (obat ARV) pada sel CD4 yang terinfeksi virus HIV sehingga dan
terjadi penyebaran virus HIV dalam tubuh manusia (endemik) dengan
=
kemudian dilanjutkan dengan memberikan pengontrol (obat ARV) pada sel CD4
Gambar 4.2 Populasi sel CD4 yang sehat sebelum diberi pengontrol (obat ARV)
Gambar 4.3 Populasi sel CD4 yang sehat setelah diberi pengontrol (obat ARV)
Gambar 4.2 menunjukkan bahwa populasi sel CD4 yang sehat sebelum
pemberian obat ARV dengan kondisi awal populasi ( ) menurun
hingga hari ke 100 dan bergerak naik turun kemudian bergerak menuju ke titik
setimbang endemik ( ) = 523,248 pada saat kurang lebih pada hari ke 800.
Sedangkan pada Gambar 4.3 terlihat bahwa populasi sel CD4 yang sehat setelah
peningkatan lebih cepat beberapa hari daripada tanpa pengontrol, kemudian
bergerak menuju titik ( ) atau dibulatkan menjadi 987 pada saat kurang
lebih 700 hari. Hal ini menunjukkan bahwa jumlah populasi sel CD4 yang sehat
meningkat karena pemberian pengontrol (obat ARV). Saat hari ke-900 menuju
hari ke-1000 terlihat bahwa sel CD4 yang sehat mengalami penurunan. Hal ini
dikarenakan virus HIV mulai bereplikasi lebih cepat dari sebelumnya sehingga
mulai menginfeksi kembali sel CD4 yang sehat, ini disebabkan pemberian dosis
obat ARV yang rendah padahal seharusnya lebih besar dari pemberian saat itu.
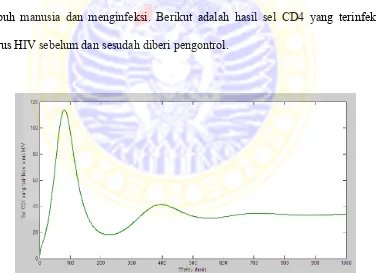
Simulasi selanjutnya yaitu kondisi dimana virus HIV masuk kedalam
tubuh manusia dan menginfeksi. Berikut adalah hasil sel CD4 yang terinfeksi
virus HIV sebelum dan sesudah diberi pengontrol.
Gambar 4.4 Populasi sel CD4 yang terinfeksi virus HIV sebelum diberi
Gambar 4.5 Populasi sel CD4 yang terinfeksi virus HIV setelah diberi pengontrol
(obat ARV)
Pada Gambar 4.4 terlihat bahwa grafik populasi sel CD4 yang terinfeksi
virus HIV dengan kondisi awal ( ) mengalami peningkatan kemudian
menurun dan bergerak konstan menuju titik setimbang ( ) atau
dibulatkan menjadi 34 pada saat kurang lebih hari ke-800 dan bergerak seterusnya
sehingga penyakit akan selalu ada sampai waktu tak terbatas. Oleh karena itu,
penyakit bersifat endemik dan tidak akan menghilang dari populasi. Peningkatan
jumlah sel CD4 yang terinfeksi virus HIV tersebut, dikarenakan menurunnya
jumlah populasi sel CD4 yang sehat pada hari pertama sampai hari ke 500
mengakibatkan populasi sel CD4 yang terinfeksi virus HIV meningkat pada
selang waktu tersebut. Namun berbeda pada Gambar 4.5, terlihat bahwa populasi
sel CD4 yang terinfeksi virus HIV dengan pengontrol yang optimal pada kondisi
awal ( ) terjadi penurunan secara drastis dibanding dengan sebelum diberi
bergerak menuju ke titik ( ) atau dibulatkan menjadi 4 pada saat
kurang lebih hari ke-100. Penurunan jumlah individu yang terinfeksi ini
dikarenakan pemberian obat ARV pada sel CD4 yang terinfeksi virus HIV.
Namun pada saat hari ke-900 menuju hari ke-1000 sel CD4 yang terinfeksi virus
mengalami peningkatan karena virus mengalami replikasi lebih cepat dari
sebelumnya sehingga virus mulai menginfeksi kembali sel CD4 yang sehat, ini
disebabkan pemberian dosis obat ARV yang rendah padahal seharusnya lebih
besar dari pemberian saat itu.
Simulasi selanjutnya yaitu kondisi dari perilaku virus HIV itu sendiri saat
menginfeksi sel CD4 dalam tubuh manusia. Berikut adalah hasil simulasi untuk
virus HIV sebelum dan sesudah diberikan pengontrol:
Gambar 4.7 Populasi virus HIV setelah diberi pengontrol (Obat ARV)
Gambar 4.6 menunjukkan bahwa grafik populasi yang sehat dengan
kondisi awal ( ) meningkat dan bergerak naik turun menuju titik
setimbang ( ) dibulatkan menjadi 15.214 pada saat kurang lebih
pada hari ke 800. Hal ini sebanding dengan laju perubahan sel CD4 yang
terinfeksi virus HIV, dikarenakan ketika virus meningkat sel CD4 yang terinfeksi
virus juga akan meningkat dan sebaliknya. Sedangkan Gambar 4.7 menunjukkan
populasi virus HIV setelah diberi pengontrol yang optimal pada kondisi awal
( ) terjadi penurunan lebih cepat daripada sebelum diberi pengontrol,
kemudian bergerak konstan menuju titik ( ) dibulatkan menjadi
1.584 pada saat kurang lebih 100 hari. Hal ini dapat terjadi karena virus HIV
diberi suatu pengontrol yang berupa obat ARV saat di dalam tubuh manusia.
Sehingga dapat disimpulkan bahwa penyebaran virus HIV dalam tubuh manusia
dapat ditekan, namun pada saat hari ke-900 menuju hari ke-1000 populasi virus
disebabkan pemberian dosis obat ARV yang rendah padahal seharusnya lebih
besar dari pemberian saat itu.
Simulasi terakhir adalah bentuk kontrol optimal (Obat ARV) saat
diberikan kepada penderita yang terinfeksi HIV. Berikut hasil yang diperoleh:
Gambar 4.8 Kondisi pengontrol (Obat ARV)
Gambar 4.8 menunujukkan bahwa pengontrol yaitu persentase
pemberian dosis obat yang diberikan pada sel CD4 yang terkena virus HIV pada
awal periode pengendalian adalah 1 atau dapat dinyatakan 100% ini berarati bobot
dari dosis obat ARV diberikan sepenuhnya, kemudian bergerak menurun lalu
konstan pada saat kurang lebih 100 hari dan mulai turun kembali kurang lebih
pada hari ke-900. Hal ini berarti pemberian obat ARV pada sel CD4 yang
terinfeksi virus HIV semakin menunjukkan keefektifannya dalam menghambat
replikasi virus HIV dalam tubuh manusia dengan selarasnya populasi virus HIV
yang menurun. Namun keefektifan pemberian obat ARV hanya berlangsung
hingga hari ke-900, karena pada waktu tersebut sel CD4 yang sehat mengalami
peningkatan namun pemberian dosis obat terus menurun. Padahal dalam
aplikasinya seharusnya pemberian dosis obat ARV menurun jika sel CD4 yang
terinfeksi virus mengalami penurunan. Hal ini dapat terjadi karena untuk jangka
waktu lebih dari 800 hari, perlu adanya tambahan obat lainnya selain ARV agar
sel CD4 yang terinfeksi terus menurun.
Dari seluruh hasil yang telah didapatkan, secara garis besar bentuk
pengontrol (Obat ARV) pada model penyebaran virus HIV dapat menekan
penyebaran virus HIV dalam tubuh manusia dalam jangka waktu kurang lebih 0
sampai dengan 900 hari sehingga dapat mengurangi populasi sel CD4 yang
terinfeksi virus HIV serta virus HIV itu sendiri, dan meningkatkan populasi sel
CD4 yang sehat dalam waktu tersebut. Sehingga dapat disimpulkan bahwa pada
hari ke-900 seharusnya pemberian bobot dari dosis obat tidak kurang dari 0.1 agar
sel CD4 yang sehat terus meningkat. Dari uraian di atas dapat disimpulkan bahwa
keefektifan pengontrol (obat ARV) pada waktu kurang lebih 0 sampai dengan 900
hari, dapat mengurangi populasi sel CD4 yang terinfeksi virus HIV sehingga
penyebaran virus HIV dapat ditekan dan dapat memaksimumkan sel CD4 yang
BAB V PENUTUP
5.1 KESIMPULAN
Dari hasil pembahasan diperoleh kesimpulan bahwa model penyebaran
virus HIV dalam tubuh manusia, maka diperoleh kesimpulan sebagai berikut:
1. Pada kestabilitan didapatkan dua titik setimbang yaitu titik setimbang
bebas penyakit = ( ) ( ) dan titik setimbang endemik
= ( ) ( ). Untuk titik setimbang bersifat
stabil asimtotis jika sedangkan titik setimbang bersifat stabil
asimtotis jika .
2. Pada optimal kontrol didapatkan bentuk kontrol yang optimal sebagai
berikut:
( ( ( )) ).
Karena model HIV nonlinier maka untuk memperoleh solusi tersebut
digunakan toolbox DOTcvp MATLAB. Hasil simulasi pada toolbox
DOTcvp MATLAB menunjukkan perilaku sistem dan keefektifan
pengontrol (obat ARV) pada waktu kurang lebih 0 sampai dengan 900
hari, dapat mengurangi populasi sel CD4 yang terinfeksi virus HIV
sehingga penyebaran virus HIV dapat ditekan dan dapat memaksimumkan
sel CD4 yang sehat dan meminimumkan biaya dalam pemberian obat
5.2 SARAN
Pada penelitian ini dibahas mengenai analisis kestabilan model penyebaran
virus HIV dengan menggunakan laju pertumbuhan sel CD4 yang konstan. Oleh
karena itu terbuka peluang untuk pembaca melakukan penelitian selanjutnya
menggunakan laju pertumbuhan sel CD4 yang tidak konstan. Selain itu juga untuk
hasil yang lebih baik, dapat menggunakan kondisi free final state dan free final
time atau dengan kata lain bebas menentukan waktu dan state akhirnya, karena
pada skripsi ini waktu akhir telah ditentukan (fix final time) dan state akhir yang
bebas (free final state), sehingga tidak dapat mengetahui pada hari ke berapa state
DAFTAR PUSTAKA
1. Anton, H., 1987, Aljabar Linier Elementer, Erlangga, Jakarta
2. Bronson R., Costa G.B., 2007, Differential Equations, The Mc Grow-Hill
Companies,Inc., New Jersey
3. Felissa R. L., Jerry D. D., 2009, The person with HIV/AIDS: nursing perspectives, Springer Publishing Company, Inggris
4. Graham, A., dan Gurghes, D.N., Introduction to Control Theory Including Optimal Control, Halsted Press, New York
5. http://kkp-balikpapan.blogspot.com/2011/05/seputar-cd4.html, 3 April 2012
6. http://www.cdc.gov/hiv/resources/qa/transmission.htm, 9 April 2012
7. Jenny P., Maylani L., Delene P., Monica J., 2006. Working with HIV/AIDS,
Juta Legal and Academic Publishers, Cape Town
8. Jones, D.S., Sleeman B.D., 2003, Differential Equations and Mathematical Biology, CRC Press, New York
9. Lewis F.L., Syrmos V.L., 1995, Optimal Control, Willy Interscience, Canada
10.Merkin, D.R., 1997, Introduction to the Theory of Stability, Springer, New
York
11. Naidu D.S., 2002, Optimal Control Systems, CRC Press, New York
12. Olsder, G.J., 1992, Mathematical System Theory, Delft, The Natherland
13. Schoub B. D., 1999, AIDS and HIV in Perspective: A Guide to Understanding the Virus and its Consequences. Cambridge University Press,
Inggris
14. Shirazian M., Farahi M. H., 2010, Optimal Control Strategy for a Fully Determined HIV Model, vol.1, Intelligent Control and Automation, pg. 15-19
15.Sontag E.D., Thoma M., 2001, Control Theory for Linier Systems, Springer,
London
16. Vandermeer, J., 1981, Elementary Mathematical Ecology, A
17. Wardah, F., 2012, http://www.voaindonesia.com/content/penderita-baru-hivaids-di-jakarta-berjumlah-1184-orang-134637773/101326.html, 15 Maret 2012
18.Weisstein, Eric W., 1999, Eigen Decomposition,
http://mathworld.wolfram.com/EigenDecomposition.html , 24 April 2012
19. Zhou, K. Doyle, J. C., dan Glover, K., 1996, Robust and Optimal Control,
Lampiran 1
Skrip M-File pada MATLAB
untuk Model Penyebaran Virus HIV Tanpa Pengontrol
% A MATLAB example described in detail in the technical report %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% %
% DOTcvp - Dynamic Optimization Toolbox with CVP approach for %
% handling continuous and mixed-integer dynamic optimization problems %
% The DOTcvp toolbox is completely free of charge under the creative %
% commons license. The conditions of the license can be found on the %
FORTRAN parameters definition, e.g. {'double precision k10, k20, ..'}
data.odes.parameters = {}; %constant parameters before ODE
{'T=300','..}
data.odes.Def_MATLAB = {}; %this option is needed only for
MATLAB parameters definition
data.odes.res(1) = {
data.odes.res(2) = {
'0.00000042163*y(1)*y(3)-data.odes.NonlinearSolver = 'Newton'; %['Newton'|'Functional']
/Newton for stiff problems; Functional for non-stiff problems
data.odes.LinearSolver = 'Dense'; %direct
['Dense'|'Diag'|'Band']; iterative ['GMRES'|'BiCGStab'|'TFQMR'] /for the Newton NLS
data.odes.LMM = 'Adams'; %['Adams'|'BDF'] /Adams for
non-stiff problems; BDF for stiff problems
data.odes.MaxNumStep = 500; %maximum number of steps
data.odes.RelTol = 1*10^(-7); %IVP relative tolerance
level
data.odes.AbsTol = 1*10^(-7); %IVP absolute tolerance
level
data.sens.SensAbsTol = 1*10^(-7); %absolute tolerance for
sensitivity variables
data.nlp.SolverSettings = 'None'; %insert the name of the file
data.nlp.approximation = 'PWC'; %['PWC'|'PWL'] PWL only for: FMINCON & without the free time problem
data.nlp.FreeTime = 'off'; %['on'|'off'] set 'on' if free
time is considered
data.nlp.t0Time = [data.odes.tf/data.nlp.RHO]; %initial
size of the time intervals, e.g. [data.odes.tf/data.nlp.RHO] or for the each time interval separately [dt1 dt2 dt3]
data.nlp.lbTime = 0.01; %lower bound of the time
taken from the last control variables, if not equal to 0 you need to use some MINLP solver ['ACOMI'|'MISQP'|'MITS']
data.nlp.eq.PenaltyCoe = [1.0];
%J0=J0+data.nlp.eq.PenaltyCoe*ViolationOfEqualityConstraint /*
data.nlp.ineq.InNUM = 1; %how many inequality constraints
are '>' else '<'
data.nlp.ineq.eq(1) = {''};
data.nlp.ineq.eq(2) = {''};
data.nlp.ineq.Tol = 0.0005; %tolerance level of violation
of INECs
data.nlp.ineq.PenaltyFun = 'off'; %['on'|'off'] INECs penalty
function
data.nlp.ineq.PenaltyCoe = [1.0 1.0];
%J0=J0+data.nlp.ineq.PenaltyCoe*ViolationOfInequalityConstraint /* for every inequality constraint one parameter */
% --- % % Options for setting of the final output:
% --- %
data.options.intermediate = 'off'; %['on'|'off'|'silent'] display
of the intermediate results
data.options.display = 'on'; %['on'|'off'] display of the