74
Pengambilan Keputusan Dengan Metode Analytic Hierarchy
Process (AHP)
Wahyu Sasmita
1,*, Rito Goejantoro
2, Ika Purnamasari
21Laboratorium Statistika Komputasi, Jurusan Matematika, FMIPA, Universitas Mulawarman 2Program Studi Statistika, Jurusan Matematika, FMIPA, Universitas Mulawarman
Email korespondensi: [email protected]
Abstract The experiment laboratory required competent assistant to provide teaching to students. The purpose of this research was to determine the order of importance and priority scale criteria of laboratory assistant statistics major and to know the results of assessment of laboratory assistant candidates in order of importance of the criteria set. By using Analytic Hierarchy Process (AHP), which will be resolved in a mind frame that is organized, so that it can be expressed to make an effective decisions on these issues. In this research, the problem of organized into a hierarchy of goals, criteria and alternatives. Alternative identification obtained from interviews with relevant matter. Alternatives in this research is the statistical students enrolled as a candidate for an assistant, or a statistics student selected by the faculty to be a candidate in the laboratory assistant Odd Semester Academic Year 2016/2017. Criteria used in the determination of priorities, which are value grade point average (GPA), teaching ability and mastery of materials, as well as the ability to communicate from a prospective assistant. From the criteria analysis, obtained variables that have a high priority is GPA and mastery of matter with a weight rating of 0.4. Meanwhile, the second priority is communication with a weight rating of 0.2. The weight alternative of each criterion will determine the end of the priority scale. The results of this research are expected to be a decision-making tool in determining the order of priority candidates statistics laboratory assistant.
Keywords: analytic hierarchy process (AHP), priorities, criteria, laboratory assistant. Pendahuluan
Dibutuhkan sebuah metode pengambilan keputusan dalam pemilihan asisten praktikum agar memudahkan tim seleksi asisten dalam menilai masing-masing calon asisten. Metode AHP adalah proses membentuk skor secara numerik untuk menyusun rangking setiap alternatif keputusan berbasis pada bagaimana sebaiknya alternatif tersebut dicocokkan dengan kriteria pembuat keputusan. AHP menciptakan kerangka yang sistematis untuk penilaian secara individu maupun pengambilan keputusan secara berkelompok dan membuat pemecahannya secara terstruktur.
Oleh karena itu, Peneliti ingin menerapkan sistem pengambilan keputusan dengan metode Analytic Hierarchy Process (AHP) untuk menentukan asisten praktikum yang terbaik di laboratorium program studi statistika berdasarkan kriteria yang telah ditentukan. Analytic Hierarchy Process
Metode Analytic Hierarchy Process (AHP) dikembangkan oleh Prof. Thomas Lorie Saaty dari Wharton Business School pada Tahun 1970, yang digunakan untuk mencari rangking atau urutan prioritas dari berbagai alternatif dalam pemecahan suatu permasalahan [4]. Berikut contoh struktur heirarki untuk mengambil suatu keputusan:
Gambar 1. Contoh Struktur Hierarki Prinsip-prinsip AHP
Menurut [3] dalam menyelesaikan persoalan dengan AHP, terdapat prinsip-prinsip yang harus dipahami, diantaranya adalah:
1. Decomposition (Penyusunan Hierarki)
2. Comparative Judgement (Penilaian
Perbandingan Berpasangan)
3. Synthesis of Priority (Sintesis Prioritas) 4. Logical Consistency (Logika Konsistensi) Nilai Skala Perbandingan
Setelah mengembangkan hierarki, responden menimbang relatif pentingnya suatu elemen dengan memberi penilaian dari angka 1 hingga 9. Pilihan yang mendapat nilai numerik tertinggi merupakan pilihan yang terbaik [5].
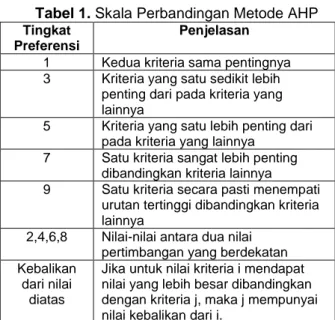
75 Tabel 1. Skala Perbandingan Metode AHP
Tingkat Preferensi
Penjelasan
1 Kedua kriteria sama pentingnya
3 Kriteria yang satu sedikit lebih
penting dari pada kriteria yang lainnya
5 Kriteria yang satu lebih penting dari
pada kriteria yang lainnya
7 Satu kriteria sangat lebih penting
dibandingkan kriteria lainnya
9 Satu kriteria secara pasti menempati
urutan tertinggi dibandingkan kriteria lainnya
2,4,6,8 Nilai-nilai antara dua nilai pertimbangan yang berdekatan Kebalikan
dari nilai diatas
Jika untuk nilai kriteria i mendapat nilai yang lebih besar dibandingkan dengan kriteria j, maka j mempunyai nilai kebalikan dari i.
Konsep Dasar AHP
Model AHP yang merupakan metode perbandingan dengan menggunakan konsep matriks. Bangun dasar konsep AHP dapat dilihat pada Tabel 2.
Tabel 2. Contoh Matriks Perbandingan
C X1 X2 X3 X4
X1 1 2 3 4
X2 1/2 1 … …
X3 1/3 … 1 …
X4 1/4 … … 1
Tabel 2 memperlihatkan perbandingan antara kolom X1 sampai dengan X4 dengan baris X1 sampai dengan X4. Perbedaannya terletak dari cara perbandingan tersebut dibaca. Misal:
Bila baris yang dibaca maka:
Jika faktor C dari X1 dibandingkan dengan faktor C dari X2 maka X1 = 2X2
Bila kolom yang dibaca maka:
Jika faktor C dari X2 dibandingkan terhadap faktor C dari X1, maka X2 = X1 / 2.
Demikian pula dengan perbandingan elemen lainnya.
Perbandingan antara keduanya merupakan perubahan posisi letak nilai perbandingan semata. Pernyataan tersebut menegaskan prinsip penting dalam model AHP atas dasar matriks perbandingan. Suatu matriks perbandingan haruslah bernilai konsisten (consistency principle). Prinsip ini dapat dilihat pada Tabel 3.
Tabel 3. Contoh Matriks Perbandingan Kualitas Motor
Kualitas Motor 1 Motor 2 Motor 3
Motor 1 1 1/2 ¼
Motor 2 2 1 ½
Motor 3 4 2 1
Jumlah 7 3,5 1,75
Nilai perbandingan yang diperlihatkan pada Tabel 3 merupakan penilaian subyektif atas dasar tingkat preferensi individual dan pengalaman yang dimiliki seseorang. Berdasarkan atas matriks tersebut, maka dapat dibuat formula matematis perbandingan sebagai berikut [1]:
Tingkat preferensi kualitas:
Motor 1 = 1/2 Motor 2 (1) Motor 1 = 1/4 Motor 3 (2) Dapat simpulkan bahwa:
1/2 Motor 2 = 1/4 Motor 3 (3) Motor 2 = Motor 3 (4) Dengan demikian:
Motor 2 = 1/2 Motor 3 (5) Setelah melakukan penilaian maka diperlukan standarisasi data untuk mendapatkan nilai prioritas dari kriteria ataupun alternatif-alternatif tersebut. Untuk mendapatkan nilai standarisasi yaitu dengan membagi nilai setiap cell dengan jumlah dari kolom cell tersebut. Nilai prioritas diperoleh dengan mencari rata-rata dari baris tersebut. Berikut contoh tabel untuk nilai standarisasi dan nilai prioritas dengan menggunakan data pada Tabel 3.
Tabel 4. Standarisasi Untuk Matriks Perbandingan Kualitas Motor
Kualitas Motor 1 Motor 2 Motor 3 Prioritas
Motor 1
Motor 2
Motor 3
Jumlah 1 1 1 1
Dari Tabel 4 tersebut, dapat disimpulkan bahwa kualitas motor Motor 3 terbaik jika dibandingan dengan motor Motor 2 ataupun motor Motor 1.
Prinsip Konsistensi
Prinsip konsistensi digunakan untuk mengetahui seberapa besar tingkat konsisten suatu penilaian hierarki tersebut. Di mana dalam kasus pembangunan model kuantitatif AHP, prinsip konsistensi lebih diutamakan dibandingkan prinsip inkonsistensi untuk memudahan melakukan evaluasi numerik bagi penentuan urutan alternatif solusi.
Saaty telah membuktikan bahwa Indeks Konsistensi dari matriks berukuran dapat diperoleh dengan rumus:
76 di mana:
IK = Indeks Konsistensi
= Nilai eigen maksimum dari matriks = Ukuran matriks
Nilai diperoleh dengan menggunakan rumus dibawah ini:
(7) di mana:
= Nilai eigen maksimum dari matriks = Nilai bobot/prioritas dari matriks yang telah distandarkan = Jumlah kolom dari matriks awal = Banyaknya baris/kolom
Apabila IK bernilai nol, maka pair-wise comparison matrix tersebut konsisten. Batas inkonsistensi yang telah ditetapkan oleh Thomas L. Saaty ditentukan dengan menggunakan rasio konsistensi (CR). Dengan demikian, rasio konsistensi dapat dirumuskan sebagai berikut: (8) di mana: CR = Rasio konsistensi IK = Indeks Konsistensi RI = Random Indeks
Tabel 5. Nilai Random Indeks (RI) Ordo Matri ks Rando m Indeks Ordo Matri ks Rando m Indeks Ordo Matri ks Rando m Indeks 1 2 3 4 5 0,000 0,000 0,580 0,900 1,120 6 7 8 9 10 1,240 1,320 1,410 1,450 1,490 11 12 13 14 15 1,510 1,480 1,560 1,570 1,590 Bila matriks pair-wise comparison dengan nilai CR 0,1 maka inkonsistensi dari
decision maker masih dapat diterima, jika tidak maka penilaian perlu diulang [2].
Praktikum
Menurut [6] manfaat praktikum untuk melatih keterampilan mahasiswa, memberi kesempatan pada mahasiswa untuk menerapkan dan mengintegrasikan pengetahuan dan keterampilan yang dimilikinya secara nyata dalam praktek, membuktikan sesuatu secara ilmiah.
Kegiatan praktikum di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Mulawarman memiliki bobot satu Sistem Kredit Semester (SKS). Satu sks praktikum memerlukan masing-masing 100 menit per minggu untuk pelaksanaannya. Dengan demikian, jika setiap praktikum memerlukan waktu 1000 menit pertemuan, maka per semester hanya diperlukan 10 kali tatap muka.
Mata kuliah program studi statistika FMIPA Universitas Mulawarman yang disertai
dengan praktikum Matematika, Statistika Komputasi, Operation Research, Aljabar Linear, Pemrograman Komputer, dll.
Metodologi
Penelitian ini dilakukan pada bulan September 2016 sampai bulan Mei 2017 di Laboratorium Statistika Komputasi Program Studi Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Mulawarman Samarinda. Penelitian ini mengambil data dari responden yaitu tim seleksi asisten, laboran, dan beberapa dosen program studi statistika FMIPA Universitas Mulawarman Samarinda. Dalam penelitian ini data yang digunakan adalah data primer dan data sekunder. Data primer dikumpulkan dengan cara melakukan survei dan wawancara dengan menggunakan alat bantu penelitian berupa kuesioner. Data sekunder diperoleh dari tim seleksi asisten setelah melakukan tes interview terhadap masing-masing calon asisten praktikum.
Variabel yang digunakan dalam penelitian ini adalah sebagai berikut:
1. Nilai IPK mahasiswa
2. Kemampuan mengajar dan penguasaan materi dari mahasiswa
3. Kemampuan berkomunikasi dari mahasiswa
Hasil dan Pembahasan
1. Struktur Hierarki Pemilihan Asisten Berikut adalah struktur hierarki untuk pemilihan asisten praktikum pada mata kuliah Matematika I untuk program studi Statistika. Pada tingkatan pertama merupakan tujuan utama dari permasalahan yaitu menentukan asisten praktikum suatu mata kuliah. Pada tingkatan kedua merupakan variabel kriteria untuk menentukan asisten yang terbaik. Pada tingkatan ketiga merupakan alternatif pilihan dari beberapa calon asisten.
Gambar 2. Struktur hierarki asisten praktikum matematika I (prodi statistika)
2. Membuat Matriks Perbandingan Untuk Kriteria
Hasil analisis dari 10 responden untuk 3 kriteria penentuan asisten terbaik untuk program
77 studi statistika Fakultas MIPA Universitas Mulawarman disusun dalam bentuk matriks perbandingan berpasangan. Matriks pembobot antar kriteria selanjutnya disederhanakan dan dihitung jumlah setiap kolom. Hasil penyederhanaan matriks pembobotan antar kriteria seperti pada Tabel 6.
Tabel 6. Matriks Perbandingan untuk Kriteria
Kriteria IPK Penguasaan
Materi Komunikasi IPK 1 1 2 Penguasaan Materi 1 1 2 Komunikasi 0,5 0,5 1 Jumlah 2,5 2,5 5
Pada baris pertama, diperoleh nilai dari pembulatan rata-rata geometric dari hasil kuisioner. Dengan menerapkan konsep dasar AHP dan Persamaan (4), baris kedua diperoleh dengan membagikan setiap nilai baris pertama terhadap nilai penguasaan materi pada baris pertama. Baris ketiga diperoleh dengan membagikan setiap nilai baris pertama terhadap nilai komunikasi pada baris pertama.
3. Membuat Matriks Perbandingan Untuk Kriteria Yang Distandarkan
Setelah nilai dari matriks perbandingan kriteria dimasukkan sesuai dengan kolomnya masing-masing, kemudian data tersebut distandarkan untuk memudahkan dalam memodifikasikan data tersebut. Berikut adalah data dari matriks perbandingan kriteria yang telah distandarkan.
Tabel 7. Matriks Perbandingan untuk Kriteria yang Distandarkan
Kriteria IPK Penguasaan Materi Komunikasi Bobot/ Prioritas
IPK 0,4 0,4 0,4 0,4
Penguasaan
Materi 0,4 0,4 0,4 0,4
Komunikasi 0,2 0,2 0,2 0,2
Jumlah 1 1 1 1
Untuk mendapatkan data yang distandarkan dapat menggunakan perhitungan seperti pada Tabel 4. Kriteria IPK dan penguasaan materi memiliki bobot prioritas yang sama yaitu 0,4, berarti bahwa kriteria IPK dan penguasaan materi memiliki urutan kepentingan yang sama. Kriteria komunikasi memiliki bobot prioritas 0,2 yang berarti bahwa kriteria komunikasi berada pada urutan prioritas kedua setelah kriteria IPK dan penguasaan materi.
4. Menguji Konsistensi Untuk Matriks Perbandingan Kriteria
Setelah mendapatkan nilai prioritas kriteria, data tersebut diuji tingkat kekonsistensiannya untuk mengetahui apakah nilai dari matriks kriteria tersebut telah konsisten atau belum. Apabila penilaian telah konsisten, maka perhitungan selanjutnya dapat diteruskan, namun apabila tidak konsisten maka penilaian harus diulang. Dengan menggunakan Persamaan 7, maka didapat nilai eigen maksimum sebagai berikut:
Karena matriks berordo (terdiri dari 3 kriteria) maka nilai n adalah 3. Dengan menggunakan Persamaan 6 dapat diketahui apakah nilai dari matriks kriteria tersebut sudah konsisten atau belum.
Dari hasil perhitungan diperoleh nilai indeks konsistensi jumlah sampel adalah 0. Karena nilai IK adalah nol, maka nilai dari matriks-matriks kriteria tersebut telah konsisten. Karena nilai dari matriks-matriks kriteria tersebut telah konsisten maka dapat dilanjutkan untuk perhitungan selanjutnya.
5. Membuat Matriks Perbandingan Alternatif Asisten Praktikum yang Distandarkan Setelah nilai dari matriks perbandingan untuk alternatif asisten praktikum dimasukkan sesuai dengan kolomnya masing-masing, kemudian data tersebut distandarkan. Berikut adalah data dari matriks perbandingan untuk alternatif asisten praktikum yang telah distandarkan pada Tabel 8.
Tabel 8. Matriks Perbandingan Alternatif Asisten Praktikum Matematika I yang Distandarkan Asiste n 1 Asiste n 2 Asiste n 3 Asiste n 4 Bobot IPK 1 0,258 0,258 0,258 0,258 0,258 2 0,239 89 0,239 89 0,239 89 0,239 89 0,239 89 3 0,249 0,249 0,249 0,249 0,249 4 0,254 0,254 0,254 0,254 0,254 Jumlah 1 1 1 1 1 Penguasa an Materi 1 0,26 0,26 0,26 0,26 0,26 2 0,245 0,245 0,245 0,245 0,245 3 0,245 0,245 0,245 0,245 0,245 4 0,251 0,251 0,251 0,251 0,251 Jumlah 1 1 1 1 1
78 Asisten 1 Asisten 2 Asisten 3 Asisten 4 Asisten 1 Asisten 2 Asisten 3 Asisten 4 n 1 n 2 n 3 n 4 t Komu nikasi 1 0,267 0,267 0,267 0,267 0,267 2 0,25 0,25 0,25 0,25 0,25 3 0,25 0,25 0,25 0,25 0,25 4 0,234 0,234 0,234 0,234 0,234 Jumlah 1 1 1 1 1
Setelah mendapatkan nilai prioritas dari alternatif pilihan asisten untuk masing-masing kriteria, data tersebut diuji tingkat konsistensiannya juga.
Pengujian konsistensi untuk alternatif dilakukan satu persatu berdasakan kriteria sebelumnya. Karena matriks alternatif untuk masing-masing kriteria berordo 4 maka nilai n adalah 4. Dan nilai indeks konsistensi sampel adalah 0 untuk masing-masing kriteria. Karena nilai IK adalah nol, maka nilai dari matriks-matriks kriteria tersebut telah konsisten.
6. Mengalikan Matriks Perbandingan Alternatif Dengan Matriks Perbandingan Kriteria
Perhitungan terakhir dalam metode AHP yaitu mengalikan nilai prioritas dari matriks perbandingan alternatif dengan nilai prioritas dari matriks perbandingan kriteria. Perkalian matriks bertujuan untuk memperoleh hasil prioritas akhir dari pemilihan asisten praktikum tersebut. Berikut hasil perkalian matriks alternatif dengan nilai prioritas matriks kriteria:
Keterangan kriteria : K1 : IPK
K2 : Penguasaan Materi K3 : Komunikasi
Dari hasil perkalian matriks diperoleh nilai 0,26067 untuk ranking/prioritas 1 atas nama Asisten 1, 0,24841 untuk ranking/prioritas 2 atas nama Asisten 4, 0,2471 untuk ranking/prioritas 3 atas nama Asisten 3, 0,24382 untuk ranking/prioritas 4 atas nama Asisten 2.
7. Perhitungan Dengan Menggunakan Program Lazarus
Langkah pertama yang dilakukan untuk membuat program Lazarus yaitu dengan membuat tampilan yang menarik untuk program tersebut. Setelah tampilan program selesai dibuat, kemudian Syntax dapat dimasukkan ke dalam program yang akan dibuat. Berikut tampilan untuk program Lazarus.
Gambar 3. Tampilan Matriks Perbandingan Kriteria
Tipe data yang digunakan untuk menghitung nilai kriteria adalah real. Pada button process, variabel dimasukkan sesuai dengan kolom edit yang diinginkan. Kemudian rumus dimasukkan untuk masing-masing kolom edit sesuai dengan rumus dari metode AHP dan variabel yang digunakan pada kolom edit tersebut.
Gambar 4. Tampilan Data Asisten Tipe data yang digunakan untuk kolom nama asisten adalah string, sedangkan kolom IPK, penguasaan materi dan komunikasi menggunakan tipe data real.
Pada button input, variabel dimasukkan sesuai dengan kolom edit yang diinginkan. Variabel dihubungkan dari kolom edit tersebut ke kolom edit yang berada pada menu IPK, penguasaan materi dan komunikasi.
Gambar 5. Tampilan Matriks Hubungan Kriteria dan Alternatif
Pada button process di menu hasil, variabel dimasukkan sesuai dengan kolom edit yang diinginkan. Kemudian pada kolom hasil, rumus dimasukkan untuk masing-masing kolom edit
sesuai dengan rumus dari metode AHP dan variabel yang digunakan pada kolom edit
tersebut. Penggunaan kondisi If untuk menunjukkan nilai tertinggi dan menampilkan K1 K2 K3 Kriteria
79 nama asisten yang memiliki nilai terbaik tersebut.
Kesimpulan
Berdasarkan analisis yang telah dilakukan, maka penulis mengambil kesimpulan bahwa kriteria nilai IPK dan kriteria penguasaan materi masing-masing memiliki bobot penilaian 0,4 yang berarti bahwa kriteria nilai IPK dan kriteria penguasaan materi tersebut sama pentingnya. Sedangkan urutan kepentingan kedua yaitu kriteria komunikasi dengan bobot penilaian 0,2.
Berdasarkan hasil analisis, diperoleh nilai prioritas untuk calon asisten praktikum yang terpilih sebagai berikut :
a. Asisten praktikum matematika I prodi statistika adalah Asisten 4 dengan nilai 0,24841 atau 24,84%
b. Asisten praktikum matematika III prodi statistika adalah Asisten 1 dengan nilai 0,2564 atau 25,64%
c. Asisten praktikum matematika I prodi kimia adalah Asisten 1 dengan nilai 0,26268 atau 26,27%
d. Asisten Praktikum Metode Statistika II adalah Asisten 3 dengan nilai 0,25682 atau 25,68%
e. Asisten Praktikum Statistika Non Parametrik adalah Asisten 2 dengan nilai 0,33672 atau 33,67%
Hasil penilaian dari calon asisten praktikum telah sesuai karena Asisten yang terpilih memiliki nilai IPK, penguasaan materi, dan
komunikasi yang lebih tinggi dan lebih baik dibandingkan dengan calon asisten yang lainnya.
Daftar Pustaka
[19] Dermawan, R. (2005). Model Kuantitatif
Pengambilan Keputusan dan
Perencanaan Strategi. Bandung: CV. Alfabeta.
[20] Leo, J. (2014). Penentuan Komoditas Unggulan Pertanian Dengan Metode Analytical Hierarchy Process (AHP). Jurnal Saintia Matematika Universitas Sumatera Utara, Vol. 02 (3), hal 213-224. ISSN: 2337-9197.
[21] Mulyono, S. (2004). Riset operasi. Jakarta: Fakultas Ekonomi, Universitas Indonesia.
[22] Saaty, TL. (1993). Pengambilan Keputusan Bagi Para Pemimpin, Proses Hierarki Analitik untuk Pengambilan Keputusan dalam Situasi yang Kompleks. Jakarta: PT.Pustaka Binaman Pressindo.
[23] Suyono, RS. (2010). Penggunaan Metode
Proses Hierarki Analitik (PHA) Dalam Pemilihan Lokasi Untuk Relokasi Bandara Rahadi Oesman Ketapang Kalimantan Barat. Jurnal Teknik Sipil Universitas Tanjungpura, Vol. 10 (1), hal 15-32. Zainuddin, M. (1996). Panduan Praktikum dalam Mengajar di Perguruan Tinggi, Bagian Empat. Jakarta: Departemen Pendidikan dan Kebudayaan.