R DNA (3.1.1) k 1. DNA NTP k 3. k 2

MODEL DAN ANALISA

MATEMATIKA

3.1

Model Matematika

Pada bab ini akan dimodelkan proses ekspresi gen dengan kontrol yang dilakukan oleh protein repressor. Kemudian kita analisis model yang diperoleh yakni mencari solusi steady-state dan kestabilannya. Sementara itu, dengan analisis numerik kita akan menentukan parameter yang sangat berpengaruh pada proses ini.

Kita misalkan protein yang dihasilkan oleh ekspresi gen ini adalah protein repressor. Sebagaimana ditulis pada Bab 2, ekspresi gen terdiri dari transkripsi dan translasi. Mula-mula ketika repressor tidak berikatan dengan DNA, DNA tersebut akan di-transkripsi berdasarkan suatu reaksi kimia sehingga terbentuk mRNA di nukleus. Reaksi kimia tersebut diberikan oleh [6] :

DN A+ρR k+1 k₋₁ R∗DN A (3.1.1) DN A+N T P k+2 k₋₂ DN A∗N T P k3 →DN A+mRN A (3.1.2)

dengan R menyatakan protein repressor, R∗DN A, DN A∗N T P adalah senyawa kompleks dan N T P adalah substansi kimia nukleotida trifosfat.

mRNA yang terbentuk dari proses transkripsi di nukleus tersebut akan menuju ribosom untuk mentranslasikan diri sehingga terbentuk protein yang dikodenya. Dalam perjalanannya menuju ribosom, mRNA harus melalui membran inti yang memiliki permeabilitas tertentu dan berdifusi di sitoplasma menuju ribosom yang diasumsikan terletak pada suatu jarak tertentu dari nukleus. Proses translasi yang terjadi dinyatakan oleh reaksi [6] :

mRN A+AAk+4

k₋₄ mRN A∗AA k₅

→mRN A+R (3.1.3)

dengan AA menyatakan asam amino.

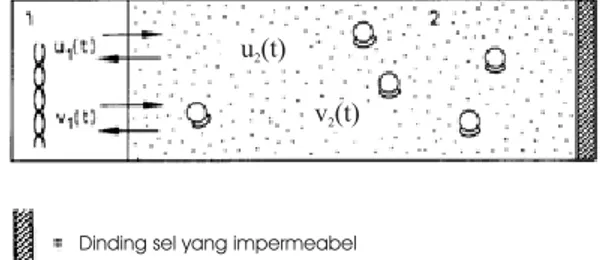
Untuk memodelkan permasalahan ini, kita bagi sel menjadi dua kompartemen (ru-ang bagian), yaitu nukleus sebagai kompartemen pertama dan sitoplasma sebagai kompartemen kedua yang mengandung ribosom, Gambar 3.1. Kedua kompartemen tersebut dipisahkan oleh membran inti yang menyelubungi nukleus. Selain itu, sel tersebut dibatasi oleh dinding sel yang impermeabel.

Pada kompartemen pertama terjadi reaksi kimia yakni reaksi pada proses

trans-Dinding sel yang impermeabel

v (t)2 u (t)2

Gambar 3.1: Model dengan 2 kompartemen

kripsi. DNA berkombinasi secara reversibel dengan sejumlah ρ molekul repressor (R) membentuk senyawa kompleks R∗DN A yang dinyatakan oleh reaksi (3.1.1) dengan konstanta laju reaksi K₁. Sehingga diperoleh :

K₁ = DN A∗Rρ

Sementara itu, DNA yang tidak berkombinasi dengan repressor berkombinasi dengan NTP (nukleotida trifosfat) membentuk mRNA berdasarkan reaksi (3.1.2) dengan konstanta K₂. Sehingga kita peroleh :

K₂ = DN A∗N T P

DN A.N T P (3.1.5)

DN AT = DN A+R∗DN A+DN A∗N T P (3.1.6) = DN A(1 +K₁.Rρ +K₂.N T P)

Secara biologi, jumlah atau konsentrasi DN AT (DNA total) tetap yang diberikan oleh persamaan (3.1.6) sedangkan konsentrasi mRNA dapat berubah-ubah tergan-tung pada kondisi sel. Jika pada sel terdapat substrat maka DNA akan meme-rintahkan untuk memproduksi enzim untuk mengubah substrat tersebut menjadi produk akhir yang diinginkan dengan membentuk salinan perintahnya yang terkan-dung dalam mRNA. Sebagai contoh, bila di sel terdapat laktosa sebagai substrat glukosa, sel akan menghidupkan lac operon-nya yang akan mencetak mRNA yang membawa perintah untuk mensintesa enzim beta-galaktosidase yang akan memecah laktosa menjadi glukosa dan galaktosa.

Jika diasumsikan laju penghancuran mRNA dan repressor terjadi secara linier maka persamaan diferensial untuk konsentrasi mRNA, pembentukan dan penghancuran, dapat dirumuskan sebagai berikut [6]. Misal u₁ menyatakan konsentrasi (molar) mRNA dan v₁ menyatakan konsentrasi (molar) repressor pada kompartemen per-tama maka diperoleh persamaan laju perubahan konsentrasi mRNA dan repressor pada kompartemen pertama sebagai berikut :

·

u₁(t) = (v₁)−b₁u₁(t) +a₁(u₂(t)−u₁(t)) ·

v₁(t) = a₂(v₂(t)−v₁(t))−b₂v₁(t)

(v₁) menyatakan laju pembentukan mRNA berdasarkan reaksi (3.1.1) dan (3.1.2),

b₁ dan b₂ masing-masing adalah konstanta laju penghancuran mRNA dan repres-sor serta a₁ dan a₂ masing-masing adalah kontanta permeabilitas yang berasosiasi dengan u₁ dan v₁.

Kita tinjau (v₁), dari reaksi (3.1.2) dan bahwa DNA pada reaksi (3.1.2) adalah DNA yang ditranskripsi sementara ada bagian lain dari DNA yang tidak dapat ditranskripsi yaitu pada reaksi (3.1.1), maka diperoleh [9] :

(v₁) =k₃ DN A∗N T P.f(v₁) (3.1.7) Dengan f(v₁) adalah fraksi dari DNA yang dapat ditranskripsi. Dari persamaan (3.1.5), (3.1.6) dan (3.1.7) diperoleh : (v₁) = τ 1 +k[v₁(t)]ρ (3.1.8) denganτ = k3K₂DN A_T.N T P 1+K2.N T P ,k = k₊₁ k−1(1+K2.N T P),K2 = k₊₂ k−2. Persamaan (3.1.8) belum

memperhitungkan waktu yang diperlukan untuk transkripsi, sebut r₁. Jika kita masukkan r₁ pada persamaan (3.1.8) maka r₁ akan menjadi waktu tunda sehingga unsur v₁(t) menjadiv₁(t−r₁).

Pada kompartemen kedua, mRNA ditranslasi oleh ribosom untuk memproduksi pro-tein. Waktu yang dibutuhkan oleh mRNA untuk berdifusi dari nukleus ke ribosom relatif kecil dibandingkan dengan waktu untuk transkripsi dan translasi. Oleh karena itu, kita abaikan proses difusi tersebut. Dari reaksi (3.1.3) diperoleh :

K₄ = mRN A∗AA

mRN A.AA (3.1.9)

Misal u₂ menyatakan konsentrasi (molar) mRNA dan v₂ menyatakan konsentrasi (molar) repressor pada kompartemen kedua maka diperoleh :

·

u₂(t) = a₃(u₁(t)−u₂(t))−b₁u₂(t) ·

v₂(t) = S(u₂)−b₂v₂(t) +a₄(v₁(t)−v₂(t))

dengana₃ dana₄ masing-masing merupakan konstanta permeabilitas yang berasosi-asi dengan u₂(t) dan v₂(t). S(u₂) menyatakan laju pembentukan protein repressor berdasarkan reaksi (3.1.3). Dengan demikian, kita peroleh :

Dari persamaan (3.1.9) dan (3.1.10) diperoleh :

S(u₂) = c₀u₂(t) (3.1.11)

dengan c₀ = k₅ K₄ AA, K₄ = k_k+4

−4. Jika pada persamaan (3.1.11) kita masukkan

waktu yang diperlukan untuk translasi, sebutr₂, makar₂ akan menjadi waktu tunda sehingga unsur u₂(t) menjadi u₂(t−r₂).

Dengan melihat keseluruhan proses, kita mendapatkan model yang dicari yaitu berupa SPD dengan waktu tunda r₁ dan r₂ sebagai berikut :

· u₁(t) = τ 1 +k[v₁(t−r₁)]ρ −b1u1(t) +a1(u2(t)−u1(t)) · v₁(t) = a₂(v₂(t)−v₁(t))−b₂v₁(t) (3.1.12) · u₂(t) = a₃(u₁(t)−u₂(t))−b₁u₂(t) · v₂(t) = c₀u₂(t−r₂)−b₂v₂(t) +a₄(v₁(t)−v₂(t))

3.2

Analisa Model

3.2.1

Analisa Masalah

_Steady-State

Pada sub bab ini akan dibahas persamaan yang independen terhadap waktu yang diperoleh dari model (3.1.12). Artinya, untuk waktu yang sangat lama model terse-but akan memberikan solusi yang konstan atau konvergen ke suatu nilai. Oleh karena itu, bentuk diferensial pada (3.1.12) bernilai nol sehingga diperoleh per-samaan steady-state sebagai berikut :

(¯v₁)−b₁u¯₁+a₁(¯u₂−u¯₁) = 0

a₂(¯v₂−v¯₁)−b₂v¯₁ = 0

a₃(¯u₁−u¯₂)−b₁u¯₂ = 0

Dari persamaan steady-state di atas terdapat empat variabel dengan empat per-samaan. Dengan demikian, dapat diperoleh solusi steady-state nya adalah :

¯ v₁ = ¯v₁ ¯ v₂ = b2+a2 a₂ v¯1 ¯ u₁ = b2+a2 a₂ u¯2 ¯ u₂ = B2 c₀v¯1 dengan ¯v₁ memenuhi (¯v₁) = B1B₂ c0 v¯1 denganB1 = b2₁+a₁b₁+a₃b₁ a3 , B2 = b2₂+a₂b₂+a₄b₂ a2 .

3.2.2

Kestabilan Lokal

Dari model (3.1.12) dengan r₂ = 0 disekitar titik kesetimbangan dapat dituliskan sebagai berikut : ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ · u₁(t) · v₁(t) · u₂(t) · v₂(t) ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ −(a₁+b₁) 0 a₁ 0 0 −(a₂+b₂) 0 a₂ a₃ 0 −(a₃+b₁) 0 0 a₄ c₀ −(a₄+b₂) ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ u₁(t) v₁(t) u₂(t) v₂(t) ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ + ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 0 (v₁(t−r₁)) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

Pertama kita analisis terlebih dahulu jika= 0. Dengan asumsi tersebut, diperoleh persamaan karakteristik :

Dengan demikian, diperoleh :

λ₁ = −b₁ λ₂ = −b₂

λ₃ = −(a₁+a₃+b₁)

λ₄ = −(a₂+a₄+b₂) Maka syarat kestabilan dari model (3.1.12) adalah :

b₁ >0

b₂ >0 (a₁+a₃ +b₁)>0 (a₂+a₄ +b₂)>0

Selanjutnya tinjau kasus = 0. Persamaan karakteristiknya adalah :

|λI−J₀−Jr1e−λr1 |= 0

denganJ₀ = _∂x∂g_(t),Jr₁ = _∂x(∂g_t−r1), ˙x=g(x(t), x(t−r1)) danx(t) = [u1(t), v1(t), u2(t), v2(t)]. Sehingga diperoleh :

(b₁+λ)(b₂+λ)(a₁+a₃+b₁+λ)(a₂+a₄+b₂+λ)−c₀a₂a₃g(x₂(t−r₁))e−λr1 _{= 0 (3.2.1)}

Tidaklah mudah untuk menentukan nilai λ yang memenuhi persamaan 3.2.1. Oleh sebab itu, analisa pengaruh parameter pada model dengan waktu tunda akan di-lakukan secara numerik dan dijelaskan pada bab selanjutnya.