MATEMATIKA DASAR 2A
MODUL 14 – VARIABEL ACAK DAN DISTRIBUSI KONTINU
Tim Matematika
TAHAP PERSIAPAN BERSAMA
INSTITUT TEKNOLOGI SUMATERA – LAMPUNG SELATAN
2019
TAHAP PERSIAPAN BERSAMA | 2018/2019 1 PENDAHULUAN
Bidang statistika berurusan dengan penarikan inferensi tentang populasi dan sifat populasi. Percobaan yang dilakukan memberikan hasil yang berkemungkinan.
Pelemparan sejumlah koin merupakan suatu contoh percobaan statistika, suatu istilah yang memberikan setiap proses yang menghasilkan pengamatan yang berkemungkinan.
Mengetahui bahwa distribusi variabel acak memberi tahu kita semua tentang variabel acak. Namun, dalam praktiknya, sering kali tidak mungkin atau tidak perlu untuk mengetahui semua peluang distribusi dari variabel acak yang menggambarkan eksperimen acak tertentu. Sebagai gantinya, mungkin cukup untuk menentukan beberapa kuantitas karakteristik, seperti nilai rata-rata dan ukuran yang menggambarkan penyebaran di sekitar nilai rata-rata.
Distribusi peluang kontinu yang terpenting dalam seluruh bidang statistika adalah distribusi normal. Grafiknya, disebut kurva normal, berbentuk lonceng yang menggambarkan dengan cukup baik banyak gejala yang muncul di alam, industri, dan penelitian. Pengukuran fisik di bidang seperti percobaan meteorologi, penelitian curah hujan, dan pengukuran suku cadang yang diproduksi sering dengan baik dapat diterangkan menggunakan distribusi normal.
Modul 14 ini memberikan materi Variabel Acak dan Distribusi Kontinu.
Perlu diketahui bahwa dalam mempelajari variabel acak dan distribusi kontinu dibutuhkan pemahaman tentang konsep dari modul-modul sebelumnya terutama tentang turunan, integral, ruang sampel, dan peluang.
Berdasarkan penjelasan di atas, tujuan instruksional yang harus dicapai mahasiswa pada pembelajaran ini antara lain mahasiswa:
1 • Mampu menghitung peluang suatu kejadian melalui variabel acak kontinu
2 • Mampu menghitung dan menggambar suatu fungsi distribusi kontinu
3
• Mampu menghitung nilai harapan (mean) dan variansi untuk suatu variabel acak yang diberikan atau suatu ruang sampel kontinu
4
• Dapat menghitung peluang kasus kontinu dan menggunakan tabel distribusi normal
TAHAP PERSIAPAN BERSAMA | 2018/2019 2 1. VARIABEL ACAK KONTINU
Pada modul sebelumnya, membahas variabel acak yang mengambil sejumlah nilai diskrit. Pada modul ini, kita akan membahas variabel acak yang mengambil nilai kontinu disebut variabel acak kontinu. Misalnya, ketika kita mempertimbangkan distribusi panjang suatu organisme: dalam interval (spesies-spesifik) yang sesuai, panjang individu dapat mengambil nilai apa pun. Sebagai ilustrasi, perhatikan contoh berikut yang diadaptasi dari de Roos (1996): Aliran air Daphnia pulex memakan alga Chlamydomonas rheinhardii. Komponen penting dari perilaku makan Daphnia adalah ketergantungan yang kuat dari jumlah makanan yang dikonsumsi pada ukuran individu.
Untuk memodelkan perilaku makan dari Daphnia, kita harus membuat kode struktur rumah populasi.
Kita melihat ukuran sebagai variabel acak, dilambangkan dengan , dan menentukan untuk semua nilai yang mungkin, fraksi Daphnia yang ukurannya kurang dari atau sama dengan . Jika ukuran populasi besar, fraksi ini dapat didekati dengan baik oleh fungsi kontinu, yang ditunjukkan dengan . Fungsi ini berfungsi sebagai fungsi distribusi, jadi .
Fungsi distribusi sepenuhnya mencirikan peluang distribusi dari variabel acak, seperti yang kita lihat di bagian sebelumnya. Sifat ini tidak berbeda untuk variabel acak kontinu. Untuk menggambarkan peluang distribusi variabel acak kontinu , kita akan menggunakan fungsi distribusinya .
Definisi.
Fungsi distribusi untuk variabel acak kontinu memiliki definisi yang sama dengan yang untuk variabel acak diskrit:
∫
yang telah memenuhi sifat fungsi distribusi dapat dilihat pada Gambar 1:
TAHAP PERSIAPAN BERSAMA | 2018/2019 3 Gambar 1. Fungsi Distribusi Variabel Acak Kontinu
Beberapa sifat fungsi distribusi yang tidak ada dalam kasus variabel acak diskrit:
1.
2.
3. adalah fungsi tak-turun dan kontinu.
Perhatikan di satu sisi, bahwa fungsi distribusi variabel acak kontinu adalah kontinu, tidak seperti fungsi distribusi variabel acak diskrit, yang sebagian konstan dan mengambil lompatan pada nilai-nilai di mana . Di sisi lain, kedua fungsi distribusi tak-turun dan mengambil nilai antara 0 dan 1.
Jika ada fungsi non-negatif sehingga fungsi distribusi dari variabel acak memiliki representasi
∫
kita mengatakan bahwa adalah variabel acak kontinu dengan fungsi kerapatan peluang (probability density function) . Perhatikan Gambar 2 berikut:
Gambar 2. Fungsi Distribusi dan Fungsi Kerapatan yang sesuai dari variabel acak kontinu
TAHAP PERSIAPAN BERSAMA | 2018/2019 4 Karena adalah fungsi distribusi, maka
∫
Setiap fungsi non-negatif pada persamaan (1) mendefinisikan fungsi kerapatan. Fungsi tidak perlu kontinu, meskipun dalam semua aplikasi akan kontinu, kecuali mungkin untuk sejumlah titik. Fungsi akan sering didefinisikan sebagai fungsi kontinu. Menggunakan Teorema Dasar Kalkulus 2, kita dapat memperoleh fungsi kerapatan dari variabel acak kontinu dari fungsi distribusi dengan membedakan fungsi distribusi. Jadi, untuk semua titik di mana dapat dibedakan. Pada titik di mana tidak dapat dibedakan, kita tetapkan , strategi yang memastikan bahwa fungsi kerapatan didefinisikan di mana-mana.
Selanjutnya,
maka
∫ Yaitu, area di bawah kurva antara dan merupakan peluang bahwa variabel acak mengambil nilai antara dan , seperti yang diilustrasikan dalam Gambar 3.
Penting untuk menyadari bahwa, dalam persamaan (2), peluang diwakili oleh bidang (luas); khususnya, integral dari , bukan itu sendiri yang memiliki interpretasi fisik. Fungsi kerapatan tidak memiliki interpretasi fisik langsung. Kemudian di bagian ini, kita akan menjelaskan bagaimana menemukan secara empiris.
Gambar 3. Area antara fungsi kerapatan dan sumbu antara dan merupakan peluang bahwa variabel acak terletak antara dan
TAHAP PERSIAPAN BERSAMA | 2018/2019 5 Berbeda dengan variabel acak diskrit, dimana dan dapat berbeda, tidak ada perbedaan untuk variabel acak kontinu, karena
∫ Oleh karena itu,
∫ Sehingga, fungsi kerapatan peluang dengan adalah variabel acak kontinu dapat didefinisikan sebagai berikut
Definisi.
Sebuah variabel acak disebut variabel acak kontinu jika variabel itu mengambil nilai kontinu. Peluang distribusi dapat digambarkan dengan fungsi kerapatan peluang , yang memiliki sifat-sifat berikut:
1. untuk semua 2. ∫
3. ∫
Contoh 1.
Diberikan fungsi distribusi variabel acak kontinu sebagai berikut:
{
a. Tentukan dan gambarkanlah fungsi kerapatan yang sesuai, b. Hitunglah .
Jawab.
a. Untuk menentukan fungsi kerapatan, kita perlu Teorema Dasar Kalkulus 2 atau Integral dengan batas fungsi. Jadi,
∫
Fungsi kerapatan dapat ditentukan dengan membedakan fungsi distribusi ke dalam interval , , dan :
TAHAP PERSIAPAN BERSAMA | 2018/2019 6 {
Untuk mendefinisikan fungsi kerapatan di mana-mana, kita tetapkan .
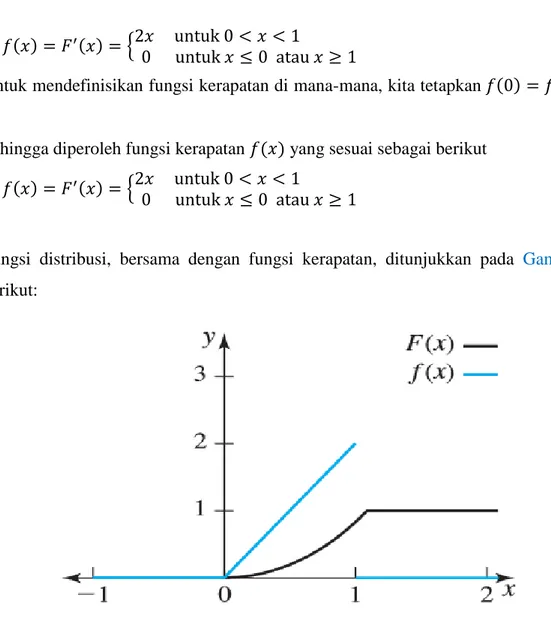
Sehingga diperoleh fungsi kerapatan yang sesuai sebagai berikut {
Fungsi distribusi, bersama dengan fungsi kerapatan, ditunjukkan pada Gambar 4 berikut:
Gambar 4. Fungsi Distribusi dan fungsi kerapatan yang sesuai
b. Dengan menggunakan fungsi distribusi, diperoleh
( ) ( ) ( )
Sebaliknya, jika kita menggunakan fungsi kerapatan, kita harus menghitung
( ) ∫
∫
∫
∫
∫ ∫
∫
] ] ( )
TAHAP PERSIAPAN BERSAMA | 2018/2019 7 Contoh 2.
Diberikan fungsi kerapatan variabel acak kontinu sebagai berikut {
a. Tentukan fungsi distribusi yang sesuai,
b. Hitunglah , c. Hitunglah . Jawab.
a. Untuk , ∫
∫
∫ ∫
∫ ]
]
Sehingga fungsi distribusi yang sesuai sebagai berikut
{
b. Dengan menggunakan fungsi distribusi,
atau dengan menggunakan fungsi kerapatan,
∫
∫
]
c. Dengan menggunakan fungsi distribusi,
TAHAP PERSIAPAN BERSAMA | 2018/2019 8 2. NILAI RATA-RATA (MEAN) DAN RAGAM (VARIANSI) DARI VARIABEL
ACAK KONTINU
Rumus untuk mean dan variansi dari variabel acak kontinu dianalisis sesuai dengan keputusan yang diambil. Nilai harapan, atau mean, dari variabel acak kontinu dengan fungsi kerapatan peluang didefinisikan sebagai
∫
Nilai harapan dari suatu fungsi variabel acak adalah
[ ] ∫
dengan adalah fungsi kerapatan peluang dari . Variansi dari variabel acak kontinu dengan mean didefinisikan sebagai
∫
Formula alternatif yang diberikan di bagian sebelumnya juga berlaku:
[ ] ∫
( ∫
)
Ingat bahwa integral ini didefinisikan pada interval yang tidak terbatas dan mungkin tidak kontinu.
Contoh 3.
Fungsi kerapatan peluang dari variabel acak diberikan sebagai berikut {
Dengan grafik seperti pada Gambar 5 berikut:
TAHAP PERSIAPAN BERSAMA | 2018/2019 9 Gambar 5. Fungsi kerapatan peluang , dengan lokasi mean X
Hitunglah nilai mean dan variansi dari ? Jawab.
Untuk menghitung nilai mean, kita hitung ∫
∫
∫ ∫
∫
∫ ∫ ∫
∫ ]
Nilai mean ditunjukkan pada Gambar 5. Untuk menghitung nilai variansi, pertama kita hitung
∫
∫
∫ ∫
∫
∫ ∫ ∫
∫ ]
Variansi dari adalah
[ ] ( )
TAHAP PERSIAPAN BERSAMA | 2018/2019 10 3. DISTRIBUSI NORMAL
Distribusi normal pertama kali diperkenalkan oleh Abraham De Moivre (1667-1754) dalam konteks peluang komputasi dalam percobaan binomial ketika banyaknya uji coba yang besar. Kemudian, Gauss menunjukkan bahwa distribusi ini penting dalam analisis kesalahan pengukuran. Distribusi ini adalah distribusi berkelanjutan yang paling penting, dan membahas aplikasi pertama kali. Genetika kuantitatif berkaitan dengan karakter metrik, seperti tinggi tanaman, ukuran volume, berat badan, dan lainnya.
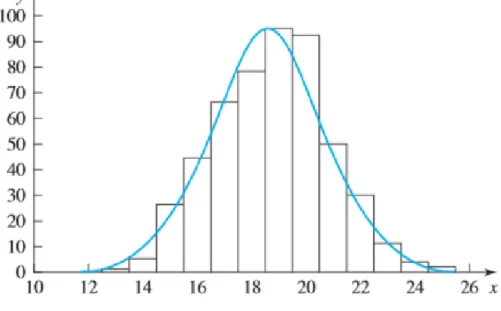
Karakter tersebut disebut karakter kuantitatif. Ada banyak karakter kuantitatif yang distribusi frekuensinya mengikuti kurva bengkok. Sebagai contoh, menghitung bulu pada bagian tertentu dari perut (sternite kelima) dari keturunan Drosophila melanogaster, Mackay (1984) menemukan bahwa banyaknya bulu bervariasi menurut kurva berbentuk lonceng disebut sebagai kurva normal. (Kurva ini ditunjukkan pada Gambar 6, yang diadaptasi dari Hartl dan Clark, 1989.)
Gambar 6. Banyaknya bulu perut
Kurva halus pada Gambar 6 yang sesuai dengan histogram sebanding dengan fungsi kerapatan dari distribusi normal. (Kurva tidak diskalakan, sehingga area di bawah kurva tidak sama dengan 1.) Fungsi kerapatan dari distribusi normal dijelaskan oleh hanya dua parameter, yang disebut dan , yang dapat diperkirakan dari data. Parameter dapat berupa bilangan real apa pun; parameter adalah bilangan real positif. Fungsi kepadatan distribusi normal dijelaskan sebagai berikut:
TAHAP PERSIAPAN BERSAMA | 2018/2019 11 Definisi.
Variabel acak kontinu biasanya terdistribusi normal dengan parameter dan jika memiliki fungsi kerapatan
√
Parameter adalah rata-rata dan parameter adalah simpangan baku (standar deviasi) dari distribusi normal.
Berikut ini adalah sifat-sifat dari : 1. adalah simetris dimana .
2. Nilai maksimum dari adalah pada .
3. Titik refleksi dari adalah pada dan .
Bentuk fungsi kerapatan dari distribusi normal ditunjukkan pada Gambar 7 berikut
Gambar 7. Kurva Normal
Karena adalah fungsi kerapatan peluang,
∫
Dengan alat yang kita miliki sejauh ini, kita tidak dapat menunjukkan bahwa fungsi kerapatan dinormalisasi menjadi 1. Mean memang nilai harapan dari ; yaitu,
∫
Selanjutnya, jika kuantitas terdistribusi normal dengan parameter dan dengan , maka
TAHAP PERSIAPAN BERSAMA | 2018/2019 12 ∫
√
Tidak mungkin untuk mengevaluasi integral ini dengan menggunakan fungsi-fungsi dasar; integral tersebut hanya dapat dievaluasi secara numerik. Ada tabel untuk distribusi normal dengan parameter dan yang mencantumkan nilai untuk
∫
√
Tabel untuk distribusi normal terdapat dalam Lampiran hal 22 dan dapat digunakan untuk memperoleh peluang untuk dan yang lebih umum.
Tabel untuk distribusi normal dengan rata-rata 0 dan standar deviasi 1 (lihat Lampiran hal 22) dapat digunakan untuk menghitung peluang ketika distribusi normal dengan rata-rata dan standar deviasi . Kita mulai dengan menjelaskan bagaimana menggunakan tabel untuk distribusi normal dengan mean 0 dan standar deviasi 1, yang disebut distribusi normal standar (distribusi normal baku), yang kerapatannya diberikan oleh
∫
√
Pada tabel mencantumkan nilai untuk ∫
√
Secara geometris, adalah area di sebelah kiri garis di bawah grafik fungsi kerapatan, seperti yang diilustrasikan dalam Gambar 8 berikut.
Gambar 8. Area di sebelah kiri di bawah grafik kerapatan normal , yang tercantum dalam tabel untuk distribusi normal.
TAHAP PERSIAPAN BERSAMA | 2018/2019 13 Kita menafsirkan sebagai peluang bahwa observasi berada di sebelah kiri . Misalnya, ketika , (Lihat Lampiran hal 22), dan kita katakan bahwa peluang pengamatan memiliki nilai kurang dari atau sama dengan 1 adalah 0.8413. Dengan kata lain, 84.13% populasi memiliki nilai kurang dari atau sama dengan 1. Seperti yang dapat dilihat, tabel tidak menyediakan entri untuk nilai negatif . Untuk menghitung nilai-nilai tersebut, kita ambil keuntungan dari sifat simetri fungsi kerapatan. Misalnya, kita melihat dari grafik fungsi bahwa area di sebelah kiri −1 sama dengan area di sebelah kanan 1. Perhatikan Gambar 9. Jadi, jika kita ingin menghitung , kita tulis
∫
√
∫
√
∫ √
∫
√
Di sini, digunakan fakta bahwa total area sama dengan 1.
Gambar 9. Luas wilayah yang diarsir sama dengan luas wilayah yang diarsir
TAHAP PERSIAPAN BERSAMA | 2018/2019 14 Kita dapat menggunakan tabel untuk menghitung area di bawah grafik kerapatan normal dengan mean μ dan deviasi standar σ. Dengan demikian, untuk menemukan nilai
∫ √
dengan , kita substitusi
Sehingga menjadi
∫ √
∫
√
(
)
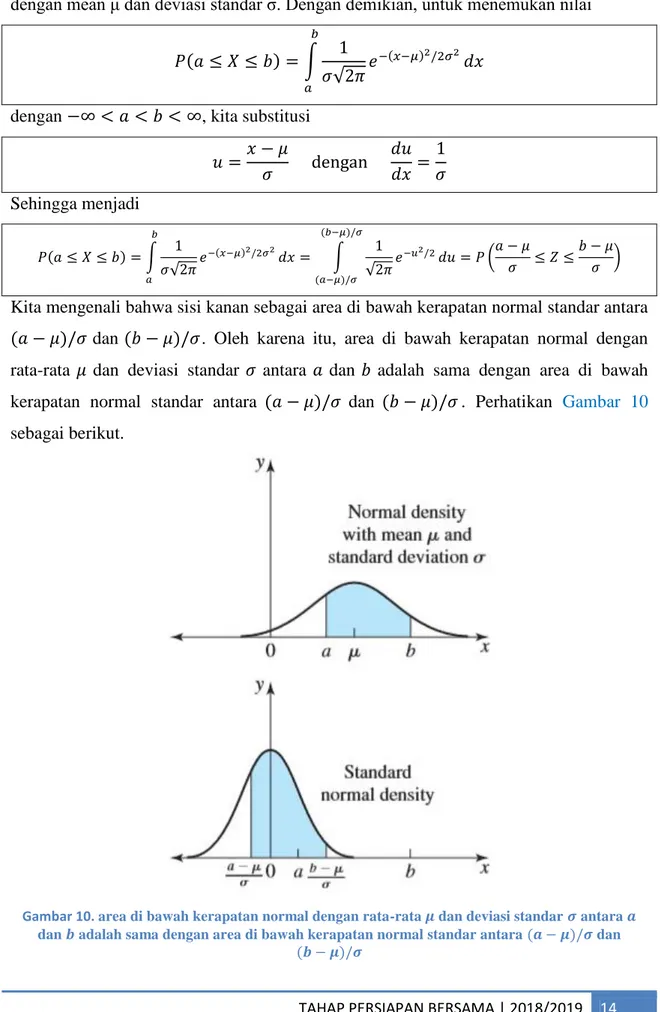
Kita mengenali bahwa sisi kanan sebagai area di bawah kerapatan normal standar antara dan . Oleh karena itu, area di bawah kerapatan normal dengan rata-rata dan deviasi standar antara dan adalah sama dengan area di bawah kerapatan normal standar antara dan . Perhatikan Gambar 10 sebagai berikut.
Gambar 10. area di bawah kerapatan normal dengan rata-rata dan deviasi standar antara dan adalah sama dengan area di bawah kerapatan normal standar antara dan
TAHAP PERSIAPAN BERSAMA | 2018/2019 15 Contoh 4.
Misalkan terdistribusi normal dengan mean 3 dan simpangan baku 2. Tentukan fraksi populasi yang masuk dalam interval [ ]; yaitu, menentukan [ ] .
Jawab.
Diketahui dan .
Untuk mengatasi masalah ini, kita harus menghitung
∫ √
Jika kita menghitung integral tersebut tidaklah mudah, maka kita gunakan transformasi
Sehingga diperoleh
Oleh karena itu, area di bawah kerapatan normal dengan rerata 3 dan deviasi standar 2 antara 2 dan 5 adalah sama dengan daerah di bawah kerapatan normal standar antara
−1/2 dan 1. Oleh karena itu, integral dalam (4) sama dengan
∫ √
∫
√
∫
√
( ) [ ( )]
( )
dan [ ] .
TAHAP PERSIAPAN BERSAMA | 2018/2019 16 Alih-alih menuliskan integral ini, lebih mudah untuk menentukan apa yang perlu kita hitung ketika kita membuat sketsa area yang relevan di bawah kurva normal standar.
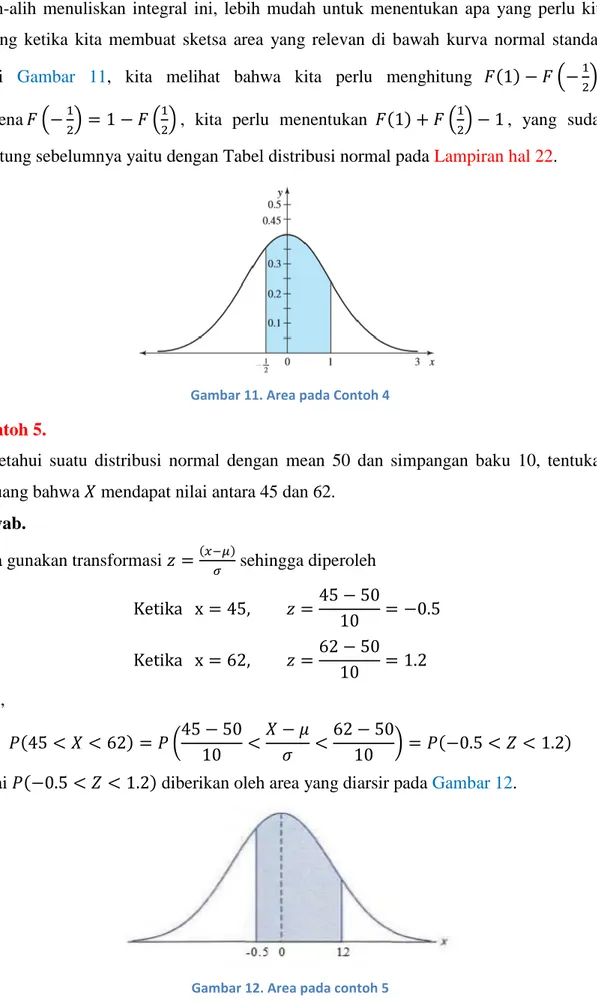
Dari Gambar 11, kita melihat bahwa kita perlu menghitung ( ) . Karena ( ) ( ) , kita perlu menentukan ( ) , yang sudah dihitung sebelumnya yaitu dengan Tabel distribusi normal pada Lampiran hal 22.
Gambar 11. Area pada Contoh 4
Contoh 5.
Diketahui suatu distribusi normal dengan mean 50 dan simpangan baku 10, tentukan peluang bahwa mendapat nilai antara 45 dan 62.
Jawab.
Kita gunakan transformasi sehingga diperoleh
Jadi,
(
) Nilai diberikan oleh area yang diarsir pada Gambar 12.
Gambar 12. Area pada contoh 5
TAHAP PERSIAPAN BERSAMA | 2018/2019 17 Area ini dapat dicari dengan mengurangkan area sebelah kiri ordinat dari seluruh luas bagian kiri . Dengan menggunakan Tabel Distribusi Normal (Lampiran hal 22), diperoleh
(
)
[ ]
Contoh 6.
Diketahui distribusi normal dengan dan , tentukan peluang bahwa mendapat suatu nilai lebih besar dari .
Jawab.
Distribusi peluang normal dengan area yang dicari diperlihatkan pada Gambar 13 berikut
Gambar 13. Area pada contoh 6
Untuk mencari , kita perlu menghitung area di bawah kurva normal di sebelah kanan .
Kita dapat menghitung dengan menransformasi ke nilai , kemudian mencari area di sebelah kiri dari Tabel Distribusi Normal (Lampiran Hal 22), dan kemudian cari selisih area ini dengan 1. Diperoleh
Sehingga
TAHAP PERSIAPAN BERSAMA | 2018/2019 18 RINGKASAN
Diskrit Fungsi
Kerapatan Peluang
∫
Sifat-sifat:
1. untuk semua 2. ∫
3.
∫ Fungsi
Distribusi
∫ . Sifat-sifat:
1.
2.
3. adalah fungsi tak-turun dan kontinu.
Nilai Harapan (Mean) dari Variabel Acak
∫
∫
[ ] ∫
Variansi dari
Variabel Acak ∫
[ ] ∫
[ ∫
]
Simpangan Baku
√
TAHAP PERSIAPAN BERSAMA | 2018/2019 19 Distribusi
Normal ∫ √
Distribusi Normal Standar
(
) ∫
√
dengan
TAHAP PERSIAPAN BERSAMA | 2018/2019 20 LATIHAN
1. Diberikan fungsi distribusi variabel acak kontinu sebagai berikut {
a. Tentukan fungsi kerapatan yang sesuai,
b. Gambarkanlah grafik fungsi distribusi dan fungsi kerapatan , c. Hitunglah .
2. Diberikan fungsi kerapatan variabel acak kontinu sebagai berikut {
a. Tentukan fungsi distribusi yang sesuai,
b. Hitunglah .
3. Permintaan mingguan Coca Cola, dalam ribuan liter, pada suatu jaringan pemasaran daerah, merupakan variabel acak kontinu dengan fungsi kerapatan peluang sebagai berikut
{ a. Tentukan ,
b. Tentukan ,
c. Tentukan simpangan baku dari .
4. Misalkan menjadi variabel acak kontinu dengan fungsi kerapatan peluang {
a. Tentukan nilai harapan dari ,
b. Tentukan variansi dari .
5. Misalkan terdistribusi normal dengan mean 3 dan simpangan baku 2. Tentukan a. ,
b. , c. , d. .
TAHAP PERSIAPAN BERSAMA | 2018/2019 21 6. Suatu jenis baterai mobil rata-rata (mean) berumur 3.0 tahun dengan simpangan
baku 0.5 tahun. Jika dianggap umur baterai berdistribusi normal, tentukan peluang suatu baterai tertentu akan berumur kurang dari 2.3 tahun?
7. Suatu perusahaan listrik menghasilkan bila lampu yang umurnya berdistribusi normal dengan rata-rata (mean) 800 jam dan simpangan baku 40 jam. Hitunglah peluang suatu bola lampu dapat menyala antara 778 dan 834 jam.
8. Suatu mesin membuat alat tahanan listrik dengan rata-rata (mean) tahanan 40 ohm dan simpangan baku 2 ohm. Misalkan bahwa tahanan berdistribusi normal dan dapat diukur sampai derajat ketelitian yang diinginkan. Berapa persentase alat yang mempunyai tahanan melebihi 43 ohm?
TAHAP PERSIAPAN BERSAMA | 2018/2019 22 Lampiran Tabel Distribusi Normal
√
TAHAP PERSIAPAN BERSAMA | 2018/2019 23 DAFTAR PUSTAKA
Neuhauser, Claudia. Calculus for Biology and Medicine 3rd Ed. Prentince Hall. 2011.
Walpole, Ronald E. Dan Myers, Raymond H. Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan, Edisi 3. Bandung: Penerbit ITB, 1995.