Mekanika Bahan Bab I

BAB I

TEGANGAN DAN REGANGAN

1.1. Tegangan

  Dalam mekanika bahan, pengertian tegangan tidak sama dengan vektor tegangan. Tegangan merupakan tensor derajat

dua, sedangkan vektor, vektor apapun, merupakan tensor

derajat satu. Besaran skalar merupakan tensor derajat nol. Tensor ialah besaran fisik yang keadaannya pada suatu titik dalam ruang, tiga dimensi, dapat dideskripsikan dengan 3n

komponennya, dengan n ialah derajat tensor tersebut. Dengan

pembebanan. Sedangkan tegangan geser ialah tegangan yang bekerja sejajar dengan bidang pembebanan. Jadi keenam tegangan yang mendeskripsikan tegangan pada suatu titik terdiri atas tiga tegangan normal, _xx , _yy , dan _zz , serta tiga tegangan geser, t_xy , t_yz , dan t_zx. Nilai tegangan bisa positif dan bisa pula negatif. Tegangan bernilai positif bila tegangan tersebut bekerja pada bidang positif dengan arah positif, atau bekerja pada bidang negatif dengan arah negatif. Selain itu, nilainya negatif.

Besar tegangan rata-rata pada suatu bidang dapat didefinisikan sebagai intensitas gaya yang bekerja pada bidang tersebut. Sehingga secara matematis tegangan normal rata-rata dapat dinyatakan sebagaii = j

(1a)

= tegangan normal rata-rata (N/mm2 = MPa₎ F_n = gaya normal yang bekerja (N)

A = luas bidang (mm2)

i, j = sumbu koordinat pada sistem sumbu silang, x, y, z

 

ij



ij Fn

Sedangkan tegangan geser rata-rata dapat dinyatakan sebagai  

(1b)

= tegangan geser rata-rata (N/mm2 = MPa)

F_t = gaya tangensial atau sejajar bidang yang bekerja (N) A = luas bidang (mm2)

i, j = x, y, z

ij Ft

A i j

  , 

ij



Bila bidang yang menerima pembebanan tersebut dipersempit sampai akhirnya mendekati nol, dalam artian limit maka akan didapat tegangan pada suatu titik. Sehingga secara matematis tegangan normal pada suatu titik dapat dinyatakan

i = j (2a)

ij

A

n n

F A

d F dA

  

 

 

0

Sedangkan tegangan geser pada suatu titik, secara matematis dapat dinyatakan sebagai

(2b)

 

ij

A

t t

F A

d F

dA i j

   

 

 

0

lim ,

Seperti halnya tegangan, regangan juga merupakan tensor derajat dua. Dengan demikian keadaan regangan ruang, tiga dimensi, pada suatu titik dapat dideskripsikan dengan kesembilan komponennya. Pada sistem koordinat sumbu silang, regangan tersebut adalah e_xx , e_yy , e_zz , g_xy , g_yx , g_xz , g_zx , g_yz , dan g_zy , sebagaimana ditunjukkan pada Gambar 1.2(a). Regangan juga dapat diklasifikasikan menjadi dua, yakni regangan normal, dengan notasi e_ij , i = j, serta regangan geser dengan simbul _ij , . Sebagaimana dengan tegangan, g_xy = g_yx , g_xz = g_zx dan g_yz = g_zy , maka keadaan regangan ruang pada suatu titik dapat dinyatakan oleh enam komponen, yakni e_xx , e_yy , e_zz , g_xy , g_yz , g_zx. Sedangkan regangan bidang, dua dimensi, dapat dideskripsikan dengan 22 komponennya, dan karena g_ij = g_ji maka regangan bidang pada suatu titik dapat dideskripsikan dengan hanya tiga komponen, Gambar 1.2(b).

Regangan normal merupakan perubahan panjang spesifik. Regangan normal rata-rata dinyatakan oleh perubahan panjang dibagi dengan panjang awal, atau secara matematis dapat dituliskan

 

, i = j (3)

 

ij

i i

i i

l l

  = regangan normal rata-rata

l = u = perubahan panjang pada arah (mm) l = panjang awal pada arah (mm)

i, j = sumbu koordinat pada sistem sumbu silang, x, y, z.  

Sedangkan regangan geser merupakan perubahan sudut dalam radial. Regangan geser bernilai positif bila sudut pada kuadran I dan atau kuadran III pada sistem koordinat sumbu silang mengecil, Gambar 1.3(a), sedangkan selain itu bernilai negatif.

ij



1.3. Transformasi Tegangan Bidang

Transformasi tegangan bidang berdasarkan pada keseimbangan gaya-gaya yang bekerja pada elemen. Perhatikan Gambar 1.5(b) berikut.

 (1.4a )



F

_x'



0

x x' '

.

A

(

xy

. sin ) cos

A

(

yy

. sin ) sin

A

(

xy

. cos ) sin

A



































_xx

. cos cos

A







0

x x' ' xx

cos

yy

sin

xy

sin cos

Dengan memasukkan harga (90o _{+ ) untuk harga } pada persamaan (1.4a), sehingga dengan identitas-identitas:

2

90

90

90

2 2

cos (

o





)



(cos

o

cos





sin

o

sin )





sin



2

9 0

9 0

9 0

2 2

sin (

o





)



(sin

o

cos





cos

o

sin )





co s



sin(₉₀o _) cos(₉₀o _) _(sin₉₀ocos_{ }cos₉₀osin )(cos_{ 90}ocos_{ } sin₉₀osin )_



sin cos





= akan didapat

 



_{y y' '}





_yy

cos

2

 



_xx

sin

2





2



_xy

sin cos





(1.4b)

(1.4c)  _Fy' 0

x y' '

.

A

(

xy

. sin ) sin

A

(

yy

. sin ) cos

A

(

xy

. cos ) cos

A



































_xx

. cos sin

A







0

x y' ' xy

(cos

sin ) (

xx yy

) sin cos

Dengan substitusi identitas trigonometri, persamaan (1.4a, b, c) bisa ditulis (1.5a)   (1.5b)   (1.5c)       

 cos2 sin2

2 2 ' ' xy yy xx yy xx x x            

 cos2 sin2

2 2 ' ' xy yy xx yy xx y y          

 sin2 cos2

2 ' ' xy yy xx y x    

1.4. Transformasi Regangan Bidang

Dari Gambar 1.6(c) akan didapat

Dan dari Gambar 1.6(d) diperoleh dx' dx dy

cos sin ,

 

  x1'x.cos ,



x

₂

'





y

.sin ,



Dengan demikian total perubahan panjang dx’ akibat adanya regangan pada sistem koordinat awalnya adalah

 

x’ = x₁’ + x₂’ + x₃’ Sedangkan

 

Sehingga

(1.6a)  

Selanjutnya, _y’ dapat diperoleh dengan mensubstitusikan harga (90o + _) untuk harga _ pada persamaan (1.6) di atas, kemudian menerapkan identitas trigonometri. Sehingga akan didapat

x x

xy

x

dx

x

dx

y

dy

dy

dy

' '

'

'

.cos

cos

.sin

sin

. .cos

sin































x x' ' xx

.cos

yy

.sin

_xy

.cos .sin







2

 



2











y y' ' xx

.cos (

o

)

yy

.sin (

o

)

_xy

.cos(

o

).sin(

o

)







2

9 0









2

9 0









9 0





9 0





y y' ' yy

.cos

xx

.sin

_xy

.cos .sin







2

 



2











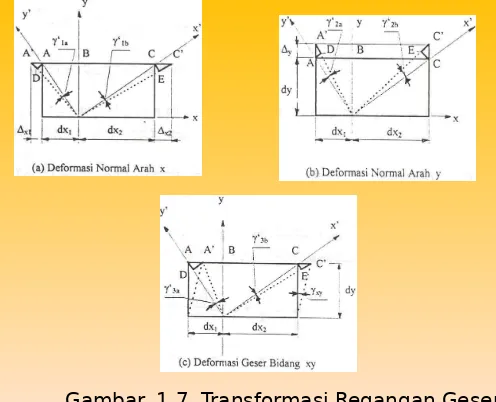
 Analisis transformasi regangan gesernya ditunjukkan pada Gambar 1.7 di bawah. Sebagaimana pada regangan normal, dalam hal ini perubahan regangan geser oleh masing-masing regangan yang terjadi ditinjau satu per satu. Pada analisis ini, panjang dx dibagi dua oleh sumbu y menjadi dx₁ dan dx₂.

[image:15.720.35.686.30.509.2]

 

Dari Gambar 1.7 didapat dan

Selanjutnya perhatikan Gambar 1.7(a), akibat terjadinya deformasi normal pada arah sumbu x saja.

  d y'₁ d x1 dy

sin cos

 

  d x

dx dy

2

'

cos sin

 2 

  1 1 1 1 1 1 1 2 2 2 2 2

1 1 1 2

a xx

b xx

x y a b xx

AD dy x d x x d x CE dx x d x x d x      _        _      _   ' ' .cos sin

sin .cos .sin .cos

'

'

.sin

cos

sin .cos .sin .cos

' _{' '} .sin .cos

   

   

  

 

[image:16.720.53.706.53.369.2]

[image:17.720.116.612.23.425.2]

Gambar. 1.7. Transformasi Regangan Geser  

Akibat deformasi normal arah sumbu y saja seperti ditunjukkan pada Gambar 1.7(b) akan diperoleh

Sedangkan dari Gambar 1.7(c), akibat terjadinya regangan geser saja, akan didapat

 

2

1

2

2

2 2 2 2

a yy

b yy

x y a b yy

AD dy y dy y dy CE dx y dy y dy      _        _      _   ' ' .sin cos

.sin .cos .sin .cos

'

'

.cos sin

.sin .cos .sin .cos

' _{' '} .sin .cos

               3 1 2 2 a xy xy

A D

d y

AA

dy

dy

dy

















'







'

'.cos

cos

.

.cos

.cos

3 2 2 2

3 3 3 2 2

b

xy

x y a b xy

CE d x CC dy dy dy xy                      ' ''.sin sin . .sin .sin

(cos sin )

Dengan demikian akan diperoleh besarnya regangan geser pada set sumbu koordinat yang baru, sebagai berikut

x y' ' x y' ' x y' ' x y' '

(

xx yy

)sin .cos

xy

(cos

sin )







₁





₂





₃











 



2





2



...(1.6c)

Selanjutnya, dengan menggunakan identitas trigonometri persamaan-persamaan (1.6a, b, c) dapat ditulis dalam bentuk lain sebagai berikut



 



x x

xx yy xx yy _xy

' '

cos

.sin



























2

2

2

2

2









y y

xx yy xx yy _xy

' '

cos

.sin



























2

2

2

2

2





x y

x y xx yy xy

' '

' '

sin

.cos























2

2

2

2

2

(1.7a)

(1.7b)

1.5. Tegangan dan Regangan Utama (Principal Stress and Strain) serta Tegangan dan Regangan Geser Maksimum

 

Tegangan Utama (Principal Stress) dan Tegangan Geser Maksimum_{Tegangan Utama (principal stress) adalah tegangan} normal yang terjadi pada set sumbu koordinat baru setelah transformasi yang menghasilkan tegangan geser nol. Tegangan-tegangan tersebut ditunjukkan sebagai s₁ dan s₂ pada Gambar 1.10. Perlu dicatat bahwa s₁ selalu diambil lebih

besar dari s₂. Sudut transformasi yang menghasilkan

tegangan utama tersebut dengan sudut utama (principal

angle). Secara analitik, besar tegangan utama dan sudut

utama dapat diturunkan dari persamaan-persamaan (1.5a, b, c).

Menurut pengertian tentang tegangan utama, dari persamaan (1.5c) akan didapat

0



2

2

2





xx yy

xy





 



atau  

(1.8)  

Dari persamaan di atas dapat dilukiskan segitiganya sebagai berikut

 

sin

cos

tan

2

2

2

2

p p

p

xy

xx yy



















[image:21.720.67.674.81.480.2]

Sehingga  

Substitusi dan penerapan prosedur yang sama terhadap persamaan (1.5b), akan didapat

x x

xx yy xx yy xx yy

xx yy xy

xy

xx yy xy

' ' ( ) ( )                        

2 2 ₄

2 4 2 2 2 2 2





x x xx yy

xx yy xy

xx yy xy ' '

. (

)

(

)

































2

1

2

2

4

2

4

2 2





x x

xx yy

xx yy xy ' '

.

(

)























2

1

2

4

2 2





y y xx yy

xx yy xy

' ' . ( )          2 1 2 4 2 2

  (1.9)  

Selanjutnya, perhatikan persamaan (1.5c). Untuk suatu titik dan jenis pembebanan tertentu dari suatu bagian konstruksi, harga-harga _xx , _yy dan _xy adalah tetap atau konstan, sehingga _x’y’ merupakan suatu fungsi , atau _x’y’ = f().Harga ekstrim fungsi tersebut akan diperoleh bila turunan pertama fungsi tersebut terhadap  sama dengan nol. Jadi

 





1 2 2 2 2 1 2 4 , . ( )

 xx yy  xx yy  xy

atau  

(1.10)  

Dari persamaan di atas dapat dilukiskan segitiganya sebagai berikut:

x y xx yy

xy d d ' ' .sin .cos           

2 2 2 0

sin cos tan max max max 2

2 2 2



 

 

   xx  yy

Dengan substitusi harga-harga sin 2 dan cos 2 pada gambar di atas ke persamaan (1.5c) akan didapat

 





x y

xx yy xx yy

xx yy xy

xy

xx yy xy

xx yy xy

xx yy xy

' '

( )

( ) ( )

. ( ) ( )

    

  



  

  

  

   

 



 



 

 

2 ₄

2

4 1

2 4 4

2 2

2

2 2

2 2

Sehingga  

 

Persamaan (1.10) juga dipenuhi bila panjang sisi di depan sudut 2 adalah (_xx  _yy) dan panjang sisi di sampingnya adalah -2_xy. Kondisi ini akan memberikan

 





x y' ' xx yy xy

. ( )

  1     

2 4

2 2





x y' ' xx yy xy

. ( )

  1     

2 4

2 2

Dengan demikian kedua persamaan tersebut dapat dituliskan menjadi satu sebagai

(1.11)  

Regangan Utama dan Regangan Geser Maksimum

 





max

. ( )

 1     

2 4

2 2

Sebagaimana pengertian tentang tegangan utama, maka

regangan utama (principal strain) adalah regangan normal yang

[image:26.720.39.694.26.514.2]

terjadi pada set sumbu koordinat baru setelah transformasi yang menghasilkan setengah regangan geser nol. Regangan-regangan tersebut ditunjukkan sebagai ₁ dan ₂ pada Gambar 1.11. Demikian juga, ₁ selalu diambil lebih besar dari ₂ , serta sudut transformasinya juga disebut sudut utama (principal angle). Secara analitik, dengan penerapan prosedur yang sama dengan yang diterapkan untuk persamaan-persamaan (1.7a, b, c), maka akan didapat hasil-hasil berikut.

 

(1.12a)  

(1.12b)

q_p = sudut utama

e_1,2 = regangan-regangan utama g_xy = 2e_xy = regangan geser

sin

cos tan 2

2 2

p p

p

xy

xx yy



 



 

 







1 2

2 2

2

1

2

,

.

(

)

(1.13a)

 

(1.13b)  

_max = sudut regangan geser maksimum

_xy = 2_xy = regangan geser

sin

cos tan

max max

max

2

2 2



 

     xx  yy

xy





max

. ( )



  

2

1 2

2 2

 xx yy  xy

1.6. Lingkaran Mohr untuk Tegangan Bidang dan Regangan Bidang

 

Lingkaran Mohr diperkenalkan oleh seorang insinyur Jerman, Otto Mohr (1835-1913). Lingkaran ini digunakan untuk melukis transformasi tegangan maupun regangan, baik untuk persoalan-persoalan tiga dimensi maupun dua dimensi. Yang perlu dicatat adalah bahwa perputaran sumbu elemen sebesar q ditunjukkan oleh perputaran sumbu pada lingkaran Mohr sebesar 2q, .dan

sumbu tegangan geser positif adalah menunjuk ke arah bawah.

Lingkaran Mohr untuk Tegangan Bidang

Pada persamaan (1.5a), bila suku dipindahkan ke ruas

kiri dan kemudian kedua ruasnya dikuadratkan, maka akan didapat

………(1.14a) Sedangkan pada persamaan (1.5c), bila dikuadratkan akan didapat

 

………(1.14b)  Penjumlahan persamaan-persamaan (1.14a) dan (1.14b) menghasilkan

(1.15)

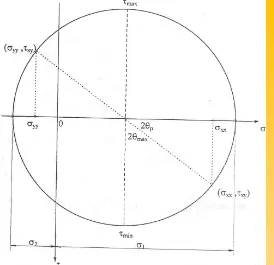
Persamaan (1.15) merupakan persamaan lingkaran pada bidang st yang pusatnya di dengan jari-jari . Lingkaran tersebut ditunjukkan pada Gambar 1.8 di bawah ini, yang dilukis dengan prosedur sebagai berikut:

  x y

2





2 2

2 2 2

2 2 2 2 2 2

x

x y x y

xy x y xy

co s sin

' sin cos

                             





2 2 ₂

2

2

2

2

2

2

2

x y xy

x y

x y xy

co s

sin

' '

sin

cos













 







 



















2 2 2 2

2

2

x x y

x y x y xy

1. Buatlah sumbu _ij , horisontal.

2. Periksa harga tegangan normal, _xx atau _yy , yang secara matematis lebih kecil. Bila bernilai negatif jadikanlah

tegangan tersebut sebagai titik yang mendekati tepi kiri batas melukis, sedangkan bila positif maka titik yang mendekati batas kiri adalah titik _ij = 0.

3. Periksa harga tegangan normal, _xx atau _yy , yang secara matematis lebih besar. Bila bernilai positif jadikanlah tegangan tersebut sebagai titik yang mendekati tepi kanan batas melukis,

sedangkan bila negatif maka titik yang mendekati batas kanan adalah titik _ij = 0.

4. Tentukan skala yang akan digunakan sehingga tempat melukis bisa memuat kedua titik tersebut dan masih tersisa ruangan di sebelah kiri dan kanannya. Tentukan titik-titik batas tersebut sesuai dengan skala yang telah ditentukan.

5. Tentukan letak titik-titik _ij = 0 dan sumbu , serta _ij terkecil dan _ij terbesar bila belum terlukis pada sumbu _ij . 6. Bagi dua jarak antara tegangan terkecil dan tegangan terbesar sehingga diperoleh pusat lingkaran, P.

7. Tentukan letak titik A pada koordinat (_ij terbesar , _xy ). 8. Lukis lingkaran Mohr dengan pusat P dan jari-jari PA.

9. Tarik garis dari A melalui P sehingga memotong lingkaran Mohr di B. Maka titik B akan terletak pada koordinat (_ij terkecil , _xy ). Garis AB menunjukkan sumbu asli,  = 0, elemen tersebut.

 

Contoh 1.1: Sebuah elemen dari bagian konstruksi yang

Diminta: a. Lukisan lingkaran Mohr.

b. Besar rotasi mengelilingi sumbu z untuk mendapatkan tegangan geser maksimum, menurut lingkaran Mohr. Periksa hasil tersebut dari persamaan (1.10).

c. Besar tegangan geser maksimum menurut lingkaran Mohr. Periksa hasil tersebut dengan rumus (1.11) dan hasil yang didapat pada b. di atas.

d. Besar perputaran mengelilingi sumbu z untuk

mendapatkan tegangan geser bernilai nol, menurut lingkaran Mohr. Periksa hasil ini dengan persamaan (1.8).

e. Besar tegangan-tegangan utama menurut lingkaran Mohr. Periksa hasil tersebut dengan persamaan-persamaan (1.9) dan dari hasil pada pada d. di atas.

Penyelesaian:

a. Lingkaran Mohr:

1) Buat sumbu s_ij , horisontal.

2) Tegangan normal terkecil, s_yy = -40 MPa, negatif, sehingga digunakan sebagai titik di dekat batas kiri.

3) Tegangan normal terbesar s_xx = 280 MPa, positif, sehingga digunakan sebagai titik di dekat batas kanan.

4) Diambil skala 1cm = 40 MPa. Kemudian ditentukan titik s_yy = - 40 MPa di sebelah kiri, dan s_xx = 280 MPa di sebelah kanan yang berjarak (s_xx + s_yy) dari titik s_yy di sebelah kiri.

5) Lukis sumbu t yang berjarak 40 MPa di sebelah kanan titik s_{yy .}

6) Dengan membagi dua sama panjang jarak s_yy ke s_xx akan didapat titik P.

7) Menentukan letak titik A pada koordinat (s_{xx ,} t_xy ) = (280,120).

8) Dengan mengambil titik pusat di P dan jari-jari sepanjang PA, lingkaran Mohr dapat dilukis.

9) Dengan menarik garis dari A lewat P yang memotong lingkaran Mohr di B, akan didapat kedudukan titik (s_{yy ,} t_xy ) = (-40,120).

[image:33.720.220.494.19.284.2]

Gambar 1.8. Lingkaran Mohr untuk Tegangan Bidang  

b. Besar rotasi mengellilingi sumbu z menurut lingkaran Mohr, dengan mengukur, didapat

_max = 0,5 x 2_max = 0,5 x (-53o) = 26o 30’.

Sedangkan menurut persamaan (1.10) didapat tan 2_max =  (280 + 40) / (2 x 120) =  43 2_max =  53o _{08’ atau }

max =  26o 34’

c. Besar tegangan geser maksimum menurut lingkaran Mohr _max = 5 x 40 MPa = 200 MPa.

Sedangkan menurut persamaan (1.11) akan didapat

d. Besar rotasi mengellilingi sumbu z menurut lingkaran Mohr, dengan mengukur, didapat

_p = 0,5 x 2_p = 0,5 x 37o = 18o 30’.

Sedangkan menurut persamaan (1.10) didapat tan 2_p = (2 x 120) / (280 + 40) = 

2_p =  36o 52’ atau _

max =  18o 26’

e. Besar tegangan-tegangan utama menurut lingkaran Mohr ₁ = 8 x 40 MPa = 320 MPa.

₂ = -2 x 40 MPa = -80 MPa.

Sedangkan menurut persamaan (1.11) akan didapat

 









1

2 ₂

2 2 2

280 40 2

1

2 280 40 120 320 280 40

2

1

2 280 40 120 80





     

     

MPa

Lingkaran Mohr untuk Regangan Bidang

Pada persamaan (1.7a), bila suku dipindahkan ke ruas kiri

dan kemudian kedua ruasnya dikuadratkan, maka akan didapat  

……… (1.16a)

Sedangkan pada persamaan (1.7c), bila dikuadratkan akan didapat

 

……… (1.16b)

 

Penjumlahan persamaan-persamaan (1.16a) dan (1.16b) menghasilkan xx yy    2





2 2 2 2 2

2 2 2 2 2 2 2 2

x x

xx yy xx yy xy

xx yy xy

' ' cos sin sin cos

                                   _      





2 2 2 2 2

2 2 2 2 2 2 2 2

x y xy xx yy

xx yy x y

' ' ' '

cos sin sin cos

(1.17)

Persamaan (1.17) merupakan persamaan lingkaran pada bidang

yang pusatnya di dengan jari-jari

Lingkaran tersebut ditunjukkan pada Gambar 1.9 di bawah ini, yang dilukis dengan prosedur sebagaimana melukis lingkaran Mohr untuk tegangan dengan mengganti_xx , _yy dan _xy berturut-turut menjadi _xx , _yy dan _xy / 2. Penerapannya, lihat Contoh 1.2 pada halaman 21.

 

2 2 2 2

2 2 2 2

x x

xx yy x y xx yy x y

' ' ' ' ' '                                      2 xx yy         

2 ,0

2 2

2 2

xx yy xy

               

1.7. Hubungan Antara Tegangan Dengan Regangan  

Apabila besar tegangan-tegangannya yang diketahui, maka hukum Hooke untuk persoalan-persoalan tiga dimensi, hubungan antara tegangan normal dengan regangan normal dapat dituliskan secara matematis sebagai berikut:

(1.18)

Dengan E dan v berturut-turut adalah modulus alastis atau modulus Young dan angka perbandingan Poisson. Sedangkan pada deformasi geser untuk G adalah modulus geser , hubungannya adalah: (1.19)  













xx xx yy zz

yy yy xx zz

zz zz xx yy

E E E                      1 1 1













xy

xy xy xy

xz xz xz

xz

yz

yz yz yz

Sedangkan untuk mencari tegangan normal yang terjadi bila regangan normal dan sifat-sifat mekanis bahannya diketahui, digunakan persamaan-persamaan:

(1.20)

Selanjutnya untuk deformasi geser, bentuk hukum Hooke adalah: (1.21)     



 







  



   



  



 







xx xx yy zz

yy yy xx zz

zz zz xx yy

E E E                                          

1 1 2 1

1 1 2 1

1 1 2 1

     

xy xy xy xy

xz xz xz xz

yz yz yz yz

E E G E E G E E G                              

1 2 1

1 2 1

Persamaan-persamaan (1.18) sampai dengan (1.21) dapat juga diberlakukan untuk persoalan-persoalan dua dan satu dimensi, yakni dengan memasukkan harga nol untuk besaran-besaran di luar dimensi yang dimaksud.

 

Contoh 2: Pembebanan seperti pada Contoh 1, untuk bahan

dengan sifat-sifat mekanis: modulus Young, E = 200 GPa dan angka perbanding-an Poisson, n = 0,29. Modulus geser ditentukan dengan, G = E / 2(1 + n).

Diminta: a. Hitunglah regangan-regangan yang terjadi.

b. Lukisan lingkaran Mohr untuk regangan yang terjadi.

c. Besar rotasi mengelilingi sumbu z untuk mendapatkan regangan geser maksimum, menurut lingkaran Mohr. Periksa hasil tersebut dari persamaan (1.10).

e. Besar perputaran mengelilingi sumbu z untuk

mendapatkan regangan geser bernilai nol, menurut lingkaran Mohr. Periksa hasil ini

dengan persamaan (1.8).

f. Besar regangan-regangan utama menurut lingkaran Mohr. Periksa hasil tersebut dengan persamaan- persamaan (1.9) dan dari hasil pada pada d. di atas._{Penyelesaian:}

a) Dari persamaan (1.18) dan (1.19) akan didapat:

b. Lingkaran Mohr:

1) Buat sumbu e_ij horisontal.

2) Regangan normal terkecil, e_yy = -606me, sehingga merupakan titik di dekat batas kiri.









xx

yy

 

 

 

   

      

1

200000 280 0,29.40 0,29.0 0,001458 1458

1

200000 40 0,29.280 0,29.0 0,000606 606

 

xy xy atau xy

         

2

1 0,29 120

3) Regangan normal terbesar e_xx = 1458me, sehingga merupakan titik di dekat batas kanan.

4) Diambil skala 1cm = 250me. Kemudian ditentukan titik e_yy = -606me di sebelah kiri, e_xx = 1458me di sebelah kanan dan berjarak (e_xx + e_yy) dari titik e_yy di sebelah kiri.

5) Lukis sumbu t yang berjarak 606me di sebelah

kanan titik e_{yy .}

6) Dengan membagi dua sama panjang jarak e_yy ke e_xx akan didapat titik P.

7) Menentukan letak titik A pada koordinat (e_{xx ,} e_xy )

= (1458,774).

8) Dengan mengambil titik pusat di P dan jari-jari sepanjang PA, lingkaran Mohr dapat di-lukis. 9) Dengan menarik garis dari A lewat P yang memotong lingkaran Mohr di B, akan di dapat kedudukan titik (e_{yy ,} e_xy ) = (-606,-774).

c. Besar rotasi mengelilingi sumbu z menurut lingkaran Mohr, dengan mengukur, didapat

_max = 0,5 x 2_max = 0,5 x (-53o) = 26o 30’.

Sedangkan menurut persamaan (1.10) didapat tan 2_max =  (1458 + 606) / (2 x 774) =  43 2_max =  53o 08’ atau _

max =  26o 34’

  d. Besar regangan geser maksimum menurut lingkaran Mohr

_xy-max = 5,2 x 250 = 1300.

Sedangkan menurut persamaan (1.11) akan didapat

e. Besar rotasi mengellilingi sumbu z menurut lingkaran Mohr, dengan mengukur, didapat

_p = 0,5 x 2_p = 0,5 x 37o = 18o 30’.

Sedangkan menurut persamaan (1.10) didapat tan 2_p = (2 x 120) / (280 + 40) = 

2_p =  36o 52’ atau _

max =  18o 26’

 

max

max (



 

2

1 2

2

1458 606) ₁₅₄₈2 1290

f. Besar regangan-regangan dasar menurut lingkaran Mohr

₁ = 6,9 x 250 = 1725. ₂ = -3,5 x 250 = -875

Sedangkan menurut persamaan (1.11) akan didapat_{ }

 

1

2

1458 606 2

1 2

2

1458 606 ₁₅₄₈2 1716 1458 606

2

1 2

2

1458 606 15482 864

 

 







   

