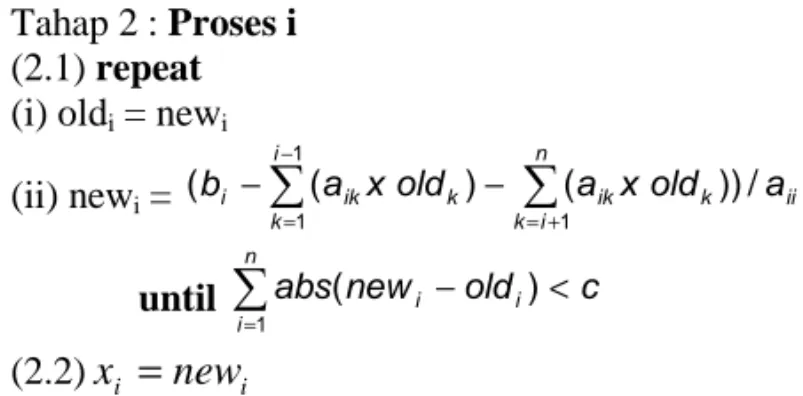Pecahan Persamaan 2-D Diffusi Secara Paralel menggunakan Metoda Modified Gauss (Mike Susmikanti)

PEMECAHAN PERSAMAAN 2-D DIFFUSI SECARA PARALEL MENGGUNAKAN METODA MODIFIED GAUSS SEIDEL

DALAM KOMPUTER KLUSTER

Mike Susmikanti

*

ABSTRAK

PEMECAHAN PERSAMAAN 2-D DIFFUSI SECARA PARALEL MENGGUNAKAN METODA MODIFIED GAUSS SEIDEL DALAM KOMPUTER KLUSTER. Paralelisasi penyelesaian diffusi 2-D dalam komputer kluster dibahas dalam tulisan ini. Perhitungan nilai karakteristik dan distribusi fluks neutron adalah pusat dari analisis fisis reaktor nuklir. Sebagai pendekatan persoalan transport neutron, metoda diffusi merupakan metoda standard yang digunakan dalam analisis ini. Dalam pemecahan persamaan diffusi, prosedur akan berhadapan dengan persoalan matriks. Dalam penyelesaian diffusi 2-D, matriks membentuk matriks penta-diagonal. Untuk membuat perhitungan diffusi lebih efektif, proses algoritma Modified Gauss Seidel difokuskan dalam unsur-unsur penta-diagonal. Metoda

Modified Gauss Seidel dalam pemecahan diffusi 2-D dengan matriks yang besar akan dipresentasikan. Sebagian besar operasi dalam metoda modifikasi Gauss Seidel dapat dikerjakan secara paralel. Komputasi paralel dari penta-diagonal untuk pemecahan model difussi 2-D diimplementasikan secara integrasi menggunakan program C dan Message Passing Interface (MPI) dalam komputer kluster.

Kata-kata kunci : Model Diffusi, Sistem Penta-Diagonal, Komputasi Paralel, Modified Gauss Seidel, Komputer Kluster

ABSTRACT

PARALLEL 2-D DIFFUSION EQUATION SOLVER USING MODIFIED GAUSS-SEIDEL METHOD IN COMPUTER CLUSTER. Parallelization of 2-D diffusion solution in Computer Cluster reported in this paper. Neutron flux distribution and eigen value calculation is the central of nuclear reactor physics analysis. As an approximation to the neutron transport problem, diffusion method is nowadays a standard method used in this analysis. In solving the neutron diffusion equation the procedure will end up with the matrix problem. For 2-D diffusion solution the matrix would be a penta-diagonal matrix. To make the 2-D diffusion calculation more effective, the process of this algorithm is focused in elements penta-diagonal. The Modified Gauss Seidel method in solving the 2-D

diffusion equation with the big matrix will be presented. Most of the operation in the modified Gauss-Seidel method can be done in parallel. The parallel computing of penta-diagonal for solving the 2-D

diffusion model are implementation with integrated used program C and Message Passing Interface (MPI) in computer cluster .\

Keywords : Diffusion Model, Penta-Diagonal System, Parallel Computing, Modification Gauss Seidel, Cluster Computer

*

PENDAHULUAN

Salah satu persoalan dalam bidang reaktor nuklir adalah pemecahan transport neutron. Perhitungan nilai karakteristik dan distribusi fluks neutron adalah pusat dari analisis fisis reaktor nuklir. Dalam perhitungan distribusi neutron dalam reaktor harus diperhatikan proses transport neutron, yaitu pergerakan alur neutron. Banyak studi reaktor mempelajari perlakuan pergerakan neutron sebagai suatu proses diffusi. Para teknik nuklir mempelajari bagaimana mendesain reaktor demikian sehingga terdapat keseimbangan antara produksi neutron dalam reaksi fisi dan hilangnya neutron karena hamburan atau diserap. Salah satu persoalan transport neutron adalah penyelesaian model diffusi 2-D. Sebagai pendekatan persoalan transport neutron, model diffusi merupakan model standard yang digunakan dalam analisis ini. Dalam pemecahan persamaan diffusi, prosedur akan berhadapan dengan persoalan matriks. Dalam penyelesaian diffusi 2-D, matriks membentuk matriks penta-diagonal. Model mengasumsikan bahwa semua neutron dapat dikarakteristik dengan perlakuan energi pada dua dimensi. Model diffusi 2-D mempunyai sistim persamaan linier penta-diagonal.

Paralelisasi penyelesaian diffusi 2-D dalam komputer kluster dibahas dalam tulisan ini. Beberapa algoritma telah dikembangkan untuk dikembangkan untuk penyelesaian paralel pada sistem penta-diagonal. Sistem penta diagonal adalah sistem persamaan linier yang memerlukan penyelesaian khusus.Untuk membuat perhitungan diffusi lebih efektif, proses algoritma Modified Gauss Seidel difokuskan dan diterapkan dalam unsur-unsur penta-diagonal. Metoda Modified Gauss Seidel dalam pemecahan diffusi 2-D dengan matriks yang besar akan dipresentasikan. Metoda ini sangat sesuai diterapkan dalam sistem komputer kluster. Sebagian besar operasi dalam metoda modifikasi Gauss Seidel dapat dikerjakan secara paralel. Komputasi paralel dari penta-diagonal untuk pemecahan model difussi 2-D diimplementasikan secara integrasi menggunakan program C dan Message Passing Interface (MPI) dalam komputer kluster. Diperoleh waktu yang sangat singkat dalam menyelesaikan sistem persamaan Diffusi 2-D untuk ukuran matriks besar dengan metoda modified Gauss Seidel secara paralel dalam komputer kluster.

METODOLOGI

Perhitungan diffusi neutron mengkhususkan perlakuan 2-D atau 3-D. Pada reaktor inti dihitung frekuensi hamburan neutron atau berapa banyak neutron diserap. Rasio jumlah neutron dalam satu generasi dan jumlah neutron pada generasi sebelumnya disebut dengan faktor multiplikasi k. Jika k = 1, jumlah neutron dalam generasi fisi sebelumnya dan sesudahnya adalah sama dan reaksi rantai tidak bergantung waktu. Karakteristik sistim dinyatakan dengan k = 1 menunjukkan reaktor kritis. Persamaan diffusi adalah persamaan diferensial parsial generasi fisi yang

menyatakan fluktuasi kerapatan material selama diffusi. Solusi numerik persamaan diffusi lebih umum dinyatakan pada persamaan (1) [2],

(1)

) (r

φ

kerapatan material diffusi pada lokasi

r

and D(r)adalah kumpulan koefisien diffusi untuk kerapatan

φ

pada lokasi r . Simbol

∇

merepresentasikan simbol operator differensial vektor pada koordinat bidang. S(r)adalah sumber pada lokasi r dan

Σ

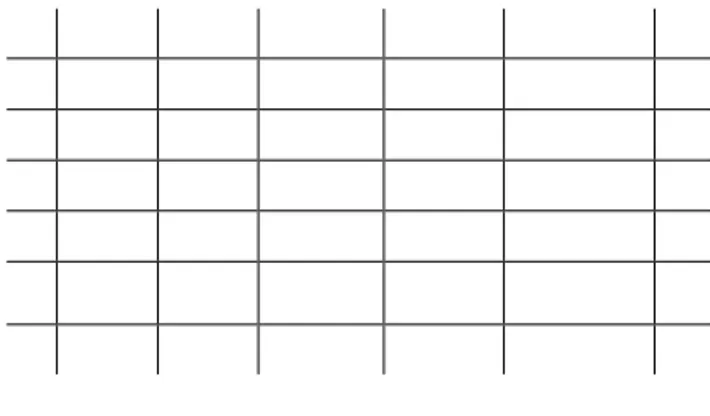
_a adalah probabilitas reaksi neuron-nuklir yang terjadi yang dinyatakan dengan nilai penampang lintang.

Geometri yang ingin diselidiki didiskritisasi kedalam mesh dari sel-sel seperti grid-grid segiempat yang dinyatakan pada Gambar 1.

Gambar 1. Grid segi empat

2-D

Jika didefinisikan D_ij adalah koefisien diffusi pada mesh titik i dan j,

) ( 2 1 j i ij D D D ≅ + ₍₂₎

Maka persamaan (1) dapat dinyatakan dalam bentuk persamaan (3)

(3)

dimana ∆_ij =jarak diantara mesh titik i dan j dengan i berjalan pada semua titik-titik mesh. Jika diperluas persamaan beda untuk persamaan diffusi 2-D dengan media mesh seragam dalam geometri segiempat dinyatakan pada persamaan (4),

(4) ) ( ) ( ) ( ) (r r r S r D ∇ +Σa = ∇ −→ →

φ

φ

i i J j ij a ij j J j ij ij S D D j = + ∆ + ∆ −

∑

∑

∑

= = φ 1 φ 2 1 2 ( ) ) , ( ) , ( 2 2 2 2 y x S y x y D x D a = ∂ ∂ − ∂ ∂ − φ φ

∑

φ

Titik-titik mesh dinyatakan dalam ruang mesh dengan pendekatan persamaan (5),

(5)

Jika nilai pada persamaan (5) disubtitusi pada persamaan (4), evaluasi terhadap titik mesh (xi,yj) diperoleh dari persamaan (6) [2],

, i=1, ..., N-1,j=1,...,M-1 (6)

Syarat batas yang digunakan,

φ

_0,j,

φ

N_,j,

φ

i_,0 dan

φ

i,M.

Pada penyelesaian persamaan diffusi 2-D, pertama-tama adalah membentuk matriks koefisien difusi dengan memberi tanda indeks tunggal untuk tiap titik mesh. Sebagai contoh dalam mesh 2-D, titik mesh diberi label (i,j)

→

k = i + (j-1)(N-1). Untuk persoalan 2-D, struktur matriks dengan jajaran mesh i x j, diperoleh parameter distribusi fluks sebanyak k = i x j, yaitu

φ

1

,

...,

φ

k

                      . . . . . . . . . . 63 52 45 44 43 41 36 34 33 32 25 23 22 21 14 12 11 a a a a a a a a a a a a a a a a a

                      k φ φ φ φ φ 4 3 2 1

=

                      k S S S S S 4 3 2 1

A

φ

=

S

Sebagai contoh, Pada baris ke-k = 14, ( i = 7 dan j =2), hasil perkalian matriks diatas dinyatakan pada persamaan (7),

2 , 1 , , 1 , 2 2 ) ( 2 x x j i j i j i i y xi ∆ + − ≅ ∂ ∂ φ φ− φ φ+ + + ∆ − + ∆ − + − ( + − ) ) ( ) ( ) ( 2 i 1,j i 1,j y 2 i,j 1 i,j 1 D x D

φ

φ

φ

φ

2 1 , , 1 , , 2 2 ) ( 2 y y j i j i j i i y xi ∆ + − ≅ ∂ ∂ φ φ − φ φ + j i j i a S y x D _{2 2}) _{, ,} ) ( 1 ) ( 1 ( 2 _ =      ∆ + ∆ + Σ + φ − ∆ + ∆ + ∆ + ∆ + − ∆ − − ∆ −

∑

) ) ( ) ( ) ( ) ( ( ) ) ( ( ) ) ( ( ₂ 12 , 7 12 , 7 2 8 , 7 8 , 7 2 6 , 7 6 , 7 2 2 , 7 2 , 7 7 2 6 , 7 6 , 7 2 2 , 7 2 , 7 D D D D D D a

) ( ) ( ) ) ( ( ) ) ( ( _{2 7 7} 12 , 7 12 , 7 2 8 , 7 8 , 7 S D D = − ∆ − − ∆ − φ ₍₇₎

Persamaan (7) digunakan dalam perhitungan kritikalitas pada persamaan (8) [2],

(8)

Penyelesaian dengan metode iterasi memberikan tebakan sumber awal dan k-effektif (keff), dinyatakan pada persamaan (9),

(9) Kemudian dihitung fluks

φ

(1) berdasarkan persamaan (10),

(10) Sumber baru dan keff dapat dihitung menggunakan persamaan (11),

(11)

Prosedur iterasi untuk menghitung keff dapat disederhanakan berikut ini [2, 5], 1. Tebakan awal untuk k0 = k eff

(0)

dan

φ

(0). 2. Kemudian pecahkan untuk

φ

(n+1) = 1/keff

(n)

x F x

φ

(n) , F =

ν

∑f 3. Hitung keff baru : keff

(n+1) = keff (n)

∫

+ dr M dr M N N ) ( ) 1 ( φ φ

Ulangi (1)-(3) sampai keduanya keff(n+1) dan

φ

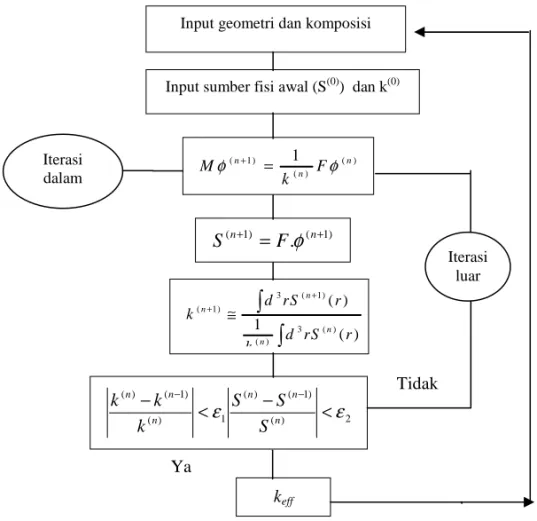
(n+1) konvergen,

Diagram alur perhitungan keff dinyatakan pada gambar 2.

)

(

)

(

r

F

S

(0)

r

S

≡

⋅

φ

≅

) 0 ( k k ≅ ) 0 ( ) 1 ( ) 1 ( ) 1 ( 2 ) 1 ( 1 ) ( S k r D M⋅

φ

≡− ∇ ⋅

φ

+Σ_a ⋅

φ

= ) 1 ( ) 1 ( ) 1 (

φ

υ

φ

f

F

S

=

⋅

=

Σ

φ φ= ⋅ ⋅ F k M 1

Gambar 2. Diagram Alur Perhitungan Kritikalitas

Sistem persamaan Aφ = S memberikan nilai fluks φ dalam vektor. Matriks A adalah matriks koefisien diffusi dan S adalah vektor nilai sumber. Nilai unsur-unsur matriks A adalah bentuk sederhana dari persamaan beda hingga. Penyelesaian diskritisasi fluks

φ

i diperoleh dari penyelesaian persamaan berikut

2 12 1 11φ a φ a +

₊

a₁₄φ₄

₌

1

S

3 23 2 22 1 21φ a φ a φ a + +

₊

a25φ5

=

S

₂

a32φ2+a33φ3+a34φ4

+

a36φ6

=

S

3 6 6 3 φ a

a₃₂φ₂+a₃₃φ₃+a₃₄φ₄

₊

a36φ6 . . aNNφN +aNNφN = SN ) ( ) ( ) 1 ( 1 n n n F k Mφ + = φ

Input geometri dan komposisi

Input sumber fisi awal (S(0)) dan k(0)

) 1 ( ) 1 ( . + + ₌ n n F S φ ) ( 1 ) ( ) ( 3 ) ( ) 1 ( 3 ) 1 ( r S r d k r S r d k n n n n

∫

∫

+ + _≅ 2 ) ( ) 1 ( ) ( 1 ) ( ) 1 ( ) ( ε ε − < < − − − n n n n n n S S S k k k keff Ya Tidak Iterasi dalam Iterasi luar

Prinsip algoritma untuk pemecahan sistim persamaan linier Ax = b diterapkan secara paralel dengan memodifikasi metoda Iteratif Gauss-Seidel dengan Modified Gauss-Seidel. Persamaan diatas dapat dinyatakan sebagai persamaan (12),

A = E + D + F (12)

dimana E, D dan F adalah matriks n x n dengan masing-masing unsur eij, dij dan ij f _berikut; ij e ₌







>

lainnya

untuk

j

i

untuk

a

ij

0

ij d ₌







=

lainnya

untuk

j

i

untuk

a

ij

0

ij f ₌







<

lainnya

untuk

j

i

untuk

a

ij

0

Persamaan Ax = b dapat dinyatakan dalam bentuk persamaan (13),

(E + D + F)x = b (13)

atau dalam bentuk persamaan (14)

Dx = b – Ex – Fx (14)

Dimulai dengan vektor x0 ( dugaan sembarang untuk x awal), penyelesaian vektor diperoleh melalui proses iteratif dimana iterasi ke-k diberikan pada persamaan (15),

Dxk = b – Exk – Fxk−1 (15)

Iterasi dikatakan konvergen jika untuk suatu k, memenuhi persamaan (16),

∑

₌n + _{− <} i k i k i x c x abs 1 1 , ) ( ₍₁₆₎

dimana c adalah nilai toleransi kesalahan.

Proses diatas dapat dimodifikasi secara umum menjadi algoritma paralel Modified Gauss Seidel yang dapat diterapkan pada sistem komputer kluster, karena didesain untuk sistem paralel Multiple Instruction Multiple Data. Berikut algoritma paralel dari metode Modified Gauss Seidel [1],

Prosedur MIMD MODIFIED GAUSS SEIDEL Tahap 1 : for i = 1 to n do (1) oldi = xi 0 (2) newi = xi 0 Hitung Proses i end for

Tahap 2 : Proses i

(2.1) repeat

(i) oldi = newi

(ii) newi = ii n i k k ik k i k ik i a xold a xold a b ( ) ( ))/ ( 1 1 1

∑

∑

+ = − = − −

until abs new old c

n i i i − <

∑

₌ ( ) 1 (2.2)

x

_i

=

new

_i

Tahap 2, menyatakan satu dari n proses dalam Tahap 1.

Misalkan untuk n = 4 (empat variabel yang ingin dicari) dan iterasi awal, k = 1, mula-mula diberikan nilai 40

0 3 0 2 0 1,x ,x ,x

x awal dan nilai toleransi c.Selama iterasi ke-k (k=1) pendekatan nilai x yang tidak diketahui, disubstitusi kedalam ruas kanan persamaan (15), yang menghasilkan nilai pendekatan baru berikut ini,

) ( 0 _{12 2}0 _{13 3}0 _{14 4}0 1 1 1 11x b a x a x a x a = − − + + ) ( ) ( 24 40 0 3 23 1 1 21 2 1 2 22x b a x a x a x a = − − + ) ( ) ( 0 4 34 1 2 32 1 1 31 3 1 3 33x b a x a x a x a = − + − 0 ) ( 43 31 1 2 42 1 1 41 4 1 4 44x =b − a x +a x +a x − a atau 11 0 4 14 0 3 13 0 2 12 1 1 1 (b 0 (a x a x a x ))/a x = − − + + 22 0 4 24 0 3 23 1 1 21 2 1 2 (b (a x ) (a x a x ))/a x = − − + . . 44 1 3 43 1 2 42 1 1 41 4 1 4 (b (a x a x a x ) 0)/a x = − + + −

Ilustrasi pekerjaan untuk masing-masing prosesor sebagai berikut, prosesor 1 memberikan nilai

old

₁

=

x

₁0 dan

new

₁

=

x

₁0. Secara simultan prosesor 2 memberikan nilai

old

₂

=

x

0₂ dan

new

₂

=

x

₂0. Demikian pula untuk prosesor 3 dan prosesor 4. Nilai

x

₁1

,

x

1₂

,...,

x

1₄ dapat dihitung dari sistim persamaan diatas yang menjadi nilai

4 2

1

,

new

,....,

new

new

pada iterasi pertama, sedangkan nilai

old

₁

=

x

₁0

,

old

₂

=

x

₂0

,

0 4 4

...,

old

=

x

. Kemudian dihitung new1 −old1 +...+ new4 −old4 <c. Jika syarat konverven belum tercapai maka iterasi dilanjutkan dengan menyimpan nilai

4 4

1

1

new

,...,

old

new

old

=

=

dan menghitung

new

1

,

new

2

,....,

new

4 dengan

menghitung 14 1 2 1

1

,

x

,...,

x

x

. Demikian selanjutnya untuk iterasi ke-k sehingga syarat konvergen terpenuhi.

HASIL DAN PEMBAHASAN

Proses simulasi paralel dilakukan dengan beberapa prosesor. Proses ini integrasi dengan program C, konsep MPI (Message Passing Interface) pada sistem Open Source LINUX dalam sistem kluster [3,4]. Geometri input dibagi dalam panjang material 25 cm dan jumlah partisi 40 per cm (n = 1000, delta(i) = 1, i = 1, 1000). Input material meliputi penampang lintang sigmaabs(i), konstanta diffusi d(i), produktivitas per fissi nusigma(i), tebakan awal

φ

(0) = 10 dan keff awal (keff(0)) = 1.

Pertama-tama dihitung unsur-unsur matriks koefisien diffusi A, dari persamaan

S

A

φ

=

. Untuk perhitungan distribusi fluks φ, digunakan metoda Modified Gauss Seidel yang diterapkan dalam komputasi paralel pada sistem kluster untuk penyelesaian sistim persamaan penta-diagonal

A

φ

=

S

dalam bentuk matriks 1000 x 1000. Sistem penta-diagonal diperoleh dari proses pembentukan matriks koefisien diffusi A. Vektor S menyatakan nilai sumber yang dinyatakan pada ruas kanan sistim persamaan. Vektor

φ

menyatakan nilai fluks yang akan dihitung dalam bentuk matriks berikut ini,

                        896 . 225 ... 593 . 234 ... 6273 . 1 044 . 452 736 . 324 044 . 452 6273 . 1 601 . 236 022 . 226 601 . 236 6273 . 1 6247 . 1 754 . 235 661 . 225 754 . 235 6273 . 1 6247 . 1 132 . 451 096 . 322 132 . 451 6247 . 1 132 . 451 149 . 616 566 . 225 6247 . 1 566 . 225 503 . 233                         .. 7 6 5 4 3 2 1 φ φ φ φ φ φ φ =                         .. 0058708 . 0.0058708 0 0058708 . 0 0058708 . 0 0058708 . 0 0058708 . 0 0058708 . 0 Nilai fluks

φ

1,

φ

2,

φ

3,

φ

4,

φ

5,

φ

6,

φ

7,

φ

8,

φ

9,

φ

10,

φ

11,

φ

12,,...,

φ

998,

φ

999,

φ

1000

dihitung dari proses Modified Gauss Seidel yang masing-masing diperoleh,

0.002035008666; 0.003048633432; 0.003553513429; 0.003804990918; 0.003930250242; 0.003992641108; 0.004023717599; 0.004039196600; ………; 0.004054567793; 0.004054567793; 0.004054567793.

Diperoleh nilai k-eff = 1,000004050544.

Proses paralel dilakukan dengan fasilitas MPI pada tiga komputer Dual Core dalam lokal jaringan (LAN) dengan sistem kluster. Kinerja paralel perhitungan kritikalitas dan distribusi fluks menggunakan metoda Modified Gauss Seidel dinyatakan pada tabel 1 pada sistem kluster untuk penyelesaian sistim persamaan penta-diagonal dengan ukuranmatriks 1000 x 1000.

Tabel 1. Kinerja Paralel Perhitungan Kritikalitas dan Distribusi Fluks

Jumlah Prosesor Waktu (detik)

Waktu Per Prosesor (detik) 2 6,64 3,32 3 6,60 2,20 4 11,24 2,81 5 13,43 2,69 6 17,97 3,00 7 16,83 2,40 8 23,01 2,88

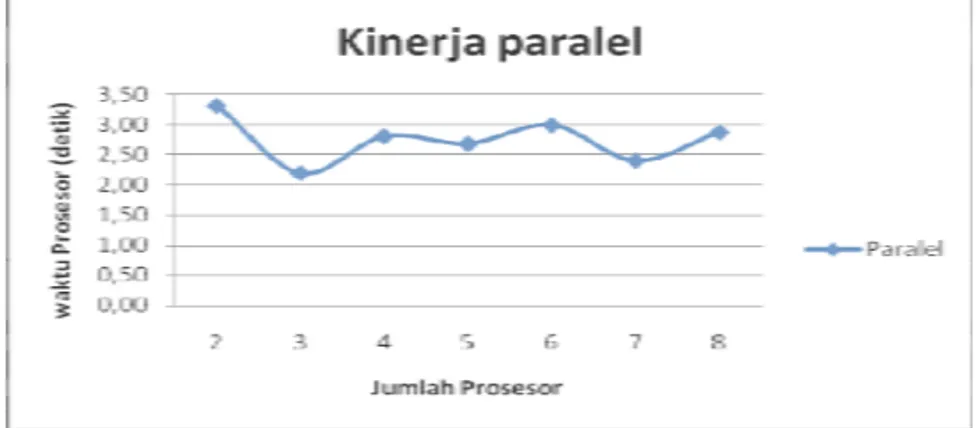
Fluktuasi kinerja paralel perhitungan kritikalitas dan distribusi fluks dengan memperhatikan jumlah prosesor terhadap waktu ditampilkan pada Gambar 3.

Gambar 3. Kinerja Paralel Perhitungan Kritikalitas

Fluktuasi kinerja paralel per-prosesor terhadap waktu ditampilkan pada Gambar 4.

Gambar 4. Kinerja Paralel Per-Prosesor

Secara umum sistim persamaan n variabel dapat diproses secara paralel menggunakan algoritma Modified Gauss Seidel yang dirancang pada sistem paralel MMID dalam sistem kluster yang mengijinkan proses didistribusi pada node-node dengan pembagian beban yang diserahkan pada sistem. Selain hal diatas secara konsep komputer dual core masing-masing berfungsi sebagai komputer dengan dua prosesor

sehingga proses dapat didistribusikan pada minimal dua node atau lebih untuk masing-masing komputer. Sehingga tiga komputer dual core berfungsi sebagai minimal enam prosesor. Simulasi paralel pada sistem kluster yang berintegrasi dengan fasilitas MPI, diperkenankan diproses pada beberapa node atau prosesor. Dilihat dari grafik kinerja paralel per prosesor bahwa kinerja paralel yang optimal diperoleh pada tiga node walaupun proses dimungkinkan dilakukan untuk enam sampai delapan node, tetapi diperoleh hasil yang tidak optimal walaupun dalam jaringan lokal sekalipun. Hal ini disebabkan waktu untuk mendistribusikan beban atau mengumpulkan hasil perhitungan akan menambah waktu proses. Tidak menutup kemungkinan pula adanya jaringan komunikasi yang tidak lancar walaupun dalam jaringan lokal sekalipun.

KESIMPULAN

Model diffusi 2-D secara numerik dinyatakan dalam sistem persamaan penta-diagonal. Metode Modified Gauss Seidel dapat diterapkan dalam penyelesaian sistem persamaan penta-diagonal. Algoritma Modified Gauss Seidel dapat diaplikasikan untuk sistem persamaan dengan ukuran matriks koefisien difusi yang besar dalam waktu singkat dengan sistim paralel Multiple Instruction Multiple Data pada sistem kluster. Dalam simulasi ini, pada tiga komputer Dual Core dengan jaringan lokal ternyata diperoleh kinerja paralel yang efisien dibebankan hanya terhadap tiga prosesor, walaupun dapat diproses pada lebih dari tiga prosesor. Hal ini dimungkinkan, dalam mendistribusikan pekerjaan dan mengumpulkan hasil akan menambah waktu proses.

DAFTAR PUSTAKA

1. SELIM G., AKL. (1989), “The Design and Analysis of Parallel Algorithms”, Prentice Hall, Inc., New Jersey.

2. DUDERSTADT, J.J., HAMILTON, L. J., (1976), “Nuclear Reactor Analysis”, John Wiley & Sons, Inc., (1976).

3. GRAMMATIKAKIS, MILTOS, D., FRANK HSU, D., and KRAETZL, MIRO (2001), “Parallel System Interconnections and Communications”, CRC Press LLC, New York.

4. KARNIADAKIS, GEORGE, E., KIRBY, LL., ROBERT, M. (2003), “Parallel Scientific Computing in C++ and MPI”, Cambridge University Press, First Published.

5. SUSMIKANTI M., SETIDIPURA, T., ADHIYAKSA, A. (2009), “The Parallel Computation for Tridiagonal System In One-Dimension Diffusion Model”, Journal of Theoritical and Computational Studies Volume 8 Number 0406, ISSN1979-3898, LIPI.

DISKUSI

KARSONO

1. Saran : Makalah seharusnya menjelaskan algoritma paralel yang digunakan dan juga penjelasan pembagian beban kerja ke prosesor-prosesor. Aspek paralelisasi ini adalah inti makalah (yang belum dijelaskan).

2. Mohon penjelasan kurva kinerja prosesor fluktuatif; menambah jumlah prosesor tidak selalu mempercepat proses /waktu hitung.

MIKE

1. Akan ditambahkan dan dimasukkan dalam makalah sebagai perbaikan.

2. Sistem paralel ini dikerjakan pada empat komputer Dual Core, tetapi dengan kemampuan berbeda, sehingga setelah dilakukan simulasi diperoleh waktu yang minimal pada tiga prosedur. JAdi pada prinsipnya ada kemungkinan bahwa kinerja salah satu komputer tidak baik dan kemungkinan lain bahwa perjalanan untuk melakukan proses pada 8 prosesor (4 komputer dengan Dual Core) lebih memakan waktu.

DAFTAR RIWAYAT HIDUP

Nama : Mike Susmikanti

Tempat & Tanggal Lahir : Jakarta, 12 November 1956

Pendidikan : S-1 Matematika, S-2 Magister Manajemen Riwayat Pekerjaan : 1980 s.d. sekarang di BATAN

Makalah : Pemecahan Persamaan 2-D Diffsusi Secara Paralel menggunakan Metoda Modified Gauss Seidel dalam Komputer Kluster