BAB II TINJAUAN PUSTAKA

BAB II

TINJAUAN PUSTAKA

2.1. Dasar –Dasar Teori

2.1.1. Hubungan tegangan dan regangan

Hubungan teganan dan regangan pertama kali dikemukakan oleh Robert Hooke pada tahun 1678. Dalam hokum hooke dijelaskan bahwa baja lunak ditarik

oleh gaya aksial tertentu pada kondisi temperatur ruang maka material tersebut akan mengalami regangan yang nilainya berbanding lurus dengan tegangan ataupun dengan beban aksial yang diberikan kondisi tersebut kemudian disebut sebagai kondisi elastis. Hubungan antara tegangan dan regangan dapat diinterpretasikan sebagai berikut:

• 𝜎 =^𝑃_𝐴 (2.1)

• ε =^(𝑙−𝑙_𝑙 ⁰⁾

0 (2.2)

• 𝜎 = 𝐸𝜀 (2.3)

Dimana: P = Beban Aksial A = Luas Profil

lo = Panjang Mula-mula

l = Panjang Batang setelah dibebani E = Modulus Young/ Modulus kekenyalan

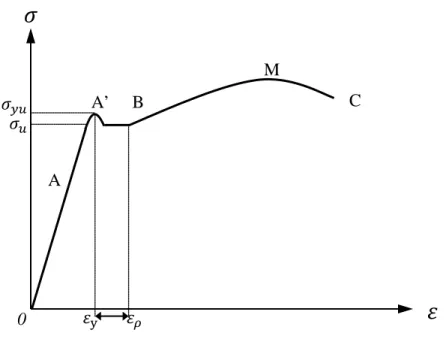
Tegangan didefinisikan sebagai intensitas gaya yang bekerja pada tiap satuan luas bahan sedangkan regangan didefinisikan sebagai suatu perbandingan antara perubahan dimensi suatu bahan dengan dimensi awalnya. Karena regangan merupakan rasio antara dua panjang, maka regangan ini merupakan besaran tak berdimensi, artinya regangan tidak mempunyai satuan. Dengan demikian, regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang yang terbuat dari bahan struktural hanya mengalami perubahan panjang yang kecil apabila dibebani. Hubungan antara regangan dan tegangan untuk lebih jelasnya dapat digambarkan pada gambar 2.1

Gambar 2.1. Hubungan tegangan dan regangan

Daerah pertama yaitu OA, merupakan garis lurus dan menyatakan daerah linear elastis. Kemiringan garis ini menyatakan besarnya modulus elastis atau disebut juga Modulus young, E. diagram tegangan- regangan untuk baja lunak

𝜎

𝜎𝑦𝑢

M

C 𝜎_𝑢 A’ B

𝜀_y 𝜀_𝜌

0

𝜀

A

umumnya memiliki titik leleh atas ( Upper Yield Point ),

σ

yu dan daerah leleh datar. Secara praktis, letak titik leleh atas ini, A’ tidaklah terlalu berarti sehingga pengaruhnya sering diabaiakan. Lebih lanjut, tegangan pada titik A disebut sebagai tegangan leleh, dimana regangan pada kondisi ini berkisar 0.00012. Dari grafik tersebut dapat dilihat bahwa bila regangan terus bertambah hingga melampaui harga ini, ternyata tegangannya dapat dikatakan tidak mengalami pertambahan. Sifat dalam daerah AB ini kemudian kemudian disebut sebagai daerah plastis. Lokasi titik B, yaitu titik akhir sebelum tegangan mengalami sedikit kenaikan, tidaklah dapat ditentukan. Tetapi, sebagai perkiraan dapat ditentukan terletak pada regangan 0,014 atau secara praktis dapat ditetapkan sebesar sepuluh kali besarnya regangan leleh.

Daerah BC merupakan daerah strain- hardening, dimana pertambahan regangan akan diikuti oleh pertambahan sedikit tegangan. Disamping itu hubungan tegangan- regangannya tidak bersifat linear. Kemiringan garis setelah titik B ini didefinisikan sebagai Es. Di titik M, tegangan mencapai titik maksimum yang disebut sebagai tegangan tarik ultimit ( ultimate tensile strength ). Pada akhirnya material akan putus ketika mencapai titik C.

Besaran- besaran pada gambar 2.1 akan tergantung pada komposisi baja, proses pembuatan pengerjaan baja dan temperature baja pada saat percobaan.

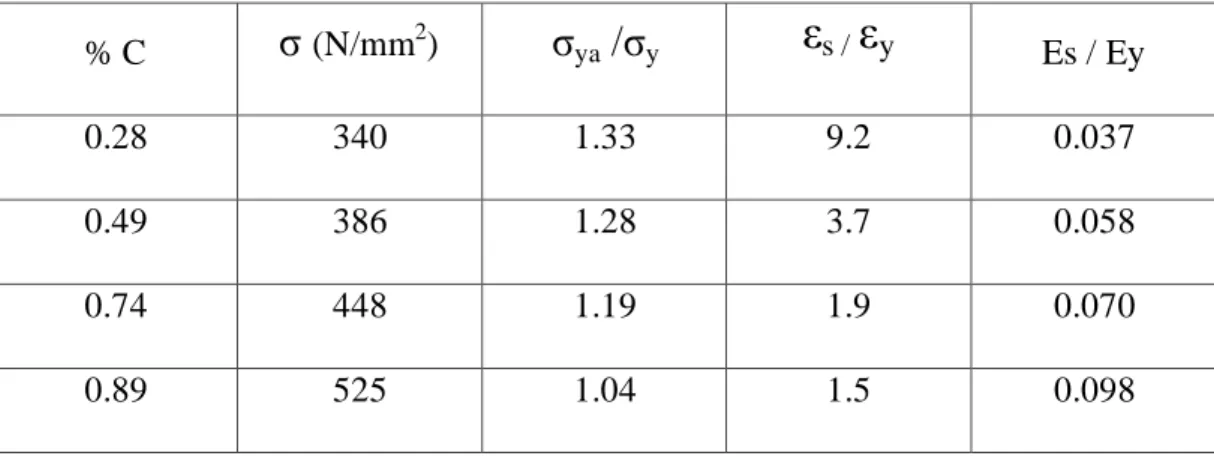
Tetapi factor- faktor tersebut tidak terlalu mempengaruhi besarnya modulus elastisitas ( E ). Roderick dan Heyman (1951), melakukan percobaan terhadap empat jenis baja dengan kadar karbon yang berbeda, data yang dihasilkan ditampilkan pada table 2.1

Table 2.1 Hubungan persentase karbon ( C ) terhadap tegangan

% C

σ

^(N/mm2)

σ

ya

/σ

y

ε

s /

ε

y Es / Ey

0.28 340 1.33 9.2 0.037

0.49 386 1.28 3.7 0.058

0.74 448 1.19 1.9 0.070

0.89 525 1.04 1.5 0.098

Dari table 2.1 dapat dilihat bahwa semakin besar tegangan lelehnya maka semakin besar kadar karbon yang dibutuhkan. Tegangan bahan akan berpengaruh pada daktalitas bahan. Semakin tinggi tegangan leleh maka semakin rendah daktalitas dari material tersebut. Daktalitas adalah perbandingan antara

ε

s dan

ε

y dimana

ε

s adalah regangan strain hardening dan

ε

y adalah regangan leleh.

Selanjutnya, apabila suatu material logam mengalami keadaan tekan dan tarik secara berulang, diagram tegangan regangannya dapat berbentuk seperti gambar 2.2. lintasan dan tekan akan sama. Hal ini menunjukkan suatu keadaan yang disebut efek bauschinger, yang pertama kali diperkenalkan oleh J.

Bauschinger dalam makalahnya yang dipublikasikan pada tahun 1886.

Gambar 2.2. Efek bauschinger

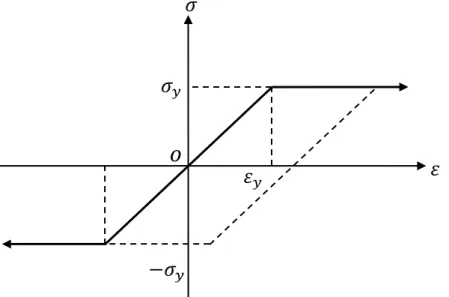
Hubungan regangan-tegangan untuk keperluan analisis ini diidealisasikan dengan mengabaikan pengaruh tegangan leleh atas (strain hardening ) dan efek bauschinger, sehingga hubungan antara tegangan dan regangan menjadi seperti

gambar 2.3. keadaan semacam ini sering disebut sebagai keadaan hubungan plastis ideal (ideal plastic relation).

𝜎

_𝑦

𝜀

𝜎

_𝑦

𝜀 𝜎

−𝜎

_𝑦

𝜀

_𝑦

𝑜

Gambar 2.3. Hubungan plastic ideal

2.1.2. Distribusi Tegangan Regangan

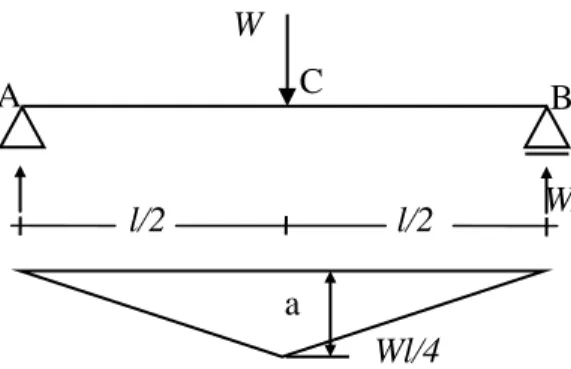
Sebuah balok diatas dua tumpuan sendi dan menahan beban terpusat W seperti gambar 2.4. dari persamaan keseimbangan, kita dapat memperoleh reaksi tumpuan sebesar W/2. Diagram momen lenturnya terdapat pada 2.4b, dengan momen maksimumnya sebesar Wl/4 yang terletak dibawah titik beban.

Gambar 2.4. Perletakan sederhana

Jika besarnya tegangan maksimum belum mencapai tegangan leleh, distribusi tegangan dan regangan dari semua penampangnya akan berupa garis lurus. Hal ini sesuai dengan hukum Bernoulli dan Navier, yaitu bersifat linear dan nol pada garis netral. Dengan demikian, tegangan dan regangan disuatu serat yang ditinjau adalah berbanding lurus terhadap jarak dari garis netral penampang.

Teganan tarik maksimum pada serat bawah dan tegangan tekan pada serat atas adalah :

𝜎𝑚𝑎𝑥 =^𝑀_𝑆 (2.4)

Dengan M = momen lentur

W

a

A C B

W/2 W/2

Wl/4

l/2 l/2

S = modulus penampang (section modulus).

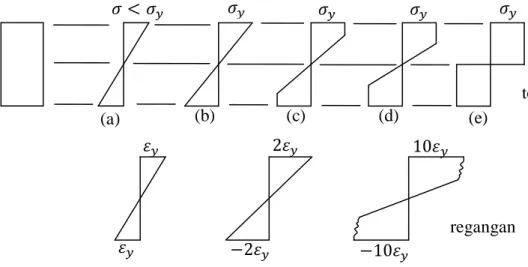
Jika beban terpusat semakin besar, tegangan di setiap serat penampang turut bertambah pula. Keadaan ini dapat kita lihat pada gambar 2.5, gambar 2.5b menunjukkan tegangan dan regangan pada serat terluar yang telah mencapai kondisi leleh. Keadaan ini terletak ditik A pada gambar 2.1, dan besarnya momen padatitik ini disebut sebagai momen leleh (yield stress), My.

Apabila beban w diperbesar lagi, tengangan lelehnya mulai menjalar keserat sebelah dalam, gambar 2.5c-d. bahwa tidak ada tegangan yang lebih besar daripada tegangan leleh, tetapi momen dalam dapat terus bertambah karena resultan gaya dalamnya bertambah besar. Dengan pemberian sedikit penambahan beban lagi, akan tercapailah keadaan dimana seluruh serat penampang mengalami tegangan leleh, gambar 2.5e. momen dalam menjadi maksimum dan merupakan momen plastis. Pada kondisi ini, penampang tadi akan mengalami rotasi yang

cukup besar tanpa terjadi perubahan momen. Dengan kata lain dititik tersebut telah terjadi sendi plastis. Titik c pada gambar 2.4 memiliki harga momen yang terbesar, sehingga titk ini akan lebih cepat untuk berubah menjadi sendi plastis dibandingkan dengan titik lainnya.

Gambar 2.5. Distribusi tegangan - regangan

2.1.3. Menentukan garis netral profil

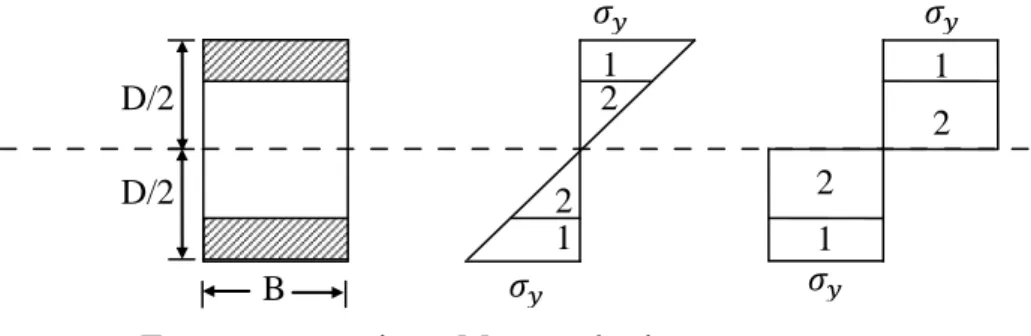
Garis netral untuk tampak yang sama pada kondisi elastis tidak akan sama dengan kondisi garis netral pada saat plastis. Pada kondisi elastis, garis netral merupakan garis yang membagi penampang menjadi dua bagian yang sama luasnya. Pada kondisi plastis, garis netral ditinjau sebagai berikut :

gambar 2.6. penentuan garis netral

• D1 = A1. σy (2.5)

regangan

𝜀𝑦 2𝜀_𝑦

𝜀_𝑦 −2𝜀𝑦

10𝜀_𝑦

−10𝜀𝑦

(a) (b) (c) (d) (e)

tegangan

𝜎 < 𝜎𝑦 𝜎𝑦 𝜎_𝑦 𝜎_𝑦 𝜎_𝑦

A1 A2

Z1

D2

𝜎𝑌

𝜎𝑌

Z2

D1

• D2 = A2. σy (2.6)

Agar terjadi keseimbangan maka D1 = D2

• Sehingga A1 = A2 = 1/2 A

• Selanjutnya Z1 = S1/A1 Z2 = S2/A2

Dimana : S1 = statis momen pada bidang A1 terhadap garis netral plastis S2 = statis momen pada bidang A2 terhadap garis netral plastis D1 = resultan gaya tekan diatas garis netral plastis

D2 = resultan gaya tarik diatas garis netral plastis Z1 = section modulus luasan 1

Z2 = section modulus luasan 2

Untuk menentunkan momen plastis batas digunakan :

• Mp = D1 (Z1 + Z2)

• Mp = σy ½ A ( Z1 + Z2 )

2.1.4. Hubungan momen kelengkungan

Pada saat terjadi sendi plastis pada suatu struktur dengan perletakan sederhana, suatu struktur akan berotasi secara tidak terbatas. Sebelun gaya luar bekerja, balok masih dalam keaadan lurus.

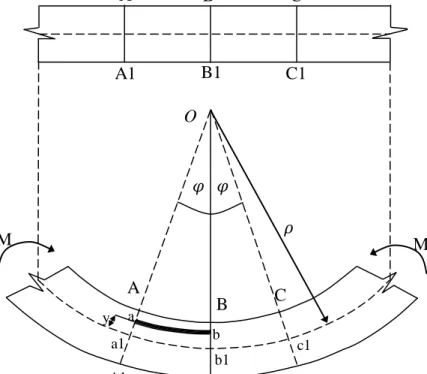
Gambar 2.7. Kelengkungan balok

Setelah gaya luar bekerja, balok akan mengalami pelenturan.

Diasumsikan bahwa material penyusun balok adalah homogen dan diasumsikan bahwa balok hanya mengalami lentur murni tanpa gaya aksial.

Perubahan kelengkungan akibat lentur murni ditunjukkan oleh gambar 2.5. titik A, B dan C akan tertekan sedangkan titik A1, B1, C1, akan meregang.

Perpanjangan titik A1-A, B1-B, C1-C akan mengalami perpotongan pada titik O.

sudut yang terbentuk akibat trjadinya perubahan kelengkungan ditik A dan B atau B dan C, dinyatakan dengan 𝜑. Kalau 𝜑 ini sangat kecil maka :

• 𝑎 𝑏 = (𝜌 − 𝑦)𝜑

• 𝑎1𝑏1 = 𝜌 𝜑

dengan 𝜌 adalah jari- jari kelengkungan ( radius of curvature )

A B C

A1 B1 C1

O

𝜑 𝜑

𝜌 M

M

B C A

y a a1 b

b1

c1 A1

B1 C1

sehingga, regangan pada arah memanjang disuatu serat sejauh y dari sumbu netral dapat dinyatakan sebagai:

• 𝜀 = ^{𝑎𝑏−𝑎1 𝑏1} _{𝑎1 𝑏1}

𝜀 =^−𝑦 _𝜌 (2.7)

Dimana 1/𝜌 menunjukkan kelengkungan ( K ). Tanda negatif menunjukkan bahwa bagian diatas garis netral, berada pada kondisi tekan, sedangkan pada kondisi dibawah garis netral berada pada kondisi tarik. Dengan

• ^𝜎

𝜀 = ^𝑦 _𝑅

1

R= _Ey^σ (2.8)

Tegangan tarik pada serat bawah dan tegangan tekan pada sera atas adalah :

• 𝜎 =^𝑀_𝑆

Dimana : S adalah modulus penampang

• 𝑦 =^𝐷₂

Akhirnya didapat ¹

𝑅=_ESD/2^M dimana S.D/2 = I (momen inersia)

• ¹_𝑅= ^M_EI= ^d_dx^2y₂ (2.9)

= Daerah yang mengalami elastis

= daerah yang berada pada kondisi elastis gambar 2.8. Distribusi tegangan pada penampang

Pada gambar 2.8. dapat dilihat bahwa regangan pada serat terluar telah mencapai tegangan leleh. Sedangkan serat terjauh Z dari garis netral belum mengalami tegangan leleh. Dengan demikian daerah sejauh 2Z materialnya masih berada pada kondisi elastis dan besarnya momen dalam dapat dicari dari resultan bagian elastis dan plastis.

Jika Z=D/2, hanya serat terluar saja yang mencapai kondisi leleh dan besar momen dalam yang ditahan disebut sebagai momen leleh (My).

• My = S . 𝜎𝑦 (2.10)

Dimana S adalah modulus penampang (section modulus)

Dari persamaan (2.6) dengan harga 𝜀 = 𝜀_𝑦 , 𝑦 = 𝑧, dapat diperoleh :

• 𝐾 = 𝜀_𝑦/𝑧 (2.11)

Selanjutnya untuk Z = ½ D diperoleh :

• 𝐾𝑦 = 2 𝜀𝑦/𝐷 (2.12)

Dimana K = kelengkungan pada kondisi plastis sebagian (partially plastic state)

Garis netral

B 𝜎𝑌

𝜎𝑌

D/2 z D/2

Ky = kelengkungan pada saat kondisi leleh

Perbandingan antara momen plastis (Mp) dengan momen leleh (My) menyatakan peningkatan kekuatan penampang akibat ditinjau dari kondisi plastis.

Perbandingan ini tergantung dari bentuk penampang (shape factor) yang dinotasikan sebagai f.

Gambar 2.9. Hubungan momen kelengkungan

dari gambar 2.9 dapat dilihat bahwa suatu kurva hubungan momen terhadap kelengkungan (M-K), dimana dari kurva tersebut dapat dilihat bahwa nilai momen ( M ) akan semakin mendekati f. My apabila harga K semakin besar. Bila nilai menjadi factor bentuk ( f ) maka harga K akan mencapai harga tidak berhingga, dimana ini menandakan bahwa nilai z dalam persaamaan 2.11 sama dengan nol, dimana y = z, maka seluruh penampang serat mencapai kondisi plastis penuh dan momen plastisnya adalah Mp = f. My. Dimana f adalah factor bentuk yang merupakan perbandingan antara momen plastis dan momen leleh menyatakan

b

c M/My

K/ky a

peningkatan kekuatan penampang akibat ditinjau dari kondisi plastis.

Perbandingan ini tergantung dari bentuk penampang.

2.1.5. Analisa penampang

Pada bagian ini akan diberikan paparan yang lebih mendetail tentang distribusi tegaganan pada keadaan leleh menuju kondisi plastis penuh yang digambarkan pada gambar 2.10.

Gambar 2.10. Distribusi tegangan pada keadaan leleh dan keadaan plastis pada tampang persegi

 Modulus elastis My = 2M1+2M2

= 2 �^𝐷₂− 𝑍� 𝐵. 𝜎𝑌1

2�^𝐷₂+ 𝑍� + 2.¹₂𝑍. 𝐵. 𝜎𝑌�²₃𝑍�

= �^𝐷₂− 𝑍� �^𝐷₂+ 𝑍� 𝐵. 𝜎_𝑌 + 𝐵. 𝜎_𝑌²₃𝑍²

= 𝐵. 𝜎𝑌���^𝐷₂�²− 𝑍²� +²₃𝑍²�

= 𝐵. 𝜎𝑌�^𝐷₄²−¹₃𝑍²�

= 𝐵. 𝜎_𝑌�^𝐷₄²−¹₃�^𝐷₂�²�

= 𝐵. 𝜎_𝑌�^3𝐷2₁₂^−𝐷2� D/2

D/2

B

1 2

2 1

2 1 1

2

Momen elastis Momen plastis 𝜎𝑦

𝜎_𝑦

𝜎𝑦

𝜎𝑦

Tampang persegi

= ¹

6𝐵. 𝐷². 𝜎𝑌 (2.13a)

 Modulus plastis

Momen plastis yaitu luasan tampang kali lengan momen Mp = 2. 𝜎_𝑌�¹₂𝐵. 𝐷� �¹₄𝐷�

= ¹

4𝐵. 𝐷². 𝜎_𝑌 (2.13b)

Jika menggunakan factor bentuk (shape factor) yang dinotasikan dengan f, maka hubungan antara kapasitas momen pada saat keadaan leleh (My) dan kapasitas momen pada keadaan plastis (Mp) akan menghasilkan :

• 𝑓 = ^𝑀𝑝_𝑀𝑦

• 𝑓 = ¹⁴1^{𝐵.𝐷2.𝜎𝑌} 6𝐵.𝐷².𝜎_𝑌

• 𝑓 = 1,5

2.2. SENDI PLASTIS 2.2.1. Umum

Sendi plastis merupakan suatu kondisi dimana terjadi perputaran (rotasi) pada suatu struktur yang berlangsung secara terus menerus sebelum pada akhirnya mencapai keruntuhan yang diakibatkan oleh pembebanan eksternal.

Dengan timbulnya sendi plastis pada suatu sturktur maka sifat dari konstruksi tersebut akan berubah, sebagai contoh:

1. Bila konstruksi semula merupakan statis tertentu, maka dengan timbulnya satu sendi plastis akan membuat konstruksi menjadi labil dan runtuh.

2. Pada suatu konstruksi yang hiperstatis berderajat n, bila timbul satu sendi plastis maka konstruksi akan berubah derajat kehiperstatis dari suatu konstruksi.

Dengan timbulnya sendi plastis pada suatu konstruksi maka momen yang yang semula dihitung dengan cara elastis harus dihitung kembali sesuai dengan perubahan sifat konstruksi yang ditimbulkan oleh sendi plastis tersebut.

2.2.2. Bentuk sendi plastis

Sendi plastis akan membentuk satu persamaan garis tertentu sebelum terjadi keruntuhan.

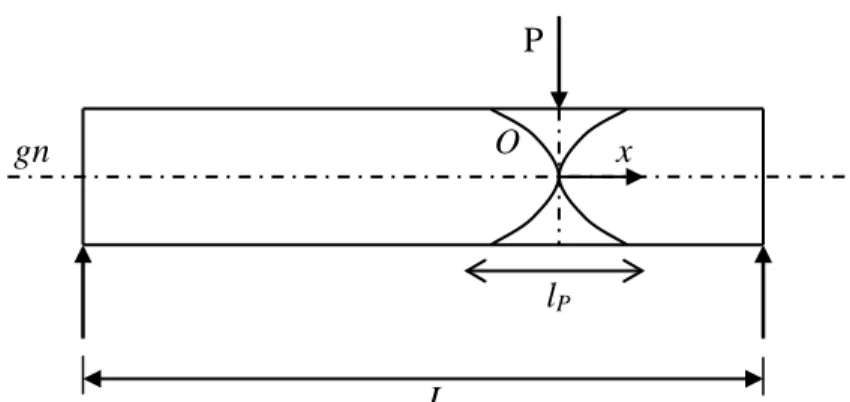
Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp ) pada balok sepanjang L dengan pembebanan terpusat asimetris

Gambar 2.11. Balok dengan pembebanan terpusat

𝑀_𝑅 = 𝑀_𝑃(1 −𝑥 𝐿) 𝑀_𝑅 = 𝑀_𝑃(1 − 𝛽𝛼²) (1 −𝑥

𝐿) = (1 − 𝛽𝛼²)

O P

lP

x gn

L

𝑥 = 𝛽𝐿𝛼² 𝛼 = 𝛽𝐿√𝑥 𝑓(𝑥) = 𝛽𝐿√𝑥

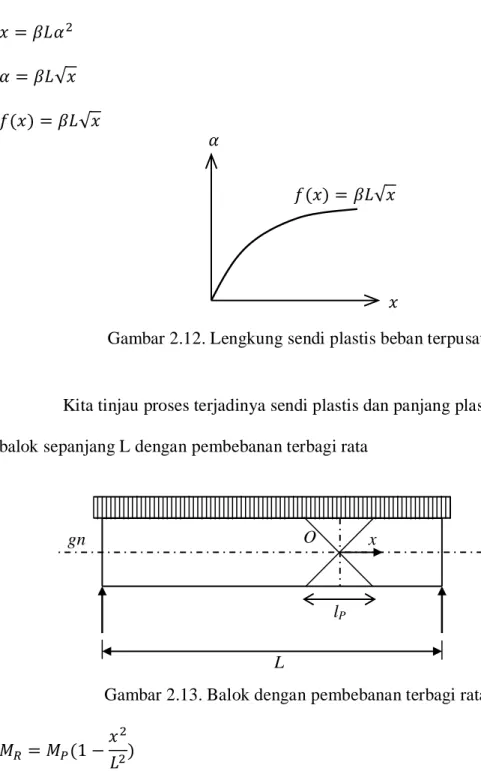
Gambar 2.12. Lengkung sendi plastis beban terpusat

Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp ) pada balok sepanjang L dengan pembebanan terbagi rata

Gambar 2.13. Balok dengan pembebanan terbagi rata 𝑀_𝑅 = 𝑀_𝑃(1 −𝑥²

𝐿²) 𝑀_𝑅 = 𝑀_𝑃(1 − 𝛽𝛼²)

(1 −𝑥²

𝐿²) = (1 − 𝛽𝛼²) 𝑥 = 𝛽𝐿²𝛼²

𝛼 = 𝛽𝐿𝑥 𝑓(𝑥) = 𝛽𝐿𝑥

𝛼

𝑥 𝑓(𝑥) = 𝛽𝐿√𝑥

O

l_P x gn

L

Gambar 2.14.Gambar dengan sendi plastis terbagi rata

Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp ) pada balok sepanjang L dengan pembebanan terbagi rata segitiga

Gambar 2.15. Balok dengan pembebanan terbagi rata segitiga

𝑀𝑅 = 𝑀𝑃(1 −𝑥³ 𝐿³) 𝑀𝑅 = 𝑀𝑃(1 − 𝛽𝛼²)

(1 −𝑥³

𝐿³) = (1 − 𝛽𝛼²) 𝑥 = 𝛽𝐿³𝛼²

𝛼 = 𝛽𝐿𝑥³² 𝑓(𝑥) = 𝛽𝐿𝑥³²

𝛼

𝑥 𝑓(𝑥) = 𝛽𝐿𝑥

O

lP

x gn

L

Gambar 2.16. Gambar sendi plastis beban segitiga

2.3. ANALISA STRUKTUR SECARA PLASTIS 2.3.1. Pendahuluan

Analisa struktur secara plastis bertujuan untuk menentukan beban batas yang dapat dipikul oleh suatu struktur ketika mengalami keruntuhan. Kruntuhan struktur dimulai dengan terjadinya sendi plastis. Keruntuhan dapat bersifat menyeluruh ataupun parsial.

Suatu struktur hiperstatis berderajat n akan mengalami mengalami keruntuhan total jika kondisinya labil, di sini telah terbentuk lebih dari n buah sendi plastis. Keruntuhan parsial terjadi apabila sendi plastis yang terjadi pada mekanisme keruntuhan tidak menyebabkan struktur hiperstatis dengan derajat yang lebih rendah dari yang semula.

Suatu struktur statis tak tentu mempunyai sejumlah mekanisme keruntuhan yang berbeda. Setiap mekanisme keruntuhan itu menghasilkan beban runtuh yang berbeda. Sehingga pada akhirnya dipilih mekanisme yang menghasilkan beban runtuh yang terkecil.

𝛼

𝑥 𝑓(𝑥) = 𝛽𝐿𝑥³²

Jumlah sendi plastis yang dibutuhkan untuk mengubah suatu struktur kedalam kondisi mekanisme runtuhnya sangat berkaitan dengan derajat statis tak tentu yang ada dalam struktur tersebut. Dalam hal ini dapat dibuat runusan sebagai berikut : 𝑛 = 𝑟 + 1

Dimana n = jumlah sendi plastis untuk runtuh r = derajat statis tak tentu

1. untuk struktur balok dua perletakan sendi- sendi (struktur statis tertentu ) dengan 𝑟 = 0 𝑑𝑎𝑛 𝑛 = 1

Gambar 2.17. struktur pembebanan dan mekanisme runtuh perletakan sendi- sendi

Struktur diatas hanya memerlukan sebuah sendi platis untuk mencapai mekanisme runtuhnya yaitu sendi plastis pad momen maksimum (dibawah beban titik).

2. Suatu balok dua perletakan sendi- jepit ( struktur statis tak tentu berderajat 1) dengan 𝑟 = 1 𝑑𝑎𝑛 𝑛 = 2

Gambar 2.18. struktur pembebanan dan mekanisme runtuh perletakan sendi- jepit P

P

Struktur perletakan ini memerlukan dua buah sendi plastis untuk mencapai mekanisme keruntuhannya . sendi plastis pada system perletakan tersebut akan terjadi pada titik dimana terjadinya momen maksimum dan pada perletakan jepit.

3. Untuk balok struktur dua perletakan jepit- jepit (struktur statis tak tentu berderajat dua) dengan 𝑟 = 2 𝑑𝑎𝑛 𝑛 = 3

Gambar 2.19. struktur pembebanan dan mekanisme runtuh perletakan jepit –jepit

Pada struktur perletakan ini diperlukan tiga buah sendi platis untuk mencapai mekanisme keruntuhannya. Sendi pada system perletakan tersebut akan terjadi pada titik dimana terjadinya momen maksimum dan pada perletakan jepit.

2.3.2. Perhitungan struktur

Pada prinsipnya, jika suatu struktur mencapai kondisi keruntuhan maka akan dipenuhi ketiga kondisi berikut:

1. Kondisi leleh (Yield Condition)

Momen lentur dalam struktur tidak ada yang melampaui momen batas (Mp)

2. Kondisi keseimbangan (Equilibrium Condition) 3. Kondisi mekanisme (mechanism condition)

Beban batas tercapai apabila terbentuk suatu mekanisme keruntuhan.

P

Ketiga kondisi diatas menjadi syarat dari teorema berikut:

1. Teorema batas bawah ( lower bound theorem)

Teorema batas bawah menetapkan atau menghitung distribusi momen dalam struktur berdasarkan kondisi keseimbangan dan leleh. Beban yang dianalisa memiliki factor beban (𝜆 ) yang memiliki nilai yang lebih kecil dari harga yang sebenarnya (𝜆_𝑐), dirumuskan 𝜆 ≤ 𝜆_𝑐 sehingga hasil yang dihasilkan mungkin aman mungkin tidak.

2. Teorema batas atas (upper bound theorem)

Jika distribusi momen yang diperoleh dihitung berdasrkan syarat yang memenuhi kondisi keseimbangan dan mekanisme, dapat dipastikan bahwa harga factor bebannya akan lebih besar atau sama dengan harga sebenarnya, (𝜆𝑐), 𝜆 ≥ 𝜆𝑐

Sehingga hasil yang dihasilkan mungkin benar atau mungkin tidak.

3. Teorema unik (unique theorem)

Distribusi momen untuk teorema ini akan memenuhi ketiga kondisi tersebut di atas sehingga akan diperoleh nilai factor beban dari mekanisme struktur yang ditinjau :𝜆 = 𝜆𝑐. Pada teorema ini terdapat 4 metode yang dapat digunakan :

a. Metode statis

b. Metode kerja virtual (virtual work method) c. Metode distribusi momen

d. Metode element hingga(finite element method)

2.3.3. Metode kerja virtual

Metode kerja virtual adalah metode yang meninjau keseimbangan energi dari struktur tersebut ketika mengalami mekanisme runtuhnya.

Persamaan kerja virtual ini dapat ditulis sebagagai berikut :

∑𝑊𝑖. ∆𝑖 = ∑𝑀𝑗. 𝜃𝑗 (2.14)

Dimana : Wi = beban luar ( beban terpusat atau terbagi rata)

∆𝑖 = deformasi struktur

∆𝑖 = 𝑙 2� tan 𝜃 , untuk sudut yang kecil tan 𝜃 = 𝜃 tan 𝜃 = 𝜃

Mj = momen pada tampang kritis 𝜃𝑗 = sudut rotasi sendi plastis

2.3.4. Metode Elemen Hingga Untuk Elemen Plane frame

Metode elemen hingga merupakan salah satu metode yang digunakan untuk menghitung gaya-gaya dalam yang terjadi dalam suatu komponen struktur.

Metode elemen hingga juga dikenal sebagai metode kekakuan ataupun displacement methode karena yang didapat terlebih dahulu dari perhitungan

adalah perpindahan baru kemudian gaya batang dicari.

Dalam hubungannya dengan tugas akhir ini, metode elemen hingga ini digunakan untuk perhitungan gaya-gaya dalam yang terjadi pada komponen struktur. Untuk itu, metode elemen hingga yang digunakan adalah metode elemen hingga untuk Elemen Plane frame dimana gaya yang bekerja pada struktur yang diperhitungkan hanya terbatas pada gaya normal, gaya lintang, dan momen pada arah z

Persamaan umum untuk metode elemen hingga ini adalah :

{𝑓} = [𝑘]{𝑑} (2.15)

dimana : {f} = Matriks gaya-gaya batang ( kg ) [k] = Matriks kekakuan struktur ( N/m² ) {d} = Matriks perpindahan ( m dan rad )

Kemudian rumus untuk menentukan kekakuan global dapat diturunkan sebagai berikut :

�𝑓̅� = [𝑇]{𝑓}

�𝑑̅� = [𝑇]{𝑑}

{𝑓} = [𝑘]{𝑑}

[𝑇]⁻¹�𝑓̅� = [𝑘][𝑇]⁻¹�𝑑̅�

�𝑓̅� = [𝑇][𝑘][𝑇]⁻¹�𝑑̅�

Maka ditentukan matriks kekakuan global adalah :

�𝑘�� = [𝑇][𝑘][𝑇]⁻¹

Dengan [𝑇] adalah suatu faktor konversi gaya-gaya ke arah sumbu global yang berbeda-beda untuk tiap jenis struktur dan akan dijabarkan kemudian. Setelah diperoleh matriks kekakuan global, maka dapat disusun suatu matriks kekakuan struktur yang memasukkan semua komponen-komponen elemen yang ada.

�𝑓₁̅

𝑓̅₂� = �𝑘�₁ 0 0 𝑘�₂� �𝑑₁̅

𝑑̅₂�

Langkah berikutnya yaitu menentukan syarat-syarat batas yang ada dan kemudian nilai perpindahan dapat diperoleh. Dengan nilai perpindahan global yang diperoleh, gaya-gaya batang untuk tiap element dapat ditentukan dengan :

{𝑓} = [𝑘]{𝑑}

dimana :

{𝑑} = [𝑇]⁻¹�𝑑̅�

Dalam menggunakan metode elemen hingga, perlu diperhatikan, bahwa pada tiap elemen / batang akan terdapat dua buah titik simpul yaitu simpul awal yang diberi tanda (1) dan simpul akhir yang diberi tanda (2) dan sebuah elemen yang diberi tanda (a) seperti tampak pada Gambar.2.14

Derajat kebebasan adalah jumlah komponen perpindahan yang dapat terjadi pada kedua simpul yang ada pada suatu elemen. Jumlah derajat kebebasan berbeda-beda untuk tiap jenis struktur. Misalnya, untuk elemen rangka, jumlah derajat kebebasannya adalah dua yaitu masing-masing satu perpindahan dalam arah sumbu batang ( biasanya disebut sebagai sumbu 1 ) pada titik simpul (1) dan (2).

Dari jumlah derajat kebebasan yang ada, suatu matriks kekakuan untuk suatu jenis struktur dapat ditentukan. Masing-masing jenis struktur memiliki suatu matriks kekakuan tersendiri dimana matriks kekakuan untuk elemen rangka

Gambar.II.11.Titik Simpul dan Elemen

1 2

Gambar 2.20. Titik simpul dan element

berbeda dengan matriks kekakuan untuk elemen frame dan lain-lainnya. Begitu pula halnya dengan matriks kekakuan untuk elemen grid. Matriks kekakuan dari elemen plane frame dapat diperoleh dengan menggabungkan Matriks kekakuan truss element dengan beam element. Memiliki 6 buah DOF dimana element- elementnya mengalami gaya normal, gaya lintang, dan momen pada arah z.

Kekakuan dalam suatu struktur terbagi dalam dua jenis yaitu kekakuan lokal dan kekakuan global. Kekakuan lokal adalah kekakuan elemen yang mengacu arah sumbu masing-masing elemen sedangkan kekakuan global adalah kekakuan elemen yang mengacu pada sistem koordinat global yaitu sistem koordinat kartesian (XYZ). Jika dalam suatu struktur terdapat lebih dari satu batang dengan arah sumbu lokal yang berbeda, maka kekakuan lokal dari tiap elemen harus diubah menjadi kekakuan global agar matriks kekakuan dari semua elemen yang ada dapat digabungkan.

Untuk elemen plane frame, seperti yang telah disebutkan di atas, kekakuan lokalnya merupakan gabungan dari kekakuan lokal untuk truss element dengan beam element.

ΕΙz ΕΑ

Sy¹ Μz¹ Sx¹

Sy² Μz²

Sx²

L

Gambar 2.21. derajat kebebasan untuk elemen plane frame

•

Syarat keseimbangan :

𝑆_𝑥1 = −𝑆_𝑥2 ; 𝑆_𝑦1 = −𝑆_𝑦2 ; 𝑀_𝑍1= −𝑀_𝑍2+ 𝑆_𝑦2. 𝐿 Menentukan Matriks Kekakuan Untuk Flane-Frame Element

dimana :

𝑆_𝑥1 =𝐸𝐴

𝐿 (𝑢1− 𝑢2) ; 𝑆_𝑥2 =𝐸𝐴

𝐿 (𝑢2− 𝑢1) 𝑆_𝑦1 =12 𝐸𝐼

𝐿³ (𝑣₁− 𝑣₂) +6 𝐸𝐼

𝐿² (𝜒₁+ 𝜒₂) ; 𝑆_𝑦2

=12 𝐸𝐼

𝐿³ (𝑣₂− 𝑣₁) −6 𝐸𝐼

𝐿² (𝜒₁+ 𝜒₂)

𝑀_𝑍1 =6 𝐸𝐼

𝐿² (𝑣₁− 𝑣2 ) +2 𝐸𝐼

𝐿 (2𝜒₁+ 𝜒2) ; 𝑀_𝑍2

= 6 𝐸𝐼

𝐿² (𝑣₁− 𝑣2 ) +2 𝐸𝐼

𝐿 (𝜒₁+ 2𝜒2)

Maka diperoleh :

⎩⎪

⎪⎨

⎪⎪

⎧𝑆_𝑥1 𝑆_𝑦1 𝑀_𝑍1

𝑆_𝑥2 𝑆_𝑦2 𝑀_𝑍2⎭⎪⎪⎬

⎪⎪

⎫

=

⎣⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎡ ^𝐸𝐴𝐿 0 0 0 ^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

𝐸𝐴

𝐿 0 0

0 ^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿 ⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤

⎩⎪

⎨

⎪⎧𝑢₁ 𝑣₁ 𝜒₁ 𝑢2

𝑣2

𝜒2⎭⎪⎬

⎪⎫

Jadi matriks kekakuan lokal untuk plane-frame element :

[𝑘] =

⎣⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎡ ^𝐸𝐴𝐿 0 0 0 ^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

𝐸𝐴

𝐿 0 0

0 ^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿 ⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤

• Menentukan Matriks Kekakuan Global Untuk Plane-Frame Element

perhatikan gambar 1.2. pada sistem koordidat batang tipikal, Untuk simpul 1 pada gambar tersebut, dapat dituliskan :

𝑓̅₁= � 𝑆̅_𝑥1 𝑆̅_𝑦1 𝑀�_𝑍1

� = �cos 𝛼 − sin 𝛼 0 sin 𝛼 cos 𝛼 0

0 0 1� �

𝑆_𝑥1 𝑆_𝑦1

𝑀_𝑍1� = [𝑇]{𝑓₁} Untuk satu element / batang berlaku :

�𝑓̅𝑒� = [𝑇𝑒]{𝑓𝑒}

�𝑓₁̅

𝑓̅2� = �𝑇 00 𝑇� �𝑓₁ 𝑓₂� dimana :

[𝑇_𝑒] = �𝑇 00 𝑇�

Maka matriks kekakuan global untuk truss element adalah :

�𝑘�𝑒� = [𝑇𝑒][𝑘𝑒][𝑇𝑒]⁻¹

Karena matriks _[𝑇𝑒] merupakan matriks ortogonal maka dapat ditulisakan sebagai :

�𝑘�𝑒� = [𝑇𝑒][𝑘𝑒][𝑇𝑒]^𝑇

�𝑘�𝑒�

=

⎣⎢

⎢⎢

⎢⎡cos 𝛼 − sin 𝛼 0 sin 𝛼 cos 𝛼 0

0 0 1 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0

cos 𝛼 − sin 𝛼 0 sin 𝛼 cos 𝛼 0 0 0 1⎦⎥⎥⎥⎥⎤

⎣⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎡ 𝐸𝐴

𝐿 0 0

0 12 𝐸𝐼 𝐿³

6 𝐸𝐼 𝐿² 0 6 𝐸𝐼

𝐿² 4 𝐸𝐼

𝐿

−𝐸𝐴

𝐿 0 0

0 −12 𝐸𝐼 𝐿³

6 𝐸𝐼 𝐿² 0 −6 𝐸𝐼

𝐿² 2 𝐸𝐼

𝐿

−𝐸𝐴

𝐿 0 0

0 −12 𝐸𝐼 𝐿³ −6 𝐸𝐼

𝐿²

0 6 𝐸𝐼

𝐿²

2 𝐸𝐼 𝐿

𝐸𝐴

𝐿 0 0

0 12 𝐸𝐼 𝐿³ −6 𝐸𝐼

𝐿² 0 −6 𝐸𝐼

𝐿² 4 𝐸𝐼

𝐿 ⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤

⎣⎢

⎢⎢

⎢⎡cos 𝛼 sin 𝛼 0

− sin 𝛼 cos𝛼 0

0 0 1 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0

cos 𝛼 sin 𝛼 0

− sin 𝛼 cos𝛼 0 0 0 1⎦⎥⎥⎥⎥⎤

Jika dimisalkan cos α = c dan sin α = s, maka matriks kekekakuan global untuk Plane-Frame Element :

�𝑘�𝑒� =

⎣⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎡

𝐴𝑐²+12𝐼

𝐿² 𝑠² �𝐴 −12𝐼

𝐿²� 𝑐𝑠 −6𝐼 𝐿 𝑠

�𝐴 −12𝐼

𝐿²� 𝑐𝑠 𝐴𝑠²+12𝐼

𝐿² 𝑐² 6𝐼 𝐿𝑐

−6𝐼

𝐿𝑠 6𝐼

𝐿𝑐 4𝐼

− �𝐴𝑐²+12𝐼

𝐿² 𝑠²� − �𝐴 −12𝐼

𝐿²� 𝑐𝑠 −6𝐼 𝐿 𝑠

− �𝐴 −12𝐼

𝐿²� 𝑐𝑠 − �𝐴𝑠²+12𝐼

𝐿² 𝑐²� 6𝐼 𝐿 𝑐 6𝐼

𝐿𝑠 −6𝐼

𝐿 𝑐 2𝐼

− �𝐴𝑐²+12𝐼

𝐿² 𝑠²� − �𝐴 −12𝐼

𝐿²� 𝑐𝑠 6𝐼 𝐿 𝑠

− �𝐴 −12𝐼

𝐿²� 𝑐𝑠 − �𝐴𝑠²+12𝐼

𝐿²𝑐²� −6𝐼 𝐿𝑐

−6𝐼

𝐿𝑠 6𝐼

𝐿𝑐 2𝐼

𝐴𝑐²+12𝐼

𝐿² 𝑠² �𝐴 −12𝐼

𝐿²� 𝑐𝑠 −6𝐼 𝐿𝑠

�𝐴 −12𝐼

𝐿²� 𝑐𝑠 𝐴𝑠²+12𝐼

𝐿² 𝑐² −6𝐼 𝐿 𝑐

−6𝐼

𝐿 𝑠 −6𝐼

𝐿𝑐 4𝐼 ⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤

Setelah matriks kekakuan diperoleh maka gaya-gaya batang untuk elemen plane frame dapat dihitung dengan terlebih dahulu menghitung besarnya perpindahan yang terjadi pada titik-titik simpul dengan menggunakan persamaan (2.15).

⎩⎪

⎪⎨

⎪⎪

⎧𝑆_𝑥1 𝑆_𝑦1 𝑀_𝑍1

𝑆_𝑥2 𝑆_𝑦2 𝑀_𝑍2⎭⎪⎪⎬

⎪⎪

⎫

=

⎣⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎡ ^𝐸𝐴𝐿 0 0 0 ^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 ^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

−^𝐸𝐴_𝐿 0 0

0 −^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 ^{6 𝐸𝐼} _𝐿2 ^{2 𝐸𝐼} _𝐿

𝐸𝐴

𝐿 0 0

0 ^{12 𝐸𝐼} _𝐿3 −^{6 𝐸𝐼} _𝐿2 0 −^{6 𝐸𝐼} _𝐿2 ^{4 𝐸𝐼} _𝐿 ⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤

⎩⎪

⎨

⎪⎧𝑢1

𝑣1

𝜒1

𝑢₂ 𝑣₂ 𝜒2⎭⎪⎬

⎪⎫

(2.16)

Setelah nilai-nilai perpindahan diperoleh dari persamaan (2.16), maka gaya-gaya dalam untuk tiap elemen dapat dicari dengan menggunakan persamaan (2.15).