TESIS KI142502
Komputasi Numerik Model Penyobekan
Dinamis Lembaran Kertas
ASTRIS DYAH PERWITA
NRP. 5114201066
PEMBIMBING I
Dr. Darlis Herumurti, S.Kom, M.Kom.
NIP. 197712172003121001
PEMBIMBING II
Rully Soelaiman, S.Kom, M.Kom. NIP. 197002131994021001
PROGRAM STUDI MAGISTER
JURUSAN TEKNIK INFORMATIKA
FAKULTAS TEKNOLOGI INFORMASI
INSTITUT TEKNOLOGI SEPULUH NOPEMBER
SURABAYA
THESIS KI142502
Numerical Scheme Computation for Paper
Sheet Adaptive Tearing
ASTRIS DYAH PERWITA
NRP. 5114201066
SUPERVISOR I
Dr. Darlis Herumurti, S.Kom, M.Kom.
NIP. 197712172003121001
SUPERVISOR II
Rully Soelaiman, S.Kom, M.Kom.
NIP. 197002131994021001
MASTER PROGRAM
DEPARTEMENT OF INFORMATICS
FACULTY OF INFORMATION TECHNOLOGY
INSTITUT TEKNOLOGI SEPULUH NOPEMBER
SURABAYA
vi
vii
Komputasi Numerik Model Penyobekan Dinamis Lembaran Kertas
Nama Mahasiswa : Astris Dyah Perwita
NRP : 5114201066
Pembimbing : 1. Dr. Darlis Herumurti, S.Kom, M.Kom.
2. Rully Soelaiman, S.Kom, M.Kom.
ABSTRAK
Untuk memproduksi detail dan variasi retakan pada berbagai macam benda
nyata masih dirasa sangat sulit. Sementara bila membangun model dengan metode
Finite Element tradisional, maka penerapan yang dilakukan juga cukup kompleks
karena membutuhkan pembaharuan setiap sebuah retakan atau sobekan terbentuk.
Oleh karena itu, pada penelitian ini akan berfokus pada teknik simulasi retakan dan
sobekan dengan arah dan besaran yang tepat sesuai dengan sifat atau properti yang
dikalkulasi dengan perhitungan matematis pada bidang tipis khususnya kertas
sesuai dengan metode dan parameter yang tepat.
Untuk dapat menghasilkan model sobekan yang tepat, maka diperlukan suatu
skema numerik yang dapat memenuhi kebutuhan (requirement) tersebut. Penelitian
ini akan melibatkan perhitungan metode Finite Element modifikasi yang
melibatkan elemen-elemen pengayaan pada proses eksekusinya. Proses yang
dilakukan akan berlangsung dinamis dengan memperhatikan hasil sobekan setiap
pada setiap waktu.
Penelitian ini berfokus pada komputasi numerik model penyobekan dinamis
lembaran kertas dengan memperhatikan variabel-variabel yang mempengaruhinya.
Metode yang diimplementasikan akan menghasilkan model dengan proses
assembly matrik kekakuan yang konvergen terhadap fungsi waktu. Hasil uji coba
penelitian ini menyatakan bahwa rata-rata waktu komputasi pembentukan sobekan
pada material tanpa inklusi adalah 21,17 detik dan lebih cepat dari pada
pembentukan sobekan dengan inklusi dengan rata-rata waktu komputasi 30,57
viii
24,75 detik dan lebih cepat daripada inklusi linier dengan rata-rata waktu komputasi
36,39 detik.
ix
Numerical Scheme Computation for Paper Sheet Adaptive Tearing
Student’s Name : Astris Dyah Perwita Student’s ID : 5114201066
Supervisor : 1. Dr. Darlis Herumurti, S.Kom, M.Kom.
2. Rully Soelaiman, S.Kom, M.Kom.
ABSTRACT
To produce detail and variation of tearing and cracking on various object is
challenging. Meanwhile using traditional Finite Element Method will need such a
complex computation caused by updated value for every crack made. To overcome
such problems, research focused on tearing and cracking simulation technique with
to predict precise tear amount and angle depend on the variables value on thin plates
such as paper.
To generate tearing model that fulfill the requirement, numeric scheme will
be needed. Modification of Finite Element Method along with enrichment element
will be adapted in this research. And this method will determine which variables
take effect on the results. Every process will be done adaptively depending on the
existing results for each iteration.
This research will be focused on numerical computation on paper sheet with
variables affects. Experiments generate a model which stiffness matrix convergent
for each time function. The stiffness matrix will also convergent for each variation
of elastic variables. Experiments show that computation time for tearing model will
works faster without inclusion as it works on average 21.17 seconds than with
inclusion with average 30.57 seconds. It also shows that computation time for
tearing model with circular inclusion works faster than linear inclusion with 24.75
seconds for circular inclusion and 36.39 seconds for linear inclusion on average.
x
xi
KATA PENGANTAR
Puji syukur kepada Allah SWT atas segala karunia dan rahmat-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul “Komputasi Numerik Model
Penyobekan Dinamis Lembaran Kertas”.
Harapan dari penulis semoga apa yang tertulis di dalam buku tesis ini dapat
bermanfaat dan dapat memberikan kontribusi yang nyata bagi pengembangan ilmu
pengetahuan saat ini. Dalam pelaksanaan penelitian dan penyusunan buku tesis
penulis mendapatkan banyak bantuan dan dukungan dari berbagai pihak. Tanpa
mengurangi rasa hormat, penulis ingin mengucapkan banyak terima kasih kepada:
1. Bapak Rully Soelaiman S.Kom, M.Kom, dan Bapak Dr. Darlis
Herumurti, S.Kom, M.Kom. selaku dosen pembimbing yang telah
memberikan banyak arahan, bantuan, nasihat, dan perhatian terhadap
penelitian penulis.
2. Bapak Waskito Wibisono S.Kom., M.Eng., Ph.D. dan Ibu Chastine
Fatichah selaku Ketua dan Sekretaris Program Studi Pascasarjana Teknik
Informatika yang telah memberikan kesempatan belajar di Teknik
Informatika di tingkat pascasarjana.
3. Pihak Pascasarjana ITS yang telah memberikan kesempatan belajar dalam
bentuk Beasiswa Fresh Graduate di ITS Surabaya.
4. Para penulis artikel ilmiah yang karyanya direferensi oleh tesis ini
sehingga membantu mempermudah terlaksananya penelitian dan
penulisan tesis.
5. Keluarga dan rekan-rekan yang selalu memberikan dukungan moral,
material, dan doa sehingga penulis mendapatkan kelancaran untuk
menyelesaikan tesis ini.
6. Serta pihak-pihak lain yang tidak dapat disebutkan satu-per-satu disini
yang telah banyak membantuk penulis dalam penyusunan tesis ini.
Penulis telah berusaha sebaik-baiknya dalam melakukan penelitian dan
menyusun tesis ini. Namun, penulis mohon maaf atas kekurangan maupun
xii
dan saran yang membangun dapat disampaikan sebagai bahan perbaikan
selanjutnya.
Surabaya, Desember 2016
xiii
DAFTAR ISI
LEMBAR PENGESAHAN... iv
ABSTRAK ... vii
1.3 Tujuan dan manfaat penelitian ... 3
1.4 Kontribusi penelitian ... 4
1.5 Batasan masalah ... 4
BAB 2 KAJIAN PUSTAKA ... 5
2.1. Tearing dan cracking ... 5
2.2. Metode Finite Element ... 6
2.2.1. eXtended Finite Element Method ... 6
2.2.2. Elemen Pengayaan ... 8
a. Pengayaan Titik Inklusi ... 8
b. Pengayaan Titik Retak dan Heaviside ... 9
2.2.3. Metode Level Set... 11
2.3. Stiffness Matrix ... 13
2.4. Model Sobekan dengan J-Integral ... 15
BAB 3 METODOLOGI PENELITIAN ... 19
3.1. Alur Metode Penelitian ... 19
3.1.1. Studi Literatur Model Peretakan dan Sobekan... 19
3.1.2. Studi Literatur Metode Finite Element ... 20
3.1.3. Perancangan Model Sobekan ... 20
3.1.4. Implementasi Model Sobekan ... 20
3.1.5. Uji Coba dan Analisis Model Sobekan ... 20
3.2. Rancangan Sistem ... 21
3.2.1. Masukan ... 21
xiv
3.2.3. Fungsi connectivity... 25
3.2.4. Fungsi LevelSet ... 26
3.2.5. Fungsi calcDOF ... 30
3.2.6. Fungsi enrElem ... 31
3.2.7. Fungsi stiffnessMatrix dan updateStiffness ... 32
3.2.8. Fungsi forceVector ... 37
3.2.9. Fungsi boundaryCond ... 38
BAB 4 UJI COBA DAN PEMBAHASAN ... 43
4.1. Lingkungan Uji Coba ... 43
4.2. Skenario Uji Coba ... 43
4.2.1. Uji Coba Model Sobekan Tanpa Inklusi ... 44
4.2.2. Uji Coba Model Sobekan dengan Inklusi ... 51
4.3. Analisis Hasil Uji Coba ... 63
BAB 5 KESIMPULAN DAN SARAN... 65
5.1. Kesimpulan ... 65
5.2. Saran ... 65
DAFTAR PUSTAKA ... 67
LAMPIRAN A ... 69
LAMPIRAN B ... 71
LAMPIRAN C ... 73
xv
DAFTAR GAMBAR
Gambar 2.1 Node-node elemen pengayaan. Fungsi Heaviside ditunjukan dengan
titik bulat dan titik sobekan ditunjukkan dengan titik kotak (Pais, 2011) ... 9
Gambar 3.1 Alur metodologi penelitian... 19
Gambar 3.2 Diagram Alir Model Sobekan ... 22
Gambar 3.3. Pseudocode fungsi utama ... 24
Gambar 3.4 Pseudocode Fungsi connectivity ... 25
Gambar 3.5 Pseudocode Inisialisasi elemen dengan metode Level Set ... 26
Gambar 3.6 Pseudocode Inisialisasi elemen dengan metode Level Set (2) ... 27
Gambar 3.7 Pseudocode Inisialisasi elemen dengan metode Level Set (3) ... 28
Gambar 3.8 Pseudocode Inisialisasi elemen dengan metode Level Set (4) ... 29
Gambar 3.9 Pseudocode fungsi untuk mendefinisikan PSI (1)... 29
Gambar 3.10 Pseudocode fungsi untuk mendefinisikan PSI (2) ... 30
Gambar 3.11. Pseudocode untuk menghitung Degree of Freedom ... 31
Gambar 3.12.Pseudocode untuk membentuk elemen pengayaan (1) ... 31
Gambar 3.13 Pseudocode untuk membentuk elemen pengayaan (2) ... 32
Gambar 3.14 Pseudocode untuk membangun matrik kekakuan (1) ... 32
Gambar 3.15 Pseudocode untuk membangun matrik kekakuan (2) ... 33
Gambar 3.16 Pseudocode untuk membangun matrik kekakuan (3) ... 34
Gambar 3.17 Pseudocode untuk membangun matrik kekakuan (4) ... 35
Gambar 3.18. Pseudocode untuk membangun matrik kekakuan (5) ... 36
Gambar 3.19 Pseudocode untuk membangun matrik kekakuan (6) ... 37
Gambar 3.20. Pseudocode fungsi forceVector(1) ... 37
Gambar 3.21 Pseudocode fungsi forceVector (2) ... 38
Gambar 3.22 Pseudocode untuk mendefinisikan boundary condition ... 38
Gambar 3.23 Pseudocode fungsi penghitungan faktor intensitas tegangan dengan J-Integral (1) ... 39
Gambar 3.24 Pseudocode fungsi penghitungan faktor intensitas tegangan dengan J-Integral (2) ... 40
xvi
Gambar 3.26. Pseudocode fungsi growCrack (1)... 41
Gambar 3.27. Pseudocode fungsi growCrack (2) ... 42
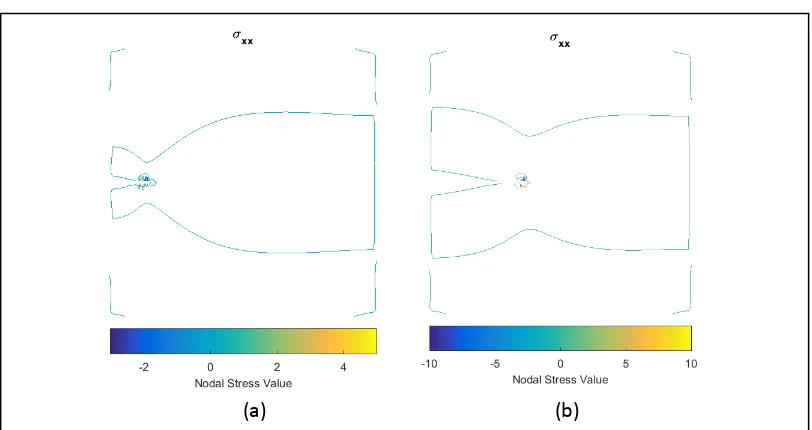
Gambar 4.1. Persebaran Stress pada proses sobekan tanpa inklusi variasi 1 (a)
iterasi ke-1 (b) iterasi ke-10 ... 45
Gambar 4.2. Persebaran Stress pada proses sobekan tanpa inklusi variasi 1 (a)
iterasi ke-20 (c) iterasi ke-30 ... 46
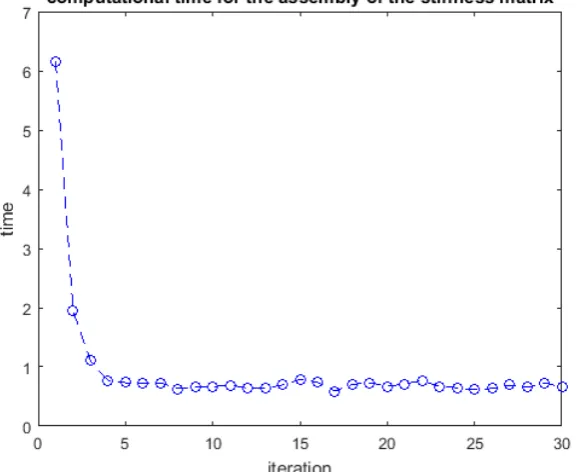
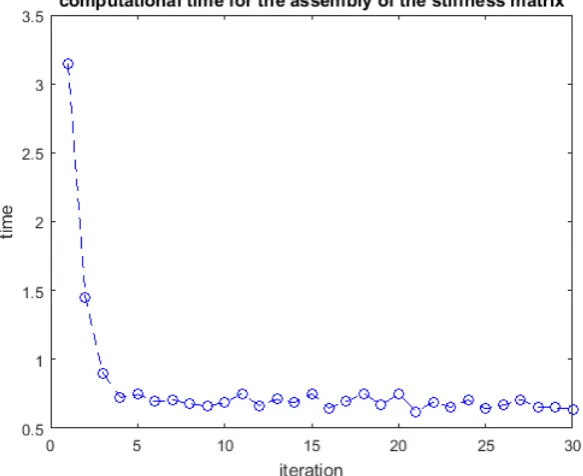
Gambar 4.3 Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan tanpa inklusi variasi 1 ... 46
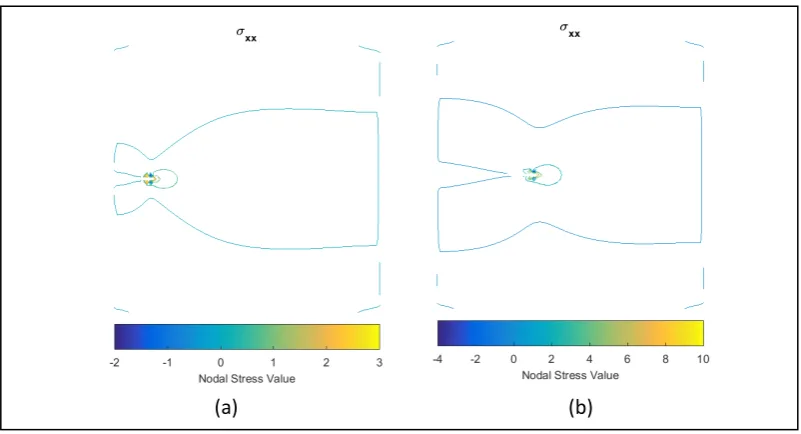
Gambar 4.4. Persebaran Stress pada proses sobekan tanpa inklusi variasi 2 (a)
iterasi ke-1 (b) iterasi ke-10 ... 47
Gambar 4.5 Persebaran Stress pada proses sobekan tanpa inklusi variasi 2 (a)
iterasi ke-20 (b) iterasi ke-30 ... 48
Gambar 4.6. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan tanpa inklusi variasi 2 ... 48
Gambar 4.7. Persebaran Stress pada proses sobekan tanpa inklusi variasi 3 (a)
iterasi ke-1 (b) iterasi ke-10 ... 49
Gambar 4.8. Persebaran Stress pada proses sobekan tanpa inklusi variasi 3 (a)
iterasi ke-20 (b) iterasi ke-30 ... 50
Gambar 4.9. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan tanpa inklusi variasi 3 ... 50
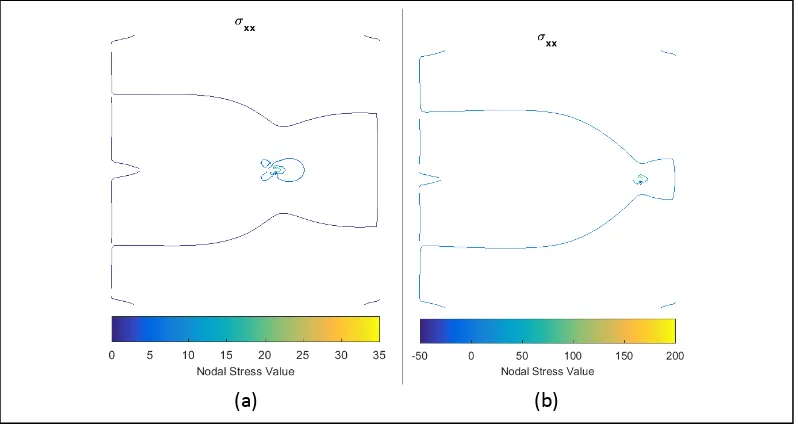
Gambar 4.10. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 1
(a) iterasi ke-1 (b) iterasi ke-10 ... 51
Gambar 4.11. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 1
(a) iterasi ke-20 (b) iterasi ke-30 ... 52
Gambar 4.12. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan dengan inklusi lingkaran variasi 1 ... 52
Gambar 4.13. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 2
(a) iterasi ke-1 (b) iterasi ke-10 ... 53
Gambar 4.14. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 2
(a) iterasi ke-20 (b) iterasi ke-30 ... 54
Gambar 4.15. Grafik implementasi assembly matrik kekakuan terhadap fungsi
xvii
Gambar 4.16. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 3
(a) iterasi ke-1 (b) iterasi ke-10 ... 55
Gambar 4.17. Persebaran Stress pada proses sobekan inklusi lingkaran variasi 3
(a) iterasi ke-20 (b) iterasi ke-30 ... 56
Gambar 4.18. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan dengan inklusi lingkaran variasi 3 ... 56
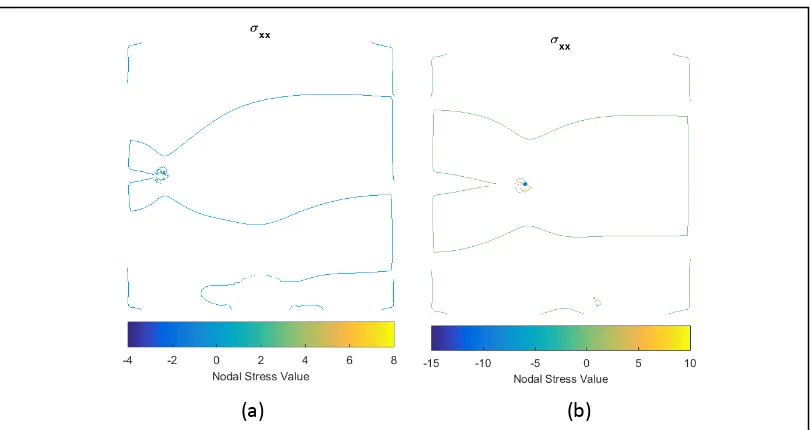
Gambar 4.19. Persebaran Stress pada proses sobekan inklusi linier variasi 1 (a)
iterasi ke-1 (b) iterasi ke-10 ... 57
Gambar 4.20. Persebaran Stress pada proses sobekan inklusi linier variasi 1 (a)
iterasi ke-20 (b) iterasi ke-30 ... 58
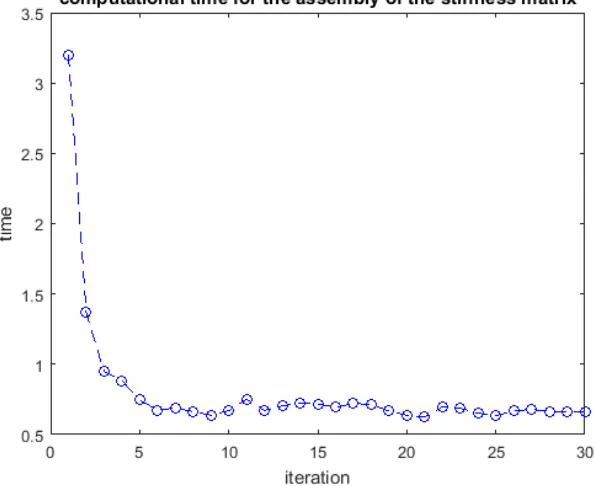
Gambar 4.21. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan dengan inklusi linier variasi 1 ... 58
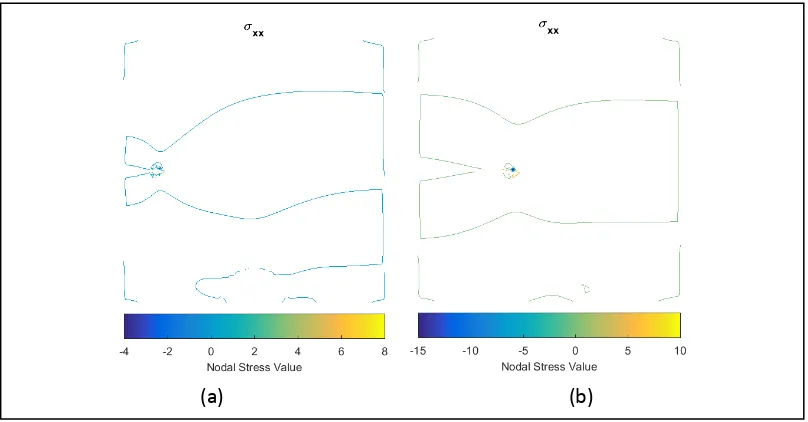
Gambar 4.22. Persebaran Stress pada proses sobekan inklusi linier variasi 2 (a)
iterasi ke-1 (b) iterasi ke-10 ... 59
Gambar 4.23. Persebaran Stress pada proses sobekan inklusi linier variasi 2 (a)
iterasi ke-20 (b) iterasi ke-30 ... 60
Gambar 4.24. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan dengan inklusi linier variasi 2 ... 60
Gambar 4.25. Persebaran Stress pada proses sobekan inklusi linier variasi 3 (a)
iterasi ke-1 (b) iterasi ke-10 ... 61
Gambar 4.26. Persebaran Stress pada proses sobekan inklusi linier variasi 3 (a)
iterasi ke-20 (b) iterasi ke-30 ... 62
Gambar 4.27. Grafik implementasi assembly matrik kekakuan terhadap fungsi
waktu percobaan dengan inklusi linier variasi 3 ... 62
Gambar A.1. Referensi nilai konstan modulus Young ... 69
Gambar B.1 Konstanta elastisitas berdasarkan Mechanic of Materials ... 71
Gambar C.1. Ilustrasi model sobekan tanpa inklusi (a) Finite Element Mesh dan
elemen pengayaan (b) Mesh deformasi... 73
Gambar C.2. Ilustrasi model sobekan dengan inklusi lingkaran (a) Finite Element
Mesh dan elemen pengayaan (b) Mesh deformasi ... 73
Gambar C.3. Ilustrasi model sobekan dengan inklusi linier (a) Finite Element
xviii
xix
DAFTAR TABEL
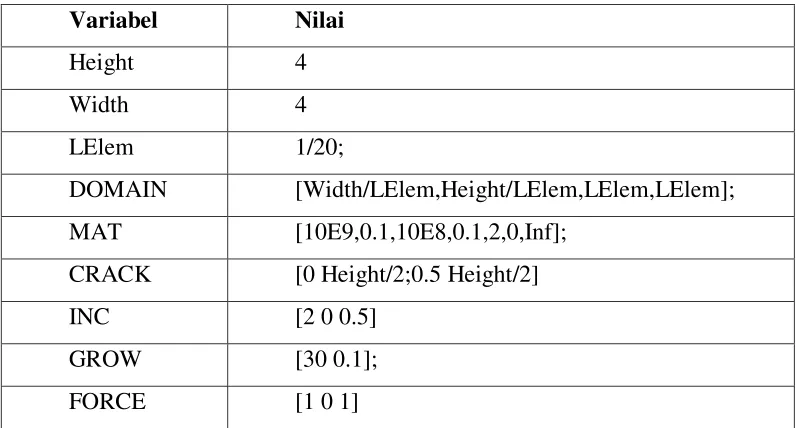
Tabel 4.1. Masukan model sobekan ... 44
Tabel 4.2. Masukan untuk percobaan sobekan tanpa inklusi variasi 1 ... 45
Tabel 4.3. Masukan untuk percobaan sobekan tanpa inklusi variasi 2 ... 47
Tabel 4.4. Masukan untuk percobaan sobekan tanpa inklusi variasi 3 ... 49
Tabel 4.5. Masukan untuk percobaan sobekan dengan inklusi lingkaran variasi 1 ... 51
Tabel 4.6. Masukan untuk percobaan sobekan dengan inklusi lingkaran variasi 2 ... 53
Tabel 4.7. Masukan untuk percobaan sobekan dengan inklusi lingkaran variasi 3 ... 55
Tabel 4.8. Masukan untuk percobaan sobekan dengan inklusi linier variasi 1 ... 57
Tabel 4.9. Masukan untuk percobaan sobekan dengan inklusi linier variasi 2 ... 59
Tabel 4.10. Masukan untuk percobaan sobekan dengan inklusi linier variasi 3 ... 61
Tabel 4.11. Waktu komputasi uji coba (1) ... 63
xx
1
1
BAB 1
PENDAHULUAN
1.1 Latar belakang
Simulasi retakan secara dinamis memiliki sejarah dan perkembangan yang
panjang pada bidang grafika komputer. Namun memproduksi detail dan variasi
retakan pada berbagai macam benda nyata masih dirasa sangat sulit (Pfaff, et al.,
2014). Sementara bila membangun model dengan metode Finite Element
tradisional, maka penerapan yang dilakukan juga cukup kompleks (Pais, et al.,
2010). Oleh karena itu, pada penelitian ini akan berfokus pada teknik simulasi
retakan dan sobekan dengan arah dan besaran yang tepat sesuai dengan sifat atau
properti yang dikalkulasi dengan perhitungan matematis pada bidang tipis
khususnya kertas sesuai dengan metode dan parameter yang tepat.
Pada tahun 1988, Terzopoulos dan Fleischer mempresentasikan teknik
pemodelan viscoelastic dan plastic deformation. Metode ini diterapkan dengan tiga
metrik tensor fundamental untuk merepresentasikan fungsi energi yang dapat
diukur untuk deformasi lekukan, bagian kulit, maupun volume sebuah obyek.
Fungsi energi ini yang memungkinkan deformasi model secara berkelanjutan
sehingga dapat disimulasikan dalam beberapa metode diskrit. Salah satu dari bentuk
metode ini diaplikasikan dengan memperhatikan teknik pembeda terbatas yang
dikontrol oleh continuity spline. Formulasi ini memungkinkan pembentukan
retakan dalam wilayah terbatas sehingga retakan ini dapat dianimasikan dengan
koefisien elastis antara titik-titik yang berdekatan sehingga menghasilkan retakan
saat jaraknya mencapai batas ambang. (O'Brien, 2000).
Saat sebuah obyek dikenai tekanan, bidang tipis dengan jenis material yang
kaku seperti kertas dan lempeng besi akan cenderung menggumpal, membentuk
pola yang saling berhubungan dengan lipatan-lipatan dan bentuk-bentuk kerucut
yang ganjil. Pola ini terjadi akibat adanya interaksi antara tingkat ketahanan
material yang rendah terhadap pembengkokan dan tingkat kekakuan material yang
tinggi. (Narain, et al., 2013).
Pada penelitian yang dilakukan Busyarev(2013), diajukan kerangka kerja
2
terdiri atas lebih dari satu lapisan. Model dibangun atas empat proses yaitu
pembangunan jejaring dasar, pembangunan model retakan, penerapan metode
penghalusan, dan pemisahan layer untuk material berlapis. Namun penelitian ini
tidak dilakukan pendekatan mendetail terhadap parameter-parameter
pembentuknya. Selain itu penelitian cenderung berfokus terhadap tujuan utamanya
yaitu membentuk model untuk bidang tipis yang berlapis. Sehingga evaluasi yang
dibahas adalah perbandingan hasil antara bidang berlapis dan bidang yang tidak
berlapis.
Finite Element harus sesuai dengan mesh yang direpresentasikan, oleh karena
itu mesh di sekitar ujung retakan harus dibentuk ulang saat sebuah retakan baru
terbentuk. Pada beberapa kasus, pergerakan yang diakibatkan diskontinuitas yang
dihitung dengan metode Finite Element tidak praktis untuk diterapkan akibat
perlunya pembaharuan untuk setiap perubahan pada geometri dari diskontinuitas
yang terjadi. Oleh karena itu beberapa penelitian menerapkan teknik penerapan
Finite Element untuk memodelkan retakan tanpa adanya remeshing untuk
meminimalkan kerja komputasi (Moes, et al., 1999).
Teknik tanpa remeshing ini diterapkan dengan memanfaatkan partisi dari sifat
unity dari Finite Element. Konsep ini memungkinkan adanya fungsi pengayaan
secara lokal yang dapat dengan mudah digabungkan ke dalam pendekatan Finite
Element. Pendekatan ini dilakukan sedemikian rupa sehingga degree of freedom
dari elemen pengayaan ini terhubung dengan mesh. Untuk kasus analisis retakan
atau sobekan, fungsi pengayaan akan difokuskan pada bidang yang berdekatan
dengan titik retakan dan fungsi diskontinuitas untuk merepresentasikan perubahan
di sepanjang retakan (Melenk & Babuska, 1996).
Untuk memodelkan diskontinuitas kuat yang merepresentasikan bidang
retakan dibutuhkan dua jenis titik pengayaan. Pertama adalah fungsi Heaviside
yang merepresentasikan diskontinuitas yang mengalir menjauhi titik ujung retakan.
Yang kedua adalah perubahan ujung retakan yang bersifat elastis linier yang
digunakan untuk memperhitungkan diskontinuitas ujung retakan. Retakan
direpresentasikan pada mesh secara independen oleh elemen pengayaan sehingga
geometri dari retakan dapat diperbaharui tanpa perlu menambah atau membentuk
3
diterapkan dengan memperhatikan gabungan jarak yang dihasilkan dari
diskontinuitas rendah dan nilai absolut dari nilai fungsi (Pais, et al., 2010).
Untuk dapat menghasilkan tahapan komputasi yang akurat dan efisien, maka
diperlukan suatu skema numerik yang dapat memenuhi kebutuhan atau requirement
yang sesuai.
Berdasarkan penelitian-penelitian sebelumnya, maka diajukan kerangka kerja
penyobekan dengan nilai-nilai parameter yang sesuai sehingga terbentuk model
yang relatif dan efisien terhadap proses perubahan yang terjadi. Setiap perubahan
yang terjadi pada objek merupakan proses yang dikerjakan berdasarkan hasil dari
proses sebelumnya. Hal ini dilakukan untuk menghasilkan model yang dinamis.
Diharapkan dengan adanya pendekatan terhadap nilai-nilai parameter yang optimal
dan adanya elemen pengayaan yang menghemat komputasi, akan didapatkan model
yang lebih efisien dibandingkan dengan penelitian-penelitian yang telah dilakukan
sebelumnya.
1.2 Perumusan masalah
Permasalahan penyusunan skema komputasi numerik model penyobekan
dinamis lembaran kertas meliputi hal-hal sebagai berikut:
1. Bagaimana representasi obyek lembaran kertas menjadi domain komputatif
yang dapat mengalami perubahan secara dinamis?
2. Bagaimana bentuk penerapan perhitungan matematis dengan
memanfaatkan elemen pengayaan pada domain sehingga dapat membentuk
sobekan dan perubahan posisi domain awal?
3. Bagaimana pengaruh variabel-variabel yang ada pada model terhadap hasil
sobekan yang terbentuk?
1.3 Tujuan dan manfaat penelitian
Tujuan dari penelitian ini adalah menghasilkan komputasi numerik model
penyobekan lembaran kertas yang berlaku secara dinamis sehingga didapatkan
4 1.4 Kontribusi penelitian
Penelitian ini memiliki kontribusi membangun kerangka kerja model
penyobekan dengan memanfaatkan elemen pengayaan pada metode modifikasi
Finite Element.
1.5 Batasan masalah
Permasalahan yang dibahas pada penelitian ini memiliki beberapa batasan,
yaitu:
1. Sobekan dialirkan pada arah koordinat x,
2. Variasi variabel yang diterapkan adalah variasi yang berkenaan dengan
modulus Young dan rasio Poisson sebagai variabel yang menentukan elastisitas
sebuah objek,
3. Objek kertas yang digunakan merupakan representasi objek rektangular 2D,
4. Jumlah iterasi pada uji coba adalah 30 kali.
5. Program XFEM yang digunakan adalah adaptasi dari program
xfemQuasiStatic dari Matthew Jon Pais yang dapat diakses pada
5
2.
BAB 2
KAJIAN PUSTAKA
Bab ini berisi pembahasan tentang kajian dan dasar teori yang digunakan
sebagai teori pendukung penelitian. Adapun pembahasannya meliputi tearing dan
cracking, metode Finite Element, dan model sobekan.
2.1.Tearing dan cracking
Retakan atau fracture telah dipelajari secara luas baik dari segi mekanisnya
maupun teknik-teknik pembangunan, simulasi, dan analisa behavior dari banyak
materi. Telah banyak teori yang menjelaskan pembentukan sebuah titik retakan dan
persebarannya. Teori-teori ini telah menerapkan berbagai metode numerik
termasuk elemen terbatas (finite element) dan finite difference methods, persamaan
integral batas, dan simulasi partikel molekular. Aplikasi rekayasa pembentukan
model grafika membutuhkan simulasi yang menampilkan dan memprediksi
behavior dari kejadian nyata dalam bentuk yang akurat dan dapat diandalkan. Pada
grafika komputer maupun animasi komputer, hal yang terpenting adalah
pengimplementasian bentuk retakan pada sebuah bidang (O'Brien & Hodgins,
1999).
Simulasi sobekan pada domain grafis memiliki banyak kompleksitas dalam
pemodelannya. Setiap obyek memiliki tingkah laku atau behavior yang unik dalam
menampilkan efek dari sobekan pada bidangnya. Behavior pada obyek-obyek ini
dapat dimodelkan dengan menggunakan thin-shell model yang merupakan sebuah
representasi obyek dalam bidang datar. Thin-shell model dapat direpresentasikan
dengan jejaring atau mesh segitiga dalam proses pemodelan grafis (Pfaff, et al.,
2014).
Program yang bertujuan untuk memodelkan sobekan dengan framework
Finite Element tradisional adalah sebuah tantangan tersendiri. Pada dasarnya,
framework Finite Element dimodifikasi untuk dapat bekerja pada diskontinuitas
yang terjadi akibat adanya sobekan, inklusi, maupun elemen kosong atau void.
Dibutuhkan penyesuaian terhadap framework Finite Element agar dapat bekerja
6
sobekan, setidaknya domain pada sekitar titik retak harus disesuaikan agar sobekan
yang baru dapat direpresentasikan dengan baik secara geometris (Pais, et al., 2010).
2.2.Metode Finite Element
Sebuah model simulasi sebuah obyek biasanya dibangun atas model
kontinyu. Namun pada kenyataannya, sebuah obyek hanya akan dapat
divisualisasikan pada komputer dalam bentuk diskrit. Oleh karena itu banyak
metode yang khusus digunakan untuk mengubah bentuk kontinyu dari obyek
menjadi bentuk diskrit. Metode yang biasa digunakan adalah finite difference dan
finite element.
Finite difference merupakan metode yang membagi domain material menjadi
kisi-kisi dan kemudian diterapkan diferensial numerik sebagai pendekatan spasial
yang nantinya akan digunakan untuk mendapatkan nilai strain dan strain tensor.
Pendekatan ini cocok untuk permasalahan yang memiliki struktur reguler atau
teratur
Finite element merupakan metode yang membagi domain menjadi
sub-domain atau elemen-elemen. Pada setiap elemen, material akan dipisahkan sesuai
dengan fungsi yang dibatasi beberapa parameter. Fungsi-fungsi tersebut diuraikan
ke dalam beberapa bagian seperti bentuk ortogonal, atau basis, fungsi yang
berhubungan dengan batas node pada elemen yang ada. Elemen yang berdekatan
akan memiliki node yang sama sehingga jejaring yang didefinisikan pada fungsi
yang sama merepresentasikan domain material (O'Brien & Hodgins, 1999).
2.2.1.eXtended Finite Element Method
XFEM atau eXtended Finite Element Method dikonsepkan dengan tujuan
untuk membangun model sobekan dan aliran sobekan tanpa perlu remeshing atau
penyesuaian mesh akibat adanya perubahan baik posisi maupun ukuran mesh.
Pembentukan sobekan tanpa remeshing termasuk dari elemen-elemen dengan
bentuk kontinu, teknik pergerakan mesh, dan teknik enrichment yang berbasis
partition-of-unity yang mencakup remeshing dengan tingkat yang minimal.
Ide utama dari metode pada XFEM ini adalah menambahkan fungsi
7
perpindahan elemen-elemen akibat terjadinya sebuah ketidaksinambungan atau
diskontinuitas.
Pada konsep elastostastis, perubahan atau perpindahan kecil yang terjadi pada
mesh direpresentasikan sebagai sebuah persamaan equilibrium yang dinotasikan
dengan Persamaan 2.1.
∇. 𝝈 + 𝒃 = 0 in Ω, 𝜎 = 𝐶: 𝜀, 𝜀 = ∇𝑠𝑢 2.1 (2.1)
Pada Persamaan, Ω ⊂ 𝑹2 adalah domain dari objek, 𝝈 adalah stress tensor
Cauchy, 𝜀 adalah small strain tensor, b adalah gaya internal objek, C adalah tensor
dari material, u adalah perpindahan, ∇ adalah operator gradien, dan ∇𝑠 adalah operator gradien simetris.
Sedangkan secara umum, pendekatan dari sebuah perpindahan atau
displacement pada XFEM diformulasikan sebagai Persamaan 2.2.
𝑢ℎ(𝑥) = ∑ 𝑁
Variabel Ω pada Persamaan 2.2 merupakan keseluruhan domain sementara
Ω𝑑 merupakan domain yang mengalami diskontinuitas. Variabel 𝑁𝐼(𝑥) adalah
fungsi Finite Element tradisional, 𝑣(𝑥) adalah fungsi diskontinuitas elemen
pengayaan, sedangkan 𝑢𝐼 dan 𝑎𝐼 merupakan degree of freedom dari masing-masing Finite Element tradisional dan elemen pengayaan. Saat terjadi kondisi Ω ∩ Ω𝑑 = ∅, fungsi pengayaan 𝑣(𝑥) akan dihilangkan. Karena diskontinuitas tidak didefinisikan
sebagai mesh, maka diskontinuitas ini didefinisikan ke dalam sebuah Level Set.
Pendekatan pada Persamaan 2.2 tidak mencakup sifat interpolasi akibat
adanya degree of freedom dari elemen pengayaan. Untuk mengatasi hal ini,
dibentuk formulasi fungsi pengayaan seperti Persamaan 2.3.
𝛶𝐼(𝑥) = 𝑣(𝑥) − 𝑣𝐼(𝑥) 2.3 (2.3)
8
formulasi mencapai elemen pengayaan, maka 𝛶𝐼(𝑥) akan bernilai nol pada node
tersebut.
Implementasi Persamaan 2.3 pada Persamaan 2.2 akan menghasilkan
Persamaan 2.4 yang merepresentasikan pendekatan dari perpindahan yang terjadi
pada mesh.
Metode Finite Element digunakan untuk menyelesaikan permasalahan yang
berkaitan dengan diskontinuitas. Pada metode Finite Element, terutama XFEM,
terdapat fungsi tambahan yang digunakan untuk memodelkan sobekan, kekosongan
atau voids, dan inhomogenitas. Fungsi-fungsi tambahan ini diaplikasikan untuk
meningkatkan akurasi pada bidang-bidang yang mementingkan penyesuaian sifat.
(Sukumar, et al., 2001)
Pada sebuah model sobekan, dapat ditentukan diskontinuitas terjadi pada
perpindahan yang berkaitan dengan mesh, tegangan yang terjadi, atau pada
keduanya. Cara terbaik untuk dapat menunjukkan sebuah diskontinuitas adalah
dengan membuat satu atau beberapa elemen sebagai penanda. Pada XFEM,
diperkenalkan penggunaan hanging nodes yang berkaitan dengan sobekan, inklusi,
dan aliran mekanik agar dapat dilakukan proses mesh refinement secara otomatis
pada titik-titik diskontinu (Fries, et al., 2011).
a. Pengayaan Titik Inklusi
Titik inklusi merupakan salah satu representasi node yang bersifat
homogenitas yang menyatakan batasan internal atau batasan yang berasal dari
bidang objek itu sendiri. Pengayaan titik inklusi ini pertama kali disesuaikan dengan
kebutuhan metode Level Set oleh Sukumar (2001). Pengayaan ini diformulasikan
dengan Persamaan 2.5.
9
Variabel 𝜁𝐼 pada Persamaan 2.5 adalah nilai node pada nilai Level Set. Namun penyelesaian dengan Persamaan 2.5 dapat menimbulkan masalah blending pada
elemen dengan pengayaan dan tanpa pengayaan. Untuk meningkatkan tingkat
konvergensi dari penyelesaian permasalahan ini, maka dilakukan optimasi.
Optimasi ini menerapkan modifikasi nilai absolut dari nilai pengayaan (Moes, et
al., 2003). Dilakukan formulasi ulang sehingga Persamaan 2.5 dapat sesuai dengan
formulasi elemen pengayaan menjadi Persamaan 2.6. Fungsi pengayaan ini akan
bernilai nol pada node yang tidak perlu melakukan perpindahan.
Υ(𝑥) = ∑ 𝑁𝐼 𝐼(𝑥)|𝜁𝐼| − | ∑ 𝑁𝐼 𝐼(𝑥)𝜁𝐼| 2.6 (2.6)
b. Pengayaan Titik Retak dan Heaviside
Sebuah displacement atau perpindahan node tertentu bisa didapatkan dengan
menggabungkan dua fungsi yang berkaitan dengan pendekatan sobekan itu sendiri.
Dua fungsi tersebut adalah fungsi elemen crack tip atau titik ujung sobekan dan
fungsi elemen Heaviside. Perbedaan kedua elemen ini berada pada fungsi yang
dilakukan dan titik yang dipengaruhinya.
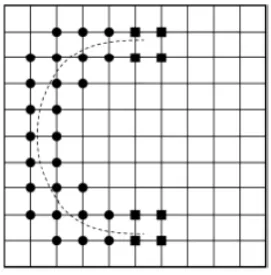
Gambar 2.1 Node-node elemen pengayaan. Fungsi Heaviside ditunjukan dengan titik bulat dan titik sobekan ditunjukkan dengan titik kotak (Pais, 2011)
Fungsi elemen Heaviside digunakan untuk merepresentasikan sobekan yang
mengalir dari titik ujung sobekan. Sebuah titik ini dinyatakan termasuk elemen
Heaviside apabila memenuhi Persamaan 2.7.
ℎ(𝑥) =
{ 1 , di atas titik sobek−1 , di bawah titik sobek
10
Untuk elemen titik ujung sobekan, terdapat fungsi dengan empat nilai
pengayaan yang digunakan untuk menyatakan perpindahan sobekan dari titik ujung
sobekan ke wilayah selanjutnya. Fungsi tersebut dinyatakan dengan Persamaan 2.8.
∅𝛼(𝑥),𝛼=1−4= √𝑟 [𝑠𝑖𝑛𝜃2 , 𝑐𝑜𝑠𝜃2 , 𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜃2 , 𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃2]
2.8 (2.8)
Variabel r dan 𝜃 menyatakan koordinat polar pada sistem koordinat ujung
sobekan lokal. Koordinat ini bermula dari titik ujung sobekan dan 𝜃 = 0 paralel
dengan sobekan.
Persamaan 2.8 akan menunjukkan diskontinuitas yang terjadi saat ujung
sobekan terbentuk sementara Persamaan 2.7 akan menunjukkan potongan yang
terjadi akibat munculnya sobekan. Pengaruh kedua fungsi ini ditunjukkan pada
Gambar 2.1.
Perhitungan kedua fungsi ini belum menyatakan sobekan pada domain objek
yang dituju. Oleh karena itu dibutuhkan metode yang merepresentasikan
fungsi-fungsi ini ke domain yang diinginkan sehingga diterapkan metode Level Set.
Terdapat dua Level Set yang dibutuhkan untuk merepresentasikan sobekan.
Pertama adalah level set dasar 𝜓(x) yang merepresentasikan fisik sobekan. Yang
kedua adalah level set dasar ∅(x) yang ortogonal dengan level set dasar 𝜓(x).
Persamaan 2.7 dan 2.8 dapat dikalkulasi mengikuti bentuk ∅(x) dan 𝜓(x) sehingga
didapatkan Persamaan 2.9.
ℎ(x) = ℎ(𝜓(x)) = { 1 untuk 𝜓−1 untuk 𝜓(x) < 0(x) > 0 2.9 (2.9)
Sedangkan koordinat polar didapatkan dengan Persamaan 2.10 dan 2.11.
𝑟 = √𝜓2(x) + ∅2(x) 2.10 (2.10)
𝜃 = arctan 𝜓(x)∅(x) 2.11 (2.11)
Node-node pengayaan yang berhubungan dengan titik ujung sobekan juga
dapat ditentukan dengan menggunakan Level Set yang mendefinisikan sobekan.
Node Heaviside dapat ditentukan dengan Persamaan 2.12. Sedangkan Node titik
ujung sobekan dapat ditentukan ketika memenuhi Persamaan 2.13.
11
∅𝑚𝑎𝑥∅𝑚𝑖𝑛 ≤ 0 dan 𝜓𝑚𝑎𝑥𝜓𝑚𝑖𝑛 ≤ 0 2.13 (2.13)
Setelah diterapkan titik ujung sobekan dan Heaviside, perubahan yang terjadi
pada domain seperti yang dinyatakan pada Persamaan 2.4 akan mengalami
penyesuaian. Penyesuaian ini dilakukan dengan menerapkan metode
Bubnov-Galerkin untuk membangun sistem persamaan dan menurunkan Persamaan 2.4
sehingga dapat merepresentasikan domain secara total. Pendekatan ini dinyatakan
dalam Persamaan 2.14.
𝑢ℎ(𝑥) = ∑ 𝑁 2.2.3. Metode Level Set
Metode Level Set adalah metode numerik yang digunakan untuk menelusuri
evolusi atau perubahan posisi yang terjadi pada antarmuka atau obyek yang tampak
oleh pengguna. Metode ini diterapkan berdasarkan kecepatan fisik yang terjadi pada
obyek sehingga menimbulkan perpindahan posisi node pada setiap iterasi
berdasarkan waktu. Kecepatan yang ada pada antarmuka objek dapat dipengaruhi
oleh posisi, waktu, geometri bidang, dan fisik yang ada pada model.
Metode Level Set digunakan untuk menentukan nilai diskrit dari domain awal
objek menjadi titik-titik diskrit. Selain itu, Level Set digunakan untuk
merepresentasikan antarmuka bidang sebagai serat atau fiber dan matrik sehingga
dapat merepresentasikan bentuk geometri dari sobekan.
Fungsi Level Set dinyatakan dengan ∅(𝑥(𝑡), 𝑡). Sesuai dengan formulasi
tersebut, fungsi ini merupakan fungsi kontinu dengan variabel 𝑥(𝑡) adalah titik pada
sebuah domain awal 𝛺. Batasan yang diterapkan untuk memenuhi fungsi Level Set
diformulasikan pada Persamaan 2.15, 2.16, dan 2.17. Variabel 𝛤 pada Persamaan
2.17 adalah representasi domain antarmuka.
∅(𝑥(𝑡), 𝑡) < 0 untuk 𝑥 𝜖 Ω 2.15 (2.15)
∅(𝑥(𝑡), 𝑡) > 0 untuk 𝑥 𝜖 Ω 2.16 (2.16)
12
Domain antarmuka dapat ditemukan pada sembarang waktu t dengan lokasi
yang sesuai dengan syarat ∅(𝑥(𝑡), 𝑡) = 0 seperti pada Persamaan 2.17. Batasan ini
biasa disebut zero level set ∅ dan bisa disimbolkan sebagai ∅0. Persamaan 2.17 inilah yang dinamakan persamaan Level Set.
Untuk mendapatkan evolusi perubahan posisi objek untuk setiap satuan
waktu, dilakukan pendekatan dengan melakukan penurunan rumus persamaan
Level Set terhadap waktu t. Penurunan ini dinyatakan dengan Persamaan 2.18.
𝜙𝑖+1−𝜙𝑖
∆𝑡 + 𝑉𝑖. ∇𝜙𝑖 = 0
2.18 (2.18)
Variabel 𝜙𝑖+1 pada Persamaan 2.18 adalah nilai Level Set pembaharuan, variabel 𝜙𝑖 adalah nilai Level Set pada titik yang sedang diproses, 𝑉𝑖 adalah vektor kecepatan, dan ∆𝑡 adalah perbedaan waktu yang terjadi antara i dan i+1. Persamaan
2.18 dapat ditulis kembali ke dalam bentuk yang lebih sesuai dengan objek dua
dimensi pada Persamaan 2.19.
𝜙𝑖+1= 𝜙𝑖− ∆𝑡 (𝑢𝑖𝜕𝜙𝜕𝑥𝑖+ 𝑣𝑖𝜕𝜙𝜕𝑦𝑖) 2.19 (2.19)
Variabel 𝑢𝑖 adalah kecepatan terhadap arah x dan 𝑣𝑖 adalah kecepatan terhadap arah y. Pada Persamaan 2.18 dan 2.19, variabel ∆𝑡 dibatasi oleh kondisi
Courant-Friedrichs-Lewy (CFL) yang memastikan bahwa pendekatan dari solusi
konvergen. Kondisi CFL dinyatakan dengan Persamaan 2.20. Variabel ∆𝑥 dan ∆𝑦
pada Persamaan 2.20 adalah nilai x dan y pada grid atau representasi matrik dasar
dari objek.
∆𝑡 <max (∆𝑥,∆𝑦)max (𝑢,𝑣) 2.20 (2.20)
Metode Level Set juga diterapkan pada elemen pengayaan. Untuk nilai
elemen pengayaan dengan bentuk material komposit yang berbentuk lingkaran,
fungsi Level Set yang diterapkan pada setiap node dinyatakan dalam fungsi 𝜁(𝑥)
seperti pada Persamaan 2.21. Pada persamaan ini, 𝑥𝑖 dan 𝑦𝑖 merupakan koordinat titik ke-i dan 𝑥𝑐 dan 𝑦𝑐 merupakan koordinat titik pusat material komposit, sedangkan 𝑟𝑐 adalah jari-jari lingkaran tersebut.
13
Sedangkan untuk elemen pengayaan yang berkenaan dengan sobekan—titik
ujung sobekan dan Heaviside, dihitung jarak antara setiap titik dengan zero level
set yang terdekat. Retakan terdefinisi apabila persyaratan pada Persamaan 2.22 dan
2.23 terpenuhi.
𝜙(𝑥(𝑡), 𝑡) ≤ 0 2.22 (2.22)
𝜓(𝑥(𝑡), 𝑡) = 0 2.23 (2.23)
2.3. Stiffness Matrix
Nilai perpindahan yang dihitung dengan Persamaan 2.14 terjadi pada wilayah
komputasi numerik. Untuk mengaplikasikan perpindahan agar dapat
direpresentasikan pada domain baik domain mesh maupun domain antarmuka,
dilakukan convert nilai perpindahan agar sesuai dengan bentuk nodalnya. Hal ini
dapat dilakukan dengan menggunakan metode Bubnov-Galerkin yang dapat
membentuk perpindahan ke dalam bentuk persamaan linier. Persamaan linier ini
dinyatakan dalam Persamaan 2.24.
𝑲. 𝒒 = 𝒇 2.24 (2.24)
Variabel K merupakan stiffness matrix global, q adalah degree of freedom
dari node, dan f adalah gaya yang berlaku pada node. Sesuai dengan urutan degree
of freedom, global stiffness matrix dapat dinyatakan dengan Persamaan 2.25.
𝐾 = [
Element tradisional, sementara a menyatakan nilai pengayaan pada elemen
Heaviside, dan b menyatakan nilai pengayaan pada titik ujung sobekan.
Sesuai dengan perumusan Persamaan 2.25 terhadap Persamaan 2.24, dapat
dilihat bahwa kekakuan pada sobekan dikerjakan oleh elemen Heaviside dan titik
ujung sobekan sehingga elemen kekakuan pada Finite Elemen tradisional 𝐾𝑢𝑢 akan konstan selama iterasi penambahan titik retak. Matrik kekakuan juga menyatakan
bahwa porsi perubahan yang diakibatkan elemen pengayaan akan lebih kecil
daripada elemen non-pengayaan. Lebih jauh, dapat dilihat bahwa setelah sebuah
iterasi-14
iterasi berikutnya. Hal ini berarti komponen kekakuan yang mengandung a akan
konstan selama iterasi pembentukan sobekan terjadi.
Oleh karena itu, matrik kekakuan dapat disederhanakan untuk dapat
menghitung evolusi pertumbuhan sobekan dan menghasilkan elemen baru berupa
titik ujung sobekan pada iterasi-iterasi yang terjadi setelah kondisi inisial. Matrik
kekakuan global yang digunakan dinyatakan dalam Persamaan 2.26.
𝐾 = [𝐾𝐾𝑢𝑢 𝐾𝑢𝑎
𝑢𝑎𝑇 𝐾𝑎𝑎]
2.26 (2.26)
Berdasarkan matrik dasar dengan Persamaan 2.26, bisa didapatkan nilai
kekakuan elemental untuk setiap anggota K. Kekakuan elemental ini dihitung
dengan Persamaan 2.27.
𝐾𝑒 = ∫ 𝐵Ωℎ 𝑢𝑇𝐶𝐵𝑎𝑑Ω 2.27 (2.27)
Variabel C adalah matrik konstitutif untuk material dengan isotropic linear
elastic. Variabel 𝐵𝑢 adalah matrik turunan dari fungsi matrik domain awal
sedangkan 𝐵𝑎 adalah matrik turunan dari matrik elemen pengayaan. Matrik 𝐵𝑢 dan
𝐵𝑎 dijabarkan pada Persamaan 2.28 dan 2.29.
15
Sesuai dengan Persamaan 2.24, formulasi akan lengkap dengan perhitungan
degree of freedom. Perhitungan degree of freedom dilakukan dengan Persamaan
2.30. Pada Persamaan 2.30, variabel u dan a adalah degree of freedom untuk elemen
tradisional dan elemen pengayaan.
𝑞𝑇 = {𝑢 𝑎}𝑇 2.30 (2.30)
Setelah matrik kekakuan dan degree of freedom didapatkan, maka tegangan
dan tekanan atau strain dan stress dapat dihitung dengan Persamaan 2.31 dan 2.32.
𝜀 = [𝐵𝑢 𝐵𝑎]{𝑢 𝑎}𝑇 2.31 (2.31)
𝜎 = 𝐶𝜀 2.32 (2.32)
2.4. Model Sobekan dengan J-Integral
Metode Finite Element mengatur dan memperhitungkan segala komputasi
numerik mulai dari implementasi objek ke dalam bentuk matrik, proses diskrit
objek, hingga penggabungan elemen-elemen yang mempengaruhi objek untuk
dapat membentuk sobekan. Pada bab ini akan dijelaskan mengenai model s yang
akan mencakup proses perhitungan nilai J sebagai energi yang dilepaskan yang
menentukan arah dan besar sobekan yang terjadi.
Sudut sobekan dihitung dengan Persamaan 2.33 dengan 𝐾𝐼 dan 𝐾𝐼𝐼 adalah faktor intensitas tegangan atau stress intensity factor
𝜃𝑐= 2arctan14(𝐾𝐾𝐼𝐼𝐼 − 𝑠𝑖𝑔𝑛(𝐾𝐼𝐼)√(𝐾𝐾𝐼𝐼𝐼) 2
+ 8) 2.33 (2.33)
Arah dari pertumbuhan sobekan ditentukan pula oleh mode-gabungan
(mixed-mode) faktor intensitas tegangan. Bentuk domain dari interaksi integral
16
metode-gabungan secara umum, hubungan antara J-Integral dan faktor intensitas
tegangan dinyatakan dengan Persamaan 2.34.
𝐽 = 𝐾𝐼2
Untuk menghitung mode-gabungan faktor intensitas tegangan, diberikan
sebuah kondisi tegangan sebagai bantuan. Bantuan ini ditumpangkan pada tegangan
dan perpindahan dari analisis XFEM. Elemen dari XFEM dinotasikan dengan tanda
(1) seperti 𝜎𝑖𝑗(1), 𝜀𝑖𝑗(1), dan 𝑢𝑖(1), sementara elemen dari kondisi bantuan dinyatakan dengan 𝜎𝑖𝑗(2), 𝜀𝑖𝑗(2), dan 𝑢𝑖(2).
Kondisi awal J-Integral dinyatakan dengan Persamaan 2.36.
𝐽𝑖 = ∫ [𝑊𝑛𝑖− 𝜎𝑗𝑘𝑛𝑗
menotasikan arah bukaan sobekan, yang diasumsikan berkorespondensi dengan
arah x secara global, yang dinotasikan dengan 𝑥𝑖. Persamaan 2.36 dapat dituliskan kembali sebagai Persamaan 2.37.
𝐽𝑖 = ∫ [𝑊𝛿1𝑗− 𝜎𝑖𝑗𝜕𝑥𝜕𝑢𝑖 1] 𝑛𝑗𝑑Γ Γ
2.37 (2.37)
Kedua kondisi tegangan 𝜎 dapat ditumpangkan pada Persamaan 2.37
sehingga membentuk Persamaan 2.38.
𝐽1(1+2)= ∫ [12(𝜎𝑖𝑗(1)+ 𝜎𝑖𝑗(2)) (𝜀𝑖𝑗(1)+ 𝜀𝑖𝑗(2)) 𝛿1𝑗− (𝜎𝑖𝑗(1)+ 𝜎𝑖𝑗(2))
𝜕(𝑢𝑖(1)+𝑢𝑖(2)) 𝜕𝑥1 ] 𝑛𝑗𝑑Γ
Γ
(2.38) 2.38
Bentuk J-Integral dengan kondisi 1 dan 2 yang terpisah dari Persamaan 2.38
17
𝐽1(1+2)= 𝐽1(1)+ 𝐽1(2)+ 𝐼(1,2) 2.39 (2.39) Variabel 𝐼(1,2) pada Persamaan 2.39 merupakan kondisi interaksi dan dihitung dengan Persamaan 2.40.
density yang dinyatakan dengan Persamaan 2.41.
𝑊(1,2) = 𝜎
𝑖𝑗(1)𝜀𝑖𝑗(2)= 𝜎𝑖𝑗(2)𝜀𝑖𝑗(1) 2.41 (2.41)
Setelah menumpangkan kedua kondisi, Persamaan 2.34 dapat diformulasi
ulang dengan Persamaan 2.42.
𝐽1(1+2)=(𝐾𝐼(1)𝐾𝐼(2))2
𝐸𝑒𝑓𝑓 +
(𝐾𝐼𝐼(1)𝐾𝐼𝐼(2))2 𝐸𝑒𝑓𝑓
2.42 (2.42)
Pengembangkan dan pengaturan ulang dilakukan untuk Persamaan 2.42
sehingga menjadi Persamaan 2.43.
𝐽1(1+2)= 𝐽1(1)+ 𝐽1(2)+2(𝐾𝐼(1)𝐾𝐼(2)+𝐾𝐼𝐼(1)𝐾𝐼𝐼(2))
𝐸𝑒𝑓𝑓
2.43 (2.43)
Faktor intensitas tegangan untuk kondisi yang sedang difokuskan dapat
dihitung dengan memisahkan kedua mode sobekan. Dengan memilih 𝐾𝐼(2) = 1 dan
𝐾𝐼𝐼(2)= 0, didapatkan penyelesaian 𝐾𝐼(1) dengan Persamaan 2.44 dan penyelesaian
𝐾𝐼𝐼(1) dengan Persamaan 2.45.
𝐾𝐼(1)=𝐼(1,𝑀𝑜𝑑𝑒 𝐼)𝐸𝑒𝑓𝑓
2 2.44
(2.44)
18
19
3.
BAB 3
METODOLOGI PENELITIAN
Bab ini memaparkan metodologi penelitian yang akan digunakan. Pada
bagian ini akan dijelaskan alur dari metodologi penelitian yang terdiri atas studi
literatur, perancangan metode, implementasi metode, pengujian, dan analisa hasil
uji coba. Selanjutnya dijelaskan rancangan sistem dan detailnya.
3.1.Alur Metode Penelitian
Penelitian ini terdiri atas beberapa tahap. Alur metodologi yang dilakukan
pada penelitian ini dijabarkan dalam Gambar 3.1.
Gambar 3.1 Alur metodologi penelitian 3.1.1. Studi Literatur Model Peretakan dan Sobekan
Studi literatur tentang model peretakan dan sobekan dilakukan untuk dapat
memahami model retakan dan sobekan yang selama ini telah dikerjakan oleh
peneliti-peneliti lain. Pada studi literatur ini dilakukan pemahaman tentang dasar
model yang harus dikerjakan. Dasar model ini meliputi pendalaman metode untuk
merepresentasikan objek ke dalam bentuk mesh, pendalaman metode yang
digunakan untuk mengekstraksi komponen-komponen objek sehingga dapat
Studi literatur model peretakan dan sobekan
Studi literatur Metode Finite Element
Perancangan model sobekan
Implementasi model sobekan
20
dikomputasi, dan pendalaman formulasi-formulasi yang harus digunakan untuk
membentuk model yang sesuai dengan tujuan penelitian.
3.1.2. Studi Literatur Metode Finite Element
Studi literatur tentang metode Finite Element dilakukan setelah pendalaman
tentang objek dan representasi mesh dilakukan. Metode ini merupakan metode
dasar yang digunakan untuk merepresentasikan bentuk nyata objek yang
merupakan bentuk kontinu menjadi bentuk diskrit sehingga
komponen-komponennya dapat dikomputasi oleh sistem. Metode ini memerlukan pemahaman
yang lebih karena pada setiap kasus pembentukan model grafis, Finite Element
yang diterapkan menyesuaikan dengan bentuk geometri serta permasalahan yang
harus diselesaikan. Literatur-literatur yang mendukung dikumpulkan dan diproses
sehingga membentuk model yang sesuai.
3.1.3. Perancangan Model Sobekan
Perancancangan model sobekan dilakukan untuk mengolaborasikan
metode-metode yang cocok menjadi sebuah sistem yang dapat merepresentasikan objek
dengan semirip mungkin. Metode-metode mulai dari pengimplementasian objek ke
dalam bentuk mesh, pengubahan bentuk kontinu ke dalam bentuk diskrit,
implementasi bentuk plastisitas, dan implementasi retakan yang dihasilkan harus
dapat dikolaborasikan agar dapat berjalan dengan baik.
3.1.4. Implementasi Model Sobekan
Implementasi dilakukan dengan membangun model secara keseluruhan.
Model dibentuk sesuai dengan kebutuhan dengan masukan-masukan yang
disesuaikan dengan kasus penelitian.
Tahapan ini dilakukan untuk mengimplementasikan metode yang diusulkan
ke dalam perangkat lunak. Proses implementasi ini meliputi penulisan kode
program, compiling, debugging, hingga dihasilkan kode program yang siap
dieksekusi. Tahapan ini dilakukan setelah dilakukan pembelajaran terhadap library
yang digunakan untuk membentuk komponen-komponen yang dibutuhkan pada
sebuah komputasi grafis.
21
Uji coba yang dilakukan terdiri atas uji coba untuk melihat keberhasilan
model membentuk sobekan pada objek penelitian. Selain itu dilakukan untuk
mengetahui variabel-variabel yang berpengaruh terhadap terbentuknya sobekan.
3.2.Rancangan Sistem
Tahap perancangan sistem ini merupakan implementasi dari metode-metode
yang telah dipelajari untuk membentuk model sobekan. Tahapan-tahapan yang
harus dilakukan untuk membentuk model sobekan dijabarkan dalam diagram alir
yang ditunjukkan pada Gambar 3.2. Sesuai dengan Gambar 3.2, terdapat beberapa
tahapan yang harus dieksekusi pada setiap iterasi. Tahapan-tahapan ini akan
dijelaskan secara rinci pada subbab Rancangan Sistem.
3.2.1. Masukan
Masukan pengguna dikategorikan ke dalam beberapa komponen. Komponen
ini adalah DOMAIN, MAT, CRACK, INC, GROW, dan FORCE. Komponen
masukan DOMAIN merupakan sebuah variabel dengan empat nilai yang
menyatakan:
1. Panjang objek pada arah x
2. Lebar objek pada arah y
3. Ukuran setiap elemen x
4. Ukuran setiap elemen y
Variabel kedua adalah MAT yang melingkupi tujuh nilai. Nilai-nilai ini
menyatakan:
1. modulus Young domain,
2. rasio Poisson domain,
3. modulus Young titik inklusi,
4. rasio Poisson titik inklusi,
5. status stress-strain,
6. nilai plane stress,
7. faktor intensitas tegangan kritis pada domain.
Variabel ketiga adalah variabel CRACK. Variabel ini menyatakan garis
22
23 1. koordinat x titik pertama
2. koordinat y titik pertama
3. koordinat x titik kedua,
4. koordinat y titik kedua.
Variabel keempat adalah variabel INC yang menyatakan inklusi. Bila
masukan pada INC berisi tiga nilai, maka nilai tersebut akan menyatakan inklusi
lingkaran dengan keterangan:
1. koordinat x titik pusat inklusi,
2. koordinat y titik pusat inklusi,
3. jari-jari inklusi.
Sementara bila variabel INC berisi empat nilai, maka nilai tersebut
menyatakan inklusi linier yang dinyatakan dengan:
1. koordinat x titik pertama,
2. koordinat y titik pertama ,
3. koordinat x titik kedua,
4. koordinat y titik kedua.
Variabel berikutnya adalah variabel GROW yang nantinya akan
mempengaruhi besar pertumbuhan sobekan pada domain. Variabel ini menyatakan:
1. jumlah iterasi,
2. crack growth increment.
Variabel terakhir adalah variabel FORCE yang akan menentukan muatan
yang dialirkan pada domain. Variabel ini menyatakan tiga keterangan:
1. uniaxial tension
2. nilai gaya yang diaplikasikan pada arah x
3. nilai gaya yang diaplikasikan pada arah y
3.2.2. Fungsi Utama
Fungsi utama diterapkan sebagai fungsi eksekusi dari keseluruhan program.
Fungsi ini mengandung skenario eksekusi fungsi-fungsi lain yang ada pada
program. Fungsi ini merupakan representasi kode dari Gambar 3.2 dan dinyatakan
dengan pseudocode pada Gambar 3.3. Fungsi-fungsi lain yang dieksekusi pada
24
Pseudocode 3.1 Fungsi utama
Masukan -
Keluaran PLOT, waktu
1. input
2. if isempty(GROW) = 1 3. iter 1
4. elseif length(GROW) = 2 5. iter GROW(1)
14. omega levelSet(i) 15. [DOF,DISP] calcDOF
16. [updElem, IElem] = enrElem(i,pHDOF) 17.
18. if i = 1
19. globalK stiffnessMatrix 20. else
21. globalK updateStiffness 22. end
23. globalF forceVector 24. freeDOF boundaryCond
25. DISP(freeDOF,:) globalK \ globalF 26. if isempty(CRACK) != 0
27. pHDOF 2*max(NODES(:,2))
28. [KI,KII] JIntegral(omega,DISP)
29. Gopt -(KI(1)^2+KII(1)^2)*(1-MAT(2)^2)/MAT(1); 30. growCrack(KI,KII,omega)
31. if i ~=1
32. if CRACK(nPt,1)>=(nXElem*lXElem-2*lXElem) %|| CRACK(nPt,1)<CRACK(nPt-1,1)
25 3.2.3. Fungsi connectivity
Fungsi connectivity dapat dikatakan fungsi inisialisasi. Fungsi ini akan
membentuk grid dari masukan yang telah diberikan pengguna. Grid inilah yang
menjadi representasi objek. Fungsi connectivity akan membentuk grid dengan
informasi masukan dan membentuk informasi-informasi lainnya seperti koordinat
titik, keterhubungan antar titik, hingga elemen serta titik-titik yang menjadi
anggotanya. Fungsi ini hanya dieksekusi pada iterasi pertama. Untuk iterasi
berikutnya, informasi yang digunakan juga merupakan hasil dari fungsi ini namun
dengan nilai-nilai yang telah diproses pada fungsi-fungsi lain.
Proses eksekusi fungsi connectivity dijelaskan dalam bentuk pseudocode
pada Gambar 3.4.
Pseudocode 3.2 Konektivitas domain
Masukan DOMAIN
Keluaran NODES, XYZ, CONNEC
1. nXElem DOMAIN(1) 2. nYElem DOMAIN(2) 3. lXElem DOMAIN(3) 4. lYElem DOMAIN(4)
5. nNode = (nXElem+1)*(nYElem+1) 6. nNode 1;
7. for iYNode 1 to nYElem+1 8. for iXNode 1 to nXElem+1 9. NN(iXNode,iYNode) nNode
10. XYZ (nNode,:) [nNode (iXNode-1)*lXElem (iYNode-1)*lYElem]
11. NODES(nNode,1) nNode 12. nNode nNode+1 18. N1 NN(iXElem, iYElem) 19. N2 NN(iXElem+1, iYElem) 20. N3 NN(iXElem+1,iYElem+1) 21. N4 NN(iXElem, iYElem+1)
22. CONNEC(nElem,1:5) [nElem N1 N2 N3 N4] 23. nElem nElem+1
24. end 25. end
26 3.2.4. Fungsi LevelSet
Fungsi levelSet merupakan fungsi yang membentuk nilai level set ∅ yang
merepresentasikan domain. Elemen dengan pengayaan titik ujung sobekan dan
Heaviside ditentukan. Pada fungsi ini akan diidentifikasi titik retakan berdasarkan
masukan pengguna. Selain itu, fungsi ini juga akan mengidentifikasi retakan yang
terjadi pada iterasi lanjut dengan titik retakan hasil iterasi sebelumnya.
Fungsi ini juga akan membentuk level set PHI dan PSI yang menyatakan
diskontinuitas yang disebabkan oleh titik ujung sobekan dan titik-titik Heaviside.
Titik-titik ini kemudian akan memiliki nilai degree of freedom sesuai dengan
pengayaan yang dimilikinya. Fungsi levelSet dieksekusi sesuai dengan pseudocode
seperti pada Gambar 3.5, Gambar 3.6, Gambar 3.7, dan Gambar 3.8.
Pseudocode 3.3. Inisialisasi elemen dengan metode Level Set
Masukan iter, CONNEC, DOMAIN, INC, NODES, XYZ, CRACK
Keluaran Omega, PHI, PSI, ZETA
1. nXElem DOMAIN(1) 2. nYElem DOMAIN(2) 3. lXElem DOMAIN(3) 4. nElem nXElem*nYElem
5. nNode (nXElem+1)*(nYElem+1); 6. nPt size(CRACK,1);
7. nBand (sqrt(2)+0.005)*lXElem
8. //Create material level set function ZETA
9. if iter = 1 10. if INC != 0
11. if INC circular 12. xc INC(1)
18. Z sqrt((xi-xc)^2+(yi-yc)^2)-rc 19. if abs(z) < 1e-6, ZETA(iNode) 0
27
Pseudocode 3.4. Inisialisasi elemen dengan metode Level Set
Masukan iter, CONNEC, DOMAIN, INC, NODES, XYZ, CRACK
Keluaran Omega, PHI, PSI, ZETA
28. l sqrt((x1-x0)^2+(y1-y0)^2) 29. for iNode = 1 to nNode
30. xi XYZ(iNode,2) 31. yi XYZ(iNode,3)
32. c (y0-y1)*x+(x1-x0)*y+(x0*y1-x1*y0) 33. ZETA(iNode) c/l
34. end
35. end ZETA min(ZETA,[],1) 36. for iElem = 1 to nElem
37. Z1 ZETA(CONNEC(iElem,2)) 38. Z2 ZETA(CONNEC(iElem,3)) 39. Z3 ZETA(CONNEC(iElem,4)) 40. Z4 ZETA(CONNEC(iElem,5)) 41. Z [Z1 Z2 Z3 Z4]
42. if max(Z)*min(Z) < 0for iNode = 2 to 5 43. if NODES(CONNEC(iElem,iNode),30) == 0 44. NODES(CONNEC(iElem,iNode),30) =
nNode+incNode;
45. NODES(CONNEC(iElem,iNode),31) = Z(iNode-1);
46. incNode = incNode+1;
47. end
48. end
49. end 50. else
51. ZETA ones(1,nNode) 52. end
53. //Create level set function PHI and PSI defining
the crack
54. if CRACK != empty
55. nCT Check for edge crack 56. Calculate crack angle
57. PHI sparse(nNode,nCT) 58. for iCT = 1: nCT
59. define radius of nodal search 60. find nodes within search radius
61. //compute PHI level set for main cracktip
62. for iNode = 1 to length of domain 63. cNode domain(iNode)
64. x XYZ(cNode,2) 65. y XYZ(cNode,3)
66. disc CRACK(nPt,:)-CRACK(nPt-1,:) 67. t 1/norm(disc)*disc
68. phi ([x y]-CRACK(nPt,:))*t’;
28
Pseudocode 3.5 Inisialisasi elemen dengan metode Level Set
Masukan iter, CONNEC, DOMAIN, INC, NODES, XYZ, CRACK
Keluaran Omega, PHI, PSI, ZETA
69. if phi = 0, phi = 1e-6; end
70. if nCT == 2
71. disc CRACK(1,:)-CRACK(2,:) 72. t 1/norm(disc)*disc
73. phi(2) ([x y]-CRACK(1,:))*t’; 74. if phi(2) = 0, phi(2) = 1e-6; end
75. end
76. if iCT = 1
77. if abs(phi(1)) < nBand
78. define psi
79. if abs(psi)<nBand
80. PHI(cNode,1) = phi(1)
81. PSI(cNode,1) = psi end
89. if abs(phi(2)) < nBand
90. define psi
91. if abs(psi)<nBand
92. PHI(cNode,1) = phi(2)
93. PSI(cNode,1) = psi
103. define the crack tip enriched nodes 104. define Heaviside enriched nodes
105. //Preliminaries to numbering enriched nodes
106. nNode nNode+1+incNode-1 107. ctNodes unique(ctNodes) 108. bmNodes unique(bmNodes) 109. hNodes unique(hNodes)
110. // Number the Heaviside nodes
111. for i = 1 to length of hNodes 112. NODES(hNodes(i),2) = nNode
29
Pseudocode 3.6 Inisialisasi elemen dengan metode Level Set
Masukan iter, CONNEC, DOMAIN, INC, NODES, XYZ, CRACK
Keluaran Omega, PHI, PSI, ZETA
113. nNode = nNode+1; 114. end
115. // Number the crack tip nodes
116. for i = 1:length(ctNodes)
117. NODES(ctNodes(i),4) = nNode; 118. NODES(ctNodes(i),6) = nNode+1; 119. NODES(ctNodes(i),8) = nNode+2; 120. NODES(ctNodes(i),10) = nNode+3; 121. nNode = nNode+4;
122. end
123. // Number the bimaterial crack tip nodes
124. for i = 1:length(bmNodes) 125. NODES(bmNodes(i),4) = nNode; 126. NODES(bmNodes(i),6) = nNode+1; 127. NODES(bmNodes(i),8) = nNode+2; 128. NODES(bmNodes(i),10) = nNode+3; 129. NODES(bmNodes(i),12) = nNode+4; 130. NODES(bmNodes(i),14) = nNode+5;
Gambar 3.8 Pseudocode Inisialisasi elemen dengan metode Level Set (4) Fungsi define PSI yang disebutkan pada Gambar 3.7 baris ke 79 dan 84
merupakan proses yang diekskusi untuk mendapatkan nilai PSI. Fungsi ini
dijabarkan dalam bentuk pseudocode pada Gambar 3.9 dan Gambar 3.10
Pseudocode 3.7. Define PSI
1. dist zeros(nPt-1,1) 2. sine dist
30
Pseudocode 3.8. Define PSI
9. if isinf(m) = 1
26. dist(iSeg) sqrt((xo-x)^2+(yo-y)^2) 27. sine(iSeg) sign(x2-x1)*sign(y-yo); 28.end
29. dMin min(abs(dist))
30. ind find(abs(dist) = dMin) 31. if length(ind) = 2
32. ind(2)[] 33. end
34. psi dist(ind)*sine(ind) 35. if psi = 0
36. psi = 1e-6 37.end
Gambar 3.10 Pseudocode fungsi untuk mendefinisikan PSI (2) 3.2.5. Fungsi calcDOF
Fungsi ini merupakan fungsi yang digunakan untuk menghitung degree of
freedom total yang mencakup degree of freedom dari Finite Element tradisional
maupun pengayaan. Setelah terbentuk level set dengan fungsi sebelumnya,
didapatkan elemen-elemen pengayaan. Hal ini yang membuat degree of freedom
tidak dapat diinisialisasi dengan uniform secara keseluruhan. Oleh karena itu,
degree of freedom untuk setiap elemen pengayaan dieksekusi sesuai dengan fungsi
pengayaannya masing-masing. Fungsi calcDOF ini dinyatakan dalam pseudocode
seperti pada Gambar 3.11. Perhitungan degree of freedom masing-masing elemen
pengayaan tampak pada baris 5, 8, dan 11. Dan baris 13 dieksekusi untuk
31
Pseudocode 3.9. Menghitung total degree of freedom
Masukan NODES
Keluaran DOF, DISP
1. heavDOF 2*nonzero(NODES(:,2)) 2. ctipDOF 2*nonzero(NODES(:,4)) 3. bmctDOF 2*nonzero(NODES(:,12)) 4. if heavDOF > 0
13. DOF 2*max(max(NODES)) 14. DISP sparse(DOF,1)
Gambar 3.11. Pseudocode untuk menghitung Degree of Freedom 3.2.6. Fungsi enrElem
Fungsi ini merupakan fungsi yang digunakan untuk membentuk elemen
pengayaan. Pada proses sebelumnya didapatkan informasi titik-titik mana saja yang
mendapatkan pengayaan baik sebagai titik ujung sobekan maupun titik Heaviside.
Dari informasi proses-proses sebelumnya tersebut dibentuk elemen sesuai dengan
titik-titik pengayaan yang berkesinambungan. Fungsi ini dieksekusi sesuai dengan
pseudocode seperti pada Gambar 3.12 dan Gambar 3.13
Pseudocode 3.10 Membentuk elemen pengayaan
Masukan i, pHDOF, NODES, CONNEC
Keluaran enrElem, IElem
1. I find NODES(:,4)>0
2. c1 intersect(I,CONNEC(:,2)’) 3. c2 intersect(I,CONNEC(:,3)’) 4. c3 intersect(I,CONNEC(:,4)’) 5. c4 intersect(I,CONNEC(:,5)’)
6. CTElem unique(vertcat(c1,c2,c3,c4))
7. if i = 1
8. I find NODES(:,2)>0
9. c1 intersect(I,CONNEC(:,2)’) 10. c2 intersect(I,CONNEC(:,3)’) 11. c3 intersect(I,CONNEC(:,4)’) 12. c4 intersect(I,CONNEC(:,5)’)
13. HElem unique(vertcat(c1,c2,c3,c4)) 14. I find NODES(:,30)>0
32
Pseudocode 3.11 Membentuk elemen pengayaan
Masukan i, pHDOF, NODES, CONNEC
Keluaran enrElem, IElem
15. c1 intersect(I,CONNEC(:,2)’) 16. c2 intersect(I,CONNEC(:,3)’) 17. c3 intersect(I,CONNEC(:,4)’) 18. c4 intersect(I,CONNEC(:,5)’)
19. IElem unique(vertcat(c1,c2,c3,c4))
20. else
21. I find NODES(:,2) > pHDOF/2 22. c1 intersect(I,CONNEC(:,2)’) 23. c2 intersect(I,CONNEC(:,3)’) 24. c3 intersect(I,CONNEC(:,4)’) 25. c4 intersect(I,CONNEC(:,5)’)
26. HElem unique(vertcat(c1,c2,c3,c4)) 27. IElem []
28. end
29. enrElem = unique(vertcat(CTElem, HElem))
Gambar 3.13 Pseudocode untuk membentuk elemen pengayaan (2) 3.2.7. Fungsi stiffnessMatrix dan updateStiffness
Fungsi yang menghitung matrik kekakuan ini dibagi menjadi 2 yaitu
stiffnessMatrix yang digunakan untuk menghitung kekakuan dasar pada iterasi
pertama dan updateStiffness yang digunakan untuk menghitung kekakuan pada
iterasi-iterasi berikutnya. Perbedaan fungsi updateStiffness adalah fungsi ini tidak
menghitung matrik kekakuan elemen inklusi karena elemen inklusi tidak
mengalami perubahan terhadap fungsi waktu. Fungsi ini dikerjakan sesuai dengan
pseudocode seperti pada Gambar 3.14, Gambar 3.15, Gambar 3.16, Gambar 3.17,
Gambar 3.18, dan Gambar 3.19
Pseudocode 3.12 Membentuk matrik kekakuan
Masukan Omega, DOF, iter, enrElem, IElem, CONNEC,
CRACK, DOMAIN, MAT, NODES, PHI, PSI, XYZ, ZETA
Keluaran globalK
33 Pseudocode 3.13 Membentuk matrik kekakuan
Masukan Omega, DOF, iter, enrElem, IElem, CONNEC, CRACK,
DOMAIN, MAT, NODES, PHI, PSI, XYZ, ZETA
Keluaran globalK
8. plane MAT(5) 9. nCT size(PHI)
10. globalK sparse matrix size globalDOF 11. if plane = 1
12. build initial plane stress stiffness matrix 13. Km = build initial plane stress stiffness fiber
matrix
14. elseif plane = 2
15. build initial plane strain stiffness matrix 16. Kf = build initial plane strain stiffness fiber
matrix 17. end
18. define crack point coordinate
19. for iElem = 1 to nYElem*nXElem
20. NN current elements nodal data 21. CN chi level set values
22. CTN number of crack tip node enrichment 23. HEN number of Heaviside node enrichment 24. IEN number of inclusion node enrichment 25. NEN number of enriched nodes
26. lokalK 0
27. local = traditional index 28. iLoc 9
29. if NEN = 0Set stiffness matrix for traditional nodes
30. //Set stiffness for enriched nodes
31. if NEN > 0
32. define nodes coordinates for current element
33. if NEN = 4 //fully enriched element 34. define crack level set values 35. define inclusion level set values
36. [gp, gw, J] = subDomain(enriched nodes) 37. for i = 1 to length of Gauss Point 38. defines Gauss elements
39. end
40. elseif min(CN)<0 //partially enriched element 41. define crack level set values
42. define inclusion level set values
43. [gp, gw, J] = subDomain(enriched nodes) 44. for i = 1 to length of Gauss Point 45. defines Gauss elements
46. end
47. else