BAB II
TINJAUAN PUSTAKA
A. Teori Graf
1. Dasar-dasar Graf
Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex) dan E adalah himpunan sisi (mungkin kosong) yang menghubungkan sepasang titik. Himpunan titik di G dinotasikan dengan V(G) dan himpunan sisi dinotasikan dengan E(G). Sisi e = (u,v) dapat ditulis e = uv (Chartrand dan Lesniak, 1996). Sebagai contoh: V(G1) = {v1, v2, v3, v4} dan E(G1) =
{v1v2, v2v3, v3v4}.
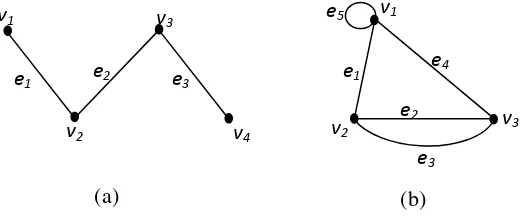
Sisi yang menghubungkan dua titik yang sama disebut loop. Jika terdapat lebih dari satu sisi yang menghubungkan dua titik, maka sisi tersebut dinamakan sisi ganda (multiple edge). Suatu graf yang mengandung loop atau mengandung sisi ganda dinamakan multigraf.
5
Gambar 2.1. Graf (a) dan Multigraf (b)
Gambar 2.1 adalah contoh multigraf karena mengandung loop, yaitu sisi e5 dan mengandung sisi ganda yaitu sisi e2 dan e3. Banyaknya unsur di V
disebut order dari G dinotasikan dengan n(G) dan banyaknya unsur di E disebut size dari G dinotasikan dengan m(G). Jika graf yang dibicarakan hanya graf G, maka order dan size dari G tersebut cukup ditulis dengan n dan m (Chartrand dan Lesniak, 1996). Gambar 2.1 terlihat bahwa, Graf G1
dengan w, titik w adjacent dengan v, titik u adjacent dengan x. Berikut merupakan titik yang bersisian (incident) pada graf G: u dan e1 serta v dan
e1, v dan e2 serta x dan e2, w dan e3 serta x dan e3, x dan e4 serta u dan e4, v
dan e5 serta w dan e5.
Derajat dari titik v di graf G, adalah banyaknya sisi di G yang bersisian (incident) dengan v (Chartrand dan Leniak, 1996). Dalam konteks pembicaraan hanya terdapat satu graf G, maka tulisan degG(v) disingkat menjadi deg(v). Titik yang berderajat genap disebut titik genap (even vertices) dan titik yang berderajat ganjil disebut titik ganjil (odd vertices). Titik yang berderajat nol disebut isolated vertices dan titik yang berderajat satu disebut titik ujung (end vertices) (Chartrand dan Leniak, 1996).
Diberikan contoh graf G yang akan ditentukan derajat titiknya:
Berdasarkan gambar 2.3, diperolah bahwa
Titik v1 dan v3 adalah titik ganjil, titik v2 dan v4 adalah titik genap.
Karena tidak ada yang berderajat 1, maka graf G tidak mempunyai titik ujung. Hubungan antara jumlah derajat semua titik dalam suatu graf G dengan banyak sisi, dinyatakan dalam teorema berikut:
Teorema 1
Jumlah derajat semua titik pada graf adalah genap, yaitu dua kali jumlah sisi pada graf tersebut. Jika G(V, E) dengan m merupakan banyaknya unsur di E maka:
Akibat 1
Pada sebarang graf, jumlah derajat titik ganjil adalah genap.
Bukti:
Misalkan graf G dengan size m. Misalkan W himpunan yang memuat titik ganjil pada G serta U himpunan yang memuat titik genap di G.
Karena deg(v) genap untuk v U, maka suku pertama dari ruas kiri persamaan selalu bernilai genap. Ruas kanan pada persamaan di atas juga bernilai genap. Nilai genap pada ruas kanan hanya benar bila suku kedua ruas kiri adalah genap sehingga
Karena deg(v) ganjil untuk v W, maka banyaknya simpul v di dalam W harus genap agar jumlah seluruh derajatnya bernilai genap. Jadi, banyaknya simpul yang berderajat ganjil selalu genap.
3. Beberapa Graf Sederhana Khusus
Graf sederhana merupakan graf yang tidak mengandung loop maupun sisi ganda. Ada beberapa graf sederhana khusus yang dijumpai seperti berikut:
a. Graf Komplit (Complete Graph)
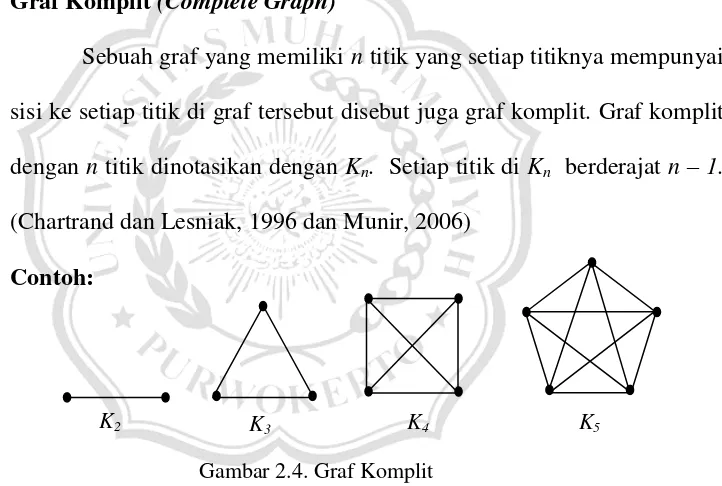
Sebuah graf yang memiliki n titik yang setiap titiknya mempunyai sisi ke setiap titik di graf tersebut disebut juga graf komplit. Graf komplit dengan n titik dinotasikan dengan Kn. Setiap titik di Kn berderajat n – 1.
(Chartrand dan Lesniak, 1996 dan Munir, 2006)
Contoh:
b. Graf Sikel
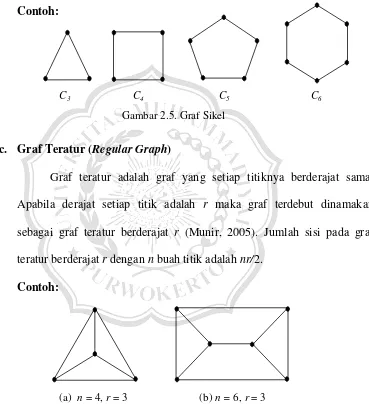
Graf sikel adalah graf sederhana yang setiap titiknya berderajat dua. Graf sikel dengan n titik dinotasikan dengan Cn. Jika titik pada Cn
adalah v1, v2, v3, …, vn maka sisi-sisinya adalah (v1v2), (v2,v3), …, (vn-1,vn),
dan (vn,v1). Dengan kata lain, ada sisi dari titik terakhir vn ke titik pertama
v1 (Munir, 2005).
Gambar 2.4. Graf Komplit
Graf sikel merupakan graf dengan n titik dengan simpul n ≥ 3 dimana setiap titik saling terhubung dan membentuk cincin. Setiap titik pada graf sikel berderajat dua (Biggs, Lloyd, and Wilson: 1936).
Contoh:
c. Graf Teratur (Regular Graph)
Graf teratur adalah graf yang setiap titiknya berderajat sama. Apabila derajat setiap titik adalah r maka graf terdebut dinamakan sebagai graf teratur berderajat r (Munir, 2005). Jumlah sisi pada graf teratur berderajat r dengan n buah titik adalah nr/2.
Contoh:
d. Graf Bipartit (Bipartite Graph)
Graf G yang himpunan titiknya dapat dikelompokan menjadi dua himpunan bagian V1 dan V2, sedemikian sehingga setiap sisi di dalam G
Gambar 2.5. Graf Sikel
C3 C4 C5 C6
menghubungkan titik di V1 ke titik di V2 yang disebut juga dengan graf
bipartit(Munir, 2005).
Contoh:
Graf G pada Gambar 2.7 adalah graf bipartit karena himpunan titik di G dapat di partisi menjadi dua himpunan, yaitu:
V1 = {a, b, c, d} dan V2 = {p, q, r}
Berdasarkan gambar 2.7 masing-masing sisi di G mempunyai ujung di V1 dan di V2. Himpunan titik dalam satu partisi tidak boleh
terhubung langsung.
e. Graf Bipartit Lengkap (Complete Bipartite Graph)
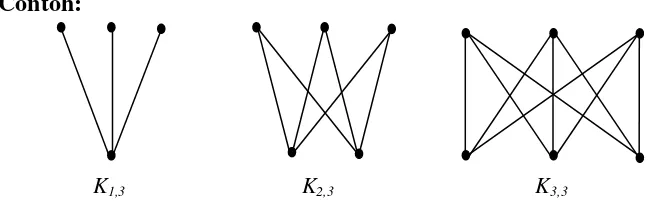
Graf bipartit lengkap adalah graf bipartit dengan setiap titik di V1
bertetangga dengan semua titik di V2. Graf bipartit lengkap dinotasikan
sebagai Kn,m dengan jumlah sisi adalah mn (Munir, 2005). Contoh:
Gambar 2.8. Graf Bipartit Lengkap K2,3
K1,3 K3,3
Gambar 2.7. Graf Bipartit
a b c d
f. Graf lintasan
Graf lintasan (path) adalah graf dengan menarik garis pada setiap titik
sehingga membentuk satu garis lurus dan graf yang terdiri dari satu lintasan.
Graf lintasan dengan n titik, dinotasikan dengan Pn, contoh dari graf lintasan
sebagai berikut:
B. Graf Terhubung
Diberikan u dan v merupakan titik di graf G. Sebuah jalan di graf G dinamakan walk dan dinotasikan dengan W. Walk u-v pada graf G adalah barisan hingga u = u0, e1, u1, e2, u2,...,uk-1, ek, un = v yang merupakan titik dan sisi,
diawali dengan titik u dan diakhiri dengan titik v, dengan e1= ui-1ui untuk i = 1, 2,
3, ..., k. k sering disebut dengan panjang dari sebuah walk (Chartrand dan Lesniak, 1996). Jika u = v maka W disebut dengan jalan tetutup. Tetapi jika u ≠ v maka W disebut dengan jalan terbuka (Chartrand dan Lesniak, 1996).
Jika terdapat jalan u-v yang semua sisinya berbeda maka jalan tersebut merupakan trail u-v. Tetapi jika jalan u-v yang semua sisi dan titiknya berbeda maka disebut dengan lintasan (path) u-v. Dengan demikian, semua lintasan adalah trail (Chartrand dan Lesniak, 1996).
Gambar 2.9. Graf Lintasan P2 :
P3 :
Trail tertutup dan tak trivial pada G disebut sirkuit di G. Sirkuit v1, v2, …, vn, v1
(n ≥ 3) dengan semua titik interval yang berbeda kecuali v1 = vndisebut siklus (cycle).
(Chartrand dan Lesniak, 1996). Graf terhubung yang tidak mengandung siklus disebut
dengan pohon. dikatakan terhubung (connected), jika terdapat lintasan u – v di G. Suatu graf G dapat dikatakan terhubung (connected), jika untuk setiap titik u dan v di G
Gambar 2.10. Graf untuk Mengilustrasikan Jalan, Jalan Tertutup, Trail, Lintasan.
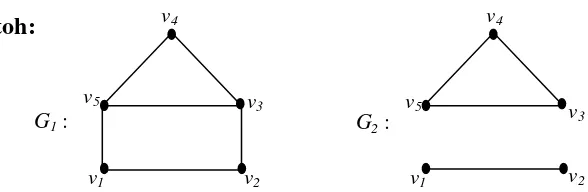
Gambar 1.11. Graf Terhubung dan Graf Tak Terhubung
Graf G1 merupakan graf terhubung karena setiap titiknya terhubung dan
terdapat lintasan dari setiap titik ke tiap titik lain di graf G1, sedangkan G2 adalah
graf tak terhubung karena terdapat titik yang tak terhubung dengan titik yang lain, yaitu titik v1 dan v2 tidak terhubung dengan titik v3,v4, dan v5.
C. Operasi pada Graf
Gabungan dua graf G1 dan G2 dinotasikan dengan G = G1 G2 yang
memiliki himpunan titik V(G) = V(G1) V(G2) dan himpunan sisi E(G) =
E(G1) E(G2). Jika suatu graf G memuat lebih dari n graf, dimana n ≥ 2 graf H,
dapat ditulis dengan G = nH (Chartrand dan Lesniak, 1996). Gambar 2.12 merupakan contoh dari gabungan graf.
Karena graf G memuat 3 graf P2 dan 2 graf C2, maka graf tersebut dapat
dinotasikan dengan 3P2 2C2. D. Graf Planar
Graf planar adalah graf pada bidang datar dimana sisi pada graf tersebut tidak bersiangan dengan sisi yang lain, jika graf yang sisinya bersilangan disebut juga graf tidak planar (Chartrand dan Lesniak, 1996).
K4 merupakan graf planar dimana sisi pada graf K4 saling bersilangan
seperti yang ditunjukan pada gambar 2.13 (a), lalu dapat digambarkan kembali tanpa ada sisi yang bersilangan pada gambar 2.13 (b).
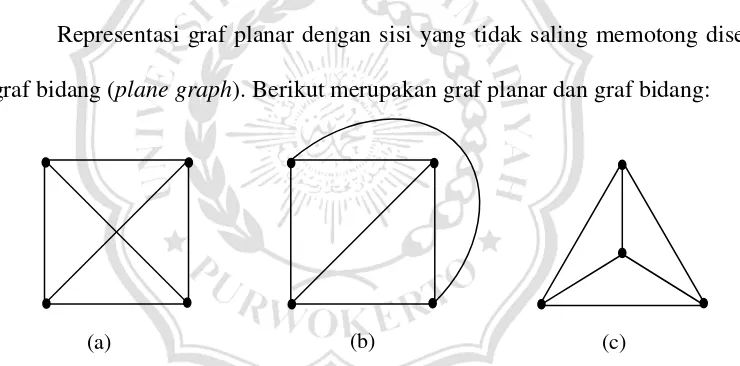
Representasi graf planar dengan sisi yang tidak saling memotong disebut graf bidang (plane graph). Berikut merupakan graf planar dan graf bidang:
Sisi pada graf bidang membagi bidang datar menjadi beberapa wilayah (region) atau disebut dengan wajah (face). Wilayah pada graf bidang dapat ditentukan dengan mudah perhatikan gambar 2.15 di bawah:
R1
R2
R4 R3
R5
R6
Gambar 2.15. Graf planar yang terdiri dari 6 wilayah Gambar 2.13. Graf planar (a)
(a) (b)
Gambar 2.14.(a) Graf planar. (b) dan (c) adalah graf bidang
Gambar 2.15 di atas merupakan graf bidang yang terdiri dari 6 wilayah (termasuk wilayah terluar).
Teorema 2 (Formula Euler)
Diketahui graf G adalah graf terhubung planar dengan v adalah titik, e adalah sisi, f adalah wajah, maka :
v – e + f = 2
Bukti:
Dibuktikan dengan menginduksi pada jumlah sisi. Jika e = 0, maka graf G hanya mempunyai satu titik, dan jumlah wajah pada graf G tersebut adalah satu. Jelas bahwa v – e + f = 2.
E. Graf Platonik
Graf platonik adalah graf sederhana karena tidak memiliki loop dan juga sisi ganda yang dibentuk dari bangun polyhedron yang semua wajahnya merupakan bangun segi-n beraturan dan semua wajah bertemu di setiap titik yang sama yang disebut platonic solid. Graf platonik dinotasikan dengan Pnd dengan n
adalah jumlah sisi pada polyhedron dan d adalah derajat titik.
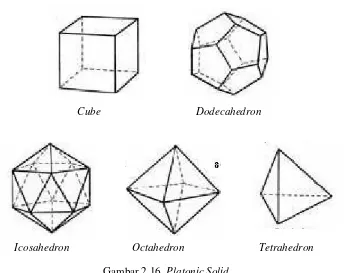
Terdapat 5 platonic solid yang meliputi cube, dodecahedron, icosahedron, octahedron, dan tetrahedron. Gambar 2.16 merupakan platonic solid.
Tabel 2.1 adalah 5 nama platonic solid, dimana V adalah banyaknya titik, E adalah banyaknya sisi, dan F adalah banyaknya wajah pada platonic solid.
Cube Dodecahedron
Gambar 2.16. Platonic Solid
Tetrahedron Octahedron
Simbol Nama polyhedron V E F
Cube 8 12 6
Dodecahedron 20 30 12
Icosahedron 12 30 20
Octahedron 8 12 8
Tetrahedron 4 6 4
Teorema 3
Hanya ada 5 platonic solid yang terdiri dari cube, dodecahedron, icosahedrons, octahedron, dan tetrahedron (Fleck, 2004).
Bukti
Dari teorema 1, jumlah derajat titik adalah 2 kali jumlah sisi dengan derajat titik adalah d, maka didapatkan
dv = 2e
dari teorema 1 untuk wajah, jumlah wilayah juga 2 kali jumlah sisinya, ini berarti
nf = 2e
Subtitusi persamaan (1) dan (2) ke formula euler v – e + f = 2, didapatkan
Kedua ruas di bagi dengan 2e:
………. (1)
Jika dianalisi persamaan di atas, dapat disimpulkan bahwa d dan n tidak dapat lebih besar dari 3. Jika d dan n adalah 4 atau lebih, maka ruas kiri pada persamaan di atas akan lebih kecil dari ½. Sehingga salah satu antara d dan n harus sama dengan 3.
Untuk d = 3,
Karena 1/e positif, ini berarti n tidak boleh lebih besar dari 5, dengan demikian jika n = 3 maka d tidak boleh lebih besar dari 5. Dapat diperoleh 5 kemungkinan untuk derajat d dan banyak sisi n yaitu: (3,3) bentuk dari tetrahedron, (3,4) bentuk dari octahedron, (3,5) bentuk dari icosahedrons. (4,3) bentuk dari cube, (5,3) bentuk dari dodecahedron
F. Graf Archimedean
Terdapat 13 Archimedean solid seperti gambar di bawah:
Great rhombicuboctahedron Great rhombicosidodecahedron
Truncated tetrahedron Truncated cube Truncated octahedron
Truncated dodecahedron Truncated icosahedron cuboctahedron
rhombicuboctahedron
icosidodecahedron rhombicosidodecahedron
11 dari 13 Archimedean solid dibentuk oleh proses pemotongan (truncation). 7 Archmedean solid dibentuk dari proses pemotongan platonic solid meliputi truncated cube, truncated dodecahedron, truncated icosahedron, truncated icosahedron, truncated tetrahedron, cuboctahedron, icosidodecahedron, 4 Archimedean solid dibentuk dari pemotongan Archimedean solid meliputi great rhombicosidodecahedron, great rhombicuboctahedron, small rhombicosidodecahedron, small rhombicuboctahedron, dan 2 Archimedean solid yang lainnya diperoleh dengan proses snubbing yaitu snub cube dan snub dodecahedron.
Snubbing adalah proses yang digunakan pada polyhedral. 3 langkah dalam proses snubbing meliputi:
a. Menarik setiap wajah secara terpisah pada setiap polyhedron
b. Mengganti sisi pada setiap wajah dengan segitiga. Masing-masing segitiga dapat dipasangkan ke kiri atau ke kanan.
c. Mengganti titik dimana n wajah bertemu dengan n sisi polygon.
Tabel 2.2 adalah 13 nama Archimedean solid, dimana V adalah banyaknya titik, E adalah banyaknya sisi, dan F adalah banyaknya wajah pada Archimedean solid.
Simbol Nama polyhedron V E F
A3.82 Truncated Cube 24 36 14
A3.102 Truncated Dodecahedron 60 90 32
A5.62 Truncated Icosahedron 60 90 32
A4.62 Truncated Octahedron 24 36 14
A3.62 Truncated Tetrahedron 12 18 8
A(3.4)2 Cuboctahedron 12 24 14
A(3.5)2 Icosidodecahedron 30 60 32
A4.6.10 Great Rhombicosidodecahedron 120 180 62
A4.6.8 Great Rhombicuboctahedron 48 72 26
A3.4.5.4 Small Rhombicosidodecahedron 60 120 62
A3.43 Small Rhombicuboctahedron 24 48 26
A34
.4 Snub Cube 24 60 38
A34.5 Snub Dodecahedron 60 150 92
G. Digraf
Digraf (Graf berarah/ Directed Graph) adalah struktur yang terdiri dari pasangan himpunan (V, E) dimana V adalah himpunan tak kosong yang disebut titik (vertex) dan E adalah himpunan sisi (mungkin kosong) yang mempunyai arah dari u ke v. Sisi berarah disebut busur (arc). Himpunan titik di D dinotasikan dengan V(D) dan himpunan busur dinotasikan dengan E(D) (Chartrand dan Lesniak, 1996).
Himpunan titik pada digraf D disebut order dari D dan dilambangkan dengan n(D) atau n. Sedangkan himpunan busur digraf D adalah size m(D) atau m (Chartrand dan Lesniak, 1996). Diberikan digraf D dengan himpunan titik V(D) = {u, v, w} dan himpunan busur E(D) = {(u, w), (w, u), (u, v)} berikut:
Gambar 2.18. Digraf D u
Misal D digraf dan u dan v adalah titik-titik pada digraf D. Jika e = (u, v) adalah busur pada digraf D, maka e dikatakan menghubungkan antara titik u dan v, u adjacent ke v dan v adjacent dari u. Jika busur e diarahkan dari u ke v maka busur e disebut incident dari u dan incident ke v. Dicontohkan pada digraf di bawah:
Digraf D dikatakan terhubung jika ada lintasan di D antara pasangan titik yang diketahui (Chartrand dan Lesniak, 1986). Suatu walk dengan panjang k pada suatu digraf D adalah rangkian k busur D dengan bentuk uv untuk (u,v) dimana uv ≠ vu. Sebuah walk, W = e1e2…ek: u v pada digraf D jika ei D
untuk semua i [i, k]. Jika semua busur (tetapi tidak perlu semua titik) suatu walk berbeda disebut trail. Jika walk dengan semua titiknya berbeda maka trail itu disebut lintasan (path) (Harju, 1994).
D1 merupakan digraf terhubung karena setiap titiknya terhubung dan
terdapat lintasan dari setiap titik ke tiap titik yang lain di digraf D1, D2 adalah
digraf tak terhubung karena terdapat titik yang tak terhubung dengan titik yang lain, yaitu titik v1 dan v2 tidak terhubung dengan titik v3 dan v4.
Gambar 2.19. Adjacent dan incident di Digraf D
u e v
Gambar 2.20. Digraf Terhubung dan Graf Tak Terhubung
H. Eksentrik Digraf
Diberikan suatu graf terhubung G, jarak (distance) antara dua titik u dan v di G adalah panjang lintasan terpendek yang menghubungkan u dan v di G. Jika tidak ada lintasan dari simpul u ke v, maka kita definisikan jarak d(u,v) = ∞ (Chartrand dan Lesniak, 1996). Eksentrisitas (eccentricity) titik v pada graf G dinotasikan dengan e(v) dari suatu titik v pada graf terhubung G adalah jarak terjauh dari titik v ke setiap titik di G dapat dituliskan e(v) = max{d(u,v)│u V(G)} (Deo, 1994).
Radius dari G adalah eksentrisitas minimum pada setiap titik di G, dapat dituliskan rad G = min{e(v),v V}. Sedangkan diameter dari graf G adalah eksentrisitas maksimum pada setiap titik di G, dapat dituliskan diamG = max{e(v), v V} (Kusmayadi dan Sudibyo, 2011).
Eksentrik digraf dari suatu graf adalah suatu graf yang mempunyai himpunan titik yang sama dengan himpunan titik di G, dan terdapat suatu busur (sisi berarah) yang menghubungkan titik u ke v jika v adalah suatu titik eksentrik dari u. Eksentrik digraf dinotasikan dengan ED(G) (Kusmayadi dan Sudibyo: 2011).
pada eksentrik digraf sama dengan himpunan titik di graf G dan jika v adalah titik eksentrik dari u, maka terdapat busur yang menghubungkan titik u ke v.
Berdasarkan gambar 2.21 dapat menentukan jarak antara titik satu dengan titik yang lain pada graf G adalah:
d(v1,v2) = 1, d(v2,v1) = 1, d(v3,v1) = 2, d(v4,v1) = 3, d(v5,v1) = 1, d(v6,v1) = 2
d(v1,v3) = 2, d(v2,v3) = 1, d(v3,v2) = 1, d(v4,v2) = 2, d(v5,v2) = 1, d(v6,v2) = 1
d(v1,v4) = 3, d(v2,v4) = 2, d(v3,v4) = 1, d(v4,v3) = 1, d(v5,v3) = 1, d(v6,v3) = 1
d(v1,v5) = 1, d(v2,v5) = 1, d(v3,v5) = 1, d(v4,v5) = 2, d(v5,v4) = 2, d(v6,v4) = 1
d(v1,v6) = 2, d(v2,v6) = 1, d(v3,v6) = 1, d(v4,v6) = 1, d(v5,v6) = 2, d(v6,v5) = 2
Jarak antara jarak titik satu dan titik lainnya seperti di atas dapat dibuat tabel seperti tabel jarak di bawah:
v1 v2 v3 v4 v5 v6
v1 1 2 3 2 1
v2 1 1 2 3 2
v3 2 1 1 2 3
v4 3 2 1 1 2
v5 2 3 2 1 1
v6 1 2 3 2 1
Gambar 2.21. Graf yang akan dicari Eksentrik Digrafnya
v1 v2 v3 v4
v6
v5
Pada gambar 2.21, setelah menentukan jarak pada setiap titik ke titik lain di graf G, maka akan didapat eksentrisitas dari titik tersebut:
Titik Eksentrisitas Titik eksentrik
v1 3 v4
v2 2 v4
v3 2 v1
v4 3 v1
v5 2 v4, v6
v6 2 v1, v5
Hasil titik eksentrik pada tabel di atas, diperoleh eksentrik digraf dari graf pada gambar 2.22 sebagai berikut:
Tabel 2.4. Tabel Eksentrisitas
Gambar 2.22. Eksentrik Digraf dari Graf G
v1 v2 v3 v4
v6